Abstract
The existing definition method of filter grid scale in a Detached Eddy Simulation (DES) hybrid model is unreasonable, which will lead to the unreasonable trigger of a boundary layer large eddy simulation and reduce computational efficiency. In view of this problem, the filter grid scale is discussed in this paper. The 90° square curved elbow is selected as the research object. The effects of three grid definition methods: geometric mean (), arithmetic mean () and quadratic mean () on the simulation results of the DES model are compared, and the velocity distribution of the flow cross section and the distribution of the flow pressure coefficient on the outer arc surface are compared with the experimental results of Taylor. The results show that the order of the three definition methods is . Meanwhile, within 30° < polar angle(θ) < 75°, the results are closer to the experiment, and the development trends and numerical values of and are closer to the experiment in general. However, when θ > 60°, the value of is slightly closer to the experimental result than . is more suitable for calculating the internal flow in a curved elbow than the other two methods.
1. Introduction
The turbulence inside the centrifugal pump shows unstable flow phenomena (flow separation and secondary flow) due to curvature and rotation. With the rapid development of Computational Fluid Dynamics (CFD), numerical simulation has become a primary way to study turbulence. According to the processing scales for turbulence in the Navier–Stokes (N-S) Equation [1], there are mainly three kinds of method, that are Direct Numerical Simulation (DNS), Reynolds Average Navier–Stokes (RANS) and Large Eddy Simulation (LES). The DNS method can accurately obtain the turbulence field and is an effective way to study the turbulence mechanism. However, the existing computing resources are often difficult to meet the needs of the high Reynolds number flow. So, the DNS method is not commonly used in the simulation of the pump [2]. In the study of Zhao [3], the RANS method performs time-average processing for the instantaneous velocity, which can greatly reduce the computing time, while neglecting the instantaneous details of turbulent flow. The research of Li [4] shows that the LES method can directly calculate the motion of large-scale vortexes, and the influence of small-scale vortexes on large scale vortexes can be reflected by establishing a model. However, LES needs to build a very fine grid to simulate a large number of small-scale fluctuations in the near-wall region, resulting in a huge amount of calculations for complex three-dimensional flow [5].
In order to combine the advantages of RANS and LES, scholars have proposed a variety of RANS/LES hybrid model methods. The basic idea of a RANS/LES hybrid model is to use RANS to efficiently and reliably simulate the near-wall region dominated by high-frequency small-scale motion, and use LES to accurately calculate the unsteady separation flow region dominated by low-frequency large-scale motion. The RANS/LES hybrid model methods mainly include Detached Eddy Simulation (DES) [6] and Scale-Adaptive Simulation (SAS) [7]. The construction form of the DES method is very simple, and it has a strong adaptability to complex models. The numerical simulation capability of DES for massive separation flows can reach the level of LES, and the grid demand is far less than LES. Although SAS has been tested for a variety of applications, it has not yet evaluated complex dynamic stall. SAS is only suitable for strongly unsteady problems such as rotation, flow around a bluff body and large separation. Compared with the DES method, the irregularity of vortex shedding in the SAS model is slightly lower. Therefore, DES is the most widely used RANS/LES hybrid model.
The transformation from RANS to LES in the DES hybrid model is completely realized through the comparison of grid scale and turbulence scale. When the boundary layer mesh is too fine, the use of large eddy simulation in the boundary layer will lead to insufficient Reynolds stress simulation. Menter [8] introduced the delay function Fsst into DES to reduce the excessive dependence on grid density based on the two-equation SST k-ω model. Although compared with the original DES hybrid model the real flow could be simulated more accurately, it was not universal. Spalart [9] constructed another kind of delay function fd. It was firstly applied in the RANS/LES switching function, which effectively delayed the switching from RANS to LES and solved the problem of grid-induced separation [10,11,12]. To further enhance the ability to resolve turbulence in the boundary layer, Shur [13] combined the Delayed Detached Eddy Simulation (DDES) with Wall-modeled Large-eddy Simulation (WMLES), namely IDDES. Although the IDDES method can improve the calculation accuracy in the boundary layer, the introduced WMLES means there is a complete LES method within the whole flow field. In a sense, this contradicts the original intention of DES-type models (RANS in the boundary layer and LES in other regions).
The filtering grid scale is the key parameter of DES, which is mostly obtained by calculating the function of mesh size. Smagorinsy [14], Deardorff [15], Scotti [16] and Ferziger [17] proposed the calculation formulas of the filtering grid scale in the LES with a direct influence of grid size and grid spacing. In the existing DES-type models, the definition method in LES was directly applied. So, it is necessary to build an extremely fine grid to simulate small-scale fluctuations and define a too-conservative RANS area outside the boundary layer. As a result, the advantages of the DES model, such as high calculation accuracy in the main flow area and small computing resource, cannot be fully utilized. On the other hand, the unreasonable division of the DES grid will inevitably lead to the mismatch between the calculated value and the appropriate value of filtering grid scale. In particular, there is still a lack of computational grid control criteria for DES in the physical sense, leading to the oversize of the local computational grid size and the loss of useful small-scale information. It is instructive to study the above problems based on the curvature of a curved elbow.
There is a problem of curvature variation in a curved elbow, the curvature has a direct influence on the turbulent structure of the boundary layer, so it affects the switching of the hybrid model. Zhao [18] carried out a study on the influencing factors of liquid–solid two-phase flow erosion and the optimization of the erosion-resistant structure of a 90° curved pipe. He found that erosion weakened as the radius of the curvature of the elbow increased. Zhang et al. [19] carried out numerical calculations and an analysis of the stress at the special point of the pipeline. The results showed that the range of stress influence was enlarged, but the stress of the curved elbow gradually decreased with the increase of the radius of curvature of the curved elbow. Li [20] studied the influence of the radius of curvature on the sound field of the curved elbow and found that the larger the radius of the curvature of the curved elbow, the smaller the exit noise. Wang et al. [21] studied the flow instability of a 90° circular cross-section curved elbow based on LES and analyzed the asymmetry of pressure distribution in a transient flow field.
In the paper, the applicability of three typical boundary layer meshes (anisotropic mesh, isotropic mesh and mesh type between them) to the DES hybrid model were firstly analyzed. Then, the filter grid scale was defined by the two methods of and . Three kinds of DES hybrid model filtering grids were compared. Furthermore, the size relationship among the three was analyzed. Finally, the effects of three definition methods on the simulated results were compared to the experimental results of the 90° curved elbow.
2. DES Grid
The general form of RANS/LES switching function based on a SST k-ω DES-type model is
where, is the turbulence length scale of RANS, marked as is the turbulence length scale of LES, marked as · is the delay function.
The turbulence length scale of DES is:
If is less than , the RANS is triggered in DES model. Otherwise, the LES is triggered in DES model.
In Equation (1), the delay function and the filtering grid scale Δ are two functions directly related to the RANS/LES switching performance. The delay function is used to delay the switching from RANS to LES in the boundary layer, thereby the entire boundary layer can be simulated only by RANS and the grid-induced separation problem can be solved. The filtering grid scale Δ is an important parameter for , which is a measure of the size of the local grid in essence.
2.1. Boundary Layer Mesh
The objection of the DES model is to adopt RANS in the boundary layer and LES in other regions. The switching functions are different in forms; however, the realization of RANS/LES switching all relies on the relations between the filtering grid scale and the distance from the wall. Therefore, for the convenience of description, the switching function in this section is expressed in the simplest form of . In order to excite the switching between RANS and LES near the outermost side of the boundary layer, three kinds of boundary layer mesh were given in Figure 1. Where, x represents the flow direction, y represents the direction perpendicular to the wall and the filtering grid scale in the z-direction is not given here, assuming .
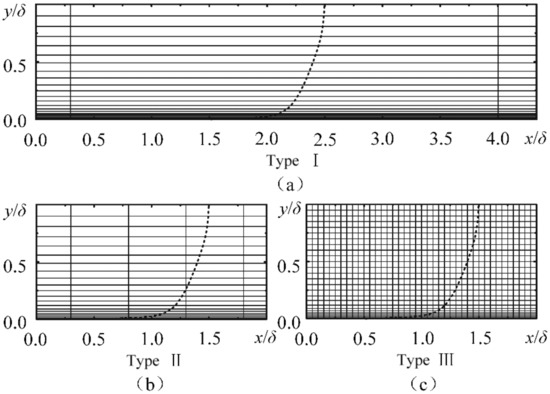
Figure 1.
Three types of grid in the boundary layer [9]. (a) Boundary layer grid type I; (b) Boundary layer grid type II; (c) Boundary layer grid type III.
Figure 1a shows mesh type I () with large size difference in different directions (), which is called an anisotropic grid. According to the maximum criterion, all the elements in the boundary layer satisfy , so the flow in the boundary layer can be stably calculated by RANS (). The boundary layer grid can meet the requirement of the DES hybrid model. Figure 1b shows mesh type II (), where in most regions of the boundary layer. The kind of meshes with approximately equal sizes in three directions are defined as isotropic grids. According to the maximum criterion, all the elements in the boundary layer satisfy . So, LES is adopted for the DES model in most areas of the boundary layer (), while RANS is in the near-wall area (). The flow field simulation is not carried out in accordance with the expected DES mode under the type of grid. Figure 1c shows mesh type III (), where in the boundary layer. For , there exists within 2/3 of upper boundary layer, i.e., LES mode. In the LES region of the boundary layer, the eddy viscosity decreases and the modeled Reynolds stress lowers. However, the mesh density in the region does not meet the requirement of LES. Thereby, the reduced modeled Reynolds stress cannot be balanced by a considerable amount of analytic stress, and the problem of insufficient modeling stress may occur, resulting in grid-induced separation. The DES model with a delay function is proposed to solve the problem. The active region of RANS is delayed outside the boundary layer in the delayed DES model.
RANS can be triggered within the boundary layer in the DES model using mesh type I and III. The reason that Type II cannot be used as a DES grid is as follows: (1) Type II will trigger the LES in most areas of the boundary layer, which does not conform to the working mode of the DES model. (2) Type II is a very fine isotropic mesh required for LES calculation, with obviously more mesh numbers and a larger computing resource.
In general, the grid in the boundary layer should satisfy . However, the thickness of the boundary layer is not constant with the development of flow in practical applications. In order to ensure the application of RANS in the boundary layer, the mesh type within the boundary layer for DES tends towards Type I (), which can further save computing resources due to the small number of meshes.
2.2. Filtering Grid Scale
The filtering grid scale in the DES model has two main functions:
- (1)
- As the main component of the DES switching function, it is used to determine whether the flow region is suitable for RANS or LES.
- (2)
- As the sub-grid grid scale of LES, large and small vortexes in the flow field are separated. There are two definition methods for filtering grid scales.
2.2.1. (Maximum Criterion)
Currently in the DES model, the most widely used filtering grid scale definition method (Maximum criterion) is the common method in LES. The filtering grid scale is defined as the local maximum grid spacing according to the criterion
For further discussion, the three-dimensional grid size in the above Equation is generalized, and represented by , and . Then, Equation (3) is expressed as
Analyzing the RANS/LES switching function of the DES model in the paper, , and . When , the DES model behaves as RANS. At this time,
where is essentially an amount proportional to the turbulence intensity, and is the local maximum grid spacing. Then, Equation (5) can be understood that the flow field can be simulated by RANS and the value is determined by the maximum size of the local grid when the turbulence intensity in the region near the boundary layer is less than a certain value.
2.2.2. (IDDES Grid Scale Definition)
Shur et al. [13] proposed the definition method of , which considers the influences of local maximum grid spacing, wall-normal grid spacing and the distance from wall on Δ.
where is an empirical constant. For the IDDES model based on SST k-ω, it is taken as 0.15. is the grid spacing normal to wall, d is the distance from the wall and is the maximum of wall-normal size and transverse element size locally along the direction of flow.
The definition is much more complex than that of . To clarify Equation (6), the channel flow field data obtained by Shur, and the possible values of are shown in Figure 2, where the x-coordinate and y-coordinate are dimensionless by half width H and , respectively.
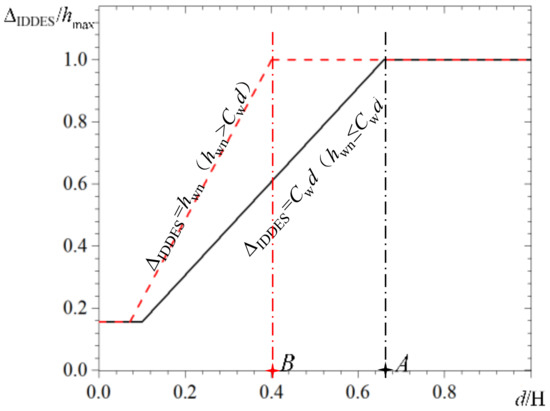
Figure 2.
Two values of ΔIDDES in the paper of Shur [13].
There are two cases for the value of ΔIDDES.
When (Black line in the picture), shows three stages of change
where is almost constant, which equals to close to the wall . In the region advancing from the wall toward main flow ), grows linearly (). When grows to equal to , remains .
When (Red line in the picture), has three similar stages.
where is always equal to in the region which is close to the wall . In the region advancing from the wall toward the main flow , increases linearly, but the growth rate is greater than case 1 (). When grows to , remains .
For the general DES cases, the advancing ratio of wall-normal grid length in the boundary layer is generally 1.2–1.3. At the time, the values obtained by two ways are close and have little influence on the calculation accuracy.
and represent two ways of filtering grid scale. For , the definition is simple, which can greatly reduce the amount of calculations. For , considering the calculation accuracy of WMLES in the boundary layer, the corresponding variation laws of two filtering grid scales are provided for the turbulence model in the boundary layer. Although is slightly better than in the verified example, its definition is too complicated. If it is applied in a more complex flow field, the computing time of the flow in the boundary layer will increase. Therefore, it is necessary to analyze and compare the existing methods of grid scale definition.
3. Comparison of Three Grid Scale Definition Methods
As can be seen from above, unlike the isotropic mesh in LES, the DES boundary layer mesh is usually anisotropic with a larger length–width ratio. Taking Type I as an example, the filtering grid scale continues to be calculated according the maximum criterion, . In the boundary layer, the of each mesh element is approximately equal, and is approximately a fixed value. For Type I, it means there will be a larger range of over conservative RANS regions outside the boundary layer for the DES method. The filtering grid scale defined by the maximum criterion is too large relative to the true geometry feature of grid. Therefore, it is necessary to analyze and compare the existing methods of grid scale definition.
3.1. Arithmetic Mean ()
For a single mesh element, the weighted average value of grid size in three directions is
where is the weight ). If the weight of each item is equal ), the weighted average is also known as the arithmetic mean.
Considering the main flow area is mainly solved through LES, which requires approximately isotropic meshes, the equivalent weight for three-dimensional mesh size was set. For convenience, the value of each weight was taken as 1, then, the weighted average of the three terms is the arithmetic mean. The filtering grid scale defined by this method is called the arithmetic mean filtering grid scale, denoted by .
3.2. Geometric Mean ()
Similar to the arithmetic average, the geometric mean is also a method to calculate the average value of a data set
where fi is the weight ().
It is applied to the filtering grid scale definition
As discussed in the previous section, the weight values of three-dimensional grid are 1. The filtering grid scale defined by this method is called the geometric mean filtering grid scale, marked as .
3.3. Quadratic Mean ()
The quadratic mean is a kind of generalized average method based on square root. It is to find the square of n data and the arithmetic mean of these squared values, then the arithmetic average values are squared. In the method, each data point in a set of numbers is regarded as an independent individual with equal weight
Applying it to mesh element, the filtering grid scale defined by quadratic mean of three-dimensional grid size is called the quadratic mean filtering grid scale, denoted by
3.4. Relations between Three Filtering Grid Scales
As can be seen from Section 1, the filtering mesh scale is the only variable of . and its size directly affects the switching position of the DES near the boundary layer. These three definitions take into account the scale of the three-dimensional grid, but the size of the filter grid is still different for the same grid. Therefore, it is necessary to get the size relations of these three filtering grid scales. Among the definition methods, the arithmetic average method is the most common and simplest in form. The size relations of filtering grid scales , and were compared.
1.
and
The size relation between and can be regarded as a simple application of arithmetic mean-geometric mean inequality (AG inequality [22]) in the three-dimensional filtering grid scale. The general form of AG inequality is
where is a positive number. The equal sign is true only when .
Equation (17) is applied to mesh element
It means the arithmetic mean mesh scale is not less than the geometric mean mesh scale .
2. and
Since , , and are all greater than 0, from the Cauchy–Buniakowsky–Schwarz Inequality, Equation (18) can be further converted to
It means the quadratic mean filtering grid scale is not less than the arithmetic mean filtering grid scale .
From Equations (14)–(17), the relations between the three filtering grid scales is
4. Internal Flow Simulation in Curved Elbow
4.1. Physical Model
The 90° square curved elbow with experimental results in the work of Taylor et al. [23] was selected as a research model, as shown in Figure 3. A cylindrical coordinate system is set at the curved section, and the Cartesian coordinate system is assigned for the straight section in the figure. In the cylindrical coordinate system, the origin is located at the curvature center of the curved section centerline, and is the polar angle. at the entrance of the curved section, and at the exit section. In the Cartesian coordinate system, x represents the length of straight section, which is positive along the flow direction. When and 90°, x is taken as 0 mm. The dimensionless coordinate in flow direction is defined as , is the radial dimensionless coordinate, and is the spanwise dimensionless coordinate ( represents half of the total length of span, that is 1/2D).
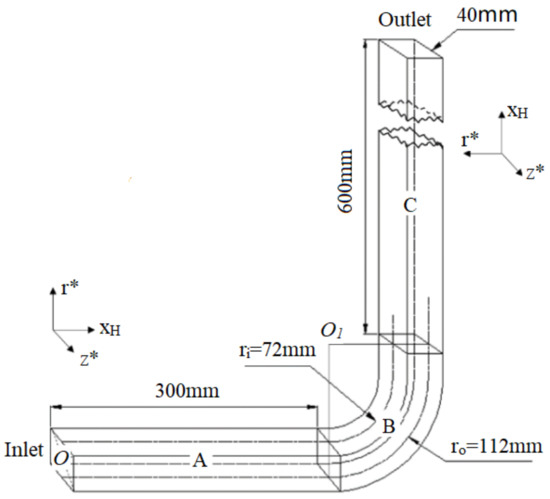
Figure 3.
Geometry structure of square curved elbow.
The side length of elbow section , and the inlet flow rate . The curvature radius of the inner arc surface , the curvature radius of the outer arc surface and the dimensionless average curvature radius . Among them, is the average radius of curved section, . The length of A and C straight segments are and , respectively. The tangents of upstream and downstream were 0.3m and 2.0 m, respectively. The dimensions of the cross-section (40 ± 0.1 × 40 ± 0.1 mm) conform closely to those of the tangents. The bulk velocities, Vc, were 1.98 cm/s and 1.00 m/s for the laminar and turbulent flows, respectively, corresponding to the Reynolds numbers, Re, of 790 and 40,000 and Dean numbers, De, of 368 and 18,700. The temperature of the liquid was maintained at 20° ± 2 °C for all the experiments.
4.2. Calculation Settings
In the paper, the structured grid partition was used for the whole fluid domain by ANSYS (Finite element analysis software). In order to meet the requirement of the DES model, the near-wall grid was refined. The thickness of first layer was set , and the grid growth rate of 1.2 was adopted to the main flow. The final total mesh number is 4,939,044, and the grid quality is above 0.65. The rationality of y+ was verified by the steady calculation according to SST k-ω turbulence model. The y+ is shown in Figure 4. As can be seen, the grid meets the requirement of the DES model.
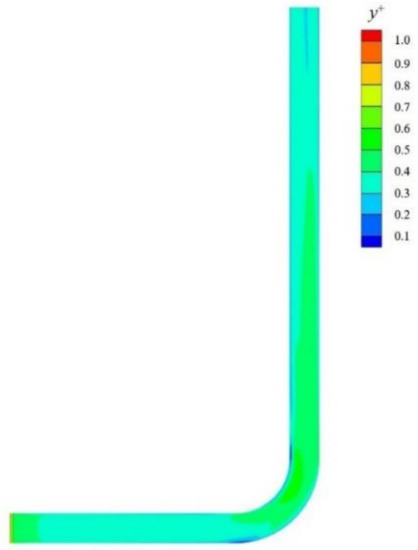
Figure 4.
y+ distribution of curved elbow.
The numerical calculation was based on OpenFOAM (Open Field Operation and Manipulation) software [24]. The inlet and outlet were set as velocity and free outflow, respectively. The wall was set to no slip boundary condition. The DES unsteady calculation was initialized with a convergent SST k-ω steady result using the SIMPLE algorithm.
The main geometric feature of grid was used in the improved definition of the filtering grid scale. The process of calling the function of grid element feature quantities in OpenFOAM is described in Figure 5.
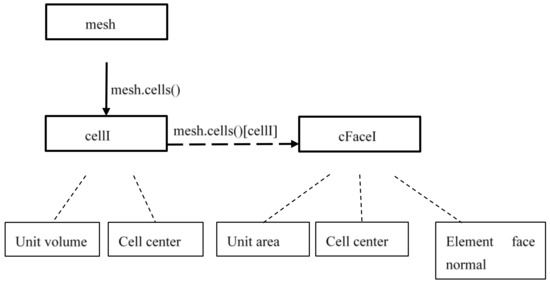
Figure 5.
Main geometric feature quantities of mesh in OpenFOAM.
No matter how many mesh cells are contained in the grid, all cell bodies in the grid objects can be located by using the forAll loop, that is, traversing the cell bodies. Here is how to use forAll:
const cellList& cells=mesh.cells();
forAll(cells,cellI)
{
;
}
The CellI above is a count variable of the total number of cells automatically updated by the software according to the cell body list (cellList& cells), and no artificial setting is required.
In forAll (cells,cellI), the current mesh cell body is mesh.cells () [cellI]. To traverse the cell surface in the cell body, another forAll loop was applied in the cell body traversal function:
const labelList& cFaces=mesh.cells()[cellI];
forAll(cFaces, cFaceI)
{
;
}
The function of cFaceI is the same as cellI.
4.3. Calculation Results
For the three filtering grid scales, the effects of definition methods (, and ) on calculation results in the DES model were compared to the experimental results. In addition, the DES result of was used as another set of comparisons.
4.3.1. Comparison of the Average Speed Curve in the Mainstream Direction
The mainstream time-averaged velocity distribution curves obtained by DES model defined by three scales are shown in Figure 6. According to Figure 6b,c, the three velocity distribution curves near the outer arc surface are close to the experimental value, and there is a big difference in the velocity curve near the inner arc surface (Figure 6a). In the inlet section of the elbow (), the three velocity curves are still close to the experimental value, which indicates that the three scale definition methods can accurately simulate the characteristics of the internal flow distribution. At the back of the pipe elbow ( ), the three speed distribution curves start to be different, among which gets the most deviation from the experimental value, is the closest to the experimental value and is in the middle.
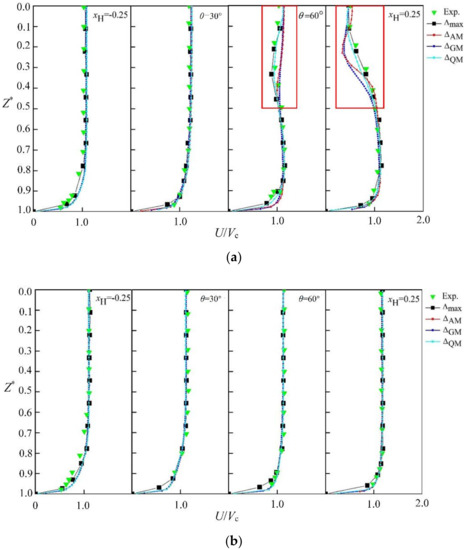
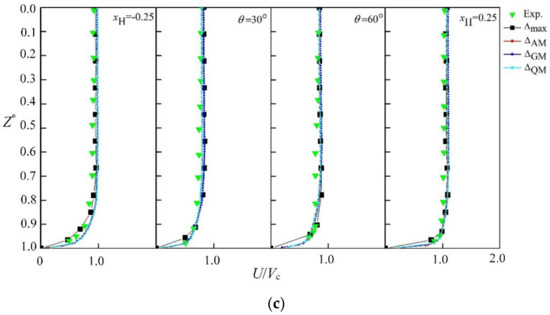
Figure 6.
Time-averaged velocity distribution of flow cross section. (a) The mainstream time-averaged velocity distribution curve obtained by the DES model at ; (b) the mainstream time-averaged velocity distribution curve obtained by the DES model at ; (c) the mainstream time-averaged velocity distribution curve obtained by the DES model at .
The difference between , and in different regions were analyzed. The three curves are close to the experimental values near the wall area () and the difference is not obvious. With the decrease of (flow close to the mainstream area), the development of the three curves changed. The curve firstly deviates significantly from the experimental value, then the curve also begins to deviate. In the mainstream area (), the and curves deviate from the experimental value by a large margin, and gradually return to the experimental value again. Compared with the and curves, the curve trend is closest to the experimental value. It can be seen that in the simulation area affected by centrifugal force, the velocity curve appears in obvious deformation ( in Figure 6a). The oscillation stability of the curve obtained by is higher than . Therefore, the curve trend and velocity results of are closer to the experimental results, and the stability is evident in the distribution of the section.
4.3.2. External Arc Surface Flow Static Pressure Distribution ()
The static pressure distribution curves on the outer arc wall surface obtained by , and are shown in Figure 7. As can be seen from the figure, the development of the three pressure distribution curves is the same. As increases firstly then decreases, takes a peak in the range when is between 50° and 60. This rule is consistent with the experimental results. Compared with the experimental values, the results of , and are close to the results of in the range of and . Within , the results of , and are closer to the experimental values.
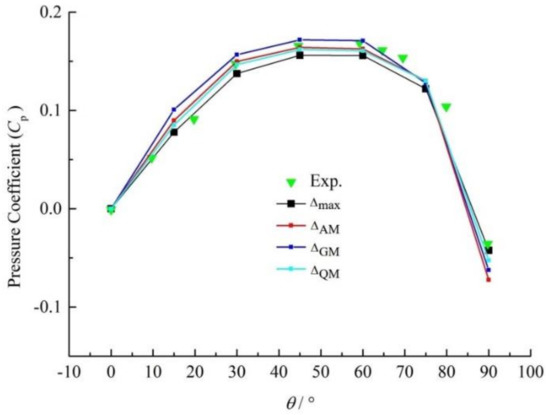
Figure 7.
Flow static pressure distribution on the outer arc surface.
Compared with the averaged speed curve in the mainstream direction, the distribution of , and is not obvious. In terms of the value on the curve, > > within . When , the relationship between the three values changes, which is related to the serious deformation of the velocity distribution on the cross section under the influence of centrifugal force. Among the three curves, the development trend and the values of the curve and the curve are closer to the experimental results. However, when , is slightly closer to the experimental value compared with the value.
Comparing Figure 6 and Figure 7, the velocity curve and pressure distribution curve of , and are all close to the experimental values in the areas where the centrifugal force is small (). When simulating the flow in the area seriously affected by centrifugal force (), the trend obtained by is closer to the experimental result. In summary, is more suitable for calculating the flow in the elbow.
5. Conclusions
The RANS/LES switching function of the DES model was studied in the paper. The characteristics of the DES grid and the influence of existing RANS/LES switching functions on the switching mode of one-dimensional grid definitions were analyzed. The length–width ratio of the three-dimensional grid size of typical DES mesh was obtained by comparing the effects of the DES boundary layer meshes on the working mode of the DES model. Then, the 90° square curved elbow was selected as the research object. The effects of three grid definition methods on the simulation results of the DES model were compared, and the velocity distribution of the flow cross section and the distribution of the flow pressure coefficient on outer arc surface was compared with the experimental results. The results show that, the three velocity curves near the wall are close to the experimental values, and the flow is close to the main flow area. The and curves deviate greatly from the experimental values at first, and the trend of the curve is the closest to the experimental values. Among the three pressure coefficient curves, the development trend and numerical values of and are the closest to the experimental results, but when °, the values of are slightly close to the experimental results. It is verified that the filter grid scale defined by the square average method can better simulate the turbulent flow under the influence of curvature compared with and .
Author Contributions
Conceptualization, L.D.; Data curation, C.G.; Formal analysis, Y.W.; writing—original draft preparation, H.L. and C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Key Research and Development Program of China (No. 2016YFB0200901), National Natural Science Foundation of China (No. 51879122, 51579117,51779106), China Postdoctoral Science Foundation (2017M611721), the association innovation fund of production, learning, and research (BY2016072-01),Zhenjiang key research and development plan (GY2017001, GY2018025), the Open Research Subject of Key Laboratory of Fluid and Power Machinery, Ministry of Education, Xihua University (szjj2017-094, szjj2016-068),Sichuan Provincial Key Lab of Process Equipment and Control (GK201614, GK201816), the Advanced Talent Foundation of Jiangsu University (15JDG052), Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and Six Talent Peaks Project in Jiangsu Province (GDZB-017).
Acknowledgments
The authors gratefully acknowledge the National Key Research and Development Program of China (No. 2016YFB0200901), National Natural Science Foundation of China (No. 51879122, 51779106), China Postdoctoral Science Foundation (2017M611721), the association innovation fund of production, learning, and research (BY2016072-01), Zhenjiang key research and development plan (GY2017001, GY2018025), the Open Research Subject of Key Laboratory of Fluid and Power Machinery, Ministry of Education, Xihua University (szjj2017-094, szjj2016-068), Sichuan Provincial Key Lab of Process Equipment and Control (GK201614, GK201816), the Advanced Talent Foundation of Jiangsu University (15JDG052) and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and Six Talent Peaks Project in Jiangsu Province (GDZB-017).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, X.G. Turbulence; Tianjin University Press: Tianjin, China, 1994. [Google Scholar]
- Xiao, Z.X.; Zhang, Y.F.; Chen, H.X.; Fu, S. Research on RANS/LES Hybrid method based on nonlinear pattern. In Proceedings of the Academic Conference of Chinese Mechanical Society (2015), Nanning, China, 19–21 November 2015. [Google Scholar]
- Zhao, R.; Wang, C.; Li, H.B.; Li, Y.J. A New Hybrid method for dynamic RANS/LES. Prop. Tech. 2017, 38, 1950–1955. [Google Scholar]
- Li, B.; Wu, S.P. Hybrid RANS/LES model based on turbulence scale. J. Beijing. Univ. Aero. Astro 2008, 7, 755–758. [Google Scholar]
- Sun, M.B.; Wang, H.B.; Liang, J.H.; Liu, W.D.; Wang, Z.G. Study on Hybrid RANS/LES method for complex turbulent flow. Aero. Comp. Tech. 2011, 41, 24–29. [Google Scholar]
- Constantinescu, G.S.; Squires, K.D. LES and DES Investigations of Turbulent Flow over a Sphere at Re = 10,000. Flow. Turbul. Combust. 2003, 70, 267–298. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. SAS turbulence modelling of technical flows. Diec. Lar. Simul. 2006, 10, 687–694. [Google Scholar]
- Menter, F.; Kuntz, M.A. Zonal SST-DES Formulation. In DES-Workshop; Petersburg Technical University: Saint Petersburg, Russia, 2003. [Google Scholar]
- Spalart, P.R.; Deck, S. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comp. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Deck, S.; Jacquin, L.; Chauvet, N. Zonal Detached Eddy Simulation of a Controlled Propulsive Jet. AIAA J. 2007, 45, 2458–2473. [Google Scholar]
- Fu, S.; Xiao, Z.X.; Chen, H.X.; Zhang, Y.F.; Huang, J.B. Simulation of wing-body junction flows with hybrid RANS/LES methods. Int. J. Heat Fluid Flow 2007, 28, 1379–1390. [Google Scholar] [CrossRef]
- Trapier, S.; Deck, S.; Duveau, P. Delayed Detached-Eddy Simulation and Analysis of Supersonic Inlet Buzz. AIAA J. 2008, 46, 118–131. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow. 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Smagorinsy, J. General Circulation Experiments with the Primitive Equations: I The Basic Experiment. Mon. Weather Rev. 1962, 91, 99–164. [Google Scholar] [CrossRef]
- Deardorff, J.W.A. Numerical study of three-dimensional turbulent channel flow at large reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Scotti, A.; Meneveau, C.; Lilly, D.K. Generalized smagorinsky model for anisotropic grids. Phys. Fluids 1992, 5, 2306–2308. [Google Scholar] [CrossRef]
- Metai, O.; Ferziger, J.H. New Tools in Turbulence Modeling; Springer Press: New York, NY, USA, 1996. [Google Scholar]
- Zhao, L.Q. Study on Liquid-Solid Two Phase Elbow Erosion and Anti-Erosion Optimization; China University of Petroleum (East China): Qingdao, China, 2016. [Google Scholar]
- Zhang, Y.N.; Ma, G.Y.; Huang, X.C.; Ning, W.Y.; Bi, Q. Numerical Simulation of the Stress of Elbow in the Beam-Mounted Straight Crossing Pipeline. J. Liaoning Univ. Petr. Chem. Tech. 2015, 35, 28–32. [Google Scholar]
- Li, L. Study on the Influence of Vortex Interaction on Sound Field in Circular Curved Pipe; Shaanxi normal University: Xian, China, 2015. [Google Scholar]
- Wang, S.; Ren, C.; Sun, Y.F.; Yang, X.T.; Tu, J.Y.; Tu, X. A Study on the Instantaneous Turbulent Flow Field in a 90-Degree Elbow Pipe with Circular Section. Sci. Tech. Nuc. Instal. 2016, 11, 1–8. [Google Scholar] [CrossRef]
- He, X.X. Classical proof of arithmetic mean-geometric mean inequality. Math. Bull. 1995, 3, 39–43. [Google Scholar]
- Taylor, A.M.K.P.; Whitelaw, J.H.; Yianneskis, M. Curved ducts with strong secondary motion—Velocity measurements of developing laminar and turbulent flow. J. Fluids Eng. 1982, 104, 350–359. [Google Scholar] [CrossRef]
- OpenFOAM. User Guide; Version v3.0+; Silicon Graphics: San Francisco, CA, USA, 8 January 2016. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).