Abstract
As an important technology in computer science, data mining aims to mine hidden, previously unknown, and potentially valuable patterns from databases.High utility negative sequential rule (HUNSR) mining can provide more comprehensive decision-making information than high utility sequential rule (HUSR) mining by taking non-occurring events into account. HUNSR mining is much more difficult than HUSR mining because of two key intrinsic complexities. One is how to define the HUNSR mining problem and the other is how to calculate the antecedent’s local utility value in a HUNSR, a key issue in calculating the utility-confidence of the HUNSR. To address the intrinsic complexities, we propose a comprehensive algorithm called e-HUNSR and the contributions are as follows. (1) We formalize the problem of HUNSR mining by proposing a series of concepts. (2) We propose a novel data structure to store the related information of HUNSR candidate (HUNSRC) and a method to efficiently calculate the local utility value and utility of HUNSRC’s antecedent. (3) We propose an efficient method to generate HUNSRC based on high utility negative sequential pattern (HUNSP) and a pruning strategy to prune meaningless HUNSRC. To the best of our knowledge, e-HUNSR is the first algorithm to efficiently mine HUNSR. The experimental results on two real-life and 12 synthetic datasets show that e-HUNSR is very efficient.
1. Introduction
Data mining is a very important technology in the field of computer science. It is a non-trivial process of revealing hidden, previously unknown and potentially valuable information from a large amount of data in the database. In recent years, utility-driven mining and learning from data has received emerging attentions from researchers due to its high potential in many applications, covering finance, biomedicine, manufacturing, e-commerce, social media, etc. Current research topics of utility-driven mining focus primarily on discovering patterns of high value (e.g., high profit) in large databases or analyzing the important factors (e.g., economic factors) in the data mining process [1]. High utility sequential pattern (HUSP) mining is an important task in utility-driven mining [2,3,4,5,6,7,8]. It focuses on extracting subsequences with a high utility (importance) from quantitative sequential databases. Current HUSP mining algorithms, however, only consider occurring events and do not take non-occurring events into account, which results in the loss of a lot of useful information [9,10,11]. Thus, high utility negative sequential pattern (HUNSP) mining is proposed to address this issue by considering both occurring events and non-occurring events. HUNSP can provide more valuable information that HUSP can not because a non-occurring event may influence its following event. For example, given HUSP and HUNSP . indicates that a first occurs, then b, and then c while indicates that a first occurs, if b does not occur, then d (not c ) will occur. That is, whether b occurs (or not) may result in the occurrence of c (or d ). Therefore, HUNSP is really important. But few studies on HUNSP have been proposed so far [12,13]. The high utility negative sequential pattern mining (HUNSPM) algorithm solved the key problem of how to calculate the utility of negative sequences by setting the utility of negative elements (not items) to 0 and choosing the maximum utility as the sequence’s utility [14]. Nevertheless, both HUSP and HUNSP have a limitation in that they cannot indicate the probability that some subsequences will occur after other subsequences occur or not. For example, we assume HUSP = and HUNSP = , where a, b, c, and d denote four symptoms, i.e., headache, , , and , and X and Y denote two diseases, i.e., and . shows that patients who have , then and then are likely to have a , whereas indicates that patients who have but not a and then probably have . Although and are useful apparently, we can not know the exact probability that patients will have disease X (or Y) after they show symptom a, then b (or not) and then c (or d) from them.
To address this issue, high utility sequential rule (HUSR) mining has been proposed in HUSP mining. HUSR, such as , can precisely tell us the probability that patients will have a after they show , then a and then . Unfortunately, research studies on HUSR mining are few. The HUSRM algorithm was proposed in HUSR mining [15]. HUSRM first scans the database to build all sequential rules for which the sizes of the antecedent and consequent are both one. Then, it recursively performs expansions starting from those sequential rules to generate sequential rules of a longer size based on the support-confidence framework and minimum utility threshold. However, the rules mined by HUSRM only guarantee the items in the consequent occur after the items in the antecedent but the items in the antecedent and consequent are internally unordered (e.g., a, b, and c are unordered in HUSR ). In addition, HUSRM has a very strict constraint for datasets, that is, an item cannot occur more than once in a sequence (e.g., is not allowed because a appears two times in the sequence), similar to the association rule mining. In fact, the constraint is too strict to be applicable for many real-life applications. Moreover, HUSRM does not take non-occurring events into account, which can lead to the loss of a lot of valuable information.
In order to mine high utility sequential rules that consider non-occurring events, high utility negative sequential rules (HUNSR) should be proposed. With HUNSR: , we can clearly know the probability that patients will have after they show a , but not a and then . Unfortunately, we have not found any existing research on HUNSR mining so far. In fact, HUNSR mining is very challenging due to the following three intrinsic complexities.
Firstly, it is very difficult to define the HUNSR mining problem because of the hidden nature of non-occurring events in HUNSR. For example, what is a valid HUNSR? There is no unified measurement to evaluate the usefulness of rules. The traditional support-confidence framework is not applicable to mine HUNSR because it does not involve the utility measure [16,17,18].Furthermore, the utility-confidence framework in high utility association rule (HUAR) mining is not applicable either because it does not involve the ordinal nature of sequential patterns [19]. So, it is very important to formalize the problem properly and comprehensively.
Secondly, it is very difficult to calculate the antecedent’s local utility value in a high utility negative sequential rule candidate (HUNSRC), which is a core step in calculating the utility-confidence of a HUNSRC. For simplicity, we take HUSP and HUSR for example to illustrate how to obtain the local utility value of in . Different from HUAR mining where all items appear only once in a rule, the ordinal nature of sequential patterns determines that and may have multiple matches in a q-sequence (such as ), which makes the problem quite complicated. In order to calculate the local utility value of in , we first need to obtain all the utility values of the matches of in , then choose the maximum one and record its items’ transaction ID (TID) (such as ) and find the TID of at this time, i.e., . Next, find the corresponding utility of this (its TID is ) in . Find and sum the utility values of in each q-sequence containing in the database using the above method, and the sum is the local utility value of in . However, it is much more difficult to calculate the antecedent’s local utility value (such as ) in a HUNSR (such as ) than a HUSR for the following two reasons. One is that it is rather difficult to determine the TID of a negative item in a q-sequence [20]. The other is that the necessary information of sequence ID (SID), TID and utility to calculate the local utility value is not saved by current algorithms as these algorithms do not need to calculate the local utility value [12,13,14].
Finally, the antecedent’s utility may not exist, that is, it may not be saved by current algorithms because it may be less than the minimum utility threshold. In fact, the antecedent’s utility is also a necessary condition to calculate the utility-confidence of HUNSRC. Therefore, we must modify the existing algorithms to save the related information of the antecedent and recalculate its utility.
To address the above intrinsic complexities, this paper proposes a comprehensive algorithm called e-HUNSR. The main ideas of e-HUNSR are as follows. First, we formalize the HUNSR problems by defining a series of important concepts, including the local utility value, utility-confidence measure, and so on. Second, a novel data structure called a SLU-list (sequence location and utility) is proposed to record all the required information to calculate the antecedent’s local utility value, including the information of SID, TID, and utility of the intermediate subsequences during the generation of HUSP which corresponds to the HUNSRC. Third, in order to efficiently calculate the local utility value and utility of the antecedent, we convert the HUNSR’s calculation problem to its corresponding HUSR’s calculation problem to simplify the calculation based on high utility negative sequential patterns discovered by the HUNSPM algorithm [14]. In addition, we propose an efficient method to generate HUNSRC based on the HUNSP mined by the HUNSPM algorithm and a pruning strategy to prune the large proportion of meaningless HUNSRC.
Our main contributions are summarized as follows.
- (1)
- We formalize the problem of HUNSR mining by proposing a series of concepts;
- (2)
- We propose a novel data structure to store the related information of HUNSRC and a method to efficiently calculate the local utility value and utility of HUNSRC’s antecedent;
- (3)
- We propose an efficient method to generate HUNSRC based on HUNSP and a pruning strategy to prune meaningless HUNSRC;
- (4)
- Based on the above, we propose an efficient algorithm named e-HUNSR to mine HUNSR. To the best of our knowledge, this is the first study to mine HUNSR. The experimental results on two real-life and 12 synthetic datasets show that the e-HUNSR is very efficient.
The rest of the paper is structured as follows. In Section 2, we briefly review the existing works proposed in the literature. In Section 3, we provide some basic preliminaries. Section 4 introduces our proposed e-HUNSR algorithm. Section 5 presents the experimental results. Finally, the paper ends with concluding remarks in Section 6.
2. Related Work
In this section, we review the existing methods of HUSR mining, HUNSP mining, HUAR mining, and HUSP mining.
2.1. High Utility Sequential Rule Mining (HUSR Mining)
In this section, we mainly introduce the HUSRM [15] algorithm in high utility sequential rule (HUSR) mining. Based on the support-confidence framework, the HUSRM algorithm combines sequential rule (SR) mining and utility-driven mining, and adds the minimum utility threshold to mine HUSR. It assumes that sequences cannot contain the same item more than once and explores the search space of sequential rules using a depth-first search. It firstly scans the database to build all the sequential rules for which the sizes of the antecedent and consequent are both one. Then, it recursively performs left/right expansions starting from these sequential rules to generate sequential rules of a longer size. It uses the sequence estimated utility measure to prune unpromising items and rules and uses the utility table structure to quickly calculate support and utility, and bit vector to calculate confidence.
However, the rules mined from HUSRM are partially-ordered sequential patterns, where the antecedent and consequent of the rules are unordered. Moreover, HUSRM can only mine HUSR instead of HUNSR.
2.2. High Utility Negative Sequential Pattern Mining (HUNSP Mining)
Negative sequential pattern (NSP) mining referring to frequent sequences with non-occurring items plays an important role in many real-life applications, such as health and medical systems and risk management [20]. Although a few algorithms [21,22,23] have been proposed to mine NSP based on a minimum support threshold, they do not consider utility. This means some important sequences with low frequencies will be lost. Thus, HUNSP mining was proposed. The HUNSPM algorithm [14] solves the key problems of how to calculate the utility of negative sequences, how to efficiently generate high utility negative sequential candidates (HUNSC), and how to store the HUNSC’s information. The utility of negative elements (not items) in a negative sequence is 0, which can simplify the utility calculation and HUNSPM chooses the maximum utility as the sequence’s utility. For a k-size HUSP, the sets of its HUNSC are generated by changing any n non-continuous elements to their corresponding negative elements based on HUSP, , not less than . To efficiently calculate the HUNSC’s utility, HUNSPM uses a novel data structure called the utility of positive and negative elements (PNU)-list to store HUNSC-related information. In fact, negative unit profit is also interesting. The work in [12] proposes an algorithm named efficient high utility itemsets mining with negative utility (EHIN) to find all high utility itemsets with negative utility. The work in [13] proposes a generalized high utility mining (GHUM) method that considers both positive and negative unit profits. The method uses a simplified utility-list data structure to store itemset information during the mining process.
Although HUNSPM takes non-occurring events and utility into account, it cannot mine HUNSR.
2.3. High Utility Association Rule Mining (HUAR Mining)
HUAR mining is an interesting topic which refers to association rule generation based on high utility itemsets (HUI). It helps organizations make decisions on sale and promotion activities and realize higher profit by analyzing their business, sale activities, and customer trends [24]. Sahoo et al. [19] proposed an approach to mine non-redundant high utility association rules and a method for reconstructing all high utility association rules. This approach consists of three steps: The first step is to mine high utility closed itemsets (HUCI) and generators; the second step is to generate high utility generic basic (HGB) association rules; and the last step is to mine all high utility association rules based on HGB. Since the approach consumes a lot of time in the third stage when the HGB list is large and each rule in HGB has many items, a lattice-based algorithm called LARM for mining high utility association rules was proposed in [25]. It has two phases: (1) Building a high utility itemsets lattice (HUIL) from a set of high utility itemsets; and (2) mining all high utility association rules from the HUIL. Lee et al. [26] determine three key elements (opportunity, effectiveness, and probability) to define user preferences and operate them as utility functions, and evaluate association rules by measuring the specific business benefits brought by association rules to enterprises.
Although several algorithms have been proposed to mine HUAR, they cannot mine HUNSR. The ordinal nature of HUNSR means that algorithms for HUAR mining cannot be directly used to mine HUNSR, rather they need to be modified.
2.4. High Utility Sequential Pattern Mining (HUSP Mining)
HUSP mining can provide more comprehensive information for decision-making and many algorithms have been proposed to mine HUSP. The work in [2] proposes UtilityLevel (UL) and UtilitySpan (US) algorithms by extending the traditional sequential pattern mining algorithm. The UL algorithm uses a level-wise candidate generation approach to mine HUSP, whereas the US algorithm adopts a pattern growth approach to avoid generating large numbers of candidates. The work in [3] proposes a lexicographic quantitative sequence tree to extract the complete set of high utility sequences and two concatenation mechanisms are designed to calculate the utility of a node with two effective pruning strategies. The work in [4] introduces a pure array structure, which reduces memory consumption compared with the utility matrix. A new pruning strategy and parallel mining strategy are also proposed. The work in [5] proposes an effective algorithm to mine HUSP from incremental databases without generating candidate data. Based on the list data structure, the algorithm scans the database only once during the mining process. The work in [6] designs an approximate algorithm memory-adaptive high utility sequential pattern mining (MAHUSP), which employs a memory adaptive mechanism to use limited memory so as to effectively discover HUSP over data streams. The work in [7] uses a lexicographic quantitative sequence tree (LQS-tree) to extract the complete set of HUSP and two pruning methods are used to reduce the search space in the LQS-tree. The work in [8] considers the negative item value in HUSP mining and an algorithm named HUSPNIV is proposed to mine HUSP with a negative item value. The work in [9] proposes an efficient sequence-utility (SU)-chain structure to improve mining performance. The work in [10] extends the occupancy measure to assess the utility of patterns in transaction databases and proposes an efficient algorithm named high-utility occupancy pattern mining (HUOPM). The work in [11] proposes a method for the effective mining of closed high utility itemsets in both dense and sparse datasets.
These algorithms, however, cannot be used to mine HUNSR because they do not take non-occurring events into account.
3. Preliminaries
In this section, we introduce some basic preliminaries.
Let be a set of distinct items. Each item is associated with a positive number , called its quality or external utility. A q-item is one in which represents an item and q is a positive number representing the quantity or internal utility of i, e.g., the purchased number of i. A q-itemset, which is a set of q-items for , is denoted and defined as . If a q-itemset contains only one q-item, the brackets can be omitted for brevity. A q-sequence is defined as , where is a q-itemset. A negative q-sequence denoted as is composed of more than one negative item, where is called a positive q-itemset, and is called a negative q-itemset. A q-sequence database D is composed of many tuples like , where s is a q-sequence and represents the unique identifier of s. represents the number of itemsets (positive or negative) in s. represents the number of items (positive or negative) in s.
We use the examples in Table 1 and Table 2 to illustrate the concepts. In q-sequence ( = 1), (a, 2), (b, 2), (f, 3), (b, 3), and (d, 3) are q-items, where 2, 2, 3, 3, and 3 represent the internal utility of a, b, f, b, and d respectively. [(b, 2)(f, 3)] is a q-itemset consisting of two q-items. According to the utility table given in Table 1, the external utilities of a, b, f, and d are respectively 2, 4, 1, and 5. For convenience, we use “q-” to name the object associated with quantity, that is, “q-item”, “q-itemset”, and “q-sequence” are related to quantity. We denote the = 1 q-sequence in Table 2 as , and the other q-sequences are numbered accordingly.

Table 1.
Utility table.

Table 2.
Q-Sequence database.
Definition 1.
For a q-sequence and a sequence . s matches t if and for , denoted as .
For example, has match in . has two matches and in . A sequence may have multiple matches in a q-sequence.
Definition 2.
The utility of a q-item is denoted as and is defined as:
For example, .
Definition 3.
The utility of a q-itemset is denoted as and is defined as:
For example, .
Definition 4.
The utility of a q-sequence is denoted as and is defined as the sum of the utilities of :
For example, .
Definition 5.
The utility of a sequence t in a q-sequence s is denoted as and is defined as:
The utility of t in a q-sequence database D is denoted as and is defined as:
For example, the utility of sequence in q-sequence is . The utility of sequence in D is .
Definition 6.
We choose the maximum utility as the sequence’s utility. The maximum utility of sequence t is denoted and defined as :
According to Definition 6, the utility of sequence in D is .
4. The e-HUNSR Algorithm
In this section, we present the framework and working mechanism of the e-HUNSR algorithm, which is illustrated in Figure 1. More specifically, we first introduce the framework of e-HUNSR, and then propose the utility-confidence concepts, the method of HUNSRC generation, the pruning strategy, the data structure to store the related information of HUNSRC, and the utility-confidence of the HUNSRC calculation.
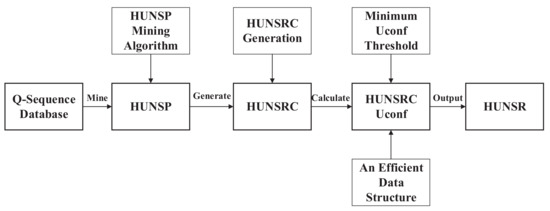
Figure 1.
The framework of the e-HUNSR (high utility negative sequential rule) algorithm.
4.1. The Framework of the e-HUNSR Algorithm
Given a q-sequence database, e-HUNSR captures HUNSR in terms of the following four steps.
- Step 1.
- Mine all HUNSP from the q-sequence database using a traditional HUNSP mining algorithm, i.e., HUNSPM algorithm;
- Step 2.
- Use a HUNSRC generation method to obtain all HUNSRC based on HUNSP;
- Step 3.
- Remove unpromising HUNSRC and calculate the utility-confidence of promising HUNSRC;
- Step 4.
- Find all HUNSR satisfying the user-specified minimum utility-confidence threshold.
4.2. The Utility-Confidence Concepts in HUNSR Mining
In this section, a series of definitions are proposed to construct the utility-confidence framework in HUNSR mining. Calculating the local utility value is the core step of calculating the utility-confidence of a rule, therefore we propose a series of definitions, i.e., Definitions 7–11 to illustrate the local utility value in HUNSR mining as follows.
Definition 7.
Given q-sequences and are subsequences of q-sequence s, where and . The local utility value of in is the sum of the utility values of q-itemset , which is denoted as and is defined as:
For example, in q-sequence , q-subsequence , q-subsequence .
Definition 8.
Given sequences X and Y such that , y is the q-sequence with the maximum utility value among all the q-sequences matching Y in q-sequence s and x is the q-sequence that matches X in q-sequence y. The local utility value of X in Y in the q-sequence s is denoted as and is defined as:
For example, we need to calculate the local utility value of sequence in sequence in q-sequence , i.e., . has two matches in , i.e., and where and , therefore has the maximum utility of the above two matches. The match of sequence in q-sequence is . Thus, .
Definition 9.
The local utility value of sequence X in Y such that in a quantitative sequence database D is denoted as and is defined as:
For example, the local utility value of sequence in sequence in D, i.e., .
In particular, if Y is a negative sequence, it is extremely difficult to calculate the local utility value due to the hidden nature of non-occurring events. In this paper, X and Y are converted to their corresponding maximum positive subsequences in order to simplify the calculation. The definition is shown below.
Definition 10.
The maximum positive subsequence of a negative sequence is denoted as and is defined as:
For example, .
Definition 11.
The local utility value of a sequence s (positive or negative) in another negative sequence such that in a database D is denoted and defined as :
where and represent the maximum positive subsequences of s and respectively. For example, .
To address the problem that the utility of the antecedent in a negative sequential rule may be less than the minimum utility threshold, we replace the antecedent with its maximum positive subsequence. The definition is shown below.
Definition 12.
The utility of a HUNSR’s antecedent is denoted and defined by:
Based on Definitions 11 and 12, we know that the antecedent’s local utility value and utility can be calculated by only using the corresponding HUSP information of the HUNSRC. Hence, there is no need to consider the problem of determining a negative item’s TID and storing the related information of HUNSP.
The utility-confidence measure is an important criterion to evaluate the usefulness of rules. The detailed definition is shown below.
Definition 13.
A high utility negative sequential rule is an implication of the form R: , where X, , X is antecedent of the rule, Y is consequent of the rule, and is a HUNSP.
The utility-confidence of the rule R is denoted by and is defined by:
where and represent the maximum positive subsequences of X and respectively.
R: is called a HUNSR if its utility-confidence, i.e., is more than or equal to the specified minimum utility-confidence () threshold.
For example, if the minimum utility () threshold is 37.8, the is 0.5, is a HUNSR since and .
4.3. e-HUNSR Candidate Generation
To generate all HUNSRC based on HUNSP, we use a straightforward method. The basic idea of the method is to divide a HUNSP into two parts, i.e., the antecedent and consequent. The detail is described as follows.
For a k-size HUNSP , the set of its corresponding HUNSRCs is generated by dividing it into two parts, i.e., the antecedent and the consequent . We can get HUNSRCs.
For example, given a HUNSP , its corresponding five HUNSRCs are listed as follows: .
4.4. Pruning Strategy
We obtain all HUNSRCs using the e-HUNSR candidate generation method. However, not all of them are promising. To avoid calculating the unpromising rules’ utility-confidence, we propose a pruning strategy to remove these rules. We define a HUNSRC as an unpromising rule if its antecedent or consequent only contains one negative element. As the utility of a negative element is 0, it is meaningless if the utility of an antecedent or consequent in a HUNSRC is 0. A HUNSRC will be removed from the list if it satisfies one of the following two conditions:
- (1)
- There is only one element in the antecedent and it is negative;
- (2)
- There is only one element in the consequent and it is negative.
For instance, and are unpromising rules, while , and are promising.
4.5. Data Structure
In order to efficiently calculate the local utility value and utility of HUNSRC’s antecedent, we design a novel data structure called the sequence location and utility list (SLU-list). It records the SID, TID, and utility information of the intermediate subsequences during the generation of HUSP which corresponds to HUNSRC. The SLU-list is composed of a Seq-table and LU-table. The Seq-table stores the intermediate subsequence of the HUSP generation process and the LU-table stores the corresponding SID, TID, and Utility. That is, each intermediate subsequence corresponds to multiple tuples like (SID, TID, and Utility).
Table 3 gives an example, showing the SID, TID, and utility information of the generation from to . Take for example, has six matching q-sequences in the database in Table 3, and the six q-sequences are from , and respectively. In , it matches two q-sequences; in the first matching q-sequence, item a is from itemset 1 (TID = 1) and item b comes from itemset 2 (TID = 2) and its utility is 12; in the second matching q-sequence, item a is from itemset 1 (TID = 1) and item b comes from itemset 3 (TID = 3) and its utility is 16. Similarly, has one and three matching sequences in and respectively.

Table 3.
The SLU-list (sequence location and utility) structure.
4.6. The Utility-Confidence of HUNSRC Calculation
We can efficiently calculate HUNSRC’s utility-confidence based on the above proposed definitions and the SLU-list structure. Firstly, we need to know the local utility value of the antecedent in HUNSRC. Then, we need to know the utility of the antecedent. Finally, the local utility value divided by the utility value is the utility-confidence.
For example, if we want to calculate the utility-confidence of HUNSRC:, the first step is to calculate , the second step is to calculate , then the can be determined. The steps are as follows.
- Step 1:
- Calculate the local utility value of the antecedent.
According to Equation (11), calculating is equal to calculating , . Firstly, sequence has two matches in and the corresponding utilities are 12 and 16 respectively in Table 3. Next, the maximum utility is 16 and the corresponding TID of 16 is {1, 3} in Table 3. Then, the TID of is {1} and the corresponding utility is 4. Finally, we can obtain the utility of in and by using the same method, i.e., 6 and 6 respectively and the sum is 16. Therefore, the local utility value of the antecedent is .
- Step 2:
- Calculate the utility of the antecedent.
- Step 1:
- Calculate the utility-confidence .
The HUNSRs extracted from the q-sequence database given in Table 1 and Table 2 with , are shown in Table 4. There are 94 HUNSRs in the mining result. Here we only show a small number of them due to the limited space.

Table 4.
Extracted HUNSRs with , .
4.7. The e-HUNSR Algorithm
The pseudocode of the e-HUNSR algorithm is shown in Algorithm 1. It takes a quantitative sequential database D, , as inputs, and outputs all the HUNSR.
e-HUNSR consists of four steps: (1) All HUNSPs are mined by the HUNSPM algorithm (Line 3); (2) all HUNSRCs are generated using the e-HUNSR candidate generation method based on HUNSP (Line 4); (3) unpromising rules are removed from HUNSRC using the pruning strategy given in Section 4.4 (Line 5–8); and (4) for each rule in HUNSRC, the antecedent’s local utility value, the antecedent’s utility, and the utility-confidence of the HUNSRC are calculated using Equations (11)–(13) (Line 9–11). If the HUNSRC’s utility-confidence satisfies the , it will be added to HUNSR (Line 12–14).
| Algorithm 1 e-HUNSR Algorithm |
|
4.8. Theoretical Analysis about the Utility-Confidence Framework
Since the utility-confidence framework is the core of our proposed e-HUNSR algorithm, we give a theoretical analysis to prove the rationality of the utility-confidence framework in this section.
Traditional association rules mining algorithms depend on support-confidence framework in which all items are given the same importance [16,21,22,23]. The goal of the algorithms is to extract all the valid association rules whose confidence has at least the user defined confidence. But they do not consider utility, this means some important patterns with low frequencies will be lost [14]. For example, consider a sequential rule in Table 2. The support of R, i.e., support() is one because the number of the q-sequences in Table 2 containing is one, i.e., . Similarly, support(f) = 5. The confidence of R is 0.2 which is calculated by confidence (R)=support()/ support(f). If the is 0.3, will be considered an invalid rule. But if we consider utility, the utility confidence of R is will be considered a valid rule when is 0.3.
Why is the same rule treated differently under different frameworks? In fact, the support-confidence framework does not provide any additional knowledge except the measures that reflects the statistical correlation among items [19,24]. is considered an invalid rule just because f only contributes one time to when f has already occurred five times in Table 2. In addition, it does not reflect their semantic implication towards the mining knowledge, that is, it does not take utility into account [25,26]. However, the indicates that the utility contribution of f to accounts for 40% of the total utility of f under the utility-confidence framework. Hence, is considered a valid rule. The support-confidence model may not measure the usefulness of a rule in accordance with a user’s objective (for example, profit) and the utility-confidence framework is more reasonable for decision-making.
5. Experiments
We conduct experiments on two real-life and 12 synthetic datasets to evaluate the efficiency of e-HUNSR. Since e-HUNSR is the first algorithm for high utility negative sequential rule mining, there are no baseline algorithms to compare with, we only test the performance of e-HUNSR in terms of execution time and number of HUNSRs under different factors. In the experiments, all HUNSPs are mined by the HUNSPM algorithm and all HUNSRs are identified by e-HUNSR. The algorithm is written in Java and implemented in Eclipse, running on Windows 10 PC with 16GB memory, Intel (R) Core (TM) i7-6700 CPU of 3.40 GHz.
5.1. Datasets
We use the following data factors: C, T, S, I, DB, and N defined in [27] to describe the impact of data characteristics.
C: Average number of elements per sequence; T: Average number of items per element; S: Average length of maximal potentially large sequences; I: Average size of items per element in maximal potentially large sequences; DB: Number of sequences; and N: Number of items.
DS1 (C8_T2_S6_I2_DB10k_N0.6k) and DS2 (C10_T2_S6 _I2 _DB10k_N1k) are synthetic datasets generated by the IBM data generator [27]. DS3 and DS4 are real-life datasets. DS3 is the BMS-WebView-2 dataset from KDDCUP 2000 [28,29]. It includes click-stream data from Gazelle.com. The dataset contains 7631 shopping sequences and 3340 products. The average number of elements in each sequence is 10, the max length of a customer’s sequence is 379, and the most popular product is ordered 3766 times. DS4 is a dataset of sign language utterance containing 800 sequences [30]. It is a dense dataset with very long sequences with 267 distinct items and the average sequence length is 93.
Table 5 shows the four datasets and their different characteristics. Since only synthetic datasets have data factors S and I (real-life datasets do not), we do not show them in Table 5. DS1 is moderately dense and contains short sequences. DS2 is moderately dense and contains medium length sequences. DS3 is a sparse dataset that contains many medium length sequences and a few very long sequences. DS4 is a dense dataset having very long sequences.

Table 5.
Data characteristics.
For all datasets, external utilities of items are generated between 0 and 50 using a log-normal distribution and the quantities are generated randomly between 1 and 10, similar to the settings of [3,28].
5.2. Evaluation of Impact
We analyze the impact of on the algorithm performance in terms of the running time and number of HUNSRs, thus the is fixed and the is varied. Since the four datasets have different characteristics, we set different and values to better reflect the impact of respectively.
Figure 2a shows that with the increase of , the execution time and number of HUNSRs decreases gradually. This is because the number of HUNSPs decreases with the increase of . Figure 2b–d show a similar trend for both synthetic and real-life datasets from DS2 to DS4. The results in Figure 2 also show that e-HUNSR can extract HUNSR under very low (e.g., 0.00092 for DS2). It is worth noting that DS4 is a very dense dataset, and the result shown in Figure 2d indicates that e-HUNSR also has good adaptability to dense datasets.
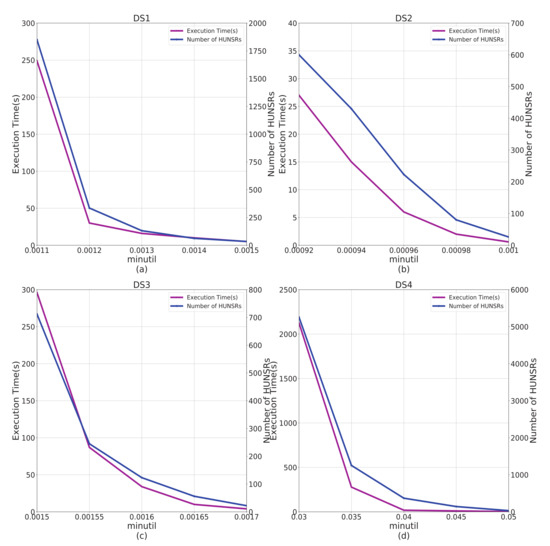
Figure 2.
Impact of on algorithm performance. This figure shows the impact of on execution time and number of HUNSRs. (a) The experiment on DS1. (b) The experiment on DS2. (c) The experiment on DS3. (d) The experiment on DS4.
5.3. Evaluation of minuconf Impact
In this experiment, we assess the impact of on the algorithm performance in terms of the running time and number of HUNSRs. The is fixed and the is varied.
Figure 3a shows that with the increase of , the number of HUNSRs decreases gradually, while the execution time does not change much. A similar trend can be found in the results of Figure 3b–d from DS2 to DS4.
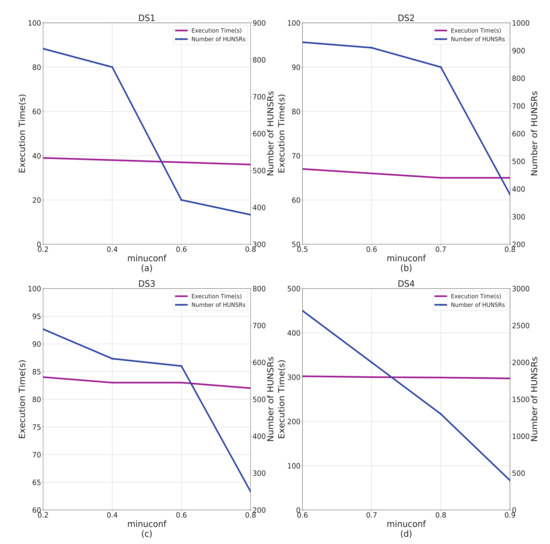
Figure 3.
Impact of on algorithm performance. This figure shows the impact of on execution time and number of HUNSRs. (a) The experiment on DS1. (b) The experiment on DS2. (c) The experiment on DS3. (d) The experiment on DS4.
5.4. Data Characteristics Analysis
In this section, we explore the impact of data characteristics on the performance of e-HUNSR as well as the sensitivity of e-HUNSR to particular data factors.
DS1 is extended to 10 new datasets by tuning each factor and we mark the different factors in bold for each dataset as shown in Table 6. For example, DS1.1 (C6_T2_S6_I2_DB10k_N0.6k) and DS1.2 (C10_T2_S6_I2_DB10k_N0.6k) have a different data factor C compared with DS1 (C8_T2_S6_I2_DB10k_N0.6k) and we test the influence of data factor C on algorithm performance through the three datasets. We analyze the performance of e-HUNSR in terms of the running time and the number of HUNSRs from the perspective of and based on different datasets respectively.

Table 6.
DS1 and its extended datasets.
According to the results shown in Figure 4, Figure 5, Figure 6 and Figure 7, factors C and T significantly affect the performance of the e-HUNSR algorithm, while factors S and I have little effect on it. In general, with the increase of factors C, T, S, and I, the running time and the number of HUNSRs increase accordingly. Taking the results in Figure 5 for example, when factor T is higher, such as DS1.4, the e-HUNSR generates more rules and takes more time than DS1. However, factor N is the opposite as the running time and the number of HUNSRs first increase and then decrease with the increase of N according to the results shown in Figure 8. Moreover, from Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the descending gradient of factors C and N is larger than that of T, S, and I. This indicates that e-HUNSR is more sensitive to factors C and N than T, S, and I.
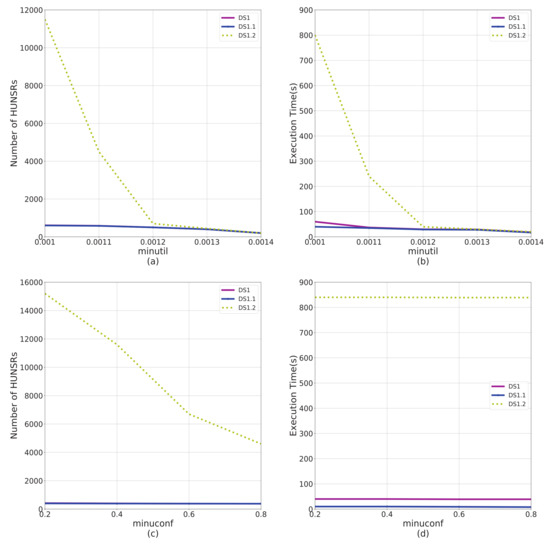
Figure 4.
Performance comparison on data factor C. This figure shows the impact of data factor C on algorithm performance in terms of execution time and number of HUNSRs from different perspectives. DS1, DS1.1, and DS1.2 have different data factor on C. (a) The impact of C on number of HUNSRs from the perspective of . (b) The impact of C on execution time from the perspective of . (c) The impact of C on number of HUNSRs from the perspective of . (d) The impact of C on execution time from the perspective of .
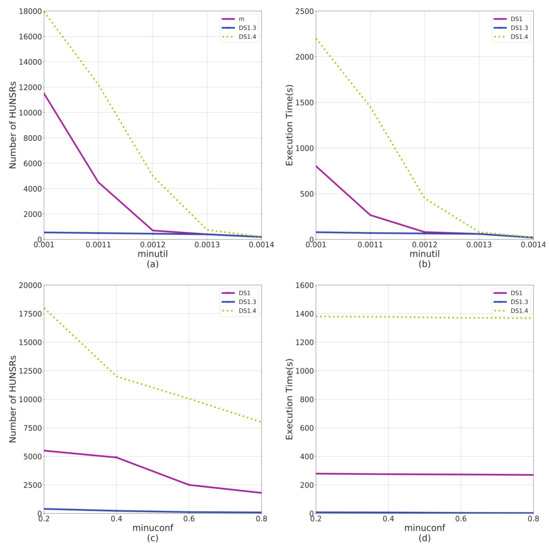
Figure 5.
Performance comparison on data factor T. DS1, DS1.3, and DS1.4 have different data factor on T. (a) The impact of T on number of HUNSRs from the perspective of . (b) The impact of T on execution time from the perspective of . (c) The impact of T on number of HUNSRs from the perspective of . (d) The impact of T on execution time from the perspective of .
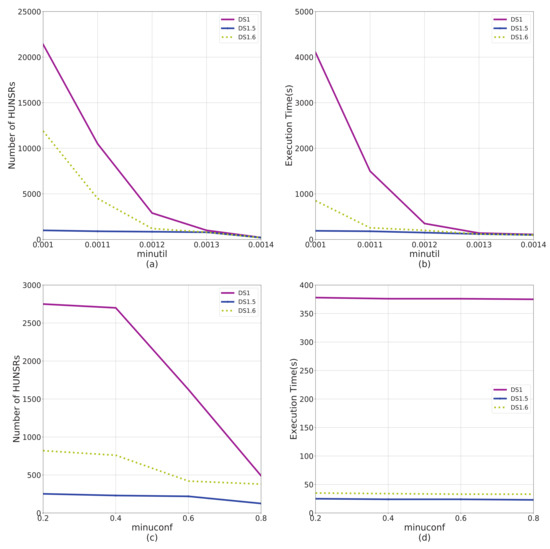
Figure 6.
Performance comparison on data factor S. Dataset DS1, DS1.5, and DS1.6 have different data factor on S. (a) The impact of S on number of HUNSRs from the perspective of . (b) The impact of S on execution time from the perspective of . (c) The impact of S on the number of HUNSRs from the perspective of . (d) The impact of S on execution time from the perspective of .
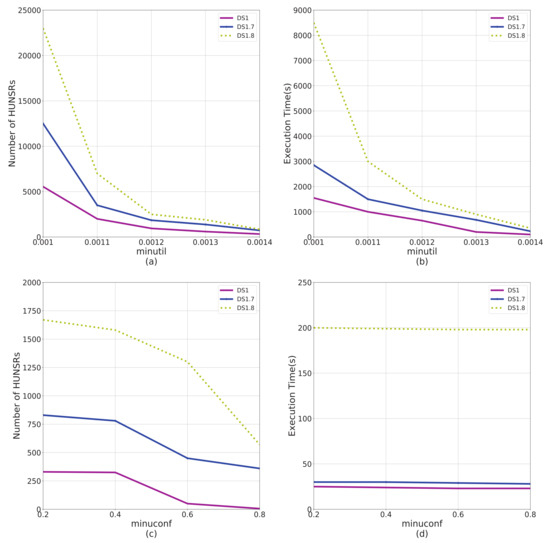
Figure 7.
Performance comparison on data factor I. Dataset DS1, DS1.7, and DS1.8 have different data factor on I. (a) The impact of I on number of HUNSRs from the perspective of . (b) The impact of I on execution time from the perspective of . (c) The impact of I on number of HUNSRs from the perspective of . (d) The impact of I on execution time from the perspective of .
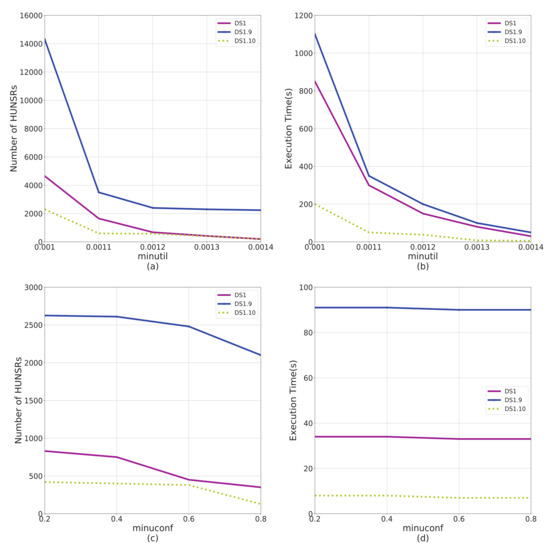
Figure 8.
Performance comparison on data factor N. Dataset DS1, DS1.9, and DS1.10 have different data factor on N. (a) The impact of N on number of HUNSRs from the perspective of . (b) The impact of N on execution time from the perspective of . (c) The impact of N on the number of HUNSRs from the perspective of . (d) The impact of N on execution time from the perspective of .
5.5. Scalability Test
Since the algorithm’s performance is affected by the dataset size, we conducted a scalability test to evaluate e-HUNSR’s performance on large q-sequence datasets. Figure 9 shows the results on datasets DS2 and DS3 based on different sizes: From 5 (i.e., 2.05 M) to 20 (41.1 M) times of DS2, and from 5 (3.78 M) to 20 (75.7 M) times of DS3.
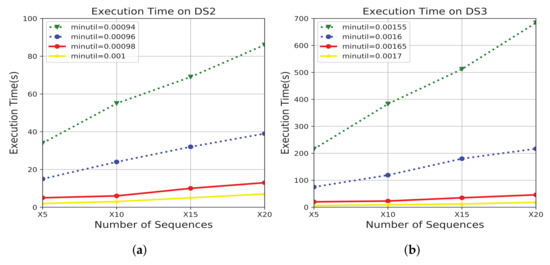
Figure 9.
Scalability test. This figure shows the impact of a number of sequences on execution time. Each curve in the figure represents a specified value. (a) The scalability test on DS2. (b) The scalability test on DS3.
The results in Figure 9 show that the growth of the runtime of e-HUNSR on large q-sequence datasets follows a roughly linear relationship with the datasets size increasing with different values. The results also show that e-HUNSR works particularly well on huge q-sequence datasets.
5.6. A Real-Life Application of the e-HUNSR Algorithm
In this section, we apply the e-HUNSR algorithm to prefabricated chunks extraction and prediction. Prefabricated chunks are composed of more than one word that occur frequently and are stored and used as a whole, such as “put off”, “by the way”, “it is important that”, etc. Prefabricated chunks has played an important role in language learning [31], including helping teachers establish some new teaching models [32], improving fluency and accuracy of an interpreter [33], increasing students’ listening predictive ability [34], etc.
The dataset used for this application is Leviathan, which is a conversion of the novel Leviathan by Thomas Hobbes (1651) as a sequence database (each word is an item) [30]. The dataset has 5834 sequences, 9025 items, and the average sequence length is 33.8. We randomly selected 100 sequences to conduct this experiment. In total, 171 rules were obtained with = 0.078 and = 0.4. Since converting items to words is time-consuming, we only show five rules to analyze the meaning of the rules. The five rules are shown in Table 7.

Table 7.
The extracted results.
Rule 1 indicates that if “controversies, the, cause, of, war ” occurs in order first (“ ¬and ” indicates that “and” does not occur), then we can predict with 90% certainty that “against, the, law” will occur next in order in the novel Leviathan. Rule 2 indicates that if “ sickness ” occurs in order first, we can predict with 70% certainty that “civil, war, death ” will occur next. Rule 3 indicates that if “cause, of, sense” occurs in order first, we can predict with 43% certainty that “ is, the, external, body” will occur next in order. Rule 4 indicates that if “several, motions, diversely” occurs in order first, we can predict with 82% certainty that “to, counterfeit, just, trust” will occur next. Rule 5 indicates that if “things, suggested” occurs in order first, we can predict with 80% certainty that “the, memory, and, equity, and, laws” will occur next in order.
In fact, there are sentences like “So, the controversies, that is, the cause of war, remains against the Law of nature", “Concord, health; sedition, sickness; and civil war, death" and so on in the original novel. This proves that our extracted rules are useful. The antecedents and consequents like “sickness" and “civil, war, death" are extracted prefabricated chunks. The value of uconf represents the possibility of the occurrence of the predictive prefabricated chunks. These prefabricated chunks can help people understand the novel better and quickly to a certain extent.
6. Conclusions and Future Work
HUSR mining can precisely tell the probability that some subsequences will happen after other subsequences happen, but it does not take non-occurring events into account, which can result in the loss of valuable information. So, this paper has proposed a comprehensive algorithm called e-HUNSR to mine high utility negative sequential rules. First, in order to overcome the difficulty of defining the HUNSR mining problem, we have defined a series of important concepts, including the local utility value, utility-confidence measure, and so on. Second, in order to overcome the difficulty of calculating the antecedent’s local utility value in a HUNSR, we proposed a novel data structure called a SLU-list to record all required information, including information of SID, TID, and utility of the intermediate subsequences during the generation of HUSP. Third, in order to efficiently calculate the local utility value and utility of the antecedent, we converted the HUNSR’s calculation problem to its corresponding HUSR’s calculation problem to simplify the calculation. In addition, we proposed an efficient method to generate HUNSRC based on the HUNSP mined by the HUNSPM algorithm and a pruning strategy to prune a large proportion of meaningless HUNSRCs. To the best of our knowledge, e-HUNSR is the first study to mine HUNSR. The experimental results on two real-life and 12 synthetic datasets show that e-HUNSR is very efficient.
From the experiments, we can see that the number of HUNSRs mined from HUNSP is very large and our recent research shows that not all of the HUNSRs can be used to make decisions. Our future work is to find strategies to select those actionable HUNSRs. In addition, many research studies are based on a quantitative database or fuzzy data and are very useful [35]. But with the development of economy and the progress of Internet technology, the amount of information generated in social media channels (e.g., Twitter, Linkedin, Instagram, etc.) or economical/business transactions exceeds the usual bounds of static databases and is in continuous movement [36]. Therefore, it is important to design a streaming rule extraction algorithm in a dynamitic databases.
Author Contributions
Conceptualization, X.D.; Investigation, T.X. and X.H.; Methodology, M.Z., T.X. and Z.L.; Software, M.Z.; Supervision, X.D.; Writing—original draft, M.Z.; Writing—review & editing, Z.L. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (61906104) and the Natural Science Foundation of the Shandong Province, China (ZR2018MF011 and ZR2019BF018).
Acknowledgments
The authors are very thankful to the editor and referees for their valuable comments and suggestions for improving the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HUNSR | High Utility Negative Sequential Rule |
| HUSR | High Utility Sequential Rule |
| HUSP | High Utility Sequential Pattern |
| HUNSP | High Utility Negative Sequential Pattern |
| HUAR | High Utility Association Rule |
| HUNSRC | High Utility Negative Sequential Rule Candidate |
| minimum utility threshold | |
| minimum utility-confidence threshold |
References
- 2nd International Workshop on Utility-Driven Mining and Learning [EB/OL]. Available online: http://www.philippe-fournier-viger.com/utility_mining_workshop_2019/ (accessed on 20 May 2020).
- Ahmed, C.F.; Tanbeer, S.K.; Jeong, B.S. A Novel Approach for Mining High-Utility Sequential Patterns in Sequence Databases. Etri J. 2010, 32, 676–686. [Google Scholar] [CrossRef]
- Yin, J.; Zheng, Z.; Cao, L. USpan: An efficient algorithm for mining high utility sequential patterns. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 660–668. [Google Scholar]
- Le, B.; Huynh, U.; Dinh, D.-T. A pure array structure and parallel strategy for high-utility sequential pattern mining. Expert Syst. Appl. 2018, 104, 107–120. [Google Scholar] [CrossRef]
- Yun, U.; Ryang, H.; Lee, G.; Fujita, H. An efficient algorithm for mining high utility patterns from incremental databases with one database scan. Knowl.-Based Syst. 2017, 124, 188–206. [Google Scholar] [CrossRef]
- Zihayat, M.; Chen, Y.; An, A. Memory-adaptive high utility sequential pattern mining over data streams. Mach. Learn. 2017, 106, 799–836. [Google Scholar] [CrossRef]
- Xu, T.; Xu, J.; Dong, X. Mining High Utility Sequential Patterns Using Multiple Minimum Utility. Int. J. Pattern Recogn. Artif. Intell. 2018, 32, 3–14. [Google Scholar] [CrossRef]
- Xu, T.; Dong, X.; Xu, J.; Dong, X. Mining High Utility Sequential Patterns with Negative Item Values. Int. J. Pattern Recogn. Artif. Intell. 2017, 31, 1750035. [Google Scholar] [CrossRef]
- Lin, C.W.; Li, Y.; Fournier-Viger, P. Efficient Chain Structure for High-Utility Sequential Pattern Mining. IEEE Access 2020, 8, 40714–40722. [Google Scholar] [CrossRef]
- Gan, W.; Lin, J.C.; Fournier-Viger, P. HUOPM: High-Utility Occupancy Pattern Mining. IEEE Trans. Cybern. 2020, 50, 1195–1208. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Vu, V.V.; Lam, M.T. An efficient method for mining high utility closed itemsets. Inf. Sci. 2019, 495, 78–79. [Google Scholar] [CrossRef]
- Singh, K.; Shakya, H.K.; Singh, A. Mining of high-utility itemsets with negative utility. Expert Syst. 2018, 35, e12296.1–e12296.23. [Google Scholar] [CrossRef]
- Krishnamoorthy, S. Efficiently mining high utility itemsets with negative unit profits. Knowl.-Based Syst. 2018, 145, 1–14. [Google Scholar] [CrossRef]
- Xu, T.; Li, T.; Dong, X. Efficient High Utility Negative Sequential Patterns Mining in Smart Campus. IEEE Access 2018, 6, 23839–23847. [Google Scholar] [CrossRef]
- Zida, S.; Fournier-Viger, P.; Wu, C.-W. Efficient Mining of High-Utility Sequential Rules. In International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Hamburg, Germany; Cham, Switzerland, 2015. [Google Scholar]
- Dong, X.; Hao, F.; Zhao, L. An efficient method for pruning redundant negative and positive association rules. Neurocomputing 2020, 393, 245–258. [Google Scholar] [CrossRef]
- Bux, N.K.; Lu, M.; Wang, J. Efficient Association Rules Hiding Using Genetic Algorithms. Symmetry 2018, 10, 576. [Google Scholar]
- Xu, J.Y.; Liu, T.; Yang, L.T. Finding College Student Social Networks by Mining the Records of Student ID Transactions. Symmetry 2019, 11, 307. [Google Scholar] [CrossRef]
- Sahoo, J.; Das, A.K.; Goswami, A. An efficient approach for mining association rules from high utility itemsets. Expert Syst. Appl. 2015, 42, 5754–5778. [Google Scholar] [CrossRef]
- Cao, L.; Dong, X.; Zheng, Z. e-NSP: Efficient negative sequential pattern mining. Artif. Intell. 2016, 235, 156–182. [Google Scholar] [CrossRef]
- Dong, X.; Qiu, P.; Lu, J.; Cao, L.; Xu, T. Mining Top-k Useful Negative Sequential Patterns via Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2764–2778. [Google Scholar] [CrossRef]
- Dong, X.; Gong, Y.; Cao, L. e-RNSP: An Efficient Method for Mining Repetition Negative Sequential Patterns. IEEE Trans. Cybern. 2018, 50, 2084–2096. [Google Scholar] [CrossRef]
- Dong, X.; Gong, Y.; Cao, L. F-NSP+: A fast negative sequential patterns mining method with self-adaptive data storage. Pattern Recogn. 2018, 84, 13–27. [Google Scholar] [CrossRef]
- Nguyen, L.T.T.; Mai, T.; Vo, B. High Utility Association Rule Mining. In Proceedings of the 17th International Conference (ICAISC 2018), Zakopane, Poland, 3–7 June 2018. [Google Scholar]
- Mai, T.; Vo, B.; Nguyen, L.T.T. A lattice-based approach for mining high utility association rules. Inf. Sci. 2017, 399, 81–97. [Google Scholar] [CrossRef]
- Lee, D.; Park, S.-H.; Moon, S. Utility-based association rule mining: A marketing solution for cross-selling. Expert Syst. Appl. 2013, 40, 2715–2725. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Mining sequential patterns. In Proceedings of the Eleventh International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1995; pp. 3–14. [Google Scholar]
- Yin, J. Mining High Utility Sequential Patterns; University of Technology Sydney: Sydney, Australia, 2015. [Google Scholar]
- Kdd Cup 2000: Online Retailer Website Clickstream Analysis [EB/OL]. Available online: http:www.sigkdd.org/kdd-cup-2000-online-retailer-websiteclickstream-analysis (accessed on 5 September 2019).
- SPMF: An Open-Source Data Mining Library [EB/OL]. Available online: http://www.philippe-fournier-viger.com/spmf/ (accessed on 15 October 2019).
- Hou, J.; Loerts, H.; Verspoor, M. Chunk use and development in advanced Chinese L2 learners of English. Lang. Teach. Res. 2018, 22, 148–168. [Google Scholar] [CrossRef]
- Wen, S. Research on the Teaching of Spoken English Based on the Theory of Prefabricated Chunks. J. Mudanjiang Coll. Educ. 2011, 2, 131–132. [Google Scholar]
- Meng, Q. Promoting Interpreter Competence through Input Enhancement of Prefabricated Lexical Chunks. J. Lang. Teach. Res. 2017, 8, 115–121. [Google Scholar] [CrossRef]
- Guan, L. Prefabricated Chunks and Second Language Listening Comprehension. J. Dalian Natl. Univ. 2014, 16, 194–196. [Google Scholar]
- Fernandezbasso, C.; Franciscoagra, A.J.; Martinbautista, M.J. Finding tendencies in streaming data using Big Data frequent itemset mining. Knowl.-Based syst. 2019, 163, 666–674. [Google Scholar] [CrossRef]
- Yen, S.J.; Lee, Y.S. Mining high utility quantitative association rules. In Proceedings of the International Conference on Data Warehousing and Knowledge Discovery, Regensburg, Germany, 3–7 September 2007; pp. 283–292. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).