On Path Homology of Vertex Colored (Di)Graphs

Abstract

In this paper, we construct the colored-path homology theory in the category of vertex colored (di)graphs and describe its basic properties. Our construction is based on the path homology theory of digraphs that was introduced in the papers of Grigoryan, Muranov, and Shing-Tung Yau and stems from the notion of the path complex. Any graph naturally gives rise to a path complex in which for a given set of vertices, paths go along the edges of the graph. We define path complexes of vertex colored (di)graphs using the natural restrictions that are given by coloring. Thus, we obtain a new collection of colored-path homology theories. We introduce the notion of colored homotopy and prove functoriality as well as homotopy invariance of homology groups. For any colored digraph, we construct the spectral sequence of colored-path homology groups which gives the effective method of computations in the general case since any (di)graph can be equipped with various colorings. We provide a lot of examples to illustrate our results as well as methods of computations. We introduce the notion of homotopy and prove functoriality and homotopy invariance of introduced vertexed colored-path homology groups. For any colored digraph, we construct the spectral sequence of path homology groups which gives the effective method of computations in the constructed theory. We provide a lot of examples to illustrate obtained results as well as methods of computations.

1. Introduction

In this paper, we apply the methods of the path homology theory of digraphs and quivers first defined in [1,2,3,4,5,6] to the category and homotopy category of vertex colored digraphs and graphs (see [7,8,9,10,11]).

We construct the collection of path homology theories for vertex colored digraphs. Then we describe the possibility of implementing this theory to the case of edge colored digraphs and non-directed graphs. We will consider vertex colored (di)graphs which from now on will be simply called colored (di)graphs unless otherwise clearly stated.

The consideration of digraphs in this theory stems from the following reasons. The path homology theory is a natural generalization of simplicial homology theory and is defined for any path complex. Any digraph naturally gives rise to a path complex in which allowed paths go along directed edges. The path homology theory for digraphs provides the path homology theory for (non-directed) graphs by applying the functorial transformation from a given graph to the corresponding symmetric digraph [2].

In the classical algebraic topology, in most cases, the homology groups have a natural filtration that is given by the n-skeleton of $CW$ or a simplicial complex. In the general case, the path homology groups do not have any structure that is similar to the n-skeleton. It follows directly from the results below that a vertex coloring of a digraph gives a functorial filtration that agrees with path homology groups. If we color a digraph in some way, then by the means of the spectral sequence constructed below, we obtain an effective method of computing the path homology groups of such a (di)graph.

Note also that the line digraph of an edge colored digraph gives the vertex colored digraph and that means in turn that the vertex colored homology theory might be applied to the edge colored digraphs and non-directed graphs. Let us mention here that the application of the colored homology theory to the case of quivers requires significant modifications. This fact follows from the generalization of the path homology theory to the category of quivers constructed in [4].

In our paper, we use the notions of the category and the functor (see, for example, ([10,12], Chapter 1) and ([13], Chapter 1)). A category $\mathcal{C}$ consists of a class of objects and for each ordered pair of objects $(A,B)$ a collection of morphisms$Hom(A,B)$. Any such morphism $f\in Hom(A,B)$ will be denoted by $f:A\to B$. For every pair of morphisms $f\in Hom(A,B)$, $g\in Hom(B,C)$, we define a composition $gf=g\circ f\in Hom(A,C)$. The morphisms satisfy the following axioms.

(i)

If $f\in Hom(A,B)$, $g\in Hom(B,C)$ and $h\in Hom(C,D)$, then $h\left(gf\right)=\left(hg\right)f\in Hom(A,D)$.

(ii)

For every object B there is a morphism ${Id}_B:B\to B$, such that if $f\in Hom(A,B)$, then ${Id}_{B}f=f$ and if $h\in Hom(B,C)$, then $h{Id}_B=h$.

Let $\mathcal{C}$ and $\mathcal{D}$ be two categories. A functor $\mathcal{F}$ from $\mathcal{C}$ to $\mathcal{D}$ assigns to any object of $\mathcal{C}$ an object $\mathcal{F}\left(\mathcal{C}\right)$ and to any morphism $f\in Hom(A,B)$ of $\mathcal{C}$ a morphism $\mathcal{F}\left(f\right)\in Hom\left(\mathcal{F}\right(A),\mathcal{F}(B\left)\right)$ in such a way that

(i)

$\mathcal{F}\left({Id}_B\right)={Id}_{\mathcal{F}\left(B\right)}$,

(ii)

$\mathcal{F}\left(gf\right)=\mathcal{F}\left(g\right)\mathcal{F}\left(f\right)$ for $f\in Hom(A,B)$, $g\in Hom(B,C)$.

It is necessary to remark that the notion of homotopy in the graph theory differs from a similar notion in the continuous topology (see Definition 4 and Example 1 below). Two digraph mappings $f,g:G\to H$ are homotopic if we can construct a sequence of digraph mappings $f=f_0,f_1,\dots ,f_n=g$ from G to H, so that any pair of sequential mappings $(f_i,f_{i+1})$ satisfies one of the following properties (see ([2], §3.1)):

(i)

$f_i\left(v\right)=f_{i+1}\left(v\right)$ or $f_i\left(v\right)\to f_{i+1}\left(v\right)$ in the digraph H for arbitrary vertex v of the digraph G,

(ii)

$f_i\left(v\right)=f_{i+1}\left(v\right)$ or $f_{i+1}\left(v\right)\to f_i\left(v\right)$ in the digraph H for arbitrary vertex v of the digraph G.

Let us point out here the main new results provided in our paper. First, we introduce the category of colored digraphs and define a notion of the colored homotopy between colored morphisms. Then we describe the basic properties of the colored homotopy and colored morphisms and construct a collection of functorial path homology theories for colored digraphs. We prove the invariance of the colored-path homology groups relative to the colored homotopy. For any colored digraph we construct the spectral sequence of colored-path homology groups which gives the effective method of computations of path homology groups of arbitrary digraphs since any (di)graph can be equipped with various colorings. We also describe the transfer of the colored-path homology theory to the category of graphs and edge colored (di)graphs.

The paper is organized as follows. In Section 2, for the sake of convenience, we recall the basic definitions from the graph theory and the path homology theory for digraphs.

In Section 3, we bring the notion of colored digraphs to your attention and introduce the notion of homotopy for colored digraphs.

In Section 4, we define several path homology theories for the categories that were introduced in the previous Section. Next, we provide examples to illustrate the difference between the path homology theory of digraphs in colored and uncolored case.

In Section 5, we construct a spectral sequence for path homology groups of a colored digraph, and describe its basic properties. We also obtain a braid of exact sequences of path homology groups for 3-colored digraphs. We give detailed computations of path homology groups in such a braid of exact sequences for a digraph G that is the one-dimensional skeleton of the minimal triangulation of the closed Möbius band.

In Section 6, we describe applications of the obtained results to the case of non-directed graphs. We also explain the possibility of applying homology of vertex colored digraph to the edge colored digraphs and edge colored graphs using the line digraphs.

Finally, in Section 7, we give conclusions and make some remarks about our results, whereas is acknowledgement section.

2. The Path Homology Theory for Digraphs

In this Section, we give preliminary material about the path homology theory for a digraph following [1,2,3,4,5,6].

Definition 1.

A digraph G is a pair $\left(V_G,E_G\right)$ of a set $V=V_G$ of vertices and a subset $E_G\subset \{V_G\times V_G\setminus diagonal\}$ of ordered pairs $(v,w)$ of vertices which are called arrows. A pair $(v,w)\in E_G$ is denoted $v\to w$. For such a pair the vertex v is called an origin of the arrow and is denoted $orig(v\to w)$ while the vertex w is called an end of the arrow and is denoted $end(v\to w)$.

Definition 2.

A digraph mapping $f:G\to H$ (or simply a mapping) from a digraph G to a digraph H is a mapping ${f|}_{V_G}:V_G\to V_H$ such that for any arrow $(v\to w)\in E_G$, we have $(f\left(v\right)\to f\left(w\right))\in E_H$ or $f\left(v\right)=f\left(w\right)\in V_H$. We call the mapping f non-degenerate if $(f\left(v\right)\to f\left(w\right))\in E_H$ for any $(v\to w)\in E_G$. For a digraph G we denote by ${Id}_G:G\to G$ the identity mapping that is the identity mapping on the set of vertices and the set of edges.

It is clear that digraphs with the digraph mappings form a category which throughout this paper will be denoted by $\mathcal{D}$. Please note that digraphs together with non-degenerated mappings form a subcategory $\mathcal{N}$ of the category $\mathcal{D}$.

Definition 3.

For two digraphs $G=(V_G,E_G)$ and $H=(V_H,E_H)$ their Box product $\Pi =G\square H=(V_{\Pi },E_{\Pi })$ is a digraph with a set of vertices $V_{\Pi }=V_G\times V_H$ and a set of arrows $E_{\Pi }$ given in the following way. For two vertices $x,x^{\prime }\in V_G$, and two vertices $y,y^{\prime }\in V_H$ there is an arrow $(x,y)\to (x^{\prime },y^{\prime })\in E_{\Pi }$ if and only if

$$\mathrm{either}{x}^{\prime }=x\mathrm{and}y\to y^{\prime },\mathrm{or}x\to x^{\prime }\mathrm{and}y=y^{\prime }.$$

In Example 1 below we give a graph interpretation of the Box product.

Fix $n\ge 0$. Denote by $I_n=(V_{I^n},E_{I^n})$ a digraph for which $V_{I^n}=\{0,1,\dots ,n\}$ and, for $i=0,1,\dots n-1$, there is exactly one arrow $i\to i+1$ or $i+1\to i$ without any other available arrows. We will refer from now on to $I_n$ as a segment digraph. Let us note here that the notion of a segment digraph coincides with the notion of a line digraph introduced in papers [1,2,3,4,5,6]. We are forced to use different terminology because the standard notion of a line digraph already exists in the graph theory and will also be used later in this paper.

Definition 4.

Two digraph mappings $f_0,f_1:G\to H$ are called homotopic if there exists a segment digraph $I_n\in \mathcal{I}(n\ge 0)$ and a digraph mapping $F:G\square I_n\to H$ called a homotopy between $f_0$ and $f_1$, such that

$${F|}_{G\square \left\{0\right\}}=f_0{:G\square \left\{0\right\}\to H,F|}_{G\square \left\{n\right\}}=f_1:G\square \left\{n\right\}\to H.$$

In such a case we write $f_0\simeq f_1$.

Example 1.

Now we give several digraphs to illustrate definitions introduced above.

(i) 

For the digraph $G=(V_G,E_G)$ presented on the diagram below

$$\begin{array}{ccccc}a& ⟶& b& ⟵& c\\ \downarrow & & \uparrow \downarrow & \nearrow \\ d& ⟵& e& \end{array}$$

(1)

we have $V_G=\{a,b,c,d,e\}$, whereas $E_G=\{a\to b,a\to d,e\to d,e\to b,b\to e,e\to c,c\to b\}$.

(ii) 

Let G be a digraph given in (1) and $H=(V_H,E_H)$ be a digraph provided below

$$\begin{array}{ccccc}& & 3& ⟵& 4\\ & & \uparrow \downarrow & \nearrow \\ 1& ⟵& 2& \end{array}$$

(2)

Let $f:V_G\to V_H$ be the mapping given by $f\left(a\right)=2,f\left(d\right)=1,f\left(b\right)=3,f\left(e\right)=2,f\left(c\right)=3$. Then the mapping f is the digraph mapping but it is not a non-degenerate digraph mapping since $f(c\to b)$ is not an arrow. Let $g:V_G\to V_H$ be the mapping given by $f\left(a\right)=2,f\left(d\right)=1,f\left(b\right)=3,f\left(e\right)=2,f\left(c\right)=4$. Then the mapping g is the non-degenerate digraph mapping.

(iii) 

The explanation of the Box product is given in the diagram below:

$$\begin{array}{ccccc}{y}^{\prime }\bullet & & \stackrel{\left(x,y^{\prime }\right)}{\bullet }& ⟶& \stackrel{\left(x^{\prime },y^{\prime }\right)}{\bullet }\\ \uparrow & & \uparrow & & \uparrow \\ y\bullet & & \stackrel{\left(x,y\right)}{\bullet }& ⟶& \stackrel{\left(x^{\prime },y\right)}{\bullet }\\ & & \\ H∕G& & \underset{x}{\bullet }& ⟶& \underset{x^{\prime }}{\bullet }\end{array}$$

where $G=(x\to x^{\prime })$ and $H=(y\to y^{\prime })$.

(iv) 

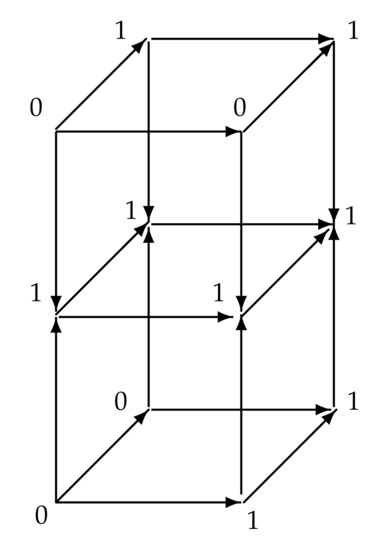
Let $G=(V_G,V_H)$ be the digraph presented on the diagram

$$\begin{array}{ccc}c& ⟶& d\\ \uparrow & & \uparrow \\ a& ⟶& b\end{array}$$

(3)

and $H=I_1$ be the line digraph $0\to 1$. Let $f:G\to H$ be the mapping given on the set of vertices $f\left(a\right)=f\left(c\right)=0,f\left(d\right)=f\left(b\right)=1$ and $g:G\to H$ be the mapping given on the set of vertices $g\left(a\right)=g\left(b\right)=0,g\left(c\right)=g\left(d\right)=1$. Let I be the segment digraph $0\to 1\leftarrow 2$. Now we define the homotopy $F:G\square I\to H$ between f and g as follows:

$$\begin{array}{c}F(a,0)=F(c,0)=0,F(b,0)=F(d,0)=1,\\ F(a,1)=F(c,1)=F(b,1)=F(d,1)=1,\\ F(a,2)=F(b,2)=0,F(c,2)=F(d,2)=1,\end{array}$$

In the Figure 1 given below we point out the images of the vertices of the digraph $G\square I$ under the homotopy mapping F.

Figure 1. Homotopy $G\square I$ in Example 1.

The relation ≃ is an equivalence relation on the set of digraph mappings from G to H. Two digraphs G and H are homotopy equivalent if there exist digraph mappings $f:G\to H$ and $g:H\to G$ such that $f\circ g\simeq {Id}_H$ and $g\circ f\simeq {Id}_G$, where ${Id}_H$ and ${Id}_G$ are the identity mappings of H and G respectively. In this case, we write $H\simeq G$ and call the mappings f and g homotopy inverses to each other.

Thus, the category ${\mathcal{D}}^{\prime }$ with the same objects as in $\mathcal{D}$ and with the morphisms given by classes of homotopy equivalent digraphs mappings is defined.

A homotopy F is non-degenerate if it is non-degenerate as a digraph mapping. We define a category ${\mathcal{N}}^{\prime }$ with the same objects as in $\mathcal{N}$ and with the morphisms that are given by classes of homotopies by means of the non-degenerate homotopy of non-degenerate mappings.

Now we define the path homology groups of a digraph $G=(V,E)$. For $p\ge 0$, we define an elementary p-path on a set V as a sequence $i_0,\dots i_p$ of $p+1$ of vertices (not necessarily different) and denote this path $e_{i_0\dots i_p}$. Let R be a commutative ring with a unity $1\in R$ and let ${\mathsf{\Lambda }}_p={\mathsf{\Lambda }}_p(V,R)$ be a free R-module generated by all elementary p-paths $e_{i_0\dots i_p}$. The elements of ${\mathsf{\Lambda }}_p$ are called p-paths. Set ${\mathsf{\Lambda }}_{-1}=0$ and for $p\ge 1$, define the boundary operator $\partial :{\mathsf{\Lambda }}_{p+1}\to {\mathsf{\Lambda }}_p$ on basic elements by

$$\partial e_{i_0\dots i_{p+1}}=\sum _{q=0}^{p+1}{\left(-1\right)}^q{e}_{i_0\dots \widehat{i_q}\dots i_{p+1}},$$

(4)

where $\widehat{i_q}$ means omitting the corresponding index. We assume that $\partial :{\mathsf{\Lambda }}_0\to {\mathsf{\Lambda }}_{-1}=0$ is trivial. It is easy to check that for any elementary p-path v, we have ${\partial }^{2}v=0$, hence the homomorphism ${\partial }^2:{\mathsf{\Lambda }}_n\to {\mathsf{\Lambda }}_{n-2}$ is trivial for $n\ge 1$. Let $p\ge 1$. An elementary p-path $e_{i_0\dots i_p}$ is called regular if $i_k\ne i_{k+1}$ for $0\le k\le p-1$. Any 0-path is regular. For $p\ge 0$, we denote by $I_p$ a submodule of ${\mathsf{\Lambda }}_p$ that is generated by all irregular elementary paths. In particular, $I_0=0$ and we set $I_{-1}=0$. It is easy to check that $\partial \left(I_{p+1}\right)\subset I_p$ for $p\ge -1$. Thus, we obtain a chain complex

$$0\leftarrow {\mathcal{R}}_1\leftarrow {\mathcal{R}}_2\leftarrow R_3\leftarrow \dots$$

where ${\mathcal{R}}_p={\mathcal{R}}_p(V,R)={\mathsf{\Lambda }}_p/I_p$ and the differential is induced by ∂.

We note here that thus obtained path complex is defined for arbitrary discrete set V but basic elements $e_{i_0\dots i_p}\in {\mathcal{R}}_p$ $(i_k\in V)$ depend on the order of the vertices $i_1,\dots ,i_p$ in the recording $e_{i_0\dots i_p}$. For example, for $V=\{i,j,k\}$ the elements $e_{ijk}$ and $e_{jik}$ are different. The differential ∂ is well defined for basic elements and, for example $\partial \left(e_{ijk}\right)=e_{jk}-e_{ik}+e_{ij}$.

Now we consider a digraph $G=(V,E)$. Let $e_{i_0\dots i_p}$ be a regular elementary p-path on the set of vertices V. For $p\ge 1$, it is called allowed if $(i_{k-1}\to i_k)\in E$ for any $k=1,\dots ,p$, and non-allowed otherwise. For $p=0$ any elementary path is regular. For $p\ge 0$, denote by ${\mathcal{A}}_p={\mathcal{A}}_p(G,R)$ a submodule of ${\mathcal{R}}_p(V,R)$ that is generated by the allowed elementary p-paths and set ${\mathcal{A}}_{-1}=0$. The elements of the modules ${\mathcal{A}}_p$ are called allowed p-paths.

Now we define the path homologies of a digraph $G=(V,E)$. Consider the following submodule of ${\mathcal{A}}_p$, namely

$${\Omega }_p={\Omega }_p(G,R)=\left\{v\in {\mathcal{A}}_p:\partial v\in {\mathcal{A}}_{p-1}\right\}.$$

(5)

The elements of ${\Omega }_p$ are called ∂-invariant p-paths. Examine now the chain complex

$$\begin{array}{cccccccccccc}0& \leftarrow & {\Omega }_0& \stackrel{\partial }{\leftarrow }& {\Omega }_1& \stackrel{\partial }{\leftarrow }& \dots & \stackrel{\partial }{\leftarrow }& {\Omega }_{p-1}& \stackrel{\partial }{\leftarrow }& {\Omega }_p& \stackrel{\partial }{\leftarrow }\dots \end{array}$$

(6)

Its homologies are called path homologies of the digraph G with the coefficients in the ring R and are denoted by

$$H_p\left(G,R\right):={ker\partial |}_{{\Omega }_p}/{Im\partial |}_{{\Omega }_{p+1}}.$$

Every elementary allowed path $e_{i_0\dots i_p}\in {\Omega }_p\left(G\right)$ of the chain complex (6) has a naturally ordered structure on the set of vertices $i_1,\dots ,i_p$ that is defined by arrows of the digraph. By definition, each pair $i_k,i_{k+1}\in V_G$ of neighboring vertices in $e_{i_0\dots i_p}$ must give an arrow $(i_k\to i_{k+1})\in E_G$. The differential ∂ in the chain complex ${\Omega }_{*}$ is well defined and preserves this ordering.

The path homology groups give a collection of (di)graphs invariants and provide deep connections of the graph theory to discrete geometry, algebraic topology, and mathematical physics (see, for example [1,6,14,15,16,17]). For the sake of convenience, we formulate the basic result of the categorical properties of path homology groups which will be used throughout this paper.

Theorem 1

([1]). The homology groups defined above are homotopy invariant and functorial for digraph mappings.

3. Categories of Colored Digraphs

In the first part of this section we recall the basic definitions concerning digraph coloring (see [7,8,9,10,11]). Then we describe several categories of colored digraphs that fit the path homology theory defined in Section 2.

Definition 5.

A coloring of a digraph $G=(V_G,E_G)$ is given by an assignment of a color to each vertex $v\in V_G$. A coloring that uses k colors is called k-coloring.

Recall that two vertices $v,w\in V_G$ are called neighbors if there exists at least one arrow $v\to w$ or $w\to v$ in G. The open neighborhood of a vertex $v\in V_G$ is a subgraph $N\left(v\right)=(V_N,E_N)$ of G, for which $V_N$ consists of all vertices which are neighbors of v while $E_N$ is constituted by the edges connecting vertices from $V_N$. A coloring of a digraph G is called proper if any vertex of the neighborhood $N\left(v\right)$ is colored differently from the vertex v for all $v\in V_G$. A coloring of a digraph G is called k-improper if the open neighborhood of any vertex v contains at most k-vertices with the same color as v. As usual, we can consider a coloring as a function $\phi :V_G\to \mathbb{N}$. In the case of k-coloring, we assume that $\phi :V_G\to \{1,2,\dots ,k\}$. We shall write $(G,\phi )$ for a digraph G with a coloring function $\phi$.

Definition 6.

Let $(G,\phi )$ and $(H,\psi )$ be two colored digraphs. A digraph mapping $f:G\to H$ is a morphism of colored digraphs if $\psi \left(f\right(v\left)\right)=\phi \left(v\right)$ for any vertex $v\in V_G$.

It is clear that colored digraphs with the morphisms defined above form a category which from now on will be denoted by $\mathcal{C}$. This category has the naturally defined subcategory ${\mathcal{C}}_0$, objects of which are given by proper colored digraphs and morphisms are given by non-degenerate mappings that satisfy Definition 6. Moreover, if we let ${\mathcal{C}}_k(k\ge 1)$ be the subcategory of $\mathcal{C}$ with the objects that are given by k-improper colored digraphs and with morphisms that are given by digraph mappings that satisfy Definition 6, then we obtain a filtration

$${\mathcal{C}}_0\subset {\mathcal{C}}_1\subset \cdots \subset \mathcal{C}$$

(7)

of the category C. In what follows, we will consider a proper coloring as the k-improper coloring with $k=0$.

For a colored digraph $(G,\phi )$, we can consider only the digraph G that now is recognized as one without any coloring. Any morphism of colored digraphs $f:(G,\phi )\to (H,\psi )$ is, in particular, a digraph mapping $f:G\to H$. Thus, we obtain a forgetful functor from the category of colored digraphs to the category of digraphs.

For any colored digraph $(G,\phi )$ and a segment digraph $I_n$, we define a coloring $\Phi$ on the digraph $G\square I_n$ by

$$\Phi (v,i)=\phi \left(v\right),v\in V_G,i\in V_{I_n}.$$

(8)

For a k-improper colored digraph $(G,\phi )$, the coloring $\Phi$ gives a $(k+1)$-improper coloring of the digraph $G\square I_n$. We shall say that two morphisms $f_0,f_1:(G,\phi )\to (H,\psi )$ of colored digraphs are colored homotopic if there exists a homotopy $F:G\square I_n\to H$ in Definition 4 such that

$$\psi \left(F\right(v,i\left)\right)=\Phi (v,i)=\phi \left(v\right).$$

(9)

We will denote this relation exactly as before, namely ≃, since the category under investigation will be clear from the given context.

Proposition 1.

The relation “to be colored homotopic” is an equivalence relation on the set of colored morphisms $f:(G,\phi )\to (H,\psi )$ and provides a relation ≃ of colored homotopy equivalence of colored digraphs.

Proof. 

Consider the set of colored morphisms $f:(G,\phi )\to (H,\psi )$. Since $I_0$ is the one-vertex digraph we obtain $G\square I_0=G$ and the colored morphism $F=f:G\square I_0=G\to H$ gives $f\simeq f$. The proof of the remaining properties follows from corresponding results for digraph mappings.

Thus, we obtain the colored homotopy category ${\mathcal{C}}^{\prime }$ in which the objects are colored digraphs and morphisms are classes of colored homotopic morphisms.

Proposition 2. 

(i) Any morphism $f:(G,\phi )\to (H,\psi )$ of proper colored digraphs is non-degenerate. (ii) Two morphisms $f_0,f_1:(G,\phi )\to (H,\psi )$ of proper colored digraphs are colored homotopic if and only if $f_0=f_1$.

Proof. 

The statement (i) is known and results directly from Definitions 2 and 6. To prove (ii), we must check only that the colored homotopic mappings $f_0\simeq f_1$ coincide. Consider the case $I_n=I_1=(0\to 1)$ and let $F:(G\square I_1,\Phi )\to (H,\psi )$ be a colored homotopy. For any vertex $v\in V_G$, due to the definition we have an arrow $[(v,0)\to (v,1)]\in E_{G\square I_1}$ and $\Phi (v,0)=\Phi (v,1)$. If $F(v,0)\ne F(v,1)$, then we are provided with an arrow $F(v,0)\to F(v,1)$ in $E_H$. This is impossible in a proper colored digraph H since, by (9), $\psi (\Phi (v,0\left)\right)=\phi \left(v\right)=\psi (\Phi (v,1\left)\right)$. Thus, $f_0\left(v\right)=F(v,0)=F(v,1)=f_1\left(v\right)$ for any vertex $v\in G$. Performing induction by n and using the same line of arguments finishes the proof. □

Now we give several examples that explain that the introduced notions are non-degenerate.

Example 2. 

(i) 

Let G be the 1-improper colored digraph presented on (10).

$$\begin{array}{ccccc}\begin{array}{c}\hfill a\end{array}& & \to & & \begin{array}{c}\hfill b\end{array}\\ & \searrow & & \nearrow \\ & & \begin{array}{c}\hfill c\end{array}& \end{array}$$

(10)

Let $f_0:G\to G$ be the identity mapping and $f_1:G\to G$ be the mapping defined on the set of vertices in the following way $f\left(a\right)=a,f\left(b\right)=f\left(c\right)=b$. Observe that thus defined, $f_0$ and $f_1$ are colored morphisms. Define the colored homotopy $F:G\square I_1\to G$ on the set of vertices by

$$f(a,0)=f(a,1)=a,f(c,0)=c,f(b,0)=b,f(c,1)=f(b,1)=b.$$

Then it follows that $f_0$ is colored homotopic to $f_1$.

(ii) 

Let G be the proper colored digraph presented on (11):

$$\begin{array}{ccc}a& \to & d\\ \uparrow & & \uparrow \\ a& \to & c\end{array}$$

(11)

By Proposition 2, any two different colored morphisms $f_0,f_1:G\to G$ are not colored homotopic. By ([2], Ex. 3.12) digraph G is contractible and, hence, any two digraph mappings to G are homotopic. It is a relatively easy exercise to construct directly a homotopy between the identity mapping $f_0$ and the mapping $f_1$ that is given on the set of vertices by

$$f_1\left(a\right)=a,f_1\left(b\right)=f_1\left(c\right)=c,f_1\left(d\right)=d.$$

(iii) 

Using the same line of arguments as in the case (ii) and the results from [2] (Section 3) it is possible to construct a lot of similar examples.

4. Path Homology of Colored Digraphs

Now we turn our attention to defining several path homology theories for colored digraphs and describe relations between them. We will provide examples that illustrate the difference between the path homology theory of digraphs in cases of colored and uncolored ones.

Let $G=(V,E)$ be a colored digraph with a given coloring $\phi :V\to \mathbb{N}$. Fix a natural number $k\ge 1$.

Definition 7.

An elementary path $e_{i_0\dots i_p}(p\ge 0)$ on the set V of vertices is calledk-colored if vertices of this path are colored with k-colors.

Example 3.

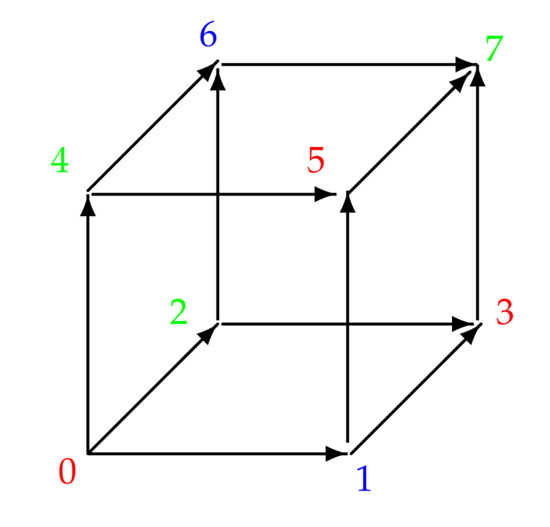
Consider the colored digraph in Figure 2. The path $e_{013}$ is 2-colored while the path $e_{046}$ is 3-colored. Please note that any regular elementary p-paths are k-colored where $k\le p+1$.

Figure 2. The proper colored digraph cube.

For $p\ge 0$, let ${\mathcal{A}}_p^k={\mathcal{A}}_p^k(G,R)={\mathcal{A}}_p^k(G,\phi )$ be a free R-module generated by all allowed regular elementary p-paths, which are colored by s colors, $1\le s\le k$. Let ${\mathcal{A}}_{-1}^k=0$. We have the following natural inclusions of the modules

$${\mathcal{A}}_p^k={\mathcal{A}}_p^k(G,R)\subset {\mathcal{A}}_p(G,R)\subset {\mathcal{R}}_p(V,R).$$

(12)

Now we define k-colored-path homologies of the colored digraph $(G,\phi )$. Let

$${\Omega }_p^k={\Omega }_p^k(G,R)=\left\{v\in {\mathcal{A}}_p^k:\partial v\in {\mathcal{A}}_{p-1}^k\right\}.$$

(13)

be a submodule of ${\mathcal{A}}_p^k$. The elements of ${\Omega }_p^k$ are called ∂-invariant k-colored paths. Similarly, to the case of path homology, we obtain that $\partial \left({\Omega }_p^k\right)\subset {\Omega }_{p-1}^k$. As a result, we have the following chain complex

$$\begin{array}{cccccccccccc}0& \leftarrow & {\Omega }_0^k& \stackrel{\partial }{\leftarrow }& {\Omega }_1^k& \stackrel{\partial }{\leftarrow }& \dots & \stackrel{\partial }{\leftarrow }& {\Omega }_{p-1}^k& \stackrel{\partial }{\leftarrow }& {\Omega }_p^k& \stackrel{\partial }{\leftarrow }\dots \end{array}$$

(14)

with the differential that is induced from the differential in ${\mathcal{R}}_{*}$. Homology groups of the chain complex (14) are called k-colored path homology groups of a digraph $(G,\phi )$ and are denoted by $H_p^k\left(G,R\right)$.

Proposition 3.

For any colored digraph $(G,\phi )$, we have a filtration

$${\Omega }_{*}^1(G,R)\subset {\Omega }_{*}^2(G,R)\subset \cdots \subset {\Omega }_{*}(G,R).$$

(15)

Moreover, for a k-colored digraph $(G,\phi )$ this filtration is finite and ${\Omega }_{*}^k(G,R)={\Omega }_{*}(G,R)$.

Proof. 

We have natural inclusions ${\mathcal{A}}_p^k(G,R)\to {\mathcal{A}}_p^{k+1}(G,R)\to {\mathcal{A}}_p(G,R)$ and the result arises from (13). □

Example 4.

Consider the proper colored digraph cube in Figure 2 with the set of vertices $V_G=\{0,1,2,3,4,5,6,7\}$. To simplify computations, we assume that $R=\mathbb{R}$. It arises from [2] that $H_0\left(G\right)=R$ and $H_n\left(G\right)=0$ for $n\ge 1$.

The module ${\Omega }_0^1\left(G\right)$ is generated by elements $e_n$, where $n\in V_G$ and, hence $rang{\Omega }_0^1\left(G\right)=8$. The modules ${\Omega }_k^1\left(G\right)$ are trivial since G is proper colored. It follows that

$$H_n^1\left(G\right)=\left\{\begin{array}{cc}{R}^8\hfill & \mathit{for}n=0,\hfill \\ 0\hfill & \mathit{for}n\ge 1.\hfill \end{array}\right.$$

The module ${\Omega }_0^2\left(G\right)$ is isomorphic to ${\Omega }_0^1\left(G\right)$ and the module ${\Omega }_1^2\left(G\right)$ is generated by all arrows. The module ${\Omega }_2^2\left(G\right)$ is generated by the elements

$$\{e_{013}-e_{023},e_{015}-e_{045},e_{237}-e_{267},e_{457}-e_{467}\}.$$

The module ${\mathcal{A}}_3^2\left(G\right)$ is generated by the elements $\{e_{0237},e_{0457}\}$ and ${\Omega }_3^2\left(G\right)=0$, since $\partial e_{0237}\notin {\mathcal{A}}_2^2,\partial e_{0457}\notin {\mathcal{A}}_2^2$. The modules ${\Omega }_n^2\left(G\right)$ are trivial for $n\ge 3$ because there are no paths of the length greater than 3 in G. For more clarity, let us write all the considerations above in the more approachable form, namely

$$rang\left({\Omega }_n^2\left(G\right)\right)=\left\{\begin{array}{cc}8\hfill & \mathit{for}n=0,\hfill \\ 12\hfill & \mathit{for}n=1,\hfill \\ 4\hfill & \mathit{for}n=2,\hfill \\ 0\hfill & \mathit{for}n\ge 3.\hfill \end{array}\right.$$

Calculating directly, we provide the following result

$$H_n^2\left(G\right)=\left\{\begin{array}{cc}R\hfill & \mathit{for}n=0,\hfill \\ R\hfill & \mathit{for}n=1,\hfill \\ 0\hfill & \mathit{for}n\ge 2.\hfill \end{array}\right.$$

Recall that by ([2], 2.5, and Th. 2.10), any digraph mapping $f:G\to H$ defines a morphism of chain complexes

$$f_{*}:{\Omega }_{*}\left(G\right)\to {\Omega }_{*}\left(H\right)$$

(16)

which on the basic elements of the module ${\mathcal{A}}_p(G,R)$ is given by

$$f_{*}\left(e_{i_0\dots i_p}\right)=\left\{\begin{array}{cc}{e}_{f\left(i_0\right)\dots f\left(i_p\right)},\hfill & \mathrm{if}{e}_{f\left(i_0\right)\dots f\left(i_p\right)}\mathrm{is}\mathrm{regular},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(17)

Theorem 2.

Let $f:(G,\phi )\to (H,\psi )$ be a morphism of colored digraphs. For $k\ge 1$, the morphism $f_{*}$ in (16) provides a morphism of chain complexes

$${\Omega }_{*}^k(G,R)\to {\Omega }_{*}^k(H,R)$$

(18)

and, hence, an induced homomorphism of k-colored homology groups

$$f_{*}:H_{*}^k(G,R)\to H_{*}^k(H,R).$$

Proof. 

It arises from ([2], Th.2.10) and the definition of ${\mathcal{A}}_p^k(G,R)={\mathcal{A}}_p\cap {\mathsf{\Lambda }}_p^k$ that $f_{*}\left({\mathcal{A}}_p^k(G,R)\right)\subset {\mathcal{A}}_p^k(H,R)$. We only must prove that $f_{*}\left({\Omega }_p^k(G,R)\right)\subset {\Omega }_p^k(H,R)$. For any $v\in {\Omega }_p^k(G,R)$, by (13) we have $v\in {\mathcal{A}}_p^k\left(G\right)$ and $\partial v\in {\mathcal{A}}_{p-1}^k\left(G\right)$. Hence $f_{*}\left(v\right)\in {\mathcal{A}}_p^k(H,R)$ and $\partial \left(f_{*}\left(v\right)\right)=f_{*}(\partial v)\in {\mathcal{A}}_{p-1}^k(H,R)$, which implies $f_{*}\left(v\right)\in {\Omega }_p^k(H,R)$. □

Now we prove the colored homotopy invariance of colored homology groups of digraphs.

Theorem 3.

Let $f_0\simeq f_1:(G,\phi )\to (H,\psi )$ be two colored homotopic digraph morphisms. Then $f_0$ and $f_1$ induce the identical homomorphisms

$${f_i}_{*}:H_p^k(G,R)\to H_p^k(H,R)(i=0,1)$$

of colored homology groups for $k\ge 1$.

Proof. 

It is sufficient to prove the statement for a homotopy in the case $I_n=I_1=(0\to 1)$. The general case follows by induction.

By Theorem 2, the colored morphisms $f_i(i=0,1)$ and F induce morphisms of chain complexes

$${f_i}_{*}:{\Omega }_{*}^k(G,R)\to {\Omega }_{*}^k(H,R)\mathrm{and}{F}_{*}:{\Omega }_{*}^k(G\square I_1,R)\to {\Omega }_{*}^k(H,R).$$

(19)

Please note that we can identify colored digraphs $G\square \left\{0\right\}$ and $G\square \left\{1\right\}$ with the colored digraph G in a natural way. We will denote vertices $(i,0)\in V_{G\square \left\{0\right\}}$ by i and vertices $(i,1)\in V_{G\square \left\{1\right\}}$ by $i^{\prime }$. Similar notations will be used for arrows and paths. By the definition of the colored homotopy, for any colored path $v\in {\Omega }_{*}^k(G\square \left\{0\right\})$, we have $F_{*}\left(v\right)={f_0}_{*}\left(v\right)$, while for any colored path $v^{\prime }\in {\Omega }_{*}(G\square \left\{1\right\}$, we have $F_{*}\left(v^{\prime }\right)={f_1}_{*}\left(v\right)$. For $p\ge 0$, define R-linear mappings

$$L_p:{\Omega }_p^k(G,R)\to {\Omega }_{p+1}^k(H,R)$$

on elementary paths in the following way

$$L_p\left(e_{i_0\dots i_p}\right)=F_{*}\left(\sum _{k=0}^p{\left(-1\right)}^k{e}_{i_0\dots i_k{i}_k^{\prime }\dots i_p^{\prime }}\right).$$

(20)

By ([2], Pr. 2.12 and §3.2) $L_p$ are well defined colored mappings and the condition

$$\partial L_p\left(v\right)+L_{p-1}\partial \left(v\right)=f_1*\left(v\right)-{f_0}_{*}\left(v\right),v\in {\Omega }_p^k(G,R).$$

is satisfied. Thus, we have a chain homotopy between the morphisms ${f_i}_{*}$ and the statement of the Theorem follows from ([13], Theorem 2.1). □

Corollary 1.

If the colored digraphs $(G,\phi )$ and $(H,\psi )$ are colored homotopy equivalent, then the colored homology groups $H_{*}^k(G,R)$ and $H_{*}^k(H,R)$ are isomorphic for $k\ge 1$ and mutually inverse isomorphisms of these groups are induced by the homotopy inverse colored morphisms.

Corollary 2.

For $k\ge 0$, the colored homology groups $H_{*}^k(·,R)$ provide a functor from the colored homotopy category ${\mathcal{C}}^{\prime }$ to the category R-modules and homomorphisms.

5. Spectral Sequence for Path Homology Groups of a Colored Digraph

In this section, we construct a spectral sequence for path homology groups of any colored digraph. Our construction is based on the concept of an exact couple of a filtered chain complex from ([18], Chapter 7).

Let $(G,\phi )$ be a vertex colored digraph. By Proposition 3 we have a filtration (15) of the chain complex ${\Omega }_{*}(G,R)$. Let ${\mathcal{K}}_{*}={\Omega }_{*}(G,R)$. We define a filtration of ${\mathcal{K}}_{*}$ by subcomplexes ${\mathcal{K}}_{*}^p$ for $p\in \mathbb{Z}$ in the following way

$${\mathcal{K}}_{*}^p=\left\{\begin{array}{cc}0\hfill & \mathrm{for}p<0,\hfill \\ {\Omega }_{*}^{p+1}(G,R)\hfill & \mathrm{for}p\ge 0.\hfill \end{array}\right.$$

(21)

Thus, we have an infinite filtration

$$\cdots \subset {\mathcal{K}}_{*}^{p-1}\subset {\mathcal{K}}_{*}^p\subset {\mathcal{K}}_{*}^{p+1}\subset \cdots \subset {\mathcal{K}}_{*}$$

(22)

Theorem 4.

The filtration (22) has the following properties.

1. 

${\mathcal{K}}_{*}^p=0$ for $p<0$.

2. 

There is a short exact sequence of chain complexes

$$0\to {\mathcal{K}}_{*}^{p-1}\to {\mathcal{K}}_{*}^p\to {\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\to 0$$

(23)

with $H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)=0$ for $q<0$.

3. 

$$\bigcup _{p\ge 0}{\mathcal{K}}_{*}^p={\mathcal{K}}_{*}.$$

Proof. 

The first statement follows from the definition (21). The elements of the module ${\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}$ are given by linear combinations of allowed paths which are colored exactly by $p+1$ colors. Any elementary allowed path $e_{i_0\dots i_s}$ can be colored at most by $s+1$ colors. Hence, for $s+1<p+1$ (that is for $s<p$) the module ${\mathcal{K}}_s^p/{\mathcal{K}}_s^{p-1}$ is trivial. Now we have $H_s\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)=H_s\left(0\right)=0$ for $s<p$ and the second statement follows. Any path has a finite number of vertices and is colored by a finite number of colors, thus the third statement is proved. □

Corollary 3.

The exact sequence (23) induces a homology long exact sequence

$$\dots \stackrel{\partial }{\to }{H}_n\left({\mathcal{K}}_{*}^{p-1}\right)\stackrel{i}{\to }{H}_n\left({\mathcal{K}}_{*}^p\right)\stackrel{j}{⟶}{H}_n\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)\stackrel{\partial }{\to }{H}_{n-1}\left({\mathcal{K}}_{*}^{p-1}\right)\to \dots$$

Now we describe the spectral sequence of the filtration (22) following [18] (Chapter 7). Let

$$D_{p,q}=H_{p+q}\left({\mathcal{K}}_{*}^p\right),E_{p,q}=H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right),$$

(24)

and $D_{*}=\left\{D_{p,q}\right\}$, $E_{*}=\left\{E_{p,q}\right\}$ be corresponding bigraded R-modules. Consider the homomorphisms of homology groups that follow from exact sequences of the Corollary 3 for various p and $n=p+q$:

$$\begin{array}{c}{i}_{p,q}:D_{p,q}=H_{p+q}\left({\mathcal{K}}_{*}^p\right)⟶H_{p+q}\left({\mathcal{K}}_{*}^{p+1}\right)=D_{p+1,q-1},\\ j_{p,q}:D_{p,q}=H_{p+q}\left({\mathcal{K}}_{*}^p\right)⟶H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)=E_{p,q},\\ k_{p,q}={\partial }_{p,q}:E_{p+q}=H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)⟶H_{p+q-1}\left({\mathcal{K}}_{*}^{p-1}\right)=D_{p-1,q}.\end{array}$$

(25)

The homomorphisms in (25) define bigraded homomorphisms

$$\begin{array}{c}{i}_{*}:D_{*}⟶D_{*},\\ j_{*}:D_{*}⟶E_{*},\\ k_{*}:E_{*}⟶D_{*}.\end{array}$$

(26)

of bidegree $(+1,-1)$, $(0,0)$, and $(-1,0)$ respectively.

Proposition 4.

The bigraded modules $D_{*}$, $E_{*}$ and the homomorphisms $i_{*},j_{*},k_{*}$ fit into the commutative diagram

$$\begin{array}{ccccc}{D}_{*}& & \stackrel{i_{*}}{⟶}& & D_{*}\\ & {}_{k_{*}}\nwarrow & & {\swarrow }_{j_{*}}\\ & & E_{*}& \end{array}$$

(27)

which is exact in each vertex. Thus, we have an exact couple of modules in the sense of [18].

Proof. 

The proof in the general case of a chain complex with filtration is given in ([18], Chapter 7). □

Corollary 4.

The exact couple in (27) defines a spectral sequence with the first differential $d^1=\left\{d_{p,q}\right\}$ where $d_{p,q}:E_{p,q}^1\to E_{p-1,q}^1$ is given by

$$j_{p-1,q}{k}_{p,q}:E_{p,q}^1=H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)⟶H_{p+q-1}\left({\mathcal{K}}_{*}^{p-1}/{\mathcal{K}}_{*}^{p-2}\right)=E_{p-1,q}^1$$

of bidegree $(-1,0)$. The group $E_{p,q}^r$ is isomorphic to the quotient group

$$\frac{Im\left(H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-r}\right)⟶H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)\right)}{Im\left(\partial :H_{p+q+1}\left({\mathcal{K}}_{*}^{p+r-1}/{\mathcal{K}}_{*}^p\right)⟶H_{p+q}\left({\mathcal{K}}_{*}^p/{\mathcal{K}}_{*}^{p-1}\right)\right)}.$$

The differential $d^{r+1}$ coincides with the composition $j_{*}{\left(i_{*}\right)}^{-r}{k}_{*}$.

Proof. 

The proof for the general case of an exact couple for a chain complex with filtration is given in ([18], Chapter 7). □

We shall call this spectral sequence a vertex colored spectral sequence of path homology groups of a colored digraph $(G,\phi )$. The general properties of the spectral sequence are described in [18]. We recall now the basic definitions and properties in our case.

We put $F_{p,q}=Im\left(H_{p+q}\left({\mathcal{K}}_{*}^p\right)\to H_{p+q}\left({\mathcal{K}}_{*}\right)\right)$. We have a natural inclusion $F_{p-1,q+1}\to F_{p,q}$, and hence, we can define a module

$$E_{p,q}^{\infty }:=F_{p,q}/F_{p-1,q+1}.$$

(28)

Theorem 5.

The vertex colored spectral sequence of a colored digraph $(G,\phi )$ converges, that is

$$\left(i\right)E_{p,q}^r=E_{p,q}^{r+1}\mathit{for}r>maxp,q+1,$$

and

$$\left(ii\right)E_{p,q}^r\cong E_{p,q}^{\infty }\mathit{for}r>maxp,q+1.$$

Proof. 

The proof follows from Theorem 4 and [18] (Chapter 7: Proposition 5, Theorem 1). □

Theorem 6.

Let $(G,\phi )$ be a 3-colored digraph. Then the filtration in (22) gives a finite filtration

$$0\subset {\mathcal{K}}_{*}^0\subset {\mathcal{K}}_{*}^1\subset {\mathcal{K}}_{*}^2={\mathcal{K}}_{*}={\Omega }_{*}(G,R).$$

(29)

Moreover, the vertex colored spectral sequence gives a commutative braid of the exact sequence

$$\begin{array}{ccccc}{\to H}_{n+1}\left({\mathcal{K}}_{*}\right)& ⟶& H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1\right)& ⟶& H_n\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)\to \\ \searrow & & \nearrow \searrow & & \nearrow \searrow \\ & H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^0\right)& & H_n\left({\mathcal{K}}_{*}^1\right)\\ \nearrow & & \searrow \nearrow & & \searrow \nearrow \\ {\to H}_{n+1}\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)& ⟶& H_n\left({\mathcal{K}}_{*}^0\right)& ⟶& H_n\left({\mathcal{K}}_{*}\right)\to \end{array}$$

which consists of the following exact sequences

$$\begin{array}{c}\to H_{n+1}\left({\mathcal{K}}_{*}\right)⟶H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^0\right)⟶H_n\left({\mathcal{K}}_{*}^0\right)⟶H_n\left({\mathcal{K}}_{*}\right)\to \\ \to H_{n+1}\left({\mathcal{K}}_{*}\right)⟶H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1\right)⟶H_n\left({\mathcal{K}}_{*}^1\right)⟶H_n\left({\mathcal{K}}_{*}\right)\to \\ \to H_{n+1}\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)\to H_n\left({\mathcal{K}}_{*}^0\right)\to H_n\left({\mathcal{K}}_{*}^1\right)\to H_n\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)\to \end{array}$$

$$\to H_{n+1}\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)\to H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^0\right)\to H_{n+1}\left({\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1\right)\to H_n\left({\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0\right)\to$$

where $H_n\left({\mathcal{K}}_{*}^0\right)=H_n^1(G,R)$, $H_n\left({\mathcal{K}}_{*}^1\right)=H_n^2(G,R)$ and $H_n\left({\mathcal{K}}_{*}\right)=H_n(G,R)$.

Proof. 

The inclusions of chain complexes in (29) follow directly from (22). By ([19], Chapter 4), these inclusions induce a short exact sequence

$$0⟶{\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0⟶{\mathcal{K}}_{*}/{\mathcal{K}}_{*}^0⟶{\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1⟶0.$$

and, hence, the commutative diagram of chain complexes

$$\begin{array}{cccccc}& 0& & 0& & 0\\ & \downarrow & & \downarrow & & \downarrow \\ 0⟶& {\mathcal{K}}_{*}^0& ⟶& {\mathcal{K}}_{*}^1& ⟶& {\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0& ⟶0\\ & \downarrow \cong & & \downarrow & & \downarrow \\ 0⟶& {\mathcal{K}}_{*}^0& ⟶& {\mathcal{K}}_{*}& ⟶& {\mathcal{K}}_{*}/{\mathcal{K}}_{*}^0& ⟶0\\ & \downarrow & & \downarrow & & \downarrow \\ & 0& ⟶& {\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1& \stackrel{\cong }{⟶}& {\mathcal{K}}_{*}/{\mathcal{K}}_{*}^1& ⟶0\\ & & \downarrow & & \downarrow \\ & & 0& & 0\end{array}$$

(30)

in which the rows and columns are short exact sequences. The homology long exact sequences of the short exact sequences from (30) give the commutative braid of exact sequences. □

Example 5.

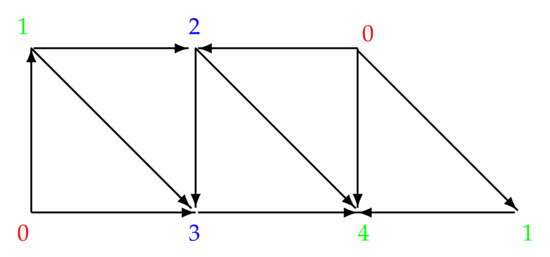
Consider a 1-improper 3-colored digraph $(G,\phi )$ in Figure 3 where the left-side arrow $0\to 1$ and the right-side arrow $0\to 1$ is identified in the natural way. Please note that the underlying non-directed graph of the digraph G is the one-dimensional skeleton of the minimal triangulation of the closed Möbius band.

Figure 3. The 1-improper 3-colored digraph.

Now we compute all homology groups in the braid of exact sequence from Theorem 6. We assume that $R=\mathbb{R}$ similarly to Example 4. In what follows we shall denote by $⟨a_1,\dots ,a_n⟩$ the R-module generated by elements $a_1,\dots ,a_n$.

Recall that in the modules of the chain complex ${\mathcal{K}}_{*}^0$, we can use only one-colored basic elements. Hence ${\mathcal{K}}_{*}^0$ has two non-trivial modules ${\mathcal{K}}_0^0=⟨e_0,\dots ,e_4⟩$ and ${\mathcal{K}}_1^0=⟨e_{14},e_{23}⟩$. The differential $\partial :{\mathcal{K}}_1^0\to {\mathcal{K}}_0^0$ is a monomorphism and, hence

$$H_n\left({\mathcal{K}}_{*}^0\right)=\left\{\begin{array}{cc}{R}^3\hfill & \mathit{for}n=0,\hfill \\ 0\hfill & \mathit{for}n\ge 1.\hfill \end{array}\right.$$

(31)

Now we describe the chain complex ${\mathcal{K}}_{*}^1$. In the modules of this chain complex we can use one-colored and two-colored basic elements. We have ${\mathcal{K}}_0^1=⟨e_0,\dots ,e_4⟩$. The module ${\mathcal{K}}_1^1$ is generated by all arrows of the digraph G that is

$${\mathcal{K}}_1^1=⟨e_{01},e_{02},e_{03},e_{04},e_{12},e_{13},e_{14},e_{23},e_{24},e_{34}⟩.$$

We can check directly that the module ${\mathcal{K}}_2^1$ is generated by the elementary paths of length two that are colored in two colors

$${\mathcal{K}}_2^1=⟨e_{014},e_{023},e_{123},e_{124},e_{134},e_{234}⟩$$

and, similarly, we obtain that ${\mathcal{K}}_3^1=⟨e_{1234}⟩$. It is clear that ${\mathcal{K}}_n^1=0$ for $n\ge 4$. We sum up the above in the following way

$$rang\left({\mathcal{K}}_n^1\right)=\left\{\begin{array}{cc}5\hfill & \mathit{for}n=0,\hfill \\ 10\hfill & \mathit{for}n=1,\hfill \\ 6\hfill & \mathit{for}n=2,\hfill \\ 1\hfill & \mathit{for}n=3,\hfill \\ 0\hfill & \mathit{for}n\ge 4.\hfill \end{array}\right.$$

We have $rang\left\{Image\{\partial :{\mathcal{K}}_1^1\to {\mathcal{K}}_1^0\}\right\}=4$ since G is a connected digraph (see [2]). The differential $\partial :{\mathcal{K}}_3^1\to {\mathcal{K}}_2^1$ is a monomorphism. Consider the differential $\partial :{\mathcal{K}}_2^1\to {\mathcal{K}}_1^1$. It is easy to see that elements $\partial e_{014}$ and $\partial e_{023}$ are independent and they are independent of the image of the restriction of ∂ to a submodule M of ${\mathcal{K}}_2^1$ generated by $⟨e_{123},e_{124},e_{134},e_{234}⟩$. Now we directly check that

$$Ker\{\partial {|}_M:M\to {\mathcal{K}}_1^1\}=Im\{:{\mathcal{K}}_3^1\to {\mathcal{K}}_2^1\}=⟨e_{234}-e_{134}+e_{124}-e_{123}⟩.$$

Thus,

$$Ker\{\partial :{\mathcal{K}}_2^1\to {\mathcal{K}}_1^1\}=Im\{:{\mathcal{K}}_3^1\to {\mathcal{K}}_2^1\}.$$

Hence,

$$H_n\left({\mathcal{K}}_{*}^1\right)=\left\{\begin{array}{cc}R\hfill & \mathit{for}n=0,\hfill \\ R\hfill & \mathit{for}n=1,\hfill \\ 0\hfill & \mathit{for}n\ge 2.\hfill \end{array}\right.$$

(32)

Now we compute the homology groups of the chain complex

$${\mathcal{K}}_{*}^{1/0}:={\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0.$$

It follows from the calculations above that ${\mathcal{K}}_0^{1/0}=0$,

$${\mathcal{K}}_1^{1/0}=⟨e_{01},e_{02},e_{03},e_{04},e_{12},e_{13},e_{24},e_{34}⟩,$$

$${\mathcal{K}}_2^{1/0}=⟨e_{014},e_{023},e_{123},e_{124},e_{134},e_{234}⟩,$$

and ${\mathcal{K}}_3^{1/0}=⟨e_{1234}⟩$. Considering the information given above, now we obtain that

$$rang\left({\mathcal{K}}_n^{1/0}\right)=\left\{\begin{array}{cc}0\hfill & \mathit{for}n=0,\hfill \\ 8\hfill & \mathit{for}n=1,\hfill \\ 6\hfill & \mathit{for}n=2,\hfill \\ 1\hfill & \mathit{for}n=3,\hfill \\ 0\hfill & \mathit{for}n\ge 4.\hfill \end{array}\right.$$

and

$$H_n\left({\mathcal{K}}_{*}^{1/0}\right)=\left\{\begin{array}{cc}0\hfill & \mathit{for}n=0,\hfill \\ R^3\hfill & \mathit{for}n=1,\hfill \\ 0\hfill & \mathit{for}n\ge 2.\hfill \end{array}\right.$$

(33)

Now we compute the homology groups of the chain complexes

$${\mathcal{K}}_{*}^{2/1}:={\mathcal{K}}_{*}^2/{\mathcal{K}}_{*}^1\mathit{and}{\mathcal{K}}_{*}^{2/0}:={\mathcal{K}}_{*}^2/{\mathcal{K}}_{*}^0.$$

First, we describe modules of the chain complex ${\mathcal{K}}_{*}^2={\Omega }_{*}$. As with the notions above, we have

$${\mathcal{K}}_0^2={\mathcal{K}}_0^1={\mathcal{K}}_0^0=⟨e_0,\dots ,e_4⟩,$$

$${\mathcal{K}}_1^2={\mathcal{K}}_1^1=⟨e_{01},e_{02},e_{03},e_{04},e_{12},e_{13},e_{14},e_{23},e_{24},e_{34}⟩,$$

$${\mathcal{K}}_2^2=⟨e_{014},e_{023},e_{123},e_{124},e_{134},e_{234},e_{012},e_{013},e_{024},e_{034}⟩\supset$$

$${\mathcal{K}}_2^1=⟨e_{014},e_{023},e_{123},e_{124},e_{134},e_{234}⟩,$$

$${\mathcal{K}}_3^2=⟨e_{0123},e_{0124},e_{0134},e_{0234},e_{1234}⟩\supset {\mathcal{K}}_3^1=⟨e_{1234}⟩,$$

$${\mathcal{K}}_4^2=⟨e_{01234}⟩,$$

and ${\mathcal{K}}_n^2=0$ for $n\ge 5$. Using these results, we get the following

$${\mathcal{K}}_n^{2/1}=\left\{\begin{array}{cc}0\hfill & \mathit{for}n=0,1,\hfill \\ ⟨e_{012},e_{013},e_{024},e_{034}⟩\hfill & \mathit{for}n=2,\hfill \\ ⟨e_{0123},e_{0124},e_{0134},e_{0234}⟩\hfill & \mathit{for}n=3,\hfill \\ ⟨e_{01234}⟩\hfill & \mathit{for}n=4,\hfill \\ 0\hfill & \mathit{for}n\ge 5.\hfill \end{array}\right.$$

(34)

Please note that in the reduced bases in (34), we have

$$\begin{array}{c}\partial \left(e_{0123}\right)=e_{013}-e_{012},\\ \partial \left(e_{0124}\right)=-e_{024}-e_{012},\\ \partial \left(e_{0134}\right)=-e_{034}-e_{013},\\ \partial \left(e_{0234}\right)=-e_{034}+e_{024},\\ \partial \left(e_{01234}\right)=-e_{0234}+e_{0134}-e_{0124}+e_{0123}.\end{array}$$

(35)

It follows directly from (35) that

$$rang\left\{Image\left(\partial :{\mathcal{K}}_3^{2/1}\to {\mathcal{K}}_2^{2/1}\right)\right\}=3,$$

whereas

$$rang\left\{Image\left(\partial :{\mathcal{K}}_4^{2/1}\to {\mathcal{K}}_3^{2/1}\right)\right\}=1$$

and, hence,

$$H_n\left({\mathcal{K}}_{*}^{2/1}\right)=\left\{\begin{array}{cc}0\hfill & \mathit{for}n\ne 2,\hfill \\ R\hfill & \mathit{for}n=2.\hfill \end{array}\right.$$

(36)

Now we turn our attention to the homology groups of the chain complex

$${\mathcal{K}}_{*}^{2/0}:={\mathcal{K}}_{*}^2/{\mathcal{K}}_{*}^0.$$

Having in mind modules of the chain complexes ${\mathcal{K}}_{*}^2$ and ${\mathcal{K}}_{*}^0$, by calculating directly, we obtain the following

$${\mathcal{K}}_n^{2/0}=\left\{\begin{array}{cc}0\hfill & \mathit{for}n=0,\hfill \\ ⟨e_{01},e_{02},e_{03},e_{04},e_{12},e_{13},e_{24},e_{34}⟩\hfill & \mathit{for}n=1,\hfill \\ ⟨e_{012},e_{013},e_{034},e_{014},e_{023},e_{024},e_{134},e_{123},e_{124},e_{234}⟩\hfill & \mathit{for}n=2,\hfill \\ ⟨e_{0123},e_{0124},e_{0134},e_{1234},e_{0234}⟩\hfill & \mathit{for}n=3,\hfill \\ ⟨e_{01234}⟩\hfill & \mathit{for}n=4,\hfill \\ 0\hfill & \mathit{for}n\ge 5.\hfill \end{array}\right.$$

(37)

Computing directly in the similar fashion, now we provide

$$rang\left\{Image\left(\partial :{\mathcal{K}}_2^{2/0}\to {\mathcal{K}}_1^{2/0}\right)\right\}=6$$

and

$$rang\left\{Image\left(\partial :{\mathcal{K}}_3^{2/0}\to {\mathcal{K}}_2^{2/0}\right)\right\}=4,$$

whereas in an obvious way

$$rang\left\{Image\left(\partial :{\mathcal{K}}_1^{2/0}\to {\mathcal{K}}_0^{2/0}\right)\right\}=0,$$

$$rang\left\{Image\left(\partial :{\mathcal{K}}_3^{2/0}\to {\mathcal{K}}_2^{2/0}\right)\right\}=1.$$

Keeping that in mind, we obtain the following results

$$H_n\left({\mathcal{K}}_{*}^{2/0}\right)=\left\{\begin{array}{cc}0\hfill & \mathit{for}n=0,\hfill \\ R^2\hfill & \mathit{for}n=1,\hfill \\ 0\hfill & \mathit{for}n\ge 2.\hfill \end{array}\right.$$

(38)

Let

$${\mathcal{K}}_{*}={\mathcal{K}}_{*}^2,{\mathcal{K}}_{*}^{1/0}={\mathcal{K}}_{*}^1/{\mathcal{K}}_{*}^0,{\mathcal{K}}_{*}^{2/0}={\mathcal{K}}_{*}^2/{\mathcal{K}}_{*}^0,{\mathcal{K}}_{*}^{2/1}={\mathcal{K}}_{*}^2/{\mathcal{K}}_{*}^1.$$

Now we can write down the braid of exact sequences for the filtration in (29) and using the diagram chasing, we compute the groups $H_{*}\left({\mathcal{K}}_{*}\right)$ and homomorphisms in this diagram. We obtain the following commutative braid of exact sequences:

$$\begin{array}{ccccc}\mathbf{0}& & 0& & 0\\ \left|\right|& & \left|\right|& & \left|\right|\\ {0\to H}_3\left({\mathcal{K}}_{*}^2\right)& ⟶& H_3\left({\mathcal{K}}_{*}^{2/1}\right)& ⟶& H_2\left({\mathcal{K}}_{*}^{1/0}\right)⟶\\ \nearrow \searrow & & \nearrow \searrow & & \nearrow \searrow \\ 0& H_3\left({\mathcal{K}}_{*}^{2/0}\right)=0& & H_2\left({\mathcal{K}}_{*}^1\right)=0& \\ \searrow \nearrow & & \searrow \nearrow & & \searrow \nearrow \\ {0\to H}_3\left({\mathcal{K}}_{*}^{1/0}\right)& ⟶& H_2\left({\mathcal{K}}_{*}^0\right)& ⟶& H_2\left({\mathcal{K}}_{*}^2\right)⟶\\ \left|\right|& & \left|\right|& & \left|\right|\\ 0& & 0& & \mathbf{0}\end{array}$$

$$\begin{array}{cccc}& 0& & \mathbf{0}\\ & \left|\right|& & \left|\right|\\ ⟶& H_1\left({\mathcal{K}}_{*}^0\right)& ⟶& H_1\left({\mathcal{K}}_{*}^2\right)& ⟶\\ & \nearrow \searrow & & \nearrow \searrow \\ H_2\left({\mathcal{K}}_{*}^{2/0}\right)=0& & H_1\left({\mathcal{K}}_{*}^1\right)=R& & H_1\left({\mathcal{K}}_{*}^{2/0}\right)=R^2\\ & \searrow {\nearrow }_{\cong }& & {\searrow }^{mono}{}^{epi}\nearrow \\ ⟶& H_2\left({\mathcal{K}}_{*}^{2/1}\right)& \stackrel{mono}{⟶}& H_1\left({\mathcal{K}}_{*}^{1/0}\right)& ⟶\\ & \left|\right|& & \left|\right|\\ & R& & R^3\end{array}$$

$$\begin{array}{ccc}0& & 0\\ \left|\right|& & \left|\right|\\ ⟶H_1\left({\mathcal{K}}_{*}^{2/1}\right)& ⟶& H_0\left({\mathcal{K}}_{*}^{1/0}\right)\\ \nearrow \searrow & & \nearrow \searrow \\ & H_0\left({\mathcal{K}}_{*}^1\right)=R& & H_0\left({\mathcal{K}}_{*}^{2/0}\right)=0\\ \searrow {}^{epi}\nearrow & & {\searrow }^{\cong }\nearrow \\ ⟶H_0\left({\mathcal{K}}_{*}^0\right)& \stackrel{epi}{⟶}& H_0\left({\mathcal{K}}_{*}^2\right)\\ \left|\right|& & \left|\right|\\ R^3& & R\end{array}$$

in which we wrote in a bold font all the groups that were provided by diagram chasing.

Proposition 5.

The spectral sequence constructed in Theorem 6 is functorial, which means that any morphism of colored digraphs induces a morphism of corresponding spectral sequences.

6. Path Homology of Colored Graphs

In this section, we apply the results obtained so far to the category of non-directed colored graphs. To do this, we need to use the isomorphism between the category of graphs and the full subcategory of symmetric digraphs. To avoid further misunderstandings in this section, we denote undirected graph and graph mapping with a bold font and continue to use the same notations for digraphs as before.

Definition 8. 

(i) 

A graph $\mathbf{G}$ is given by a set ${\mathbf{V}}_{\mathbf{G}}$ of vertices and a subset ${\mathbf{E}}_{\mathbf{G}}\subset {\mathbf{V}}_{\mathbf{G}}\times {\mathbf{V}}_{\mathbf{G}}$ of non-ordered pairs of vertices $(v,w)$ with $v\ne w$ that are called edges.

(ii) 

A mapping $\mathbf{f}:\mathbf{G}\to \mathbf{H}$ is a mapping $\mathbf{f}:{\mathbf{V}}_{\mathbf{G}}\to {\mathbf{V}}_{\mathbf{H}}$ such that for any edge $(v,w)\in {\mathbf{E}}_{\mathbf{G}}$ we have either $\mathbf{f}\left(v\right)=\mathbf{f}\left(w\right)$ or $(\mathbf{f}\left(v\right),\mathbf{f}\left(w\right))\in {\mathbf{E}}_{\mathbf{H}}$.

The set of all graphs with graph mappings forms a category $\mathcal{G}$. We can associate each graph $\mathbf{G}=({\mathbf{V}}_{\mathbf{G}},{\mathbf{E}}_{\mathbf{G}})$ with a symmetric digraph $G=\mathcal{O}\left(\mathbf{G}\right)=(V_G,E_G)$ where $V_G={\mathbf{V}}_{\mathbf{G}}$ and $E_G$ is defined by the condition $\{v\to w\}\iff \{(v,w)\in {\mathbf{E}}_{\mathbf{G}}\}$. Thus, we obtain a functor $\mathcal{O}$ that provides an isomorphism of the category $\mathcal{G}$ and the full subcategory of symmetric digraphs of the category $\mathcal{D}$.

Definition 9. 

(i) 

A coloring of a graph $\mathbf{G}=({\mathbf{V}}_{\mathbf{G}},{\mathbf{E}}_{\mathbf{G}})$ is given by an assignment of a color to each vertex $v\in {\mathbf{V}}_{\mathbf{G}}$. A coloring that uses k colors is called k-coloring. We denote by $(\mathbf{G},\phi )$ a graph $\mathbf{G}$ with a coloring function $\phi :{\mathbf{V}}_{\mathbf{G}}\to \mathbb{N}$.

(ii) 

Let $(G,\phi )$ and $(\mathbf{H},\psi )$ be two colored graphs. A digraph mapping $\mathbf{f}:\mathbf{G}\to \mathbf{H}$ is a morphism of colored graphs if $\psi \left(f\right(v\left)\right)=\phi \left(v\right)$ for any vertex $v\in {\mathbf{V}}_{\mathbf{G}}$.

The colored graphs with the defined above morphisms form a category which we denote $\mathcal{CG}$. For any colored graph $(\mathbf{G},\phi )$, we define a colored digraph $\mathcal{O}(\mathbf{G},\phi )=(G,\phi )$ by setting $G=\mathcal{O}\left(\mathbf{G}\right)$ and attaching the same coloring map $\phi$ on the set of vertices $V_G={\mathbf{V}}_{\mathbf{G}}$. Now we have the following result.

Proposition 6.

Any morphism of colored graphs $\mathbf{f}:(G,\phi )\to (\mathbf{H},\psi )$ provides a morphism of colored digraphs $\left(O\right)\left(\mathbf{f}\right)=f:(G.\phi )\to (H,\psi )$ defined on the set of vertices by the morphism $\mathbf{f}$ and we have the functor $\mathcal{O}:\mathcal{CG}\to \mathcal{C}$.

The Box product $\mathbf{G}\square \mathbf{H}$ of two graphs $\mathbf{G}=({\mathbf{V}}_{\mathbf{G}},{\mathbf{E}}_{\mathbf{G}})$ and $\mathbf{H}=\left({\mathbf{V}}_{\mathbf{H}}{\mathbf{E}}_{\mathbf{H}}\right)$ is defined similarly to the Box product of digraphs. We put ${\mathbf{V}}_{\mathbf{G}\square \mathbf{H}}={\mathbf{V}}_{\mathbf{G}}\times {\mathbf{V}}_{\mathbf{H}}$ and $[(x,y),(x^{\prime },y^{\prime })]\in {\mathbf{E}}_{\mathbf{G}\square \mathbf{H}}$ if and only if

$$\mathrm{either}{x}^{\prime }=x\mathrm{and}y\sim y^{\prime },\mathrm{or}x\sim x^{\prime }\mathrm{and}y=y^{\prime }$$

where $x,x^{\prime }\in {\mathbf{V}}_{\mathbf{G}},y,y^{\prime }\in {\mathbf{V}}_{\mathbf{H}}$. Please note that the functor $\mathcal{O}$ preserves Box products (see [2], Lemma 6.3), that is $\mathcal{O}(\mathbf{G}\square \mathbf{H})=G\square H$.

We introduce now the notion of segment graph which is equivalent to the notion of the line graph in [2] since we shall use the classical notion of a line graph below. A segment graph ${\mathbf{J}}_n=(\mathbf{V},\mathbf{E})$ of the length $n\ge 0$ is defined as follows: $\mathbf{V}=\{0,1,\dots ,n\}$ and $\mathbf{E}=\left\{\right(k,k+1\left)\right|0\le k\le n-1\}$.

Definition 10

([2,20]). (i) Two graph mappings ${\mathbf{f}}_{\mathbf{0}},{\mathbf{f}}_{\mathbf{n}}:\mathbf{G}\to \mathbf{H}$ are called homotopic if there exists a segment graph ${\mathbf{J}}_n$ and a graph mapping $\mathbf{F}:\mathbf{G}\square {\mathbf{J}}_n\to \mathbf{H}$ such that

$${\mathbf{F}|}_{\mathbf{G}\square \left\{0\right\}}={\mathbf{f}}_0{\mathrm{and}\mathbf{F}|}_{\mathbf{G}\square \left\{n\right\}}={\mathbf{f}}_n.$$

In this case, we shall write $\mathbf{f}\simeq \mathbf{g}$. Now the homotopy equivalence of graphs is defined in a natural way.

Remark 1.

The relation ”≃" is an equivalence relation on the set of graph mappings and it induces the notion of homotopy equivalence on the set of graphs. The functor $\mathcal{O}$ preserves the relation of homotopy equivalence (see [2]), that is two graph mappings $\mathbf{f},\mathbf{g}:\mathbf{G}\to \mathbf{H}$ are homotopic if and only if the digraph mappings $f=\mathcal{O}\left(\mathbf{f}\right)$ and $g=\mathcal{O}\left(\mathbf{g}\right)$ are homotopic.

We define the k-colored homology groups $H_{*}^k(\mathbf{G},R)$ of a colored graph $(\mathbf{G},\phi )$ in the following way

$$H_{*}^k(\mathbf{G},R):=H_{*}^k(\mathcal{O}\left(\mathbf{G}\right),R).$$

(39)

Example 6.

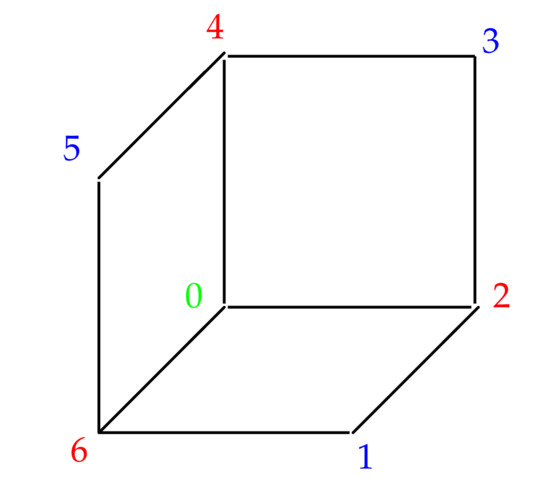
Consider the 3-proper colored graph $\mathbf{G}$ in Figure 4 which has 7 vertices and 9 edges. We now compute now the homology groups $H_1^2(\mathbf{G},R)$ and $H_1^3(\mathbf{G},R)$ for $R=\mathbb{R}$.

Figure 4. The 3-proper colored graph.

Using the notations of Section 4 and Section 5, we have

$${\Omega }_0^3={\Omega }_0^2=⟨e_0,e_1,\dots ,e_6⟩,$$

$${\Omega }_1^3={\Omega }_1^2=⟨e_{02},e_{20},e_{04},e_{40},e_{06},e_{60},e_{12},e_{21},$$

$$e_{16},e_{61},e_{23},e_{32},e_{34},e_{43},e_{45},e_{54},e_{56},e_{65}⟩,$$

$${\Omega }_2^2=⟨e_{020},e_{202},e_{204}-e_{234},e_{206}-e_{216},e_{040},e_{404},e_{402}-e_{432},$$

$$e_{406}-e_{456},e_{060},e_{606},e_{602}-e_{612},e_{604}-e_{654},e_{121},e_{212},$$

$$e_{161},e_{616},e_{232},e_{323},e_{343},e_{434},e_{454},,e_{545},e_{565},e_{656}⟩,$$

and

$${\Omega }_2^3={\Omega }_2^2\oplus ⟨e_{021}-e_{061},e_{023}-e_{043},e_{045}-e_{065},e_{120}-e_{160},e_{320}-e_{340},e_{540}-e_{560}⟩.$$

We compute ranks of the kernels and the images of the differential directly. These calculations lead us to homology groups $H_1^2(\mathbf{G},\mathbb{R})=\mathbb{R}$ and $H_1^3(\mathbf{G},\mathbb{R})=0.$

Equation (39), Remark 1, and the results of Section 5 together give the following result.

Theorem 7.

For any $n\in \mathbb{N}$, the k-colored homology groups $H_n^k(·,R)$ provide the homotopy invariant functors from the category $\mathcal{CG}$ to the category of R-modules. Moreover, all algebraic results of Section 5 can be transferred to the category of colored graphs.

Now we describe an application of the above developed methods for constructing a path homology theory for edge colored (di)graphs. At first, we recall several standard definitions.

Definition 11.

An edge coloring of a digraph $G=(V_G,E_G)$ is given by an assignment of a color to each edge $(v\to w)\in E_G$. We can identify the colors with natural numbers and denote this digraph by $(G,\phi )$ where $\phi :E_G\to \mathbb{N}$ is the coloring.

A morphism $f:(G,\phi )\to (H,\psi )$ of edge colored digraphs is a non-degenerate digraph mapping $f:G\to H$ such that $\psi \circ f\left(e\right)=\phi \left(e\right)$ for all $e\in E_G$.

Thus, we obtain a category $\mathcal{CE}$ in which objects are edge colored digraphs and morphisms are given by non-degenerate digraph mappings that commute with colorings.

Definition 12.

The line digraph of a digraph $G=(V_G,E_G)$ is the digraph $L\left(G\right)=G^{*}=(V^{*},G^{*})$ obtained from G by associating with each edge $e=(v\to w)\in E_G$ a vertex $e^{*}\in G^{*}$, and there is a directed edge $e_1^{*}\to e_2^{*}$ for $e_1=(v_1\to w_1),e_2=(v_2\to w_2)\in E_G$ if and only if $w_1=v_2$.

An edge coloring $\phi$ of a digraph G induces a vertex coloring $L\phi ={\phi }^{*}$ of the digraph $G^{*}=(V^{*},G^{*})$ by the rule ${\phi }^{*}\left(e^{*}\right)=\phi \left(e\right)=\phi (v\to w)$ for $e=(v\to w)\in E_G$. The example of the application of the functor L is given in Figure 4. Directly from the definitions above we obtain the following result.

Lemma 1.

Any morphism $f:(G,\phi )\to (H,\psi )$ of edge colored digraphs define a morphism $Lf=f^{*}:(G^{*},{\phi }^{*})\to (H^{*},{\psi }^{*})$ of vertex colored digraphs given on the set of vertices by the rule $f^{*}\left(e^{*}\right)={\left[f\left(e\right)\right]}^{*}$. Thus, we obtain a functor $L:\mathcal{CE}\to \mathcal{C}$

Now we define k-colored homology groups ${\mathcal{H}}_{*}^k(G,\phi )$ of the edge colored digraph putting

$${\mathcal{H}}_{*}^k(G,\phi )=H_{*}^k(LG,L\phi ).$$

(40)

Theorem 8.

The k-colored homology groups ${\mathcal{H}}_{*}^k(G,\phi )$ of edge colored digraphs define a functor from the category $\mathcal{CE}$ to the category R-modules.

Proof. 

Follows from Theorem 2 and Lemma 1. □

Example 7.

Consider the edge colored digraph G in Figure 5 with the set of edges $E_G=\{0,1,2,3,4\}$. The vertex colored digraph $LG$ is presented now in Figure 5. Let $R=\mathbb{R}$. Now similarly to computing in Section 4 and Section 5 we find

$${\mathcal{H}}_n^1(G,\phi )=\left\{\begin{array}{cc}{\mathbb{R}}^5\hfill & \mathit{for}n=0,\hfill \\ 0\hfill & \mathit{for}n\ge 1,\hfill \end{array}\right.$$

and

$${\mathcal{H}}_n^2(G,\phi )=\left\{\begin{array}{cc}\mathbb{R}\hfill & \mathit{for}n=0,\hfill \\ {\mathbb{R}}^2\hfill & \mathit{for}n=1,\hfill \\ 0\hfill & \mathit{for}n\ge 2.\hfill \end{array}\right.$$

Figure 5. The edge colored digraph G and vertex colored digraph $LG$.

Remark 2.

Any edge colored graph defines a symmetric edge colored digraph and it is an easy exercise to construct the k-colored path homology theory using the notion of the line graph and the methods of Section 5.

7. Conclusions

The discrete algebraic topology stems from the problems provided by discrete mathematical physics, discrete differential geometry, and analysis [14,16,17,21]. The first results for the discrete homotopy theory were obtained in [15,20,22]. The path homology theory has been constructed recently in [2,3,5,6]. This theory is a natural generalization of the simplicial homology theory and satisfies the properties that are similar to Eilenberg–Steenrod axioms [1]. First applications of discrete algebraic topology to graph coloring are given in ([2], §5) and ([23], §6). These results are based on the discrete homotopy theory and discrete fundamental groupoid of the digraph.

In the present paper, we have constructed a collection of new homology invariants of colored digraphs using homology of path complexes with the natural restriction that is given by digraph coloring. We have described functorial properties of introduced homologies and constructed a spectral sequence for colored homology groups. To our knowledge, before the results given in this paper, no effective methods for computing path homology groups by using natural filtrations were known. The spectral sequence gives an effective tool for computing path homology groups of an arbitrary (di)graph. In our paper, the main constructions are given for colored digraphs but in Section 6 we describe the possibility of transferring this theory to the category of graphs and the category of edge colored (di)graphs.