Abstract
Recent a few years have witnessed the rapid expansion of the peer-to-peer lending marketplace. As a new field of investment and a novel channel of financing, it has drawn extensive attention throughout the world. Many investors have shown great enthusiasm for this field. However, investors are at the disadvantage of information asymmetry, which is a key issue in this marketplace that is unavoidable and can lead to moral hazard or adverse selection. In this paper, we propose an -regularized weighted logistic regression model for default prediction of peer-to-peer lending loans from investors’ perspective, which can reduce the impact of information asymmetry in the process of loan decision. Rather than solely focus on the accuracy of the prediction, we take into consideration the different risk preferences of different investors. We try to find a trade-off between the risk of losing principal and that of losing potential investment opportunities on the basis of investors’ risk preferences. Meanwhile, due to the nature of peer-to-peer lending loans, we add an -regularization term to reduce the chance of overfitting. Xu’s algorithm for -regularization problems is applied to solve our model. We perform training, in-sample test, and out-of-sample test with data from LendingClub. Numerical experiments demonstrate that regularization could enhance out-of-sample the area under the Precision–Recall curve (AUPRC). By applying the proposed model, the risk-averse investors could apply a higher penalty factor to lower the risk of losing principal at the cost of the loss of some potential investment opportunities according to their own risk preferences. This model can help investors reduce the impact of information asymmetry to a great extent.
1. Introduction
Peer-to-peer lending (also known as people-to-people lending, person-to-person lending, or social lending), often shorted as P2PL, a form of crowdfunding, is an online practice of individuals or businesses lending money to other individuals or businesses without going through a traditional financial intermediary. A classical P2PL model involves three basic elements: investors (supply), borrowers (demand), and a platform. In the modern financial market, investors have a variety of choices, such as stocks, bonds, futures. However, P2PL enables small investments as low as $25, which may have little chance of investment elsewhere. Meanwhile, it would help investors diversify their traditional portfolios. Additionally, interest rates offered by P2PL are usually more competitive than those of traditional banks while it can build connections between borrowers and investors faster and cheaper than any bank. Compared to stock markets, P2PL investments enjoy lower volatility and correlation. These merits make it a good alternative to traditional investments.
However, investors in this marketplace should be extremely cautious since its special risk characteristics. Loan applicants are individuals with all kinds of uncertainty. Default is more likely to happen than bonds or T-bills. Information asymmetry is a key issue in this marketplace, which can result in moral hazard or adverse selection [1]. As it comes to the loan decision, investors are at a disadvantage to the borrower, where the borrower has near-complete information while the investors can only access the information provided by the platform. Though P2PL platforms seek to reduce the impact of information asymmetry via many mechanisms, investors should also take information asymmetry into consideration in loan decision. From investors’ perspective, an effective default prediction would help to protect their profits and principle in such a marketplace. P2PL platforms usually provide a mass of information, thought not as much as that possessed by the borrower, which will help investors in loan decision making.
In the next section, we will introduce the peer-to-peer lending marketplace in detail.
2. Theoretical Background
2.1. Development of Peer-to-Peer Lending in Marketplace
As a novel financial model, P2PL has attracted public attention over the past decade when many P2PL companies came into being across the world.
The first company to offer peer-to-peer loans in the world, ZOPA, was founded in Britain in 2005. The name, ZOPA, which stands for “zone of possible agreement”, is a negotiating term that identifying the bounds within which agreement can be reached between the two parties [2]. Prosper Marketplace, the first P2PL company in the United States, was also founded in 2005. It began operations in February 2006 and was the only P2PL company in the United States until May 2007, when LendingClub was founded. In the beginning, Prosper issued loans to anyone who had the interest to get a loan, which caused most of its investors to get negative returns. At that time, Prosper offered only unsecured consumer loans but not small- and medium-sized enterprise (SME) loans. In 2008, Prosper was temporarily shut down because of scrutiny by the Securities and Exchange Commission (SEC). SEC issued a formal cease-and-desist letter to explain that Prosper should be considered as a seller of securities and should be regulated by the SEC [3].
LendingClub was first introduced as a Facebook application. With rapid growth, it emerged as a standalone website within a couple of months. It was the first P2PL company that registered its offerings as securities with SEC. It offers loans from $1000 to $35,000 for individuals and from $15,000 to $300,000 for SME. Currently, LendingClub is the largest P2PL platform in the world.
In 2007, TrustBuddy, the first P2PL company in Sweden, began operations. Now it is a peer-to-peer group that operates in five European countries under three different brand names (Geldvoorelkaar, Crowdfunding Society and TrustBuddy).
The first P2PL company in China was also set up in the year 2007, named “Paipaidai”. This marketplace has undergone extremely rapid growth in the past few years. In 2015, the national P2P net loans turnover has increased 258.62% compared to the year 2014 and reached RMB 1180.6 billion and 3844 platforms reported to be operating [4].
Funding Circle, a P2PL platform founded in the UK in August 2010, entered the US in October 2013. It only processes SME loans and operates in the US, UK, Germany, and the Netherlands.
Upstart, founded in April 2012 in San Carlos, California, by a group of ex-Googlers, was first launched with an Income Share Agreement (ISA) product that enabled individuals to raise money by contracting to share a portion of future income. Later, it pivoted away toward the personal loan marketplace. Upstart operates differently in many ways from other P2PL platforms. The firm specifies its target niche as young professionals. It applies unique grading criteria taking into consideration not only Fair Issac Credit Organization (FICO) scores but also educational background information and employs a so far remarkably accurate modeling system at predicting future defaults and returns. This helps the firm enjoy the lowest default rates across the P2PL industry up to 2017.
Some other countries also opened up P2PL industry in recent years, such as Australia, India, Israel, Canada, and Brazil.
2.2. Literature Review
Although P2PL is a relatively young field of research, it has been extensively studied in the past decade. Since the first P2PL platform ZOPA launched, research on this new lending pattern gains increasing attention. Wang et al. [5] provide an overview of the concepts and discussed some different P2PL marketplace models in detail. Prosper and LendingClub gave great impetus to research on P2PL by giving full public access to their data. Traditional research work on P2PL mainly focused on funding success, that is, looking for the features with which loan applicants are more likely to succeed, such as [6,7]. Among a variety of research topics on P2PL, default prediction has always been in the spotlight since its significance for borrowers. Ajay et al. [8] propose a credit scoring model to perform default prediction based on artificial neural networks. They are also aiming to reduce the risk of investment failure. The numerical results show a 64.47% of the non-default loans and 74.75% of the default loans are correctly classified for training data while 62.70% of the non-default loans and 74.38% of the default loans are correctly classified for testing data. Jiang et al. [9] apply a tex analysis method and latent Dirichlet allocation (LDA) model to extract soft information from text to be combined with hard information. Then they present a prediction model based on a two-stage feature selection method. Kim and Cho [10] consider an ensemble semi-supervised learning method taking into account both labeled data and unlabeled data.
Other research mainly includes investment strategy designation, the role of P2PL in financial market, information asymmetry, interest rate, etc., to name a few [11,12,13,14,15].
2.3. Peer-to-Peer Lending Process
For a potential borrower, the first step is to submit an application to a P2PL platform, which usually contains the information about the borrower and the loan he would like to apply for, such as loan amount, annual income, and Social Security Number (SSN).
After receiving the application, the platform will access the status of the potential borrower with its own system taking into account information provided by the applicant and also the information obtained through the applicant’s SSN, such as Fair Issac Credit Organization (FICO) score, debt-to-income (DTI) ratio, and other credit information. Based on this information, the platform decides whether to approve the loan. This process is usually called loan application processing. Different platforms may differ in loan application processing scheme and also in the way to set the interest rate.
Once a loan is approved by the platform, detailed information about the loan and the applicant will go public online. Potential investors have a period of time to review the loan information and make the decision to invest or not. A loan is issued if it collects enough funding within this period of time; otherwise, the loan is dismissed and the money collected will go back to investors’ accounts.
After the loan is issued, the borrower gets the money collected and makes monthly payment to repay. The platform charges a scheduled rate of fee for service.
Although platforms tried to provide qualified loans with complex loan application processing systems, investors may get negative returns at the maturity of the loan due to the investment risks involved in P2PL.
2.4. Investment Risk of Peer-to-Peer Lending
Investment in P2PL may face many types of risks, just as other financial instruments do, including but not limited to: default risk, bankruptcy risk, regulatory risk, interest rate risk, prepayment risk, and liquidity risk.
The main risk in P2PL is default risk, which related to the loans selected to invest, i.e., investors’ investment strategies will affect the default risk exposure of a portfolio to a great extent. Other types of risks may not have as much effect as default risk since the risk events may be unlikely to happen or measured in the sense of opportunity costs. We would like to introduce several main risks to investors below.
2.4.1. Default Risk
Default risk is the chance that borrowers may be unable to repay their loans entirely or partially, and it is the main risk that investors in P2PL will encounter. Many works have investigated into default prediction, see [16], including default prediction in P2PL [17,18,19]. However, these works depend on meta-level phone usage data, which is not available for general investors.
2.4.2. Bankruptcy Risk of P2PL Platform
Investors of P2PL may face the risk that platforms shut down, especially when the P2PL industry goes crazy. For example, in 2011, Quakle, a UK P2PL company closed down with a nearly 100% default rate due to the unsuccessful attempt to measure borrowers’ creditworthiness. This type of risk is closely related to default risk. We could go further and say bankruptcy risk of P2PL platforms mainly caused by borrows default.
However, this type of risk is fairly low in the current stable economic environment. With the improving regulatory enforcement, choosing a legal compliance P2PL platform could help to reduce the bankruptcy risk of the platform to a negligible level.
2.4.3. Regulatory Risk
Regulatory risk is the risk that a change in regulations or laws which will materially impact the whole industry. Generally, events which involve regulatory risk occur in the early years of market establishment, when the market is premature or when notable events happen. LendingClub temporarily shut down lending operations from April 2008 to October 2008 and Prosper did not offer investment opportunity from October 2008 to July 2009. Both platforms were preparing to file the registration statement with the SEC [20]. In China, at least 246 P2PL platforms were shut down during the first half of 2016 since tightening of regulation according to a report by cnr.cn.
However, most of the time, regulatory risk is unpredictable and uncontrollable. Fortunately, it is unlikely to happen when the market is in normal operation.
2.4.4. Interest Rate Risk
Interest rate risk is the risk that arises for fixed income securities owners from interest rates fluctuation. As reported by SEC, all bonds are subject to interest rate risk, even if they are insured or government guaranteed. This type of risk is mainly affected by the overall economic climate and maturity of the security. That is, securities in the same market and with the same maturity face similar interest rate risk. Loans on one platform in P2PL are of this kind of situation.
2.4.5. Prepayment Risk
Platforms usually allow extra payments and full prepayment. These payments could be made any time and would be applied directly to the borrower’s principal balance. It would decrease the total cost of the loan by reducing the principal balance and the total interest that borrowers pay on this amount. That is, for investors, prepayment would reduce the return lower than a prospective return.
2.4.6. Liquidity Risk
Investors of P2PL would also face liquidity risk, which is the risk that stems from the lack of marketability. In the case of LendingClub, investors should be prepared to hold any note purchased through to its maturity. Even though there is a secondary market, Folio Investing, there is no guarantee that investors will find buyers for their notes. This type of risk is common in most bond markets.
Due to the risk characteristics involved, default events happen from time to time. This makes default prediction necessary for investors, especially for this marketplace has a high level of information asymmetry. From historical statistics, we can see that default loans are relatively few compared to loans successfully repaid. Taken default prediction as a binary classification problem would confront the problem of class imbalance. Meanwhile, overfitting is another problem since there are too many features in P2PL data, especially considering the introduction of dummy variables, while simply deleting some of them may cause loss of information. Additionally, different investors may have different risk preferences, which makes traditional classification models impracticable for every investor.
In this paper, from the investors’ perspective, we develop an -regularized weighted logistic regression model for default prediction of P2PL loans. A penalty factor on the negative class is applied to deal with class imbalance. Additionally, by adjusting this parameter, investors can weigh the risk of losing principal and that of potential investment opportunities according to their own risk preferences. The introduction of regularizer help to reduce the chance of overfitting. We also give out a proof of the convergence of Algorithm 1 for this model. Finally, we test the performance of -regularized weighted logistic regression model by applying it to the data from LendingClub.
| Algorithm 1 Xu’s Algorithm |
|
The rest of this paper is organized as follows. In Section 3, we establish the -regularized weighted logistic regression model and explain its application in default prediction. We apply Algorithm 1 to solve this model, and we give out a proof of the convergence result. In Section 4, we explain the performance measure in use. We carry out numerical experiments with the data from LendingClub to test the performance in Section 5. Finally, we come to a conclusion in Section 6.
3. Default Prediction by Regularized Weighted Logistic Regression
Throughout the duration of a loan, there would be several types of loan statuses. Here, we only focus on the statuses possibly at the expiration.
For LendingClub, loans may take one of the following statuses (For more details of loan statuses on LendingClub, see https://help.lendingclub.com/hc/en-us/articles/215488038-What-do-the-different-Note-statuses-mean-) at its predetermined maturity date.
- Fully Paid: The loan has been fully repaid, either at the expiration of the 36- or 60-month term, or as a result of a prepayment.
- Current: The loan is up to date on all outstanding payment.
- In Grace Period: There will be a 15-day grace period if the loan past due.
- Late (16–30): The loan has not been current for 16 to 30 days.
- Late (31–120): The loan has not been current for 31 to 120 days.
- Default: The loan has past due for more than 121 days.
- Charged Off: The loan for which there is no longer a reasonable expectation of further payments. Upon Charge Off, the remaining principal balance of the note is deducted from the account balance.
Usually, the platform has a complicated loan applications processing scheme to determine whether to issue or reject a loan application. It helps to distinguish qualified loan applications from unqualified ones to a great extent. For example, up to the first quarter of 2019, LendingClub has issued about 2 million loans, while more than 30 million loans have been declined which account for 93.78% of total loan applications. However, among the issued loans, only about 0.96 million loans have been fully paid, and about 1.1 million are with the status “Current”, which means the loan is up to date on all outstanding payment. There are still about 0.28 million loans not likely to be paid back with statuses “In Grace Period”, “Late (16–30)”, “Late (31–120)”, “Default”, or “Charged Off”, which would lead to significant capital loss to investors. Detailed loan status statistics of the loans issued up to the first quarter of 2019 are shown in Table 1 (Data are drawn from LendingClub, https://www.lendingclub.com).

Table 1.
Loan status statistics up to the 1st quarter of 2019.
We train the model with loans that already past the predetermined maturity, where “Current” means the borrower must have missed or been late for at least one payment. Throughout this paper, we take “Fully Paid” as one category and all the others as the other category, named “Not Fully Paid”. As shown in Table 1, the datasets are highly imbalanced. Therefore, the default prediction turns into a binary classification problem with class imbalance. In this binary classification, we take the status of loans as the target variable, where 1 denotes Fully Paid and 0 denotes Not Fully Paid; while, the independent variables are chosen from features of loans accessible to investors. We will discuss the features in detail later in Section 5.1.
Notation: Suppose we have a sample of size n,
where and . Here, represents the jth feather of the ith loan and is the loan status of the ith loan taken from , where 0 represents Not Fully Paid (negative class) and 1 represents Fully Paid (positive class). Without loss of generality, we assume any two loans are independent. That is, if one borrower defaults, it is not likely to affect the probability of a default event of any other borrower.
3.1. Standard Logistic Regression
Logistic regression is a machine learning algorithm borrowed from statistics. It is an important topic in both fields. Since y is the label, it is an indicator variable taking value from . Obviously, . Then, the conditional probability is the conditional expectation of the indicator, i.e., . Denote the p-value involved with some parameter as , where .
From the independence of , we have
In the standard logistic regression model, the conditional probability distribution of the label y given the feature vector can be formed as
and
where . Here, is the logistic function (also known as sigmoid function) defined as
The standard logistic regression model can be built by minimizing the negative log-likelihood (NLL) ,
3.2. Weighted Logistic Regression
In loan default prediction, the Type I error (also known as False Positive), which happens when a classifier incorrectly classifies a Not Fully Paid loan as a Fully Paid loan, is more serious than the Type II error (also known as False Negative), which is the misclassification of a Fully Paid loan as a Not Fully Paid loan. That is because the Type I error will lead to real loss of capital and it is what we want to avoid at all cost; while the Type II error means loss of potential investment opportunities, which is not as dangerous as the Type I error. Thus, we are more reluctant to accept Type I errors.
Since for a given sample size, the probability of making a Type I error and that of making a Type II error cannot be reduced simultaneously, we need to judge and weight Type I and Type II errors.
Tsai, Ramiah, and Singh state that precision is a more suitable statistical measure of performance in this situation and introduce a penalty factor into log-likelihood [21] as,
where, is a penalty factor (weight) on the negative class.
Obviously, for a given sample size, a high will decrease the probability of a Type I error, even if meanwhile it will increase the probability of a Type II error. This modification could yield higher precision at the cost of recall and prediction accuracy. Their numerical experiments on the data of LendingClub also suggest that for this problem weighted Logistic Regression outperforms LibSVM, Naïve Bayes, and Random Forest.
3.3. Regularized Weighted Logistic Regression
Since classical logistic regression may cause over-fitting when the sample size is not large enough compared to the dimension of features [22], i.e., does not hold. The introduction of a penalty factor on the negative class can cope with the problem of data imbalance but cannot alleviate the problem of over-fitting.
Let us consider some techniques, such as regularization, which is one of several useful techniques to overcome this weakness [23] taking the form,
where is a loss function; denotes the quasi-norm. Here, is the regularization parameter used to weight between the loss function and the regularization term .
Zongben et al. [22] introduce an regularizer since it can be solved easier than regularizer, which yields the most sparse solutions but faces the problem of combinatory optimization. Meanwhile, regularizer is more sparse and stable than the regularizer which often yields solutions less sparse than regularizer and is inefficient when the error follows a fat tail distribution. Moreover, Xu shows the unbiasedness and Oracle properties, and presents an iteration algorithm to solve the regularizer.
Hence, by taking advantages of regularizer, our objective is
Zongben et al. [22] also present an iteration algorithm which transforms the solution of the regularizer into a series of convex weighted Lasso. Here, we apply this algorithm to solve the default prediction by a modification of the termination criterion. However, we use to approximate the regularizer instead of which would help to correct the proof in their work.
In order to avoid the error of , has been replaced by , where is an arbitrary small number.
In the iterative process, some of may become zero.
Theorem 1.
Given , converges to the set of stationary points of .
Proof.
From the definition of p,
we have
Then, the gradient and Hessian matrix of the function are as below,
and
Since , we have . That is, is positive semi-definite.
Now, we define a function associated with as,
where, and are the positive part and negative part of , respectively. Obviously, it holds, , and
Similarly, we have the gradient and Hessian matrix of as,
and
From the positive definiteness of , we have . Thus, the function is convex in , i.e.,
Denote and , where and . Similarly, we define functions associated with and associated with as,
and
Clearly, we have,
and
Further, we define associated with and associated with as,
Thus, it holds
and
Hence,
From the optimality condition of , we have
In order to show the concavity of with respect to , we can easily compute the gradient based on its definition in Equation (13) as follows,
Since we know that,
where, , . Then, the Hessian of is,
and ,
Therefore, is concave with respect to , .
It follows directly from the concavity of that
which, in view of Equations (14) and (25), implies that
From the definition of , we can see , . That is, is monotonically decreasing function and bounded below. As stated in [22], by the LaSalleś Invariance Principle, converges to the set of stationary points of as . □
4. Performance Measure: Accuracy, Precision, and Recall
Since assessing the performance of a classifier is crucial in evaluating a classification model, we need to choose one or more proper performance measures.
For binary classification, a confusion matrix is usually used [24]. It summarizes the classification performance of a classifier in four categories: true positive (TP), false positive (FP), false negative (FN), and true negative (TN), as shown in Table 2. TP and TN outcomes are those classified correctly while FP and FN represent Type I error and Type II error, respectively.

Table 2.
Confusion Matrix.
A variety of common evaluation metrics can be derived from the confusion matrix, such as:
and
For imbalanced data, the application of accuracy and error rate results in a poor performance for the minority class, see [25].
Later, to cope with measure of classifiers for imbalance data, people develop some other evaluation metrics, to name a few, recall (also known as true positive rate (TPR), sensitivity), precision (also known as positive predictive value (PPV)), false positive rate (FPR), defined as:
Thereafter, based on these metrics, the receiver operating characteristic (ROC) curve, the area under the ROC curve (AUROC, or just AUC), the Precision–Recall (PR) curve and the area under the PR curve (AUPRC) are developed. The ROC curve is a two-dimensional plot of classifier performance, which is obtained by plotting the TPR vs. the FPR for every possible classification threshold. It is useful for visualizing and evaluating the overall classification performance. To facilitate comparison, AUROC has been proposed, which summarizes the classification performance into a single number. The PR curve is an alternative of the ROC curve that can visualize the performance of binary classification while AUPRC is its counterpart of AUROC.
As shown in Table 1, the data set is highly imbalanced. To balance between the risk of losing principal with potential investment opportunities, we care both the recall and precision. Therefore, AUPRC is more informative [25] in this case. Accuracy is also presented and we explain why it is not suitable here.
5. Experiments
We present the numerical results based on the historical loan information and data from LendingClub.
5.1. Data Description
LendingClub regularly updates the status of loans currently listed in data set available to download on a monthly basis and adds new loans data quarterly. In the data, the features include not only standard hard financial information commonly used by bank, such as annual income, debt-to-income ratio, FICO score range, but also non-standard information, such as description of the purpose of raising the loan, professional title. There are 151 features available in total. For more details of features available, we refere to the data dictionary provided by LendingClub (Data dictionary can be downloaded at https://resources.lendingclub.com/LCDataDictionary.xlsx). The number of features available may change over time.
The target variable of this experiment is loan status, while independent variables are carefully chosen from these 151 features. We take only the features can be described numerically into account, including numeric features and categorical features. Free text fields, such as emp_title, purpose, are removed. We finally take 62 features into consideration. To name a few,
- dti: Data to income ratio, a ratio calculated using the borrower’s total monthly debt payments on the total debt obligations, excluding mortgage and the requested LendingClub loan, divided by the borrower’s self-reported monthly income;
- emp_length: Employment length in years. Possible values are between 0 and 10 where 0 means less than one year and 10 means ten or more years;
- fico_range_high: The upper boundary range the borrower’s FICO at loan origination belongs to;
- fico_range_low: The lower boundary range the borrower’s FICO at loan origination belongs to;
- last_fico_range_high: The upper boundary range the borrower’s last FICO pulled belongs to;
- last_fico_range_low: The lower boundary range the borrower’s last FICO pulled belongs to;
- funded_amnt: The total amount committed to that loan at that point in time;
- last_pymnt_amnt: Last total payment amount received;
- max_bal_bc: Maximum current balance owed on all revolving accounts;
- inq_fi: Number of personal finance inquiries;
- zip_code: The first 3 numbers of the zip code provided by the borrower in the loan application;
- home_ownership: The home ownership status provided by the borrower during registration or obtained from the credit report. This is a categorical variable and possible values are: RENT, OWN, MORTGAGE, OTHER.
Here, we transform categorical features into binary features with dummy variables since they cannot be entered directly into a regression model and meaningfully interpreted. For more details about dummy variables, we refer to [26]. In addition, normalization of features is recommended to put different variables on the same scale in case there may be some features with far greater values than others, for instance, loan amount and annual income.
In this experiment, we choose data from the loans that already past the predetermined maturity. We consider loans with a 36-month maturity issued from 2013 to the first quarter of 2016 (2016Q1). The training sample size is 1000, while the testing sample size is 300. After gathering the data we first need to clean and prepare the data. Upon addressing missing data, special attention should be paid since we may introduce bias at this step if the data are not missing at random. We transform date information to time length from the date to the day we perform this experiment. In particularly, the feature emp_length seems numeric, since it ranges from 0 to 10. However, since 0 means less than one year and 10 means ten or more years, it is actually a categorical feature. We transform such categorical features into binary features with dummy variables by replace a feature of c categories with dummy variables. Then, we apply normalization. Later, highly correlated predictors should be removed in order to reduce multicollinearity. Finally, we split the data into training sample set and testing sample set for in-sample tests and out-of-sample tests, separately.
As mentioned above, the datasets we considerate are highly imbalanced. Table 3 shows the imbalance ratios of sample sets, defined as the ratio of the number of instances in major class to the number of examples in the minority class. Here, the major class is Fully Paid; the minority class is Not Fully Paid.

Table 3.
Imbalance ratio.
5.2. Numerical Results
This section contains training, in-sample test, and out-of-sample test results for the year 2013, 2014, and 2015. We performed in-sample tests with instances sampled from the training sample set, while we conducted out-of-sample tests with examples sampled from the next period.
Here, we chose five different values for the penalty factor on the negative class, , based on the imbalance ratio of the dataset and five different values for the regularization parameter, , based on the value of loss function and the regularization term. When and , the model reduces to a standard logistic regression.
Figure 1, Figure 2 and Figure 3 show the AUPRC, accuracy, precision, and recall results of training, in-sample test, and out-of-sample test for 2013, 2014, and 2015. We also present the AUPRC results in Table 4.
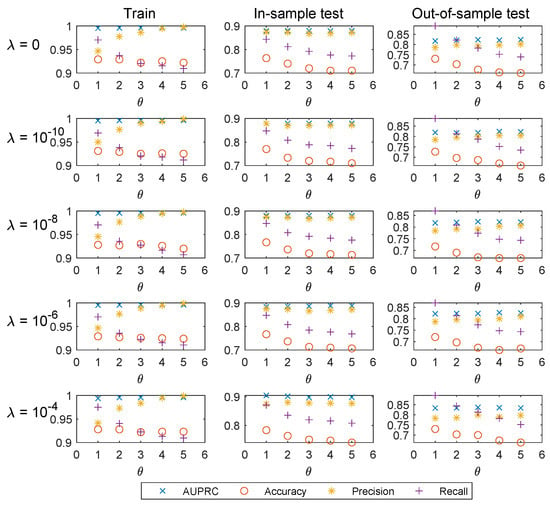
Figure 1.
Area under the Precision–Recall curve (AUPRC), accuracy, precision, and recall results of training, in-sample test, and out-of-sample test for 2013.
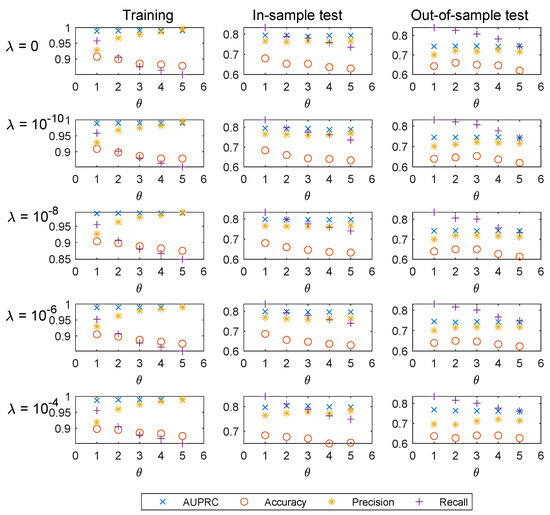
Figure 2.
AUPRC, accuracy, precision, and recall results of training, in-sample test, and out-of-sample test for 2014.
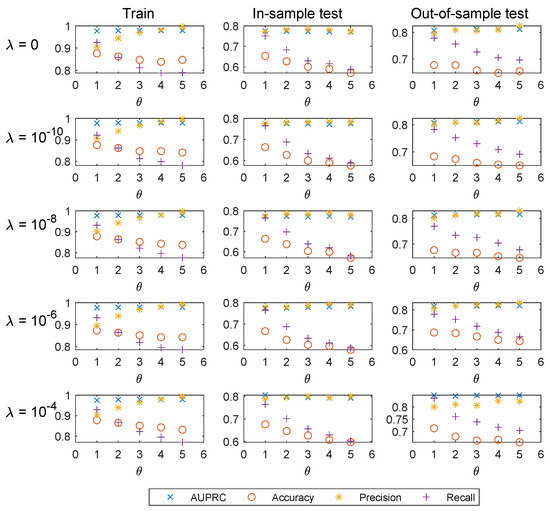
Figure 3.
AUPRC, accuracy, precision, and recall results of training, in-sample test, and out-of-sample test for 2015.

Table 4.
AUPRC results of training, in-sample test, and out-of-sample test for 2013, 2014, and 2015.
From these scatter plots, we can see accuracy performs poorly for imbalanced data. Tests with nearly the same accuracy may be far different in the number of FP samples and that of FN samples. Accuracy only shows the percentage of samples correctly classified and do not distinguish between FP and FN samples, which makes it simply does not work in our case.
As mentioned above, the probability of making a Type I error and that of making a Type II error cannot be reduced simultaneously for a given sample. Recall and precision in general change in opposite directions. As shown in the figures, for a fixed , precision results tend to increase with the increase of at the cost of the reduction in recall. Investors that are more risk-averse could apply a higher to keep the principal safer, while it may cause loss of investment opportunities.
Since the number of features taken into consideration is considerable, overfitting may happen under the standard logistic regression. Regularization could help to reduce the chance of, or the amount of, overfitting. As shown in Table 4, we present the AUPRC results of training, in-sample test, and out-of-sample test for 2013, 2014, and 2015. For a fixed , a higher regularization parameter in general yields higher out-of-sample AUPRC.
6. Discussion
The objective of this paper was to provide a method for investors in the P2PL marketplace to perform default prediction, where there exists a high-level of information asymmetry. We considered LendingClub since the availability of historical data. Since investors in P2PL are mostly individuals and small businesses. When involved in P2PL marketplace, investors are frequently adversely affected by the information asymmetry. Additionally, not every investor has a solid background in investment or quantitative finance. This makes a relatively easy and straightforward model needed.
We propose an -regularized weighted logistic model. Via only adjusting the penalty factor and the regularization parameter , investors can find a trade-off between the risk of losing principal and that of losing potential investment opportunities according to their own risk preferences and lessen the chance of, or amount of, overfitting in the meantime.
Numerical experiment shows that a higher regularization parameter yields better out-of-sample AUPRC and investors that are more risk-averse could lower the risk of losing principal at the cost of potential investment opportunities by increasing the penalty factor on the negative class according to their own risk preferences. This default prediction could help investors protect their profits and principle in the disadvantage of information asymmetry.
7. Limitations and Further Research
Since we solve the proposed model with an iterative algorithm, it has the shortcomings of longer calculation, especially when the sample size is large. Further, high performance computing could be applied to improve computing efficiency.
Author Contributions
Methodology, X.W., data curation, X.W., data curation, X.W., writing–original draft, X.W., writing–review and editing, Y.L., visualization, X.W., supervision, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (11971092).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lynn, T.; Mooney, J.G.; Rosati, P.; Cummins, M. Disrupting Finance: Fintech and Strategy in the 21st Century; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Lai, L.S.; Turban, E. Groups formation and operations in the Web 2.0 environment and social networks. Group Decis. Negot. 2008, 17, 387–402. [Google Scholar] [CrossRef]
- Smith, A.M. SEC Cease-and-Desist Orders. Adm. Law Rev. 1999, 51, 1197–1228. [Google Scholar]
- Yang, H. Comprehensive Evaluation of Online Peer-to-Peer Lending on the Province-Level Regions in China Based on Generalized Principle Component Analysis. Open J. Bus. Manag. 2016, 4, 171–176. [Google Scholar] [CrossRef]
- Wang, H.; Greiner, M.; Aronson, J.E. People-to-people lending: The emerging e-commerce transformation of a financial market. In Value Creation in E-business Management; Springer: Berlin/Heidelberg, Germany, 2009; pp. 182–195. [Google Scholar]
- Barasinska, N.; Schäfer, D. Is crowdfunding different? Evidence on the relation between gender and funding success from a German peer-to-peer lending platform. Ger. Econ. Rev. 2014, 15, 436–452. [Google Scholar] [CrossRef]
- Xia, Y. A Novel Reject Inference Model Using Outlier Detection and Gradient Boosting Technique in Peer-to-Peer Lending. IEEE Access 2019, 7, 92893–92907. [Google Scholar] [CrossRef]
- Byanjankar, A.; Heikkilä, M.; Mezei, J. Predicting credit risk in peer-to-peer lending: A neural network approach. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 719–725. [Google Scholar]
- Jiang, C.; Wang, Z.; Wang, R.; Ding, Y. Loan default prediction by combining soft information extracted from descriptive text in online peer-to-peer lending. Ann. Oper. Res. 2018, 266, 511–529. [Google Scholar] [CrossRef]
- Kim, A.; Cho, S.B. An ensemble semi-supervised learning method for predicting defaults in social lending. Eng. Appl. Artif. Intell. 2019, 81, 193–199. [Google Scholar] [CrossRef]
- Wei, X.; Gotoh, J.Y.; Uryasev, S. Peer-To-Peer Lending: Classification in the Loan Application Process. Risks 2018, 6, 129. [Google Scholar] [CrossRef]
- Wei, Z.; Lin, M. Market mechanisms in online peer-to-peer lending. Manag. Sci. 2016, 63, 4236–4257. [Google Scholar] [CrossRef]
- Liu, H.L.; Chen, H.Z.; Ding, Y.J.; Zhang, X. Research on Investment Model of Internet Financial Loan Platform. In Proceedings of the International Conference on Artificial Intelligence and Computing Science, Hangzhou, China, 24–25 May 2019; DEStech Publications: Lancaster, PA, USA; pp. 311–315. [Google Scholar]
- Cho, P.; Chang, W.; Song, J.W. Application of instance-based entropy fuzzy support vector machine in peer-to-peer lending investment decision. IEEE Access 2019, 7, 16925–16939. [Google Scholar] [CrossRef]
- Ren, K.; Malik, A. Investment Recommendation System for Low-Liquidity Online Peer to Peer Lending (P2PL) Marketplaces. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, Australia, 11–15 February 2019; ACM: New York, NY, USA, 2019; pp. 510–518. [Google Scholar]
- Calabrese, R.; Osmetti, S.A. Modelling small and medium enterprise loan defaults as rare events: The generalized extreme value regression model. J. Appl. Stat. 2013, 40, 1172–1188. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, X.; Zhou, Z.; Liu, Y. A new aspect on P2P online lending default prediction using meta-level phone usage data in China. Decis. Support Syst. 2018, 111, 60–71. [Google Scholar] [CrossRef]
- Lin, M.; Prabhala, N.R.; Viswanathan, S. Judging borrowers by the company they keep: Friendship networks and information asymmetry in online peer-to-peer lending. Manag. Sci. 2013, 59, 17–35. [Google Scholar] [CrossRef]
- Ge, R.; Feng, J.; Gu, B.; Zhang, P. Predicting and deterring default with social media information in peer-to-peer lending. J. Manag. Inf. Syst. 2017, 34, 401–424. [Google Scholar] [CrossRef]
- Smith, C.E. If it’s not broken, don’t fix it: The SEC’s regulation of peer-to-peer lending. Bus. Law Brief 2009, 6, 21. [Google Scholar]
- Tsai, K.; Ramiah, S.; Singh, S. Peer Lending Risk Predictor. CS229 Autumn. 2014. Available online: https://www.researchgate.net/profile/Sudhanshu_Singh8/publication/269699712_Peer_Lending_Risk_Predictor/links/549321420cf286fe3125b7d3/Peer-Lending-Risk-Predictor.pdf (accessed on 10 December 2016).
- Xu, Z.B.; Zhang, H.; Wang, Y.; Chang, X.Y.; Liang, Y. L1/2 regularization. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, S.; Wang, Y.; Xu, Z. L1/2 regularization: Convergence of iterative half thresholding algorithm. IEEE Trans. Signal Process. 2014, 62, 2317–2329. [Google Scholar] [CrossRef]
- Ting, K. Confusion Matrix. Encycl. Mach. Learn. 2010, 1, 209. [Google Scholar]
- Fayzrakhmanov, R.; Kulikov, A.; Repp, P. The Difference Between Precision-recall and ROC Curves for Evaluating the Performance of Credit Card Fraud Detection Models. In Proceedings of the 6th International Conference on Applied Innovations in IT, Koethen, Germany, 13 May 2018; pp. 17–22. [Google Scholar]
- Suits, D.B. Use of dummy variables in regression equations. J. Am. Stat. Assoc. 1957, 52, 548–551. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).