Discrete-Time Stochastic Quaternion-Valued Neural Networks with Time Delays: An Asymptotic Stability Analysis
Abstract
1. Introduction
2. Mathematical Fundamentals and Definition of the Problem
2.1. Notations
2.2. Quaternion Algebra
- (i)
- Addition:
- (ii)
- Subtraction:
- (iii)
- Multiplication:
2.3. Problem Definition
3. Main Results
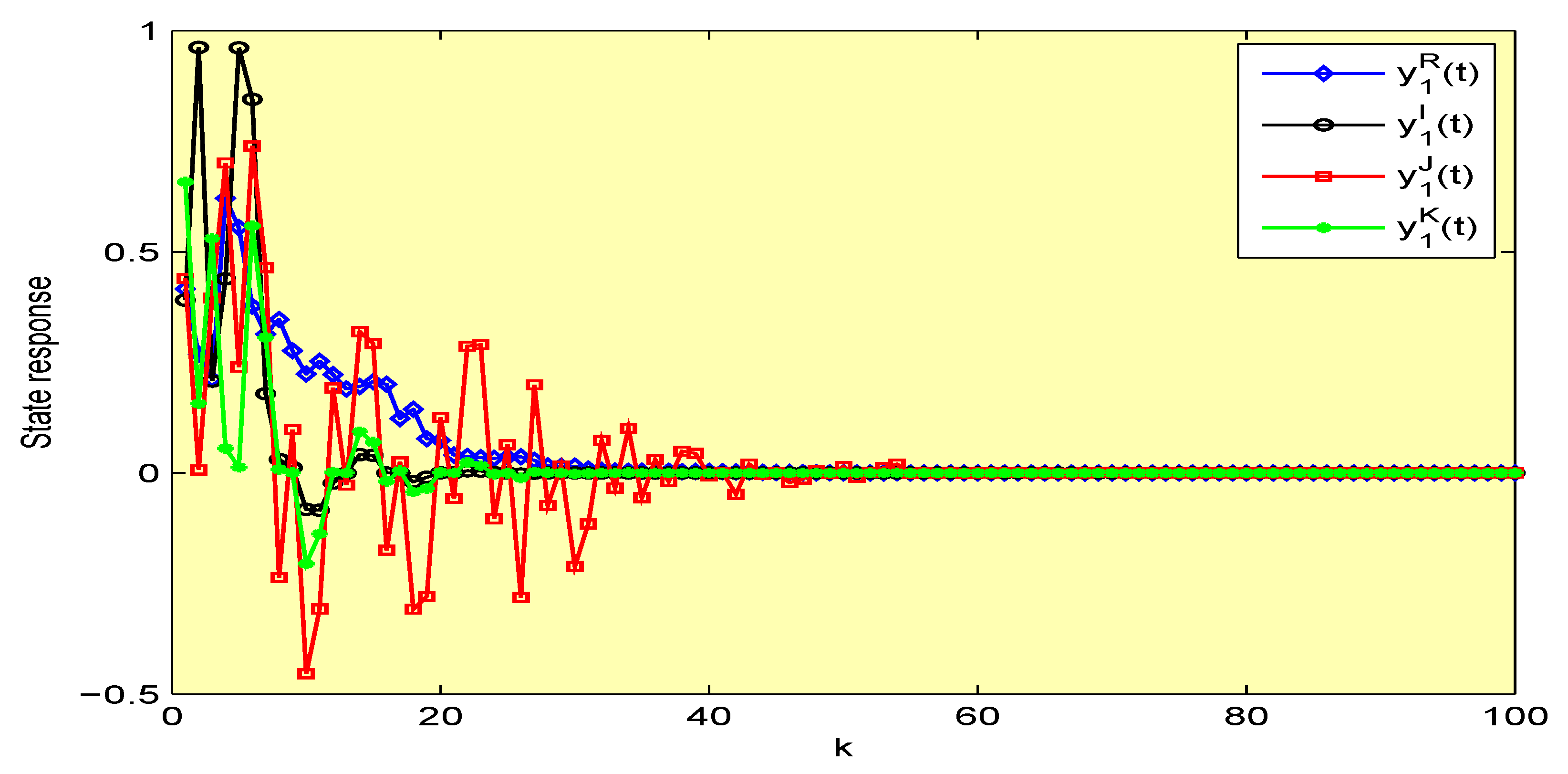
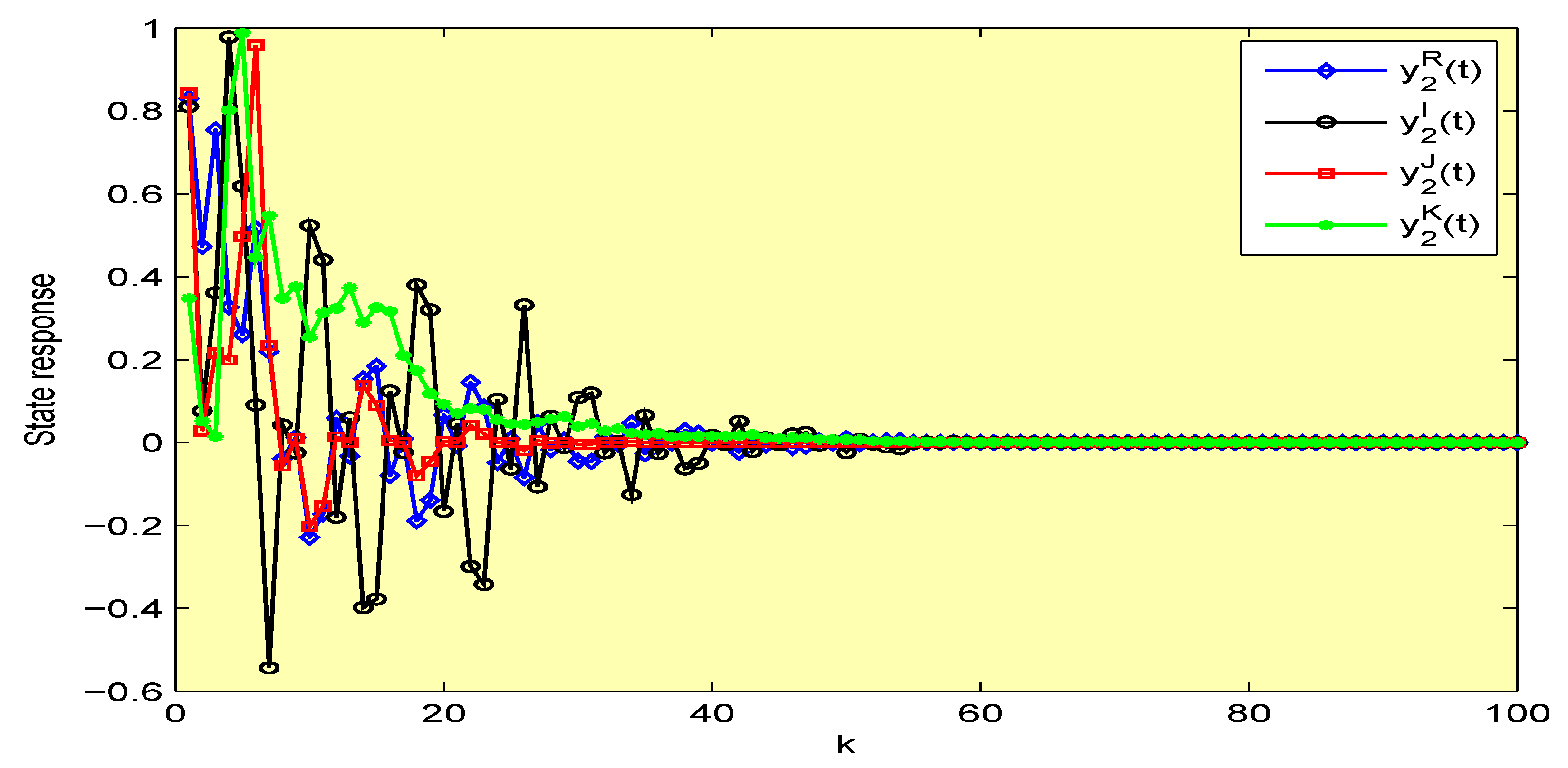
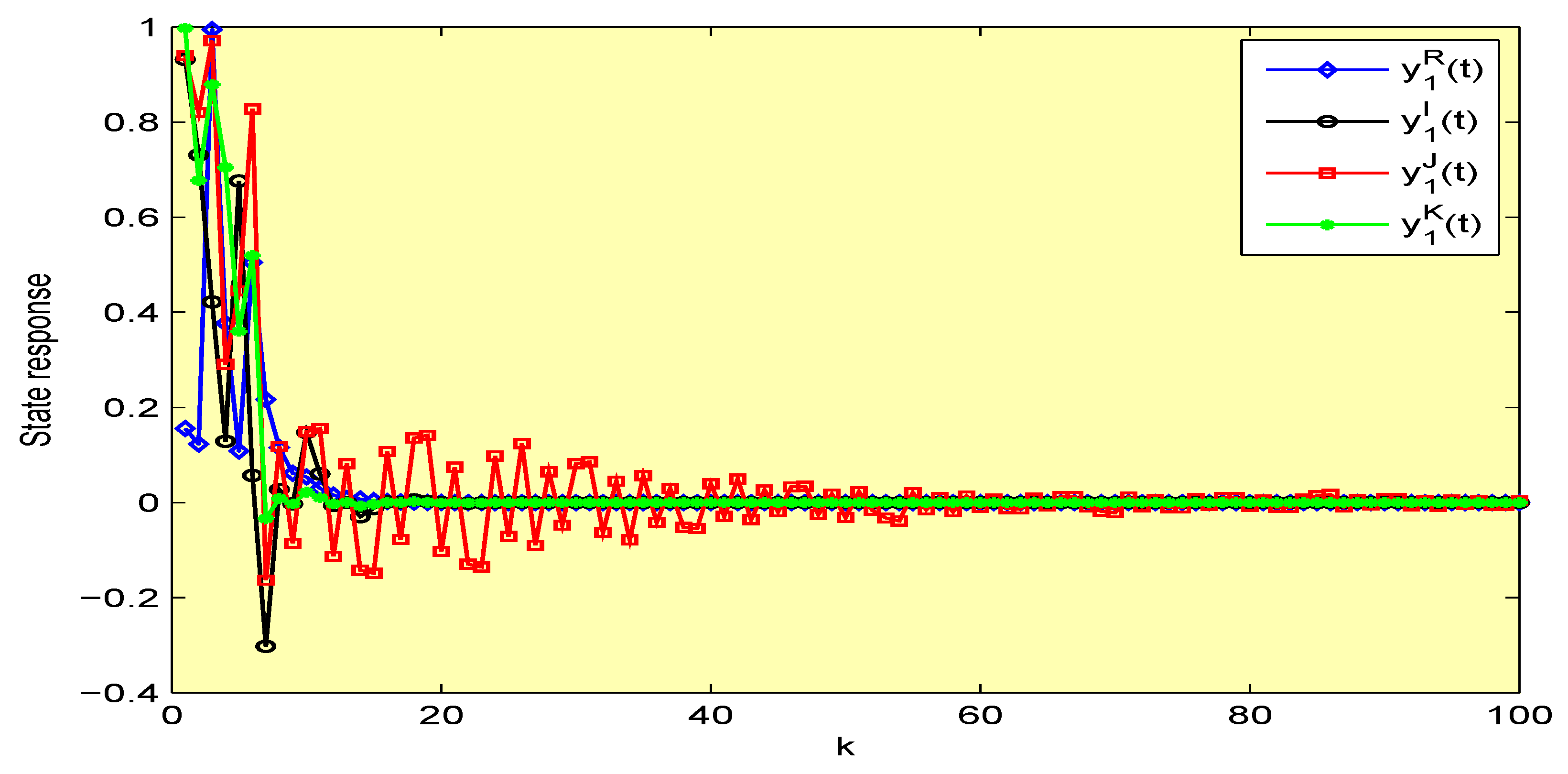
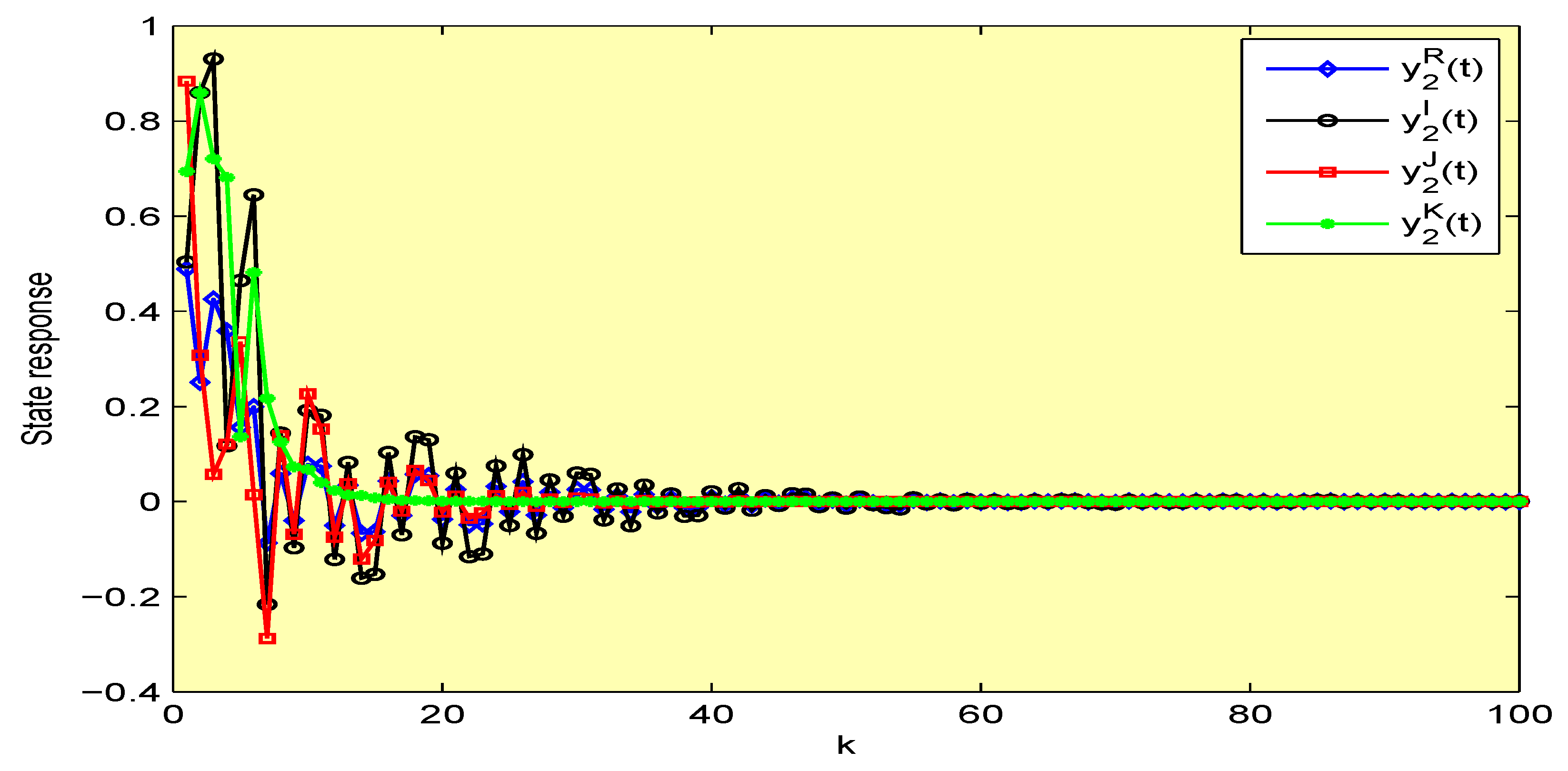
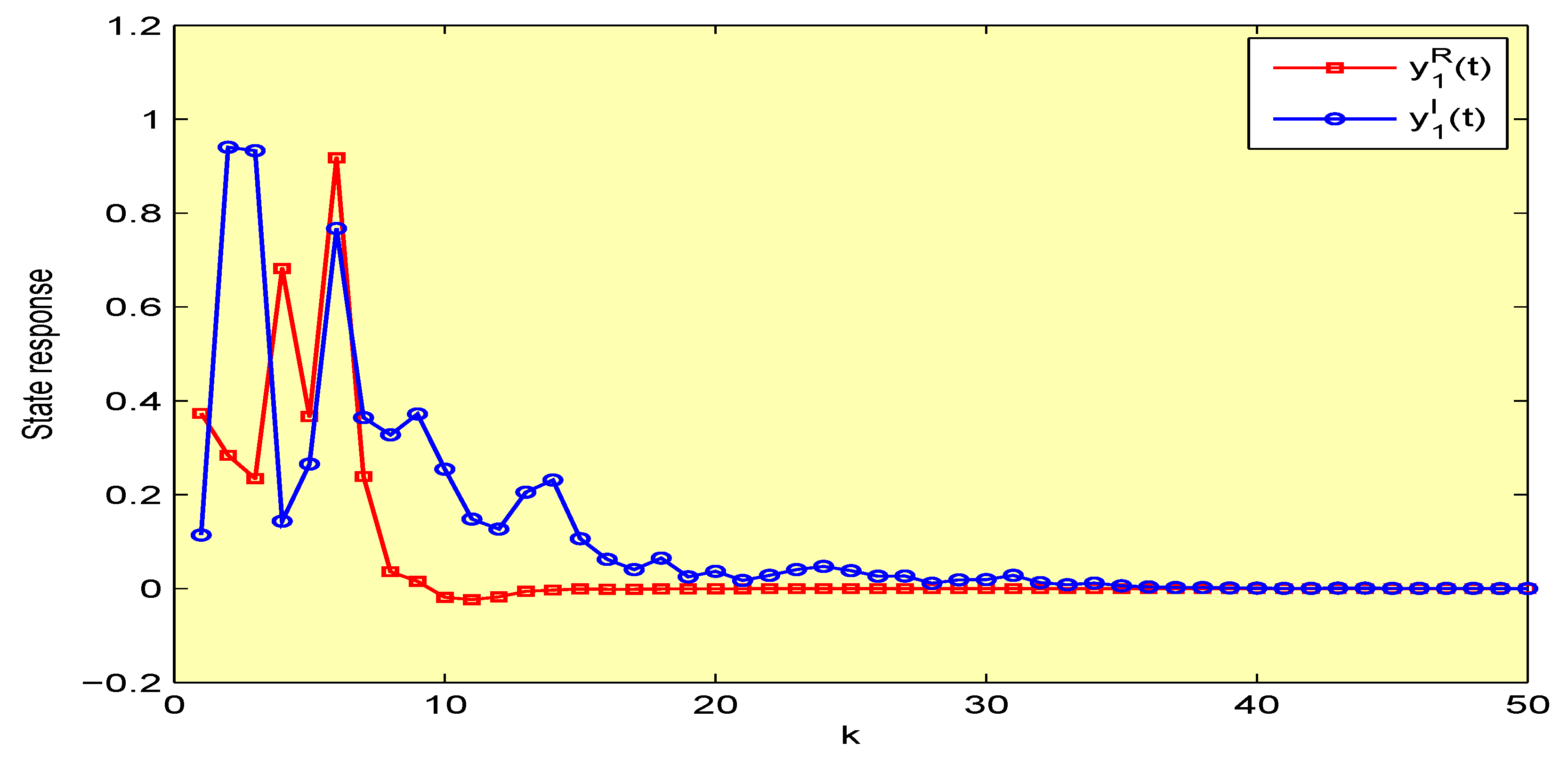
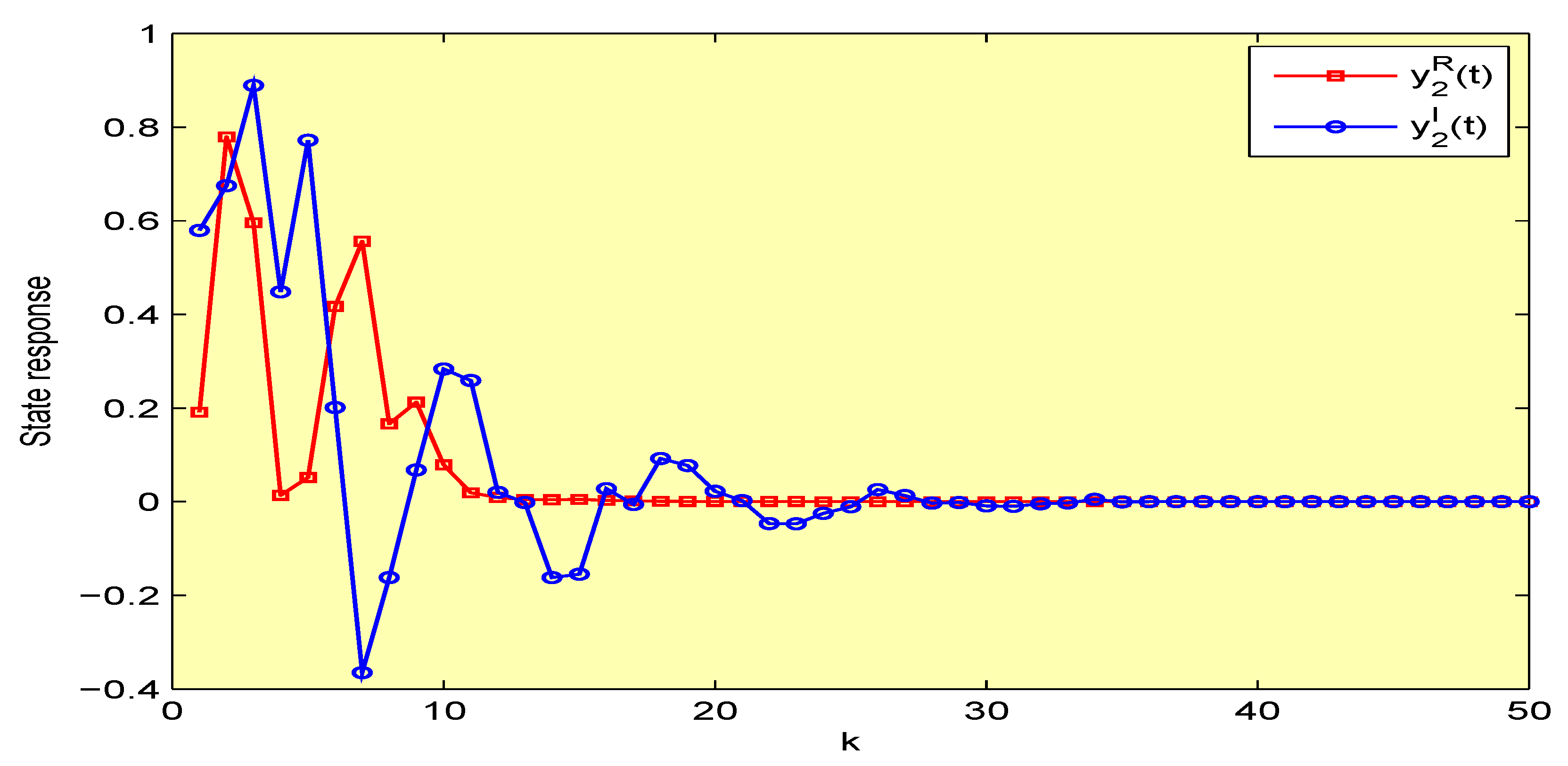
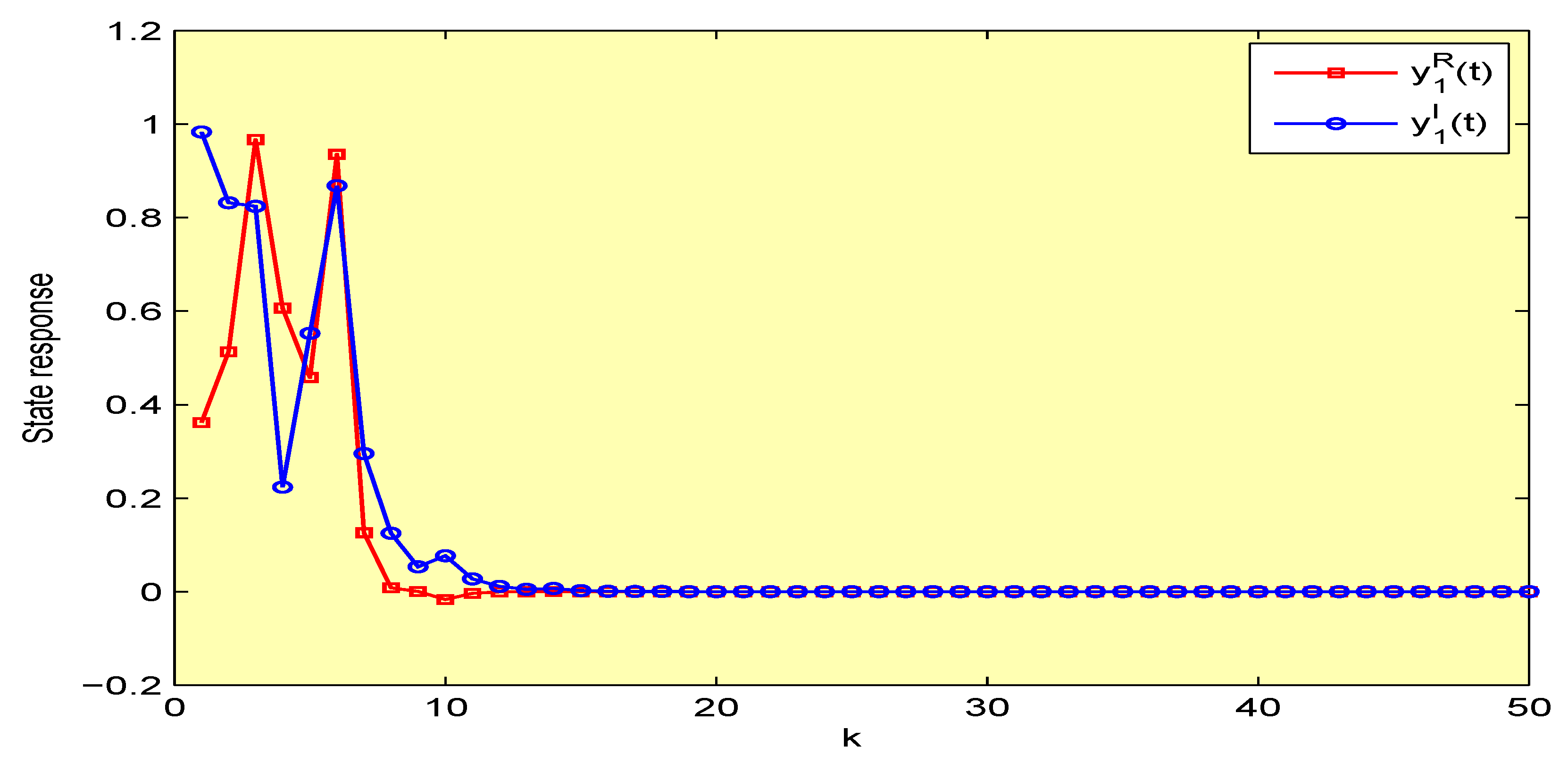
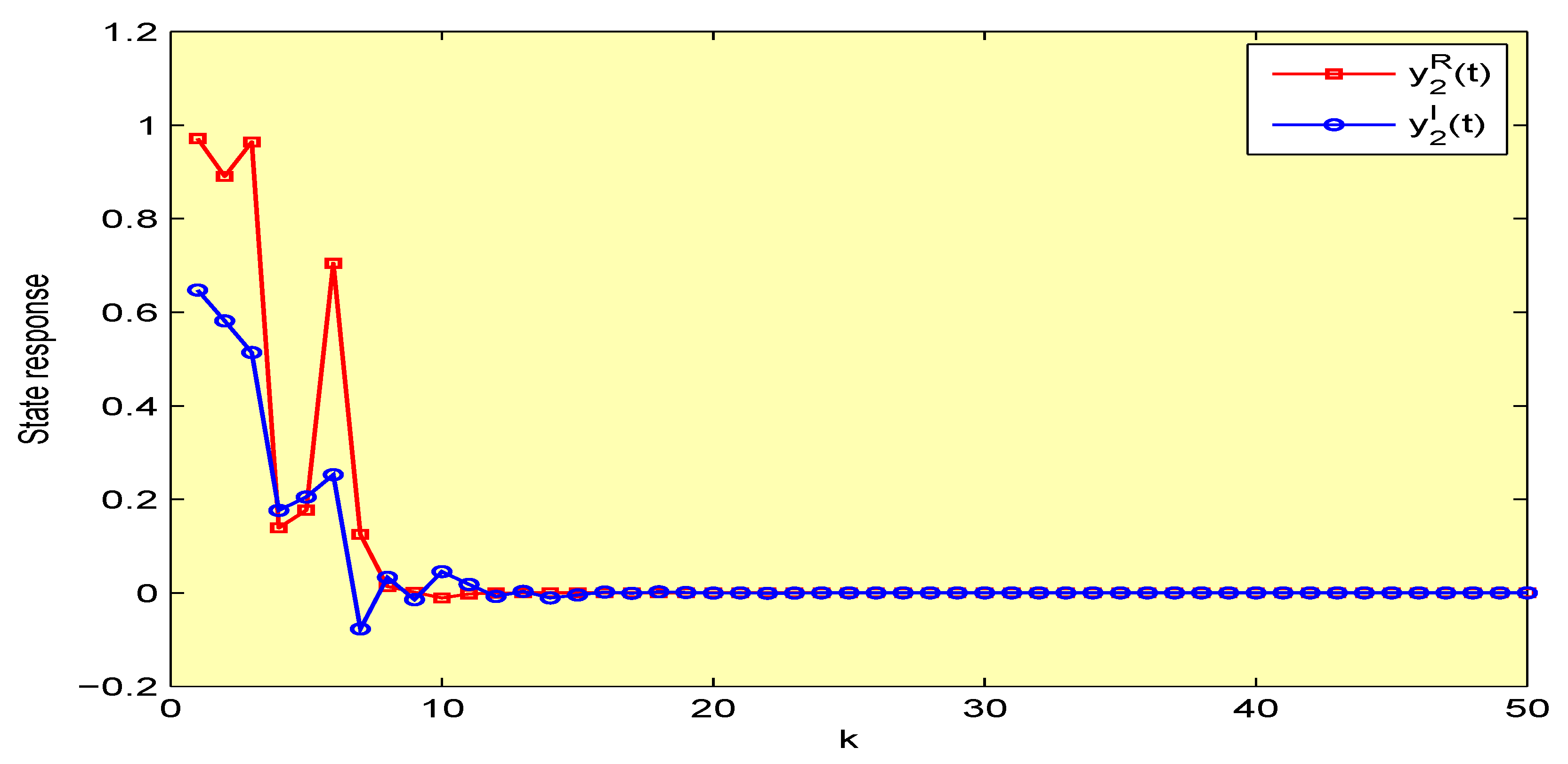
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- , ,
- , ,
- ,
References
- Feng, C.; Plamondon, R. On the stability analysis of delayed neural networks systems. Neural Netw. 2001, 14, 1181–1188. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, J.H. Exponential stability analysis for uncertain neural networks with interval time-varying delays. Appl. Math. Comput. 2009, 212, 530–541. [Google Scholar] [CrossRef]
- Cao, J.; Wang, J. Global asymptotic stability of a general class of recurrent neural networks with time-varying delays. IEEE Trans. Circuits Syst. I 2003, 50, 34–44. [Google Scholar]
- Gunasekaran, N.; Syed Ali, M.; Pavithra, S. Finite-time L∞ performance state estimation of recurrent neural networks with sampled-data signals. Neural Process. Lett. 2020, 51, 1379–1392. [Google Scholar] [CrossRef]
- Syed Ali, M.; Gunasekaran, N.; Esther Rani, M. Robust stability of Hopfield delayed neural networks via an augmented L-K functional. Neurocomputing 2017, 19, 1198–1204. [Google Scholar] [CrossRef]
- Mohamad, S. Global exponential stability in continuous-time and discrete-time delayed bidirectional neural networks. Phys. D 2001, 159, 233–251. [Google Scholar] [CrossRef]
- Mohamad, S.; Gopalsamy, K. Exponential stability of continuous-time and discrete-time cellular neural networks with delays. Appl. Math. Comput. 2003, 135, 17–38. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, M.J.; Park, J.H.; Lee, S.M.; Cha, E.J. New criteria on delay-dependent stability for discrete-time neural networks with time-varying delays. Neurocomputing 2013, 121, 185–194. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Ho, D.W.C. Discrete-time bidirectional associative memory neural networks with variable delays. Phys. Lett. A 2005, 335, 226–234. [Google Scholar] [CrossRef]
- Xiong, W.; Cao, J. Global exponential stability of discrete-time Cohen-Grossberg neural networks. Neurocomputing 2005, 64, 433–446. [Google Scholar] [CrossRef]
- Song, Q.; Wang, Z. A delay-dependent LMI approach to dynamics analysis of discrete-time recurrent neural networks with time-varying delays. Phys. Lett. A 2007, 368, 134–145. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liu, X. Asymptotic stability for neural networks with mixed time-delays: The discrete-time case. Neural Netw. 2009, 22, 67–74. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Liu, X.; Shi, Y. Robust state estimation for discrete-time stochastic neural networks with probabilistic measurement delays. Neurocomputing 2010, 74, 256–264. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Cao, J.; Tu, Z. Effects of leakage delay on global asymptotic stability of complex-valued neural networks with interval time-varying delays via new complex-valued Jensen’s inequality. Int. J. Adapt. Control Signal Process. 2018, 32, 1294–1312. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Zhou, D.; Lin, C.; Chen, J.; Wang, H. Finite-time stabilizability and instabilizability for complex-valued memristive neural networks with time delays. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2371–2382. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Zhu, S. Leakage delay-dependent stability analysis for complex-valued neural networks with discrete and distributed time-varying delays. Neurocomputing 2019, 338, 262–273. [Google Scholar] [CrossRef]
- Tu, Z.; Cao, J.; Alsaedi, A.; Alsaadi, F.E.; Hayat, T. Global Lagrange stability of complex-valued neural networks of neutral type with time-varying delays. Complexity 2016, 21, 438–450. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Zhai, G. Sampled-data state-estimation of delayed complex-valued neural networks. Int. J. Syst. Sci. 2020, 51, 303–312. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Zhai, G. Stability analysis for uncertain switched delayed complex-valued neural networks. Neurocomputing 2019, 367, 198–206. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.Y.; Lin, X.H.; Liu, C.X. Stability and synchronization for discrete-time complex-valued neural networks with time-varying delays. PLoS ONE 2014, 9, e93838. [Google Scholar] [CrossRef]
- Duan, C.; Song, Q. Boundedness and stability for discrete-time delayed neural network with complex-valued linear threshold neurons. Discrete Dyn. Nat. Soc. 2010, 2010, 368379. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Global exponential periodicity and stability of discrete-time complex-valued recurrent neural networks with time-delays. Neural Netw. 2015, 66, 119–130. [Google Scholar] [CrossRef]
- Chen, X.; Song, Q.; Zhao, Z.; Liu, Y. Global μ-stability analysis of discrete-time complex-valued neural networks with leakage delay and mixed delays. Neurocomputing 2016, 175, 723–735. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Z.; Liu, Y. Impulsive effects on stability of discrete-time complex-valued neural networks with both discrete and distributed time-varying delays. Neurocomputing 2015, 168, 1044–1050. [Google Scholar] [CrossRef]
- Ramasamy, S.; Nagamani, G. Dissipativity and passivity analysis for discrete-time complex-valued neural networks with leakage delay and probabilistic time-varying delays. Int. J. Adaptive Control Signal Process. 2017, 31, 876–902. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, H.; Cao, J. Global synchronization of fractional-order quaternion-valued neural networks with leakage and discrete delays. Neurocomputing 2019, 385, 211–219. [Google Scholar] [CrossRef]
- Tu, Z.; Zhao, Y.; Ding, N.; Feng, Y.; Zhang, W. Stability analysis of quaternion-valued neural networks with both discrete and distributed delays. Appl. Math. Comput. 2019, 343, 342–353. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Liang, J.; Liu, Y.; Alsaadi, F.E. Global μ-stability of quaternion-valued neural networks with mixed time-varying delays. Neurocomputing 2018, 290, 12–25. [Google Scholar] [CrossRef]
- Shu, H.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Global μ-stability of quaternion-valued neural networks with non-differentiable time-varying delays. Neurocomputing 2017, 247, 202–212. [Google Scholar] [CrossRef]
- Tan, M.; Liu, Y.; Xu, D. Multistability analysis of delayed quaternion-valued neural networks with nonmonotonic piecewise nonlinear activation functions. Appl. Math. Comput. 2019, 341, 229–255. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Chen, J.; Huang, J. Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Netw. 2018, 105, 88–103. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Bao, H.; Cao, J. Exponential input-to-state stability of quaternion-valued neural networks with time delay. Appl. Math. Comput. 2019, 358, 382–393. [Google Scholar] [CrossRef]
- Tu, Z.; Yang, K.; Wang, L.; Ding, N. Stability and stabilization of quaternion-valued neural networks with uncertain time-delayed impulses: Direct quaternion method. Physica A Stat. Mech. Appl. 2019, 535, 122358. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Alzabut, J.; Dianavinnarasi, J.; Cao, J.; Rajchakit, G. Finite-time Mittag-Leffler stability of fractional-order quaternion-valued memristive neural networks with impulses. Neural Process. Lett. 2020, 52, 1485–1526. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Kaewmesri, P.; Sriraman, R.; Lim, C.P. Global Mittag–Leffler stability and stabilization analysis of fractional-order quaternion-valued memristive neural networks. Mathematics 2020, 8, 422. [Google Scholar] [CrossRef]
- Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Global stability analysis of fractional-order quaternion-valued bidirectional associative memory neural networks. Mathematics 2020, 8, 801. [Google Scholar] [CrossRef]
- Chen, X.; Song, Q.; Li, Z.; Zhao, Z.; Liu, Y. Stability analysis of continuous-time and discrete-time quaternion-valued neural networks with linear threshold neurons. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2769–2781. [Google Scholar] [CrossRef]
- Li, L.; Chen, W. Exponential stability analysis of quaternion-valued neural networks with proportional delays and linear threshold neurons: Continuous-time and discrete-time cases. Neurocomputing 2020, 381, 52–166. [Google Scholar] [CrossRef]
- Hu, J.; Zeng, C.; Tan, J. Boundedness and periodicity for linear threshold discrete-time quaternion-valued neural network with time-delays. Neurocomputing 2017, 267, 417–425. [Google Scholar] [CrossRef]
- Song, Q.; Liang, J.; Wang, Z. Passivity analysis of discrete-time stochastic neural networks with time-varying delays. Neurocomputing 2009, 72, 1782–1788. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Liu, X. Robust stability of discrete-time stochastic neural networks with time-varying delays. Neurocomputing 2008, 71, 823–833. [Google Scholar] [CrossRef]
- Sowmiya, C.; Raja, R.; Cao, J.; Li, X.; Rajchakit, G. Discrete-time stochastic impulsive BAM neural networks with leakage and mixed time delays: An exponential stability problem. J. Franklin Instit. 2018, 355, 4404–4435. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S. Stochastic dissipativity and passivity analysis for discrete-time neural networks with probabilistic time-varying delays in the leakage term. Appl. Math. Comput. 2016, 289, 237–257. [Google Scholar] [CrossRef]
- Ramasamy, S.; Nagamani, G.; Zhu, Q. Robust dissipativity and passivity analysis for discrete-time stochastic T-S fuzzy Cohen-Grossberg Markovian jump neural networks with mixed time delays. Nonlinear Dyn. 2016, 85, 2777–2799. [Google Scholar] [CrossRef]
- Luo, M.; Zhong, S.; Wang, R.; Kang, W. Robust stability analysis for discrete-time stochastic neural networks systems with time-varying delays. Appl. Math. Comput. 2009, 209, 305–313. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Fraser, K.; Liu, X. Stochastic stability of uncertain Hopfield neural networks with discrete and distributed delays. Phys. Lett. A 2006, 354, 288–297. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, S.; Chang, W. Global exponential stability of stochastic memristor-based complex-valued neural networks with time delays. Nonlinear Dyn. 2017, 90, 915–934. [Google Scholar] [CrossRef]
- Sriraman, R.; Cao, Y.; Samidurai, R. Global asymptotic stability of stochastic complex-valued neural networks with probabilistic time-varying delays. Math. Comput. Simulat. 2020, 171, 103–118. [Google Scholar] [CrossRef]
- Zhu, Q.; Cao, J. Mean-square exponential input-to-state stability of stochastic delayed neural networks. Neurocomputing 2014, 131, 157–163. [Google Scholar] [CrossRef]
- Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Stochastic memristive quaternion-valued veural vetworks with time delays: An analysis on mean square exponential input-to-state stability. Mathematics 2020, 8, 815. [Google Scholar] [CrossRef]
- Hirose, A. Complex-Valued Neural Networks: Theories and Applications; World Scientific Pub Co Inc.: Singapore, 2003. [Google Scholar]
- Nitta, T. Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw. 2003, 16, 1101–1105. [Google Scholar] [CrossRef]
- Goh, S.L.; Chen, M.; Popovic, D.H.; Aihara, K.; Obradovic, D.; Mandic, D.P. Complex-valued forecasting of wind profile. Renewable Energ. 2006, 31, 1733–1750. [Google Scholar] [CrossRef]
- Kusamichi, H.; Isokawa, T.; Matsui, N.; Ogawa, Y.; Maeda, K. A new scheme for color night vision by quaternion neural network. In Proceedings of the 2nd International Conference on Autonomous Robots and Agents (ICARA), Palmerston North, New Zealand, 13–15 December 2004; pp. 101–106. [Google Scholar]
- Isokawa, T.; Nishimura, H.; Kamiura, N.; Matsui, N. Associative memory in quaternionic Hopfield neural network. Int. J. Neural Syst. 2008, 18, 135–145. [Google Scholar] [CrossRef] [PubMed]
- Matsui, N.; Isokawa, T.; Kusamichi, H.; Peper, F.; Nishimura, H. Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 2004, 15, 149–164. [Google Scholar]
- Mandic, D.P.; Jahanchahi, C.; Took, C.C. A quaternion gradient operator and its applications. IEEE Signal Proc. Lett. 2011, 18, 47–50. [Google Scholar] [CrossRef]
- Konno, N.; Mitsuhashi, H.; Sato, I. The discrete-time quaternionic quantum walk on a graph. Quantum Inf. Process. 2016, 15, 651–673. [Google Scholar] [CrossRef]
- Navarro-Moreno, J.; Fernández-Alcalá, R.M.; Ruiz-Molina, J.C. Semi-widely simulation and estimation of continuous-time -proper quaternion random signals. IEEE Trans. Signal Process. 2015, 63, 4999–5012. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Their Applications; Chichester: Horwood, UK, 1997. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sriraman, R.; Rajchakit, G.; Lim, C.P.; Chanthorn, P.; Samidurai, R. Discrete-Time Stochastic Quaternion-Valued Neural Networks with Time Delays: An Asymptotic Stability Analysis. Symmetry 2020, 12, 936. https://doi.org/10.3390/sym12060936
Sriraman R, Rajchakit G, Lim CP, Chanthorn P, Samidurai R. Discrete-Time Stochastic Quaternion-Valued Neural Networks with Time Delays: An Asymptotic Stability Analysis. Symmetry. 2020; 12(6):936. https://doi.org/10.3390/sym12060936
Chicago/Turabian StyleSriraman, Ramalingam, Grienggrai Rajchakit, Chee Peng Lim, Pharunyou Chanthorn, and Rajendran Samidurai. 2020. "Discrete-Time Stochastic Quaternion-Valued Neural Networks with Time Delays: An Asymptotic Stability Analysis" Symmetry 12, no. 6: 936. https://doi.org/10.3390/sym12060936
APA StyleSriraman, R., Rajchakit, G., Lim, C. P., Chanthorn, P., & Samidurai, R. (2020). Discrete-Time Stochastic Quaternion-Valued Neural Networks with Time Delays: An Asymptotic Stability Analysis. Symmetry, 12(6), 936. https://doi.org/10.3390/sym12060936





