Abstract
Calibration is a critical step in structured light 3D imaging systems. However, in the traditional calibration process, since the calibration plate is based on a two-dimensional model, the flatness of the calibration plate and the angle of the photo will affect the subsequent stitching steps based on the feature points. The number of photos also affects the calibration results. To improve the calibration accuracy, multiple photos need to be taken. The primary objective of this study was to achieve the simple and fast calibration of system parameters, so a method obtaining a large number of calibration data by homography matrix is presented, and a corresponding stereo target is designed in symmetry. First, using the relationship between the corner coordinates of the left and right parts of the stereo calibration plate and the coordinates of the world coordinate system, the homography matrix of the left and right calibration plates from the image coordinates to the world coordinates is calculated. Second, all the pixels in the stereo calibration plate are matched to the world coordinate system by using the homography matrix. In addition, we also compared the results of this method with those of traditional calibration methods. The experimental results show that the 3D geometric surface of the reconstruction result is smooth, it avoids the missing parts and the visual effect is excellent. Furthermore, the error range of small and complex objects can be reduced to 0.03 mm~0.05 mm. This method simplifies the calibration steps, reduces the calibration costs and has practical application value.
1. Introduction
Camera calibration is a key content of computer vision research [1,2,3]. It is the process of determining the mapping relationship between two-dimensional image coordinate points and three-dimensional space points. As an acquisition device for the original image, the charge-coupled device (CCD) camera must be systematically calibrated. The CCD is an image sensor that converts an optical signal into an electrical signal. How to improve the calibration accuracy and simplify the calibration procedure has always been a concern of scholars at home and abroad. Tsai [4] proposed a classic two-step method to simplify the calibration target to two dimensions. The two-step method is based on radial correction constraints, taking into account the camera’s distortion factor and improving the calibration accuracy, but camera calibration often requires expensive calibration equipment. Zhang [5] proposed a calibration method based on a two-dimensional checkerboard plane target; this method relies on the position of the corner plate coordinates of the checkerboard image and the two-dimensional image of the checkerboard in different spatial positions, and optimizes the internal parameter matrix of the camera through iterative calculations. Since the checkerboard calibration image is in different spatial positions, the feature points of different corner points can be extracted.
In Zhang’s calibration method based on the two-dimensional checkerboard plane target, the iterative calculation of camera parameters can be simplified by increasing the feature point size of the two-dimensional image, so as to achieve the purpose of improving the accuracy of the calibration camera. Zhang and Huang proposed a novel method that uses a projector to capture an image like a camera, and uses absolute phase to map camera pixels to projector pixels [6,7,8]. The selection of the camera pose for acquiring the calibration object image has a greater influence on the accuracy of calibration. Peng S. proposed a system to guide users through a simple graphical user interface (GUI) to move the camera to the most suitable posture for calibrating the camera [9]. The system can calculate the best pose for each new image acquired and add the latest information about the inherent parameters. A posture selection method suitable for interactive calibration was proposed by Rojtberg P [10]. This method can deduce a set of compact and robust calibration postures, which indeed avoids the calibration uncertainty caused by the singular calibration postures. In the above method, since the camera is required to accurately obtain the reflected light of the measured object when the encoded pattern is projected as the basis for solving the phase, the material and shape of the calibration plate will affect the final calibration result. Tian Miao et al. designed a black and white ring fan disc calibration template and calibrated the template design center circle using a 1/4 gap black circle in order to eliminate the influence of the calibration template rotation on the corner point sorting [11]. Fang Xu et al. introduced polar coordinates to represent the positional relationship of feature points in world coordinates, improving the convenience of multicamera calibration and the diversity of the reference calibration plates [12]. Jason Geng used a planer calibration plate, where the camera does not have to be pre-calibrated [13]. The camera and the projector are calibrated at the same time according to the same reference point on the calibration board, so as to avoid the error caused by camera calibration affecting the projector calibration. The disadvantage of this method is that it is susceptible to the effects of the noise generated by different surface areas due to the light intensity changing over time and the reflection parameters. The above method is relatively difficult to operate and the calibration accuracy is limited by the accuracy of the target. In addition, the image is fixed when the picture is captured, which is inconvenient for demonstration purposes and is susceptible to environmental factors.
In view of the above problems, this paper proposes a new calibration method based on a structured light three-dimensional measurement system. Based on phase profilometry, a stereo calibration plate was designed. The calibration data are obtained by using the homography matrix, and the corresponding relationship between the image coordinates and the world coordinates is obtained according to the perspective projection constraint relationship of the corners of the rectangular frame. This helps in obtaining the coordinate correspondence relationship of the other remaining pixel points in the calibration plate, and completes the calibration of the structured light system.
2. Basic Principles
2.1. Camera Calibration
Any object encountered in real life can be represented by a coordinate system, that is, a coordinate system can be used to represent the whole world, and a world coordinate system is established based on this. We can take a 2D picture from a camera and use the camera coordinate system to identify the location of the object that it acquired. The changes between the coordinate systems are shown in Figure 1.
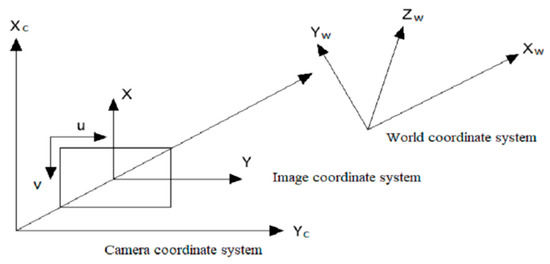
Figure 1.
Relationships between coordinate systems.
The world coordinate system is rotated and translated by the rigid body to obtain the camera coordinate system.
where , , and .
The camera coordinate system is converted to the image coordinate system through perspective projection.
In Formula (5), is a scale factor and its value not equal to 0.
and are effective focal length of the scale factor in the direction of the pixel coordinates of ,. It is assumed here that . is the homogeneous coordinate of the spatial point in the camera coordinate system. denotes the homogeneous coordinate of image point in the image coordinate system. The reason for citing the homogeneous coordinate system is that it can represent a vector that is originally dimensions in dimensions, which can be used to clearly distinguish between vectors and points, and it is also easier to use for linear geometric changes. refers to the pixel coordinates of the center of the facet. is the tilt which expresses the deviation of the two axes from orthogonality, i.e., the skewness of the coordinate system. Here,
where refers to the parameter matrix of the camera, , and . is known as the internal parameter matrix for the projector, is the outer parameter matrix of the projector, which represents the rotation and translation relationship from the world coordinate system to the camera coordinate system.
To improve the solution convenience, the internal parameter matrix of the camera is decomposed, and the pixel coordinates of the center of the phase plane are separated from the effective focal length. They are represented by separate matrices and , where, are all reversible matrices.
Here, ,.
The image coordinate system is converted to the pixel coordinate system.
Here, and are the physical size of the pixel in the and axis directions, respectively; and are the coordinates of the main point, that is, the original coordinates of the image.
2.2. Accurate Estimation of the Internal and External Parameter Matrix
The calibration method described in this paper can be divided into two steps to obtain an accurate estimation of the parameter matrix via stepwise optimization. The first step is to estimate the effective focal length under ideal conditions. Suppose the principal point is at the center of the image pixel coordinate system. When in an ideal state, the value of the skewness factor is 0. We estimate and optimize using the linear and nonlinear least squares focal length . Second, using the scale factor values obtained in the previous step, the orthogonality of the rotation matrix is used to obtain the constraint conditions, and the coordinates of the principal points and other parameters are obtained. Since each picture can calculate a set of data, multiple images can be optimized and fitted by a nonlinear optimization algorithm. Finally, the nonlinear optimization of the global parameters is performed according to the maximum likelihood estimation criterion.
The detailed process is as follows. The first step is to solve using the least squares method, assuming that the main point of the image is at the center of the pixel coordinates. and . The resolution of the camera is . After this, matrix .
where and are the first two column vectors of the rotation matrix. Then, we set up the auxiliary matrix as follows:
Simultaneously, the auxiliary matrix can also be expressed as
Subsequently, multiply both sides by matrix and expand the formula to
In the above formula, and are the first two column vectors of the set auxiliary matrix. Since the rotation matrix has orthogonality, the following constraints can be obtained:
By expanding and sorting the above two formulas, the following linear equation can be obtained.
During the calibration process, for each image used, the corresponding homography matrix can be obtained. Then, Equation (10) is used to obtain matrix . After this, Formula (14) can be used to obtain the constraints that further solve . When multiple images are acquired, fitting using the least squares method can estimate a more accurate .
The second step is as follows. First, find the coordinates of the principal points and . Second, acquire step from step one. Using the unit orthogonality of the rotation matrix combined with Equation (9), the following constraints can be obtained:
After Formulas (16) and (17) are expanded and sorted, the following formula can be obtained.
where , , and .
It can be seen from Equation (19) that is a nonlinear combination of and , and so they are not independent of each other. The solution to the principal position can be completed in two steps. The first step is to use more than two images to calculate more than two homography matrices, and then use the least square method to linearly estimate the three-dimensional vector according to Equation (18); In the second step, the result obtained in the first step is used as the initial condition. The Levenberg–Marquardt algorithm is used to solve Equation (20), and the final solution is the center coordinates of the phase plane .
where , , ; ; represents the relevant elements in the matrix and vector calculated using the image , respectively. Finally, on the basis of the known internal parameter matrix , the external parameters are obtained by combining it with Equation (10) and using the orthogonality of the rotation matrix.
3. Improved Stereo Calibration Plate and Resulting Calibration Method
3.1. Structure of the Stereo Calibration Plate
As shown in Figure 2, this paper designs a stereo calibration plate that can be quickly calibrated. The calibration plate has two mutually perpendicular planes, and the image of the feature points on the calibration plate can be obtained by the camera. Subsequently, the parameters of the camera are calculated by the conversion relationship between the world coordinate system of the feature points on the calibration plate and the image coordinate system. For this reason, for cameras with different focal lengths, different sized plastic plates are customized, and the designed printing tape is pasted on the surface of the calibration plate. During the pasting process, it should be kept as flat as possible to avoid surface bubbles and distortion errors. The size of the printing tape should be the same as the plane of the calibration plate. The printed calibration paper is pasted on the left and right planes with five * seven dots on each side. The physical structure is shown in Figure 2. The patterns on both sides of the calibration plate need to be symmetrical about the center point of the vertical line, which can minimize the error.

Figure 2.
(Left) Front view of the solid calibration plate (right) Top view of the stereo calibration plate.
3.2. Homography Matrix from the Phase Plane to the Stereo Calibration Plate Plane
In computer vision, homography is defined as the projection mapping from one plane to another. It plays a very important role in camera calibration, image correction, image stitching, camera pose estimation, visual SLAM and other fields [14,15]. With the homography matrix, images taken at different angles can be converted to the same viewing angle to conduct image stitching. That is, the homography matrix has the function of converting the viewing angle. Thus, the two planes of the three-dimensional calibration plate designed in this paper are perpendicular to each other as shown in Figure 3. The relationship between the of each side plane of the stereo calibration plate and the corresponding pixel coordinate system can be represented by a homography matrix .
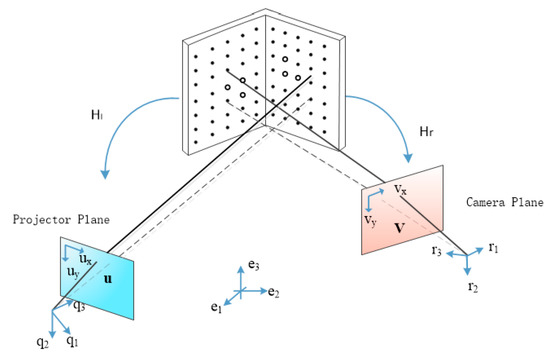
Figure 3.
Positional relationship between the homography matrix and the projector camera.
Taking the right plane as an example, the homography matrix is a nonsingular 33 matrix. The homography matrix H that defines the right phase plane to the spatial plane of the stereo calibration plate is as follows:
Then,
The matrix is expanded as
Next, multiply Equation (19) by the denominator to get
If the modulus of the homography matrix H is changed to one, the homography matrix with eight degrees of freedom requires at least four corner points to be calculated.
In practical applications, the calculated point pairs will contain noise. For example, the position of a point may deviate by a few pixels. If only four point pairs are used to calculate the homography matrix, the probability of an error will be very large. To obtain more accurate data, generally, more than four points are used to calculate the homography matrix. In addition, using a direct linear solution to solve linear equations is usually not sufficient to obtain the optimal solution. Therefore, in actuality, we use the singular value decomposition calculation and then apply all the data collected to the matrix to obtain the entire matrix in the matrix box on the right side of the stereo calibration plate.
Through the stereo calibration plate, the image coordinates of the corner points of the rectangular frame and the corresponding world coordinates are obtained, and the homography matrix of the phase plane to the space plane is obtained. Furthermore, according to the characteristics of the designed stereo calibration plate, the remaining part in the rectangular frame is obtained by the homography matrix. The image coordinates of the element and the corresponding world coordinates are calibrated. Therefore, the method does not need to acquire a large number of coded pictures for the phase decoding in each pose.
4. Experimental Results and Analysis
4.1. Experimental Layout
The experiment described in this paper adopts the structure cursor positioning system to verify the accuracy and experimental effect of the improved stereo calibration plate on the object reconstruction. The experimental object is a screw model. The system uses an MV-UB130M black and white camera with a resolution of 1280 pixel 1024 pixel, a DLP projector with a resolution of 1366768, a two-way swing arm control system, a PC software system and a stereo calibration board. The physical construction of the 3D reconstruction system is shown in Figure 4.

Figure 4.
(Left) Top view of experimental equipment (right) Left view of experimental equipment.
A certain frequency of structured light is projected onto the surface of the object by a projector, and a deformed raster image is generated on the surface of the object. Then, a CCD camera is used to obtain a two-dimensional distorted image of the object. Finally, the distorted raster image is compared with the reference grating, and after conducting Fourier transform dephasing, the 3D profile of the object can be obtained. The structure cursor system diagram and the multifrequency structure raster projection diagram are shown in Figure 5.

Figure 5.
(Left) Structured light calibration system diagram. (right) Multifrequency structure grating projection.
4.2. Stereo-Calibration Results
According to the solution algorithm of the homography matrix above, a homography matrix from the image plane to the spatial plane can be obtained, as shown in Table 1. In addition, OpenCV can very accurately calculate the homography matrix between the corresponding pairs of points. Usually, these corresponding point pairs are automatically calculated using a feature matching algorithm such as SIFT or SURF. However, some location information is manually selected here. The experiment can obtain multiple sets of calibration data, and the data can be input into the above formula to obtain the parameter matrix of the camera and the parameter matrix of the projector, as shown in Table 2.

Table 1.
Uniform matrix of the image plane to the space plane.

Table 2.
System calibration data.
The ease of operation of this method is compared with that of the traditional two-dimensional calibration method. The basic steps of the traditional two-dimensional calibration method can be divided into the following steps. First, print a checkerboard and paste it on a flat plate. Second, use a checkerboard to collect calibration data for eight poses. Each pose requires a camera picture. The projector needs to project sinusoidal phase shift coded pictures at three frequencies. Third, the projection of sine-coded pictures in both horizontal and vertical directions create the target image of the projector. In addition, the system dephases the multi-frequency grating based on the four-step phase shift method. A total of 192 pictures are projected (). At the same time, ensure that the calibration plate cannot move during scanning. This is also inconvenient for a two-position calibration board that cannot be fixed. In the method proposed in this paper, first, a standard four-step phase-shift method is used to project a raster projection of three frequencies. Only 24 pictures need to be projected, and the stereo calibration plate does not need to concern the fixation problem. After this, the camera perspective of one of the attitudes is collected, and the relationship between the camera and the projector is obtained by solving the phase using the multi-frequency extrapolation method, and then a picture of the perspective of the projector is generated. Camera calibration is implemented based on MATLAB’s own toolkit CameraCalibrator. The comparison result of the back projection error after calibration is shown in Figure 6.
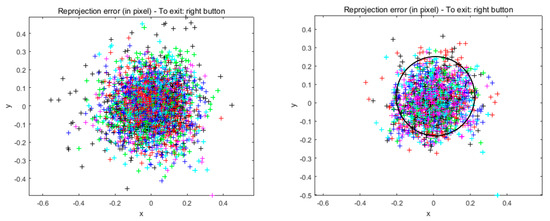
Figure 6.
Comparison of reprojection errors between the two methods. (The referenced line represents the radius of a 0.1-pixel circle).
Each corner point is subjected to back projection imaging after applying the calibrated model, and the error magnitude can be visually represented by a reprojection error map [16,17]. Reprojection error refers to the error between the point projected theoretically and the measurement point on the image. The reprojection error graph reflects the accuracy of the calibration. In the calibration, we often use the reprojection error as the evaluation standard of the final calibration effect [18,19]. As can be seen from Figure 6, the backprojection error radius decreases to 0.2.
4.3. Three Dimensional-Surface Reconstruction Results
To verify the measurement accuracy of the calibration method of this paper, a model with a small volume and a localized complex irregular screw part is scanned, and the screw scanning process is shown in Figure 7.

Figure 7.
Multi-frequency grating projected onto screw model.
The original picture of the screw is shown in Figure 8. The reconstruction result obtained after calibration is better than the traditional calibration method. A smaller amount of reconstructed object information is lost, and the splicing success rate is higher. In Figure 9a, the inaccuracy of the calibration may make the subsequent splicing steps based on the feature points difficult, resulting in the lack of fused information after reconstruction. In Figure 9b, after the calibration of the stereo icon fixed plate used in the figure, the surface of the screw is smooth, no information is missing, and the visual effect is good. The comparison of reconstruction parameters is shown in Table 3. According to the table data, the accuracy reached 0.03 mm–0.05 mm.

Figure 8.
Physical picture of the screw.

Figure 9.
(Left) traditional calibration method screw model fusion results. (right) Screw model fusion result after the calibration of the stereo calibration plate.

Table 3.
Comparison of reconstruction parameters.
5. Conclusions
In this paper, a fast and simple calibration method for a structured light 3D system is proposed. Through the improved stereo calibration plate, a large amount of calibration data is obtained using the homography matrix. Subsequently, through the internal constraints of perspective projection, the internal and external parameters are optimized. The calibration of the structured optical system is realized. The experimental results show that the object can be accurately measured and reconstructed in three dimensions through the calibration method. Moreover, compared with the original method, the calibration time is shortened and the calibration step is simplified. However, there are still some shortcomings in the method of this paper. There is a great need for the surface of the homemade three-dimensional board to be flat. In the follow-up work, this aspect will be further studied to improve the calibration efficiency.
Author Contributions
M.L., Z.Y. conceived this article, completed relevant experiments, and wrote a paper. H.Y. and W.S. helped to establish the mathematical model and revised the article. J.L. helped with the capital acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 61701296 and Grant U1831133, in part by the Natural Science Foundation of Shanghai under Grant 17ZR1443500, and in part by the Shanghai Aerospace Science and Engineering Fund under Grant SAST2017-062.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hao, X.Y.; Li, H.B.; Shan, H.T. Stratified Approach to Camera Auto-calibration Based on Image Sequences. J. Geomat. Sci. Technol. 2007, 24, 5–9. [Google Scholar]
- Song, Z.; Qin, X.I.; Songlin, L.I.U. Joint Calibration Method of 3D Laser Scanner and Digital Camera Based on Tridimensional Target. J. Geomat. Sci. Technol 2012, 29, 430–434. [Google Scholar]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Tsai, R.Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 2003, 3, 323–344. [Google Scholar] [CrossRef]
- Zhang, Z.Y. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern. Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Li, F.; Sekkati, H.; Deglint, J.; Scharfenberger, C.; Lamm, M.; Clausi, D.; Zelek, J.; Wong, A. Simultaneous Projector-Camera Self-Calibration for Three-Dimensional Reconstruction and Projection Mapping. IEEE Trans. Comput. Imaging 2017, 3, 74–83. [Google Scholar] [CrossRef]
- Merner, L.; Wang, Y.; Zhang, S. Accurate calibration for 3D shape measurement system using a binary defocusing technique. Opt. Lasers Eng. 2013, 51, 514–519. [Google Scholar] [CrossRef]
- Li, B.; Karpinsky, N.; Zhang, S. Novel calibration method for structured-light system with an out-of-focus projector. Appl. Opt. 2014, 53, 3415–3426. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Sturm, P. Calibration Wizard: A Guidance System for Camera Calibration Based on Modelling Geometric and Corner Uncertainty. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1497–1505. [Google Scholar]
- Rojtberg, P.; Kuijper, A. Efficient Pose Selection for Interactive Camera Calibration. In Proceedings of the 2018 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 16–20 October 2018; pp. 31–36. [Google Scholar]
- Miao, M.; Hao, X.Y.; Liu, S.L. Automatic Extraction and Sorting of Corners by Black and White Annular Sector Disk Calibration Patterns. J. Geomat. Sci. Technol. 2016, 33, 285–289. [Google Scholar]
- Fang, X.; Da, F.P.; Guo, T. Camera calibration based on polar coordinate. J. Southeast Univ. 2012, 42, 41–44. [Google Scholar]
- Geng, J. DLP-Based Structured Light 3D Imaging Technologies and Applications. In Proceedings of the Emerging Digital Micromirror Device Based Systems and Applications III, International Society for Optics and Photonics, San Francisco, CA, USA, 26 January 2011; Volume 7932, pp. 8–9. [Google Scholar] [CrossRef]
- Finlayson, G.; Gong, H.; Fisher, R.B. Color Homography: Theory and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 20–33. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Song, W.Q.; Li, M.; Kudreyko, A.; Zio, E. Fractional Lévy stable motion: Finite difference iterative forecasting model. Chaos Solitons Fractals 2020, 133, 109632. [Google Scholar] [CrossRef]
- Huang, Y.H. A method for image denoising based on new wavelet thresholding function. Transducer Microsyst. Technol. 2011, 9, 76–78. [Google Scholar]
- Song, W.Q.; Cattani, C.; Chi, C.H. Multifractional Brownian Motion and Quantum-Behaved Particle Swarm Optimization for Short Term Power Load Forecasting: An Integrated Approach. Energy 2020, 194, 116847. [Google Scholar] [CrossRef]
- Wang, H.Y.; Song, W.Q.; Zio, E.; Wu, F.; Zhang, Y.J. Remaining Useful Life Prediction for Lithium-ion Batteries Using Fractional Brownian Motion and Fruit-fly Optimization Algorithm. Measurement 2020. [Google Scholar] [CrossRef]
- Song, W.Q.; Cheng, X.X.; Zio, C.C. Multifractional Brownian Motion and Quantum-Behaved Partial Swarm Optimization for Bearing Degradation Forecasting. Complexity 2020, 1–9. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).