Abstract
We show that the addition of correlated phases to the recently developed method of randomized dynamical decoupling pulse sequences can improve its performance in quantum sensing. In particular, by correlating the relative phases of basic pulse units in dynamical decoupling sequences, we are able to improve the suppression of the signal distortion due to pulse imperfections and spurious responses due to finite-width pulses. This enhances the selectivity of quantum sensors such as those based on NV centers in diamond.
1. Introduction
Dynamical decoupling (DD) techniques [1] have important applications in quantum information [2,3], quantum simulation [4] and quantum sensing [5,6,7,8]. In particular, a sequence of DD pulses is able to adjust the resonance frequency of a qubit in a controlled manner by periodically flipping its quantum state. In this manner, the qubit can be detuned from resonance with respect to the frequencies of its surrounding noise, which results in an extended coherence time. At the same time, when a DD sequence imprints a qubit flipping rate that matches the frequency of a certain electromagnetic signal, the internal quantum state of the qubit gets modified, leading to quantum detection. For example, under DD control the nitrogen-vacancy (NV) center qubit [9] in diamond has already demonstrated long coherence times [10,11,12,13], and an excellent sensitivity to AC magnetic fields [14]. This makes NV centers under DD control highly promising probes for detecting, identifying and controlling nearby single nuclear spins [15,16,17,18,19,20,21,22,23] and spin clusters [24,25,26,27].
One of the major factors limiting the performance of DD techniques is the unavoidable presence of errors in the applied control, which include detuning and amplitude deviations on the applied pulses. The effects of these errors can be partially compensated by robust DD sequences that make use of different pulse phases [10,28,29,30]. In addition, even if control pulses were ideally displayed (i.e., in absence of detuning and amplitude errors) the finite-width character of each pulse will introduce a spurious harmonic response [31,32,33,34]. Importantly, this spurious response accumulates coherently when a basic DD pulse unit is repeated times. At this point, it is important to remark that repeating several DD pulse units is the standard set-up used to achieve longer detection times. The accumulated spurious response can lead to a false identification of certain nuclear spins; e.g., the presence of C nuclei in a sample can be interpreted as the existence of H nuclei, as the ratio of the magnetic moments are almost precisely integers. All this has a negative impact on the reliability of general DD methods. In this respect, a recent theoretical and experimental study shows that the application of random global phases to each basic DD pulse unit of DD sequences suppresses, up to some extent, the spurious harmonic response while enhancing the sequence robustness against control errors [35].
In this work, we introduce correlated phases to further enhance the performances of DD sequences for quantum sensing purposes. In particular, instead of using M uncorrelated random phases (one for each of the M basic DD pulse units present in a DD sequence) we impose constraints over these M phases. This leads to a superior suppression of accumulated errors and spurious responses, even when the number M of basic DD pulse units is small.
2. Results
2.1. The Effect of Controlled Imperfection
Let us consider the periodic repetition of a basic pulse unit with a time duration T and containing a number N of pulses (see Figure 1a). In the case of ideal pulse sequences, each pulse is instantaneous and rotates the qubit by an angle along an axis in the plane. In realistic situations, however, the control Hamiltonian for the pulses in the rotating frame lreads
where () is a Pauli matrix, is the Rabi frequency and is the pulse phase of the control. Between the pulses the control field is switched off with . Here the frequency detuning introduces a rotational axis and rotation-angle errors. In addition, amplitude fluctuations on the control field change the value of the Rabi frequency , thereby further altering the rotation angle of the pulse. The ideal value of the Rabi frequency is for a pulse duration , which we assume to be the same for all the pulses. We will consider the strengths of frequency detuning and amplitude fluctuation errors in terms of .
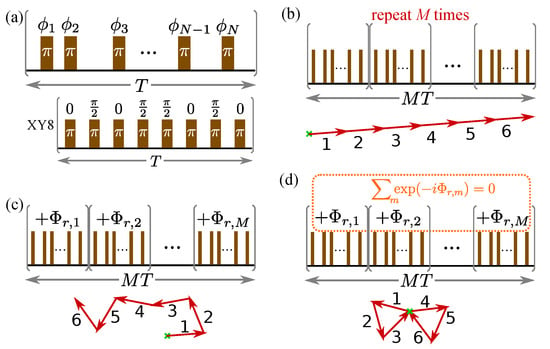
Figure 1.
Repetition of a basic dynamical decoupling (DD) pulse unit. (a) A basic unit of DD pulse sequence, which is defined by the positions and phases of the pulses. The lower panel is the example of an XY8 sequence. (b) The standard protocol to construct a longer DD sequence is to repeat the same basic pulse unit illustrated in (a) M times. Because the error contribution has the same phase factor for each DD pulse unit, the errors coherently add up (see the lower panel for the case of ). (c) The randomization protocol shifts all the pulses within each unit by a common, independent, random phase . Because of the random phases, the error terms of the basic DD pulse unit add up incoherently, suppressing the growing of error contribution (see the lower panel for an example). (d) The correlated randomization protocol imposes constraint on the phases on the random phases , such that the sum of their random phase factors vanishes. The lower panel illustrates an example in which the sum of random phase factors of every three successive DD pulse units is zero.
For the sake of simplicity in the presentation, we do not consider the environment (e.g., a nuclear spin bath) of the qubit, and directly show the effect of pulse errors. However, the presence of nuclear spins will be taken into account in our numerical simulations of quantum sensing. Using Equation (1), the evolution matrix of a single pulse reads . It is tedious to write down the expression of in terms of the amplitude error and detuning error . However, has the general form [30,35]
where the real numbers , and depend on the explicit realization of the pulse but are independent of the pulse phase . Because static fluctuations in the detuning and Rabi frequency are the dominant sources of pulse errors [36], we follow the standard procedure of robust sequence design [30,37] by assuming that each pulse has the same static errors; that is, , and are the same for all the pulses. When , the pulse corresponds to a perfect pulse up to a drift (which can be caused by the detuning error ) on the pulse phase. The pulse phase is fully tunable by changing the phase of the applied control field, and we assume that the phases of the pulses are applied in order with the values , , …, .
We consider the widely-used basic DD pulse units to lead to the identity operation on the qubit after their application. Typical examples of these basic DD pulse units are the pulse arrangements belonging to the XY family [28], the YY8 sequence [34] and the Carr–Purcell sequence [38], which contain an even number of pulses. To the first order of , the evolution matrix of a DD pulse unit reads [30,35]
where C is a complex number that depends on the structure of the employed DD pulse unit. One example of a DD pulse unit (i.e., the widely used XY8 sequence) can be found in the lower panel of Figure 1a. In addition, we note that if one introduces a global phase shift to the phases of all pulses, the constant C changes as .
2.1.1. Standard Protocol
In the standard protocol where the basic pulse unit is repeated M times as , the control errors accumulate coherently. Using Equation (3), we obtain the evolution matrix of the whole sequence, i.e., of :
2.1.2. Randomisation Protocol
In the randomization protocol [35], a random global phase is imposed to all pulses of each mth basic DD pulse unit. Now, by using Equation (3), the evolution matrix of the whole sequence reads [35]
where , with being a set of phases. Due to the random value that each phase takes, the quantity becomes a (normalized) 2D random walk with [35]. This suppresses the effect of control errors (see Figure 1c).
2.1.3. Correlated Randomization Protocol
Now, we impose a constraint on the random phases , such that . In this manner, the effect of control errors will be suppressed more efficiently as compared to a fully random scheme, and irrespective of the value of M. Note that, in the randomization protocol in [35], a larger M provides a better improvement, as is demonstrated in the previous section with the expression . In this correlated randomization protocol, , which means that the leading-order static error in the perturbative parameter is fully eliminated. To cancel the effect of slowly fluctuating errors more efficiently, we choose a smaller number of subsequent random phases such that for some integer k. Our method also improves the performance of the method over static errors since, by developing in the perturbative parameter , one can see that: Sequences with a low number G cancel high-order-error terms better in .
An example of a possible target sequence is in Figure 1d. Here we impose a constraint for every three subsequent random phases (i.e., ) such that the sum of their phase factors vanishes. Note that it is not necessary to choose the same value of G for all the subsequent random phases in a single DD sequence. But for simplicity, we will use one fixed G for each DD sequence in our simulations and call the value of G as the elimination size.
2.2. Comparison of Different Protocol Performances
The sequence performance can be studied by the survival probability of the quantum sensor in the initial state (note this is initialised in an eigenstate of ) after the application of the whole sequence. This survival probability is the directly measured value in experiments. Explicitly, we use , an eigenstate of , as the initial state. After the sequence evolution , the state evolves to , where is the qubit evolution operator. A measurement with respect to the eigenstates of gives the measured survival probability
In Figure 2, we compare the robustness of different protocols against control imperfections by numerically simulating the sequence fidelity. In particular, the fidelity is defined as the survival probability because, in the absence of external signals to detect, the quantum state of the sensor should remain unaffected after the application of the protocol and . In addition, we clarify that white regions in these figures have lower fidelities (out of the range of each plot) such that their values are not shown for clarity.
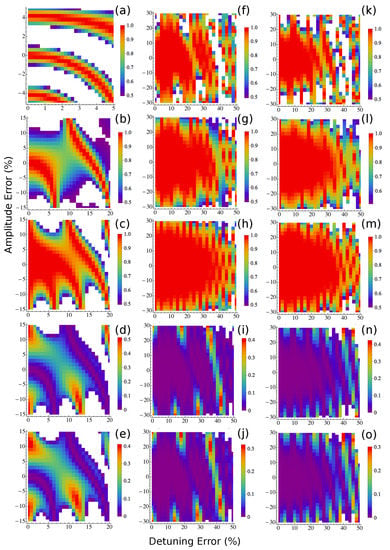
Figure 2.
Robustness of the protocols for a small M. The fidelity (the value of in the absence of an external signal) of Carr-Purcell sequences as a function of detuning and amplitude (Rabi frequency) errors for standard protocol (a), randomization protocol in [35] (b), and correlated randomization protocol with the elimination size (c). (d) difference between the fidelity of the correlated protocol in (c) and the uncorrelated protocol in (b). (e), as (d) but for the elimination size for the correlated randomization protocol. (f–j) (k–o), as (a–e), but for the XY8 [YY8 [34] sequences. In all figures, the regions in white have values out of the ranges shown in the color bars. All the sequences consists of 48 pulses (that is, for XY8 and YY8 sequences). The time duration of each pulse is 15 ns, and the inter pulse spacing is 200 ns. All the plots for the protocols with random phases are average results of 100 random sequences.
An inspection of the panels in Figure 2 shows that: even with a small number of repetitions for the DD sequences, our method using correlated random phases presents an improved fidelity over the standard protocol and the randomization protocol in [35]. For larger M the fidelities of the randomization protocol and our correlated random phases protocol are expected to be similar. However, for our protocol is still better than the randomization protocol (see Figure 3). We have also observed that our protocol using correlated random phases performs slightly better when one uses a small elimination size G, which is consistent with our theory (compare the results of and 3 in Figure 2 and Figure 3). While the smallest would be the optimal number with respect to the robustness enhancement, a slightly larger G (e.g., ) also performs well. This implies that the correlated randomization protocol with different values of small G for the subsequent random phases in a single DD sequence would also enhance sequence robustness.
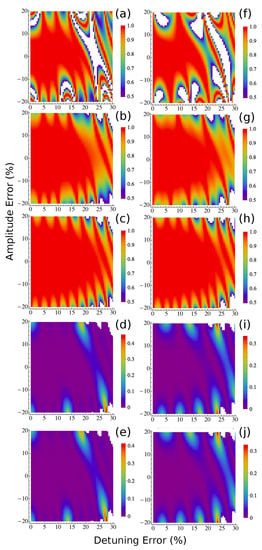
Figure 3.
Robustness of the XY8 and YY8 [34] protocols for . (a–e) Results for XY8 sequences. (a–c) show the fidelity of XY8 sequences as a function of detuning and amplitude (Rabi frequency) errors for standard protocol (a), randomization protocol [35], and correlated randomization protocol (c), respectively. (d,e) are the fidelity enhancement over the randomization protocol by using the correlated randomization protocol for elimination sizes and , respectively. (f–j), as (a–e), but for YY8 sequences. The control parameters are the same as those used in Figure 2 but with a larger . In all figures, the regions in white have values out of the ranges shown in the color bars. All the plots for the protocols with random phases are average results of 100 random sequences.
In Figure 4, we simulate the results of quantum sensing with XY8 sequences. In these simulations, we considered an NV quantum sensor in diamond. In the rotating frame of NV electron spin, the electron spin and its nearby nuclear spins have the Hamiltonian
where and are components of the hyperfine field at the location of the nth nucleus; and are nuclear spin operators; the gyromagnetic ratio; is the maganetic field applied along the symmetry axis of the NV center. See [29,35] for more information on the model. The target is to sense a proton () spin outside of the diamond sample. Due to limited control power, the Rabi frequency of control pulses has a finite value, and consequently, the pulses are not instantaneous and have a non-zero time duration. In addition, in our numerical simulations we also consider static errors on the control (see caption). The non-zero pulse duration can leads to spurious resonances [31] of sensing signal at the presence of other nuclear spins (e.g., a spin in our simulation) (see Figure 4a for a simulation). This signal error can be suppressed by the use of randomization protocol (Figure 4b). As shown in Figure 4c,d, the enhancement of the control robustness by using the correlated randomization protocol can significantly further improve the signal fidelity in quantum sensing.
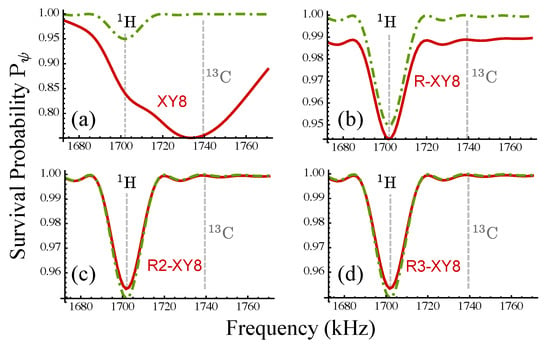
Figure 4.
Quantum spectroscopy with DD. (a) Simulated survival probability (red solid line) as a function of the DD frequency [ for pulse spacing ] for the standard XY8 protocol with a total number of 200 pulses. The DD pulses have a non-zero time duration of 100 ns. The frequency detuning and amplitude errors of the pulses have a static value of 10% of the ideal Rabi frequency. The spin to be sensed is coupled to the NV center via the hyperfine-field components [29] kHz. A spin representing a noise source is coupled to the NV center via the hyperfine-field components kHz. The presence of spin and imperfect control perturbs sensing signal and generates a spurious peak around 1740 kHz (compare it with the green dash-dotted line obtained by an ideal error-free DD sequence). (b) The use of randomization protocol suppresses the effect of pulse imperfection. The effect of errors is further suppressed in (c,d) by the use of correlated random phases elimination sizes and , respectively. A magnetic field 400 G is applied along the symmetry axis of the NV center in the simulation. The hyperfine fields used for the H and C atoms correspond to relative separation of 3.1 and 0.52 nm respectively away from the NV center in our simulation. All the plots for the protocols with random phases are average results of 100 random sequences.
3. Conclusions
We showed that the robustness of randomization DD protocol can be further improved if the random phases of the DD pulse units are chosen such that their phase factors have an average of zero. This reduces harmful effects due to amplitude fluctuations and frequency detuning of the DD control. In addition, we have demonstrated that our correlated randomization DD protocol provides better signals in DD based quantum sensing, even at the presence of nuclear spins that otherwise generate spurious peaks.
Author Contributions
Conceptualization, M.B.P.; Investigation, Z.W.; Supervision, J.C. and M.B.P.; Writing—original draft, Z.W.; Writing—review & editing, Z.W., J.C. and M.B.P. All authors have contributed substantially to the work reported. All authors have read and agreed to the published version of the manuscript.
Funding
M.B.P. acknowledges support by the ERC Synergy grant BioQ (grant number 319130); the EU project HYPERDIAMOND and AsteriQs; the QuantERA project NanoSpin; the BMBF project DiaPol; the state of Baden-Württemberg through bwHPC; and the German Research Foundation (DFG) through grant number INST 40/467-1 FUGG. J.C. acknowledges financial support from Spanish Government via PGC2018-095113-B-I00 (MCIU/AEI/FEDER, UE); the UPV/EHU grant EHUrOPE; the Basque Government via IT986-16; QMiCS (820505) and OpenSuperQ (820363) of the EU Flagship on Quantum Technologies; and the EU FET Open Grant Quromorphic.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NV | nitrogen-vacancy |
| DD | dynamical decoupling |
| CP | Carr–Purcell |
References
- Viola, L.; Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 1998, 58, 2733. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Z.-Y.; Liu, R.-B. Preserving qubit coherence by dynamical decoupling. Front. Phys. 2010, 6, 2–14. [Google Scholar] [CrossRef]
- Suter, D.; Álvarez, G.A. Colloquium: Protecting quantum information against environmental noise. Rev. Mod. Phys. 2016, 88, 041001. [Google Scholar] [CrossRef]
- Cai, J.M.; Retzker, A.; Jelezko, F.; Plenio, M.B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 2013, 9, 168–173. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.P.; Hingant, T.; Roch, J.F.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Jelezko, F.; Plenio, M.B.; Weil, T. Diamond Quantum Devices in Biology. Angew. Chem. Int. Ed. 2016, 55, 6586–6598. [Google Scholar] [CrossRef] [PubMed]
- Suter, D.; Jelezko, F. Single-spin magnetic resonance in the nitrogen-vacancy center of diamond. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 98–99, 50–62. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C.L. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Ryan, C.A.; Hodges, J.S.; Cory, D.G. Robust Decoupling Techniques to Extend Quantum Coherence in Diamond. Phys. Rev. Lett. 2010, 105, 200402. [Google Scholar] [CrossRef]
- de Lange, G.; Wang, Z.; Riste, D.; Dobrovitski, V.; Hanson, R. Universal Dynamical Decoupling of a Single Solid-State Spin from a Spin Bath. Science 2010, 330, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Bar-Gill, N.; Pham, L.M.; Jarmola, A.; Budker, D.; Walsworth, R.L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 2013, 4, 1743. [Google Scholar] [CrossRef] [PubMed]
- Abobeih, M.H.; Cramer, J.; Bakker, M.A.; Kalb, N.; Markham, M.; Twitchen, D.J.; Taminiau, T.H. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 2018, 9, 2552. [Google Scholar] [CrossRef] [PubMed]
- de Lange, G.; Riste, D.; Dobrovitski, V.V.; Hanson, R. Single-Spin Magnetometry with Multipulse Sensing Sequences. Phys. Rev. Lett. 2011, 106, 080802. [Google Scholar] [CrossRef]
- Taminiau, T.H.; Wagenaar, J.J.T.; van der Sar, T.; Jelezko, F.; Dobrovitski, V.V.; Hanson, R. Detection and Control of Individual Nuclear Spins Using a Weakly Coupled Electron Spin. Phys. Rev. Lett. 2012, 109, 137602. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Unterreithmeier, Q.P.; Bennett, S.D.; Lukin, M.D. Sensing Distant Nuclear Spins with a Single Electron Spin. Phys. Rev. Lett. 2012, 109, 137601. [Google Scholar] [CrossRef]
- Zhao, N.; Honert, J.; Schmid, B.; Klas, M.; Isoya, J.; Markham, M.; Twitchen, D.; Jelezko, F.; Liu, R.B.; Fedder, H.; et al. Sensing single remote nuclear spins. Nat. Nanotechnol. 2012, 7, 657. [Google Scholar] [CrossRef]
- Müller, C.; Kong, X.; Cai, J.-M.; Melentijevic, K.; Stacey, A.; Markham, M.; Isoya, J.; Pezzagna, S.; Meijer, J.; Du, J.; et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 2014, 5, 4703. [Google Scholar] [CrossRef]
- Casanova, J.; Wang, Z.-Y.; Plenio, M.B. Noise-Resilient Quantum Computing with a Nitrogen-Vacancy Center and Nuclear Spins. Phys. Rev. Lett. 2016, 117, 130502. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Casanova, J.; Plenio, M.B. Delayed entanglement echo for individual control of a large number of nuclear spins. Nat. Commun. 2017, 8, 14660. [Google Scholar] [CrossRef]
- Haase, J.F.; Wang, Z.-Y.; Casanova, J.; Plenio, M.B. Soft Quantum Control for Highly Selective Interactions among Joint Quantum Systems. Phys. Rev. Lett. 2018, 121, 050402. [Google Scholar] [CrossRef] [PubMed]
- Lang, J.E.; Broadway, D.A.; Hall, G.A.L.W.L.T.; Stacey, A.; Hollenberg, L.L.; Monteiro, T.S.; Tetienne, J.-P. Quantum Bath Control with Nuclear Spin State Selectivity via Pulse-Adjusted Dynamical Decoupling. Phys. Rev. Lett. 2019, 123, 210401. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.E.; Randall, J.; Abobeih, M.H.; Berrevoets, R.C.; Degen, M.J.; Bakker, M.A.; Markham, M.; Twitchen, D.J.; Taminiau, T.H. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 2019, 9, 031045. [Google Scholar] [CrossRef]
- Zhao, N.; Hu, J.-L.; Ho, S.-W.; Wan, J.T.K.; Liu, R.B. Atomic-scale magnetometry of distant nuclear spin clusters via nitrogen-vacancy spin in diamond. Nat. Nanotechnol. 2011, 6, 242. [Google Scholar] [CrossRef]
- Shi, F.; Kong, X.; P, P.W.; Kong, F.; Zhao, N.; Liu, R.B.; Du, J. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 2014, 10, 21–25. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Haase, J.F.; Casanova, J.; Plenio, M.B. Positioning nuclear spins in interacting clusters for quantum technologies and bioimaging. Phys. Rev. B 2016, 93, 174104. [Google Scholar] [CrossRef]
- Abobeih, M.H.; Randall, J.; Bradley, C.E.; Bartling, H.P.; Bakker, M.A.; Degen, M.J.; Markham, M.; Twitchen, D.J.; Taminiau, T.H. Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 2019, 576, 411–415. [Google Scholar] [CrossRef]
- Gullion, T.; Barker, D.B.; Conradi, M.S. New, compensated Carr-Purcell sequences. J. Magn. Reson. 1990, 89, 479–484. [Google Scholar] [CrossRef]
- Casanova, J.; Wang, Z.-Y.; Haase, J.F.; Plenio, M.B. Robust dynamical decoupling sequences forindividual-nuclear-spin addressing. Phys. Rev. A 2015, 92, 042304. [Google Scholar] [CrossRef]
- Genov, G.T.; Schraft, D.; Vitanov, N.V.; Halfmann, T. Arbitrarily Accurate Pulse Sequences for Robust Dynamical Decoupling. Phys. Rev. Lett. 2017, 118, 133202. [Google Scholar] [CrossRef]
- Loretz, M.; Boss, J.M.; Rosskopf, T.; Mamin, H.J.; Rugar, D.; Degen, C.L. Spurious Harmonic Response of Multipulse Quantum Sensing Sequences. Phys. Rev. X 2015, 5, 021009. [Google Scholar] [CrossRef]
- Haase, J.F.; Wang, Z.-Y.; Casanova, J.; Plenio, M.B. Pulse-phase control for spectral disambiguation in quantum sensing protocols. Phys. Rev. A 2016, 94, 032322. [Google Scholar] [CrossRef]
- Lang, J.E.; Casanova, J.; Wang, Z.-Y.; Plenio, M.B.; Monteiro, T.S. Enhanced Resolution in Nanoscale NMR via Quantum Sensing with Pulses of Finite Duration. Phys. Rev. Appl. 2017, 7, 054009. [Google Scholar] [CrossRef]
- Shu, Z.; Zhang, Z.; Cao, Q.; Yang, P.; Plenio, M.B.; Müller, C.; Lang, J.; Tomek, N.; Naydenov, B.; McGuinness, L.P.; et al. Unambiguous nuclear spin detection using an engineered quantum sensing sequence. Phys. Rev. A 2017, 96, 051402. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Lang, J.E.; Schmitt, S.; Lang, J.; Casanova, J.; McGuinness, L.; Monteiro, T.S.; Jelezko, F.; Plenio, M.B. Randomization of Pulse Phases for Unambiguous and Robust Quantum Sensing. Phys. Rev. Lett. 2019, 122, 200403. [Google Scholar] [CrossRef]
- Cai, J.M.; Naydenov, B.; Pfeiffer, R.; McGuinness, L.P.; Jahnke, K.D.; Jelezko, F.; Plenio, M.B.; Retzker, A. Robust dynamical decoupling with concatenated continuous driving. New J. Phys. 2012, 14, 113023. [Google Scholar] [CrossRef]
- Souza, A.M.; Álvarez, G.A.; Suter, D. Robust dynamical coupling. Philos. Trans. R. Soc. A 2012, 370, 4748. [Google Scholar] [CrossRef]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).