An Interactive Decision-Making Method for Third-Party Logistics Provider Selection under Hybrid Multi-Criteria
Abstract
1. Introduction
2. Preliminaries
2.1. Selection Criteria for 3PL Providers
2.2. Related Definitions
- (1)
- ;
- (2)
- if and only if;
- (3)
- .
- (1)
- ;
- (2)
- if and only if;
- (3)
- .
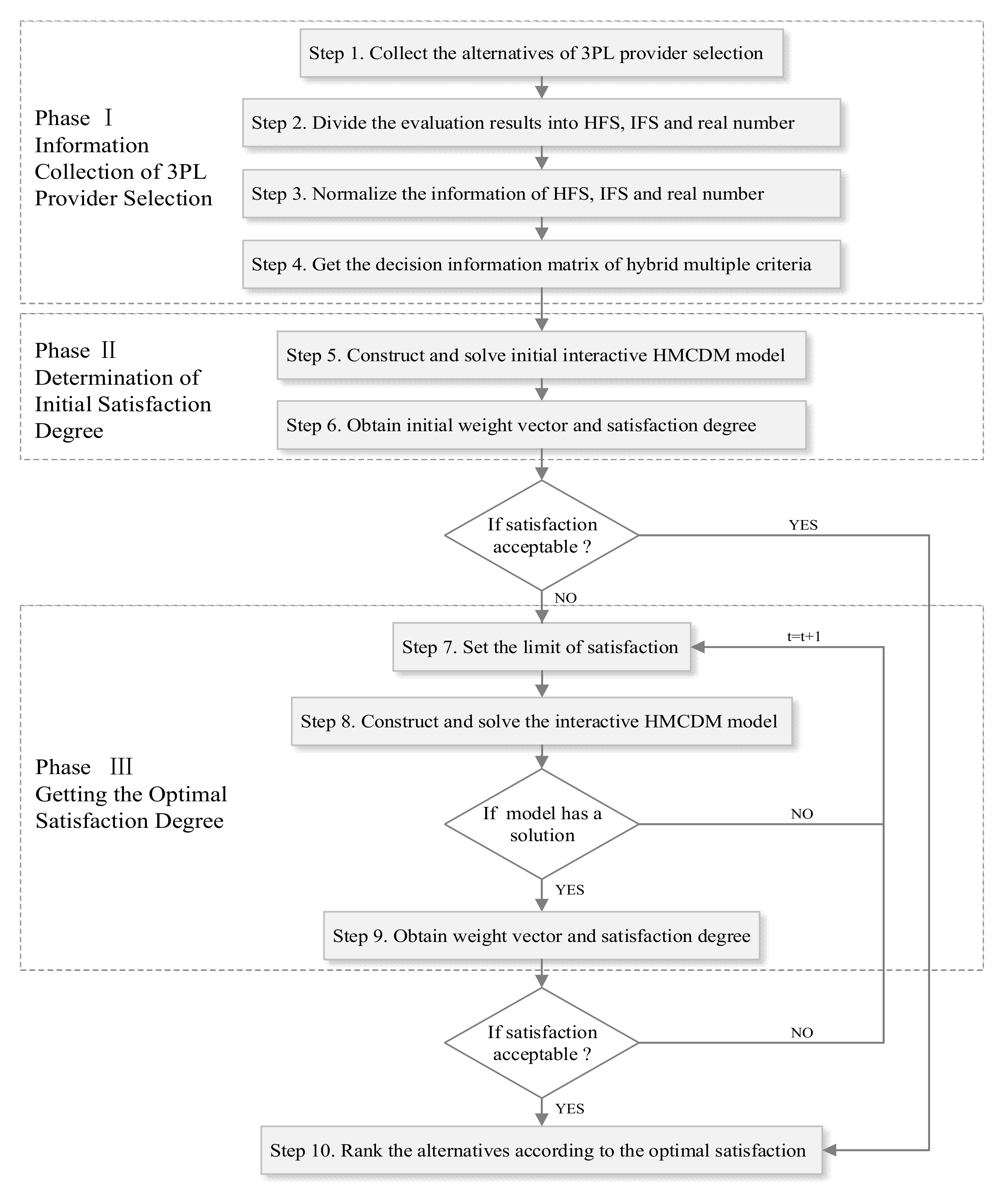
3. Interactive HMCDM Method
3.1. Description of a HMCDM Problem
3.2. Setting the Ideal Solution of Hybrid Multi-Criteria
3.3. Interactive Decision-Making Process
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
4. Case Study
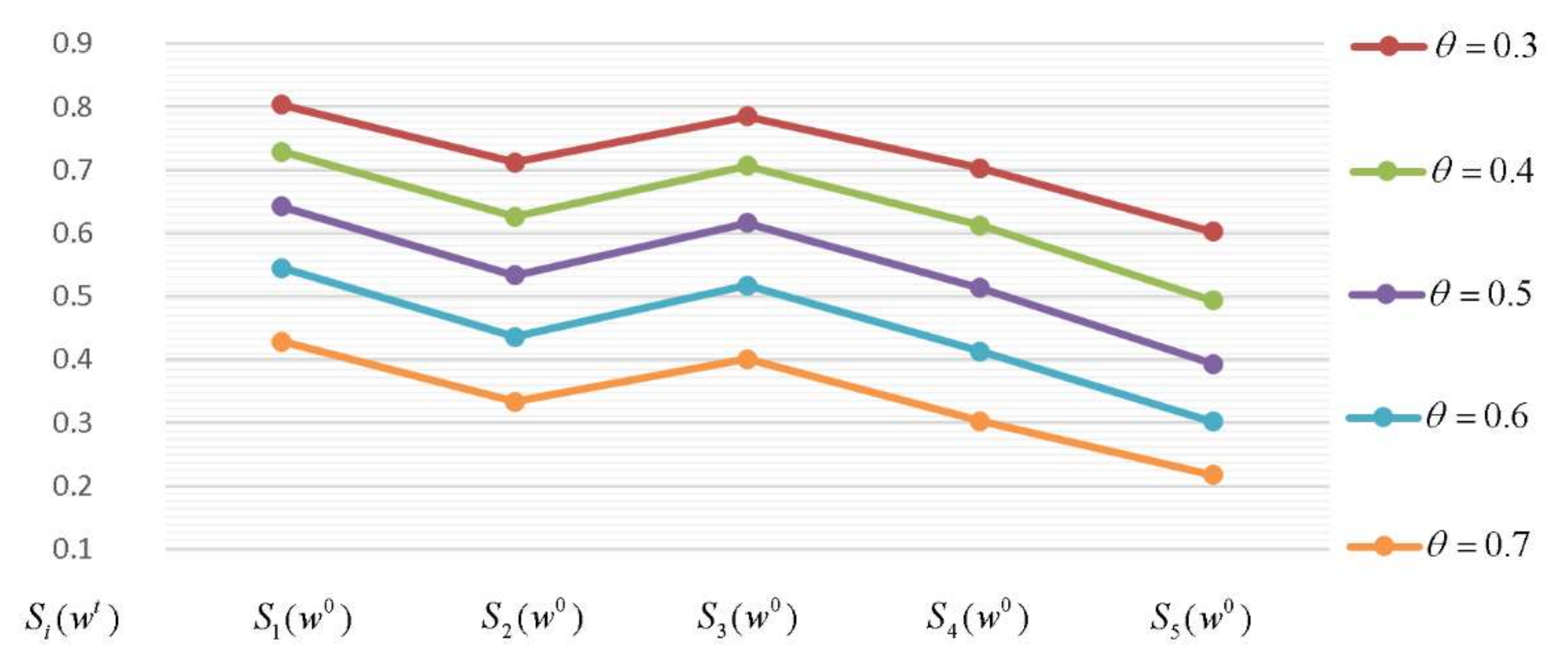
5. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Lyons, A.C. An analysis of third-party logistics performance and service provision. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 547–570. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Chen, M. Optimisation of partial collaborative transportation scheduling in supply chain management with 3PL using ACO. Expert Syst. Appl. 2017, 71, 173–191. [Google Scholar] [CrossRef]
- Kampf, R.A.H.M. Optimization of Production Logistics. Adv. Sci. Technol. Res. J. 2018, 12, 151–156. [Google Scholar] [CrossRef]
- Govindan, K.; Agarwal, V.; Darbari, J.D. An integrated decision making model for the selection of sustainable forward and reverse logistic providers. Ann. Oper. Res. 2019, 273, 607–650. [Google Scholar] [CrossRef]
- Rajesh, R.; Pugazhendhi, S.; Ganesh, K.; Ducq, Y. Generic Balanced Scorecard Framework for Third Party Logistics Service Provider. Int. J. Prod. Econ. 2012, 140, 269–282. [Google Scholar] [CrossRef]
- Gupta, R.; Sachdeva, A.; Bhardwaj, A. A Framework for the Selection of Logistic Service Provider Using Fuzzy Delphi and Fuzzy Topsis. Intell. Autom. Syst. Eng. 2011, 103, 189–202. [Google Scholar]
- Boutkhoum, O.; Hanine, M.; Tikniouine, A. Multi-criteria Decisional Approach of the OLAP Analysis by Fuzzy Logic: Green Logistics as a Case Study. Arab. J. Sci. Eng. 2015, 40, 2345–2359. [Google Scholar] [CrossRef]
- Yayla, A.Y.; Oztekin, A.; Gumus, A.T. A hybrid data analytic methodology for 3PL transportation provider evaluation using fuzzy multi-criteria decision making. Int. J. Prod. Res. 2015, 53, 6097–6113. [Google Scholar] [CrossRef]
- Jovčić, S.; Průša, P.; Dobrodolac, M. A Proposal for a Decision-Making Tool in Third-Party Logistics (3PL) Provider Selection Based on Multi-Criteria Analysis and the Fuzzy Approach. Sustainability 2019, 11, 4236. [Google Scholar] [CrossRef]
- Jung, H. Evaluation of Third Party Logistics Providers Considering Social Sustainability. Sustainability 2017, 9, 777. [Google Scholar] [CrossRef]
- Qu, Q.; Wang, W.; Tang, M. A Performance Evaluation Study of Human Resources in Low-Carbon Logistics Enterprises. Sustainability 2017, 9, 632. [Google Scholar] [CrossRef]
- Yu, M.; Wang, C.; Ho, N. A Grey Forecasting Approach for the Sustainability Performance of Logistics Companies. Sustainability 2016, 8, 866. [Google Scholar] [CrossRef]
- Bajec, P.; Tuljak-Suban, D. An Integrated Analytic Hierarchy Process—Slack Based Measure-Data Envelopment Analysis Model for Evaluating the Efficiency of Logistics Service Providers Considering Undesirable Performance Criteria. Sustainability 2019, 11, 2330. [Google Scholar] [CrossRef]
- Wang, C.; Ho, H.T.; Luo, S. An Integrated Approach to Evaluating and Selecting Green Logistics Providers for Sustainable Development. Sustainability 2017, 9, 218. [Google Scholar] [CrossRef]
- Sremac, S.; Stević, Ž.; Pamučar, D. Evaluation of a Third-Party Logistics (3PL) Provider Using a Rough SWARA–WASPAS Model Based on a New Rough Dombi Aggregator. Symmetry 2018, 10, 305. [Google Scholar] [CrossRef]
- Prakash, C.; Barua, M.K. An analysis of integrated robust hybrid model for third-party reverse logistics partner selection under fuzzy environment. Res. Conserv. Recycl. 2016, 108, 63–81. [Google Scholar] [CrossRef]
- Singh, R.K.; Gunasekaran, A.; Kumar, P. Third party logistics (3PL) selection for cold chain management: A fuzzy AHP and fuzzy TOPSIS approach. Ann. Oper. Res. 2018, 267, 531–553. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Q.; Wang, X. Lean Path for High-Quality Development of Chinese Logistics Enterprises Based on Entropy and Gray Models. Entropy 2019, 21, 641. [Google Scholar] [CrossRef]
- Sasikumar, P.; Haq, A. Integration of closed loop distribution supply chain network and 3PRLP selection for the case of battery recycling. Int. J. Prod. Res. 2011, 49, 3363–3385. [Google Scholar] [CrossRef]
- Prakash, C.; Barua, M.K. A combined MCDM approach for evaluation and selection of third-party reverse logistics partner for Indian electronics industry. Sustain. Prod. Consum. 2016, 7, 66–78. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kumar, V. Optimal selection of third-party logistics service providers using quality function deployment and Taguchi loss function. Benchmarking 2015, 22, 1281–1300. [Google Scholar] [CrossRef]
- Chen, M.; Hsu, C.; Hsu, C. Ensuring the quality of e-shopping specialty foods through efficient logistics service. Trends Food Sci. Technol. 2014, 35, 69–82. [Google Scholar] [CrossRef]
- Du, W.; Zhou, X.; Wang, C. Research on ecological logistics evaluation model based on BCPSGA-BP neural network. Multimed. Tools Appl. 2019, 78, 30271–30295. [Google Scholar] [CrossRef]
- Li, Q.J. A Novel Logistics Supplier Selection Model Based on BP. Key Eng. Mater. 2011, 460–461, 735–740. [Google Scholar] [CrossRef]
- Jin, F.W.; Xue, Q.Z.; Li, J.F. Identification of Security Status of Production Logistics System in Coal Mine Based on RS-SVM. J. Appl. Sci. 2013, 13, 5452–5457. [Google Scholar]
- Vahdani, B.; Behzadi, S.S.; Mousavi, S.M. An artificial intelligence model based on LS-SVM for third-party logistics provider selection. Int. J. Ind. Math. 2015, 7, 301–311. [Google Scholar]
- Pamucar, D.; Chatterjee, K.; Zavadskas, E.K. Assessment of third-party logistics provider using multi-criteria decision-making approach based on interval rough numbers. Comput. Ind. Eng. 2019, 127, 383–407. [Google Scholar] [CrossRef]
- Bulgurcu, B.; Nakiboglu, G. An extent analysis of 3PL provider selection criteria: A case on Turkey cement sector. Cogent Bus. Manag. 2018, 5, 1. [Google Scholar] [CrossRef]
- Shan, L. Research on green logistics service providers selection based on intuitionistic language fuzzy entropy. J. Comput. 2012, 7, 540–546. [Google Scholar] [CrossRef]
- Dhouib, D. An extension of MACBETH method for a fuzzy environment to analyze alternatives in reverse logistics for automobile tire wastes. Omega 2014, 42, 25–32. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.Q.; Tian, Z.P. A multihesitant fuzzy linguistic multicriteria decision-making approach for logistics outsourcing with incomplete weight information. Int. Trans. Oper. Res. 2018, 25, 831–856. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z. Development of TOPSIS Method to Solve Complicated Decision-Making Problems—An Overview on Developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Akman, G.; Baynal, K. Logistics Service Provider Selection through an Integrated Fuzzy Multicriteria Decision Making Approach. J. Ind. Eng. 2014, 2014, 1–16. [Google Scholar] [CrossRef]
- Jatoth, C.; Gangadharan, G.; Fiore, U. SELCLOUD: A hybrid multi-criteria decision-making model for selection of cloud services. Soft Comput. 2019, 23, 4701–4715. [Google Scholar] [CrossRef]
- Kamble, S.J.; Singh, A.; Kharat, M.G. A hybrid life cycle assessment based fuzzy multi-criteria decision making approach for evaluation and selection of an appropriate municipal wastewater treatment technology. Euro Mediterr. J. Environ. Integr. 2017, 2, 9. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Wang, H. Multi-criteria group decision-making based on quasi-order for dual hesitant fuzzy sets and professional degrees of decision makers. Appl. Soft Comput. 2018, 71, 20–35. [Google Scholar] [CrossRef]
- Rashid, T.; Faizi, S.; Xu, Z. ELECTRE-Based Outranking Method for Multi-criteria Decision Making Using Hesitant Intuitionistic Fuzzy Linguistic Term Sets. Int. J. Fuzzy Syst. 2018, 20, 78–92. [Google Scholar] [CrossRef]
- Sarkar, S.; Pratihar, D.K.; Sarkar, B. An integrated fuzzy multiple criteria supplier selection approach and its application in a welding company. J. Manuf. Syst. 2018, 46, 163–178. [Google Scholar] [CrossRef]
- Uygun, Ö.; Dede, A. Performance evaluation of green supply chain management using integrated fuzzy multi-criteria decision making techniques. Comput. Ind. Eng. 2016, 102, 502–511. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, X.; Chen, F. Extended TODIM method for hybrid multiple attribute decision making problems. Knowl. Based Syst. 2013, 42, 40–48. [Google Scholar] [CrossRef]
- Wei, G. Grey relational analysis model for dynamic hybrid multiple attribute decision making. Knowl. Based Syst. 2011, 24, 672–679. [Google Scholar] [CrossRef]
- Ko, W. Construction of house of quality for new product planning: A 2-tuple fuzzy linguistic approach. Comput. Ind. 2015, 73, 117–127. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, Z.S.; Ni, M. Hybrid fuzzy multiple attribute decision making. Inf. Int. Interdiscip. J. 2009, 12, 1033–1044. [Google Scholar]
- Herrera, F.; Martinez, L. An Approach for Combining Linguistic and Numerical Information Based on the 2-Tuple Fuzzy Linguistic Representation Model in Decision-Making. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2000, 8, 539–562. [Google Scholar] [CrossRef]
- Yucesan, M.; Mete, S.; Serin, F. An Integrated Best-Worst and Interval Type-2 Fuzzy TOPSIS Methodology for Green Supplier Selection. Mathematics 2019, 7, 182. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Wei, Y. Models for Green Supplier Selection with Some 2-Tuple Linguistic Neutrosophic Number Bonferroni Mean Operators. Symmetry 2018, 10, 131. [Google Scholar] [CrossRef]
- Deveci, M.; Ozcan, E.; John, R. Interval type-2 hesitant fuzzy set method for improving the service quality of domestic airlines in Turkey. J. Air Transp. Manag. 2018, 69, 83–98. [Google Scholar] [CrossRef]
- Deveci, M.; Öner, S.C.; Canıtez, F. Evaluation of service quality in public bus transportation using interval-valued intuitionistic fuzzy QFD methodology. Res. Transp. Bus. Manag. 2019, 100387. [Google Scholar] [CrossRef]
- Asan, U.; Kadaifci, C.; Bozdag, E. A new approach to DEMATEL based on interval-valued hesitant fuzzy sets. Appl. Soft Comput. 2018, 66, 34–49. [Google Scholar] [CrossRef]
- Jiang, F. An Approach to Evaluating Three-Dimension Reconstruction Image Quality with Hesitant Fuzzy Information. Int. J. Sci. 2017, 4, 7. [Google Scholar] [CrossRef]
- Ccedil, D.; Er, H.; Uuml, Y. Analyzing the Global Risks for the Financial Crisis after the Great Depression Using Comparative Hybrid Hesitant Fuzzy Decision-Making Models: Policy Recommendations for Sustainable Economic Growth. Sustainability 2018, 10, 3126. [Google Scholar]
- Singh, S.; Lalotra, S. On generalized correlation coefficients of the hesitant fuzzy sets with their application to clustering analysis. Comput. Appl. Math. 2019, 38, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, L.; Zhu, F. A Multi-Criteria Group Decision Making Model for Green Supplier Selection under the Ordered Weighted Hesitant Fuzzy Environment. Symmetry 2019, 11, 17. [Google Scholar] [CrossRef]
- Lin, M.; Wang, H.; Xu, Z. TODIM-based multi-criteria decision-making method with hesitant fuzzy linguistic term sets. Artif. Intell. Rev. 2019, 4, 1–25. [Google Scholar] [CrossRef]
- Sakawa, M. Large Scale Interactive Multiobjective 0–1 Programming with Fuzzy Numbers; Physica-Verlag: Heidelberg, Germany, 2000. [Google Scholar]
- Park, K.S.; Kim, S.H. Tools for interactive multiattribute decisionmaking with incompletely identified information. Eur. J. Oper. Res. 1997, 98, 111–123. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An interactive method for fuzzy multiple attribute group decision making. Inf. Sci. 2007, 177, 248–263. [Google Scholar] [CrossRef]
- Xu, Z. An interactive procedure for linguistic multiple attribute decision making with incomplete weight information. Fuzzy Optim. Decis. Mak. 2007, 6, 17–27. [Google Scholar] [CrossRef]
- Xu, Z. Interactive group decision making procedure based on uncertain multiplicative linguistic preference relations. J. Syst. Eng. Electron. 2010, 21, 408–415. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Multiattribute Decision Making: An Interactive Method. IEEE Trans. Fuzzy Syst. 2012, 20, 514–525. [Google Scholar]
- Liao, H.; Xu, Z. Satisfaction Degree Based Interactive Decision Making under Hesitant Fuzzy Environment with Incomplete Weights. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2014, 22, 553–572. [Google Scholar] [CrossRef]
- Ding, J.; Xu, Z.; Zhao, N. An interactive approach to probabilistic hesitant fuzzy multi-attribute group decision making with incomplete weight information. J. Intell. Fuzzy Syst. 2017, 32, 2523–2536. [Google Scholar] [CrossRef]
- Guarnieri, P.; Sobreiro, V.A.; Nagano, M.S. The challenge of selecting and evaluating third-party reverse logistics providers in a multicriteria perspective: A Brazilian case. J. Clean. Prod. 2015, 96, 209–219. [Google Scholar] [CrossRef]
- Aguezzoul, A. Third-party logistics selection problem: A literature review on criteria and methods. Omega 2014, 49, 69–78. [Google Scholar] [CrossRef]
- Zarbakhshnia, N.; Soleimani, H.; Ghaderi, H. Sustainable third-party reverse logistics provider evaluation and selection using fuzzy SWARA and developed fuzzy COPRAS in the presence of risk criteria. Appl. Soft Comput. 2018, 65, 307–319. [Google Scholar] [CrossRef]
- Li, Y.; Ying, C.; Chin, K. Third-party reverse logistics provider selection approach based on hybrid-information MCDM and cumulative prospect theory. J. Clean. Prod. 2018, 195, 573–584. [Google Scholar] [CrossRef]
- Senthil, S.; Srirangacharyulu, B.; Ramesh, A. A robust hybrid multi-criteria decision making methodology for contractor evaluation and selection in third-party reverse logistics. Expert Syst. Appl. 2014, 41, 50–58. [Google Scholar] [CrossRef]
- Zouggari, A.; Benyoucef, L. Simulation based fuzzy TOPSIS approach for group multi-criteria supplier selection problem. Eng. Appl. Artif. Intell. 2012, 25, 507–519. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Z.; Tian, G. A Novel Hybrid Fuzzy Grey TOPSIS Method: Supplier Evaluation of a Collaborative Manufacturing Enterprise. Appl. Sci. 2019, 9, 3770. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xu, Z.; Xia, M. Distance and similarity measures for hesitant fuzzy sets. Inf. Sci. 2011, 181, 2128–2138. [Google Scholar] [CrossRef]
- Ijadi Maghsoodi, A.; Ijadi Maghsoodi, A.; Mosavi, A. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA Approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Wang, H. Heterogeneous Multiple Criteria Group Decision Making with Incomplete Weight Information: A Deviation Modeling Approach. Inf. Fusion 2014, 25, 49–62. [Google Scholar] [CrossRef]
| Variable | Criterion | Definition | Authors |
|---|---|---|---|
| Y1 | Total assets | All assets owned by a logistics enterprise | Wang et al. [14], Prakash and Barua [16], Huang et al. [18], Guarnieri et al. [63], Aguezzoul and Aicha [64] |
| Y2 | Transport cost | Costs related to logistics activities | Stefan et al. [9], Yu et al. [12], Patricija and Suban [13], Sremac et al. [15], Guarnieri et al. [63], Zarbakhshnia et al. [65] |
| Y3 | On time rate | Logistics delivery on time rate | Stefan et al. [9], Patricija and Suban [13], Sremac et al. [15], Guarnieri et al. [63], Zarbakhshnia et al. [65], Li et al. [66] |
| Y4 | Customer satisfaction | Matching degree of customer expectation and customer experience | Patricija and Suban et al. [13], Guarnieri et al. [63], Aguezzoul and Aicha [64], Zarbakhshnia et al. [65], Li et al. [66] Senthil et al. [67], Zouggari and Benyoucef [68] |
| Y5 | Personalized service | Diversification degree of logistics products and services | Prakash and Barua [20], Guarnieri et al. [63], Aguezzoul and Aicha [64], Zarbakhshnia et al. [65], Li et al. [66], Senthil et al. [67], Zouggari and Benyoucef [68] |
| Y6 | User compatibility | Degree of information sharing with user | Shan [29], Feng et al. [69] |
| Y7 | Transport equipment | Number of transportation equipment | Shan [29], Feng et al. [69] |
| Y8 | Employee structure | Proportion of employees with bachelor degree or above in the total number of employees | Sremac et al. [15], Huang et al. [18], Guarnieri et al. [63], Zarbakhshnia [65], Li et al. [66], Senthil [67] |
| Y9 | Technology level | Technical development ability to monitor and implement logistics activities | Stefan et al. [9], Sremac et al. [15], Prakash and Barua et al. [20], Guarnieri et al. [63], Aguezzoul and Aicha [64], Arpachshad et al. [65] |
| Alternative | Criteria | ||||
|---|---|---|---|---|---|
| Y1 | Y2 | Y3 | Y4 | Y5 | |
| X1 | 0.57 | 0.45 | (0.8, 0.2) | (0.7, 0.75, 0.8, 0.9) | (0.5, 0.7, 0.9, 0.9) |
| X2 | 0.48 | 0.47 | (0.6, 0.4) | (0.6, 0.7, 0.7, 0.7) | (0.3, 0.5, 0.5, 0.5) |
| X3 | 0.66 | 0.46 | (0.6, 0.4) | (0.7, 0.75, 0.8, 0.8) | (0.5, 0.7, 0.9, 0.9) |
| X4 | 0.08 | 0.33 | (0.8, 0.2) | (0.6, 0.7, 0.8, 0.8) | (0.5, 0.7, 0.9, 0.9) |
| X5 | 0.01 | 0.51 | (0.6, 0.4) | (0.1, 0.2, 0.2, 0.2) | (0.5, 0.7, 0.9, 0.9) |
| Parameter | Satisfaction | Ranking Order | ||||
|---|---|---|---|---|---|---|
| 0.8032 | 0.712 | 0.7848 | 0.7028 | 0.6026 | ||
| 0.7292 | 0.626 | 0.7067 | 0.6127 | 0.4933 | ||
| 0.6422 | 0.5334 | 0.6163 | 0.5133 | 0.3936 | ||
| 0.5448 | 0.4365 | 0.5171 | 0.4128 | 0.3021 | ||
| 0.4284 | 0.3331 | 0.4011 | 0.3028 | 0.2178 | ||
| Limit | Satisfaction | Ranking Order | ||||
|---|---|---|---|---|---|---|
| 0.4348 | 0.3351 | 0.4077 | 0.3113 | 0.2177 | ||
| 0.4360 | 0.3413 | 0.4081 | 0.3106 | 0.2055 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhou, P.; Li, L.; Zhu, F. An Interactive Decision-Making Method for Third-Party Logistics Provider Selection under Hybrid Multi-Criteria. Symmetry 2020, 12, 729. https://doi.org/10.3390/sym12050729
Liu Y, Zhou P, Li L, Zhu F. An Interactive Decision-Making Method for Third-Party Logistics Provider Selection under Hybrid Multi-Criteria. Symmetry. 2020; 12(5):729. https://doi.org/10.3390/sym12050729
Chicago/Turabian StyleLiu, Yumin, Peng Zhou, Liyuan Li, and Feng Zhu. 2020. "An Interactive Decision-Making Method for Third-Party Logistics Provider Selection under Hybrid Multi-Criteria" Symmetry 12, no. 5: 729. https://doi.org/10.3390/sym12050729
APA StyleLiu, Y., Zhou, P., Li, L., & Zhu, F. (2020). An Interactive Decision-Making Method for Third-Party Logistics Provider Selection under Hybrid Multi-Criteria. Symmetry, 12(5), 729. https://doi.org/10.3390/sym12050729




