Abstract
The physical problem under consideration is the boundary layer problem of an incompressible, laminar flow, taking place over a flat plate in the presence of a pressure gradient and radiation. For the mathematical formulation of the problem, the partial differential equations of continuity, energy, and momentum are taken into consideration with the boundary layer simplifications. Using the dimensionless Falkner–Skan transformation, a nonlinear, nonhomogeneous, coupled system of partial differential equations (PDEs) is obtained, which is solved via the homotopy analysis method. The obtained analytical solution describes radiation and pressure gradient effects on the boundary layer flow. These analytical results reveal that the adverse or favorable pressure gradient influences the dimensionless velocity and the dimensionless temperature of the boundary layer. An adverse pressure gradient causes significant changes on the dimensionless wall shear parameter and the dimensionless wall heat-transfer parameter. Thermal radiation influences the thermal boundary layer. The analytical results are in very good agreement with the corresponding numerical ones obtained using a modification of the Keller’s-box method.
Keywords:
boundary layer; approximate solution; homotopy analysis method; pressure gradient; thermal radiation MSC:
76D10; 76M99; 35C10; 35Q35
1. Introduction
The mathematical description of the laminar, incompressible boundary layer flow remains a challenging problem with several aspects still unexplored. The first to describe the steady two-dimensional boundary layer flow over a semi-infinite flat plate was Blasius [1]. The adverse pressure gradient on the laminar boundary layer flow was numerically examined by Howarth [2]. Other studies on the effects of adverse pressure gradients, heat transfer, or thermal radiation on the fluid flow include, although not limited to, [3,4,5,6,7,8]. The effect of radiation in the presence of a magnetic field or with temperature dependent viscosity was studied in [9,10].
At high temperatures, thermal radiation has a significant effect on the flow field, which has important applications in many areas of engineering. This effect has been reported in several works where various flows in the presence of radiation have been studied, such as the free convective laminar flow in [11,12] and [13], the flow of an optically thin gray fluid in [14,15], and [10] or the flow past a moving vertical plate or a vertical oscillating plate in [16,17].
In [18], a computational model was presented for convective and radiative heat transfer of very high temperature gas cooled and gaseous core reactors, with results that are in very good agreement with experimentally based correlations. In [19,20], the interaction of flow with radiation was studied in hypersonic boundary layer flows. In [21,22], a comprehensive numerical analysis of heat transfer in a rectangular enclosure was performed, and several effects on the fluid flow and heat transfer have been extensively studied, such as the effects of the Rayleigh number, thermal conductivity ratio, as well as internal surface emissivity. These analyses revealed a significant cooling effect of the internal volume together with an increase in the thermal conductivity ratio [22]. In [23], it was shown that the thermal behavior of a compressible turbulent flow was influenced by radiation and that the radiative heat flux plays a role in the recirculating zone. More recent studies show the impact of thermal radiation and the viscous dissipation effect on the dynamic three-dimensional rotating flow of carbon nanotubes [24]. In [25], the slip effects on magnetohydrodynamic (MHD) axisymmetric buoyant nanofluid flow over a stretching sheet in the presence of radiation and a chemical reaction were studied. In [26], the mixed convection stagnation-point flow of a nanofluid past a permeable stretching or shrinking sheet was numerically examined with suction, radiation, and a heat source/sink.
In this study, the standard formulation of the boundary layer equations is used and analytically solved until the point of flow separation, for the steady state, two-dimensional, laminar, boundary layer flow of an incompressible fluid over a flat plate under radiation, and pressure gradient effects. The nondimensional form of the corresponding equations with pressure gradient and thermal radiation are obtained in Section 2, utilizing the Falkner–Skan transformation [8]. The resulting nondimensional equations form a nonlinear, coupled system of partial differential equations (PDEs), accompanied by adequate boundary conditions. Such kinds of systems have been studied in the literature using mostly numerical methods since finding an analytical solution is very difficult, if at all possible. However, instead of using a numerical method in order to solve this system of PDEs, one may choose an approximate technique instead. The main advantage when using an approximate technique instead of a numerical is that a closed form approximate formula for the solution is obtained. This may lead to useful formulae, even if they are approximations, for quantities of physical interest. In addition, the implementation of approximate techniques is highly facilitated nowadays by the use of symbolic computation software, such as Mathematica or Maple.
Approximate methods have been successfully applied in the past in order to study fluid mechanics problems. The most well known approximate methods are the perturbation techniques [27,28]. For recent applications of perturbation techniques to fluid mechanics problems, one may refer to [29,30,31,32,33,34]. Other approximate techniques have also been applied in the study of various physical problems, including boundary layer flows. The references of the present paper are confined to few indicative papers of the last decade. The variational iteration method was utilized in [35] for solving the Blasius equation and in [36] for studying the magnetohydrodynamic flow over a nonlinear stretching sheet. The Adomian decomposition method was used not only for the solution of the Blasius equation in [37] but also for the study of micropolar flow in a porous channel [38]. Also, the differential transform method was used in [39] and [40] for the study of specific wedge flow and magnetohydrodynamic flow problems. It is worth mentioning that the differential transform method, combined with the method of steps, has been successfully applied for solving partial differential equations [41], as well as delayed differential equations and systems [42,43].
Maybe a breakthrough for the approximate methods was Liao’s homotopy analysis method (HAM), which was introduced in [44]. Since then, it has been extensively used for a variety of physical problems, such as beam problems, oscillation problems, wave propagation problems, and of course, fluid mechanics problems. A thorough description of HAM can be found in the books [45,46], where it is also shown how other approximate methods can be unified by HAM. Probably the first papers where HAM was used for the study of boundary layer problems were [47,48,49], where the Blasius and the Falkner Skan equations were solved. Ever since, HAM has been successfully used, literally in hundreds of papers, for the study of boundary layer flows. Indicatively, it is mentioned that recently HAM has been used for the study of flows of nanofluids [24,50,51,52,53,54,55] and flows in porous media [56,57,58,59].
In the vast majority of the papers regarding boundary layer flows where HAM was used, the nonlinear equations under consideration were homogeneous with boundary conditions at ∞. There are, however, also papers of this kind where the solved nonlinear equations are nonhomogeneous, but in most cases, the nonhomogeneous term is a constant. Even less are the papers of this kind, where the boundary conditions are not placed at ∞ but at some finite point.
In this paper, the steady state, two-dimensional, laminar, boundary layer flow of an incompressible fluid over a flat plate under radiation and pressure gradient effects, is solved for the first time using HAM, an analytical technique. This problem is mathematically described by a nonlinear, nonhomogeneous, and coupled system of PDEs. The nonhomogeneous terms in the momentum and energy equations are nonconstants, and in addition, the boundary conditions are placed not at ∞ but at the edge of the boundary layer. The appearance of such nonhomogeneous terms as well the specific type of boundary conditions, increase the difficulty of applying HAM. To the best of the authors’ knowledge, only in [60] were similar equations and boundary conditions solved via HAM, where the two-dimensional, steady, boundary layer flow of a heat-conducting perfect gas was studied. However, no radiation effects were taken into consideration in the aforementioned paper.
The rest of the paper is organized as follows: In Section 2, the physical problem is given and the mathematical equations that describe it are derived. In Section 3, a short description of HAM is given together with its specific application for the physical problem studied in this paper. Finally, in Section 4, a thorough discussion of the obtained results is given with respect not only to the effect of a pressure gradient and radiation but also to numerical results concerning similar but not identical physical problems [3,5,6,19,20,61,62]. The presented results are novel, especially concerning the radiation effect on the boundary layer flow under the effect of a pressure gradient. More precisely, the obtained analytical results, reveal that the adverse and favorable pressure gradients substantially influence the dimensionless velocity of the boundary layer. Pressure gradient also plays a significant role in the changes of the dimensionless temperature of the boundary layer. Furthermore, the adverse pressure gradient causes significant changes on the dimensionless wall shear parameter and the dimensionless wall heat-transfer parameter, leading to boundary layer separation. Thermal radiation significantly influences the thermal boundary layer.
2. Mathematical Formulation
Consider the steady state, two-dimensional laminar flow of an incompressible fluid in the boundary layer that forms over a flat plate parallel to the free stream velocity, . In a Cartesian coordinate system, , the surface is located at as shown in Figure 1.
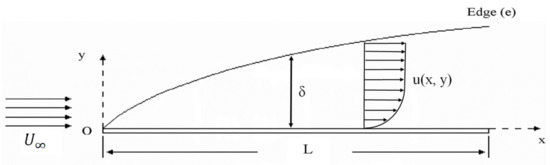
Figure 1.
Flow configuration and coordinate system.
The governing equations, after the boundary layer simplifications, form a parabolic system that constitutes of the continuity equation:
the x-momentum equation:
and the energy equation:
with boundary conditions defined as follows:
where u, v are the velocity components, T the temperature, p the pressure, the density, the kinematic viscosity, the viscosity, the specific temperature of the fluid under constant pressure, k the coefficient of thermal conductivity, the local radiant absorption, the temperature of the flat plate, , the velocity and the temperature at the edge of the boundary layer, respectively, and the boundary layer thickness.
Assuming that the temperature differences within the flow are sufficiently small, using the Taylor series of about and neglecting higher-order terms, can be expressed as a linear function of the temperature of the form [10]. Then, the local radiant absorption is given by the expression:
where is the absorption coefficient and is the Stefan–Boltzmann constant [4].
At the edge of the boundary layer, Howarth’s flow is considered, where the external velocity varies linearly with x, and at the edge, the velocity is , where is the free stream velocity. By using Bernoulli’s equation, the flow at the edge of the boundary layer and the pressure drop are associated:
Moreover, introducing the dimensionless Falkner–Skan transformation and the dimensionless stream function [3]:
as well as the dimensionless quantity
the following system of PDEs is obtained:
accompanied by the boundary conditions
where the prime denotes partial differentiation with respect to , is the Prandtl number, , and is again the boundary layer thickness, resulting now from Equation (7).
3. Application of Homotopy Analysis Method
3.1. A Short Description of HAM
As already mentioned, one of the most powerful approximate methods for solving nonlinear differential equations (DEs) is the Homotopy Analysis Method (HAM) as proposed by Liao, see [44,45,46]. According to HAM, instead of solving the original nonlinear DE, a series of linear DEs is solved and the solution of the nonlinear DE is expressed as a series of the solutions of these linear DEs. In the following, a short description of HAM is given, whereas in Section 3.2, it is demonstrated how it can be applied to System (12)–(14).
In order to keep things simple, HAM will be demonstrated by applying it to the nonlinear ordinary differential equation of th order
accompanied by the initial conditions
where is the unknown function and , are known constants.
According to HAM, an initial approximation of should be constructed together with a homotopy , so that
- is a solution of equation
Since depends not only on t but also on q, it can be expressed in the form of a series as
where satisfy the linear ODEs
called high-order deformation equations, where
and
Thus, if all can be found explicitly and the series on the right hand side of Equation (20) converges for , the solution of Equation (15) is given in the form of the so-called homotopy series
In practice, K terms of the homotopy series are calculated, in order to obtain an adequate approximation of . The corresponding series
is called the approximate solution of order.
The HAM gives great freedom in choosing the initial approximation , the convergence control parameter ℏ, the linear operator , and the auxiliary function . In order to choose these functions and operators, a set of base functions, for example
is first chosen. This set is supposed to adequately describe the expected solution of Equations (15) and (16). Then, should be chosen in such a way so that it a) can be expressed only in terms of and b) should satisfy the initial conditions (16), i.e.,
The linear ODEs of Equation (21) are accompanied by the homogeneous initial conditions
In this way, the homotopy Series (24) satisfies Equation (16). Then and are chosen in such a way so that every , is expressed as a series of , i.e.,
where , coefficients. In this way, is also expressed in the form
where , coefficients.
Moreover, ℏ is chosen in such a way so that the series on the right hand side of Equation (24) is convergent. One way to choose ℏ, is to find the optimum ℏ for which the so-called “discrete squared residual" error defined by
is minimized, where and is the step used to discretize the interval of t using . This has been proven to be a very good approximation of the total squared residual error; see, for example, [50] and [46] (Chapter 3).
Another way to choose ℏ is to use the so-called curves, which were proposed in [45] and have been used in a great amount of research papers. The curves are graphs of quantities of calculated at specific values of t, which usually have a physical meaning. For example, may be used. If the Series (24) is convergent, should always have the same value, which of course depends on ℏ. This means that in the graph of against ℏ, a horizontal line segment will be apparent, which is called the valid region of ℏ. If a value of ℏ is chosen from this region, it is quite certain that the Series (24) converges. Of course, maybe more than one important quantities with physical meaning can exist. Thus, more than one curves can be used.
3.2. Application of HAM to System (12)–(14)
As initial approximations, the following functions
may be considered. It should be noted that the multiplicative term , as well as the term in , are due to the boundary conditions at .
The corresponding linear and nonlinear operators are chosen to be
where the prime denotes partial differentiation with respect to .
Then, the higher-order deformation equations take the form
and
accompanied by the boundary conditions
and
where , is defined by Equation (22), the auxiliary functions , are both chosen to be equal to 1, and the terms and are determined via Equation (23) and are found to be:
and
Thus, beginning with , and solving Equations (31), (33) and (32), (34), several approximations of f and can be found. It should be mentioned that the nonhomogeneous terms and , appearing in (12) and (13), respectively, result in the appearance of the terms and in and , respectively. These terms greatly increase the complexity of Equations (31) and (32), and as a consequence, the computational time needed for obtaining several approximations of f and is also considerably increased. For example, in the case where both homogeneous terms for the pressure gradient and the radiation are considered, the computational time was 50% more compared to the homogeneous case, i.e., in the absence of the pressure gradient and/or radiation effect.
Regarding the convergence of the method, the following is true
Theorem 1.
The proof of this theorem is omitted since it is similar to the proof of the general convergence theorem given in [45].
The values of the convergence control parameters and are chosen in such a way so that the “discrete square residual” errors defined by
are minimized for both f and , where , and . Due to the fact that does not appear in Equation (31), the optimum value for can be found independently and then used in order to find the optimum value for .
Table 1 shows the optimum values of and , as well as the corresponding errors for several values of the order K from 2 up to 12, in the case where , , , , , , , , and . As the order increases, the error reduces for both equations, as expected.

Table 1.
Optimum values of , , and corresponding errors.
The values for the convergence control parameters are in accordance with the ℏ-curves of the 15th order approximations, as shown in Figure 2. In this study, all the figures presented in the next section show results obtained utilizing the 15th order approximation for both dimensionless quantities, velocity, , and temperature, . It is worth mentioning that in the case of no pressure gradient and/or no radiation effect, i.e., in the absence of nonhomogeneous terms, it suffices to consider only seven terms for f and only six terms for in order to obtain a good approximation of the solution.
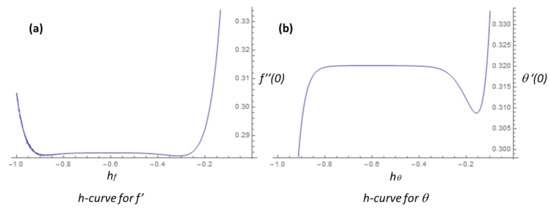
Figure 2.
(a) curve for the dimensionless velocity, for 15 terms. (b) curve for the dimensionless temperature, for 15 terms.
4. Results and Discussion
To show the combined effect of a pressure gradient (adverse or favorable) and thermal radiation on the boundary layer flow, it is important to examine the dimensionless quantities of the problem under consideration, such as the dimensionless velocity, , and the dimensionless temperature, . The shape of the boundary layer under adverse or favorable pressure gradient is clearly described by these quantities, and it turns out that it is very different from the shape of the boundary layer in the case with no pressure gradient.
In this study, the adverse pressure effect is achieved by changing the length, L () and retaining the free stream velocity, constant. The free-stream temperature was considered to be , , and . The temperature difference between the plate and the free stream was considered to be, . The radiation parameter, R, is given by the expression, , where a is the absorption coefficient (), is the Stefan–Boltzman constant (), L is a characteristic length (the length of the flat plate), is the velocity at the edge of the boundary layer, is the free stream velocity, is the specific heat under constant pressure, and is the density of the fluid [10,61,62] (see Equation (13)).
The pressure gradient effect plays a significant role on the flow, as indicated in Figure 3. The dimensionless velocity, , is presented in Figure 3a. Adverse pressure gradient (APG) decreases the dimensionless flow velocity, while a favorable pressure gradient (FPG) increases the dimensionless velocity compared to the case with no pressure gradient (PG). The same effect is observed for the dimensionless temperature, , as shown in Figure 3b. The thermal boundary layer follows the behavior of the boundary layer. Numerically a similar problem has been studied without the effect of radiation [3,5,6].
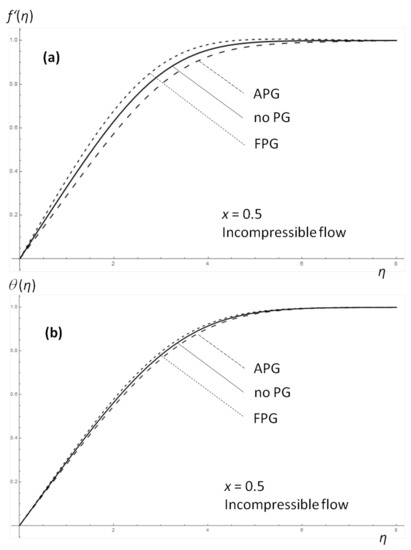
Figure 3.
(a) The dimensionless velocity, with respect to . (b) The dimensionless temperature, with respect to , for the case where , for adverse pressure gradient (APG) and favorable pressure gradient (FPG) cases.
A quantitative comparison of the analytical results obtained from HAM, with numerical results for the problem with the adverse pressure gradient, is presented in Figure 4. The numerical approach utilized is a modification of the Keller’s-box method [5], where the governing equations are reduced to a first order system and then are approximated using central differences of second order accuracy. A multi-dimensional Newton–Raphson iteration scheme is then implemented for the solution of the resulting non-linear algebraic system, and the corresponding Jacobian matrix is not prescribed by the programmer but computed numerically. It can be observed that the numerical solution is in very good agreement with the analytical one, utilizing only 20 terms from HAM.
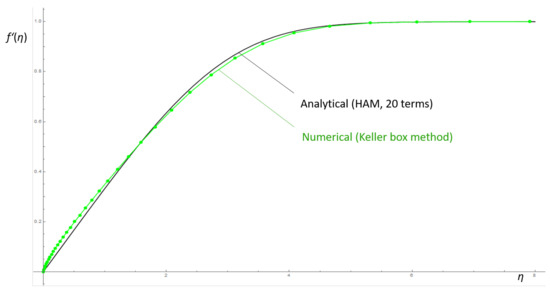
Figure 4.
Comparison of the dimensionless velocity, with respect to the dimensionless distance for the analytical (HAM, 20 terms), and the numerical solution obtained with the numerical approach introduced in [5].
Additionally, the most important parameters for engineering applications are the skin friction coefficient, and the local Stanton number, , defined per unit width of the plate, for the cases of a heating or cooling wall [5,6]. These parameters are functions of the dimensionless wall shear parameter, , and the dimensionless wall heat-transfer parameter, .
Figure 5 shows the effect of adverse pressure gradient on the skin friction coefficient, with the dimensionless x-distance. It is observed that with different adverse pressure gradients, the dimensionless provides substantially different behavior. More precisely, as the APG is increased, the flow can separate faster concerning the x-direction, as indicated in Figure 5 for different realizations of the edge fluid velocity, , representing the adverse pressure effect (ADV). Separation of the boundary layer, as shown in the case, could lead to adverse effects and boundary layer separation.
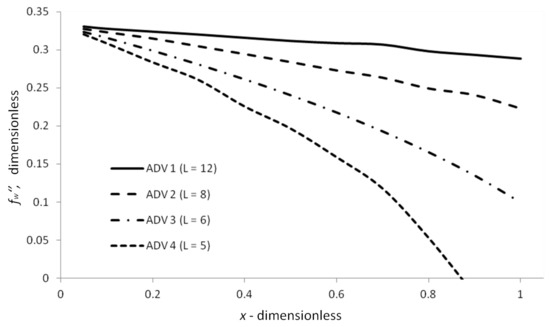
Figure 5.
Skin friction coefficient, with respect to the dimensionless x-direction.
Figure 6 shows the effect of APG on the dimensionless wall heat-transfer parameter, with the dimensionless x-distance. It is observed that the dimensionless wall heat-transfer parameter is appreciably influenced by the adverse pressure gradient, following the boundary layer behavior. This effect is more pronounced close to the separation region, as indicated in Figure 6.
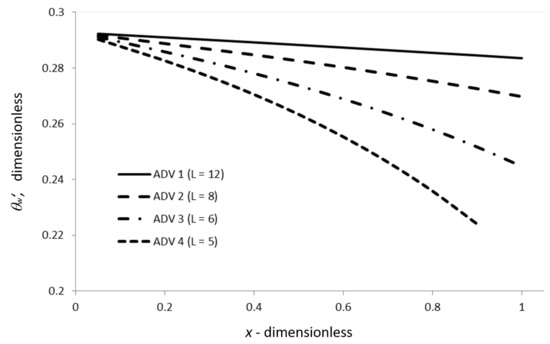
Figure 6.
Heat transfer coefficient, with respect to the dimensionless x-direction.
Finally, Figure 7 shows the effect of radiation on the thermal boundary layer. The flow is under the influence of an adverse pressure gradient. Close to the separation area (), a significant cooling effect of the thermal boundary layer is observed, which is mainly due to the influence of thermal radiation. This phenomenon was also observed in previous numerical and theoretical studies regarding compressible and turbulent flows [19,20,61,62].
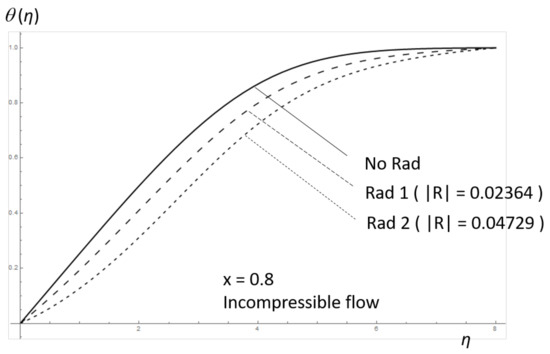
Figure 7.
Effect of radiation on the dimensionless temperature, , depending on the parameter, R, and the adverse pressure gradient, with respect to .
5. Conclusions
The main goal of this work was to study the boundary layer problem of the incompressible, laminar flow past a flat plate in the presence of a pressure gradient and radiation. The physical problem is described by the continuity, the momentum, and the energy equations with the boundary layer simplifications. Under specific assumptions on the radiation effect and using the Bernoulli equation for the pressure drop and the Falkner–Skan transformation, a nonlinear, nonhomogeneous, and coupled set of PDEs is obtained, accompanied by boundary conditions at the edge of the boundary layer.
This system is solved using the HAM, although the specific form of the boundary conditions, increase the complexity of the initial approximations and , which together with the existence of the nonhomogeneous terms, increase the complexity of the higher-order deformation Equations (31) and (32). As a consequence, the computational time needed for obtaining several approximations of f and is considerably increased. It is indicative that in one of the cases, where both homogeneous terms for the pressure gradient and the radiation are considered, the computational time was 50% more compared to the homogeneous case. Moreover, the nonhomogeneous terms also affect the number of terms required in order to obtain a good approximation, which also increases the computational time. In some cases, only half terms are needed in the homogenous case.
To the best of the authors’ knowledge, in only one previous study were similar equations and boundary conditions solved via HAM, highlighting the novelty of the current work. Additionally, no radiation effects were taken into consideration in the aforementioned paper. A short description of this mathematical method is given together with its specific application for the problem studied.
The obtained analytical results show that the pressure gradient plays a significant role in the changes of the dimensionless velocity and temperature of the boundary layer. An adverse pressure gradient causes significant alterations on important engineering parameters, such as the dimensionless wall shear parameter, , and the dimensionless wall heat-transfer parameter, , leading to adverse effects and flow separation. An essential cooling of the boundary layer was found, revealing that thermal behavior is influenced by radiation. This finding is important because it could be utilized in many engineering applications, such as the high temperature, gas-cooled, and gaseous fuel nuclear reactors, as discussed in the introduction section. Thermal radiation could influence the flow field and thermal boundary layer rendering the above application as a possible control technique.
Author Contributions
Conceptualization by M.A.X., E.N.P.; investigation by M.A.X., E.N.P., A.S., U.S.M.; methodology by M.A.X., E.N.P., A.S., U.S.M.; supervision by M.A.X., E.N.P.; validation by M.A.X., E.N.P., A.S.; visualization by M.A.X., E.N.P., A.S.; writing—original draft preparation by M.A.X., E.N.P., A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Mahabaleshwar (USM) wishes to thank Professor Pradeep G. Siddheshwar, F.N.A.Sc., F.I.M.A.(UK), Department of Mathematics, Bangalore University, Bangalore, India. We dedicate this work to him on the occasion of his retirement. The authors would also like to thank the reviewers for their valuable feedback.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PDE(s) | Partial Differential Equation(s) |
| MHD | Magnetohydrodynamic |
| HAM | Homotopy Analysis Method |
| DE(s) | Differential Equation(s) |
| ODE(s) | Ordinary Differential Equation(s) |
| APG | Adverse Pressure Gradient |
| FPG | Favorable Pressure Gradient |
| PG | Pressure Gradient |
| ADV | Adverse Pressure Effect |
| RAD | Radiation |
| e | Edge |
| coordinate system | |
| x, y | coordinates |
| free stream velocity | |
| L | length of the plate |
| dimensional boundary layer thickness | |
| u, v | dimensional velocity components of the fluid |
| density of the fluid | |
| p | pressure of the fluid |
| kinematic viscosity of the fluid | |
| dynamic viscosity of the fluid | |
| specific temperature of the fluid under constant pressure | |
| T | temperature of the fluid |
| k | coefficient of thermal conductivity |
| local radiant absorption | |
| radiative energy flux | |
| temperature of the flat plate | |
| temperature of the fluid at the edge of the boundary layer | |
| velocity of the fluid at the edge of the boundary layer | |
| absorption coefficient | |
| Stefan–Boltzmann constant | |
| dimensionless coordinate variable | |
| stream function | |
| f | dimensionless stream function |
| dimensionless temperature of the fluid | |
| Prandtl number | |
| dimensionless coordinate variable | |
| dimensionless velocity of the fluid at the edge of the boundary layer | |
| dimensionless boundary layer thickness | |
| homotopy | |
| q | embedding parameter |
| auxiliary linear operator | |
| auxiliary nonlinear operator | |
| , , | auxiliary functions |
| ℏ, , | convergence control parameters |
| set of base functions | |
| , , | “discrete square residual” errors |
| R | radiation parameter |
| local skin friction coefficient | |
| local Stanton number |
References
- Blasius, H. Grenzschichten in flüssigkeiten mit kleiner reibung. Z. Angew. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Howarth, L. On the solution of the laminar boundary layer equations. Proc. R. Soc. Lond. Ser. A 1938, 164, 547–579. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer; Springer: New York, NY, USA, 1984. [Google Scholar]
- Howell, J.R.; Siegel, R.; Mengüç, M.P. Thermal Radiation, Heat Transfer, 5th ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Kafoussias, N.; Karabis, A.; Xenos, M. Numerical study of two dimensional laminar boundary layer compressible flow with pressure gradient and heat and mass transfer. Int. J. Eng. Sci. 1999, 37, 1795–1812. [Google Scholar] [CrossRef]
- Kafoussias, N.; Xenos, M. Numerical study of two-dimensional turbulent boundary layer compressible flow with adverse pressure gradient and heat and mass transfer. Acta Mech. 2000, 141, 201–223. [Google Scholar] [CrossRef]
- Raptis, A.; Perdikis, C.; Takhar, H.S. Effect of thermal radiation on MHD flow. Appl. Math. Comput. 2004, 153, 645–649. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary–Layer Theory, 8th ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Raptis, A.; Perdikis, C.; Leontitsis, A. Effects of radiation in an optically thin gray gas flowing past a vertical infinite plate in the presence of magnetic field. Heat Mass Transf. 2003, 39, 771–773. [Google Scholar] [CrossRef]
- Xenos, M. Radiation Effects on flow past a stretching plate with temperature dependent viscosity. Appl. Math. 2013, 4, 1–5. [Google Scholar] [CrossRef][Green Version]
- Ali, M.M.; Chen, T.S.; Armaly, B.F. Natural convection-radiation interaction in boundary-layer flow over horizontal surfaces. AIAA J. 1984, 22, 1797–1803. [Google Scholar] [CrossRef]
- Raptis, A.; Toki, C.J. Thermal radiation in the presence of free convective flow past a moving vertical porous plate: An analytical solution. Int. J. Appl. Mech. Eng. 2009, 14, 1115–1126. [Google Scholar]
- Raptis, A.; Perdikis, C. Radiation and free convection flow past a moving plate. Appl. Mech. Eng. 1999, 4, 817–821. [Google Scholar]
- Raptis, A.; Perdikis, C. Thermal radiation of an optically thin gray gas. Int. J. Appl. Mech. Eng. 2003, 8, 131–134. [Google Scholar]
- Seddeek, M.A.; Abdelmeguid, M.S. Effects of radiation and thermal diffusivity on heat transfer over a stretching surface with variable heat flux. Phys. Lett. A 2006, 348, 172–179. [Google Scholar] [CrossRef]
- Muthucumaraswamy, R. The interaction of thermal radiation on vertical oscillating plate with variable temperature and mass diffusion. Theor. Appl. Mech. 2006, 33, 107–121. [Google Scholar] [CrossRef][Green Version]
- Muthucumaraswamy, R.; Chandrakala, P. Effects of thermal radiation on moving vertical plate in the presence of an optically thin gray gas. Forschung im Ingenieurwesen 2005, 69, 205–208. [Google Scholar] [CrossRef]
- Anghaie, S.; Chen, G. Application of computational fluid dynamics for thermal analysis of high temperature gas cooled and gaseous core reactors. Nucl. Sci. Eng. 1998, 130, 361–373. [Google Scholar] [CrossRef]
- Duan, L.; Martin, M.P.; Feldick, A.M.; Modest, M.F.; Levin, D.A. Study of turbulence-radiation interaction in hypersonic turbulent boundary layers. AIAA J. 2012, 50, 447–453. [Google Scholar] [CrossRef]
- Duan, L.; Martin, M.P.; Sohn, I.; Levin, D.A.; Modest, M.F. Study of emission turbulence-radiation interaction in hypersonic boundary layers. AIAA J. 2011, 49, 340–348. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A. Numerical simulation of turbulent natural convection combined with surface thermal radiation in a square cavity. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1600–1618. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Mohamad, A.A. Numerical simulation of a conjugate turbulent natural convection combined with surface thermal radiation in an enclosure with a heat source. Int. J. Therm. Sci. 2016, 109, 172–181. [Google Scholar] [CrossRef]
- Kim, S.S.; Baek, S.W. Radiation affected compressible turbulent flow over a backward facing step. Int. J. Heat Mass Transfer 1996, 39, 3325–3332. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple slip effects on magnetohydrodynamic axisymmetric buoyant nanofluid flow above a stretching sheet with radiation and chemical reaction. Symmetry 2019, 11, 1171. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Dyke, M.V. Perturbation Methods in Fluid Mechanics; Parabolic Press: Stanford, CA, USA, 1975. [Google Scholar]
- Housiadas, K.D. Steady sedimentation of a spherical particle under constant rotation. Phys. Rev. Fluids 2019, 4, 103301. [Google Scholar] [CrossRef]
- Housiadas, K.D.; Ioannou, I.; Georgiou, G.C. Lubrication solution of the axisymmetric Poiseuille flow of a Bingham fluid with pressure-dependent rheological parameters. J. Non-Newton. Fluid Mech. 2018, 260, 76–86. [Google Scholar] [CrossRef]
- Housiadas, K.D.; Tanner, R.I. A high-order perturbation solution for the steady sedimentation of a sphere in a viscoelastic fluid. J. Non-Newton. Fluid Mech. 2016, 233, 166–180. [Google Scholar] [CrossRef]
- Housiadas, K.D.; Tanner, R.I. Viscoelastic shear flow past an infinitely long and freely rotating cylinder. Phys. Fluids 2018, 30, 073101. [Google Scholar] [CrossRef]
- Si, X.; Yuan, L.; Cao, L.; Zheng, L.; Shen, Y.; Li, L. Perturbation solutions for a micropolar fluid flow in a semi-infinite expanding or contracting pipe with large injection or suction through porous wall. Open Phys. 2016, 14, 231–238. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, P.; Si, X.-H. Perturbation solutions for asymmetric laminar flow in porous channel with expanding and contracting walls. Appl. Math. Mech.-Engl. Ed. 2014, 35, 203–220. [Google Scholar] [CrossRef]
- Liu, Y.; Kurra, S.N. Solution of Blasius equation by variational iteration. Appl. Math. 2011, 1, 24–27. [Google Scholar] [CrossRef]
- Xu, L.; Lee, E.W.M. Variational iteration method for the magnetohydrodynamic flow over a nonlinear stretching sheet. Abstr. Appl. Anal. 2013, 2013, 573782. [Google Scholar] [CrossRef]
- Abbasbandy, S. A numerical solution of Blasuis equation by Adomians decomposition method and comparison with homotopy perturbation method. Chaos Solitons Fractals 2007, 31, 257–260. [Google Scholar] [CrossRef]
- Aski, F.S.; Nasirkhani, S.J.; Mohammadiand, E.; Asgari, A. Application of Adomian decomposition method for micropolar flow in a porous channel. Prop. Power Res. 2014, 3, 15–21. [Google Scholar] [CrossRef]
- Kuo, B.-L. Application of the differential transformation method to the solutions of Falkner-Skan wedge flow. Acta Mech. 2003, 164, 161–174. [Google Scholar] [CrossRef]
- Thiagarajan, M.; Senthilkumar, K. DTM-Padé approximants for MHD Flow with suction/blowing. J. Appl. Fluid Mech. 2012, 6, 724–728. [Google Scholar]
- Rebenda, J.; Šmarda, Z. Convergence analysis of an iterative scheme for solving initial value problem for multidimensional partial differential equations. Comp. Math. Appl. 2015, 70, 1772–1780. [Google Scholar] [CrossRef]
- Rebenda, J.; Šmarda, Z. A differential transformation approach for solving functional differential equations with multiple delays. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 246–257. [Google Scholar] [CrossRef]
- Rebenda, J.; Šmarda, Z. Numerical algorithm for nonlinear delayed differential systems of nth order. Adv. Differ. Equ. 2019, 2019, 26. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotoy Analysis Method; Chapman & Hall/CRC, CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Springer: Berlin, Germany, 2011. [Google Scholar]
- Liao, S.J. A kind of approximate solution technique which does not depend upon small parameters-II. An application in fluid mechanics. Int. J. Nonlin. Mech. 1997, 32, 815–822. [Google Scholar] [CrossRef]
- Liao, S.J. An explicit totally analytic solution of laminar viscous flow over a semi-infinite flat plate. Commun. Nonlinear Sci. Numer. Simul. 1999, 3, 53–57. [Google Scholar] [CrossRef]
- Liao, S.J. A uniformly valid analytic solution of 2D viscous flow past a semi-infinite flat plate. J. Fluid Mech. 1999, 385, 101–128. [Google Scholar] [CrossRef]
- Farooq, U.; Hayat, T.; Alsaedi, A.; Liao, S.J. Series solutions of non-similarity boundary layer flows of nano-fluids over stretching surfaces. Numer. Algor. 2015, 70, 43–59. [Google Scholar]
- Jawad, M.; Shah, Z.; Kahn, A.; Kumam, P.; Islam, S. Entropy generation and heat transfer analysis in MHD unsteady rotating flow for aqueous suspensions of carbon nanotubes with nonlinear thermal radiation and viscous dissipation effect. Entropy 2019, 21, 492. [Google Scholar] [CrossRef]
- Naz, R.; Noor, M.; Hayat, T.; Javed, M.; Alsaed, A. Dynamism of magnetohydrodynamic cross nanofluid with particulars of entropy generation and gyrotactic motile microorganisms. Int. Commun. Heat Mass Transf. 2020, 2020 110, 104431. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.O.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of Reiner-Philippoff fluid over an unstable stretching surface with Brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD nanofluid thin film flow over an unsteady vertical stretching sheet with entropy generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef]
- Waqas, M.; Dogonchi, A.S.; Shehzad, S.A.; Khan, M.I.; Hayat, T.; Alsaedi, A. Nonlinear convection and joule heating impacts in magneto-thixotropic nanofluid stratified flow by convectively heated variable thicked surface. J. Molecular Liquids 2020, 300, 1111945. [Google Scholar] [CrossRef]
- Hussain, M.; Ashraf, M.; Nadeem, S.; Khan, M. Radiation effects on the thermal boundary layer flow of a micropolar fluid towards a permeable stretching sheet. J. Franklin Inst. 2013, 350, 194–210. [Google Scholar] [CrossRef]
- Sharma, R.P.; Seshadri, R.; Mishra, S.R.; Munjam, S.R. Effect of thermal radiation on magnetohydrodynamic three-dimensional motion of a nanofluid past a shrinking surface under the influence of a heat source. Heat Transfer-Asian Res. 2019, 48, 2105–2121. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. Application of non-Fourier double diffusions theories to the boundary-layer flow of a yield stress exhibiting fluid model. Physica A 2020, 537, 122573. [Google Scholar] [CrossRef]
- Sravanthi, C.S. Effect of heat source/sink on MHD flow due to porous rotating disk with variable thickness in the presence of cross diffusion. Heat Transf.-Asian Res. 2019, 48, 4016–4032. [Google Scholar] [CrossRef]
- Nargund, A.L.; Madhusudhan, R.; Sathyanarayana, S.B. Study of compressible fluid flow in boundary layer region by homotopy analysis method. Int. J. Latest Trend Eng. Technol. 2017, 9, 28–39. [Google Scholar]
- Xenos, M. Thermal radiation effect on the MHD turbulent compressible boundary layer flow with adverse pressure gradient, heat transfer and local suction. Open J. Fluid Dyn. 2017, 7, 1–14. [Google Scholar] [CrossRef][Green Version]
- Xenos, M.; Pop, I. Radiation effect on the turbulent compressible boundary layer flow with adverse pressure gradient. Appl. Math. Comput. 2017, 299, 153–164. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).