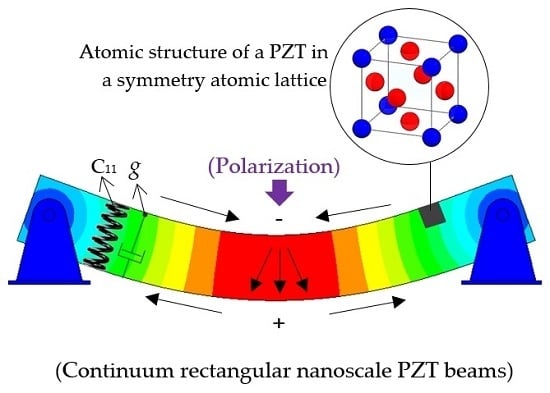
On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam
Abstract
1. Introduction
2. The Visco–Piezo–Flexoelectric Model
2.1. Piezo–Flexoelectricity
2.2. Size-Dependent Model
2.3. Internal Viscoelasticity Coupling
3. The Solution Process
4. Result Validation
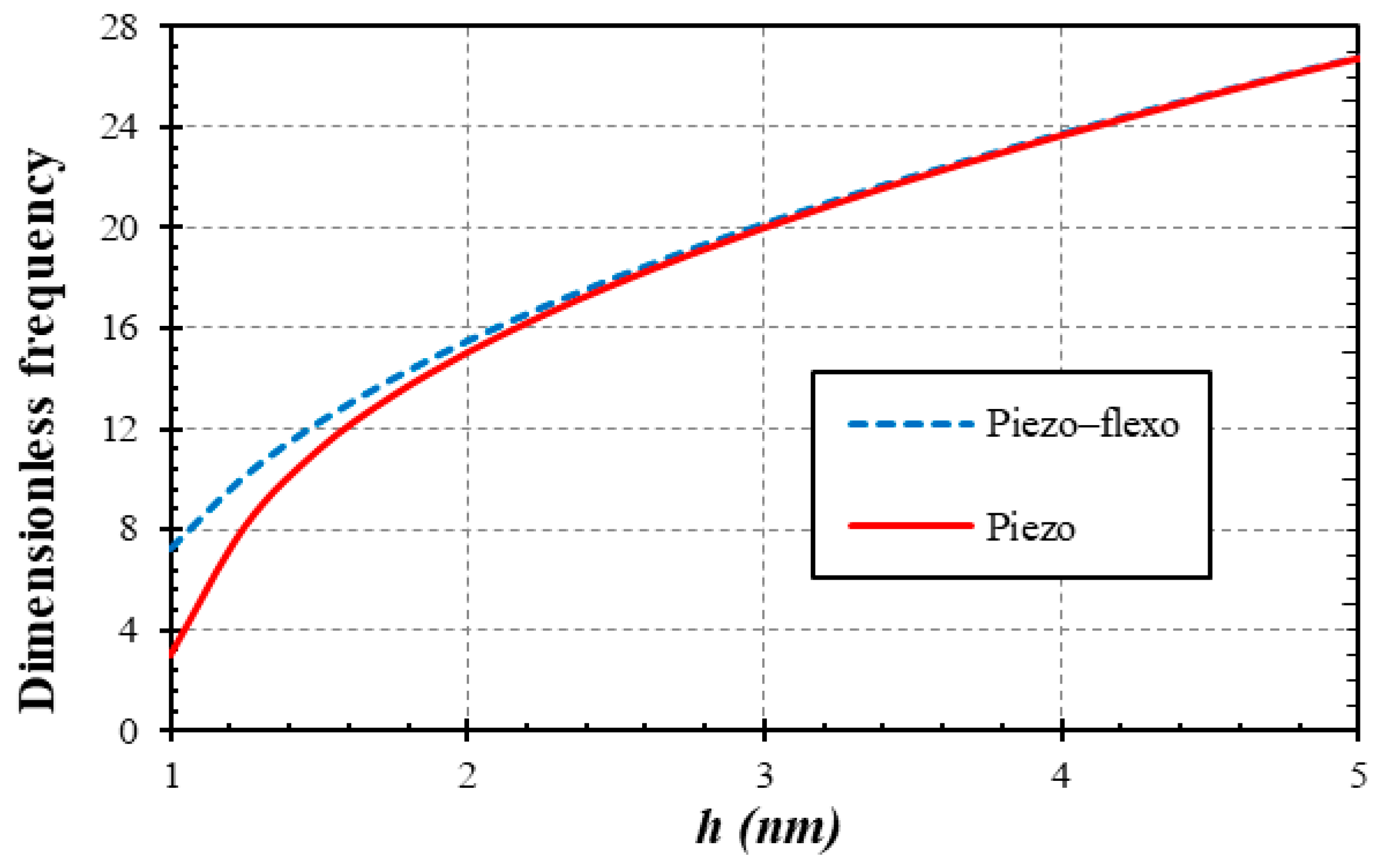
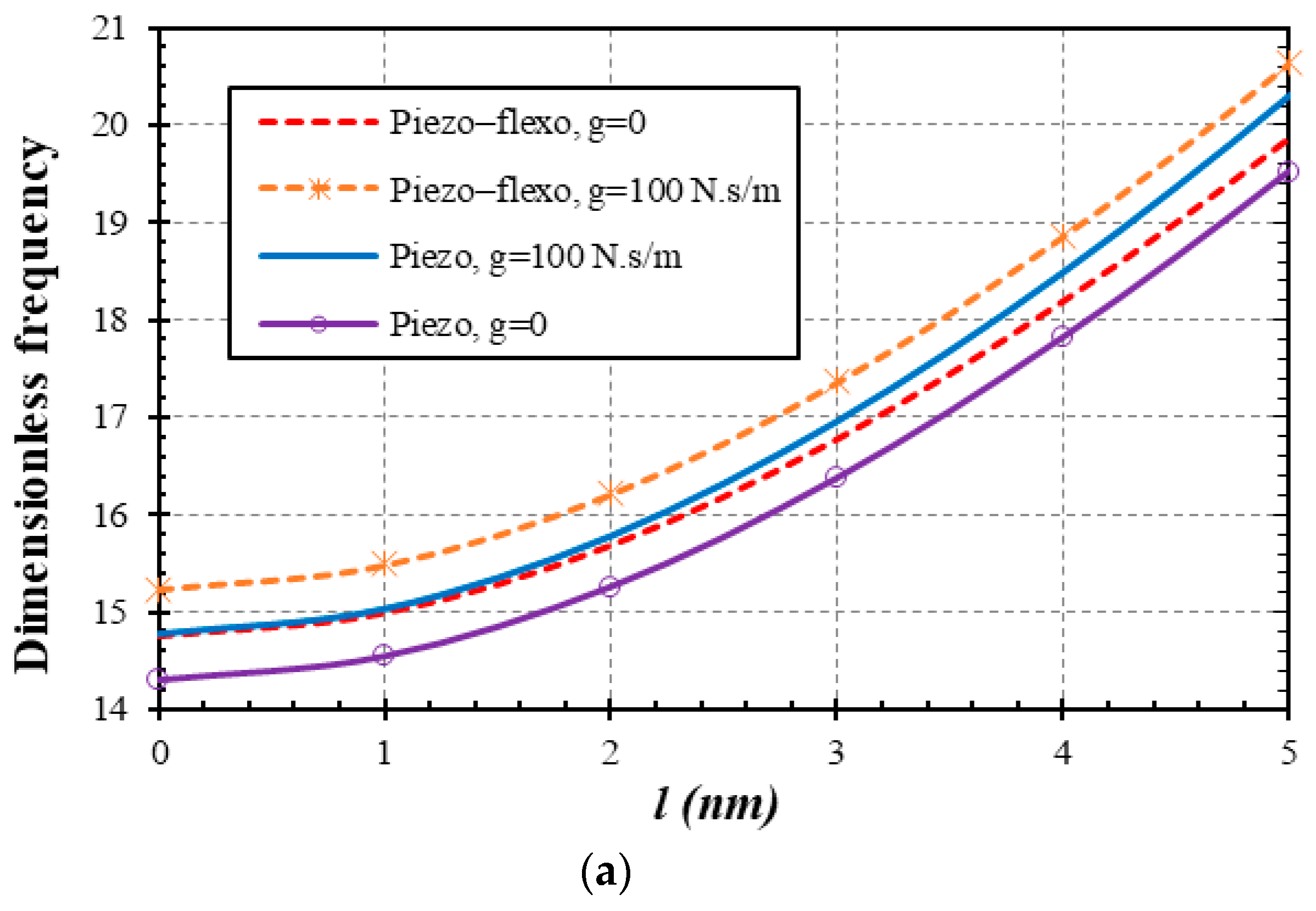
5. Frequency Analysis
6. Conclusions
- ∗
- The smaller the thickness, the larger the impact of flexoelectricity.
- ∗
- The lesser the SGLP values, the greater the flexoelectric effect.
- ∗
- The larger the length of the nanobeam, the larger the influence of flexoelectricity.
- ∗
- The greater the inner viscoelastic values, the greater the role of flexoelectricity.
- ∗
- The larger the SGLP values, the greater the inner viscoelastic impact.
- ∗
- The higher the mode number, the larger the influence of flexoelectricity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, W. Flexoelectricity: Strain gradient effects in ferroelectrics. Phys. Scripta 2007, T129, 180–183. [Google Scholar] [CrossRef]
- Lee, D.; Yoon, A.; Jang, S.Y.; Yoon, J.-G.; Chung, J.-S.; Kim, M.; Scott, J.F.; Noh, T.W. Giant Flexoelectric Effect in Ferroelectric Epitaxial Thin Films. Phys. Rev. Lett. 2011, 107, 057602. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Mao, S.; Yeh, Y.-W.; Purohit, P.K.; McAlpine, M.C. Nanoscale Flexoelectricity. Adv. Mater. 2013, 25, 946–974. [Google Scholar] [CrossRef] [PubMed]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric Effect in Solids. Ann. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Tagantsev, A.K. Flexoelectric nano-generators: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Yurkov, A.S.; Tagantsev, A.K. Strong surface effect on direct bulk flexoelectric response in solids. Appl. Phys. Lett. 2016, 108, 022904. [Google Scholar] [CrossRef]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L.-Q. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Cross, L. Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J. Mater. Sci. 2006, 41, 53–63. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Observation of the flexoelectric effect in relaxor Pb (Mg1/3Nb2/3)O3 ceramics. Appl. Phys. Lett. 2001, 78, 2920–2921. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Buckley, A.; Welche, P.R.L.; Scott, J.F. Strain-gradient-induced polarization in SrTiO3 single crystals. Phys. Rev. Lett. 2007, 99, 167601. [Google Scholar] [CrossRef] [PubMed]
- Eremeyev, V.A.; Ganghoffer, J.-F.; Konopinska-Zmysłowska, V.; Uglov, N.S. Flexoelectricity and apparent piezoelectricity of a pantographic micro-bar. Int. J. Eng. Sci. 2020, 149, 103213. [Google Scholar] [CrossRef]
- Malikan, M. Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Model. 2017, 48, 196–207. [Google Scholar] [CrossRef]
- Malikan, M. Temperature influences on shear stability of a nanosize plate with piezoelectricity effect. Multidiscip. Model. Mater. Struct. 2018, 14, 125–142. [Google Scholar] [CrossRef]
- Malikan, M. Electro-thermal buckling of elastically supported double-layered piezoelectric nanoplates affected by an external electric voltage. Multidiscip. Model. Mater. Struct. 2019, 15, 50–78. [Google Scholar] [CrossRef]
- Liu, C.; Kea, L.-L.; Yang, J.; Kitipornchaic, S.; Wang, Y.-S. Buckling and post-buckling analyses of size-dependent piezoelectric nanoplates. Theor. Appl. Mech. Lett. 2016, 6, 253–267. [Google Scholar] [CrossRef]
- Ansari, R.; Faraji Oskouiea, M.; Gholami, R.; Sadegh, F. Thermo-electro-mechanical vibration of postbuckled piezoelectric Timoshenko nanobeams based on the nonlocal elasticity theory. Compos. Part B Eng. 2016, 89, 316–327. [Google Scholar] [CrossRef]
- Tadi Beni, Y. Size-dependent analysis of piezoelectric nanobeams including electro-mechanical coupling. Mech. Res. Commun. 2016, 75, 67–80. [Google Scholar] [CrossRef]
- Malekzadeh Fard, K.; Khajehdehi Kavanroodi, M.; Malek-Mohammadi, H.; Pourmoayed, A. Buckling and vibration analysis of a double-layer Graphene sheet coupled with a piezoelectric nanoplate. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Craciun, E.M.; Baesu, E.; Soós, E. General solution in terms of complex potentials for incremental antiplane states in prestressed and prepolarized piezoelectric crystals: Application to Mode III fracture propagation. IMA J. Appl. Math. 2004, 70, 39–52. [Google Scholar] [CrossRef]
- Palacios, A.; In, V.; Longhini, P. Symmetry-Breaking as a Paradigm to Design Highly-Sensitive Sensor Systems. Symmetry 2015, 7, 1122–1150. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Li, L.; Karami, M.; Janghorban, M. Thermal buckling of embedded sandwich piezoelectric nanoplates with functionally graded core by a nonlocal second-order shear deformation theory. Proc. Inst. Mech. Eng. C-J. Mech. Eng. Sci. 2019, 233, 287–301. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Zhang, R.; Liang, X.; Shen, S. A Timoshenko dielectric beam model with flexoelectric effect. Meccanica 2016, 51, 1181–1188. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, S.; Li, A. Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 2016, 135, 167–175. [Google Scholar] [CrossRef]
- Sneha Rupa, N.; Ray, M.C. Analysis of flexoelectric response in nanobeams using nonlocal theory of elasticity. Int. J. Mech. Mater. Des. 2017, 13, 453–467. [Google Scholar] [CrossRef]
- Xiang, S.; Li, X.-F. Elasticity solution of the bending of beams with the flexoelectric and piezoelectric effects. Smart Mater. Struct. 2018, 27, 105023. [Google Scholar] [CrossRef]
- Zarepour, M.; Hosseini, S.A.H.; Akbarzadeh, A.H. Geometrically nonlinear analysis of Timoshenko piezoelectric nanobeams with flexoelectricity effect based on Eringen’s differential model. Appl. Math. Model. 2019, 69, 563–582. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Wang, B.; Zhang, B. A finite-element method of flexoelectric effects on nanoscale beam. Int. J. Multiscale Comp. 2019, 17, 29–43. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, S.; Li, Z. Size-dependent nonlinear bending and vibration of flexoelectric nanobeam based on strain gradient theory. Smart Mater. Struct. 2019, 28, 075027. [Google Scholar] [CrossRef]
- Basutkar, R.; Sidhardh, S.; Ray, M.C. Static analysis of flexoelectric nanobeams incorporating surface effects using element free Galerkin method. Eur. J. Mech. A-Solid 2019, 76, 13–24. [Google Scholar] [CrossRef]
- Ghobadi, A.; Tadi Beni, Y.; Golestanian, H. Size dependent thermo-electro-mechanical nonlinear bending analysis of flexoelectric nano-plate in the presence of magnetic field. Int. J. Mech. Sci. 2019, 152, 118–137. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Karimiasl, M. Nonlocal and surface effects on the buckling behavior of flexoelectric sandwich nanobeams. Mech. Adv. Mater. Struct. 2018, 25, 943–952. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, B.L.; Wang, K.F. Static stability analysis of nanoscale piezoelectric shells with flexoelectric effect based on couple stress theory. Microsyst. Technol. 2018, 24, 2957–2967. [Google Scholar] [CrossRef]
- Barati, M.R. On non-linear vibrations of flexoelectric nanobeams. Int. J. Eng. Sci. 2017, 121, 143–153. [Google Scholar] [CrossRef]
- Arefi, M.; Pourjamshidian, M.; Ghorbanpour Arani, A.; Rabczuk, T. Influence of flexoelectric, small-scale, surface and residual stress on the nonlinear vibration of sigmoid, exponential and power-law FG Timoshenko nano-beams. J. Low Freq. Noise Vib. Act. Control 2019, 38, 122–142. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Surface effects on the vibration behavior of flexoelectric nanobeams based on nonlocal elasticity theory. Eur. Phys. J. Plus 2017, 132, 19. [Google Scholar] [CrossRef]
- Amiri, A.; Vesal, R.; Talebitooti, R. Flexoelectric and surface effects on size-dependent flow-induced vibration and instability analysis of fluid-conveying nanotubes based on flexoelectricity beam model. Int. J. Mech. Sci. 2019, 156, 474–485. [Google Scholar] [CrossRef]
- Parsa, A.; Mahmoudpour, E. Nonlinear free vibration analysis of embedded flexoelectric curved nanobeams conveying fluid and submerged in fluid via nonlocal strain gradient elasticity theory. Microsyst. Technol. 2019, 25, 4323–4339. [Google Scholar] [CrossRef]
- Vaghefpour, H.; Arvin, H. Nonlinear free vibration analysis of pre-actuated isotropic piezoelectric cantilever Nano-beams. Microsyst. Technol. 2019, 25, 4097–4110. [Google Scholar] [CrossRef]
- Fattahian Dehkordi, S.; Tadi Beni, Y. Electro-mechanical free vibration of single-walled piezoelectric/flexoelectric nano cones using consistent couple stress theory. Int. J. Mech. Sci. 2017, 128–129, 125–139. [Google Scholar] [CrossRef]
- Joseph, R.P.; Zhang, C.; Wang, B.L. Samali, Fracture analysis of flexoelectric double cantilever beams based on the strain gradient theory. Compos. Struct. 2018, 202, 1322–1329. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Transient response of oscillated carbon nanotubes with an internal and external damping. Compos. Part B Eng. 2019, 158, 198–205. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Civalek, Ö. On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int. J. Eng. Sci. 2019, 143, 14–32. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Hygrothermal effects on vibration characteristics of viscoelastic FG nanobeams based on nonlocal strain gradient theory. Compos. Struct. 2017, 159, 433–444. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.J.; Cheng, M.; Fan, X.L. Nonlocal vibrations and stabilities in parametric resonance of axially moving viscoelastic piezoelectric nanoplate subjected to thermo-electro-mechanical forces. Compos. Part B Eng. 2017, 116, 153–169. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Sobhy, M. Nonlocal piezo-hygrothermal analysis for vibration characteristics of a piezoelectric Kelvin–Voigt viscoelastic nanoplate embedded in a viscoelastic medium. Acta Mech. 2018, 229, 3–19. [Google Scholar] [CrossRef]
- Tadi Beni, Z.; Hosseini Ravandi, S.A.; Tadi Beni, Y. Size-dependent nonlinear forced vibration analysis of viscoelastic/piezoelectric nano-beam. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Argatov, I.; Butcher, E.A. On the separation of internal and boundary damage in slender bars using longitudinal vibration frequencies and equivalent linearization of damaged bolted joint response. J. Sound Vib. 2011, 330, 3245–3256. [Google Scholar] [CrossRef]
- Qiao, G.; Rahmatallah, S. Identification of the viscoelastic boundary conditions of Euler-Bernoulli beams using transmissibility. Eng. Rep. 2019, 1, e12074. [Google Scholar] [CrossRef]
- Song, X.; Li, S.-R. Thermal buckling and post-buckling of pinned–fixed Euler–Bernoulli beams on an elastic foundation. Mech. Res. Commun. 2007, 34, 164–171. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A Higher-order nonlocal elasticity and strain gradient theory and Its Applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Lett. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Akbarzadeh Khorshidi, M. The material length scale parameter used in couple stress theories is not a material constant. Int. J. Eng. Sci. 2018, 133, 15–25. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Dimitri, R.; Tornabene, F. Dynamic modeling of non-cylindrical curved viscoelastic single-walled carbon nanotubes based on the second gradient theory. Mater. Res. Express 2019, 6, 075041. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B. Buckling analysis of piezo-magnetoelectric nanoplates in hygrothermal environment based on a novel one variable plate theory combining with higher-order nonlocal strain gradient theory. Phys. E 2018, 102, 8–28. [Google Scholar] [CrossRef]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. Post-critical buckling of truncated conical carbon nanotubes considering surface effects embedding in a nonlinear Winkler substrate using the Rayleigh-Ritz method. Mater. Res. Express 2020, 7, 025005. [Google Scholar] [CrossRef]
- Malikan, M. On the plastic buckling of curved carbon nanotubes. Theor. Appl. Mech. Lett. 2020, 10, 46–56. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Electromagnetic forced vibrations of composite nanoplates using nonlocal strain gradient theory. Mater. Res. Express 2018, 5, 075031. [Google Scholar] [CrossRef]
- Lei, Y.; Adhikari, S.; Friswell, M.I. Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams. Int. J. Eng. Sci. 2013, 66–67, 1–13. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Yang, J. Vibration of FG magneto-electro-viscoelastic porous nanobeams on visco-Pasternak foundation. Compos. Part B Eng. 2018, 155, 244–256. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Effect of sinusoidal corrugated geometries on the vibrational response of viscoelastic nanoplates. Appl. Sci. 2018, 8, 1432. [Google Scholar] [CrossRef]
- Soltani, P.; Kassaei, A.; Taherian, M.M. Nonlinear and quasi-linear behavior of a curved carbon nanotube vibrating in an electric force field; analytical approach. Acta Mech. Solida Sin. 2014, 27, 97–110. [Google Scholar] [CrossRef]
- Zare Jouneghani, F.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory. Int. J. Eng. Sci. 2017, 116, 12–24. [Google Scholar] [CrossRef]
- Mehralian, F.; Tadi Beni, Y.; Karimi Zeverdejani, M. Nonlocal strain gradient theory calibration using molecular dynamics simulation based on small scale vibration of nanotubes. Phys. B 2017, 514, 61–69. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng. Sci. Technol. Int. J. 2018, 21, 778–786. [Google Scholar] [CrossRef]
- Yang, W.; Liang, X.; Shen, S. Electromechanical responses of piezoelectric nanoplates with flexoelectricity. Acta Mech. 2015, 226, 3097–3110. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Rouhi, H. Rayleigh–Ritz axial buckling analysis of single-walled carbon nanotubes with different boundary conditions. Phys. Lett. A 2011, 375, 1255–1263. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology 2007, 18, 385704. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 24305. [Google Scholar] [CrossRef]






| Configuration | Conditions |
|---|---|
| S | w(0, L) = 0, Mx(0, L) = 0, Nx(0, L) = 0 |
| L/h | (e0a)2 | Present | Euler–Bernoulli [68] |
|---|---|---|---|
| 5 | 0 | 9.7112 | 9.7112 |
| 1 | 9.2647 | 9.2647 | |
| 2 | 8.8747 | 8.8747 | |
| 3 | 8.5301 | 8.5301 | |
| 4 | 8.2228 | 8.2228 | |
| 10 | 0 | 9.8293 | 9.8293 |
| 1 | 9.3774 | 9.3774 | |
| 2 | 8.9826 | 8.9826 | |
| 3 | 8.6338 | 8.6338 | |
| 4 | 8.3228 | 8.3228 | |
| 20 | 0 | 9.8595 | 9.8595 |
| 1 | 9.4062 | 9.4062 | |
| 2 | 9.0102 | 9.0102 | |
| 3 | 8.6604 | 8.6604 | |
| 4 | 8.3483 | 8.3483 |
| L/D | [69] (MD-Armchair CNT) | Nonlocal Strain Gradient Theory | ||
|---|---|---|---|---|
| [69] (FSDT, Navier) | [70] (OVFSDT, Navier) | Present | ||
| 4.86 | 1.138 | 1.209 | 1.25535 | 1.23117 |
| 8.47 | 0.466 | 0.448 | 0.43207 | 0.49103 |
| 13.89 | 0.190 | 0.192 | 0.19004 | 0.21306 |
| 17.47 | 0.122 | 0.126 | 0.12431 | 0.13213 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malikan, M.; Eremeyev, V.A. On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam. Symmetry 2020, 12, 643. https://doi.org/10.3390/sym12040643
Malikan M, Eremeyev VA. On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam. Symmetry. 2020; 12(4):643. https://doi.org/10.3390/sym12040643
Chicago/Turabian StyleMalikan, Mohammad, and Victor A. Eremeyev. 2020. "On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam" Symmetry 12, no. 4: 643. https://doi.org/10.3390/sym12040643
APA StyleMalikan, M., & Eremeyev, V. A. (2020). On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam. Symmetry, 12(4), 643. https://doi.org/10.3390/sym12040643