A Fuzzy Bivariate Poisson Control Chart

Abstract

In the present paper, we develop a fuzzy bivariate Poisson (FBP) control chart based on a fuzzy c chart. The FBP chart is used to monitor the sum of the nonconformities of each quality characteristic. There are two contributions of this work. First, we propose a new fuzzy parameter estimation to create a triangular fuzzy number (TFN). Second, our control chart is flexible, because we involve the ${\alpha }^{cut}$ to measure the level of tightness of inspection. Furthermore, the statistic of FBP is being able to visualise the monitoring process in a graphical form. In addition, the simulation study indicates that the performance of our proposed chart, based on average run length (ARL), is more sensitive than the performance of a conventional bivariate Poisson (BP) chart. Moreover, an illustration example shows that the FBP chart has relatively more sensitive performance compared to the conventional BP chart.

1. Introduction

Statistical quality control is one of the most important factors in monitoring the stability of the quality production process in manufacturing. These quality characteristics can be divided into two categories based on the type of monitored data: namely, variables and attributes [1]. In this study, we focus on attribute control charts. Conformity judgment usually involves a great deal of subjectivity by the operators, which results in ambiguous data [2]. Under such conditions, fuzzy control charts are useful tools to overcome the problems caused by the inability of conventional charts to handle ambiguous data for monitoring the process [3].

Various fuzzy, univariate, attribute control charts have been developed, such as the $c$ chart (for monitoring the average number of nonconformities) and the u chart (for monitoring the average number of nonconformities per unit). These control charts usually assume that the occurrence of nonconformities in samples of constant size is well modelled by the Poisson distribution [1]. Gulbay, Kahraman, and Ruan [4] developed fuzzy ${\alpha }^{cut}$ charts, using the triangular membership function called triangular fuzzy number (TFN). Gulbay and Kahraman [5] proposed a $c$ control chart by employing the principles of the direct fuzzy approach (DFA) for asymmetric data. Meanwhile, Zarandi, Turksen, and Kashan [6] suggested a combination of fuzzy c and u charts using the defuzzifier index based on the distance between the fuzzy sets. Hsieh Ting and Wang [7] created a fuzzy c chart through two approaches: the number of nonconformities, and an index grouping of nonconformities. Fadaei and Pooya [8] introduced a fuzzy $u$ chart based on fuzzy rule, and evaluated its performance using an operating characteristics (OC) curve. Furthermore, Truong et al. [9] developed a fuzzy u chart with a classification mechanism. Alakoc and Apaydin [10] proposed a fuzzy approach that integrates fuzzy set theory and the basics of Shewhart control charts. Recently, Aslam, Bantan, and Kan [11] introduced a Shewhart attribute control chart using the neutrosophic statistical interval method.

In reality, the monitoring process often involves two or more correlated attributes. This requires the development of an appropriate control chart. Nevertheless, the development of multi-attribute fuzzy control charts is limited. The existing multi-attribute fuzzy control chart in the literature is the fuzzy multinomial chart. Amirzadeh [12] adopted the concept of Shewhart-type control charts. Pandurangan [13] proposed a fuzzy multinomial chart for variable sample sizes. Taleb and Limam [14] considered fuzzy, multivariate, multinomial control charts based on $T^2$ Hotelling statistics. Pratap and Mohapatra [15] created fuzzy control charts for correlated multi-attribute quality characteristics. These charts are used to identify the quality characteristics that cause a process to go out-of-control, based on the ordering of fuzzy numbers and the concepts of possibility. Also, necessity measures are used to identify the quality characteristics that cause a process to go out of control. Fernández, García and Barzola [16] proposed control chart for correlated multi-attribute quality characteristics, through the use of a Hotelling $T^2$ control chart. Nevertheless, such multi-attribute control charts cannot be applied to processes that follow a multivariate Poisson distribution. In this study, we propose an FBP control chart. The unit sample observed in the monitoring process is the number of non-conformities or defects of the critical to quality. To develop this FPB chart, we need to form a membership function, in particular, a TFN. In this work, we use a form of TFN based on fuzzy estimation parameters. By adopting the concept of the fuzzy $c$ chart for value ${\alpha }^{cut},$ the FBP chart has two parts—the left and the right control charts, which make the chart more sensitive. The value of ${\alpha }^{cut}$ in this paper is with respect to the tightness level of inspection, which is commonly used in fuzzy logic as ${\alpha }^{cut}.$ Furthermore, the chart’s performance will be evaluated in terms of in-control and out-of-control average run length (ARL). The results will be compared with a conventional bivariate Poisson (BP) chart, which has been studied by Chiu and Kuo [17]. In this study, we focused on a bivariate Poisson chart, even though multivariate analysis can also be studied further. In addition, the multivariate analysis requires forming a membership function with more complexity to develop fuzzy parameter estimation, such that it requires further development for fuzzy multivariate Poisson values.

The rest of this paper is structured as follows. Section 2 reviews the development of fuzzy c control charts. We present our proposed chart in Section 3. In Section 4, we conduct a comparative study. First, we evaluate our proposed method compared to the conventional BP chart. Second, we apply the real case of the production process of a bottle. Conclusions and further research are presented in Section 5.

2. Fuzzy c Control Charts

This section describes the fuzzy attribute control charts used as the basis for the development of the FBP chart. In univariate cases, it is appropriate to use Poisson distribution, as reviewed by Zarandi, Turksen and Kashan [6] and Hsieh Ting and Wang [7]. One of the fuzzy control charts developed based on the Poisson distribution is the fuzzy c control chart. Gulbay, Kahraman and Ruan [4] proposed a fuzzy $c{\alpha }^{cut}$ chart with a triangular membership function (TFN). The principle of this chart is to construct the TFN representation of $\overline{c}$, where $\overline{c}$ is the number of average nonconformities for the samples initially available. In the shape of the TFN, $c_{min}$ is the minimum value of $c$, $c_{max}$ is the maximum value of $c$, and $\overline{c}$ is the crisp with a membership function equal to 1 (see Figure 1). The Shewhart control limits are adopted to construct the control limits of the fuzzy c chart.

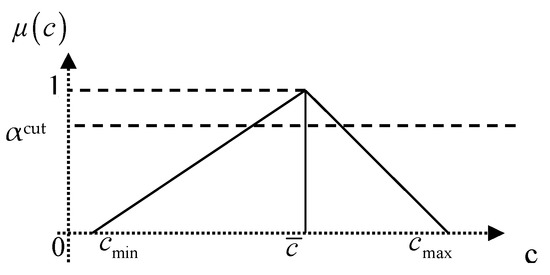
Figure 1. Triangular fuzzy number (TFN) representations of $\overline{c}$.

Meanwhile, for the fuzzy $c{\alpha }^{cut}$ chart, each observation is expressed in the form of the TFN representation denoted as $\left(c_{jmin},c_j,c_{jmax}\right)$, $j=1,2,\dots ,m$ (see Table 1). The statistics of the fuzzy $c$ control charts consist of two parts that are defined as follows:

$$L_j\left({\alpha }^{cut}\right)=c_{jmin}+\left(c_j-c_{jmin}\right){\alpha }^{cut}$$

(1)

$$R_j\left({\alpha }^{cut}\right)=c_{jmax}+\left(c_j-c_{jmax}\right){\alpha }^{cut}$$

Table 1. TFN representations of $c$.

$\mathit{j}$	${\mathit{c}}_{\mathit{j}\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{c}}_{\mathit{j}}$	${\mathit{c}}_{\mathit{j}\mathit{m}\mathit{a}\mathit{x}}$
1	$c_{1min}$	$c_1$	$c_{1max}$
2	$c_{2min}$	$c_2$	$c_{2max}$
3	$c_{3min}$	$c_3$	$c_{3max}$
$⋮$	$⋮$	$⋮$	$⋮$
j	$c_{jmin}$	$c_j$	$c_{jmax}$
$⋮$	$⋮$	$⋮$	$⋮$
m	$c_{mmin}$	$c_m$	$c_{mmax}$

The control limit (CL) for a value of ${\alpha }^{cut}$ is comprised of the boundary control for the left $\left(L\right)$ and the right $\left(R\right)$ part of the control limits, with $c_j$ as the number of observations in the part corresponding to $j.$ If $c_{min}\le c_j\le \overline{c,}$ the gained control limits are obtained as follows:

$$Control Limits=\{\begin{array}{c}C{L}^L\left({\alpha }^{cut}\right)=c_{min}+\left(\overline{c}-c_{min}\right){\alpha }^{cut}\\ LC{L}^L\left({\alpha }^{cut}\right)=max\left\{C{L}^L-3\sqrt{C{L}^L},0\right\}\\ UC{L}^L\left({\alpha }^{cut}\right)=\left\{C{L}^L+3\sqrt{C{L}^L}\right\},\end{array}$$

(2)

whereas for $\overline{c}\le c_j\le c_{max}$, the control limits are obtained as follows:

$$Control Limits=\{\begin{array}{c}C{L}^R\left({\alpha }^{cut}\right)=c_{max}+\left(\overline{c}-c_{max}\right){\alpha }^{cut}\\ LC{L}^R\left({\alpha }^{cut}\right)=max\left\{C{L}^R-3\sqrt{C{L}^R},0\right\}\\ UC{L}^R\left({\alpha }^{cut}\right)=\left\{C{L}^R+3\sqrt{C{L}^R}\right\},\end{array}$$

(3)

where $c_{min}$ is the minimum value of $c_{jmin}$, and $c_{max}$ is the maximum value of $c_{jmax}$. This process is detected as out of control when $LC{L}^L\left({\alpha }^{cut}\right)\le L_j\left({\alpha }^{cut}\right)\le UC{L}^L\left({\alpha }^{cut}\right)$ and $LC{L}^R\left({\alpha }^{cut}\right)\le L_R\left({\alpha }^{cut}\right)\le UC{L}^R\left({\alpha }^{cut}\right).$ Some concepts of the fuzzy c chart will be adopted to establish the FBP control charts.

3. The Proposed Chart: Fuzzy Bivariate Poisson (FBP) Control Chart

This section describes the design of FBP control charts, which starts by determining the estimation of fuzzy parameters for the bivariate Poisson distribution. This estimate will be used to determine the shape of the TFN.

3.1. Fuzzy Estimation of Parameters

Let $X_1$ and $X_2$ be the numbers of nonconformities with respect to certain quality characteristics. Assume that $X=\left(X_1,X_2\right)$ is a bivariate Poisson random vector. Variable $X_1$ and $X_2$ marginally follow a Poisson distribution, with a mean ${\lambda }_1$ and ${\lambda }_2$, respectively, and $\theta$ is the covariance between $X_1$ and $X_2$. As the variance is equal to the mean, $V\left(X_1\right)={\lambda }_1$ and $V\left(X_2\right)={\lambda }_2$, then the correlation between $X_1$ and $X_1$ is $\rho =\theta /\sqrt{{\lambda }_1{\lambda }_2}$. Define statistics $D$ as the sum of $X_1$ and $X_2$; $D=X_1+X_2.$ According to McKendrick [18], Maritz [19] and the work in [17], the form of the probability distribution function of $D$ is as follows:

$$P\left(D=d\right)=exp\left[-\left({\lambda }_1+{\lambda }_2-\theta \right)\right]{{\displaystyle \sum }}_{j=0}^{d/2}\frac{{\left(\left({\lambda }_1+{\lambda }_2-2\theta \right)\right)}^{d-2j}{\theta }^j}{\left(d-2j\right)!j!}, d=0,1,2,\dots ,$$

(4)

where ${\lambda }_1, {\lambda }_2,\theta >0.$ Because $X_1$ and $X_2$ are countable (the number of nonconformities), $D=X_1+X_2$ is also countable, so $\mu =E\left(D\right)$ and ${\sigma }^2=V\left(D\right)$, where $E\left(D\right)$ and $V\left(D\right)$ are the expected value and the variance of the random variable D, respectively, and have the same unit. Furthermore, given available constant $a_1$ and $a_2$, we make the following decomposition $\mu =a_1+2a_2$ and ${\sigma }^2=a_1+4a_2,$ with $a_2=\left({\sigma }^2-\mu \right)/2$ and $a_1=2\mu -{\sigma }^2,$ as shown in [20], Equation (4) can be expressed as

$$P\left(D=d\right)=exp\left[-\left(a_1+a_2\right)\right]{\displaystyle \sum }_{j=0}^{\lfloor d/2\rfloor }\frac{{\left(a_1\right)}^{d-2j} {\left(a_2\right)}^j}{\left(d-2j\right)!j!},$$

(5)

where $a_1={\lambda }_1+{\lambda }_2-2\theta$ and $a_2=\theta .$

Define $\kappa$, the coefficient of dispersion, as $\kappa =\frac{V\left(D\right)}{E\left(D\right)}=\frac{a_1+4a_2}{a_1+2a_2}=1+\frac{2a_2}{a_1+2a_2}$. Hence, the parameterisation can also be written in terms of $\mu$ and $\kappa , a_2=\frac{\mu \left(\kappa -1\right)}{2}$ and $a_2=\mu \left(2-\kappa \right)$. Therefore, the probability mass function (pmf) of $D$ can be formulated as

$$P\left(D=d\right)=exp\left(-\left(\mu \left(2-\kappa \right)+\frac{\mu \left(\kappa -1\right)}{2}\right)\right){{\displaystyle \sum }}_{j=0}^{\lfloor d/2\rfloor }\frac{{\left(\mu \left(2-\kappa \right)\right)}^{d-2j} {\left(\frac{\mu \left(\kappa -1\right)}{2}\right)}^j}{\left(d-2j\right)!j!},$$

(6)

where $\mu ,\kappa >0.$

Based on the assumptions of m random samples and the coefficient of dispersion, $\widehat{\kappa }=V\left(D\right)/\overline{D}$ being known, the maximum likelihood estimator for $\mu$ is

$$\widehat{\mu }=\frac{{{\displaystyle \sum }}_{i=1}^m{d}_i}{m},$$

(7)

and the asymptotic variance for $\widehat{\mu }$ can be written as $asvar\left(\widehat{\mu }\right)=\frac{\mu \kappa }{m}$. Thus, the confidence interval of $\mu$ is equal to

$$P\left(\left|\overline{d}-\mu \right|\le z_{\frac{\beta }{2}}\sqrt{\frac{\mu \kappa }{m}}\right).$$

(8)

If $\widehat{\kappa }$ is an estimate of $\kappa ,$ based on [21] the confidence interval for $\mu$ is

$$\left(\overline{d}+\frac{\widehat{\kappa }{z}_{\frac{\beta }{2}}^2}{2m}\right)\pm z_{\frac{\beta }{2}} \frac{\sqrt{\widehat{\kappa }\left(\widehat{\kappa }{z}_{\frac{\beta }{2}}^2+4m\overline{d}\right)}}{2m}.$$

(9)

Referring to the theorem proposed by Klir and Yuan [22] and Falsafatain, Taheri and Mashinchi [23], and based on the confidence interval in Equation (9), the membership functions of the parameter estimation $\mu$ can be obtained using Proposition 1.

Proposition 1.

Suppose that$d_1,d_2,d_3,\dots ,d_{m,}$are observations of$m$random samples (the sum of a bivariate Poisson distribution), where$\mu$is an unknown parameter, and$\kappa$is known. If$\left[{\mu }_1\left(\beta \right),{\mu }_2\left(\beta \right)\right]$is the$\left(1-\beta \right)100\%$confidence interval (CI) for the parameter$\mu$, the fuzzy estimation of$\mu$ is a fuzzy set with a unique membership function, as follows:

$$\tilde{\mu }\left(u\right)=2F\left(-\left|\frac{u-{\overline{d}}^{*}}{{\sigma }^{*}}\right|\right),u\in R,$$

(10)

where $F(.)$ is a distribution function of the standard normal distribution. The proof of this proposition is given in Appendix A.

Based on Proposition 1, for a value of ${\alpha }^{cut}$, the estimated fuzzy parameter can be expressed as $\tilde{\mu }=\left({\widehat{d}}_{left},\overline{d}, {\widehat{d}}_{right}\right).$ Xie et al. (2002) in Chiu and Kuo stated that the normal distribution approach may be used if the average value of the Poisson distribution is greater than five [17]. Therefore, the mean and variance of the random variable $D$ are $E\left(D\right)={\lambda }_1+{\lambda }_2$ and $E\left(D\right)=V\left(X_1\right)+V\left(X_2\right)+2cov\left(X_1,X_2\right),$ respectively. Thus, we obtain the $\left(1-\beta \right)100\%$ confidence interval for parameter $\mu$ as

$$\left[\left({\overline{x}}_1+{\overline{x}}_2\right)\pm z_{1-\beta /2}\sqrt{\frac{\left({\overline{x}}_1+{\overline{x}}_2+2s_{12}\right)}{m}}\right],$$

(11)

where $s_{12}$ is covariance between $X_1$ and $X_2.$ As a result, the confidence interval based on a normal approach will be obtained from the membership function parameter $\mu$ and the corollary of Proposition 1 below.

A Corollary of Proposition 1:

Suppose that $x_{11},x_{12},x_{13},\dots ,x_{1m}$ are $m$ random samples from a Poisson distribution with parameter ${\lambda }_1,$ and $x_{21},x_{22},x_{23},\dots ,x_{2m}$ are $m$ random samples from a Poisson distribution with parameter ${\lambda }_2$, and the joint probability of $\left(X_1,X_2\right)$ is a bivariate Poisson distribution. If $D=X_1+X_2$, and $\mu$ is an unknown parameter, then the estimator of $\tilde{\mu }$ is a fuzzy set with a membership function:

$$\tilde{\mu }\left(u\right)=2F\left(-\left|\frac{u-\left({\overline{x}}_1+{\overline{x}}_2\right)}{\sqrt{\left({\overline{x}}_1+{\overline{x}}_2+2s_{12}\right)/m}}\right|\right),u\in R.$$

(12)

The proof of the corollary is provided in Appendix B. In the same way, for a value ${\alpha }^{cut},$ the fuzzy parameter estimation is expressed as $\tilde{\mu }=\left({\widehat{d}}_{left},\overline{d}, {\widehat{d}}_{right}\right).$

3.2. Design of the Fuzzy Bivariate Poisson Control Chart

FBP control charts were developed based on a conventional $c$ chart and a univariate fuzzy $c$ chart. Suppose that $X_1$ and $X_2$ are the two quality characteristics, and the joint distribution of $X_1$ and $X_2$ is defined as a bivariate Poisson distribution. Define $D$ as the sum of the number of defects for each quality characteristic, with the fuzzy parameter estimate $\tilde{\mu }=\left({\widehat{d}}_{left},\overline{d}, {\widehat{d}}_{right}\right)$. If we define ${\delta }_1=\overline{d}-{\widehat{d}}_{left},{\delta }_2={\widehat{d}}_{left}-\overline{d}$, these ${\delta }_1$ and ${\delta }_2$ values will be used to transform each observation into a triangular fuzzy number (TFN).

The TFN is defined for each observation and has the form $\left(d_{jmin},d_j,d_{jmax}\right),$ where $d_{jmin}=d-{\delta }_1,d_{jmax}=d+{\delta }_2.$ The value of the constant $k=3$ is associated with a false alarm rate of 0.0027. The proposed control charts are formed with two control charts, the left and right control charts. Based on the shape of the TFN in [4], the statistics of the right and left sides of the proposed chart are:

$$\begin{gathered} L_j\left({\alpha }^{cut}\right)=d_{jmin}+\left(d_j-d_{jmin}\right){\alpha }^{cut} \\ {R}_j\left({\alpha }^{cut}\right)=d_{jmax}+\left(d_j-d_{jmax}\right){\alpha }^{cut}. \end{gathered}$$

(13)

The control limit for the value of ${\alpha }^{cut}$ consists of the left control limit $\left(L\right)$ and the right control limit $\left(R\right)$, where $d_j$ is the number of nonconformities in the $j^{th}$ sample. If $d_{min}\le d_j\le \overline{d,}$ the control limits are defined as

$$Control Limits=\{\begin{array}{c}C{L}^L\left({\alpha }^{cut}\right)=d_{min}+\left(\overline{d}-d\right){\alpha }^{cut}\\ LC{L}^L\left({\alpha }^{cut}\right)=max\left\{C{L}^L-3\sqrt{C{L}^L},0\right\}\\ UC{L}^L\left({\alpha }^{cut}\right)=\left\{C{L}^L+3\sqrt{C{L}^L}\right\},\end{array}$$

(14)

and for $\overline{d }\le d_j\le d_{max}$, the control limit is defined as

$$Control Limits=\{\begin{array}{c}C{L}^R\left({\alpha }^{cut}\right)=d+\left(\overline{d}-d_{max}\right){\alpha }^{cut}\\ LC{L}^R\left({\alpha }^{cut}\right)=max\left\{C{L}^R-3\sqrt{C{L}^R},0\right\}\\ UC{L}^R\left({\alpha }^{cut}\right)=\left\{C{L}^R+3\sqrt{C{L}^R}\right\},\end{array}$$

(15)

This process is detected as out of control when $LC{L}^L\left({\alpha }^{cut}\right)\le L_j\left({\alpha }^{cut}\right)\le UC{L}^L\left({\alpha }^{cut}\right)$ and $LC{L}^R\left({\alpha }^{cut}\right)\le L_R\left({\alpha }^{cut}\right)\le UC{L}^R\left({\alpha }^{cut}\right).$

3.3. Average Run Length of the FBP Chart

Simulation studies are used to evaluate the performance of the FBP control chart based on the value of ARL, which is the average number of the sample until finding the first sample outside of the control limit. There are two types of ARLs: an in-control ARL (ARL₀) and an out-of-control ARL (ARL₁). Simulations are carried out for several scenarios (e.g., several values of ${\alpha }^{cut}$ (0.1 to 0.9 with an increment of 0.1) and the correlation coefficients $\left(\rho \right)$ equal to 0, 0.5 and 0.8. The algorithm for ARL calculation is defined as follows:

• Step 1. Generate data $\left(X_1,X_2\right)$ that follows a bivariate Poisson distribution with $m=1000$ observations for each combination value of $\rho ,{\alpha }^{cut}$ as well as parameters $\left({\lambda }_1,{\lambda }_2\right).$
• Step 2. Calculate the value of $D_i=X_{1i}+X_{2i}$.
• Step 3. Estimate the fuzzy parameter $\tilde{\mu }=\left({\widehat{d}}_{left},\widehat{d},{\widehat{d}}_{right}\right)$ by using Proposition 1.
• Step 4. Transform each observation into $\left(d_{jmin},d_j,d_{jmax}.\right)$.
• Step 5. Calculate the statistics in Equation (13):
• Step 6. Calculate the control limit in Equation (14) and Equation (15).
• Step 7. Evaluate the FBP chart using the ARL, as follows:
  • For each combination value of ${\alpha }^{cut}$, $\rho$ and parameter $\left({\lambda }_1,{\lambda }_2\right),$ generate $m=1000$ observations that follow a bivariate Poisson distribution. Repeating and comparing statistics $L_j\left({\alpha }^{cut}\right)$ and $L_R\left({\alpha }^{cut}\right)$ with control limits obtained from step 6. If the statistics are out-of-control the first time, then the value Run Length (RL) is obtained.
  • Repeat step 7(a) 1000 times and calculate the average run length for the in-control condition (ARL₀).
  • Repeat steps 7(a) and (b) for the level shift of parameters ${\lambda }_1^{*}={\lambda }_1+\mathsf{\Delta }$ and ${\lambda }_2^{*}={\lambda }_2+\mathsf{\Delta }$, with an increment of $\mathsf{\Delta }=1$ to obtain the average run length for the out-of-control condition (ARL₁).
  • Plot the ARL₀ and ARL₁.

Section 3.3 presents the results of the simulation study to evaluate the performance of the FBP control chart based on an in-control ARL (ARL₀) and an out-of-control ARL (ARL₁). The proposed chart is simulated from a process with bivariate Poisson parameters ${\lambda }_1$ = 1, ${\lambda }_2=2$ based on several schemes for $\rho$ and ${\alpha }^{cut}$. The first scheme is selected for two independent Poisson distributions $\left(\rho =0\right)$ and the second and third schemes are selected with $\rho$ as 0.5 and 0.8. The overall scheme is simulated with ${\alpha }^{cut}$ between $0.1$ and $0.9$ with an increment of 0.1. To obtain the value of ARL₁, the parameters are shifted by Δ = 1. The result shows in Table 2 and Figure 2, Figure 3 and Figure 4.

Table 2. Average run length (ARL) values of the Fuzzy Bivariate Poisson (FBP) control charts.

$\mathit{\rho }$	${\mathit{\lambda }}_1^{*}$	${\mathit{\lambda }}_2^{*}$	$\Delta$	${\mathit{\alpha }}^{\mathit{c}\mathit{u}\mathit{t}}$
				0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0	1	2	0	500.5000	500.5000	500.5000	500.3762	499.6700	499.2309	494.9235	475.8822	220.7956
	2	3	1	499.2822	498.5563	494.5448	445.4966	340.1151	341.7502	180.4167	73.7003	15.3764
	3	4	2	420.4424	427.5666	312.8545	82.0889	36.2809	34.4991	19.3954	9.9167	3.5195
	4	5	3	90.3181	80.7588	46.8710	14.0316	8.0395	7.7880	5.1136	3.6686	1.8113
	5	6	4	17.0719	18.5737	10.4823	4.2816	3.3956	3.1855	2.3477	1.8376	1.2132
	6	7	5	6.1447	5.8631	4.2326	2.4632	1.9245	1.7552	1.5059	1.3105	1.0865
	7	8	6	2.9205	2.9935	2.2925	1.6491	1.2869	1.3602	1.2232	1.0714	1.0769
	8	9	7	1.7298	1.9136	1.6197	1.2092	1.1747	1.1357	1.0686	1.0227	1.0000
	9	10	8	1.3452	1.4130	1.4331	1.1140	1.0606	1.0706	1.0000	1.0000	1.0000
	10	11	9	1.2727	1.2072	1.0826	1.1304	1.0435	1.0833	1.0000	1.0000	1.0000
	11	12	10	1.0976	1.0632	1.0270	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
	12	13	11	1.0444	1.0303	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
	13	14	12	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
0.5	1	2	0	500.5000	500.4438	500.2137	500.2686	491.5374	491.5374	497.9363	440.4627	339.3639
	2	3	1	496.3325	487.9893	470.2235	488.5853	239.3342	239.3342	352.3361	56.3104	29.7720
	3	4	2	393.0880	301.4079	178.3637	294.5800	32.8209	32.8209	54.1805	11.6062	7.4959
	4	5	3	95.5691	55.1628	34.1244	57.5133	8.6225	8.6225	14.4826	4.2045	3.2586
	5	6	4	24.3012	15.9264	12.0475	15.6603	3.7615	3.7615	4.9493	2.4232	1.9244
	6	7	5	8.9751	6.5880	4.7337	6.3533	2.4211	2.4211	2.8989	1.6003	1.3769
	7	8	6	4.4603	3.4896	2.7533	3.1933	1.6544	1.6544	1.9817	1.3096	1.2010
	8	9	7	2.8164	2.2916	1.9074	2.3437	1.2638	1.2638	1.5943	1.1623	1.0909
	9	10	8	1.8460	1.6450	1.4289	1.6855	1.2512	1.2512	1.2698	1.0667	1.0714
	10	11	9	1.5119	1.3694	1.2569	1.4331	1.1096	1.1096	1.1500	1.0600	1.0400
	11	12	10	1.2474	1.2258	1.1973	1.2424	1.0233	1.0233	1.1600	1.0435	1.0000
	12	13	11	1.1356	1.1622	1.0735	1.0784	1.0000	1.0000	1.0789	1.0000	1.0000
	13	14	12	1.0500	1.0274	1.0600	1.1250	1.0000	1.0000	1.0000	1.0000	1.0000
	14	15	13	1.0238	1.0588	1.0000	1.0345	1.0000	1.0000	1.0000	1.0000	1.0000
0.8	1	2	0	500.1596	500.1514	500.2378	499.6190	496.4722	473.6515	434.2774	354.6419	206.9041
	2	3	1	484.9163	484.0479	459.7577	422.8506	337.2877	136.9043	68.0762	38.9847	22.0416
	3	4	2	290.3477	282.2958	186.3935	102.5621	58.8145	22.6175	14.6593	9.4666	6.4562
	4	5	3	59.2883	63.3660	37.6905	24.0107	15.9634	7.6190	5.4739	3.8403	3.0144
	5	6	4	19.1030	17.6349	11.9913	9.4512	6.7731	3.7473	2.8958	2.2732	1.9483
	6	7	5	6.9379	7.8796	5.4919	4.2981	3.7087	2.2773	1.9121	1.5686	1.3836
	7	8	6	3.9895	4.2529	3.2495	2.7780	2.2431	1.6430	1.4298	1.3440	1.3223
	8	9	7	2.6617	2.6448	2.2773	1.9415	1.6178	1.3566	1.2623	1.1795	1.1327
	9	10	8	1.9186	1.8547	1.7790	1.5094	1.3815	1.1759	1.1348	1.0598	1.1129
	10	11	9	1.6305	1.6224	1.3197	1.3099	1.1855	1.1085	1.0625	1.0448	1.0345
	11	12	10	1.3713	1.3718	1.2817	1.1304	1.1216	1.0694	1.0250	1.0455	1.0000
	12	13	11	1.1865	1.2045	1.1260	1.0777	1.1026	1.0000	1.0000	1.0000	1.0000
	13	14	12	1.0847	1.1322	1.0667	1.0725	1.1111	1.0000	1.0000	1.0000	1.0000
	14	15	13	1.1127	1.0200	1.0435	1.0476	1.0400	1.0000	1.0000	1.0000	1.0000

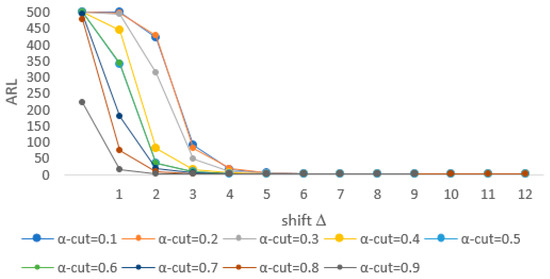
Figure 2. ARL Plot of the FBP control chart for $\rho =0$.

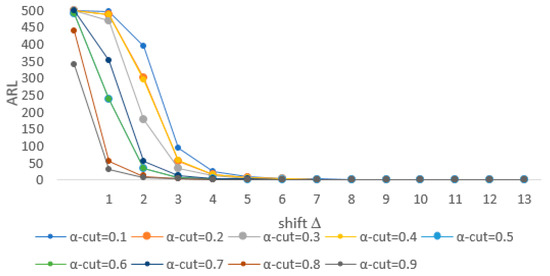
Figure 3. ARL plot of the FBP control chart for $\rho =0.5$.

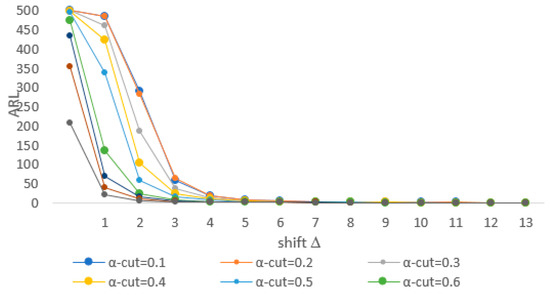
Figure 4. ARL Plot of the FBP control chart for $\rho =0.8$.

Table 2 first block presents the ARL values for the FBP control chart for the first scheme. ARL₀ is the expected number of samples until finding the first out-of-control sample, given that the process is in control. By applying ${\alpha }^{cut}$ from 0.1 to 0.8, an ARL₀ of around 500 is obtained, and the value of ARL₀ is lower than 300 for ${\alpha }^{cut}$ equal to 0.9. In the other hand, for the highest value of ${\alpha }^{cut}=0.9,$ the value of ARL₀ is 220, meaning that the false alarm rate is high. With higher values of ${\alpha }^{cut}$, the value of ARL₀ decreases.

The ARL₁ criterion is used to determine the sensitivity of the proposed control chart in order to detect a shift in the process. According to the first block in Table 2 and Figure 2, the trend in ARL decreases sharply for the proposed chart. The significant digits of the ARL value are varied from hundred to unit, and these indicate that the proposed chart is sensitive to detect the shifted of the parameter process. The smaller the ARL₁ value, the faster the proposed chart to find an out-of-control signal. Among these results, the higher the value of ${\alpha }^{cut}$, the smaller the value of ARL₁. Generally, by using ${\alpha }^{cut}$ values of 0.7, 0.8 and 0.9, the proposed chart shows a faster drop than the other charts. Since the simulation study uses a significance level equal to 0.0027, the theoretical value of ARL₀ is around 370. Therefore, among the values of ${\alpha }^{cut}$, the values of ARL₀ are higher than the theoretical values.

The second scheme generates data from a bivariate Poisson distribution with parameters ${\lambda }_1=1$, ${\lambda }_2=2$ and $\rho =0.5$. Table 2 second block and Figure 3 present the ARL values of the proposed chart in the second scheme. Based on this Table, with values of ${\alpha }^{cut}$ between 0.1 to 0.7, the first out-of-control observation occurs at around the 500^th observation (ARL₀). Meanwhile, when the value of ${\alpha }^{cut}$ is equal to 0.8, the ARL₀ value is smaller than 500. Looking at ARL₁, when the parameters ${\lambda }_1=1$, ${\lambda }_2=2$ are shifted by $\Delta$, the ARLs of the proposed chart decrease sharply. Among the overall ARLs shown in Figure 2, the greater the value ${\alpha }^{cut}$, the quicker the proposed control charts detect the shifting process. In the second scenario, despite the ability to discover values that become out-of-control more quickly, this procedure produces a low ARL₀, which means that an ${\alpha }^{cut}$ equal to 0.9 has a high false alarm rate.

Table 2 third block and Figure 4 provide the ARL values for the third scheme (the scheme with a higher coefficient of correlation). In this scheme, data with $\rho$ equal to 0.8 are generated. Among all the ARL plots, the value of ARL₀ is around 500 for an ${\alpha }^{cut}$ equal 0.1 to 0.5. In this scheme, the proposed control chart with an ${\alpha }^{cut}$ value equal to 0.8 has a value of ARL₀ closer to 350. However, with an ${\alpha }^{cut}$ smaller than 0.6, the chart has a higher value of ARL₀ (closer to 500). However, when ${\alpha }^{cut}$ is equal to 0.9, the value of ARL₀ is equal to 206, which indicates a high false alarm rate. Briefly, based on Figure 4, the ARL for the proposed chart drops sharply. For the fifth level shift of the parameters, the value of ARL₁ is nearly 135. The proposed chart using an ${\alpha }^{cut}$ equal to 0.8 gives better performance than the other charts. In general, based on the results of the three schemes, the proposed chart provides the best performance when the correlation coefficient of the quality characteristics is higher.

4. Comparative Study

Here, the FBP control chart performance is compared to the conventional bivariate Poisson (BP) chart proposed by Chiu and Kuo [17]. The performance of BP control charts is evaluated through a simulation study based on the value of ARL. This simulation calculates the value of ARL BP control charts for several values of the correlation coefficient $\left(\rho \right)$: $\rho =0,\rho =0.5$ and $\rho =0.8.$ The algorithm for the ARL BP chart calculation is defined as follows:

• Step 1. Generate data $\left(X_1,X_2\right)$ that follow a bivariate Poisson distribution with $m=1000$ observations, for each combination value of the correlation coefficients $\rho =0,\rho =0.5$ and $\rho =0.8$ and parameters $\left({\lambda }_1,{\lambda }_2\right).$
• Step 2. Calculate the statistics: $D_i=X_{1i}+X_{2i}.$
• Step 3. Calculate the control limits based on the following equations:

  $$\begin{array}{ll}P\left(D>UCL\right)& ={\displaystyle {\displaystyle \sum }_{d=UCL}^{\infty }}exp\left\{-\left[{\displaystyle {\displaystyle \sum }_{j=1}^J}{\lambda }_j-\theta \right]\right\}{\displaystyle {\displaystyle \sum }_{i=0}^{\lfloor d/2\rfloor }}\frac{{\left({{\displaystyle \sum }}_{j=1}^J{\lambda }_j-2\theta \right)}^{d-2i}{\theta }^i}{\left(d-2i\right)!i!}\le \frac{\alpha }{2}\\ & =1-{\displaystyle {\displaystyle \sum }_{d=0}^{UCL-1}}exp\left\{-\left[{\displaystyle {\displaystyle \sum }_{j=1}^J}{\lambda }_j-\theta \right]\right\}{\displaystyle {\displaystyle \sum }_{i=0}^{\lfloor d/2\rfloor }}\frac{{\left({{\displaystyle \sum }}_{j=1}^J{\lambda }_j-2{\theta }_o\right)}^{d-2i}{\theta }^i}{\left(d-2i\right)!i!}\le \frac{\alpha }{2} ,\end{array}$$

  (16)

  and

  $$P\left(D<LCL\right)={\displaystyle \sum }_{d=0}^{LCL}exp\left\{-\left[{\displaystyle \sum }_{j=1}^J{\lambda }_j-\theta \right]\right\}{\displaystyle \sum }_{i=0}^{\lfloor d/2\rfloor }\frac{{\left({{\displaystyle \sum }}_{j=1}^J{\lambda }_j-2\theta \right)}^{d-2i}{\theta }^i}{\left(d-2i\right)!i!}\le \frac{\alpha }{2} ,$$

  (17)

  where $\theta$ is the covariance between $X_1$ and $X_2.$
• Step 4. Evaluation of the BP chart using ARL as follows:
  • For each combination value of $\rho$ and parameter $\left({\lambda }_1,{\lambda }_2\right),$ generate $m=1000$ observations that follow a bivariate Poisson distribution. Repeat and compare the statistics of $D_i$ with the control limits obtained from step 3. If the statistics are out-of-control the first time, then the value for Run Length (RL) is obtained.
  • Repeat step 4a 1000 times and calculate the average run length for the in-control condition (ARL₀).
  • Repeat steps 4(a) and (b) for the level shift of parameters ${\lambda }_1^{*}={\lambda }_1+\mathsf{\Delta }$ and ${\lambda }_2^{*}={\lambda }_2+\mathsf{\Delta }$, with an increment of $\Delta =1,$ to obtain the average run length for an out-of-control condition (ARL₁).
  • Plot the ARL₀ and ARL₁.

The ARL values of the existing control charts are compared with those of the proposed chart for ${\alpha }^{cut}$ equal to 0.8. This comparison is shown in Table 3 and Figure 5. There are three schemes used to evaluate the performance of the conventional chart. These schemes are based on coefficient correlation values $\left(\rho \right),$ which are divided into 0.0, 0.5 and 0.8. The results show that the values of the ARL of the conventional chart do not significantly decrease when the process is shifted. Among these schemes, the ARL₀ of the conventional chart is close to the theoretical ARL₀ for $\rho =0.5$. Furthermore, the performance of the proposed chart with ${\alpha }^{cut}$ equal to 0.8 is compared to the conventional BP chart, with $\rho =0.5.$ The comparison shows that the proposed chart is more sensitive to detecting shifts than the conventional BP chart.

Table 3. ARL values of the BP chart.

${\mathit{\lambda }}_1^{*}$	${\mathit{\lambda }}_2^{*}$	$\Delta$	$\mathit{\rho }$
			0	0.5	0.8
1	2	0	761.3600	381.5000	586.7870
2	3	1	487.9755	274.1520	370.0240
3	4	2	338.6280	197.5360	261.0067
4	5	3	256.9445	152.0770	199.9752
5	6	4	206.5924	123.0724	161.6114
6	7	5	172.6343	103.2250	135.4560
7	8	6	148.2440	88.8520	116.5456
8	9	7	129.8954	77.9851	102.2551
9	10	8	115.5977	69.4892	91.0911
10	11	9	104.1505	62.6713	82.1280
11	12	10	94.7784	57.0829	74.7811
12	13	11	86.9658	52.4195	68.6478
13	14	12	80.3536	48.4702	63.4546

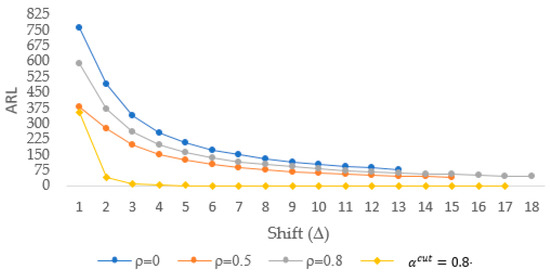
Figure 5. The ARL Plot of the FBP and BP control chart for various correlation coefficients.

Application FBP Control Charts

Based on the performance of the FBP chart described in Section 3.3, as well as the comparison presented in Section 4, the performance of FBP is better than that of the conventional BP. In this section, the proposed control chart is applied to data gathered from the Quality Control Division during the sorting process at a Glass Bottle Company for one type of bottle. In this case, the characteristics of bottle ring defects are classified into crack on ring $\left(X_1\right)$ and crack under ring $\left(X_2\right)$. In the context of glass bottle manufacturing, the crack under ring defect will cause the crack on ring defect. Here, the proposed chart will be compared with the existing chart.

In practice, during the production of a bottle, a crack under the ring will cause a crack on the ring. There are 48 observations used, where each observation contains 192 bottles. First, to estimate the fuzzy parameter, the number of defects in each observation is calculated. Thereafter, each observation is formed into triangular fuzzy numbers using the FBP procedures outlined in Section 3.2. The monitoring result for ${\alpha }^{cut}$ equal to 0.8 is shown in Figure 6.

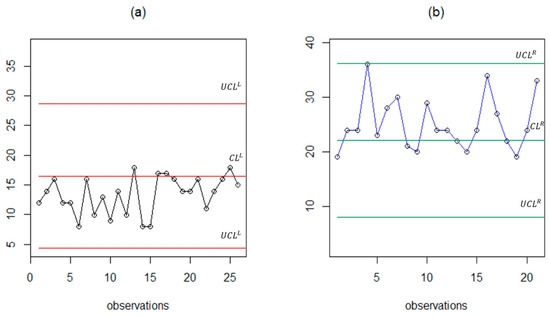
Figure 6. FBP chart for monitoring the bottle production data: (a) FBP left side chart, (b) FBP right side chart.

The proposed chart is represented by two forms of the control limit, namely the left and right control limits. The left control limits are denoted by $LC{L}^L , C{L}^L \mathrm{and}UC{L}^L$. On the other hand, the right control limits are denoted by $LC{L}^R , C{L}^R \mathrm{and}UC{L}^R$. The vertical axis on each chart represents the value of the FBP statistics, while the horizontal axis represents the observations. The values of both the left and right control limits are shown in Figure 6. The left chart (Figure 6a) shows all points within the control limit, but in the right chart (Figure 6b), there is one point outside the upper control limit. Therefore, this chart suggests that the production process for the bottles is out of control. Meanwhile, Figure 7 shows the result using the BP chart. For the same real case, all the observations fall between the lower control limit and the upper control limit. This indicates that when using the BP chart, the bottle production process remains in control. Thus, this real case shows that the proposed chart is more sensitive than the existing control chart.

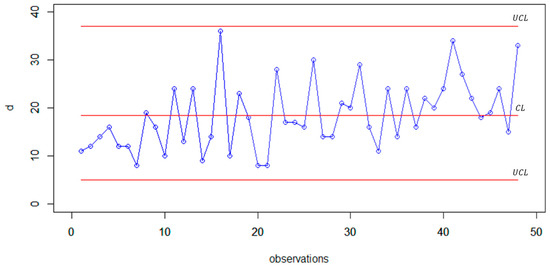
Figure 7. BP control chart for monitoring the bottle production data.

5. Conclusions

In this paper, a fuzzy bivariate Poisson (FBP) control chart based on fuzzy parameter estimation is proposed. The crisp value for the FBP is transformed using TFN based on the estimated fuzzy parameter involving the normal distribution function. The average run length (ARL) is employed to evaluate the performance of the proposed chart. Simulations were carried out for three scenarios of correlation coefficients and nine values of ${\alpha }^{cut}$. The performance of the FBP chart for each correlation value combined with ${\alpha }^{cut}$ is not effective due to the high false alarm rate. Meanwhile, for an ${\alpha }^{cut}$ value between 0.1 to 0.4, the proposed chart has a consistent ARL₀ value of about 500. For an ${\alpha }^{cut}$ value between 0.5 to 0.8, in general, the proposed chart has an ARL₀ value above 370 and less than 500. The best conditions for the FBP chart are found for a condition when the $\rho =0.8$ and ${\alpha }^{cut}=0.8.$

The simulation study shows that the proposed chart is better than the conventional chart. The BP chart is better than FB in terms of its ARL₀ (no shifting parameter). But, for the shifting of parameter process, the BP chart is slower to detect the shift compared to the proposed charts. In the real application, the FBP chart is more sensitive than the BP chart. For further research, the control limits of the FBP control charts could be modelled using intermediate criteria, such as “in-control”, “rather in-control”, “rather out-of-control” and “out-of-control”. Also, the proposed chart could be extended to a fuzzy multivariate Poisson control chart.