Symmetry Evolution in Chaotic System
Abstract
1. Introduction
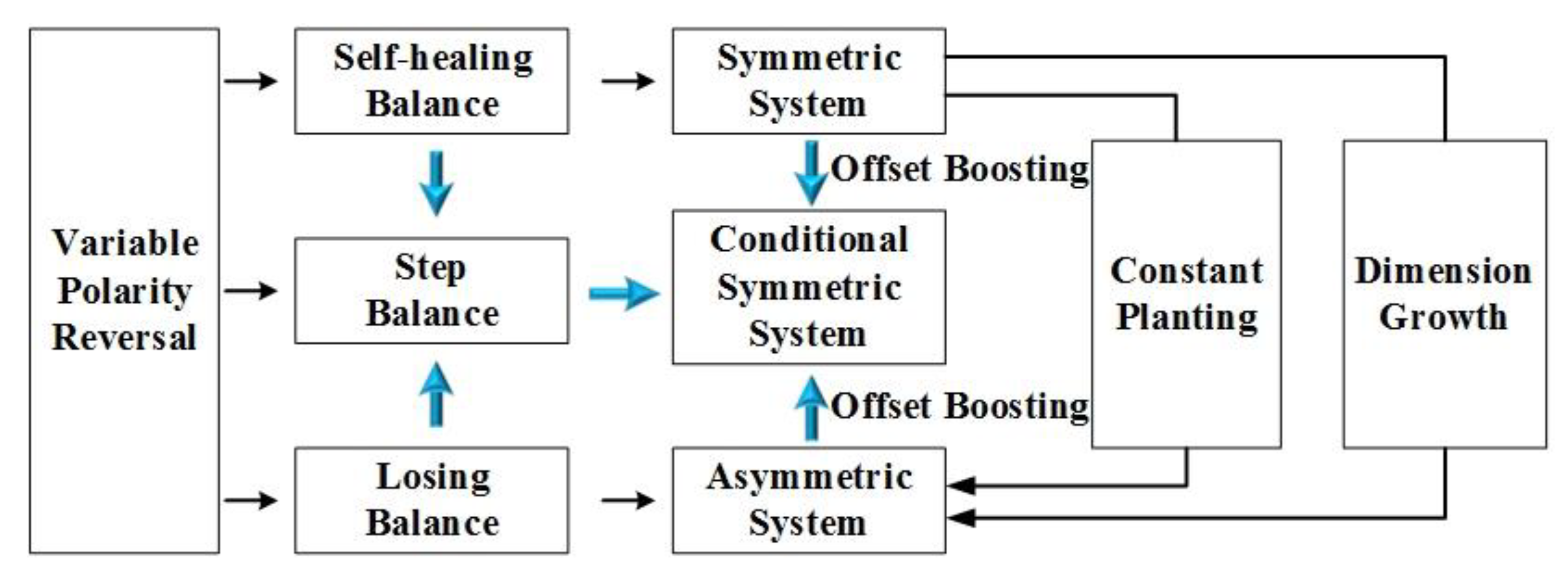
2. Conditional Symmetry from Asymmetry
3. Constructing Conditional Symmetry from Symmetry
4. Recovering Conditional Symmetry from Destroyed Symmetry
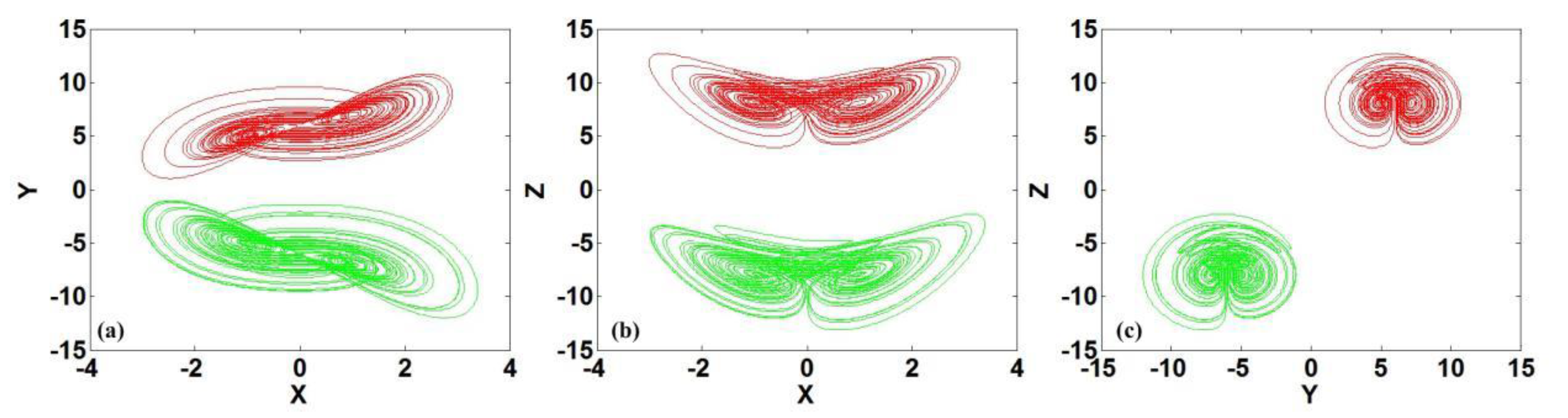
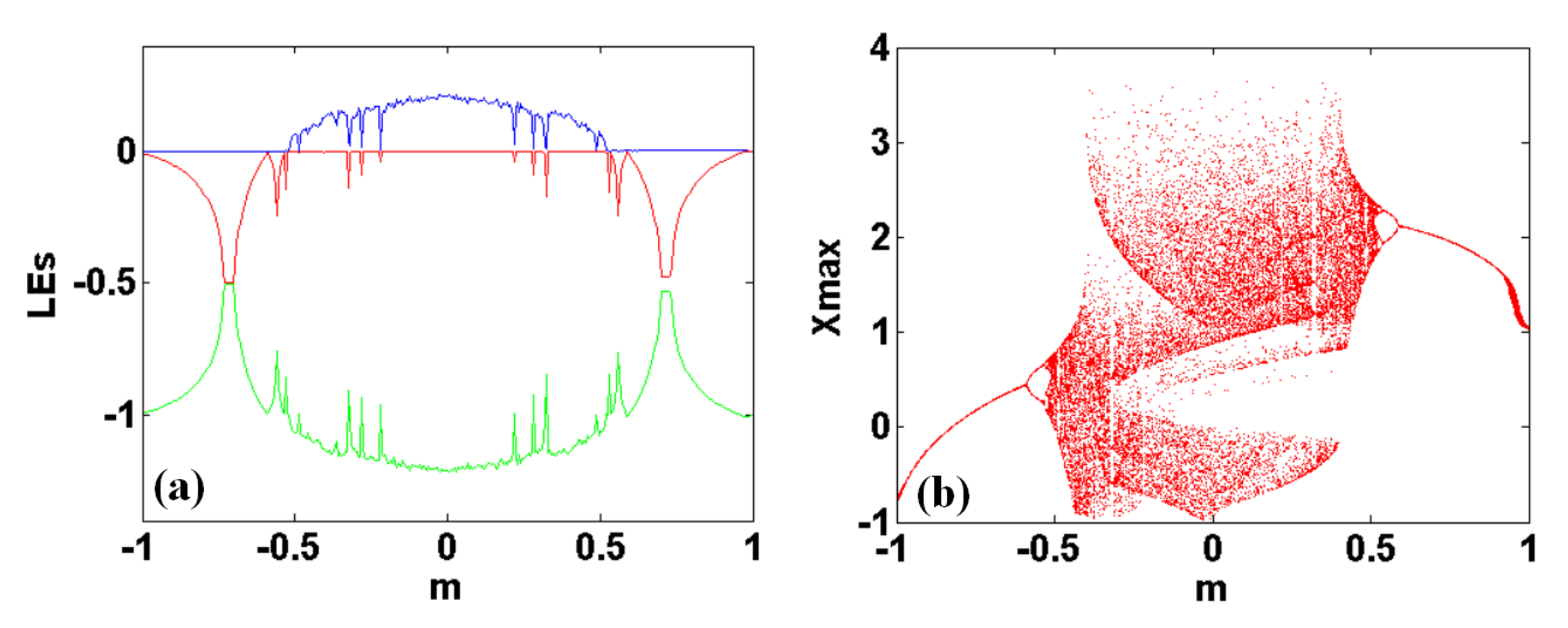
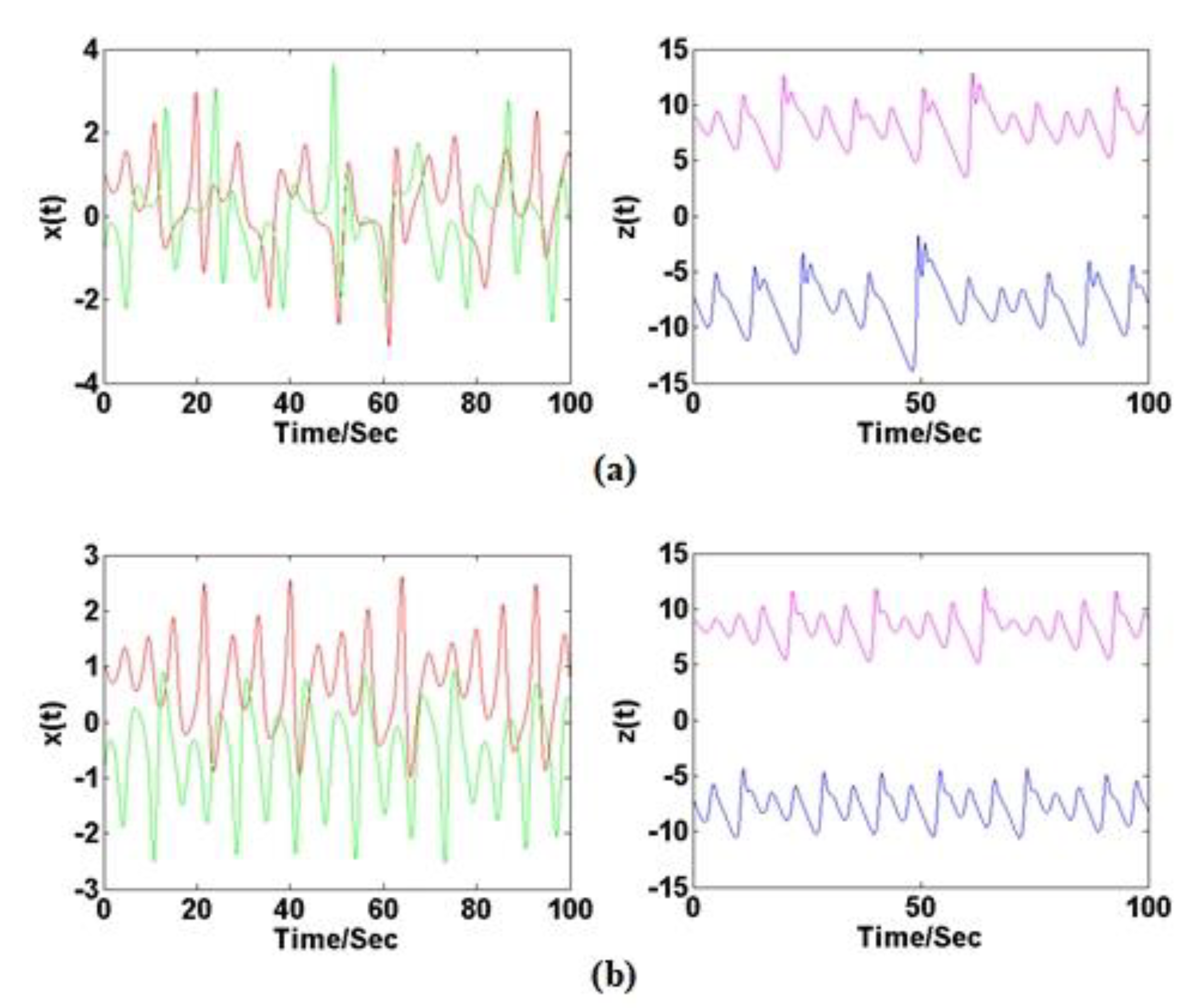
4.1. Symmetry Destroyed by the Constant Planting
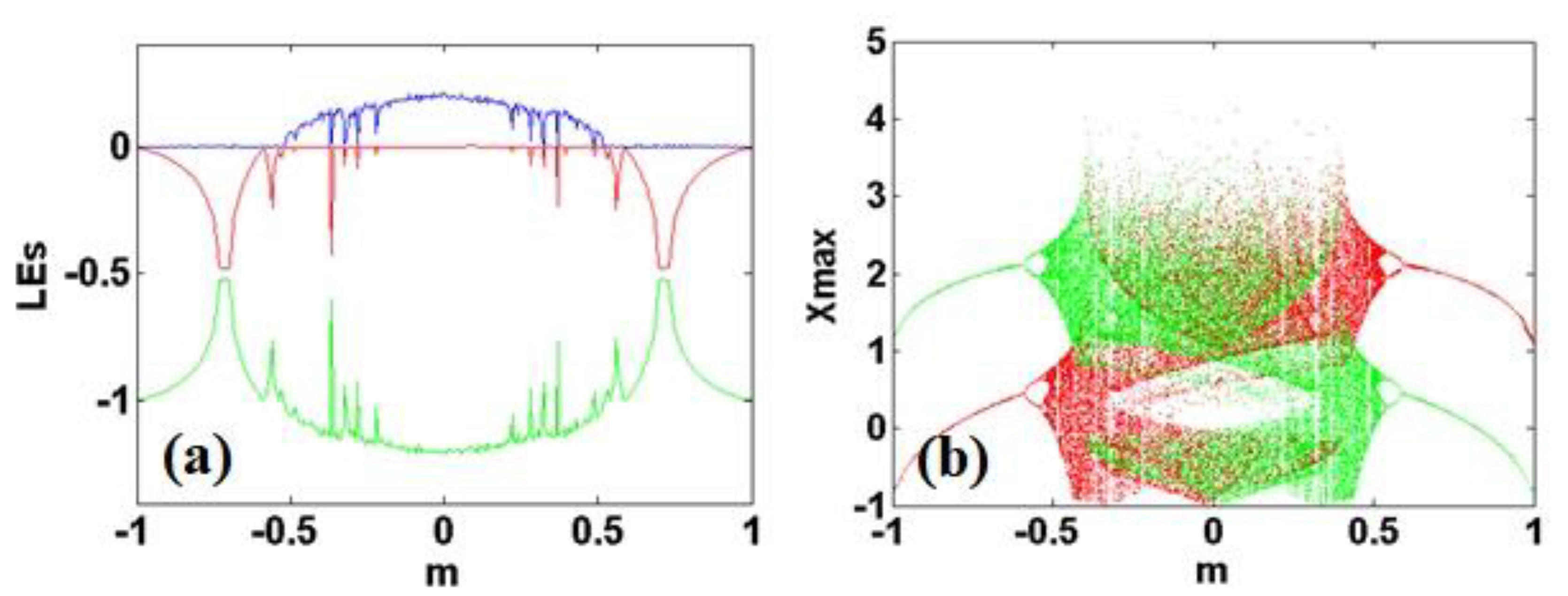
4.2. Symmetry Evolution Induced by the Dimension Growth
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lai, Q.; Chen, S. Generating multiple chaotic attractors from Sprott B system. Int. J. Bifurc. Chaos 2016, 26, 1650177. [Google Scholar] [CrossRef]
- Bao, B.C.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solit Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.H. Multiscroll Hyperchaotic System with Hidden Attractors and Its Circuit Implementation. Int. J. Bifurc. Chaos 2019, 29, 1950117. [Google Scholar] [CrossRef]
- Deng, Q.L.; Wang, C.H. Multi-scroll hidden attractors with two stable equilibrium points. Chaos 2019, 29, 093112. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, J.; Liu, H.J.; Zhang, F.F. Dynamic Analysis of a One-parameter Chaotic System in Complex Field. IEEE Access 2020, 8, 28774–28781. [Google Scholar] [CrossRef]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010; pp. 1–40. [Google Scholar]
- Sprott, J.C. Simplest chaotic flows with involutional symmetries. Int. J. Bifurc. Chaos 2014, 24, 1450009. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.H.; Yao, W.; Lin, H.R. Chaotic system with bondorbital attractors. Nonlinear Dyn. 2019, 97, 2159–2174. [Google Scholar] [CrossRef]
- Li, C.; Lu, T.; Chen, G.; Xing, H. Doubling the coexisting attractors. Chaos 2019, 29, 051102. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Serrano, S. Qualitative analysis of the Rössler equations: Bifurcations of limit cycles and chaotic attractors. Physica D 2009, 238, 1087–1100. [Google Scholar] [CrossRef]
- Sprott, J.C.; Li, C. Asymmetric bistability in the Rӧssler system. Acta Phys. Pol. B 2017, 48, 97–107. [Google Scholar] [CrossRef]
- Sprott, J.C.; Wang, X.; Chen, G. Coexistence of point, periodic and strange attractors. Int. J. Bifurc. Chaos 2013, 23, 1350093. [Google Scholar] [CrossRef]
- Jafari, S.; Ahmadi, A.; Panahi, S.; Rajagopal, K. Extreme multistability: When imperfection changes quality. Chaos Solitons Fractals 2018, 108, 182–186. [Google Scholar] [CrossRef]
- Karthikeyan, R.; Jafari, S.; Karthikeyan, A.; Srinivasan, A.; Ayele, B. Hyperchaotic Memcapacitor Oscillator with Infinite Equilibria and Coexisting Attractors. Circuits Syst. Signal. Process. 2018, 37, 1–23. [Google Scholar]
- Li, C.; Sprott, J.C. Variable-boostable chaotic flows. Opt. Int. J. Light Electron. Opt. 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
- Gu, Z.; Li, C.; Iu, H.H.C.; Min, F.; Zhao, Y.B. Constructing hyperchaotic attractors of conditional symmetry. Eur. Phys. J. B 2019, 92, 221. [Google Scholar] [CrossRef]
- Lu, T.; Li, C.; Jafari, S.; Min, F. Controlling Coexisting Attractors of Conditional Symmetry. Int. J. Bifurc. Chaos 2019, 29, 1950207. [Google Scholar] [CrossRef]
- Zhang, X. Constructing a chaotic system with any number of attractors. Int. J. Bifurc. Chaos 2017, 27, 1750118. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Xing, H. Constructing chaotic systems with conditional symmetry. Nonlinear Dyn. 2017, 87, 1351–1358. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Liu, Y.; Gu, Z.; Zhang, J. Offset Boosting for Breeding Conditional Symmetry. Int. J. Bifurc. Chaos 2018, 28, 1850163. [Google Scholar] [CrossRef]
- Schrier, G.V.D.; Maas, L.R.M. The diffusionless Lorenz equations; Shil’nikov bifurcations and reduction to an explicit map. Physica D 2000, 141, 19–36. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Thio, W. Linearization of the Lorenz System. Phys. Lett. A 2015, 379, 888–893. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. Eur. Phys. J. Spec. Top. 2015, 224, 1421–1458. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N.; Prasad, A.; Shrimali, M.D. Finite-time Lyapunov dimension and hidden attractor of the Rabinovich system. Nonlinear Dyn. 2018, 92, 267–285. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Mokaev, T.N. Numerical analysis of dynamical systems: Unstable periodic orbits, hidden transient chaotic sets, hidden attractors, and finite-time Lyapunov dimension. J. Phys. Conf. Ser. 2019, 1205, 012034. [Google Scholar] [CrossRef]








| Cases | System Equations | Parameters | Initial Condition | Lyapunov Exponents |
|---|---|---|---|---|
| CS1 | a = 0.4, b = 1.75, c = 3 | (3, −1.5, −2) (3, −1.5, 1) | 0.1191, 0, −1.2500 | |
| CS2 | a = 1.22, b = 8.48 | (3, 1, 0.5) (−3, 1, 0.5) | 0.2335, 0, −1.2335 | |
| CS3 | a = 2.6, b = 2 | (0.5, 4, −1) (0.5, −4, −1) | 0.0463, 0, −2.6463 | |
| CS4 | a = 1.24, b = 1 | (4, 0.8, −2) (−4, 0.8, 2) | 0.0645, 0, −1.2582 | |
| CS5 | a = 0.22 | (−1, 1, −1) (2, 6, −1) | 0.0729, 0, −1.6732 | |
| CS6 | a = 3, b = 1.2 | (0, −6 −6) (0, 6, 6) | 0.0506, 0, −0.2904 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Sun, J.; Lu, T.; Lei, T. Symmetry Evolution in Chaotic System. Symmetry 2020, 12, 574. https://doi.org/10.3390/sym12040574
Li C, Sun J, Lu T, Lei T. Symmetry Evolution in Chaotic System. Symmetry. 2020; 12(4):574. https://doi.org/10.3390/sym12040574
Chicago/Turabian StyleLi, Chunbiao, Jiayu Sun, Tianai Lu, and Tengfei Lei. 2020. "Symmetry Evolution in Chaotic System" Symmetry 12, no. 4: 574. https://doi.org/10.3390/sym12040574
APA StyleLi, C., Sun, J., Lu, T., & Lei, T. (2020). Symmetry Evolution in Chaotic System. Symmetry, 12(4), 574. https://doi.org/10.3390/sym12040574





