A Comparison of Complete Parts on m-Idempotent Hyperrings

Abstract

On a particular class of m-idempotent hyperrings, the relation ${\xi }_m^{*}$ is the smallest strongly regular equivalence such that the related quotient ring is commutative. Thus, on such hyperrings, ${\xi }_m^{*}$ is a new representation for the ${\alpha }^{*}$-relation. In this paper, the ${\xi }_m$-parts on hyperrings are defined and compared with complete parts, $\alpha$-parts, and m-complete parts, as generalizations of complete parts in hyperrings. It is also shown how the ${\xi }_m$-parts help us to study the transitivity property of the ${\xi }_m$-relation. Finally, ${\xi }_m$-complete hyperrings are introduced and studied, stressing on the fact that they can be characterized by ${\xi }_m$-parts. The symmetry plays a fundamental role in this study, since the protagonist is an equivalence relation, defined using also the symmetrical group of permutations of order n.

1. Introduction

A congruence relation on an algebraic structure is an equivalence relation that is compatible with the given structure, that is, all operations of the structure are well-defined on the equivalence classes. The set of the equivalence classes forms the associated quotient structure, that, in the case of a group, is a quotient group, while in the case of a ring it is a ring. In algebraic hypercompositional structures, where the operations are substituted by hyperoperations (i.e., multi-valued operations), this role of the equivalences is played by the strongly regular relations. Such a relation $\rho$ is defined on a hypergroup $(H,\circ )$ by the property: if $a\rho b$ and $c\rho d$, for $a,b,c,d\in H$, then, for any $x\in a\circ c$ and any $y\in b\circ d$, there is $x\rho y$. A strongly regular relation on a hyperring R is strongly regular with respect to both hyperoperations of R. The mathematical concept of hyperring was defined by M. Krasner [1] in 1956 in the same paper where the hyperfields were introduced in order to solve an important problem dealing with approximations of complete valued fields by sequences of such fields. This algebraic hypercompositional structure has a similar behaviour as a ring and it contains an additive part $(R,+)$, which is a canonical hypergroup and a multiplicative one $(R,·)$, that is a semigroup, while the multiplication is bilaterally distributive with respect to the addition. Besides, a Krasner hyperring is also known as an additive hyperring. There are also other types of hyperrings [2] and the most general one is the so called general hyperring, introduced by Vougiouklis [3], where both addition and multiplication are hyperoperations. A short review on the historical part, terminology and the importance of hyperrings is presented by Massouros [4] or Nakassis [5] in their expository papers. The quotient structure associated to a hypergroup modulo a strongly regular relation is a group. This is a strong relationship between hypergroups and groups, that permits to study properties of hypergroups using already known properties of groups. In 1970 Koskas [6] defined the $\beta$-relation and its transitive closure ${\beta }^{*}$ on a hypergroup H, proving that it is the smallest (with respect to inclusion) strongly regular relation on H such that the quotient $H/{\beta }^{*}$ is a group. The idea was then extended to the class of hyperrings, where Vougiouklis [3] defined in 1990 a new strongly regular relation, the $\Gamma$-relation, on a general hyperring, such that the quotient structure modulo the transitive closure ${\Gamma }^{*}$ is a ring. Both associated quotient structures modulo ${\beta }^{*}$ and ${\Gamma }^{*}$ are not commutative. That is why, new strongly regular relations were defined—first the $\gamma$-relation on (semi)hypergroups and then the $\alpha$-relation on a hyperring in order to obtained commutative quotient structures [7,8]. The same symbol $\gamma$ was (unfortunately) used to define two different relations, one on hyperrings, and the other one on (semi)hypergroups. In order to avoid confusion, some authors, for example see Reference [9], which prefers denoting the strongly regular relation on hyperrings with capital $\Gamma$ and we also adopt this notation in our current study.

Because of their “fundamental role”, that is, connecting hypercompositional structures with the corresponding classical structures, Vougiouklis [3,10] named all these strongly regular relations fundamental relations. Thus a fundamental relation defined on a hypercompositional structure is the smallest equivalence (with respect to inclusion) so that the associated quotient is a classical structure of the same type of the hypercompositional structure. The fundamental relations ${\beta }^{*}$ and ${\gamma }^{*}$ defined on a (semi)hypergroup H lead to a (semi)group $H/{\beta }^{*}$ and a commutative (semi)group $H/{\gamma }^{*}$ as quotient structure, while the fundamental relations ${\Gamma }^{*}$ and ${\alpha }^{*}$ on a hyperring are the tool to obtain a ring and a commutative ring, respectively. In 2017, Norouzi and Cristea [11] introduced a particular class of hyperrings where the fundamental relation ${\Gamma }^{*}$ is not anymore the smallest equivalence such that the associated quotient structure is a ring. On this type of hyperrings they defined the fundamental relation ${\epsilon }_m^{*}$, smaller than ${\Gamma }^{*}$, but with the associated quotient structure non-commutative in general. Thereby, the fundamental relation ${\xi }_m^{*}$ was introduced on such hyperrings, obtaining a commutative quotient ring [12].

On the other hand, all the above mentioned strongly regular relations are not transitive in general. Already in 1970 Koskas [6] had studied the transitivity property of the $\beta$-relation on hypergroups by using the complete parts, that were used as open subsets of suitable topologies on hypergroups. So they play an important role in defining topological hypercompositional structures [13]. Inspired by these studies, in this article we first define the concept of ${\xi }_m$-part on hyperrings and study it in comparison with the complete part, $\alpha$-part and m-complete part. In particular, we find conditions under which the relation ${\xi }_m$ is transitive and prove that the equivalence class, modulo the relation ${\xi }_m$, of any element of a general hyperring is a ${\xi }_m$-part. Finally, we introduce the class of ${\xi }_m$-complete hyperrings, characterize them using the ${\xi }_m$-parts and present their connections with complete, $\alpha$-complete, and $\epsilon$-complete hyperrings.

2. Preliminaries on the ${\mathit{\xi }}_{\mathit{m}}$-Relation on Hyperrings

This section contains the basic definitions and results concerning the ${\xi }_m$-relation on hyperrings that will be used throughout the paper. For more details about hyperstructures theory, specially hyperrings, we refer the readers to References [3,10,14,15] and references therein.

Definition 1.

[15] An algebraic system $(R,+,·)$ is said to be a

(1) 

(general) hyperring, if $(R,+)$ is a hypergroup, $(R,·)$ is a semihypergroup, and the hypermultiplication · is distributive with respect to the hyperaddition +. If $(R,+)$ is a semihypergroup, then $(R,+,·)$ is called a semihyperring.

(2) 

Krasner hyperring, if $(R,+)$ is a canonical hypergroup and $(R,·)$ is a semigroup such that 0 is a zero element (called also absorbing element), that is, for all $x\in R$, we have $x·0=0$, and the multiplication · is distributive over the hyperaddition +.

On a hyperring R, the $\Gamma$-relation was defined by Vougiouklis [3] as follows:

$$\begin{array}{cc}\hfill x\Gamma y& ⟺\exists n\in \mathbb{N},\exists k_i\in \mathbb{N},\exists z_{i1},\dots ,z_{i{k}_i}\in R(i=1,\dots ,n):\{x,y\}\subseteq \sum _{i=1}^n\left(\prod _{j=1}^{k_i}{z}_{ij}\right).\hfill \end{array}$$

Its transitive closure ${\Gamma }^{*}$ is the smallest strongly regular relation on R such that the associated quotient $R/{\Gamma }^{*}$ is a classical ring, but it is not commutative in general. Later on Davvaz and Vougiouklis [7] introduced the relation $\alpha$ in order to obtain a commutative quotient ring. First set ${\alpha }_0=\{(x,x)\mid x\in R\}$ and then, for any natural number n, we say that $x{\alpha }_{n}y$ if and only if there exist $k_1,\dots ,k_n\in \mathbb{N}$, a permutation $\sigma \in {\mathbb{S}}_n$ and the elements $z_{i1},\dots ,z_{i{k}_i}\in R$ and the permutations ${\sigma }_i\in {\mathbb{S}}_{k_i}$, for $1\le i\le n$, such that ${\displaystyle x\in \sum _{i=1}^n\left(\prod _{j=1}^{k_i}{z}_{ij}\right)}$ and ${\displaystyle y\in \sum _{i=1}^n{A}_{\sigma \left(i\right)}}$, where ${\displaystyle A_i=\prod _{j=1}^{k_i}{z}_{i{\sigma }_i\left(j\right)}}$. Take then ${\displaystyle \alpha =\bigcup _{n\ge 0}{\alpha }_n}$. The quotient structure $R/{\alpha }^{*}$ is a commutative ring.

In Reference [11] the authors defined a new relation on (semi)hyperrings, denoted by ${\epsilon }_m$, smaller than the $\Gamma$-relation, such that its transitive closure on a particular class of hyperrings is the smallest strongly regular relation endowing the quotient set with a ring structure. Let us remember here its definition. Select a constant m, such that $2\le m\in \mathbb{N}$. For two elements x and y in R, consider $x{\epsilon }_{m}y$ if and only if $\{x,y\}\subseteq {\sum }_{i=1}^n{z}_i^m$, for $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\{(x,x)\mid x\in R\}\subseteq {\epsilon }_m$. If $(R,+,·)$ is a hyperring such that $(R,·)$ is commutative and $B\subseteq {\sum }_{i=1}^n{A}_i^m$ implies that there exists $x_i\in A_i$ for $1\le i\le n$ such that ${\displaystyle B\subseteq \sum _{i=1}^n{x}_i^m}$ for all $B,A_1,\dots ,A_n\subseteq R$, then the relation ${\epsilon }_m^{*}$ is the smallest strongly regular equivalence on R such that the quotient set $R/{\epsilon }_m^{*}$ is a ring (not necessary commutative). Besides, since the quotient ring $R/{\epsilon }_m^{*}$ is not commutative in general, similar to the role of the $\alpha$-relation, in Reference [12], a strongly regular relation, smaller than the ${\alpha }^{*}$-relation, was defined in order to obtain commutative quotient rings as follows:

$$(x,y)\in {\xi }_m⟺\exists n\in \mathbb{N},\exists z_1,\dots ,z_n\in R,\exists \sigma \in {\mathbb{S}}_n:x\in \sum _{i=1}^n{z}_i^m\wedge y\in \sum _{i=1}^n{z}_{\sigma \left(i\right)}^m.$$

(1)

A new type of hyperring $(R,+,·)$ was introduced, where the transitive closure ${\xi }_m^{*}$ is strongly regular. Their multiplicative part is commutative and they satisfy the condition—for any nonempty subsets $B,C,A_1,\dots ,A_n$ of R and a permutation $\sigma \in {\mathbb{S}}_n$, if $B\subseteq {\sum }_{i=1}^n{A}_i^m$ and $C\subseteq {\sum }_{i=1}^n{A}_{\sigma \left(i\right)}^m$, then there exist $x_i\in A_i$, for $1\le i\le n$, such that

$$B\subseteq \sum _{i=1}^n{x}_i^{m}andC\subseteq \sum _{i=1}^n{x}_{\sigma \left(i\right)}^m.$$

(2)

The quotient $R/{\alpha }^{*}$ is always a commutative ring [15], while the quotient $R/{\xi }_m^{*}$ is not commutative in general [12]. Actually, if $(R,+,·)$ is an m-idempotent hyperring satisfying relation (2), then ${\xi }_m^{*}$ is the smallest strongly regular equivalence relation on R such that the quotient $R/{\xi }_m^{*}$ is a commutative ring. In Reference [12], it is shown that the four fundamental relations defined on hyperrings are not equal in general, but for all m-idempotent Krasner hyperrings, it holds $\Gamma ={\epsilon }_m={\xi }_m=\alpha$. Moreover, it is proved that ${\xi }_m=\alpha$ on m-idempotent hyperrings satisfying relation (2), which states that the relation ${\xi }_m^{*}$ is a new representation for the ${\alpha }^{*}$-relation on m-idempotent hyperrings satisfying relation (2).

3. ${\mathit{\xi }}_{\mathit{m}}$-Parts and Transitivity of the ${\mathit{\xi }}_{\mathit{m}}$-Relation

Generally, the ${\xi }_m$-relation is not transitive [12], as well as the relations $\beta$, $\Gamma$, $\alpha$, or ${\epsilon }_m$, so there is the necessity to find a tool, a method to show when these relations are transitive. Koskas was the first to deal with this problem, which was resolved in Reference [6] by introducing the notion of complete parts on (semi)hypergroups. A nonempty subset A of a semihypergroup $(H,·)$ is called a complete part of H, if $A\cap {\prod }_{i=1}^n{a}_i\ne \varnothing$ implies ${\prod }_{i=1}^n{a}_i\subseteq A$, for any nonzero natural number n and any elements $a_1,\dots ,a_n\in H$. In particular, the equivalence class ${\beta }^{*}\left(x\right)$ of any element of H is a complete part of H.

The transitivity property of the $\Gamma$-relation was studied by Anvariyeh et al. [16], using complete parts on hyperrings. A nonempty subset M of ahyperring $(R,+,·)$ is a complete part of R if from $M\cap {\sum }_{i=1}^n\left({\prod }_{j=1}^{k_i}{z}_{ij}\right)\ne \varnothing$ it follows that ${\sum }_{i=1}^n\left({\prod }_{j=1}^{k_i}{z}_{ij}\right)\subseteq M$, for $n,k_i\in \mathbb{N}$, $i=1,2,\dots ,n$ and $z_{i1},\dots ,z_{i{k}_i}\in R$.

Next $\alpha$-parts [17] were introduced on hyperrings to show when the $\alpha$-relation [7] is transitive. A nonempty subset M of a hyperring R is an $\alpha$-part, if for every $n,k_i\in \mathbb{N}$, $i=1,2,\dots ,n$, $z_{i1},\dots ,z_{i{k}_i}\in R$, $\sigma \in S_n$ and ${\sigma }_i\in S_{k_i}$, there is

$$\sum _{i=1}^n\left(\prod _{j=1}^{k_i}{z}_{ij}\right)\cap M\ne \varnothing ⟹\sum _{i=1}^n{A}_{\sigma \left(i\right)}\subseteq M,$$

where $A_i={\prod }_{j=1}^{k_i}{z}_{i{\sigma }_i\left(j\right)}$.

Moreover, the m-complete parts [18] were defined with respect to the transitivity of the ${\epsilon }_m$-relation. In this case, a nonempty subset M of R is an m-complete part if $M\cap {\sum }_{i=1}^n{z}_i^m\ne \varnothing$ implies that ${\sum }_{i=1}^n{z}_i^m\subseteq M$, for a constant $2\le m\in \mathbb{N}$.

In this section, the ${\xi }_m$-part of a hyperring R is introduced in order to establish a condition for transitivity of the ${\xi }_m$-relation. In this regard, some properties of ${\xi }_m$-parts and some of their differences from complete parts, m-complete parts and $\alpha$-parts are presented.

Definition 2.

Let M be a nonempty subset of a hyperring R. We say that M is an ${\xi }_m$-part, if ${\sum }_{i=1}^n{z}_i^m\cap M\ne \varnothing$ implies ${\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m\subseteq M$, for every $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\delta \in S_n$.

To start with, a characterization of ${\xi }_m$-parts is stated.

Proposition 1.

Let R be a hyperring. The following conditions are equivalent:

(i) 

A nonempty subset M of R is a ${\xi }_m$-part.

(ii) 

For any $x\in M$ with the property $x{\xi }_{m}y$ it follows that $y\in M$.

(iii) 

For any $x\in M$ with the property $x{\xi }_m^{*}y$ it follows that $y\in M$.

Proof. 

$\left(i\right)⟹\left(ii\right)$ Let M be a ${\xi }_m$-part of R and $x{\xi }_{m}y$ for $x\in M$ and $y\in R$. Hence there exist $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\delta \in S_n$ such that $x\in {\sum }_{i=1}^n{z}_i^m$ and $y\in {\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m$. Since $x\in {\sum }_{i=1}^n{z}_i^m\cap M$, it follows that ${\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m\subseteq M$ and so $y\in M$.

$\left(ii\right)⟹\left(iii\right)$ Let $x\in M$ such that $x{\xi }_m^{*}y$. Thus there exist $k\in \mathbb{N}$, $z_0,\dots ,z_k\in R$ such that $z_0=x$, $z_k=y$ and $x=z_0{\xi }_m{z}_1{\xi }_m{z}_2\dots {\xi }_m{z}_k=y$. The following implications hold:

$$\begin{array}{cc}\hfill x=z_0\in M,z_0{\xi }_m{z}_1& ⟹z_1\in M,\hfill \\ \hfill z_1\in M,z_1{\xi }_m{z}_2& ⟹z_2\in M,\hfill \\ \hfill & ⋮\hfill \\ \hfill z_{k-1}\in M,z_{k-1}{\xi }_m{z}_k& ⟹z_k=y\in M.\hfill \end{array}$$

$\left(iii\right)$ Now, let M be a nonempty subset of R. If ${\sum }_{i=1}^n{z}_i^m\cap M\ne \varnothing$, then there exists $t\in {\sum }_{i=1}^n{z}_i^m\cap M$. For $\delta \in S_n$ and every $w\in {\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m$, we have $t{\xi }_{m}w$. Thus $t\in M$ and $t{\xi }_m^{*}w$. By the hypothesis, it follows that $w\in M$ and so ${\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m\subseteq M$. Therefore, M is an ${\xi }_m$-part of R.  □

Example 1.

Consider the hyperring $R=\{a,b,c,d,e,f,g\}$ as follows:

$$\begin{array}{cccccccc}+& a& b& c& d& e& f& g\\ a& \{a,b\}& \{a,b\}& c& d& e& f& g\\ b& \{a,b\}& \{a,b\}& c& d& e& f& g\\ c& c& c& \{a,b\}& f& g& d& e\\ d& d& d& g& \{a,b\}& f& e& c\\ e& e& e& f& g& \{a,b\}& c& d\\ f& f& f& e& c& e& g& \{a,b\}\\ g& g& g& d& e& c& \{a,b\}& f\end{array}$$

and define $x·y=\{a,b\}$ for every $x,y\in R$. Then, ${\xi }_m\left(a\right)=\{a,b\}$ and ${\xi }_m\left(x\right)=\left\{x\right\}$ for all $x\in R\setminus \{a,b\}$. By Proposition 1, we can see that $M=\{a,b,c\}$ is a ${\xi }_m$-part, but $N=\left\{a\right\}$ is not a ${\xi }_m$-part of R, for any $m\ge 2$.

Proposition 2.

Every α-part is a ${\xi }_m$-part, for every $2\le m\in \mathbb{N}$.

Proof. 

Proposition 1 is similarly valid for the $\alpha$-relation and $\alpha$-parts ([15]). Therefore, the proof is completed because ${\xi }_m\subseteq \alpha$.  □

In the following example we can see that the converse of Proposition 2 is not generally valid:

Example 2.

In the hyperring R defined in Example 1, the set $M=\{a,b,f\}$ is a ${\xi }_m$-part, but it is not an α-part because $\alpha \left(f\right)=\{a,b,f,g\}$, with $f\in M$, while $f\alpha g$ and $g\notin M$.

Proposition 3.

Every ${\xi }_m$-part is an m-complete part, for every $2\le m\in \mathbb{N}$.

Proof. 

It follows immediately by using $\delta =id\in {\mathbb{S}}_N$ in the definition of ${\xi }_m$-parts.  □

The following example shows that the converse of Proposition 3 is not valid. Moreover, we can see that ${\xi }_m\ne {\epsilon }_m$.

Example 3.

On the set $R=\{a,b\}$ define the following hyperoperations

$$\begin{array}{ccc}+& a& b\\ a& \left\{a\right\}& \left\{a\right\}\\ b& \left\{b\right\}& \left\{b\right\}\end{array}\begin{array}{ccc}·& a& b\\ a& \left\{a\right\}& \left\{a\right\}\\ b& \left\{a\right\}& \left\{b\right\}\end{array}$$

Then $(R,+,·)$ is a noncommutative semihyperring. Put $m=2$, hence ${\sum }_{i=1}^n{z}_i^2=\left\{a\right\}\mathrm{or}\left\{b\right\}$, for every $z_1,\dots ,z_n\in R$. Thus, ${\sum }_{i=1}^n{z}_i^2\cap \left\{a\right\}\ne \varnothing$ implies ${\sum }_{i=1}^n{z}_i^2\subseteq \left\{a\right\}$, and so $\left\{a\right\}$ is a 2-complete part of R. But, $a^2+\left(b^2+b^2\right)=\left\{a\right\}$ and so $[a^2+\left(b^2+b^2\right)]\cap \left\{a\right\}\ne \varnothing$, while $\left(b^2+a^2\right)+b^2=\left\{b\right\}⊈\left\{a\right\}$. Therefore, $\left\{a\right\}$ is not a ${\xi }_2$-part of R. Moreover, we have ${\epsilon }_2\left(a\right)=\left\{a\right\}$ and ${\xi }_2\left(a\right)=\{a,b\}$, which implies that ${\epsilon }_2\ne {\xi }_2$.

It is easy to see that Proposition 1 is valid also to characterize complete parts with respect to the $\Gamma$-relation on hyperrings. That is, a nonempty subset M is a complete part if and only if, for any $x\in M$ such that $x\Gamma y$ it follows that $y\in M$, equivalently with, for any $x\in M$ such that $x{\Gamma }^{*}y$ it follows that $y\in M$.

Example 4.

Consider the hyperring R in Example 1 and the subset $M=\{c,d\}$. It can be seen that M is a complete part and also a ${\xi }_m$-part, but is not an α-part, since $e\alpha d$, but $e\notin M$.

Comparing the definitions of the complete parts and m-complete parts, it is easy to see that a complete part of every (semi)hyperring is an m-complete part. But the converse implication is not generally true [18]. Besides, from the following example, we can state that not all ${\xi }_m$-parts are complete parts.

Example 5.

Consider the following hyperoperations on the set $R=\{a,b,c,d\}$:

$$\begin{array}{ccccc}+& a& b& c& d\\ a& \{b,c\}& \{b,d\}& \{b,d\}& \{b,d\}\\ b& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\\ c& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\\ d& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\end{array}\begin{array}{ccccc}·& a& b& c& d\\ a& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\\ b& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\\ c& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}\\ d& \{b,d\}& \{b,d\}& \{b,d\}& \{b,d\}.\end{array}$$

Then, $(R,+,·)$ is a semihyperring. We have ${\sum }_{i=1}^n{z}_i^m=\{b,d\}={\sum }_{i=1}^n{z}_{\delta \left(i\right)}^m$ for all $z_1,\dots z_n\in R$, $\delta \in {\mathbb{S}}_N$ and $2\le m\in \mathbb{N}$. Hence, $M=\{a,b,d\}$ is an m-complete part and also a ${\xi }_m$-part, but it is not a complete part of R since $b\Gamma c$, but $c\notin M$.

Example 6.

Consider the hyperring $R=\{a,b\}$ in Example 3, where $M=\left\{a\right\}$ is not a ${\xi }_2$-part, but it is a complete part of R since $\Gamma \left(a\right)=\left\{a\right\}$.

By the above mentioned examples about various type of complete parts in a hyperring, the connections between complete parts, m-complete parts, $\alpha$-parts and ${\xi }_m$-parts in hyperrings may be represented as in Figure 1.

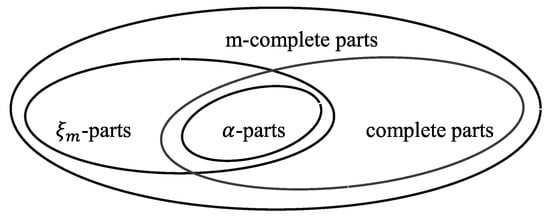
Figure 1. Generalizations of complete parts.

Theorem 1.

Let R be an m-idempotent hyperring (for $2\le m\in \mathbb{N}$) satisfying condition (2). Then a nonempty subset M of R is a ${\xi }_m$-part if and only if M is an α-part of R.

Proof. 

By Proposition 2, every $\alpha$-part is a ${\xi }_m$-part.

Now, let M be a ${\xi }_m$-part such that $M\cap {\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}\ne \varnothing$, for $n,k_i\in \mathbb{N}$, $1\le i\le n$, $1\le j\le k_i$, and arbitrary elements $z_{ij}\in R$. Since R is an m-idempotent hyperring, it follows that $z_{ij}\in z_{ij}^m$ for every $i,j$, thus ${\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}\subseteq {\sum }_{i=1}^n{\left({\prod }_{j=1}^{k_i}{z}_{ij}\right)}^m$ and

$$\sum _{i=1}^n\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\subseteq \sum _{i=1}^n{\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\right)}^m=\sum _{i=1}^n{\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right)j}\right)}^m,$$

for every $\sigma \in S_n$. Set $A_i={\prod }_{j=1}^{k_i}{z}_{ij}$ and $A_{\sigma \left(i\right)}={\prod }_{j=1}^{k_{\sigma \left(i\right)}}{z}_{{\sigma }_{\left(i\right)}\left(j\right)}$. Thus we have

$$\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\subseteq \sum _{i=1}^n{A}_i^m\mathrm{and}\sum _{i=1}^n\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\subseteq \sum _{i=1}^n{A}_{\sigma \left(i\right)}^m,$$

and by condition (2) there exist $t_i\in A_i$ (and $t_{\sigma \left(i\right)}\in A_{\sigma \left(i\right)}$) such that ${\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}\subseteq {\sum }_{i=1}^n{t}_i^m$. So $M\cap {\sum }_{i=1}^n{t}_i^m\ne \varnothing$ and we have ${\sum }_{i=1}^n{t}_{\sigma \left(i\right)}^m\subseteq M$ because M is an ${\xi }_m$-part. Hence, ${\sum }_{i=1}^n{\prod }_{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\subseteq M$, which means that M is an $\alpha$-part.  □

Now we are starting the process of finding conditions under which the ${\xi }_m$-relation is transitive. For this, first we define the following set for every element x in R and $2\le m\in \mathbb{N}$.

$${\mathcal{A}}_m\left(x\right)=\bigcup \left\{\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m|x\in \sum _{i=1}^n{z}_i^m,z_1,\dots ,z_n\in R,\sigma \in S_n,n\in \mathbb{N}\right\}.$$

Then, we obtain a different characterization of the set ${\mathcal{A}}_m\left(x\right)$.

Lemma 1.

${\mathcal{A}}_m\left(x\right)=\left\{y\in R\mid x{\xi }_{m}y\right\}$, for every $x\in R$.

Proof. 

For any arbitrary elements $x,y\in R$ such that $x{\xi }_{m}y$, there exist $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\sigma \in S_n$ such that $x\in {\sum }_{i=1}^n{z}_i^m$ and $y\in {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$. Thereby there exists $n\in \mathbb{N}$ such that $y\in {\mathcal{A}}_m\left(x\right)$, that is, $\left\{y\in R\mid y{\xi }_{m}x\right\}\subseteq {\mathcal{A}}_m\left(x\right)$. On the other hand, if $y\in {\mathcal{A}}_m\left(x\right)$, then there exists $n\in \mathbb{N}$ such that $y\in {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$ for $\sigma \in S_n$, $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $x\in {\sum }_{i=1}^n{z}_i^m$, which means that $x{\xi }_{m}y$. This completes the proof.  □

Theorem 2.

Let R be a hyperring. If ${\xi }_m$ is transitive, then ${\mathcal{A}}_m\left(x\right)={\xi }_m^{*}\left(x\right)$, for every $x\in R$.

Proof. 

If ${\xi }_m$ is transitive, then ${\xi }_m={\xi }_m^{*}$. By Lemma 1, we have $y\in {\xi }_m^{*}\left(x\right)$, equivalently with $x{\xi }_m^{*}y$ if and only if $y\in {\mathcal{A}}_m\left(x\right)$.  □

The next result states a necessary condition for the set ${\mathcal{A}}_m\left(x\right)$ to be a ${\xi }_m$-part of R.

Theorem 3.

Let R be a hyperring and $x\in R$. If ${\mathcal{A}}_m\left(x\right)={\xi }_m^{*}\left(x\right)$, then ${\mathcal{A}}_m\left(x\right)$ is a ${\xi }_m$-part of R.

Proof. 

Let $z_1,\dots ,z_n\in R$ and $\sigma \in S_n$ such that ${\sum }_{i=1}^n{z}_i^m\cap {\mathcal{A}}_m\left(x\right)\ne \varnothing$ and take $y\in {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$. Hence, there exists $t\in {\sum }_{i=1}^n{z}_i^m\cap {\mathcal{A}}_m\left(x\right)$ such that $t{\xi }_{m}y$ which implies that $t{\xi }_m^{*}y$. Then $y\in {\xi }_m^{*}\left(t\right)$. Also, $t\in {\mathcal{A}}_m\left(x\right)={\xi }_m^{*}\left(x\right)$ and thus ${\xi }_m^{*}\left(t\right)={\xi }_m^{*}\left(x\right)$. It follows that $y\in {\xi }_m^{*}\left(x\right)={\mathcal{A}}_m\left(x\right)$, implying that ${\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m\subseteq {\mathcal{A}}_m\left(x\right)$. This proves that ${\mathcal{A}}_m\left(x\right)$ is a ${\xi }_m$-part of R.  □

In the next result the transitivity of the ${\xi }_m$-relation is discussed.

Theorem 4.

Let R be hyperring and $x\in R$. If ${\mathcal{A}}_m\left(x\right)$ is a ${\xi }_m$-part, then ${\xi }_m$ is transitive.

Proof. 

Let $x,y,z\in R$ such that $x{\xi }_{m}y$ and $y{\xi }_{m}z$. Since $x\in {\mathcal{A}}_m\left(x\right)$, by Lemma 1, it follows that $y\in {\mathcal{A}}_m\left(x\right)$. And using once again Lemma 1 we obtain $z\in {\mathcal{A}}_m\left(x\right)$, implying $z{\xi }_{m}x$. Therefore, ${\xi }_m$ is transitive.  □

Summarizing the above theorems we can discuss the transitivity property of the ${\xi }_m$-relation on hyperrings by the next result.

Corollary 1.

Let R be a hyperring. Then the following statements are equivalent:

(1) 

The ${\xi }_m$-relation is transitive;

(2) 

${\xi }_m^{*}\left(x\right)={\mathcal{A}}_m\left(x\right)$, for all $x\in R$;

(3) 

The set ${\mathcal{A}}_m\left(x\right)$ is a ${\xi }_m$-part of R, for every $x\in R$.

4. ${\mathit{\xi }}_{\mathit{m}}$-Complete Hyperrings

In this section, the concept of ${\xi }_m$-complete hyperrings is introduced by meaning of the ${\xi }_m$-relation and some characterizations are provided using properties of ${\xi }_m$-parts. We present several examples that illustrate the fact that ${\xi }_m$-complete hyperrings are different from ${\epsilon }_m$-complete hyperrings and ${\alpha }_n$-complete hyperrings.

Let recall first the definition of n-complete hyperrings, ${\alpha }_n$-complete hyperrings and ${\epsilon }_m$-complete hyperrings.

For an arbitrary natural number n, a hyperring R is said to be an n-complete hyperring ([17]) if

$$\Gamma \left(\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\right)=\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij},$$

for all $k_i\in \mathbb{N}$ and $z_{i1},\dots ,z_{i{k}_i}\in R$.

R is called an ${\alpha }_n$-complete hyperring [17] if, for all $k_i\in \mathbb{N}$, $z_{i1},\dots ,z_{i{k}_i}\in R$, $\sigma \in S_n$ and ${\sigma }_i\in S_{k_i}$ with $1\le i\le n$, there is

$$\alpha \left(\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\right)=\sum _{i=1}^n{A}_{\sigma \left(i\right)},$$

where $A_i={\prod }_{j=1}^{k_i}{z}_{i{\sigma }_i\left(j\right)}$.

For any natural number m, $2\le m\in \mathbb{N}$, the hyperring R is an ${\epsilon }_m$-complete hyperring if

$${\epsilon }_m\left(\sum _{i=1}^n{z}_i^m\right)=\sum _{i=1}^n{z}_i^m,$$

for all $z_1,\dots ,z_n\in R$ and $n\in \mathbb{N}$.

Similarly, we can define the concept of ${\xi }_m$-complete hyperrings based on ${\xi }_m$-relation as follows.

Definition 3.

For any natural number m, $2\le m\in \mathbb{N}$, we say that a (semi)hyperring R is ${\xi }_m$-complete, if it satisfies the condition

$${\xi }_m\left(\sum _{i=1}^n{z}_i^m\right)=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m,$$

for any $n\in \mathbb{N}$, arbitrary elements $z_1,\dots ,z_n\in R$ and an arbitrary permutation $\sigma \in S_n$.

Example 7.

Consider the hyperring $(R,+,·)$ in Example 1. We can see that

$$\sum _{i=1}^n{z}_i^m=\{a,b\}=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^{m}and{\xi }_m\left(\{a,b\}\right)=\{a,b\},$$

for arbitrary $m,n\in \mathbb{N}$, $\sigma \in S_n$ and $z_1,\dots ,z_n\in R$. So, R is a ${\xi }_m$-complete hyperring.

Example 8.

Consider now the semihyperring $(R,+,·)$ in Example 3. Since $a^2+(b^2+b^2)=\left\{a\right\}$ and $(b^2+a^2)+b^2=\left\{b\right\}$, it follows that ${\xi }_2\left(a\right)=R$ and so

$${\xi }_2(a^2+(b^2+b^2))=R\ne \left\{b\right\}=(b^2+a^2)+b^2.$$

Therefore R is not ${\xi }_2$-complete.

Corollary 2.

Every ${\alpha }_n$-complete hyperring is a ${\xi }_m$-complete hyperring.

Proof. 

Let R be an ${\alpha }_n$-complete hyperring. For all $1\le i\le n$, take $z_{i1}=\dots =z_{i{k}_i}=z_i$ elements in R, $Id={\sigma }_i\in S_{k_i}$ the identical permutation, and $k_i=m$. Then ${\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}={\sum }_{i=1}^n{z}_i^m$ and ${\sum }_{i=1}^n{A}_{\sigma \left(i\right)}={\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$, where $A_i={\prod }_{j=1}^{k_i}{z}_{i{\sigma }_i\left(j\right)}$. Hence,

$${\xi }_m\left(\sum _{i=1}^n{z}_i^m\right)\subseteq \alpha \left(\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\right)=\sum _{i=1}^n{A}_{\sigma \left(i\right)}=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m.$$

Clearly, ${\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m\subseteq {\xi }_m\left({\sum }_{i=1}^n{z}_i^m\right)$. This completes the proof.  □

Generally, a ${\xi }_m$-complete hyperring is not an ${\alpha }_n$-complete hyperring, as illustrated by the following example.

Example 9.

Consider the hyperring R in Example 1. We know by Example 7 that R is an ${\xi }_m$-complete hyperring. Since we have $\alpha \left(a\right)=\{a,b,f,g\}$, it follows that

$$\alpha (a+a)=\alpha \left(\right\{a,b\left\}\right)=\alpha \left(a\right)\cup \alpha \left(b\right)=\{a,b,f,g\}\ne a+a.$$

Hence the hyperring R is not ${\alpha }_2$-complete.

For any m, $2\le m\in \mathbb{N}$, we say that a hyperring R is strongly m-idempotent, if $x^m=\left\{x\right\}$, for every $x\in R$. It is known [12] that ${\xi }_m=\alpha$ in any m-idempotent hyperring satisfying condition (2). Then, we can present the converse case of Corollary 2.

Theorem 5.

Any strongly m-idempotent hyperring satisfying condition (2) that is ${\xi }_m$-complete is also an ${\alpha }_n$-complete hyperring, for every $n\in \mathbb{N}$.

Proof. 

Let R be a strongly m-idempotent hyperring satisfying condition (2) and such that R is ${\xi }_m$-complete. For every $n,k_i\in \mathbb{N}$, $1\le i\le n$, $z_{i1},\dots ,z_{i{k}_i}\in R$, $\sigma \in S_n$ and ${\sigma }_i\in S_{k_i}$, let $x\in \alpha \left({\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}\right)$. This means that there exists $y\in {\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}$ such that $x\in \alpha \left(y\right)$. Since R is a strongly m-idempotent hyperring, it follows that

$$\begin{array}{c}\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\subseteq \sum _{i=1}^n{\left(\prod _{j=1}^{k_i}{z}_{ij}\right)}^m,\hfill \\ \sum _{i=1}^n\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\subseteq \sum _{i=1}^n{\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\right)}^m=\sum _{i=1}^n{\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right)j}\right)}^m.\hfill \end{array}$$

Put $A_i={\prod }_{j=1}^{k_i}{z}_{ij}$ and $A_{\sigma \left(i\right)}={\prod }_{j=1}^{k_{\sigma \left(i\right)}}{z}_{{\sigma }_{\left(i\right)}\left(j\right)}$. Then, by condition (2), there exist $t_i\in A_i$ for every $1\le i\le n$ (and $t_{\sigma \left(i\right)}\in A_{\sigma \left(i\right)}$ for $\sigma \in S_n$) such that

$$\sum _{i=1}^n\left(\prod _{j=1}^{k_i}{z}_{ij}\right)\subseteq \sum _{i=1}^n{t}_i^{m}and\sum _{i=1}^n\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\right)\subseteq \sum _{i=1}^n{t}_{\sigma \left(i\right)}^m.$$

Hence,

$$\begin{array}{cc}\hfill \alpha \left(y\right)& \subseteq \alpha \left(\sum _{i=1}^n\prod _{j=1}^{k_i}{z}_{ij}\right)\subseteq \alpha \left(\sum _{i=1}^n{t}_i^m\right)=\sum _{i=1}^n{t}_{\sigma \left(i\right)}^m\hfill \\ & \subseteq \sum _{i=1}^n{\left(\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}\right)}^m=\sum _{i=1}^n\prod _{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}.\hfill \end{array}$$

Therefore, $\alpha \left({\sum }_{i=1}^n{\prod }_{j=1}^{k_i}{z}_{ij}\right)\subseteq {\sum }_{i=1}^n{\prod }_{j=1}^{k_{\sigma \left(i\right)}}{z}_{\sigma \left(i\right){\sigma }_{\sigma \left(i\right)}\left(j\right)}$. This concludes that R is an ${\alpha }_n$-complete hyperring.  □

In the following, we discuss the relationship between ${\xi }_m$-complete hyperrings and ${\epsilon }_m$-complete hyperrings.

Corollary 3.

Every ${\xi }_m$-complete hyperring is an ${\epsilon }_m$-complete hyperring.

Proof. 

The proof follows immediately from the definition of a ${\xi }_m$-complete hyperring, taking the permutation $\sigma =Id\in {\mathbb{S}}_n$.  □

Clearly if R is a commutative hyperring, then we have ${\xi }_m={\epsilon }_m$ and so any ${\epsilon }_m$-complete hyperring is ${\xi }_m$-complete. But the converse of Corollary 3 is not valid in general, as shown in the following example.

Example 10.

Consider the hyperring R in Example 3. By Example 8, we know that R is not a ${\xi }_2$-complete hyperring. Besides we have ${\sum }_{i=1}^n{z}_i^2=\left\{c\right\}$ or $\left\{f\right\}$ or $\left\{d\right\}$ or $\{b,e\}$, for all $z_i\in R$ and $1\le i\le n$. On the other side, one founds that ${\epsilon }_2\left(c\right)=\left\{c\right\}$, ${\epsilon }_2\left(f\right)=\left\{f\right\}$, ${\epsilon }_2\left(d\right)=\left\{d\right\}$ and ${\epsilon }_2\left(\{b,e\}\right)=\{b,e\}$. Hence, ${\epsilon }_2\left({\sum }_{i=1}^n{z}_i^2\right)={\sum }_{i=1}^n{z}_i^2$, meaning that R is an ${\epsilon }_2$-complete hyperring.

We conclude this study with a characterization of ${\xi }_m$-complete hyperrings based on the notion of ${\xi }_m$-parts.

Theorem 6.

A hyperring R is ${\xi }_m$-complete if and only if ${\xi }_m\left(x\right)={\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$ for all $x\in {\sum }_{i=1}^n{z}_i^m$ where $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\sigma \in {\mathbb{S}}_n$.

Proof. 

Let R be a ${\xi }_m$-complete hyperring and take an arbitrary $x\in {\sum }_{i=1}^n{z}_i^m$. Then

$${\xi }_m\left(x\right)\subseteq {\xi }_m\left(\sum _{i=1}^n{z}_i^m\right)=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m.$$

Moreover, if $y\in {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$, then $x{\xi }_{m}y$, because $x\in {\sum }_{i=1}^n{z}_i^m$. Hence, $y\in {\xi }_m\left(x\right)$ and so ${\xi }_m\left(x\right)={\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$.

Conversely, by hypothesis we have

$${\xi }_m\left(\sum _{i=1}^n{z}_i^m\right)=\bigcup _{x\in {\sum }_{i=1}^n{z}_i^m}{\xi }_m\left(x\right)=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m.$$

Therefore, R is a ${\xi }_m$-complete hyperring.  □

Theorem 7.

Let R be a ${\xi }_m$-complete hyperring for any m, $2\le m\in \mathbb{N}$. Then ${\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$ is a ${\xi }_m$-part of R, for every $n\in \mathbb{N}$, $z_1,\dots ,z_n\in R$ and $\sigma \in {\mathbb{S}}_n$.

Proof. 

For $k\in \mathbb{N}$ and $x_1,\dots ,x_k\in R$, let ${\sum }_{i=1}^k{x}_i^m\cap {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m\ne \varnothing$. Then there exists $y\in {\sum }_{i=1}^k{x}_i^m\cap {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$. For every $u\in {\sum }_{i=1}^k{x}_{\delta \left(i\right)}^m$, with $\delta \in {\mathbb{S}}_k$, we have $u{\xi }_{m}y$. Hence,

$$u\in {\xi }_m\left(y\right)={\xi }_m\left(\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m\right)=\sum _{i=1}^n{z}_{\sigma \left(i\right)}^m,$$

and there by ${\sum }_{i=1}^k{x}_{\sigma \left(i\right)}^m\subseteq {\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$ which implies that ${\sum }_{i=1}^n{z}_{\sigma \left(i\right)}^m$ is a ${\xi }_m$-part of R.  □

5. Conclusions

Ten years after the introduction of the fundamental relation ${\alpha }^{*}$ in [7] on general hyperrings, Norouzi and Cristea [11] defined a new class of m-idempotent hyperrings satisfying a certain condition, where ${\alpha }^{*}$ is no longer the smallest strongly regular relation such that the associated quotient structure is a commutative ring. For this reason, they introduced the ${\xi }_m^{*}$-relation, as the transitive closure of the ${\xi }_m$-relation, as a fundamental relation on such hyperrings. Since ${\xi }_m$ is not generally transitive, it is useful to find conditions under which the transitivity property holds, too. In this respect, the well-known tool of complete parts has been studied in this paper, but in a general form. After defining the ${\xi }_m$-parts and presenting the relationships with complete parts, m-complete parts, and $\alpha$-parts, the study has focused on finding conditions when ${\xi }_m$ is transitive. The second part of the article has dealt with the study of ${\xi }_m$-complete hyperrings and their connections with ${\alpha }_n$- and ${\epsilon }_m$-complete hyperrings. The results have been supported by illustrative examples.