A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems

Abstract

The main objective of this article is to propose a new method that would extend Popov’s extragradient method by changing two natural projections with two convex optimization problems. We also show the weak convergence of our designed method by taking mild assumptions on a cost bifunction. The method is evaluating only one value of the bifunction per iteration and it is uses an explicit formula for identifying the appropriate stepsize parameter for each iteration. The variable stepsize is going to be effective for enhancing iterative algorithm performance. The variable stepsize is updating for each iteration based on the previous iterations. After numerical examples, we conclude that the effect of the inertial term and variable stepsize has a significant improvement over the processing time and number of iterations.

1. Introduction

Let C to be a nonempty convex, closed subset of a Hilbert space $\mathbb{E}$ and $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ be a bifunction with $f(u,u)=0$ for each $u\in C.$ The equilibrium problem for f upon C is defined as follows:

$$\mathrm{Find}{p}^{*}\in C\mathrm{such}\mathrm{that}f(p^{*},y)\ge 0,\forall y\in C.$$

(1)

The equilibrium problem ($EP$) has many mathematical problems as a particular case, for example, the fixed point problems, complementarity problems, the variational inequality problems ($VIP$), the minimization problems, Nash equilibrium of noncooperative games, saddle point problems and problem of vector minimization (see [1,2,3,4]). The unique formulation of an equilibrium problem was specifically defined in 1992 by Muu and Oettli [5] and further developed by Blum and Oettli [1]. An equilibrium problem is also known as the Ky Fan inequality problem. Fan [6] presents a review and gives specific conditions on a bifunction for the existence of an equilibrium point. Many researchers have provided and generalized many results corresponding to the existence of a solution for the equilibrium problem (see [7,8,9,10]). A considerable number of methods are the earliest set up over the last few years concentrating on the different equilibrium problem classes and other particular forms of an equilibrium problem in abstract spaces (see [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]).

The Korpelevich and Antipin’s extragradient method [30,31] are efficient two-step methods. Flam [12,20] employed the auxiliary problem principle to set up the extragradient method for the monotone equilibrium problems. The consideration on the extragradient method is to figure out two natural projections on C to achieve the next iteration. If the computing of a projection on a feasible set C is hard to compute, it is a challenge to solve two minimal distance problems for the next iteration, which may have an effect on method${}^{\prime }$s performance and efficiency. In order to overcome it, Censor initiated a subgradient extragradient method [32] where the second projection is replaced by a half-plane projection that can be computed effectively. Iterative sequences set up with the above-mentioned extragradient-like methods need to make use of a certain stepsize constant based on the Lipschitz-type constants of a cost bifunction. The prior knowledge about these constant imposes some restrictions on developing an iterative sequence because these Lipschitz-type constants are normally not known or hard to compute.

In 2016, Lyashko et al. [33] developed an extragradient method for solving pseudomonotone equilibrium problems in a real Hilbert space. It is required to solve two optimization problems on a closed convex set for each next iteration, with a reasonable fixed stepsize depends upon on the Lipschitz-type constants. The superiority of the Lyashko et al. [33] method compared to the Tran et al. [20] extragradient method is that the value of the bifunction f is to determine only once for each iteration. Inertial-type methods are based on the discrete variant of a second-order dissipative dynamical system. In order to handle numerically smooth convex minimization problem, Polyak [34] proposed an iterative scheme that would require inertial extrapolation as a boost ingredient to improve the convergence rate of the iterative sequence. The inertial method is commonly a two-step iterative scheme and the next iteration is computed by use of previous two iterations and may be pointed out to as a method of pacing up the iterative sequence (see [34,35]). In the case of equilibrium problems, Moudafi established the second-order differential proximal method [36]. These inertial methods are employed to accelerate the iterative process for the desired solution. Numerical studies indicate that inertial effects generally enhance the performance of the method in terms of the number of iterations and execution time in this context. There are many methods established for the different classes of variational inequality problems (for more details see [37,38,39,40,41]).

In this study, we considered Lyashko et al. [33] and Liu et al. [42] extragradient methods and present its improvement by employing an inertial scheme. We also improved the stepsize to its second step. The stepsize was not fixed in our proposed method, but the stepsize was set up by an explicit formula based on some previous iterations. We formulated a weak convergence theorem for our proposed method for dealing with the problems of equilibriums involving pseudomonotone bifunction within specific conditions. We also examined how our results are linked to variational inequality problems. Apart from this, we considered the well-known Nash–Cournot equilibrium model as a test problem to support the validity of our results. Some applications for variational inequality problems were considered and other numerical examples were explained to back the appropriateness of our designed results.

The rest of the article is set up as follows: In Section 2 we give a few definitions and significant results to be utilized in this paper. Section 3 includes our first algorithm involving pseudomonotone bifunction, and gives the weak convergence result. Section 4 illustrates some application of our results in variational inequality problems. Section 5 sets out numerical examinations to describe numerical performance.

2. Preliminaries

In this part we cover some relevant lemmas, definitions and other notions that will be employed throughout the convergence analysis and numerical part. The notion $⟨.,.⟩$ and $\parallel .\parallel$ presents for the inner product and norm on the Hilbert space $\mathbb{E}$. Let $G:\mathbb{E}\to \mathbb{E}$ be a well-defined operator and $VI(G,C)$ is the solution set of a variational inequality problem corresponding operator G over the set C. Moreover $EP(f,C)$ stands for the solution set of an equilibrium problem over the set C and $p^{*}$ is any arbitrary element of $EP(f,C)$ or $VI(G,C).$

Let $g:C\to \mathbb{R}$ be a convex function with subdifferential of g at $u\in C$ defined as:

$$\partial g\left(u\right)=\{z\in \mathbb{E}:g(v)-g(u)\ge ⟨z,v-u⟩,\forall v\in C\}.$$

A normal cone of C at $u\in C$ is given as

$$N_C\left(u\right)=\{z\in \mathbb{E}:⟨z,v-u⟩\le 0,\forall v\in C\}.$$

We consider various conceptions of a bifunction monotonicity (see [1,43] for details).

Definition 1.

The bifunction $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ on C for $\gamma >0$ is

(i) 

strongly monotone if $f(u,v)+f(v,u)\le {-\gamma \parallel u-v\parallel }^2,\forall u,v\in C;$

(ii) 

monotone if $f(u,v)+f(v,u)\le 0,\forall u,v\in C;$

(iii) 

strongly pseudomonotone if $f(u,v)\ge 0⟹f(v,u)\le {-\gamma \parallel u-v\parallel }^2,\forall u,v\in C;$

(iv) 

pseudomonotone if $f(u,v)\ge 0⟹f(v,u)\le 0,\forall u,v\in C;$

(v) 

satisfying the Lipschitz-type condition on C if there are two real numbers $c_1,c_2>0$ such that

$$f(u,w)\le f(u,v)+f(v,w)+c_1{\parallel u-v\parallel }^2+c_2{\parallel v-w\parallel }^2,\forall u,v,w\in C,$$

holds.

Definition 2.

[44] A metric projection $P_C\left(u\right)$ of u onto a closed, convex subset C of $\mathbb{E}$ is defined as follows:

$$P_C\left(u\right)=\underset{v\in C}{argmin}\{\parallel v-u\parallel \}$$

Lemma 1.

[45] Let $P_C:\mathbb{E}\to C$ be metric projection from $\mathbb{E}$ upon $C.$ Thus

(i) 

For each $u\in C,$ $v\in \mathbb{E},$

$$\parallel u-P_C{\left(v\right)\parallel }^2+\parallel P_C{\left(v\right)-v\parallel }^2\le {\parallel u-v\parallel }^2.$$

(ii) 

$w=P_C\left(u\right)$ if and only if

$$⟨u-w,v-w⟩\le 0,\forall v\in C.$$

This portion concludes with a few crucial lemmas which are advantageous in investigating the convergence of our proposed results.

Lemma 2.

[46] Let C be a nonempty, closed and convex subset of a real Hilbert space $\mathbb{E}$ and $h:C\to \mathbb{R}$ be a convex, subdifferentiable and lower semi-continuous function on $C.$ Moreover, $x\in C$ is a minimizer of a function h if and only if $0\in \partial h\left(x\right)+N_C\left(x\right)$ where $\partial h\left(x\right)$ and $N_C\left(x\right)$ stands for the subdifferential of h at x and the normal cone of C at x respectively.

Lemma 3

([47], Page 31). For every $a,b\in \mathbb{E}$ and $\xi \in \mathbb{R}$ the following relation is true:

$${\parallel \xi a+(1-\xi )b\parallel }^2={\xi \parallel a\parallel }^2+{(1-\xi )\parallel b\parallel }^2-\xi (1-\xi ){\parallel a-b\parallel }^2.$$

Lemma 4.

[48] If ${\alpha }_n$, ${\beta }_n$ and ${\gamma }_n$ are sequences in $[0,+\infty ),$

$${\alpha }_{n+1}\le {\alpha }_n+{\beta }_n({\alpha }_n-{\alpha }_{n-1})+{\gamma }_n,\forall n\ge 1,with\sum _{n=1}^{+\infty }{\gamma }_n<+\infty$$

holds with $\beta >0$ such that $0\le {\beta }_n\le \beta <1,$ $\forall n\in \mathbb{N}.$ The following items are true.

$\left(i\right)$

${\displaystyle \sum _{n=1}^{+\infty }{[{\alpha }_n-{\alpha }_{n-1}]}_{+}<+\infty ,}$ with ${\left[p\right]}_{+}:=max\{p,0\};$

$\left(ii\right)$

${lim}_{n\to +\infty }{\alpha }_n={\alpha }^{*}\in [0,\infty ).$

Lemma 5.

[49] Let $\left\{{\eta }_n\right\}$ be a sequence in $\mathbb{E}$ and $C\subset \mathbb{E}$ such that

$\left(i\right)$

For each $\eta \in C,$ ${lim}_{n\to \infty }\parallel {\eta }_n-\eta \parallel$ exists;

$\left(ii\right)$

All sequentially weak cluster point of $\left\{{\eta }_n\right\}$ lies in C;

Then $\left\{{\eta }_n\right\}$ weakly converges to a element of $C.$

Lemma 6.

[50] Assume $\left\{a_n\right\},\left\{b_n\right\}$ are real sequences such that $a_n\le b_n$ $\forall n\in \mathbb{N}.$ Take $\varrho ,\sigma \in (0,1)$ and $\mu \in (0,\sigma ).$ Then there is a sequence ${\lambda }_n$ in a manner that ${\lambda }_n{a}_n\le \mu b_n$ and ${\lambda }_n\in (\varrho \mu ,\sigma ).$

Due to Lipschitz-like condition on a bifunction f through above lemma, we have the following inequality.

Corollary 1.

Assume that bifunction f satisfy the Lipschitz-type condition on C through positive constants $c_1$ and $c_2.$ Let $\varrho \in (0,1),$ $\sigma <min\left\{\frac{1-3\theta }{{(1-\theta )}^2+4c_1(\theta +{\theta }^2)},\frac{1}{2c_2+4c_1(1+\theta )}\right\}$ where $\theta \in [0,\frac{1}{3})$ and $\mu \in (0,\sigma ).$ Then there exits a positive real number λ such that

$$\lambda \left(f(u,w)-f(u,v)-c_1{\parallel u-v\parallel }^2-c_2{\parallel v-w\parallel }^2\right)\le \mu f(v,w)$$

and $\varrho \mu <\lambda <\sigma$ where $u,v,w\in C.$

Assumption 1.

Let a bifunction $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ satisfies

$f_1.$

$f(v,v)=0$ for all $v\in C$ and f is pseudomonotone on feasible set $C.$

$f_2.$

f satisfy the Lipschitz-type condition on $\mathbb{E}$ with constants $c_1$ and $c_2.$

$f_3.$

$\underset{n\to \infty }{lim\; sup}f(x_n,v)\le f(x^{*},v)$ for all $v\in C$ and $\left\{x_n\right\}\subset C$ satisfy $x_n\rightharpoonup x^{*}.$

$f_4.$

$f(u,.)$ need to be convex and subdifferentiable over $\mathbb{E}$ for all fixed $u\in \mathbb{E}.$

Since $f(u,.)$ is convex and subdifferentiable on $\mathbb{E}$ for each fixed $u\in \mathbb{E}$ and subdifferential of $f(u,.)$ at $x\in \mathbb{E}$ defined as:

$${\partial }_{2}f(u,.)\left(x\right)={\partial }_{2}f(u,x)=\{z\in \mathbb{E}:f(u,v)-f(u,x)\ge ⟨z,v-x⟩,\forall v\in \mathbb{E}\}.$$

3. An Algorithm and Its Convergence Analysis

We develop a method and provide a weak convergence result for it. We consider bifunction f that satisfies the conditions of Assumption 1 and $EP(f,C)\ne \varnothing .$ The detailed method is written below.

Lemma 7.

If a sequence $\left\{u_n\right\}$ is set up by Algorithm 1. Then the following relationship holds.

$$\mu {\lambda }_{n}f(v_n,y)-\mu {\lambda }_{n}f(v_n,u_{n+1})\ge ⟨w_n-u_{n+1},y-u_{n+1}⟩,\forall y\in E_n.$$

Proof. 

By definition of $u_{n+1}$ we have

$$u_{n+1}=\underset{y\in E_n}{argmin}\{\mu {\lambda }_{n}f(v_n,y)+\frac{1}{2}\parallel w_n-y{\parallel }^2\}.$$

By using Lemma 2, we obtain

$$0\in {\partial }_2\left\{\mu {\lambda }_{n}f(v_n,y)+\frac{1}{2}{\parallel w_n-y\parallel }^2\right\}\left(u_{n+1}\right)+N_{E_n}\left(u_{n+1}\right).$$

From the above expression there is a $\omega \in {\partial }_{2}f(v_n,u_{n+1})$ and $\overline{\omega }\in N_{E_n}\left(u_{n+1}\right)$ such that

$$\mu {\lambda }_n\omega +u_{n+1}-w_n+\overline{\omega }=0.$$

Thus, we have

$$⟨w_n-u_{n+1},y-u_{n+1}⟩=\mu {\lambda }_n⟨\omega ,y-u_{n+1}⟩+⟨\overline{\omega },y-u_{n+1}⟩,\forall y\in E_n.$$

Since $\overline{\omega }\in N_{E_n}\left(u_{n+1}\right)$ then $⟨\overline{\omega },y-u_{n+1}⟩\le 0,$ for all $y\in E_n.$ Thus, we have

$$\mu {\lambda }_n⟨\omega ,y-u_{n+1}⟩\ge ⟨w_n-u_{n+1},y-u_{n+1}⟩,\forall y\in E_n.$$

(2)

Since $\omega \in {\partial }_{2}f(v_n,u_{n+1})$ we obtain

$$f(v_n,y)-f(v_n,u_{n+1})\ge ⟨\omega ,y-u_{n+1}⟩,\forall y\in \mathbb{E}.$$

(3)

Combining the expressions of Equations (2) and (3) we get

$$\mu {\lambda }_{n}f(v_n,y)-\mu {\lambda }_{n}f(v_n,u_{n+1})\ge ⟨w_n-u_{n+1},y-u_{n+1}⟩,\forall y\in E_n.$$

□

Lemma 8.

Let sequence $\left\{v_n\right\}$ be generated by Algorithm 1. Then the following inequality holds.

$${\lambda }_{n+1}f(v_n,y)-{\lambda }_{n+1}f(v_n,v_{n+1})\ge ⟨w_{n+1}-v_{n+1},y-v_{n+1}⟩,\forall y\in C.$$

Proof. 

By definition of $v_{n+1},$ we have

$$0\in {\partial }_2\left\{{\lambda }_{n+1}f(v_n,y)+\frac{1}{2}{\parallel w_{n+1}-y\parallel }^2\right\}\left(v_{n+1}\right)+N_C\left(v_{n+1}\right).$$

Thus, there is a $\omega \in {\partial }_{2}f(v_n,v_{n+1})$ and $\overline{\omega }\in N_C\left(v_{n+1}\right)$ such that

$${\lambda }_{n+1}\omega +v_{n+1}-w_{n+1}+\overline{\omega }=0.$$

The above expression implies that

$$⟨w_{n+1}-v_{n+1},y-v_{n+1}⟩={\lambda }_{n+1}⟨\omega ,y-v_{n+1}⟩+⟨\overline{\omega },y-v_{n+1}⟩,\forall y\in C.$$

Since $\overline{\omega }\in N_C\left(v_{n+1}\right)$ then $⟨\overline{\omega },y-v_{n+1}⟩\le 0,$ for all $y\in C.$ This implies that

$${\lambda }_{n+1}⟨\omega ,y-v_{n+1}⟩\ge ⟨w_{n+1}-v_{n+1},y-v_{n+1}⟩,\forall y\in C.$$

(4)

By $\omega \in {\partial }_{2}f(v_n,v_{n+1}),$ we can obtain

$$f(v_n,y)-f(v_n,v_{n+1})\ge ⟨\omega ,y-v_{n+1}⟩,\forall y\in \mathbb{E}.$$

(5)

Combining the expressions in Equations (4) and (5) we get

$${\lambda }_{n+1}f(v_n,y)-{\lambda }_{n+1}f(v_n,v_{n+1})\ge ⟨w_{n+1}-v_{n+1},y-v_{n+1}⟩,\forall y\in C.$$

□

Algorithm 1 (The Modified Popov’s subgradient extragradient method for pseudomonotone $EP$)

Initialization: Choose $u_{-1},v_{-1},u_0,v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{\frac{1-3\theta }{{(1-\theta )}^2+4c_1(\theta +{\theta }^2)},\frac{1}{2c_2+4c_1(1+\theta )}\right\}$ for a nondecreasing sequence ${\theta }_n$ such that $0\le {\theta }_n\le \theta <\frac{1}{3}$ and ${\lambda }_0>0.$ Iterative steps: Let $u_{n-1},v_{n-1},u_n$ and $v_n$ are known for $n\ge 0.$ Construct a half-space $$E_n=\{z\in \mathbb{E}:⟨w_n-{\lambda }_n{\omega }_{n-1}-v_n,z-v_n⟩\le 0\},$$ where ${\omega }_{n-1}\in {\partial }_{2}f(v_{n-1},v_n)$ and $w_n=u_n+{\theta }_n(u_n-u_{n-1}).$ Step 1: Compute $$u_{n+1}=\underset{y\in E_n}{argmin}\{\mu {\lambda }_{n}f(v_n,y)+\frac{1}{2}\parallel w_n-y{\parallel }^2\}.$$ Step 2: Revised the stepsize as follows $${\lambda }_{n+1}=min\left\{\sigma ,\frac{\mu f(v_n,u_{n+1})}{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)-c_1\parallel v_{n-1}-v_n{\parallel }^2-c_2{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}$$ (6) and compute $$v_{n+1}=\underset{y\in C}{argmin}\{{\lambda }_{n+1}f(v_n,y)+\frac{1}{2}\parallel w_{n+1}-y{\parallel }^2\},$$ where $w_{n+1}=u_{n+1}+{\theta }_{n+1}(u_{n+1}-u_n).$ Step 3: If $v_n=v_{n-1}$ and $u_{n+1}=w_n$, then stop. Else, take $n:=n+1$ and return back to Iterative steps.

Lemma 9.

Let $\left\{u_n\right\}$ and $\left\{v_n\right\}$ are sequences generated by Algorithm 1. Then the following inequality is true.

$${\lambda }_n\left\{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)\right\}\ge ⟨w_n-v_n,u_{n+1}-v_n⟩.$$

Proof. 

Since $u_{n+1}\in E_n$ then by the definition of $E_n$ gives that

$$⟨w_n-{\lambda }_n{\omega }_{n-1}-v_n,u_{n+1}-v_n⟩\le 0.$$

The above implies that

$${\lambda }_n⟨{\omega }_{n-1},u_{n+1}-v_n⟩\ge ⟨w_n-v_n,u_{n+1}-v_n⟩.$$

(7)

By ${\omega }_{n-1}\in \partial f(v_{n-1},v_n)$ with $y=u_{n+1},$ we reach the following

$$f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)\ge ⟨{\omega }_{n-1},u_{n+1}-v_n⟩,\forall y\in \mathbb{E}.$$

(8)

By combining Equations (7) and (8), we obtain

$${\lambda }_n\left\{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)\right\}\ge ⟨w_n-v_n,u_{n+1}-v_n⟩.$$

□

Lemma 10.

If $u_{n+1}=w_n$ and $v_n=v_{n-1}$ in Algorithm 1. Then, $v_n$ is the solution of Equation (1).

Proof. 

Setting $u_{n+1}=w_n$ and $v_n=v_{n-1}$ in Lemma 9, we get

$${\lambda }_{n}f(v_n,u_{n+1})\ge 0.$$

(9)

By the means of $u_{n+1}=w_n$ in Lemma 7, we get

$$\mu {\lambda }_{n}f(v_n,y)\ge \mu {\lambda }_{n}f(v_n,u_{n+1})\ge 0,\forall y\in E_n.$$

(10)

Since $\mu \in (0,1)$ and ${\lambda }_n\in (0,\infty )$ then $f(v_n,y)>0,$ for all $y\in C\subset E_n.$□

Remark 1.

(i). If $u_{n+1}=v_n=w_n$ in Algorithm 1, then $v_n\in EP(f,C).$ It is obvious from Lemma 7.

(ii). If $w_{n+1}=v_{n+1}=v_n$ in Algorithm 1, then $v_n\in EP(f,C).$ It is obvious from Lemma 8.

Lemma 11.

Let a bifunction $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ is satisfying the assumptions ($f_1$–$f_4$). Thus, for each $p^{*}\in EP(f,C)\ne \varnothing ,$ we have

$$\begin{array}{cc}\parallel u_{n+1}-p^{*}{\parallel }^2\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-{\lambda }_{n+1})\parallel u_{n+1}-w_n{\parallel }^2+4c_1{\lambda }_{n+1}{\lambda }_n{\parallel w_n-v_{n-1}\parallel }^2\hfill \\ \hfill & -{\lambda }_{n+1}(1-4c_1{\lambda }_n)\parallel w_n-v_n{\parallel }^2-{\lambda }_{n+1}(1-2c_2{\lambda }_n){\parallel u_{n+1}-v_n\parallel }^2.\hfill \end{array}$$

Proof. 

By substituting $y=p^{*}$ into Lemma 7, we get

$$\mu {\lambda }_{n}f(v_n,p^{*})-\mu {\lambda }_{n}f(v_n,u_{n+1})\ge ⟨w_n-u_{n+1},p^{*}-u_{n+1}⟩,\forall y\in E_n.$$

(11)

By make use of $p^{*}\in EP(f,C)$ implies that $f(p^{*},v_n)\ge 0$. Due to the pseudomonotonicity of a bifunction f we get $f(v_n,p^{*})\le 0.$ Therefore, from Equation (11) we get

$$⟨w_n-u_{n+1},u_{n+1}-p^{*}⟩\ge \mu {\lambda }_{n}f(v_n,u_{n+1}).$$

(12)

Corollary 1 implies that ${\lambda }_{n+1}$ in Equation (6) is well-defined and

$$\begin{array}{cc}\hfill & \mu f(v_n,u_{n+1})\hfill \\ \hfill & \ge {\lambda }_{n+1}\left(f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)-c_1\parallel v_{n-1}-v_n{\parallel }^2-c_2{\parallel v_n-u_{n+1}\parallel }^2\right).\hfill \end{array}$$

(13)

The expressions in Equations (12) and (13) imply that

$$\begin{array}{cc}⟨w_n-u_{n+1},u_{n+1}-p^{*}⟩\ge \hfill & {\lambda }_{n+1}[{\lambda }_n\left\{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)\right\}\hfill \\ \hfill & -c_1{\lambda }_n\parallel v_{n-1}-v_n{\parallel }^2-c_2{\lambda }_n{\parallel u_{n+1}-v_n\parallel }^2].\hfill \end{array}$$

(14)

Since $u_{n+1}\in E_n$ and using Lemma 9, we have

$${\lambda }_n\left\{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)\right\}\ge ⟨w_n-v_n,u_{n+1}-v_n⟩.$$

(15)

Combining the expressions in Equations (14) and (15) we get

$$\begin{array}{cc}⟨w_n-u_{n+1},u_{n+1}-p^{*}⟩\hfill & \ge {\lambda }_{n+1}[⟨w_n-v_n,u_{n+1}-v_n⟩\hfill \\ \hfill & -c_1{\lambda }_n\parallel v_{n-1}-v_n{\parallel }^2-c_2{\lambda }_n{\parallel u_{n+1}-v_n\parallel }^2].\hfill \end{array}$$

(16)

By vector algebra we have the following facts:

$$2⟨w_n-u_{n+1},u_{n+1}-p^{*}⟩=\parallel w_n-p^{*}{\parallel }^2-\parallel u_{n+1}-w_n{\parallel }^2-{\parallel u_{n+1}-p^{*}\parallel }^2.$$

$$2⟨w_n-v_n,u_{n+1}-v_n⟩=\parallel w_n-v_n{\parallel }^2+\parallel u_{n+1}-v_n{\parallel }^2-{\parallel w_n-u_{n+1}\parallel }^2.$$

From the above last two inequalities and Equation (16) we obtain

$$\begin{array}{cc}\parallel u_{n+1}-p^{*}{\parallel }^2\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-{\lambda }_{n+1})\parallel u_{n+1}-w_n{\parallel }^2-{\lambda }_{n+1}(1-2c_2{\lambda }_n){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & -{\lambda }_{n+1}\parallel w_n-v_n{\parallel }^2+{\lambda }_{n+1}\left(2c_1{\lambda }_n\right){\parallel v_{n-1}-v_n\parallel }^2\hfill \end{array}$$

By triangle inequality and elementary algebra gives the following inequality

$$\parallel v_{n-1}-v_n{\parallel }^2\le {\left(\parallel v_{n-1}-w_n\parallel +\parallel w_n-v_n\parallel \right)}^2\le 2\parallel v_{n-1}-w_n{\parallel }^2+2{\parallel w_n-v_n\parallel }^2.$$

From the above two inequalities we have the desired result

$$\begin{array}{cc}\parallel u_{n+1}-p^{*}{\parallel }^2\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-{\lambda }_{n+1})\parallel u_{n+1}-w_n{\parallel }^2+4c_1{\lambda }_n{\lambda }_{n+1}{\parallel w_n-v_{n-1}\parallel }^2\hfill \\ \hfill & -{\lambda }_{n+1}(1-4c_1{\lambda }_n)\parallel w_n-v_n{\parallel }^2-{\lambda }_{n+1}(1-2c_2{\lambda }_n){\parallel u_{n+1}-v_n\parallel }^2.\hfill \end{array}$$

□

Theorem 1.

Suppose a bifunction $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ is satisfying the Assumption 1. Then for all $p^{*}\in EP(f,C)\ne \varnothing ,$ the sequences $\left\{w_n\right\},$ $\left\{u_n\right\}$ and $\left\{v_n\right\}$ are generated by Algorithm 1 weakly converge to $p^{*}\in EP(f,C).$

Proof. 

From Lemma 11 we have

$$\begin{array}{cc}\parallel u_{n+1}-p^{*}{\parallel }^2\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-{\lambda }_{n+1})\parallel u_{n+1}-w_n{\parallel }^2+4c_1{\lambda }_n{\lambda }_{n+1}{\parallel w_n-v_{n-1}\parallel }^2\hfill \\ \hfill & -{\lambda }_{n+1}(1-4c_1{\lambda }_n)\parallel w_n-v_n{\parallel }^2-{\lambda }_{n+1}(1-2c_2{\lambda }_n){\parallel u_{n+1}-v_n\parallel }^2.\hfill \end{array}$$

(17)

By definition of $w_n$ in the Algorithm 1 we may write

$$\begin{array}{cc}\parallel w_n-v_{n-1}{\parallel }^2\hfill & =\parallel u_n+{\theta }_n(u_n-u_{n-1})-v_{n-1}{\parallel }^2\hfill \\ \hfill & =\parallel (1+{\theta }_n)(u_n-v_{n-1})-{\theta }_n(u_{n-1}-v_{n-1}){\parallel }^2\hfill \\ \hfill & =(1+{\theta }_n)\parallel u_n-v_{n-1}{\parallel }^2-{\theta }_n\parallel u_{n-1}-v_{n-1}{\parallel }^2+{\theta }_n(1+{\theta }_n){\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & \le (1+\theta )\parallel u_n-v_{n-1}{\parallel }^2+\theta (1+\theta ){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(18)

Adding the value $4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2$ on both sides of expression in Equation (17) and for each $n\ge 1,$ we obtain

$$\begin{array}{cc}\hfill & \parallel u_{n+1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-\sigma )\parallel u_{n+1}-w_n{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & +4c_1\sigma {\lambda }_n\left[(1+\theta )\parallel u_n-v_{n-1}{\parallel }^2+\theta (1+\theta ){\parallel u_n-u_{n-1}\parallel }^2\right]\hfill \\ \hfill & -{\lambda }_{n+1}(1-4c_1\sigma )\parallel w_n-v_n{\parallel }^2-{\lambda }_{n+1}(1-2c_2\sigma ){\parallel u_{n+1}-v_n\parallel }^2\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-\sigma )\parallel u_{n+1}-w_n{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2\hfill \\ \hfill & +4c_1\sigma (\theta +{\theta }^2)\parallel u_n-u_{n-1}{\parallel }^2-{\lambda }_{n+1}(1-4c_1\sigma ){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & -{\lambda }_{n+1}(1-2c_2\sigma -4c_1\sigma (1+\theta )){\parallel u_{n+1}-v_n\parallel }^2\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-\sigma )\parallel u_{n+1}-w_n{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2\hfill \\ \hfill & +4c_1\sigma (\theta +{\theta }^2){\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & -\frac{{\lambda }_{n+1}}{2}(1-2c_2\sigma -4c_1\sigma (1+\theta ))\left[2\parallel u_{n+1}-v_n{\parallel }^2+2{\parallel w_n-v_n\parallel }^2\right]\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-\sigma )\parallel u_{n+1}-w_n{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2\hfill \\ \hfill & +4c_1\sigma (\theta +{\theta }^2){\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & -\frac{{\lambda }_{n+1}}{2}(1-2c_2\sigma -4c_1\sigma (1+\theta )){\parallel u_{n+1}-w_n\parallel }^2.\hfill \end{array}$$

(22)

By Algorithm 1, $0<{\lambda }_n\le \sigma <\frac{1}{2c_2+4c_1(1+\theta )}$ and the above inequality ensures

$$\begin{array}{cc}\hfill & \parallel u_{n+1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & \le \parallel w_n-p^{*}{\parallel }^2-(1-\sigma )\parallel u_{n+1}-w_n{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta )\parallel u_n-v_{n-1}{\parallel }^2+4c_1\sigma (\theta +{\theta }^2){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(23)

From definition of $w_n$ in Algorithm 1 we obtain

$$\begin{array}{cc}\parallel w_n-p^{*}{\parallel }^2\hfill & =\parallel u_n+{\theta }_n(u_n-u_{n-1})-p^{*}{\parallel }^2\hfill \\ \hfill & =\parallel (1+{\theta }_n)(u_n-p^{*})-{\theta }_n(u_{n-1}-p^{*}){\parallel }^2\hfill \\ \hfill & =(1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+{\theta }_n(1+{\theta }_n){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(24)

By definition of $w_{n+1}$ and through Cauchy inequality, we achieve

$$\begin{array}{cc}\parallel u_{n+1}-w_n{\parallel }^2\hfill & =\parallel u_{n+1}-u_n-{\theta }_n(u_n-u_{n-1}){\parallel }^2\hfill \\ \hfill & =\parallel u_{n+1}-u_n{\parallel }^2+{\theta }_n^2{\parallel u_n-u_{n-1}\parallel }^2-2{\theta }_n⟨u_{n+1}-u_n,u_n-u_{n-1}⟩\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \ge \parallel u_{n+1}-u_n{\parallel }^2+{\theta }_n^2\parallel u_n-u_{n-1}{\parallel }^2-2{\theta }_n\parallel u_{n+1}-u_n\parallel \parallel u_n-u_{n-1}\parallel \hfill \\ \hfill & \ge \parallel u_{n+1}-u_n{\parallel }^2+{\theta }_n^2\parallel u_n-u_{n-1}{\parallel }^2-{\theta }_n\parallel u_{n+1}-u_n{\parallel }^2-{\theta }_n{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & =(1-{\theta }_n)\parallel u_{n+1}-u_n{\parallel }^2+({\theta }_n^2-{\theta }_n){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(26)

By combining the expressions of Equations (23), (24) and (26) we have

$$\begin{array}{cc}\hfill & \parallel u_{n+1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & \le (1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+{\theta }_n(1+{\theta }_n){\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & -(1-\sigma )\left[(1-{\theta }_n)\parallel u_{n+1}-u_n{\parallel }^2+({\theta }_n^2-{\theta }_n){\parallel u_n-u_{n-1}\parallel }^2\right]\hfill \\ \hfill & +4c_1\sigma {\lambda }_n(1+\theta )\parallel u_n-v_{n-1}{\parallel }^2+4c_1\sigma (\theta +{\theta }^2){\parallel u_n-u_{n-1}\parallel }^2\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & \le (1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2\hfill \\ \hfill & +\left[\theta (1+\theta )-(1-\sigma )({\theta }_n^2-{\theta }_n)+4c_1\sigma (\theta +{\theta }^2)\right]{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & -(1-\sigma )(1-{\theta }_n){\parallel u_{n+1}-u_n\parallel }^2\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \le (1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2\hfill \\ \hfill & +{\varphi }_n\parallel u_n-u_{n-1}{\parallel }^2-{\psi }_n{\parallel u_{n+1}-u_n\parallel }^2,\hfill \end{array}$$

(29)

where

$${\varphi }_n=\left[\theta (1+\theta )-(1-\sigma )({\theta }_n^2-{\theta }_n)+4c_1\sigma (\theta +{\theta }^2)\right];$$

$${\psi }_n=(1-\sigma )(1-{\theta }_n).$$

Suppose that

$${\mathsf{\Psi }}_n={\mathsf{\Phi }}_n+{\varphi }_n{\parallel u_n-u_{n-1}\parallel }^2$$

where ${\mathsf{\Phi }}_n=\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_n(1+\theta ){\parallel u_n-v_{n-1}\parallel }^2.$ We compute the following by expression in Equation (29) we obtain

$$\begin{array}{cc}\hfill & {\mathsf{\Psi }}_{n+1}-{\mathsf{\Psi }}_n\hfill \\ \hfill & =\parallel u_{n+1}-p^{*}{\parallel }^2-{\theta }_{n+1}\parallel u_n-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta )\parallel u_{n+1}-v_n{\parallel }^2+{\varphi }_{n+1}{\parallel u_{n+1}-u_n\parallel }^2\hfill \\ \hfill & -\parallel u_n-p^{*}{\parallel }^2+{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2-4c_1\sigma {\lambda }_n(1+\theta )\parallel u_n-v_{n-1}{\parallel }^2-{\varphi }_n{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & \le \parallel u_{n+1}-p^{*}{\parallel }^2-(1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2+{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & +{\varphi }_{n+1}\parallel u_{n+1}-u_n{\parallel }^2-4c_1\sigma {\lambda }_n(1+\theta )\parallel u_n-v_{n-1}{\parallel }^2-{\varphi }_n{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & \le -({\psi }_n-{\varphi }_{n+1}){\parallel u_{n+1}-u_n\parallel }^2.\hfill \end{array}$$

(30)

Next, we are going to compute

$$\begin{array}{cc}({\psi }_n-{\varphi }_{n+1})\hfill & =(1-\sigma )(1-{\theta }_n)-\theta (1+\theta )+(1-\sigma )({\theta }_{n+1}^2-{\theta }_{n+1})-4c_1\sigma (\theta +{\theta }^2)\hfill \\ \hfill & \ge (1-\sigma ){(1-\theta )}^2-\theta (1+\theta )-4c_1\sigma (\theta +{\theta }^2)\hfill \\ \hfill & ={(1-\theta )}^2-\theta (1+\theta )-\sigma {(1-\theta )}^2-4c_1\sigma (\theta +{\theta }^2)\hfill \\ \hfill & =1-3\theta -\sigma \left({(1-\theta )}^2+4c_1(\theta +{\theta }^2)\right)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

(31)

Equations (30) and (31) with some $\delta \ge 0,$ imply that

$${\mathsf{\Psi }}_{n+1}-{\mathsf{\Psi }}_n\le -({\psi }_n-{\varphi }_{n+1})\parallel u_{n+1}-u_n{\parallel }^2\le -\delta {\parallel u_{n+1}-u_n\parallel }^2\le 0.$$

(32)

The relationship in Equation (32) implies that the sequence $\left\{{\mathsf{\Psi }}_n\right\}$ is nonincreasing. Furthermore, by definition of ${\mathsf{\Psi }}_{n+1}$ we have

$$\begin{array}{cc}{\mathsf{\Psi }}_{n+1}\hfill & =\parallel u_{n+1}-p^{*}{\parallel }^2-{\theta }_{n+1}\parallel u_n-p^{*}{\parallel }^2+{\varphi }_{n+1}\parallel u_{n+1}-u_n{\parallel }^2+4c_1\sigma {\lambda }_{n+1}(1+\theta ){\parallel u_{n+1}-v_n\parallel }^2\hfill \\ \hfill & \ge -{\theta }_{n+1}{\parallel u_n-p^{*}\parallel }^2.\hfill \end{array}$$

(33)

Additionally, by definition of ${\mathsf{\Psi }}_n$ we have

$$\begin{array}{cc}\parallel u_n-p^{*}{\parallel }^2\hfill & \le {\mathsf{\Psi }}_n+{\theta }_n{\parallel u_{n-1}-p^{*}\parallel }^2\hfill \\ \hfill & \le {\mathsf{\Psi }}_1+\theta {\parallel u_{n-1}-p^{*}\parallel }^2\hfill \\ \hfill & \le \cdots \le {\mathsf{\Psi }}_1({\theta }^{n-1}+\cdots +1)+{\theta }^n{\parallel u_0-p^{*}\parallel }^2\hfill \\ \hfill & \le \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\theta }^n{\parallel u_0-p^{*}\parallel }^2.\hfill \end{array}$$

(34)

On the basis of Equations (33) and (34) we have

$$\begin{array}{cc}-{\mathsf{\Psi }}_{n+1}\hfill & \le {\theta }_{n+1}{\parallel u_n-p^{*}\parallel }^2\hfill \\ \hfill & \le \theta \parallel u_n-p^{*}{\parallel }^2\hfill \\ \hfill & \le \theta \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\theta }^{n+1}{\parallel u_0-p^{*}\parallel }^2.\hfill \end{array}$$

(35)

It follows from expressions in Equations (32) and (35) we have

$$\begin{array}{cc}\delta \sum _{n=1}^k{\parallel u_{n+1}-u_n\parallel }^2\hfill & \le {\mathsf{\Psi }}_1-{\mathsf{\Psi }}_{k+1}\hfill \\ \hfill & \le {\mathsf{\Psi }}_1+\theta \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\theta }^{k+1}{\parallel u_0-p^{*}\parallel }^2\hfill \\ \hfill & \le \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\parallel u_0-p^{*}\parallel }^2,\hfill \end{array}$$

(36)

letting $k\to \infty$ in Equation (36) we have

$$\sum _{n=1}^{\infty }\parallel u_{n+1}-u_n{\parallel }^2<+\infty \mathrm{implies}\underset{n\to \infty }{lim}\parallel u_{n+1}-u_n\parallel =0.$$

(37)

By the relationship in Equations (25) with (37) we have

$$\parallel u_{n+1}-w_n\parallel \to 0\mathrm{as}n\to \infty .$$

(38)

The expression in Equation (35) implies that

$$-{\mathsf{\Phi }}_{n+1}\le \theta \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\theta }^{n+1}\parallel u_0-p^{*}{\parallel }^2+{\varphi }_{n+1}{\parallel u_{n+1}-u_n\parallel }^2.$$

(39)

By Equation (21) we have

$$\begin{array}{cc}\hfill & {\lambda }_{n+1}(1-2c_2\sigma -4c_1\sigma (1+\theta ))\left[\parallel u_{n+1}-v_n{\parallel }^2+{\parallel w_n-v_n\parallel }^2\right]\hfill \\ \hfill & \le {\mathsf{\Phi }}_n-{\mathsf{\Phi }}_{n+1}+\theta (1+\theta )\parallel u_n-u_{n-1}{\parallel }^2+4c_1\sigma \theta (1+\theta ){\parallel u_{n+1}-u_n\parallel }^2.\hfill \end{array}$$

(40)

Fix $k\in \mathbb{N}$ and use above equation for $n=1,2,\cdots ,k.$ Summing up, we get

$$\begin{array}{cc}\hfill & {\lambda }_{n+1}(1-2c_2\sigma -4c_1\sigma (1+\theta ))\sum _{n=1}^k\left[\parallel u_{n+1}-v_n{\parallel }^2+{\parallel w_n-v_n\parallel }^2\right]\hfill \\ \hfill & \le {\mathsf{\Phi }}_0-{\mathsf{\Phi }}_{k+1}+\theta (1+\theta )\sum _{n=1}^k\parallel u_n-u_{n-1}{\parallel }^2+4c_1\sigma \theta (1+\theta )\sum _{n=1}^k{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & \le {\mathsf{\Phi }}_0+\theta \frac{{\mathsf{\Psi }}_1}{1-\theta }+{\theta }^{k+1}\parallel u_0-p^{*}{\parallel }^2+{\varphi }_{k+1}{\parallel u_{k+1}-u_k\parallel }^2\hfill \\ \hfill & +\theta (1+\theta )\sum _{n=1}^k\parallel u_n-u_{n-1}{\parallel }^2+4c_1\sigma \theta (1+\theta )\sum _{n=1}^k{\parallel u_{n+1}-u_n\parallel }^2,\hfill \end{array}$$

(41)

letting $k\to \infty$ in above expression we have

$$\sum _n\parallel u_{n+1}-v_n{\parallel }^2<+\infty \mathrm{and}\sum _n{\parallel w_n-v_n\parallel }^2<+\infty$$

(42)

and

$$\underset{n\to \infty }{lim}\parallel u_{n+1}-v_n\parallel =\underset{n\to \infty }{lim}\parallel w_n-v_n\parallel =0.$$

(43)

By using the triangular inequality we can easily derive the following from the above-mentioned expressions

$$\underset{n\to \infty }{lim}\parallel u_n-v_n\parallel =\underset{n\to \infty }{lim}\parallel u_n-w_n\parallel =\underset{n\to \infty }{lim}\parallel v_{n-1}-v_n\parallel =0.$$

(44)

Moreover, we follow the relationship in Equation (27) such that

$$\begin{array}{cc}\parallel u_{n+1}-p^{*}{\parallel }^2\hfill & \le (1+{\theta }_n)\parallel u_n-p^{*}{\parallel }^2-{\theta }_n\parallel u_{n-1}-p^{*}{\parallel }^2+\theta (1+\theta ){\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & +4c_1\sigma (1+\theta )\parallel u_n-v_{n-1}{\parallel }^2+4c_1\sigma (\theta +{\theta }^2){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(45)

The above expression with Equations (37) and (42) and Lemma 4 suggest that limits of $\parallel u_n-p^{*}\parallel ,$ $\parallel w_n-p^{*}\parallel$ and $\parallel v_n-p^{*}\parallel$ exist for each $p^{*}\in EP(f,C)$ and imply that the sequences $\left\{u_n\right\}$, $\left\{w_n\right\}$ and $\left\{v_n\right\}$ are bounded. We require to establish that every weak sequential limit point of the sequence $\left\{u_n\right\}$ lies in $EP(f,C).$ Take z to be any sequential weak cluster point of the sequence $\left\{u_n\right\},$ i.e., if there exists a weak convergent subsequence $\left\{u_{n_k}\right\}$ of $\left\{u_n\right\}$ that converges to $z,$ it implies that $\left\{v_{n_k}\right\}$ also weakly converge to $z.$ Our purpose is to prove $z\in EP(f,C).$ Using Lemma 7 with Equations (13) and (15) we obtain

$$\begin{array}{cc}\mu {\lambda }_{n}f(v_{n_k},y)\hfill & \ge \mu {\lambda }_{n}f(v_{n_k},u_{n_k+1})+⟨w_{n_k}-u_{n_k+1},y-u_{n_k+1}⟩\hfill \\ \hfill & \ge {\lambda }_n{\lambda }_{n+1}f(v_{n_k-1},u_{n_k+1})-{\lambda }_n{\lambda }_{n+1}f(v_{n_k-1},v_{n_k})-c_1{\lambda }_n{\lambda }_{n+1}{\parallel v_{n_k-1}-v_{n_k}\parallel }^2\hfill \\ \hfill & -c_2{\lambda }_n{\lambda }_{n+1}{\parallel v_{n_k}-u_{n_k+1}\parallel }^2+⟨w_{n_k}-u_{n_k+1},y-u_{n_k+1}⟩\hfill \\ \hfill & \ge {\lambda }_{n+1}⟨w_{n_k}-v_{n_k},u_{n_k+1}-v_{n_k}⟩-c_1{\lambda }_n{\lambda }_{n+1}{\parallel v_{n_k-1}-v_{n_k}\parallel }^2\hfill \\ \hfill & -c_2{\lambda }_n{\lambda }_{n+1}{\parallel v_{n_k}-u_{n_k+1}\parallel }^2+⟨w_{n_k}-u_{n_k+1},y-u_{n_k+1}⟩\hfill \end{array}$$

(46)

for any member y in $C\subset E_n.$ The expressions in Equations (38), (43) and (44) as well as the boundedness of the sequence $\left\{u_n\right\}$ mean the right side of the above-mentioned inequality is zero. Taking $\mu ,{\lambda }_n>0,$ condition ($f_3$) in (Assumption 1) and $v_{n_k}\rightharpoonup z,$ we obtain

$$0\le \underset{k\to \infty }{lim\; sup}f(v_{n_k},y)\le f(z,y),\forall y\in E_n.$$

(47)

Then $z\in C$ implies that $f(z,y)\ge 0$ for all $y\in C\subset E_n.$ This determines that $z\in EP(f,C).$ By Lemma 5, the sequences $\left\{u_n\right\},$ $\left\{v_n\right\}$ and $\left\{w_n\right\}$ weakly converges to $p^{*}\in EP(f,C).$□

We make ${\theta }_n=0$ in the Algorithm 1 and by following Theorem 1 we have an improved variant of Liu et al. [42] extragradient method in terms of stepsize.

Corollary 2.

Let a bifunction $f:\mathbb{E}\times \mathbb{E}\to \mathbb{R}$ satisfies Assumption 1. For every $p^{*}\in EP(f,C)\ne \varnothing ,$ the sequence $\left\{u_n\right\}$ and $\left\{v_n\right\}$ are set up in the subsequent manner:

• Initialization: Given $u_0,v_{-1},v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{1,\frac{1}{2c_2+4c_1}\right\},$ $\mu \in (0,\sigma )$ and ${\lambda }_0>0.$
• Iterative steps: For given $u_n,v_{n-1}$ and $v_n,$ construct a half-space

  $$E_n=\{z\in \mathbb{E}:⟨u_n-{\lambda }_n{\omega }_{n-1}-v_n,z-v_n⟩\le 0\},$$
• where ${\omega }_{n-1}\in {\partial }_{2}f(v_{n-1},v_n).$
• Step 1: Compute

  $$u_{n+1}=\underset{y\in E_n}{argmin}\{\mu {\lambda }_{n}f(v_n,y)+\frac{1}{2}\parallel u_n-y{\parallel }^2\}.$$
• Step 2: Update the stepsize as follows

  $$\begin{array}{cc}\hfill {\lambda }_{n+1}=& min\left\{\sigma ,\frac{\mu f(v_n,u_{n+1})}{f(v_{n-1},u_{n+1})-f(v_{n-1},v_n)-c_1\parallel v_{n-1}-v_n{\parallel }^2-c_2{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}\hfill \end{array}$$
• and compute

  $$v_{n+1}=\underset{y\in C}{argmin}\{{\lambda }_{n+1}f(v_n,y)+\frac{1}{2}\parallel u_{n+1}-y{\parallel }^2\}.$$
• Then $\left\{u_n\right\}$ and $\left\{v_n\right\}$ weakly converge to the solution $p^{*}\in EP(f,C).$

4. Solving Variational Inequality Problems with New Self-Adaptive Methods

We consider the application of our above-mentioned results to solve variational inequality problems involving pseudomonotone and Lipschitz-type continuous operator. The variational inequality problem is written in the following way:

$$\mathrm{find}{p}^{*}\in C\mathrm{so}\mathrm{that}⟨G\left(p^{*}\right),v-p^{*}⟩\ge 0,\forall v\in C.$$

An operator $G:\mathbb{E}\to \mathbb{E}$ is

$\left(i\right).$

monotone on C if $⟨G\left(u\right)-G\left(v\right),u-v⟩\ge 0,\forall u,v\in C$;

$\left(ii\right).$

L-Lipschitz continuous on C if $\parallel G\left(u\right)-G\left(v\right)\parallel \le L\parallel u-v\parallel ,\forall u,v\in C$;

$\left(iii\right).$

pseudomonotone on C if $⟨G\left(u\right),v-u⟩\ge 0\Rightarrow ⟨G\left(v\right),u-v⟩\le 0,\forall u,v\in C.$

Note: If we choose the bifunction $f(u,v):=⟨G\left(u\right),v-u⟩$ for all $u,v\in C$ then the equilibrium problem transforms into the above variational inequality problem with $L=2c_1=2c_2.$ This means that from the definitions of $v_{n+1}$ in the Algorithm 1 and according to the above definition of bifunction f we have

$$\begin{array}{cc}\hfill v_{n+1}& =\underset{y\in C}{argmin}\left\{{\lambda }_{n+1}f(v_n,y)+\frac{1}{2}{\parallel w_{n+1}-y\parallel }^2\right\}\hfill \\ \hfill & =\underset{y\in C}{argmin}\left\{{\lambda }_{n+1}⟨G\left(v_n\right),y-v_n⟩+\frac{1}{2}{\parallel w_{n+1}-y\parallel }^2\right\}\hfill \\ \hfill & =\underset{y\in C}{argmin}\left\{{\lambda }_{n+1}⟨G\left(v_n\right),y-w_{n+1}⟩+\frac{1}{2}{\parallel w_{n+1}-y\parallel }^2+{\lambda }_{n+1}⟨G\left(v_n\right),w_{n+1}-v_n⟩\right\}\hfill \\ \hfill & =\underset{y\in C}{argmin}\left\{\frac{1}{2}\parallel y-(w_{n+1}-{\lambda }_{n+1}G\left(v_n\right){\parallel }^2\right\}-\frac{{\lambda }_{n+1}^2}{2}{\parallel G\left(v_n\right)\parallel }^2\hfill \\ \hfill & =P_C(w_{n+1}-{\lambda }_{n+1}G\left(v_n\right)).\hfill \end{array}$$

(48)

Similarly to the expression in Equation (48) the value $u_{n+1}$ from Algorithm 1 converts into

$$u_{n+1}=P_{E_n}(w_n-\mu {\lambda }_{n}G\left(v_n\right)).$$

Due to ${\omega }_{n-1}\in {\partial }_{2}f(v_{n-1},v_n)$ and by subdifferential definition we obtain

$$\begin{array}{cc}\hfill ⟨{\omega }_{n-1},z-v_n⟩& \le ⟨G\left(v_{n-1}\right),z-v_{n-1}⟩-⟨G\left(v_{n-1}\right),v_n-v_{n-1}⟩,\forall z\in \mathbb{E}\hfill \\ \hfill & =⟨G\left(v_{n-1}\right),z-v_n⟩,\forall z\in \mathbb{E}\hfill \end{array}$$

(49)

and consequently $0\le ⟨G\left(v_{n-1}\right)-{\omega }_{n-1},z-v_n⟩$ for all $z\in \mathbb{E}.$ This implies that

$$\begin{array}{cc}\hfill & ⟨w_n-{\lambda }_{n}G\left(v_{n-1}\right)-v_n,z-v_n⟩\hfill \\ \hfill & \le ⟨w_n-{\lambda }_{n}G\left(v_{n-1}\right)-v_n,z-v_n⟩+{\lambda }_n⟨G\left(v_{n-1}\right)-{\omega }_{n-1},z-v_n⟩\hfill \\ \hfill & =⟨w_n-{\lambda }_n{\omega }_{n-1}-v_n,z-v_n⟩.\hfill \end{array}$$

(50)

Assumption 2.

We assume that G is satisfying the following assumptions:

$G_1^{*}$.

G is monotone on C and $VI(G,C)$ is nonempty;

$G_1$.

G is pseudomonotone on C and $VI(G,C)$ is nonempty;

$G_2$.

G is L-Lipschitz continuous on C through positive parameter $L>0;$

$G_3$.

$\underset{n\to \infty }{lim\; sup}⟨G\left(u_n\right),v-u_n⟩\le ⟨G\left(x^{*}\right),v-x^{*}⟩$ for every $v\in C$ and $\left\{u_n\right\}\subset C$ satisfying $u_n\rightharpoonup x^{*}.$

We have reduced the following results from our main results applicable to solve variational inequality problems.

Corollary 3.

Assume that $G:C\to \mathbb{E}$ is satisfying ($G_1,G_2,G_3$) in Assumption 2. Let $\left\{w_n\right\},$ $\left\{u_n\right\}$ and $\left\{v_n\right\}$ be the sequences obtained as follows:

• Initialization: Choose $u_{-1},v_{-1},u_0,v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{\frac{1-3\theta }{{(1-\theta )}^2+2L(\theta +{\theta }^2)},\frac{1}{3L+2\theta L)}\right\}$ for a nondecreasing sequence ${\theta }_n$ such that $0\le {\theta }_n\le \theta <\frac{1}{3}$ and ${\lambda }_0>0.$
• Iterative steps: For given $u_{n-1},v_{n-1},u_n$ and $v_n,$ construct a half space

  $$E_n=\{z\in \mathbb{E}:⟨w_n-{\lambda }_{n}G{v}_{n-1}-v_n,z-v_n⟩\le 0\}$$
• where $w_n=u_n+{\theta }_n(u_n-u_{n-1}).$
• Step 1: Compute

  $$u_{n+1}=P_{E_n}(w_n-\mu {\lambda }_{n}G\left(v_n\right)).$$
• Step 2: The stepsize ${\lambda }_{n+1}$ is updated as follows

  $$\begin{array}{cc}\hfill {\lambda }_{n+1}=& min\left\{\sigma ,\frac{\mu ⟨G{v}_n,u_{n+1}-v_n⟩}{⟨G{v}_{n-1},u_{n+1}-v_n⟩-\frac{L}{2}\parallel v_{n-1}-v_n{\parallel }^2-\frac{L}{2}{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}\hfill \end{array}$$
• and compute

  $$v_{n+1}=P_C(w_{n+1}-{\lambda }_{n+1}G\left(v_n\right))where{w}_{n+1}=u_{n+1}+{\theta }_{n+1}(u_{n+1}-u_n).$$
• Then the sequence $\left\{w_n\right\},$ $\left\{u_n\right\}$ and $\left\{v_n\right\}$ weakly converge to $p^{*}$ of $VI(G,C).$

Corollary 4.

Assume that $G:C\to \mathbb{E}$ is satisfying ($G_1,G_2,G_3$) in Assumption 2. Let $\left\{u_n\right\}$ and $\left\{v_n\right\}$ be the sequences obtained as follows:

• Initialization: Choose $v_{-1},u_0,v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{1,\frac{1}{3L}\right\}$ and ${\lambda }_0>0.$
• Iterative steps: For given $v_{n-1},u_n$ and $v_n,$ construct a half space

  $$E_n=\{z\in \mathbb{E}:⟨u_n-{\lambda }_{n}G{v}_{n-1}-v_n,z-v_n⟩\le 0\}.$$
• Step 1: Compute

  $$u_{n+1}=P_{E_n}(u_n-\mu {\lambda }_{n}G\left(v_n\right)).$$
• Step 2: The stepsize ${\lambda }_{n+1}$ is updated as follows

  $$\begin{array}{cc}\hfill {\lambda }_{n+1}=& min\left\{\sigma ,\frac{\mu ⟨G{v}_n,u_{n+1}-v_n⟩}{⟨G{v}_{n-1},u_{n+1}-v_n⟩-\frac{L}{2}\parallel v_{n-1}-v_n{\parallel }^2-\frac{L}{2}{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}\hfill \end{array}$$
• and compute

  $$v_{n+1}=P_C(u_{n+1}-{\lambda }_{n+1}G\left(v_n\right)).$$
• Thus $\left\{u_n\right\}$ and $\left\{v_n\right\}$ converge weakly to the solution $p^{*}$ of $VI(G,C).$

We examine that if G is monotone then condition ($G_3$) can be removed. The assumption ($G_3$) is required to specify $f(u,v)=⟨G\left(u\right),v-u⟩$ complies with the condition ($f_3$). In addition, condition ($f_3$) is required to show $z\in EP(f,C)$ after the inequality in Equation (47). This implies that the condition ($G_3$) is used to prove $z\in VI(G,C).$ Now we will prove that $z\in VI(G,C)$ by using the monotonicity of operator $G.$ Since G is monotone, we have

$$⟨G\left(y\right),y-v_n⟩\ge ⟨G\left(v_n\right),y-v_n⟩,\forall y\in \mathbb{E}.$$

(51)

By $f(u,v)=⟨G\left(u\right),v-u⟩$ and Equation (46) we have

$$\underset{k\to \infty }{lim\; sup}⟨G\left(v_{n_k}\right),y-v_{n_k}⟩\ge 0,y\in E_n.$$

(52)

Combining Equations (51) with (52), we deduce that

$$\underset{k\to \infty }{lim\; sup}⟨G\left(y\right),y-v_{n_k}⟩\ge 0,y\in E_n.$$

(53)

Since $v_{n_k}\rightharpoonup z\in C$ and $⟨G\left(y\right),y-z⟩\ge 0$ for all $y\in C.$ Let $v_t=(1-t)z+ty$ for all $t\in [0,1].$ Due to convexity of C the value $v_t\in C$ for each $t\in (0,1).$ We obtain

$$0\le ⟨G\left(v_t\right),v_t-z⟩=t⟨G\left(v_t\right),y-z⟩$$

(54)

That is $⟨G\left(v_t\right),y-z⟩\ge 0$ for all $t\in (0,1).$ By $v_t\to z$ as $t\to 0$ and the continuity of G gives $⟨G\left(z\right),y-z⟩\ge 0$ for each $y\in C,$ which implies that $z\in VI(G,C).$

Corollary 5.

Assume that $G:C\to \mathbb{E}$ is satisfying ($G_1^{*},G_2$) in Assumption 2. Let $\left\{w_n\right\},$ $\left\{u_n\right\}$ and $\left\{v_n\right\}$ be the sequences obtained as follows:

• Initialization: Choose $u_{-1},v_{-1},u_0,v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{\frac{1-3\theta }{{(1-\theta )}^2+2L(\theta +{\theta }^2)},\frac{1}{3L+2\theta L)}\right\}$ for a nondecreasing sequence ${\theta }_n$ such that $0\le {\theta }_n\le \theta <\frac{1}{3}$ and ${\lambda }_0>0.$
• Iterative steps: For given $u_{n-1},v_{n-1},u_n$ and $v_n,$ construct a half space

  $$E_n=\{z\in \mathbb{E}:⟨w_n-{\lambda }_{n}G{v}_{n-1}-v_n,z-v_n⟩\le 0\}$$
• where $w_n=u_n+{\theta }_n(u_n-u_{n-1}).$
• Step 1: 

  $$u_{n+1}=P_{E_n}(w_n-\mu {\lambda }_{n}G\left(v_n\right)).$$
• Step 2: The stepsize ${\lambda }_{n+1}$ is updated as follows

  $$\begin{array}{cc}\hfill {\lambda }_{n+1}=& min\left\{\sigma ,\frac{\mu ⟨G{v}_n,u_{n+1}-v_n⟩}{⟨G{v}_{n-1},u_{n+1}-v_n⟩-\frac{L}{2}\parallel v_{n-1}-v_n{\parallel }^2-\frac{L}{2}{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}\hfill \end{array}$$

   
• and compute

  $$v_{n+1}=P_C(w_{n+1}-{\lambda }_{n+1}G\left(v_n\right))where{w}_{n+1}=u_{n+1}+{\theta }_{n+1}(u_{n+1}-u_n).$$
• Then the sequences $\left\{w_n\right\},$ $\left\{u_n\right\}$ and $\left\{v_n\right\}$ converges weakly to $p^{*}$ of $VI(G,C).$

Corollary 6.

Assume that $G:C\to \mathbb{E}$ is satisfying ($G_1^{*},G_2$) in Assumption 2. Let $\left\{u_n\right\}$ and $\left\{v_n\right\}$ be the sequences obtained as follows:

• Initialization:  Choose $v_{-1},u_0,v_0\in \mathbb{E},$ $\varrho \in (0,1),$ $\sigma <min\left\{1,\frac{1}{3L}\right\}$ and ${\lambda }_0>0.$
• Iterative steps: For given $v_{n-1},u_n$ and $v_n,$ construct a half space

  $$E_n=\{z\in \mathbb{E}:⟨u_n-{\lambda }_{n}G{v}_{n-1}-v_n,z-v_n⟩\le 0\}.$$
• Step 1: 

  $$u_{n+1}=P_{E_n}(u_n-\mu {\lambda }_{n}G\left(v_n\right)).$$
• Step 2: The stepsize ${\lambda }_{n+1}$ is updated as follows

  $$\begin{array}{cc}\hfill {\lambda }_{n+1}=& min\left\{\sigma ,\frac{\mu ⟨G{v}_n,u_{n+1}-v_n⟩}{⟨G{v}_{n-1},u_{n+1}-v_n⟩-\frac{L}{2}\parallel v_{n-1}-v_n{\parallel }^2-\frac{L}{2}{\parallel u_{n+1}-v_n\parallel }^2+1}\right\}\hfill \end{array}$$
• and compute

  $$v_{n+1}=P_C(u_{n+1}-{\lambda }_{n+1}G\left(v_n\right)).$$
• Then $\left\{u_n\right\}$ and $\left\{v_n\right\}$ converge weakly to $p^{*}$ of $VI(G,C).$

5. Computational Experiment

Numerical results produced in this section show the performance of our proposed methods. The MATLAB codes were running in MATLAB version 9.5 (R2018b) on a PC Intel(R) Core(TM)i5-6200 CPU @ 2.30GHz 2.40GHz, RAM 8.00 GB. In these examples, the x-axis indicates the number of iterations or the execution time (in seconds) and y-axes represents the values $D_n=\parallel u_{n+1}-u_n\parallel .$ We present the comparison of Algorithm 1 (Algo3) with the Lyashko et al. [33] (Algo1) and Liu et al. [42] (Algo2).

Example 1.

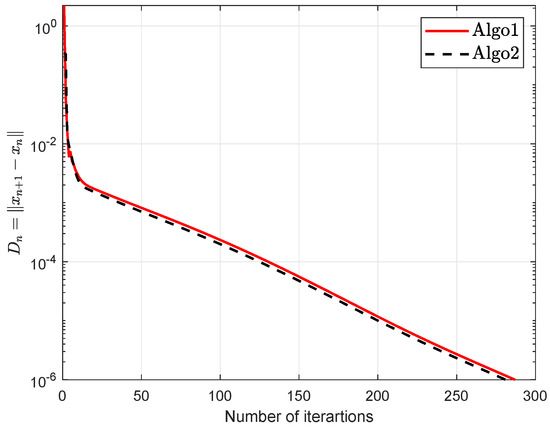
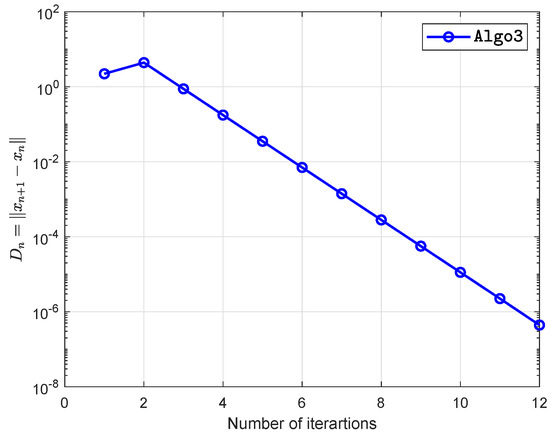
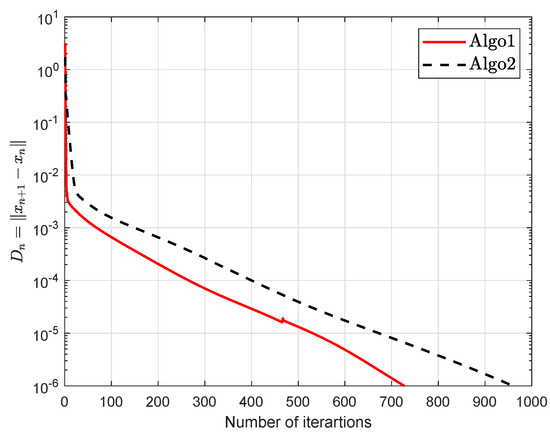
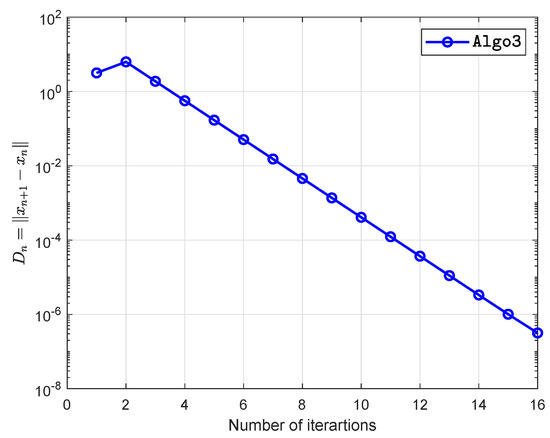
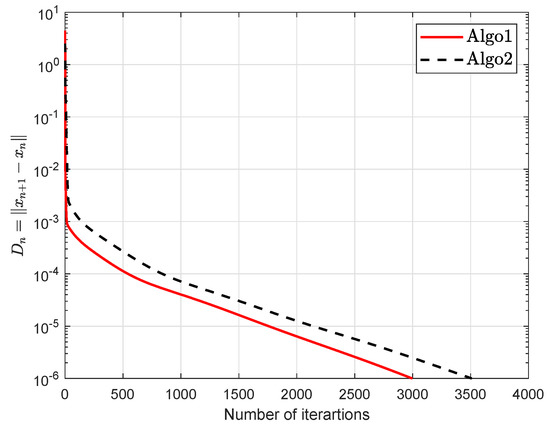
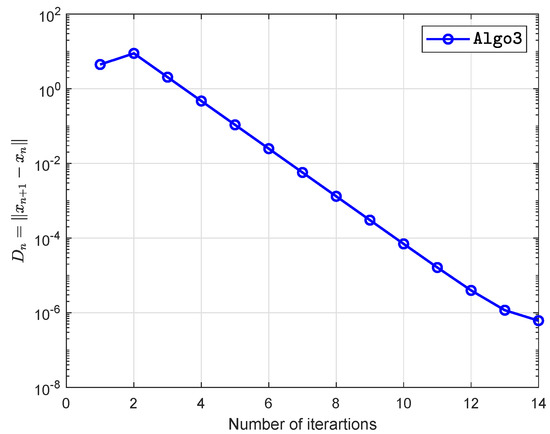
Suppose that $f:C\times C\to \mathbb{R}$ is defined by

$$f(u,v)=⟨Au+Bv+d,v-u⟩,$$

where $d\in {\mathbb{R}}^n$ and A, B are matrices of order n where B an symmetric positive semidefinite and $B-A$ is symmetric negative definite with Lipschitz constants are $c_1=c_2=\frac{1}{2}\parallel A-B\parallel$ (for more details see [20]). During Example 1, matrices $A,B$ are randomly produced (Two matrices are randomly generated E and F with entries from $[-1,1].$ The matrix $B=E^{T}E,$ $S=F^{T}F$ and $A=S+B.$) and entries of d randomly belongs to $[-1,1].$ The constraint set $C\subset {\mathbb{R}}^n$ as

$$C:=\{u\in {\mathbb{R}}^n:-10\le u_i\le 10\}.$$

The numerical findings are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 and Table 1 with $v_{-1}=(4,\cdots ,4),$ $u_{-1}=(3,\cdots ,3),$ $u_0=(1,\cdots ,1),$ $v_0=(2,\cdots ,2),$ $\lambda =\frac{1}{12c_1},$ $\sigma =\frac{5}{42c_1},$ $\mu =\frac{5}{44c_1},$ ${\theta }_n=0.12$ and ${\lambda }_0=\frac{1}{4c_1}.$

Figure 1. Example 1 when $n=5.$

Figure 2. Example 1 when $n=5.$

Figure 3. Example 1 when $n=10.$

Figure 4. Example 1 when $n=10.$

Figure 5. Example 1 when $n=20.$

Figure 6. Example 1 when $n=20.$

Table 1. Example 1: The numerical results for Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

	Algo1		Algo2		Algo3
n	Iter.	Exeu.time.	Iter.	Exeu.time.	Iter.	Exeu.time.
5	287	5.9342	281	3.5302	12	0.1204
10	727	19.8789	960	12.8186	16	0.1584
20	2997	72.7622	3510	3510	14	0.1624

Example 2.

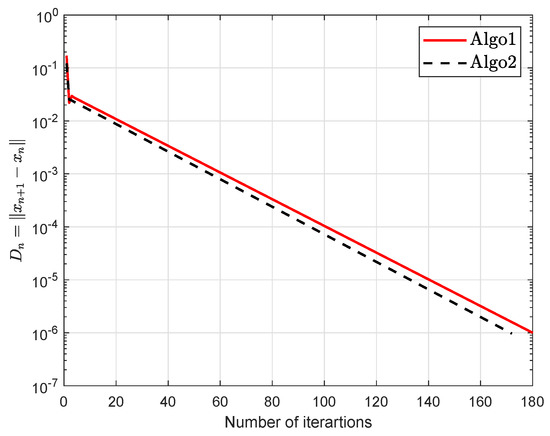
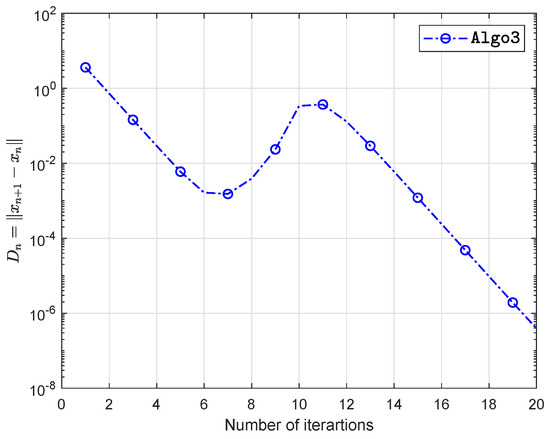
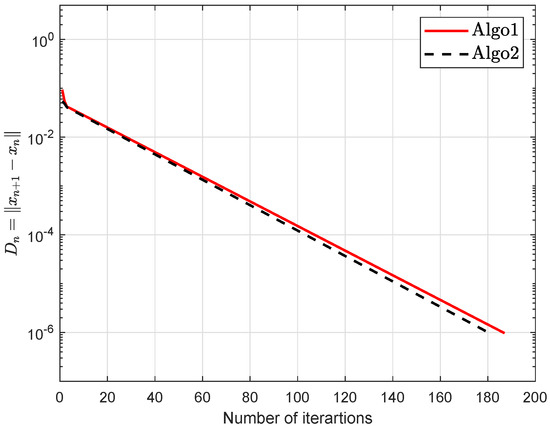
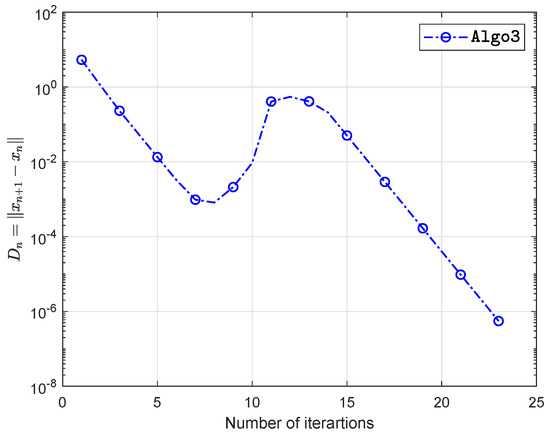
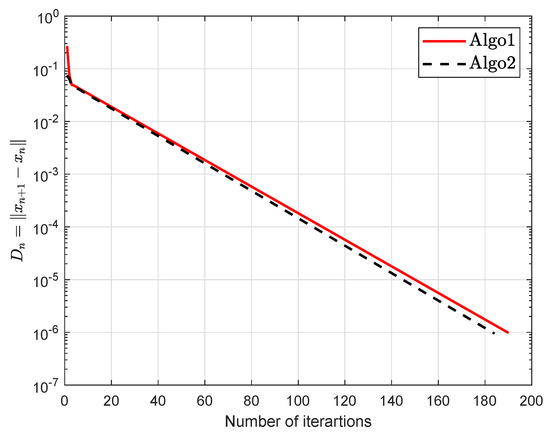
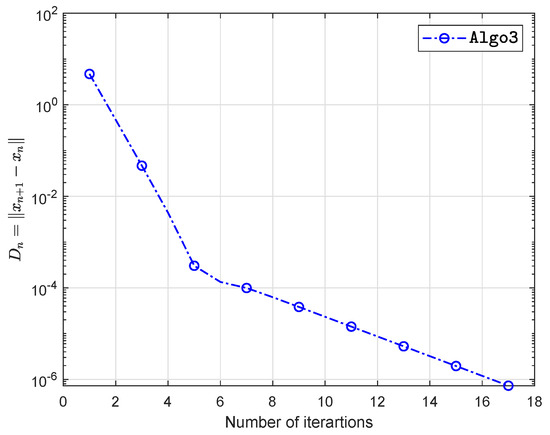
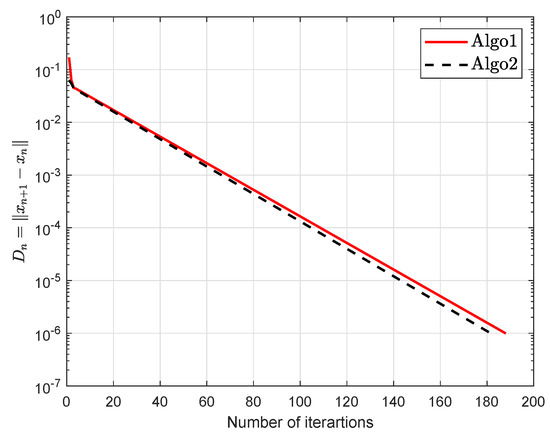
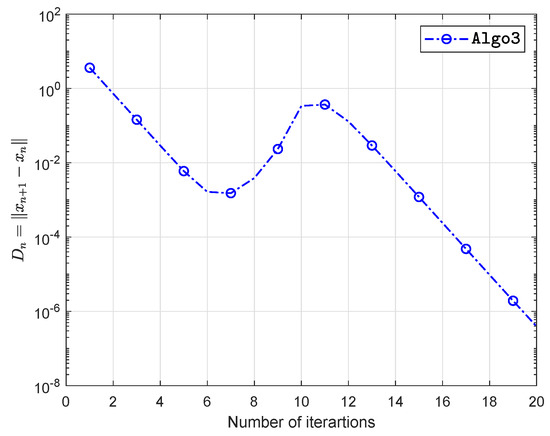
Let $f:C\times C\to \mathbb{R}$ be defined as

$$f(u,v)=(u_1+u_2-1)(v_1-u_1)+(u_1+u_2-1)(v_2-u_2)$$

where $C=[-2,5]\times [-2,5].$ We see that

$$f(u,v)+f(v,u)=-{(u_1-v_1+u_2-v_2)}^2\le 0$$

which gives that bifunction f is monotone. The numerical findings are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 and Table 2 with $v_{-1}=u_{-1}=u_0=(-1,1),$ $\lambda =0.03,$ $\sigma =0.476,$ $\mu =0.455,$ ${\theta }_n=0.15$ and ${\lambda }_0=0.1.$

Figure 7. Example 2 when $v_0=(-1.0,2.0).$

Figure 8. Example 2 when $v_0=(-1.0,2.0).$

Figure 9. Example 2 when $v_0=(1.5,1.7).$

Figure 10. Example 2 when $v_0=(1.5,1.7).$

Figure 11. Example 2 when $v_0=(2.7,4.6).$

Figure 12. Example 2 when $v_0=(2.7,4.6).$

Figure 13. Example 2 when $v_0=(2.0,3.0).$

Figure 14. Example 2 when $v_0=(2.0,3.0).$

Table 2. Example 2: The numerical results for Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.

	Algo1		Algo2		Algo3
v0	Iter.	Exeu.time.	Iter.	Exeu.time.	Iter.	Exeu.time.
(−1.0, 2.0)	180	1.7844	172	0.7740	20	0.1025
(1.5, 1.7)	187	2.1016	181	0.8069	23	0.1125
(2.7, 4.6)	190	1.9044	184	0.7979	17	0.0881
(2.0, 3.0)	188	1.8635	182	0.7792	20	0.1063

Example 3.

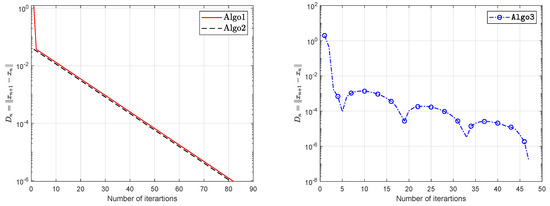
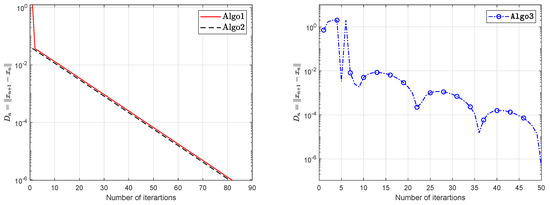
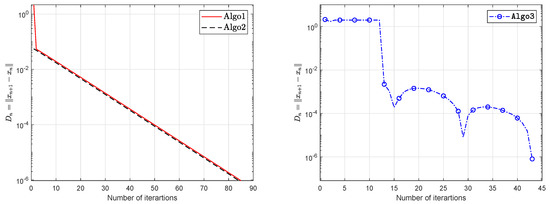
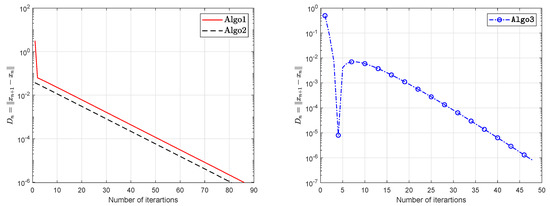
Let $G:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be defined by

$$G\left(u\right)=\left(\begin{array}{c}0.5u_1{u}_2-2u_2-{10}^7\\ -4u_1-0.1u_2^2-{10}^7\end{array}\right)$$

and let $C=\{u\in {\mathbb{R}}^2:{(u_1-2)}^2+{(u_2-2)}^2\le 1\}.$ The operator G is Lipschitz continuous with $L=5$ and pseudomonotone. During this experiment we use $u_{-1}=(1,1),$ $v_{-1}=(2,2),$ $u_0={(3,4)}^T$ with stepsize $\lambda ={10}^{-8}$ according Lyashko et al. [33] and Liu et al. [42]. We take ${\lambda }_0=0.1$, $\sigma =0.0392$ and $\mu =0.0377.$ The experimental results are shown in Table 3 and Figure 15, Figure 16, Figure 17 and Figure 18.

Table 3. Example 3: The numerical results for Figure 15, Figure 16, Figure 17 and Figure 18.

	Algo1		Algo2		Algo3
v0	Iter.	Exeu.time.	Iter.	Exeu.time.	Iter.	Exeu.time.
(1.5, 1.7)	82	2.6525	81	1.3557	47	0.9015
(2.0, 3.0)	82	2.7698	81	1.3698	50	1.4948
(1.0, 2.0)	85	2.9042	84	1.4026	43	1.2657
(2.7, 2.6)	86	2.8937	81	1.3990	48	1.4540

Figure 15. Example 3 when $u_0=(1.5,1.7).$

Figure 16. Example 3 when $u_0=(2.0,3.0).$

Figure 17. Example 3 when $u_0=(1.0,2.0).$

Figure 18. Example 3 when $u_0=(2.7,2.6).$

Example 4.

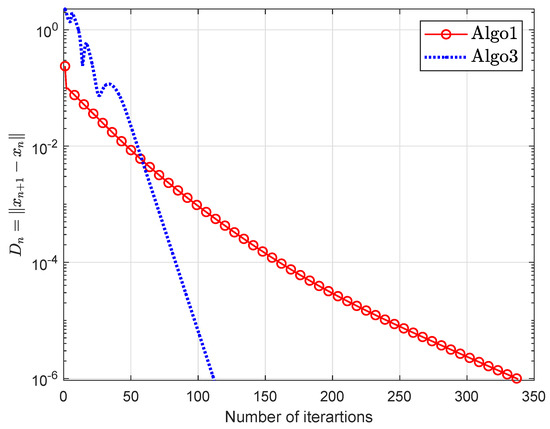
Take $G:{\mathbb{R}}^n\to {\mathbb{R}}^n$ to be defined through

$$G\left(u\right)=Au+B\left(u\right)$$

where A is a $n\times n$ symmetric semidefinite matrix and $B\left(u\right)$ is the proximal mapping through the function $h\left(u\right)=\frac{1}{4}{\parallel u\parallel }^4$ such that

$$B\left(u\right)=\underset{v\in {\mathbb{R}}^n}{argmin}\left\{\frac{{\parallel v\parallel }^4}{4}+\frac{1}{2}{\parallel v-u\parallel }^2\right\}$$

The property of A and the proximal mapping B implies that G is monotone upon C [45]. The following is a feasible set

$$C:=\{u\in {\mathbb{R}}^5:-2\le u_i\le 5\}.$$

The numerical results are shown in Table 4 and Figure 19.

Table 4. Example 4: The numerical results for Figure 19.

	Algo1		Algo3
n	Iter.	Exeu.time.	Iter.	Exeu.time.
5	338	12.6364	112	8.8393

Figure 19. Example 4 when $n=5.$

6. Conclusions

We have developed extragradient-like methods to solve pseudomonotone equilibrium problems and different classes of variational inequality problems in real Hilbert space. The advantage of our method is in designing an explicit formula for step size evaluation. For each iteration the stepsize formula is updated based on the previous iterations. Numerical results were reported to demonstrate numerical effectiveness of our results relative to other methods. These numerical studies suggest that inertial effects in this sense also generally improve the effectiveness of the iterative sequence.