General Multiplicative Zagreb Indices of Graphs with a Small Number of Cycles

Abstract

We present lower and upper bounds on the general multiplicative Zagreb indices for bicyclic graphs of a given order and number of pendant vertices. Then, we generalize our methods and obtain bounds for the general multiplicative Zagreb indices of tricyclic graphs, tetracyclic graphs and graphs of given order, size and number of pendant vertices. We show that all our bounds are sharp by presenting extremal graphs including graphs with symmetries. Bounds for the classical multiplicative Zagreb indices are special cases of our results.

1. Introduction

Molecular descriptors called topological indices have been investigated because of their numerous applications. Topological indices are graph invariants which play a significant role in chemistry, pharmaceutical sciences, materials science and engineering, since they can be correlated with many physico-chemical properties of molecules. We use graph theory to characterize these chemical structures.

We consider connected graphs without loops and multiple edges. The vertex set and the edge set of a graph G are denoted by $V(G)$ and $E(G)$, respectively. We use the vertices and edges of G for the representation of the atoms and bonds of chemical structures. The order n is the number of vertices of a graph G and the size m is the number of edges of G. The number of edges incident with a vertex $u\in V(G)$ is called the degree $d_G(u)$. A vertex of degree one is a pendant vertex. A bicyclic graph is a connected graph with $n+1$ edges, a tricyclic graph is a connected graph with $n+2$ edges and a tetracyclic graph is a connected graph with $n+3$ edges (and n vertices). The symbols $P_n$ and $K_n$ denote the path and complete graph of order n, respectively. Let $C_k=u_1{u}_2\dots u_k$ be the cycle with $V(C_k)=\{u_1,u_2,\dots ,u_k\}$ and $E(C_k)=\{u_1{u}_2,u_2{u}_3,\dots ,u_{k-1}{u}_k,u_k{u}_1\}$.

Multiplicative Zagreb indices have been extensively studied. Sharp upper and lower bounds on the multiplicative Zagreb indices for trees of given number of vertices with maximum degree were presented by Wang et al. [1], sharp upper and lower bounds for trees, unicyclic graphs and bicyclic graphs with given order were given by Xu and Hua [2], tight bounds for unicyclic graphs of given order and number of pendant vertices/diameter/k-cycle were presented by Alfuraidan, Balachandran and Vetrík [3], tight upper bounds for graphs of prescribed order and size were obtained by Liu and Zhang [4], bounds for graphs with prescribed number of bridges were given by Wang et al. [5], molecular graphs were considered by Kazemi [6] and derived graphs were investigated by Basavanagoud and Patil [7]. Bounds on the total multiplicative sum Zagreb index and first multiplicative sum Zagreb coindex for unicyclic and bicyclic graphs were presented by Božović, Vukićević and Popivoda [8]. Reformulated Zagreb indices were investigated Liu et al. [9] and De, Nayeem and Pal [10].

Recently, Vetrík and Balachandran [11] generalized multiplicative Zagreb indices by introducing the first and second general multiplicative Zagreb indices of a graph G, $P_1^a(G)$ and $P_2^a(G)$, respectively.

$$P_1^a(G)=\prod _{u\in V(G)}{d}_G{(u)}^a$$

and

$$P_2^a(G)=\prod _{u\in V(G)}{d}_G{(u)}^{a{d}_G(u)}=\prod _{uv\in E(G)}{(d_G(u)d_G(v))}^a,$$

where $a\in \mathbb{R}$, $a\ne 0$. Note that $P_1^1(G)$ is the Narumi-Katayama index, $P_1^2(G)$ is the first multiplicative Zagreb index and $P_2^1(G)$ is the second multiplicative Zagreb index. These indices are special cases of our general indices. A lot of research has been done on these special cases and the importance of our general indices is that any result on the general multiplicative Zagreb indices yields results also for the first and second multiplicative Zagreb indices and for the Narumi-Katayama index.

We study graphs with a small number of cycles which are particularly important in chemistry, since they can represent chemical structures. Our work is motivated by the paper of Zhao and Li [12] who presented bounds on the Zagreb indices for bicyclic graphs of given order and number of pendant vertices. In Section 3, we use our new methods to obtain lower and upper bounds on the general multiplicative Zagreb indices for bicyclic graphs of order n with k pendant vertices. Then in Section 4, we generalize our techniques and present bounds for $P_1^a$ and $P_2^a$ indices of tricyclic graphs, tetracyclic graphs and graphs of given order, size and number of pendant vertices. In Section 2, Section 3 and Section 4, we consider the case $a>0$ and in Section 5 we give similar results for $a<0$. We show that all our bounds are best possible by presenting extremal graphs. The cases $k=n-6,n-5,n-4$ for tricyclic graphs and $k=n-4$ for bicyclic graphs are particularly interesting.

2. Preliminary Results

Let $X=(x_1,x_2,\dots ,x_n)$ be the degree sequence with $x_1\ge x_2\ge \cdots \ge x_n$. Let us define

$$P_{1^{\prime }}^a(X)=\prod _{i=1}^n{x}_i^a \mathrm{and} P_{2^{\prime }}^a(X)=\prod _{i=1}^n{x}_i^{a{x}_i}.$$

If there exists a graph G having the vertices with degrees $x_1,x_2,\dots ,x_n$, then the sequence X is graphical and therefore $P_1^a(G)=P_{1^{\prime }}^a(X)$ and $P_2^a(G)=P_{2^{\prime }}^a(X)$.

The following lemma and corollaries about degree sequences will be used to prove some results in Section 3 and Section 4.

Lemma 1.

Let X and $X^{\prime }$ be the degree sequences which differ in two coordinates, where $x_i,x_j$ are in X and $x_i+1,x_j-1$ are in $X^{\prime }$, with $x_i\ge x_j\ge 2$ and $1\le i<j\le n$. For $a>0$ we obtain $P_{1^{\prime }}^a(X^{\prime })<P_{1^{\prime }}^a(X)$ and $P_{2^{\prime }}^a(X^{\prime })>P_{2^{\prime }}^a(X)$.

Proof. 

Let $a>0$. We get

$$\frac{P_{1^{\prime }}^a(X)}{P_{1^{\prime }}^a(X^{\prime })}=\frac{x_i^a{x}_j^a}{{(x_i+1)}^a{(x_j-1)}^a}={\left(\frac{x_i{x}_j}{x_i{x}_j+x_j-x_i-1}\right)}^a>1,$$

because $x_j-x_i-1<0$. Moreover,

$$\begin{array}{ccc}\hfill 0<\frac{P_{2^{\prime }}^a(X)}{P_{2^{\prime }}^a(X^{\prime })}& =& \frac{x_i^{a{x}_i}{x}_j^{a{x}_j}}{{(x_i+1)}^{a(x_i+1)}{(x_j-1)}^{a(x_j-1)}}={\left[\frac{x_i^{x_i}{x}_j^{x_j}}{{(x_i+1)}^{x_i+1}{(x_j-1)}^{x_j-1}}\right]}^a\hfill \\ \hfill & =& {\left[{\left(1-\frac{1}{x_i+1}\right)}^{x_i+1}{\left(1+\frac{1}{x_j-1}\right)}^{x_j-1}\frac{x_j}{x_i}\right]}^a<1,\hfill \end{array}$$

because ${(1-\frac{1}{x_i+1})}^{x_i+1}<\frac{1}{e}$, ${(1+\frac{1}{x_j-1})}^{x_j-1}<e$ and $\frac{x_j}{x_i}\le 1$. Thus $P_{1^{\prime }}^a(X)>P_{1^{\prime }}^a(X^{\prime })$ and $P_{2^{\prime }}^a(X)<P_{2^{\prime }}^a(X^{\prime })$. □

Corollary 1.

Let $a>0$ and X be the degree sequence with the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index), where $k\ge 0$ coordinates of X are 1 and ${\sum }_{i=1}^n{x}_i=2(n+ϵ)$ for some $ϵ\in \mathbb{N}$. Then $X=(k+2ϵ+2,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$.

Proof. 

Let us show by contradiction that the degree sequence X having the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index) contains at most one coordinate which is at least 3.

Suppose that X is the sequence having the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index) with at least two coordinates being at least 3. Then $X=(x_1,x_2,\dots ,x_r$, $\underset{n-r-k}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$, with $r\ge 2$ and $x_1,x_2,\dots ,x_r\ge 3$. From Lemma 1, $X^{\prime }=(x_1+1,x_2,\dots ,x_r-1,\underset{n-r-k}{\underbrace{2,\dots ,2}}$, $\underset{k}{\underbrace{1,\dots ,1}})$ has smaller $P_{1^{\prime }}^a$ index (larger $P_{2^{\prime }}^a$ index). Thus X is not the sequence having the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index).

So $X=(x_1,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$. We have ${\sum }_{i=1}^n{x}_i=x_1+2(n-k-1)+k=2(n+ϵ)$, hence $x_1=k+2ϵ+2$. □

Corollary 2.

Let $a>0$ and X be the degree sequence with the largest $P_{1^{\prime }}^a$ index (the smallest $P_{2^{\prime }}^a$ index), where $k\ge 0$ coordinates are 1 and ${\sum }_{i=1}^n{x}_i=2(n+ϵ)$ for some $ϵ\in \mathbb{N}$. Then $X=(x_1,x_2,\dots ,x_{n-k}$, $\underset{k}{\underbrace{1,\dots ,1}})$ with $x_i-x_j\le 1$ for $1\le i<j\le n-k$.

Proof. 

Let $X^{\prime }=(x_1,x_2,\dots ,x_{n-k},\underset{k}{\underbrace{1,\dots ,1}})$ be the degree sequence with the largest $P_{1^{\prime }}^a$ index (the smallest $P_{2^{\prime }}^a$ index), where k coordinates are 1. We have $x_1\ge x_2\ge \cdots \ge x_{n-k}$, so we need to prove that $x_1-x_{n-k}\le 1$.

Assume that $x_1-x_{n-k}\ge 2$. From Lemma 1, there is a sequence such containing $x_1-1$ and $x_{n-k}+1$ having larger $P_{1^{\prime }}^a$ index (smaller $P_{2^{\prime }}^a$ index), a contradiction. □

We will also use a very known equality relating the degrees and the number of edges m of a graph G,

$$\sum _{u\in V(G)}{d}_G(u)=2m.$$

(1)

3. Bicyclic Graphs with Given Number of Pendant Vertices

Let us present bounds on the general multiplicative Zagreb indices for bicyclic graphs of given order and number of pendant vertices. Since at least 4 vertices are contained in two cycles, those vertices are not pendant. Thus for the number k of pendant vertices in a bicyclic graph we have $0\le k\le n-4$.

Theorem 1.

Let G be any bicyclic graph of order n with k pendant vertices, where $0\le k\le n-4$. For $a>0$ we have

$$P_1^a(G)\le {(r+2)}^{a[n-(n-k)r+2]}{(r+1)}^{a[(n-k)r-k-2]}$$

and

$$P_2^a(G)\ge {(r+2)}^{a(r+2)[n-(n-k)r+2]}{(r+1)}^{a(r+1)[(n-k)r-k-2]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+2}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-2}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+2}{n-k}\rfloor$.

Proof. 

Let G be any bicyclic graph of order n with k pendant vertices. Thus G contains k vertices having degree one. From Corollary 2, the degree sequence with the largest $P_{1^{\prime }}^a$ index (the smallest $P_{2^{\prime }}^a$ index) is $X=(x_1,x_2,\dots ,x_{n-k},\underset{k}{\underbrace{1,\dots ,1}})$ with $x_1-x_{n-k}\le 1$.

Thus we can suppose that $x_j=l$ or $l+1$, where $j=1,2,\dots ,n-k$ and $l\ge 2$. We denote the number of coordinates in X which are i by $n_i$. So

$$X=(\underset{n_{l+1}}{\underbrace{l+1,\dots ,l+1}},\underset{n_l}{\underbrace{l,\dots ,l}},\underset{k}{\underbrace{1,\dots ,1}}).$$

Then

$$n_{l+1}+n_l+k=n.$$

(2)

Obviously $k<n$, thus we can suppose that $n_l\ge 1$. Since every bicyclic graph has $n+1$ edges, from (1) we obtain

$$\sum _{j=1}^n{x}_j=(l+1)n_{l+1}+l{n}_l+k=2(n+1).$$

(3)

From (2) and (3), we get $n_l+lk=ln-n-2$, which gives $l=\frac{n+2}{n-k}+\frac{n_l}{n-k}$. By (2) we obtain $n_l\le n-k$, thus $l=\lfloor \frac{n+2}{n-k}\rfloor +1$. Therefore,

$$n_l=(n-k)l-n-2=(n-k)⌊\frac{n+2}{n-k}⌋-k-2 \mathrm{and} n_{l+1}=n-(n-k)⌊\frac{n+2}{n-k}⌋+2.$$

Hence

$$X=(\underset{n-(n-k)r+2}{\underbrace{r+2,\dots ,r+2}},\underset{(n-k)r-k-2}{\underbrace{r+1,\dots ,r+1}},\underset{k}{\underbrace{1,\dots ,1}})$$

with $r=\lfloor \frac{n+2}{n-k}\rfloor$.

Let us prove that there exists a graph $G^{\prime }$ with the degree sequence X. Let $G^{\prime }$ be a graph which contains the cycle $C=v_1{v}_2\dots v_{n-k}$, also the edge $v_1{v}_3$ and k pendant vertices are attached to the vertices of C in such a way that the degrees of any two vertices in C differ by at most 1. Then

$$P_1^a(G^{\prime })={(r+2)}^{a[n-(n-k)r+2]}{(r+1)}^{a[(n-k)r-k-2]}$$

and

$$P_2^a(G^{\prime })={(r+2)}^{a(r+2)[n-(n-k)r+2]}{(r+1)}^{a(r+1)[(n-k)r-k-2]}.$$

The proof is complete. □

Example 1.

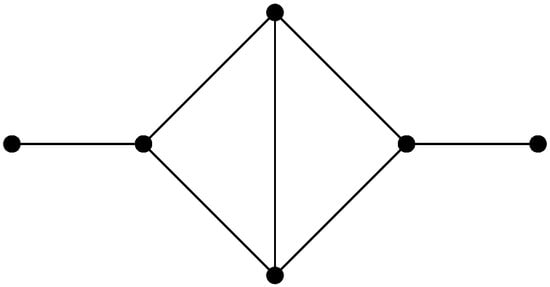
If $n=6$ and $k=2$, then in Theorem 1 we get $r=2$ and the extremal bicyclic graphs have the degree sequence $(3,3,3,3,1,1)$. The example of a graph with this degree sequence is given in Figure 1.

Figure 1. Graph with the degree sequence $(3,3,3,3,1,1)$.

Let $B_n$ be the graph of order n which contains one vertex, say v, adjacent to all the other $n-1$ vertices and one of those $n-1$ vertices is adjacent to two other neighbours of v. Let $H^1$ be the bicyclic graph containing two cycles of length 3 which have one vertex, say v, in common, and v is adjacent to k pendant vertices. So $H^1$ has $k+5$ vertices; see Figure 2. Let $S_{n,k}^1$ be the set containing all the graphs which can be obtained from $H^1$ by $n-k-5$ consecutive subdivisions of any edges. Note that one particular edge of $H^1$ can be subdivided many times, once or zero times in the process of obtaining a graph in $S_{n,k}^1$. Those subdivisions yield $n-k-5$ vertices of degree 2, so every graph in $S_{n,k}^{ϵ}$ has $n-k-1$ vertices of degree 2.

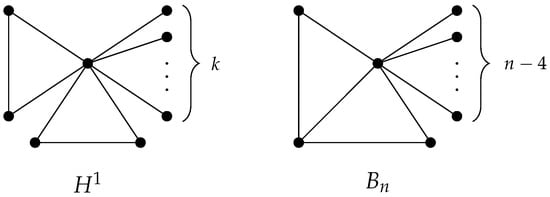
Figure 2. Graphs $H^1$ and $B_n$.

Theorem 2.

Let $a>0$ and G be any bicyclic graph of order n with k pendant vertices.

If $0\le k\le n-5$, then

$$P_1^a(G)\ge {(k+4)}^a{2}^{a(n-k-1)} and P_2^a(G)\le {(k+4)}^{a(k+4)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is any graph in $S_{n,k}^1$.

If $k=n-4$, then

$$P_1^a(G)\ge {(n-1)}^a{3}^a{2}^{2a} and P_2^a(G)\le {(n-1)}^{a(n-1)}{3}^{3a}{2}^{4a}.$$

The equalities hold if and only if G is $B_n$.

Proof. 

Let G be any bicyclic graph of order n with k pendant vertices. Then G contains k vertices having degree one. From Corollary 1, the degree sequence with the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index) is $(k+4,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$.

For $0\le k\le n-5$, the only graphs with the sequence $(k+4,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$ are the graphs in the set $S_{n,k}^1$. Therefore, the graphs $G^{\prime }\in S_{n,k}^1$ are the bicyclic graphs with the smallest $P_1^a$ index (the largest $P_2^a$ index). We get

$$P_1^a(G)\ge P_1^a(G^{\prime })={(k+4)}^a{2}^{a(n-k-1)} \mathrm{and} P_2^a(G)\le P_2^a(G^{\prime })={(k+4)}^{a(k+4)}{2}^{2a(n-k-1)}.$$

For $k=n-4$, obviously there is no graph with the degree sequence $(k+4,\underset{n-k-1}{\underbrace{2,\dots ,2}}$, $\underset{k}{\underbrace{1,\dots ,1}})=(n,2,2,2,\underset{n-4}{\underbrace{1,\dots ,1}})$. From Corollary 1 we know that the degree sequence with the second smallest $P_{1^{\prime }}^a$ index (the second largest $P_{2^{\prime }}^a$ index) is $(k+3,3,\underset{n-k-2}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})=(n-1,3,2,2,\underset{n-4}{\underbrace{1,\dots ,1}})$. The only graph with this sequence is $B_n$, so the bicyclic graph with the smallest $P_1^a$ index (the largest $P_2^a$ index) is $B_n$. Hence

$$P_1^a(G)\ge P_1^a(B_n)={(n-1)}^a{3}^a{2}^{2a} \mathrm{and} P_2^a(G)\le P_2^a(B_n)={(n-1)}^{a(n-1)}{3}^{3a}{2}^{4a}.$$

The proof is complete. □

Example 2.

If $k=n-5$, then the extremal bicyclic graph for Theorem 2 is the graph $H^1$. If $k=n-4$, then $B_n$ is the extremal bicyclic graph; see Figure 2.

4. Graphs with Given Number of Pendant Vertices and Small Number of Edges

Bicyclic graphs are connected graphs with $n+1$ edges, tricyclic graphs are connected graphs with $n+2$ edges and tetracyclic graphs are connected graphs with $n+3$ edges (and n vertices). In this section we study graphs with $n+ϵ$ edges for small $ϵ\in \mathbb{N}$.

We define some tricyclic graphs of order n. Let $T_n$ be the graph which contains one vertex of degree $n-1$ and the subgraph induced by all the other vertices contains $P_3$, $P_2$ and $n-6$ isolated vertices (pendant vertices of $T_n$). Let $T_n^{\prime }$ contain one vertex of degree $n-1$ and the subgraph induced by the other $n-1$ vertices contains a star with 3 edges and $n-5$ isolated vertices. Let $T_n^{″}$ be the graph which contains $K_4$ and one of the vertices of that $K_4$ is adjacent to $n-4$ pendant vertices; see Figure 3.

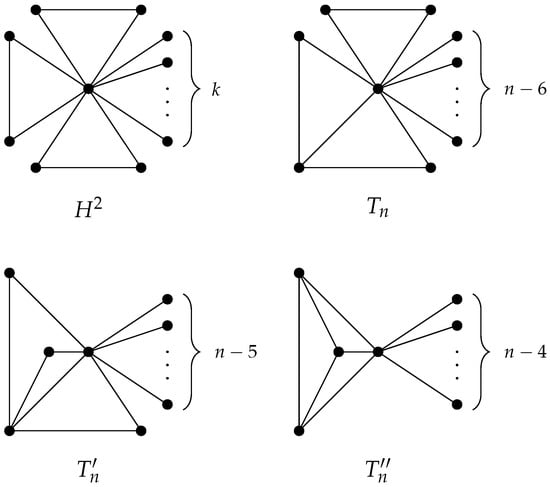
Figure 3. Graphs $H^2$, $T_n$, $T_n^{\prime }$ and $T_n^{″}$.

Let $H^2$ be the tricyclic graph containing 3 cycles of length 3 which have one vertex, say v, in common, and v is adjacent to k pendant vertices. So $H^2$ has $k+7$ vertices; see Figure 3. Let $S_{n,k}^2$ be the set containing all the graphs which can be obtained from $H^2$ by $n-k-7$ consecutive subdivisions of any edges of $H^2$.

Since at least 4 vertices are contained in a graph with more than one cycle, those vertices are not pendant. Thus for the number k of pendant vertices in a tricyclic graph we get $0\le k\le n-4$.

Theorem 3.

Let $a>0$ and G be any tricyclic graph of order n and k pendant vertices.

If $0\le k\le n-7$, then

$$P_1^a(G)\ge {(k+6)}^a{2}^{a(n-k-1)} and P_2^a(G)\le {(k+6)}^{a(k+6)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^2$.

If $k=n-6$, then

$$P_1^a(G)\ge {(n-1)}^a{3}^a{2}^{4a} and P_2^a(G)\le {(n-1)}^{a(n-1)}{3}^{3a}{2}^{8a}.$$

The equalities hold if and only if G is $T_n$.

If $k=n-5$, then

$$P_1^a(G)\ge {(n-1)}^a{2}^{5a} and P_2^a(G)\le {(n-1)}^{a(n-1)}{2}^{14a}.$$

The equalities hold if and only if G is $T_n^{\prime }$.

If $k=n-4$, then

$$P_1^a(G)\ge {(n-1)}^a{3}^{3a} and P_2^a(G)\le {(n-1)}^{a(n-1)}{3}^{9a}.$$

The equalities hold if and only if G is $T_n^{″}$.

Proof. 

Let G be any tricyclic graph of order n and k pendant vertices. Thus G contains k vertices having degree one. From Corollary 1, the degree sequence with the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index) is $(k+6,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$.

For $0\le k\le n-7$, the only graphs with the sequence $(k+6,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$ are the graphs in the set $S_{n,k}^2$. Therefore, the graphs $G^{\prime }\in S_{n,k}^2$ are the tricyclic graphs with the smallest $P_1^a$ index (the largest $P_2^a$ index). Thus

$$P_1^a(G)\ge P_1^a(G^{\prime })={(k+6)}^a{2}^{a(n-k-1)}$$

and

$$P_2^a(G)\le P_2^a(G^{\prime })={(k+6)}^{a(k+6)}{2}^{2a(n-k-1)}.$$

For $k=n-6$, obviously there is no graph with the degree sequence $(k+6,\underset{n-k-1}{\underbrace{2,\dots ,2}}$, $\underset{k}{\underbrace{1,\dots ,1}})=(n,2,2,2,2,2,\underset{n-6}{\underbrace{1,\dots ,1}})$. From Corollary 1 we know that the sequence with the second smallest $P_{1^{\prime }}^a$ index (the second largest $P_{2^{\prime }}^a$ index) is $(k+5,3,\underset{n-k-2}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})=(n-1,3,2,2,2,2,\underset{n-6}{\underbrace{1,\dots ,1}})$. The graph $T_n$ is the only graph with this sequence, thus the tricyclic graph with the smallest $P_1^a$ index (the largest $P_2^a$ index) is $T_n$. Hence

$$P_1^a(G)\ge P_1^a(T_n)={(n-1)}^a{3}^a{2}^{4a} \mathrm{and} P_2^a(G)\le P_2^a(T_n)={(n-1)}^{a(n-1)}{3}^{3a}{2}^{8a}.$$

For $k=n-5$, there is no graph with the degree sequence $(k+6,\underset{n-k-1}{\underbrace{2,\dots ,2}}$, $\underset{k}{\underbrace{1,\dots ,1}})=(n+1,2,2,2,2,\underset{n-5}{\underbrace{1,\dots ,1}})$. Note that the degree of every vertex is at most $n-1$. The degree sequences of the form $(n-1,x_2,x_3,x_4,x_5,\underset{n-5}{\underbrace{1,\dots ,1}})$ satisfying ${\sum }_{i=1}^n{x}_i=2(n+2)$ are $X_1=(n-1,4,2,2,2,\underset{n-5}{\underbrace{1,\dots ,1}})$ and $X_2=(n-1,3,3,2,2,\underset{n-5}{\underbrace{1,\dots ,1}})$. From Lemma 1 we know that $P_{1^{\prime }}^a(X_1)<P_{1^{\prime }}^a(X_2)$ and $P_{2^{\prime }}^a(X_1)>P_{2^{\prime }}^a(X_2)$. The graph $T_n^{\prime }$ is the only graph with the degree sequence $X_1$, thus the tricyclic graph with the smallest $P_1^a$ index (the largest $P_2^a$ index) is $T_n^{\prime }$. Therefore,

$$P_1^a(G)\ge P_1^a(T_n^{\prime })={(n-1)}^a{4}^a{2}^a{2}^a{2}^a={(n-1)}^a{2}^{5a}$$

and

$$P_2^a(G)\le P_2^a(T_n^{\prime })={(n-1)}^{a(n-1)}{4}^{4a}{2}^{2a}{2}^{2a}{2}^{2a}={(n-1)}^{a(n-1)}{2}^{14a}.$$

For $k=n-4$, the only tricyclic graph with a vertex of degree $n-1$ and $n-4$ pendant vertices is $T_n^{″}$ and the degree squence of this graph is $(n-1,3,3,3,\underset{n-4}{\underbrace{1,\dots ,1}})$. Hence

$$P_1^a(G)\ge P_1^a(T_n^{″})={(n-1)}^a{3}^a{3}^a{3}^a={(n-1)}^a{3}^{3a}$$

and

$$P_2^a(G)\le P_2^a(T_n^{″})={(n-1)}^{a(n-1)}{3}^{3a}{3}^{3a}{3}^{3a}={(n-1)}^{a(n-1)}{3}^{9a}.$$

The proof is complete. □

Example 3.

If $k=n-7$, then the extremal tricyclic graph for Theorem 3 is the graph $H^2$. If $k=n-6$, then $T_n$ is the extremal tricyclic graph, if $k=n-5$, then $T_n^{\prime }$ is the extremal graph and if $k=n-4$, then $T_n^{″}$ is the extremal graph; see Figure 3.

For any $ϵ\ge 1$ let $H^{ϵ}$ be the graph containing $ϵ+1$ cycles of length 3 which have one vertex, say v, in common, and v is adjacent to k pendant vertices. So $H^{ϵ}$ has $k+2ϵ+3$ vertices. Let $S_{n,k}^{ϵ}$ be the set containing all the graphs which can be obtained from $H^{ϵ}$ by $n-k-2ϵ-3$ consecutive subdivisions of any edges. Note that one particular edge of $H^{ϵ}$ can be subdivided many times, once or zero times in the process of obtaining a graph in $S_{n,k}^{ϵ}$. Those subdivisions yield $n-k-2ϵ-3$ vertices of degree 2, so every graph in $S_{n,k}^{ϵ}$ has $n-k-1$ vertices of degree 2.

The following bound holds for $ϵ\le \frac{n-3}{2}$ which follows from the inequality $0\le n-2ϵ-3$ presented in Theorem 4.

Theorem 4.

Let G be any graph of order n and size $n+ϵ$ with k pendant vertices, where $0\le k\le n-2ϵ-3$ and $ϵ\in \mathbb{N}$. For $a>0$ we have

$$P_1^a(G)\ge {(k+2ϵ+2)}^a{2}^{a(n-k-1)} and P_2^a(G)\le {(k+2ϵ+2)}^{a(k+2ϵ+2)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^{ϵ}$.

Proof. 

Let G be any graph of order n and size $n+ϵ$ with k pendant vertices. Thus G contains k vertices having degree one. From Corollary 1 we know that the degree sequence with the smallest $P_{1^{\prime }}^a$ index (the largest $P_{2^{\prime }}^a$ index) is $(k+2ϵ+2,\underset{n-k-1}{\underbrace{2,\dots ,2}},\underset{k}{\underbrace{1,\dots ,1}})$. The only graphs with this sequence are the graphs in the set $S_{n,k}^{ϵ}$. Therefore, all the graphs $G^{\prime }\in S_{n,k}^{ϵ}$ are the graphs with the smallest $P_1^a$ index (the largest $P_2^a$ index). Hence

$$P_1^a(G)\ge P_1^a(G^{\prime })={(k+2ϵ+2)}^a{2}^{a(n-k-1)}$$

and

$$P_2^a(G)\le P_2^a(G^{\prime })={(k+2ϵ+2)}^{a(k+2ϵ+2)}{2}^{2a(n-k-1)}.$$

The proof is complete. □

Note that if $k=0$, Theorem 4 gives bounds also for graphs of given order and size which do not contain pendant vertices. From this general Theorem 4, we can obtain the first statements of Theorems 2 and 3. Since a tetracyclic graph is a connected graph with $n+3$ edges, using $ϵ=3$ in Theorem 4, we obtain the following theorem for tetracyclic graphs.

Theorem 5.

Let G be any tetracyclic graph of order n with k pendant vertices, where $0\le k\le n-9$. For $a>0$ we obtain

$$P_1^a(G)\ge {(k+8)}^a{2}^{a(n-k-1)} and P_2^a(G)\le {(k+8)}^{a(k+8)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^3$.

Example 4.

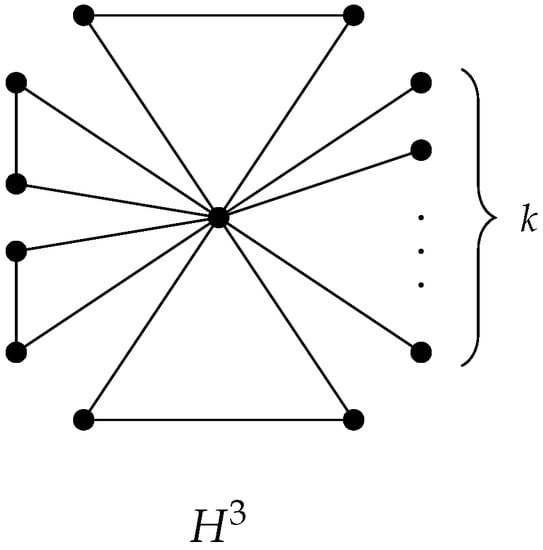
If $ϵ=3$ and $k=n-9$, then the extremal graph for Theorems 4 and 5 is the tetracyclic graph $H^3$; see Figure 4.

Figure 4. Graph $H^3$.

Let us bound the number of edges in a graph with k pendant vertices. If G has k pendant vertices, these vertices yield k edges. The subgraph of G induced by all the other $n-k$ vertices has at most $\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)$ edges, therefore G has at most $\left(\genfrac{}{}{0pt}{}{n-k}{2}\right)+k$ edges. Now we generalize Theorem 1.

Theorem 6.

Let G be any graph of order n, size $m=n+ϵ$ having k pendant vertices, where $k\ge 0$, $ϵ\ge 1$ and $m\le \left(\genfrac{}{}{0pt}{}{n-k}{2}\right)+k$. For $a>0$ we have

$$P_1^a(G)\le {(r+2)}^{a[n-(n-k)r+2ϵ]}{(r+1)}^{a[(n-k)r-k-2ϵ]}$$

and

$$P_2^a(G)\ge {(r+2)}^{a(r+2)[n-(n-k)r+2ϵ]}{(r+1)}^{a(r+1)[(n-k)r-k-2ϵ]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+2ϵ}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-2ϵ}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+2ϵ}{n-k}\rfloor$.

Proof. 

Let G be a graph of order n, size $n+ϵ$ having k pendant vertices. Then G contains k vertices having degree one. From Corollary 2, the degree sequence with the largest $P_{1^{\prime }}^a$ index (the smallest $P_{2^{\prime }}^a$ index) is $X=(x_1,x_2,\dots ,x_{n-k},\underset{k}{\underbrace{1,\dots ,1}})$ with $x_1-x_{n-k}\le 1$.

Thus we can suppose that $x_j=l$ or $l+1$, where $j=1,2,\dots ,n-k$ and $l\ge 2$. We denote the number of coordinates in X being i by $n_i$. So $X=(\underset{n_{l+1}}{\underbrace{l+1,\dots ,l+1}},\underset{n_l}{\underbrace{l,\dots ,l}}$, $\underset{k}{\underbrace{1,\dots ,1}})$. Therefore,

$$n_{l+1}+n_l+k=n.$$

(4)

Obviously $k<n$, thus we can suppose that $n_l\ge 1$. Since we study graphs with $n+ϵ$ edges, from (1) we get

$$\sum _{j=1}^n{x}_j=(l+1)n_{l+1}+l{n}_l+k=2(n+ϵ).$$

(5)

From (4) and (5), we have $n_l+lk=ln-n-2ϵ$, thus $l=\frac{n+2ϵ}{n-k}+\frac{n_l}{n-k}$. By (4), we obtain $n_l\le n-k$, thus $l=\lfloor \frac{n+2ϵ}{n-k}\rfloor +1$. Then

$$n_l=(n-k)l-n-2ϵ=(n-k)⌊\frac{n+2ϵ}{n-k}⌋-k-2ϵ \mathrm{and} n_{l+1}=n-(n-k)⌊\frac{n+2ϵ}{n-k}⌋+2ϵ.$$

Hence

$$X=(\underset{n-(n-k)r+2ϵ}{\underbrace{r+2,\dots ,r+2}},\underset{(n-k)r-k-2ϵ}{\underbrace{r+1,\dots ,r+1}},\underset{k}{\underbrace{1,\dots ,1}}),$$

such that $r=\lfloor \frac{n+2ϵ}{n-k}\rfloor$.

Let us prove that there exists a graph $G^{\prime }$ with the sequence X. Let $G^{\prime }$ be a graph containing the cycle $C=v_1{v}_2\dots v_{n-k}$, also $ϵ$ edges between some vertices in C and k pendant vertices are attached to the vertices of C in such a way that the degrees of any two vertices in C differ by at most 1. Then

$$P_1^a(G^{\prime })={(r+2)}^{a[n-(n-k)r+2ϵ]}{(r+1)}^{a[(n-k)r-k-2ϵ]}$$

and

$$P_2^a(G^{\prime })={(r+2)}^{a(r+2)[n-(n-k)r+2ϵ]}{(r+1)}^{a(r+1)[(n-k)r-k-2ϵ]}.$$

The proof is complete. □

Proofs of the following two theorems can be easily obtained when using $ϵ=2$ and $ϵ=3$ in the proof of Theorem 6.

Theorem 7.

Let G be any tricyclic graph of order n having k pendant vertices, where $0\le k\le n-4$. Then for $a>0$,

$$P_1^a(G)\le {(r+2)}^{a[n-(n-k)r+4]}{(r+1)}^{a[(n-k)r-k-4]}$$

and

$$P_2^a(G)\ge {(r+2)}^{a(r+2)[n-(n-k)r+4]}{(r+1)}^{a(r+1)[(n-k)r-k-4]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+4}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-4}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+4}{n-k}\rfloor$.

Note that any tetracyclic graph has at most $n-5$ pendant vertices.

Theorem 8.

Let G be any tetracyclic graph of order n having k pendant vertices, where $0\le k\le n-5$. For $a>0$ we have

$$P_1^a(G)\le {(r+2)}^{a[n-(n-k)r+6]}{(r+1)}^{a[(n-k)r-k-6]}$$

and

$$P_2^a(G)\ge {(r+2)}^{a(r+2)[n-(n-k)r+6]}{(r+1)}^{a(r+1)[(n-k)r-k-6]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+6}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-6}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+6}{n-k}\rfloor$.

Example 5.

If $n=8$ and $k=2$, then in Theorem 7 we get $r=2$ and the extremal tricyclic graphs have the degree sequence $(3,3,3,3,3,3,1,1)$. If $n=6$ and $k=0$, then in Theorem 8 we get $r=2$ and the extremal tetracyclic graphs have the degree sequence $(3,3,3,3,3,3)$. The examples of graphs with these degree sequences are given in Figure 5. These cases are special cases of Theorem 6 for $ϵ=2$ and $ϵ=3$.

Figure 5. Graphs with the degree sequences $(3,3,3,3,3,3,1,1)$ and $(3,3,3,3,3,3)$.

5. Bounds for $\mathit{a}<\mathbf{0}$

In the proof of Lemma 1 for $y>1$ and $a>0$, we obtain $y^a>1$. Moreover, for $0<y<1$ and $a>0$, we get $0<y^a<1$.

Obviously, $y^a$ represents $\frac{P_{j^{\prime }}^a(X)}{P_{j^{\prime }}^a(X^{\prime })}$ for $j=1,2$. All the terms in $P_{j^{\prime }}^a(X)$ and $P_{j^{\prime }}^a(X^{\prime })$ are greater than zero, thus y and $y^a$ are greater than zero.

Let us give a lemma for $a<0$. A proof is analogous to the proof of Lemma 1 since for $y>1$ and $a<0$, we have $0<y^a<1$. Similarly, for $0<y<1$ and $a<0$, we obtain $y^a>1$.

Lemma 2.

Let X and $X^{\prime }$ be the degree sequences which differ in two coordinates, where $x_i,x_j$ are in X and $x_i+1,x_j-1$ are in $X^{\prime }$, with $x_i\ge x_j\ge 2$ and $1\le i<j\le n$. For $a<0$ we obtain $P_{1^{\prime }}^a(X^{\prime })>P_{1^{\prime }}^a(X)$ and $P_{2^{\prime }}^a(X^{\prime })<P_{2^{\prime }}^a(X)$.

Lemma 2 and results similar to Corollaries 1 and 2 can be used to get the following results for $a<0$.

Theorem 9.

Let G be any graph of order n and size $n+ϵ$ with k pendant vertices, where $0\le k\le n-2ϵ-3$ and $ϵ\in \mathbb{N}$. For $a<0$ we have

$$P_1^a(G)\le {(k+2ϵ+2)}^a{2}^{a(n-k-1)} and P_2^a(G)\ge {(k+2ϵ+2)}^{a(k+2ϵ+2)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^{ϵ}$.

Theorem 10.

Let G be any graph of order n, size $m=n+ϵ$ having k pendant vertices, where $k\ge 0$, $ϵ\ge 1$ and $m\le \left(\genfrac{}{}{0pt}{}{n-k}{2}\right)+k$. For $a<0$ we have

$$P_1^a(G)\ge {(r+2)}^{a[n-(n-k)r+2ϵ]}{(r+1)}^{a[(n-k)r-k-2ϵ]}$$

and

$$P_2^a(G)\le {(r+2)}^{a(r+2)[n-(n-k)r+2ϵ]}{(r+1)}^{a(r+1)[(n-k)r-k-2ϵ]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+2ϵ}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-2ϵ}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+2ϵ}{n-k}\rfloor$.

Finally, we present bounds for bicyclic, tricyclic and tetracyclic graphs.

Theorem 11.

Let $a<0$ and G be any bicyclic graph of order n with k pendant vertices.

If $0\le k\le n-5$, then

$$P_1^a(G)\le {(k+4)}^a{2}^{a(n-k-1)} and P_2^a(G)\ge {(k+4)}^{a(k+4)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is any graph in $S_{n,k}^1$.

If $k=n-4$, then

$$P_1^a(G)\le {(n-1)}^a{3}^a{2}^{2a} and P_2^a(G)\ge {(n-1)}^{a(n-1)}{3}^{3a}{2}^{4a}$$

The equalities hold if and only if G is $B_n$.

Theorem 12.

Let $a<0$ and G be any tricyclic graph of order n and k pendant vertices.

If $0\le k\le n-7$, then

$$P_1^a(G)\le {(k+6)}^a{2}^{a(n-k-1)} and P_2^a(G)\ge {(k+6)}^{a(k+6)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^2$.

If $k=n-6$, then

$$P_1^a(G)\le {(n-1)}^a{3}^a{2}^{4a} and P_2^a(G)\ge {(n-1)}^{a(n-1)}{3}^{3a}{2}^{8a}.$$

The equalities hold if and only if G is $T_n$.

If $k=n-5$, then

$$P_1^a(G)\le {(n-1)}^a{2}^{5a} and P_2^a(G)\ge {(n-1)}^{a(n-1)}{2}^{14a}.$$

The equalities hold if and only if G is $T_n^{\prime }$.

If $k=n-4$, then

$$P_1^a(G)\le {(n-1)}^a{3}^{3a} and P_2^a(G)\ge {(n-1)}^{a(n-1)}{3}^{9a}.$$

The equalities hold if and only if G is $T_n^{″}$.

Theorem 13.

Let G be any tetracyclic graph of order n with k pendant vertices, where $0\le k\le n-9$. For $a<0$ we obtain

$$P_1^a(G)\le {(k+8)}^a{2}^{a(n-k-1)} and P_2^a(G)\ge {(k+8)}^{a(k+8)}{2}^{2a(n-k-1)}.$$

The equalities hold if and only if G is in $S_{n,k}^3$.

Theorem 14.

Let G be any bicyclic graph of order n with k pendant vertices, where $0\le k\le n-4$. For $a<0$ we have

$$P_1^a(G)\ge {(r+2)}^{a[n-(n-k)r+2]}{(r+1)}^{a[(n-k)r-k-2]}$$

and

$$P_2^a(G)\le {(r+2)}^{a(r+2)[n-(n-k)r+2]}{(r+1)}^{a(r+1)[(n-k)r-k-2]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+2}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-2}{\underbrace{r+1,\dots ,r+1}},\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+2}{n-k}\rfloor$.

Theorem 15.

Let G be any tricyclic graph of order n having k pendant vertices, where $0\le k\le n-4$. Then for $a<0$,

$$P_1^a(G)\ge {(r+2)}^{a[n-(n-k)r+4]}{(r+1)}^{a[(n-k)r-k-4]}$$

and

$$P_2^a(G)\le {(r+2)}^{a(r+2)[n-(n-k)r+4]}{(r+1)}^{a(r+1)[(n-k)r-k-4]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+4}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-4}{\underbrace{r+1,\dots ,r+1}},\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+4}{n-k}\rfloor$.

Theorem 16.

Let G be any tetracyclic graph of order n having k pendant vertices, where $0\le k\le n-5$. For $a<0$ we have

$$P_1^a(G)\ge {(r+2)}^{a[n-(n-k)r+6]}{(r+1)}^{a[(n-k)r-k-6]}$$

and

$$P_2^a(G)\le {(r+2)}^{a(r+2)[n-(n-k)r+6]}{(r+1)}^{a(r+1)[(n-k)r-k-6]}.$$

The equalities hold if and only if G has the degree sequence $(\underset{n-(n-k)r+6}{\underbrace{r+2,\dots ,r+2}}$, $\underset{(n-k)r-k-6}{\underbrace{r+1,\dots ,r+1}}$, $\underset{k}{\underbrace{1,\dots ,1}})$, where $r=\lfloor \frac{n+6}{n-k}\rfloor$.

6. Conclusion

In this paper, we used our new methods to obtain lower and upper bounds on the general multiplicative Zagreb indices for bicyclic graphs of given order and number of pendant vertices. Then we generalized our techniques and presented bounds for $P_1^a$ and $P_2^a$ indices of tricyclic graphs, tetracyclic graphs and graphs of given order, size and number of pendant vertices. We showed that all our bounds are sharp by presenting extremal graphs. Let us note that bounds for the classical multiplicative Zagreb indices are special cases of our results.