Ritz Method in Vibration Analysis for Embedded Single-Layered Graphene Sheets Subjected to In-Plane Magnetic Field
Abstract
1. Introduction
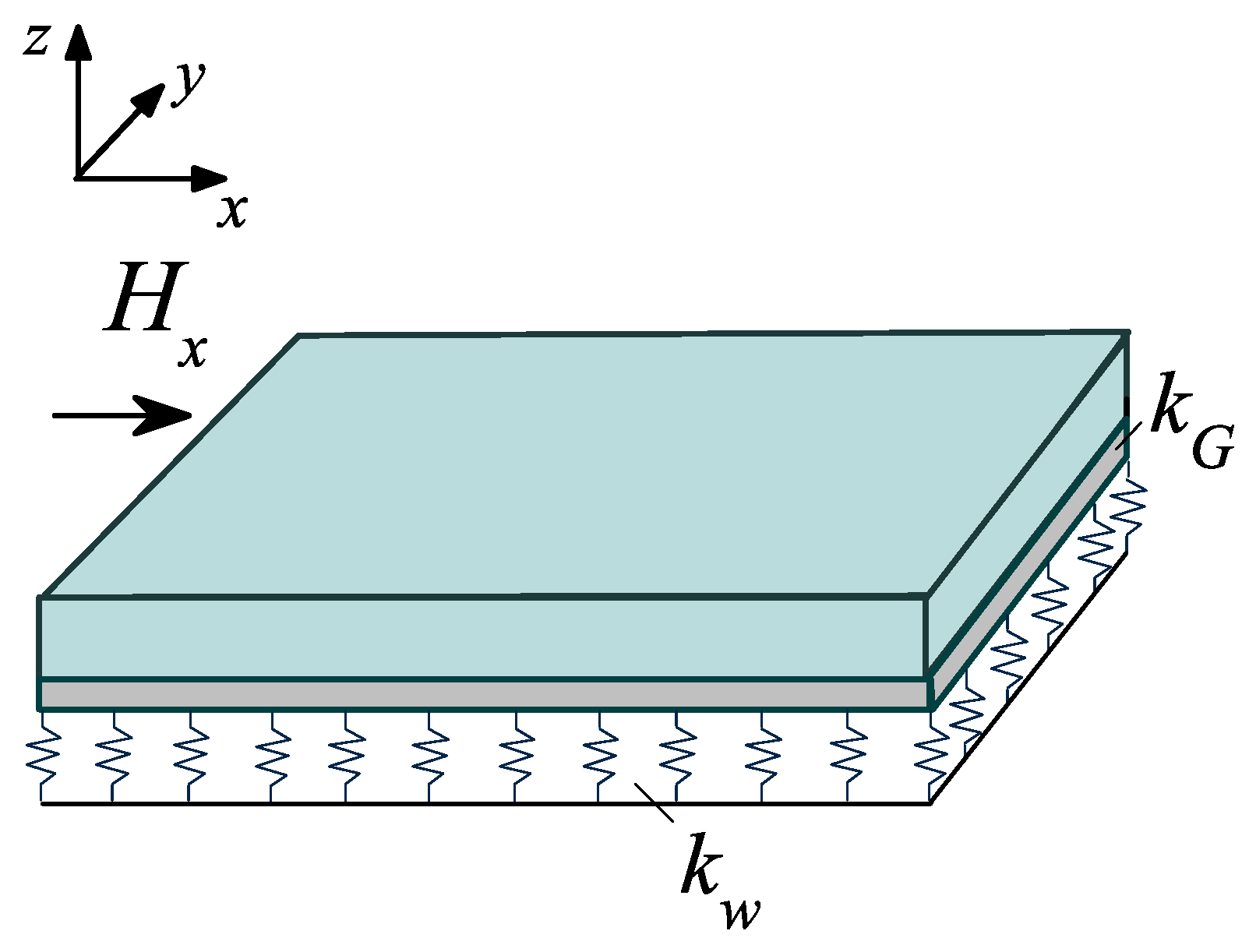
2. Formulation of the Problem
3. Influence of the Magnetic Field
4. Application of the Ritz Method
5. Solution by the Navier Method
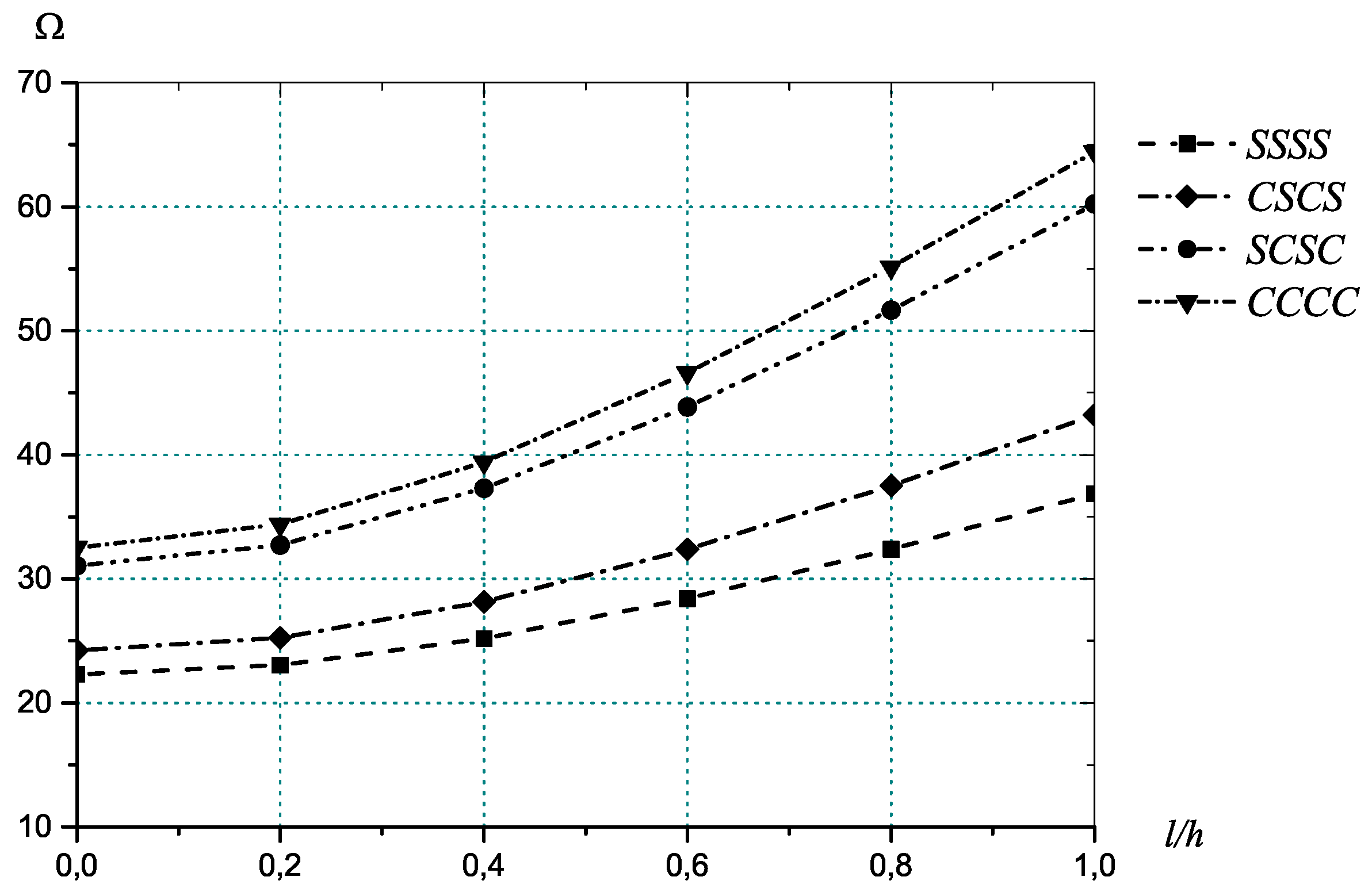
6. Results and Discussions
7. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NEMS | nano-electro mechanical systems |
| MEMS | micro-electro mechanical systems |
| SSSS | all edges are simply supported |
| CCCC | all edges are clamped |
| SSSC | three edges are simply supported and one is clamped |
| SCSC | two opposite sides are simply supported, the other two ones are clamped |
| SCSF | two opposite sides are simply supported, one is clamped and one is free |
| SSSF | the sides except one are simply supported and one is free |
| CSCS | two opposite sides are clamped, the other two ones are simply supported |
References
- Bu, I.; Yang, C. High-performance ZnO nanoflake moisture sensor. Superlattices Microstruct. 2012, 51, 745–753. [Google Scholar] [CrossRef]
- Hoa, N.; Duy, N. Hieu NCrystalline mesoporous tungsten oxide nanoplate monoliths synthesized by directed soft template method for highly sensitive NO2 gas sensor applications. Mater. Res. Bull. 2013, 48, 440–448. [Google Scholar] [CrossRef]
- Kriven, W.; Kwak, S.; Wallig, M.; Choy, J. Bio-resorbable nanoceramics for gene and drug delivery. Mrs Bull. 2004, 29, 33–37. [Google Scholar] [CrossRef]
- Bi, L.; Rao, Y.; Tao, Q.; Dong, J.; Su, T.; Liu, F.; Qian, W. Fabrication of large-scale gold nanoplate films as highly active SERS substrates for label-free DNA detection. Biosens. Bioelectron. 2013, 43, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Guo, Q.; Li, S.; Shi, J.; Liu, L. Heat transfer enhancement of paraffin wax using graphite foam for thermal energy storage. Sol. Energy Mater. Sol. Cells 2010, 94, 1011–1014. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Chong, A.C.M.; Yang, F.; Lam, D.C.C.; Tong, P. Torsion and bending of micron-scaled structures. J. Mater. Res. 2001, 16, 1052–1058. [Google Scholar] [CrossRef]
- Stölken, J.S.; Evans, A.G. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Theory of Deformable Bodies; Delphenich, D.H., Ed.; Scientific Library A. Herman and Sons: Paris, France, 1909. [Google Scholar]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration Mech. Anal. 1962, 11. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple stresses. Arch. Ration Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Koiter, W.T. Couple stresses in the theory of elasticity, I and II. Proc. K Ned. Akad. Wet B 1964, 67, 17–44. [Google Scholar]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Tsiatas, G.C. A new Kirchhoff plate model based on a modified couple stress theory. Int. J. Solids Struct. 2009, 46, 2757–2764. [Google Scholar] [CrossRef]
- Yin, L.; Qian, Q.; Wang, L.; Xia, W. Vibration analysis of microscale plates based on modified couple stress theory. Acta Mech. Solida Sin. 2010, 23, 386–393. [Google Scholar] [CrossRef]
- Simsek, M.; Aydın, M.; Yurtcu, H.H.; Reddy, J.N. Size-dependent vibration of a microplate under the action of a moving load based on the modified couple stress theory. Acta Mech. 2015, 226, 3807–3822. [Google Scholar] [CrossRef]
- Jomehzadeh, E.; Noori, H.R.; Saidi, A.R. The size-dependent vibration analysis of micro-plates based on a modified couple stress theory. Physica E 2011, 43, 877–883. [Google Scholar] [CrossRef]
- Tsiatas, A.J.; Yiotis, G.C. A Microstructure-Dependent Orthotropic Plate Model Based on a Modified Couple Stress Theory Recent Developments in Boundary Element Methods; Sapountzakis, E.J., Ed.; National Technical University of Athens: Athens, Greece, 2010; pp. 295–308. [Google Scholar]
- Ziaee, S. Linear free vibration of micro-/nano-plates with cut-out in thermal environment via modified couple stress theory and Ritz method. Ain Shams Eng. J. 2018, 9, 2373–2381. [Google Scholar] [CrossRef]
- Tsiatas, G.C.; Yiotis, A.J. Size effect on the static, dynamic and buckling analysis of orthotropic Kirchhoff-type skew micro-plates based on a modified couple stress theory: Comparison with the nonlocal elasticity theory. Acta Mech. 2015, 226, 1267–1281. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Free vibration analysis for single-layered graphene sheets in an elastic matrix via modified couple stress theory. Mater. Des. 2012, 42, 164–171. [Google Scholar] [CrossRef]
- Bastami, M.; Behjat, B. Ritz Solution of Buckling and Vibration Problem of nanoplates embedded in an elastic medium. Sigma J. Eng. Nat. Sci. 2017, 35, 285–302. [Google Scholar]
- Mohammadi, M.; Moradi, A.; Ghayour, M.; Farajpour, A. Exact solution for thermo-mechanical vibration of orthotropic mono-layer graphene sheet embedded in an elastic medium. Lat. Am. J. Solids Struct. 2014, 11, 437–458. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.; Goodarzi, M.; Ghayour, M.; Alivand, S. Small Scale effect on the vibration of orthotropic plates embedded in an elastic medium and under biaxial in-plane pre-load via nonlocal elasticity theory. J. Solid Mech. 2012, 4, 128–143. [Google Scholar]
- Behfar, K.; Naghdabadi, R. Nanoscale vibrational analysis of a multi-layered graphene sheet embedded in an elastic medium. Compos. Sci. Technol. 2005, 65, 1159–1164. [Google Scholar] [CrossRef]
- Choi, E.; Brooks, J.; Eaton DAl-Haik, M.; Hussaini, M.; Garmestani, H.; Li DDahmen, K. Enhancement of thermal and electrical properties of carbon nanotube polymer composites by magnetic field processing. J. Appl. Phys. 2003, 94, 6034–6039. [Google Scholar] [CrossRef]
- Lee, S.; Ma, C.; Yuen, S.; Teng, C.; Liao, S.; Huang, Y.; Tsai, M.; Su, A.; Wang, I. Magnetic field enhances the graphitized structure and field emission effect of carbon nanotubes. Thin Solid Film. 2011, 519, 4166–4173. [Google Scholar] [CrossRef]
- Faugeras, C.; Kossacki, P.; Basko, D.; Amado, M.; Sprinkle, M.; Berger, C.; De Heer, W.; Potemski, M. Effect of a magnetic field on the two-phonon Raman scattering in graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 155436. [Google Scholar] [CrossRef]
- Wang, Y.; Hoang, Y.; Song, Y.; Zhang, X.; Ma, Y.; Liang, J.; Chen, Y. Room-temperature ferromagnetism of graphene. Nano Lett. 2009, 9, 220–224. [Google Scholar] [CrossRef]
- Murmu, T.; McCarthy, M.A.; Adhikari, S. In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach. Compos. Struct. 2013, 96, 57–63. [Google Scholar] [CrossRef]
- Kiani, K. Revisiting the free transverse vibration of embedded single-layer graphene sheets acted upon by an in-plane magnetic field. J. Mech. Sci. Technol. 2014, 28, 3511–3516. [Google Scholar] [CrossRef]
- Ghorbanpour Arani, A.H.; Maboudi, M.J.; Ghorbanpour Arani, A.; Amir, S. 2D-Magnetic Field and Biaxiall In-Plane Pre-Load Effects on the Vibration of Double Bonded Orthotropic Graphene Sheets. J. Solid Mech. 2013, 5, 193–205. [Google Scholar]
- Atanasov, M.S.; Karlicic, D.; Kozic, P. Forced transverse vibrations of an elastically connected nonlocal orthotropic double-nanoplate system subjected to an in-plane magnetic field. Acta Mech. 2017, 228, 2165–2185. [Google Scholar] [CrossRef]
- Vol’mir, A.S. Nonlinear Dynamics of Plates and Shells; Nauka: Moscow, Russia, 1972. [Google Scholar]
- Baferani, A.H.; Saidi, A.R.; Ehteshami, H. Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]
- Parida, S.; Mohanty, S.C. Nonlinear free vibration analysis of functionally graded plate resting on elastic foundation in thermal environment using higher-order shear deformation theory. Sci. Iran. B 2019, 26, 815–833. [Google Scholar] [CrossRef]
- Rossi, R.E.; Bambill, D.V.; Laura, P.A.A. Vibrations of a rectangular orthotropic plate with a free edge: A comparison of analytical and numerical results. Ocean Eng. 1998, 25, 521–527. [Google Scholar] [CrossRef]

| Method | SSSS | SSSC | SCSC | SCSF | SSSF | ||
|---|---|---|---|---|---|---|---|
| [36] | 0 | 0 | 19.737 | 23.643 | 28.944 | 12.693 | 11.69 |
| [37] | 19.735 | 23.659 | 28.995 | - | 11.677 | ||
| RS | 19.739 | 23.646 | 28.949 | 12.687 | 11.418 | ||
| [36] | 100 | 48.615 | 51.318 | 54.674 | 37.977 | 37.152 | |
| [37] | 48.547 | 51.253 | 54.617 | - | 37.102 | ||
| RS | 48.615 | 51.323 | 54.679 | 37.981 | 37.129 | ||
| [36] | 1000 | 141.873 | 144.2 | 146.719 | 112.481 | 111.745 | |
| [37] | 140.182 | 142.439 | 144.877 | - | 110.424 | ||
| RS | 141.873 | 144.479 | 146.74 | 112.672 | 111.746 | ||
| [36] | 100 | 0 | 22.126 | 25.671 | 30.623 | 16.149 | 15.383 |
| [37] | 22.125 | 25.687 | 30.672 | - | 15.373 | ||
| RS | 22.127 | 25.673 | 30.628 | 16.155 | 15.178 | ||
| [36] | 100 | 49.633 | 52.283 | 55.581 | 39.272 | 38.474 | |
| [37] | 49.566 | 52.22 | 55.524 | - | 38.426 | ||
| RS | 49.633 | 52.289 | 55.586 | 39.276 | 38.453 | ||
| [36] | 1000 | 142.225 | 144.547 | 147.06 | 112.925 | 112.192 | |
| [37] | 140.538 | 142.789 | 145.222 | - | 110.876 | ||
| RS | 142.225 | 144.824 | 147.081 | 113.115 | 112.193 | ||
| [36] | 1000 | 0 | 37.276 | 39.483 | 42.869 | 34.075 | 33.714 |
| [37] | 37.274 | 39.493 | 42.902 | - | 33.708 | ||
| RS | 37.277 | 39.485 | 42.873 | 34.073 | 33.621 | ||
| [36] | 100 | 57.995 | 60.278 | 63.160 | 49.419 | 48.789 | |
| [37] | 57.936 | 60.222 | 63.109 | - | 48.749 | ||
| RS | 57.995 | 60.283 | 63.165 | 49.420 | 48.771 | ||
| [36] | 1000 | 145.355 | 147.627 | 150.088 | 116.842 | 116.134 | |
| [37] | 143.704 | 145.906 | 148.288 | - | 114.862 | ||
| RS | 145.355 | 147.899 | 150.109 | 117.026 | 116.135 |
| Method | ||||
|---|---|---|---|---|
| [21] | 0 | 17.543 | 36.034 | 45.660 |
| [38] | 17.860 | 36.295 | 45.683 | |
| RS | 17.880 | 36.299 | 45.704 | |
| [21] | 0.1 | 18.432 | 37.326 | 47.920 |
| RS | 18.687 | 37.441 | 47.734 | |
| [21] | 0.2 | 20.697 | 40.921 | 53.832 |
| RS | 20.802 | 40.629 | 53.060 | |
| [21] | 0.3 | 23.745 | 46.228 | 62.111 |
| RS | 23.717 | 45.350 | 60.470 | |
| [21] | 0.4 | 27.258 | 52.708 | 71.983 |
| RS | 27.114 | 51.122 | 69.194 |
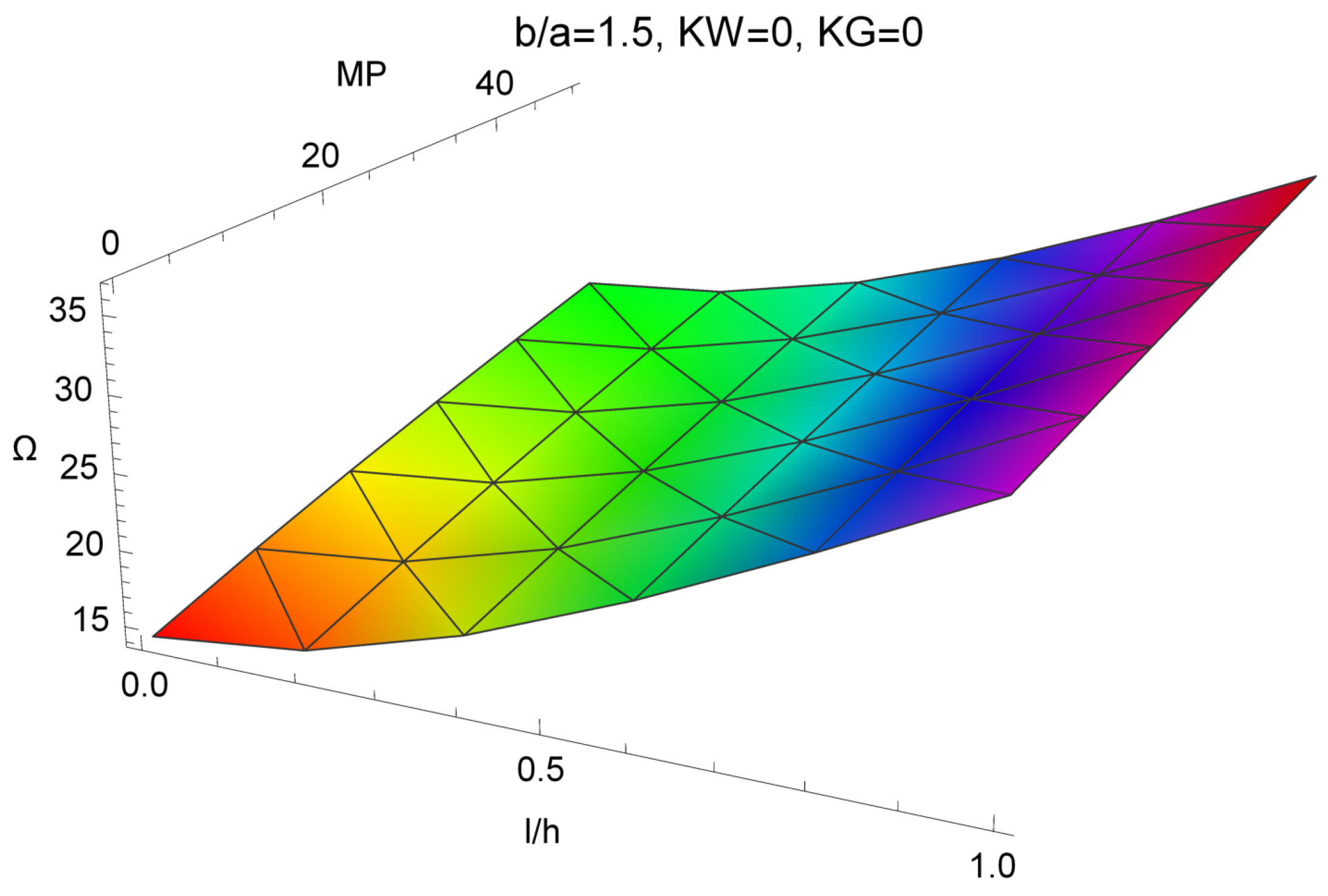
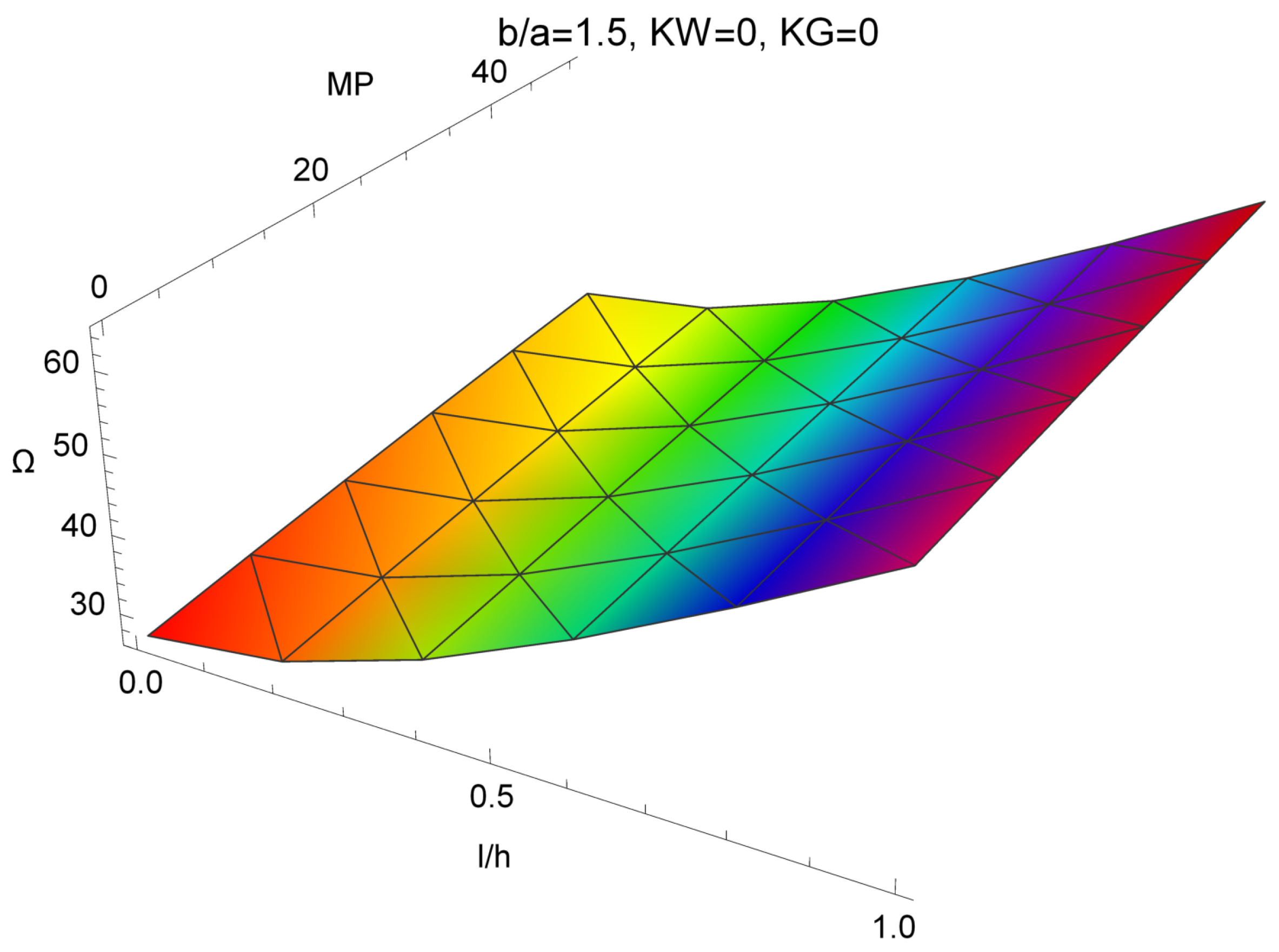
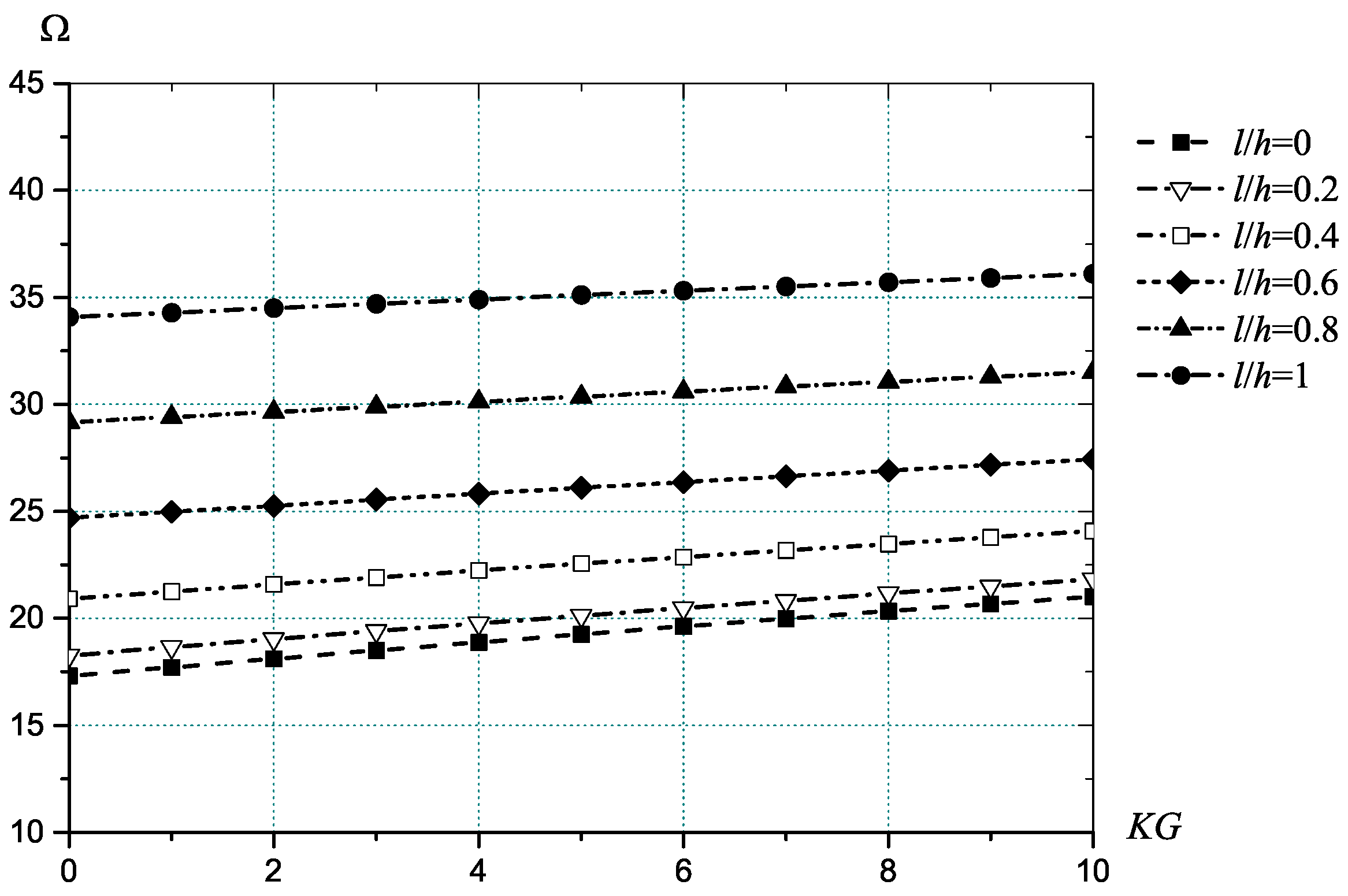
| Method | MP | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | ||
| RS | 0 | 21.0203 | 21.8251 | 24.0784 | 27.4257 | 31.5203 | 36.1088 |
| NS | 21.0205 | 21.8253 | 24.0788 | 27.4262 | 31.5209 | 36.1096 | |
| RS | 25 | 24.0608 | 24.767 | 26.7739 | 29.8201 | 33.6244 | 37.9594 |
| NS | 24.0612 | 24.7674 | 26.7744 | 29.8207 | 33.6251 | 37.9602 | |
| RS | 50 | 26.7581 | 27.3948 | 29.2218 | 32.0361 | 35.6043 | 39.7239 |
| NS | 26.7585 | 27.3953 | 29.2223 | 32.036 | 35.6051 | 39.7248 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazur, O.; Awrejcewicz, J. Ritz Method in Vibration Analysis for Embedded Single-Layered Graphene Sheets Subjected to In-Plane Magnetic Field. Symmetry 2020, 12, 515. https://doi.org/10.3390/sym12040515
Mazur O, Awrejcewicz J. Ritz Method in Vibration Analysis for Embedded Single-Layered Graphene Sheets Subjected to In-Plane Magnetic Field. Symmetry. 2020; 12(4):515. https://doi.org/10.3390/sym12040515
Chicago/Turabian StyleMazur, Olga, and Jan Awrejcewicz. 2020. "Ritz Method in Vibration Analysis for Embedded Single-Layered Graphene Sheets Subjected to In-Plane Magnetic Field" Symmetry 12, no. 4: 515. https://doi.org/10.3390/sym12040515
APA StyleMazur, O., & Awrejcewicz, J. (2020). Ritz Method in Vibration Analysis for Embedded Single-Layered Graphene Sheets Subjected to In-Plane Magnetic Field. Symmetry, 12(4), 515. https://doi.org/10.3390/sym12040515






