Abstract
We consider the magnetic monopole in the axionic dark matter environment (axionic dyon) in the framework of the Reissner-Nordström-de Sitter model. Our aim is to study the distribution of the pseudoscalar (axion) and electric fields near the so-called folds, which are characterized by the profiles with the central minimum, the barrier on the left, and the maximum on the right of this minimum. The electric field in the fold-like zones is shown to change the sign twice, i.e., the electric structure of the near zone of the axionic dyon contains the domain similar to a double electric layer. We have shown that the described fold-like structures in the profile of the gravitational potential, and in the profiles of the electric and axion fields can exist, when the value of the dyon mass belongs to the interval enclosed between two critical masses, which depend on the cosmological constant.
PACS:
04.20.Jb; 04.40.Nr; 14.80.Hv
1. Introduction
Global and local phenomena in our Universe are interrelated. When we speak about the cosmological constant , first of all we think about the global structure of the Universe and about the rate of its expansion [1]. On the other hand, the cosmological constant is associated with one of the models of the dark energy [2,3,4], and the influence of the term on the structure of compact objects, black holes and wormholes can be interpreted as the dark energy fingerprints [5]. Specific details of the causal structure of spherically symmetric objects, the number and types of the horizons can also be associated with the cosmological constant. For instance, in the framework of non-minimal extensions of the Einstein–Maxwell and Einstein–Yang–Mills models with non-vanishing cosmological constant the solutions regular at the center appear, if the parameters of the non-minimal coupling are linked by specific relationships with the cosmological constant [6,7]. In other words, the regularity at the center is connected with the appropriate asymptotic behavior.
The dark matter, the second key element of all modern cosmological scenaria [8,9,10], can play the unique role in the problem of identification of the relativistic compact objects with strong electromagnetic fields. When one studies the properties of the gravitational field of the object, the standard theoretical tool is based on the analysis of the dynamics of test particles; usually, one studies the trajectories of massive and massless particles reconstructing the fine details of the gravitational fields. When we deal with the axions, the light pseudo-bosons [11,12,13], as the possible representatives of the dark matter [14,15,16,17,18,19,20,21], we can not monitor the motion of an individual particle, and the analysis of the dark matter halos comes to the fore.
The dark matter particles are not yet identified. There are few candidates, which can be classified as WIMPs and non-WIMPs (Weekly Interacting Massive Particles); the sets of candidates include light bosons and fermions; these candidates can compose the systems indicated as cold, warm and hot dark matter components. In fact, one can assume that there are a few different fractions, which are united by a common term dark matter. We analyze the axionic fraction of the dark matter, and below we use the short terms axionic dark matter and axions. For the description of the axionic dark matter, we use the master equations for the interacting pseudoscalar and electromagnetic field [22]; over the last thirty years, they have been known as the equations of axion electrodynamics [23,24]. Furthermore, we follow the idea that the axionic fraction of the dark matter behaves as a correlated system, in particular, the axions can form the Bose–Einstein condensate [25].
The dark matter forms specific cosmological units: halos, sub-halos, filaments, walls, the structure of which admits the recognition of the type of the corresponding central elements. We assume that compact relativistic objects with strong gravitational and electromagnetic fields distort the axionic fraction of the dark matter halos, which surround them (see, e.g., [26,27] for details). For instance, when the magnetic field of the star possesses the dipolar component, the axionic halo is no longer spherically symmetric and is characterized by dipole, quadruple, etc. moments. In other words, the modeling of the halo profiles for the magnetic stars can be useful in the procedure of identification of these objects, as well as, in the detailing of their structures.
Our goal is to analyze specific details of the axionic dark matter profiles, which can be formed near the folds in the profile of the gravitational potential. The axion distribution near the folds is non-monotonic, thus the electric field induced by the strong magnetic field in the axionic environment can signal about the appearance of the inverted layers analogous to the ones in the axionically active plasma [28]. We show that, when the spacetime is characterized by the non-vanishing cosmological constant, the folds in the profiles of the gravitational potential appear, the solutions to the equations for the pseudoscalar (axion) field inherit the fold-like behavior, and the axionically induced electric field changes the sign in these domains in analogy with the phenomena of stratification in the axionically active plasma [28].
The paper is organized as follows. In Section 2, we discuss mathematical details, describing the magneto-electro-statics of the axionic dyons. In Section 3, we introduce and mathematically describe the idea of folds in the profile of the gravitational potential. In Section 4, we analyze the solutions to the key equations of the model and illustrate the appearance of the fold-like structures in the profiles of axion and electric fields. Section 5 contains discussion.
2. Description of the Axionic Dark Matter Profiles
2.1. The Total Action Functional
We consider the model, which can be described by the total action functional
Here is the Einstein–Hilbert functional with the Ricci scalar R and cosmological constant
and describes the contribution of a matter and/or fields, which form the background spacetime. The action functional of the axiono-electromagnetic subsystem is represented in the form
where is the Maxwell tensor and is its dual tensor; denotes the dimensionless pseudoscalar (axion) field, V is the potential of the pseudoscalar field, and is the parameter reciprocal to the constant of the axion-photon coupling .
2.2. Background State
We follow the hierarchical approach, according to which the background gravitational field is considered to be fixed, and the axionic dark matter is distributed in this given spacetime. Why we do it? The relativistic objects of the neutron star type are compact, but the mass density inside these objects is very high, about . The average mass density of the dark matter is known to be estimated as , but, in contrast to the dense objects, the dark matter is distributed quasi-uniformly in the whole Universe. Thus, the gravitational field in the vicinity of the dense magnetic stars is predetermined by the baryonic matter and by the magnetic field with very high energy. From the mathematical point of view, in order to describe the background state we use only two elements of the total action functional (1), namely, , and consider the known solutions to the corresponding master equations. As for the axionic and electric subsystems, we obtain the master equations and analyze their solutions with the assumption that the gravity field is already found.
2.3. Master Equations of the Axion Electrodynamics
In this work we assume that the potential of the axion field is of the form . More sophisticated periodic potential is considered in the papers [27,28]. Mention should be made, that we use the system of units, in which , , ; in this case the dimensionality of the axion mass coincides with the one of the inverse length. In the standard system of units we have to replace with . Variation of the action functional (3), with respect to pseudoscalar field gives the known master equation
Variation procedure associated with the electromagnetic potential gives the equation
This equation, being supplemented by the equation
can, as usual, be transformed into
2.4. Static Spacetime with Spherical Symmetry
We assume that the background spacetime is static and spherically symmetric, and is described by the metric
When the pseudoscalar and electromagnetic fields inherit the spacetime symmetry, we obtain that is the function of the radial variable only, , and the potential of the electromagnetic field can be presented in the form
When one deals with the magnetic monopole of the Dirac type, the azimuthal component of the potential is considered to be chosen in the form
where is the magnetic charge (see, e.g., [24,29]). The Equations (7) and (6) can be reduced to one equation only, which contains the electrostatic potential
The Equation (4) takes now the form
Integration of the Equation (11) gives
where K is the constant of integration. The function plays here the role of an effective electric charge, which is virtually distributed around the object at the presence of the axion field. This idea allows us to use the term axionically induced electric field.
As the next step, we replace the term in the right-hand side of (12) with (13), and obtain the master equation for the pseudoscalar (axion) field
Below, we analyze the solutions to the Equation (14) for models, in which the known metric function contains the non-vanishing cosmological constant.
3. On the Features of the Exact Solution Describing the Dirac Magnetic Monopole in the Spacetime with Cosmological Constant
3.1. Geometrical Aspects and Definition of the Fold
The magnetic monopole forms the background spacetime with the well-known metric
Since we work with the units with and , the asymptotic mass M and the magnetic charge of the monopole have the formal dimensionality of the length. The metric (15) covers the following exact solutions.
1. When and , we obtain the de Sitter metric in the so-called -representation.
It is well-known that using the coordinate transformations
one can obtain the de Sitter metric in the form:
When the cosmological constant is positive, , the coordinate transformation (17) is defined for the domain, in which the argument of the logarithm is positive, i.e., when , in other words, indicates the cosmological horizon. When , we deal with the anti-de Sitter spacetime, which has no horizons.
2. When , we obtain the Schwarzschild-de Sitter metric
When , depending on the value of the mass M, the spacetime can have two, one or zero horizons. When , there is one horizon. When = 0, we deal with the Schwarzschild model, which is characterized by one event horizon at r = 2M.
3. General case: The Schwarzschild–Reissner–Nordström–de Sitter solution. Searching for the horizons from the equation , we happen to be faced with the algebraic equation of the fourth order, and this spacetime is known to be equipped by three horizons as maximum. But our goal is more detailed: we would like to find the sets of parameters M, and , for which the profile contains folds. We define the fold as the domain, which is characterized by the following two features:
- 1.
- the profile has the central minimum, the barrier on the left of the minimum, and the maximum on the right;
- 2.
- this domain is inside the cosmological horizon, but it is not hidden inside the event horizon, i.e., in this domain.
We have to stress, that when = 0, the metric function can have the barrier on the left, the minimum, but there is no maximum on the right-hand side, there is only the monotonic curve, which tends asymptotically to the horizontal line . Furthermore, one can imagine the folds of the second kind, for which the barrier is on the right-hand side of the minimum, and the maximum on the left-hand side, respectively. In this paper we consider the first variant of the fold only.
3.2. Horizons
3.2.1. Auxiliary Function Indicating the Number of Horizons
The analysis of the causal structure and of the folds appearance is based on the following approach (this approach was successfully applied in [6,7] for the case with the equation of the sixth order). First, we consider that , and rewrite the equation in the form
The auxiliary function starts from infinity at and tends to minus infinity at ; it can possess two or zero local extrema depending on the value of the dimensionless guiding parameter .
3.2.2. The Case
When , the function has minimum and maximum, respectively, on the spheres, indicated as
The sketch of this function is depicted on the Figure 1a. The number of horizons is predetermined by the number of the intersection points of the horizontal mass line and of the graph of the function .
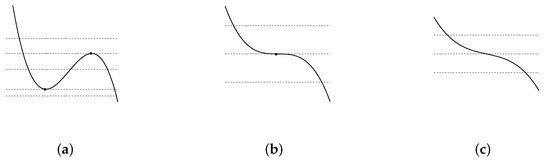
Figure 1.
Typical sketches of the auxiliary function (20), which illustrate the number of horizons depending on the values of the guiding parameter and of the asymptotic mass M. Panel illustrates the case ; panel relates to the case , and panel corresponds to .
According to the sketch , the values and define two critical values of the mass:
Let us analyze the ratio as a function of the dimensionless parameter :
Clearly, we deal with defined on the interval monotonic function, which takes it maximal value at , and tends to at . In other words, when , the ratio does not exceed one, and the critical mass belongs to the interval . In the standard units we have to replace and , where is the vacuum permittivity; thus, the condition reads .
For different values of the asymptotic mass of the object, M, we obtain the following results.
- When , the mass line crosses the indicated graph in one point, i.e., there is only one (cosmological) horizon.
- When , the mass line is the tangent one with respect to the minimum of this graph, thus, there are two horizons: the double event horizon and the simple cosmological one.
- When , there are three intersection points, thus, there are three horizons: the inner and outer event horizons and the cosmological one.
- When there are two horizons: the simple event horizon and the double cosmological one.
- When , there is only one horizon; but in contrast to the case , it is the specific case, when all the apparent Universe is inside the event horizon (see, e.g., [30,31] for some analogy).
3.2.3. The Case
For this case the values and coincide, ; the critical masses also coincide, . Now, according to the panel of Figure 1, there are simple cosmological horizons for every , and the event horizons are absent. In the case the graph of the function has the cubic inflexion point, when the minimum and maximum coincide; now one has triple horizon, i.e., the inner, outer horizons coincide with the cosmological one.
3.2.4. The Case
For this case the values and are complex, thus, the extrema of the auxiliary function are absent, and according to the panel of Figure 1. for every mass M there is only one intersection point corresponding to the cosmological horizon.
Short Resume
If we search for the models with the cosmological horizon, but without the event horizons, we can choose one of the following conditions:
- 1.
- , ;
- 2.
- , ;
- 3.
- .
We consider below the first case.
3.3. Folds
The next point of our analysis is the study of the folds. We consider now the derivative of the metric function
and rewrite the equation as follows:
When we consider the extrema of the auxiliary function , we obtain that there exists the minimum at , which corresponds to the critical value of the mass
When , it is simply to show that . Indeed, the ratio can be rewritten as follows:
where . This ratio is equal to one, when , and tends monotonically to infinity at , in other words, the graph of the function locates above the horizontal line , when .
Taking into account these features, we can state the following.
- When , the horizontal mass line crosses the graph of the function twice; this means that there are two extrema: the minimum and maximum.
- When , two extrema coincide forming the cubic inflexion point.
- When , the profile is monotonic.
We are interested to study the case , since only this case relates to the presence of the fold, which we search for. At the same time we hope to find the solution without event horizons (only the cosmological horizon can exist). It is possible when .
3.4. Final Remarks about the Features of the Spacetime Geometry
3.4.1. The Choice of the Appropriate Scale for the Radial Variable
In order to clarify the possibility of the folds existence, we rewrite the basic equations using the replacement
Keeping in mind that that there are two specific radii: first, the quantity , which relates to the cosmological scale, second, , which is the Reissner-Nordström radius, we see that (28) can be rewritten using the geometric mean value . In terms of the new dimensionless variable x we obtain
This representation of the Reissner-Nordström-de Sitter metric shows explicitly that there are, in fact, two dimensionless guiding parameters of the model: the parameter and the reduced mass . In Figure 2, we present three illustrations of the folds in the profile of the metric function , which has no event horizons, but possesses the cosmological horizon.
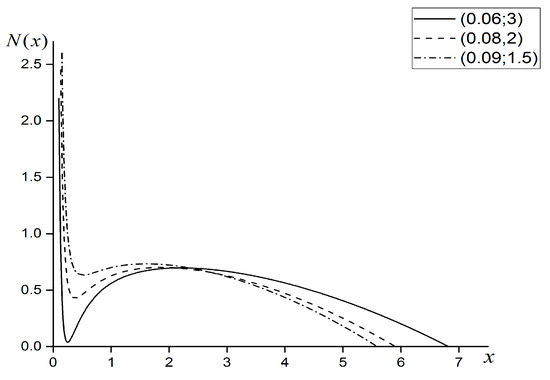
Figure 2.
Folds in the profiles of the metric function (29). There exists the infinite barrier on the left-hand side, the central minimum, and the maximum on the right-hand side. The fold is situated in the domain with positive and is not harbored by the event horizon. The dimensionless guiding parameters and are presented near the graphs in the box.
3.4.2. On the Problem of Naked Singularity and Cosmic Censorship Conjecture
The point is singular for the metric with the coefficient (29). Since we consider the spacetime without event horizons, this point should be indicated as the naked singularity, which is typical for the Reissner–Nordström metric with dominating charge (the so-called super-extremal case). The discussions about physical sense of such solutions were activated by Roger Penrose, who has formulated the cosmic censorship conjecture [32]. Active debates concerning the physical status of the naked singularity continue until now, and there are three groups of disputants. The representatives of the first group insist that the solutions describing the naked singularity are non-physical. Scientists from the second group admit that such naked singularities exist in the nature, that it is still open problem, and they propose the tests to verify this hypothesis (see, e.g., [33,34,35,36] and references therein). We belong to the third group, and we believe that the paradigm of the non-minimal coupling of the photons with the spacetime curvature removes this problem at all. In the paper [37] we have shown, that in the model of non-minimal Dirac monopole an additional horizon, formed due to the coupling of the photons to the curvature, appears, so that the point inevitably becomes hidden inside this non-minimal horizon; in other words, the non-minimal interaction plays the role of the cosmic censor. Then in the work [6] we have found the exact solution to the non-minimally extended Einstein equations, which is regular at the center. For that solution the metric coefficient has the form
where q is the non-minimal coupling parameter. The solution (30) with was obtained in [38], and then we studied it in [39,40]. Clearly, for the solution (30) we obtain , i.e., the solution is regular at the center, and the question about the naked singularity disappears. To be more precise, we can attract attention of the Reader to the curve III in Figure 2 presented in the paper [6]: one can see the analog of the fold, but the function is regular at the center. Why in the presented paper we considered the non-regular metric, if we have the example of the regular one? The explanation is very simple: the non-minimal scale associated with the coupling parameter q is estimated to be extremely small (of the order of the Compton radius of electron). This means that the folds, which we search for in the presented paper, are arranged rather far from the non-minimal zone, and the metric (15) gives the appropriate approximation for (30) in the fold zone.
4. Analysis of Solutions to the Key Equation of the Axion Field
4.1. The Profile of the Axion Field Distribution
Keeping in mind that the function is the polynomial of the fourth order, and that it has no zeros in the domain inside the cosmological horizon, , we can see that this equation has only two singular points, and , which are situated on the edges of the admissible interval . Equation (31) belongs to the class of the Fuchs equations [41].
When , we can not prolong the values of the radial variable to the infinity; we have to stop the analysis on the cosmological horizon . In other words, when we speak about the far zone, we mean the requirement , and . One can see, that in this limit the axion field tends to the value given by
The results for the near zone can be obtained numerically. Numerical simulation includes the variation of the following set of guiding parameters: first, the parameter (it already appeared in the analysis of the function ); second, the parameter ; third, the parameter , fourth, the coupling constant . The analysis has shown that the graphs inherit the fold-like structure of the gravitational potential; for illustration, we presented three graphs in Figure 3.
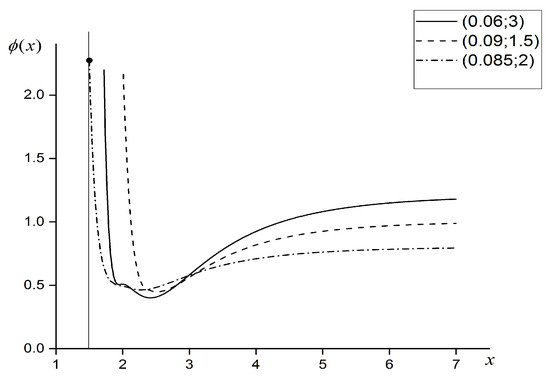
Figure 3.
Axion field profiles , as the solutions to the master Equation (31). The guiding parameters of the model: , and are fixed in the box near the graphs; for the simplicity of illustration we put and in the chosen system of units. The vertical line symbolizes the delimiter associated with the boundary of the solid body of the object, and its intersection with the graph defines the boundary value . In the far zone, the graph of the function tends to the horizontal asymptotic line, which corresponds to given by (32). The profiles of the axion field distribution inherit the fold-like structure of the profiles of the metric function .
4.2. The Profile of the Energy-Density of the Axionic Dark Matter
The scalar of the axion field energy density is standardly defined as , where is the global four-velocity vector, coinciding with the normalized time-like Killing vector . Normalization of this Killing four-vector gives . The quantity is the stress-energy tensor of the pseudoscalar axion field. The energy density scalar can be written as
In the static spherically symmetric case we obtain
Using the profiles of the functions and we can illustrate the typical behavior of the profile of the function (see Figure 4). These profiles happen to be more sophisticated than the fold-like profile of the function , since the extrema of the functions and do not coincide.
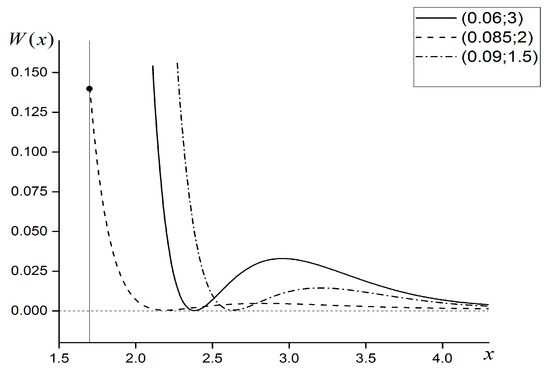
Figure 4.
Typical profiles of the energy density scalar of the axion field (34). The basic profile has the typical fold-like structure: the minimum, the barrier on the left of the minimum, the maximum on its right-hand side. In the far zone the axion energy density tends to a constant, and the graphs have the horizontal asymptotes. The vertical line relates to the object boundary and defines the corresponding boundary value .
4.3. Profiles of the Axionically Induced Electric Field
When the profile of the axion field is found, we can reconstruct the profile of the axionically induced electric field using the formula
The electric field changes the sign on the surfaces , for which . The typical profiles of the electric field are presented on Figure 5; these profiles look like the inverted fold-like structure (the fold-like structure will be recovered, if we change the sign of the magnetic charge and the parameter K simultaneously). On these profiles one can see two values of , in which the electric field changes the sign. Near the cosmological horizon, the behavior of this electric field is of the Coulombian type, i.e., .
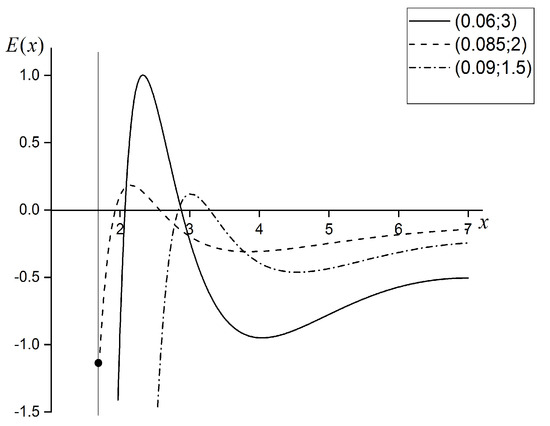
Figure 5.
Typical profiles of the axionically induced electric field. The profiles have inverted fold-like structure. The electric field changes sign twice; its profile tends to the Coulombian curve in the far zone near the cosmological horizon. The vertical line relates to the boundary of the solid body of the object; the dot relates to the boundary value of the electric field.
5. Discussion
We described an example of a new specific substructure, which can appear in the outer zone of the axionic dyon; we indicated it as a fold. The fold is presented in the profile of the metric function as a specific zone, which contains the minimum, the barrier on the left, and the maximum on the right of this minimum. The fold is entirely located in the outer zone, i.e., it can not be harbored by the event horizon. The necessary condition of the fold appearance is the inequality , where M is the asymptotic mass of the dyon, and , are the critical masses given by the formulas
Both of the critical masses and contain only two model parameters: the cosmological constant and the magnetic charge . When the fold can not be formed, since the maximum on the right of the central minimum disappears. On the fold bottom the derivative of the gravitational potential vanishes, thus there the massive particle does not feel the gravitational force and can be at rest. The width and depth of the fold are regulated, according to the Formula (29), by two dimensionless parameters and .
Then we analyzed the solution to the key equation for the axion field (31), and have found that the profile of the axion field reveals the substructure of the same type. To be more precise, the fold-like zones are found in the profile of the function , and in the energy density profile (see Figure 3 and Figure 4, respectively). In other words, the axionic distribution bears the imprint of the fold in the gravitational potential.
Finally, we studied the profile of the electric field, induced by the magnetic field in the axionic environment. Again, the fold-like structure has been found in this profile (see Figure 5). In more detail, we have seen, that the electric field changes the sign twice in this zone; such a behavior is typical for the double electric layers. Similar results are obtained in the paper [28], where the change of the electric field direction was associated with the stratification of plasma in the axionic dyon magnetosphere. We think that development of this idea can be interesting for the procedure of identification of the magnetars based on the fine spectroscopic analysis of obtained data. Why do we think so? The magnetars possess huge magnetic field of the order –; this magnetic field produces spectroscopic effects, such as Zeeman effect [42]. If the dark matter has the axionic nature, the axionically induced electric field appears in the vicinity of magnetic star. The corresponding coefficient of transformation is estimated to be less than ; however, the axionically induced electric field near magnetars is able to produce the quite distinguishable Stark effect. When one has both effects in the magnetic and electric fields (parallel and/or crossed), then the possibility appears to combine the well-elaborated methods and to organize an extended diagnostics [43]. Clearly, the standard Coulombian type radial electric field can be produced in many standard charged astrophysical objects, but if we hope to identify, say, the axionic dyon, we have to find some very specific detail distinguishing this object. In this sense the fold-like structure of the profile of the electric field of the axionic dyon, which is described in our work, gives just such a specific detail. Of course, this idea needs detailed estimations and description of the corresponding diagnostics, however, the discussion of such questions goes beyond the scope of this work.
Author Contributions
Conceptualization, A.B.; formal analysis, A.B. and D.G.; investigation, A.B. and D.G.; writing–original draft preparation, A.B.; writing–review and editing, A.B.; visualization, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation grant number 16-12-10401.
Acknowledgments
The work was supported by Russian Science Foundation (Project No. 16-12-10401), and, partially, by the Program of Competitive Growth of Kazan Federal University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weinberg, S. Cosmology; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–24. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological Constant. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Dark energy fingerprints in the non-minimal Wu-Yang wormhole structure. Phys. Rev. D 2014, 90, 044049. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Regular non-minimal magnetic black holes in spacetimes with a cosmological constant. Phys. Rev. D 2016, 93, 024008. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Magnetic black holes and monopoles in a non-minimal Einstein-Yang-Mills theory with a cosmological constant: Exact solutions. Phys. Rev. D 2016, 93, 084004. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-baryonic dark matter in cosmology. Int. J. Mod. Phys. D 2014, 23, 1430005. [Google Scholar] [CrossRef]
- Khlopov, M. Fundamentals of Cosmic Particle Physics; CISP-Springer: Cambridge, UK, 2012. [Google Scholar]
- Deliyergiyev, M.; Del Popolo, A.; Tolos, L.; Le Delliou, M.; Lee, X.; Burgio, F. Dark compact objects: An extensive overview. Phys. Rev. D 2019, 99, 063015. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP conservation in the presence of instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Weinberg, S. A new light boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Sikivie, P. Axion Cosmology. Lect. Notes Phys. 2008, 741, 19–50. [Google Scholar]
- Battesti, R.; Beltran, B.; Davoudiasl, H.; Kuster, M.; Pugnat, P.; Rabadan, R.; Ringwald, A.; Spooner, N.; Zioutas, K. Axion searches in the past, at present, and in the near future. Lect. Notes Phys. 2008, 741, 199–237. [Google Scholar]
- Steffen, F.D. Dark Matter candidates—Axions, neutralinos, gravitinos, and axinos. Eur. Phys. J. C 2009, 59, 557–588. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of Inflation with Dark Energy in f(R) Gravity and Axion Dark Matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Ni, W.-T. Equivalence principles and electromagnetism. Phys. Rev. Lett. 1977, 38, 301–304. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental Tests of the “Invisible” Axion. Phys. Rev. Lett. 1983, 51, 1415–1417. [Google Scholar] [CrossRef]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799–1802. [Google Scholar] [CrossRef] [PubMed]
- Sikivie, P.; Yang, Q. Bose-Einstein Condensation of Dark Matter Axions. Phys. Rev. Lett. 2009, 103, 111301. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. Magnetoelectrostatics of axionically active systems: Induced field restructuring in magnetic stars. Phys. Rev. D 2020, 101, 023009. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. New application of the Killing vector field formalism: Modified periodic potential and two-level profiles of the axionic dark matter distribution. Eur. Phys. J. C 2020, 80, 145. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. Polarization and stratification of axionically active plasma in a dyon magnetosphere. Phys. Rev. D 2019, 99, 023006. [Google Scholar] [CrossRef]
- Lee, K.; Nair, V.; Weinberg, E. Black holes in magnetic monopoles. Phys. Rev. D 1992, 45, 2751. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D. Supermassive Neutron Stars in Axion F(R) Gravity. Mon. Not. R. Astron. Soc. 2020, 493, 78–86. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Geometric Inflation and Dark Energy with Axion F(R) Gravity. Phys. Rev. D 2020, 101, 044010. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Nuovo Cimento 1969, 1, 252–276. [Google Scholar]
- Shaikh, R.; Joshi, P.S. Can we distinguish black holes from naked singularities by the images of their accretion disks? JCAP 2019, 10, 064. [Google Scholar] [CrossRef]
- Chakraborty, C.; Kocherlakota, P.; Patil, M.; Bhattacharyya, S.; Joshi, P.S.; Królak, A. Distinguishing Kerr naked singularities and black holes using the spin precession of a test gyro in strong gravitational fields. Phys. Rev. D 2017, 95, 084024. [Google Scholar] [CrossRef]
- Ortiz, N.; Sarbach, O.; Zannias, T. Shadow of a naked singularity. Phys. Rev. D 2015, 92, 044035. [Google Scholar] [CrossRef]
- Kovacs, Z.; Harko, T. Can accretion disk properties observationally distinguish black holes from naked singularities? Phys. Rev. D 2010, 82, 124047. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Non-minimal monopoles of the Dirac type as realization of the censorship conjecture. Phys. Rev. D 2009, 79, 024007. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Non-minimal Wu-Yang monopole. Phys. Lett. B 2007, 644, 294–298. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Non-minimal Einstein-Yang-Mills-Higgs theory: Associated, color and color-acoustic metrics for the Wu-Yang monopole model. Phys. Rev. D 2007, 76, 124011. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Ray optics in the field of non-minimal Dirac monopole. Grav. Cosmol. 2008, 14, 86–94. [Google Scholar] [CrossRef]
- Ince, E.L. Ordinary Differential Equations; Dover Publications: New York, NY, USA, 1920. [Google Scholar]
- Borra, E.F.; Deschatelets, D. Measurements of stellar magnetic fields using autocorrelation of spectra. Astron. J. 2015, 150, 146. [Google Scholar] [CrossRef]
- Thorman, A. Polarization of the Balmer-α emission in crossed electric and magnetic fields. J. Quant. Spectrosc. Radiat. Transf. 2018, 207, 8. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).