Abstract
In this paper, particle swarm optimization is incorporated into an improved bacterial foraging optimization algorithm, which is applied to classifying imbalanced data to solve the problem of how original bacterial foraging optimization easily falls into local optimization. In this study, the borderline synthetic minority oversampling technique (Borderline-SMOTE) and Tomek link are used to pre-process imbalanced data. Then, the proposed algorithm is used to classify the imbalanced data. In the proposed algorithm, firstly, the chemotaxis process is improved. The particle swarm optimization (PSO) algorithm is used to search first and then treat the result as bacteria, improving the global searching ability of bacterial foraging optimization (BFO). Secondly, the reproduction operation is improved and the selection standard of survival of the cost is improved. Finally, we improve elimination and dispersal operation, and the population evolution factor is introduced to prevent the population from stagnating and falling into a local optimum. In this paper, three data sets are used to test the performance of the proposed algorithm. The simulation results show that the classification accuracy of the proposed algorithm is better than the existing approaches.
1. Introduction
In machine learning the imbalanced distribution of categories is called an imbalanced problem. When conventional algorithms are directly applied to this problem, the classification results tend to be biased towards most classes, resulting in a few classes not being correctly identified. Moreover, most of the traditional algorithms train classifiers based on the maximization of overall accuracy, meaning they ignore the misclassification of a few samples, thus affecting the classification results of traditional classifiers [1,2,3]. However, in many practical applications, a few samples are often more valuable than most samples, such as in bank fraud user identification, medical cancer diagnosis, and network hacker intrusion [4,5,6,7,8,9].
Imbalanced data mining is an important problem in data mining. Various algorithms, including k nearest neighbor (KNN), decision tree (DT), artificial neural network (ANN), and the genetic algorithm (GA), have been recommended for data mining [10,11,12,13,14,15,16,17]. However, these algorithms usually assume that datasets are distributed evenly among different classes and that some classes may be ignored. In the literature, some methods for dealing with imbalanced data have been proposed. These methods include adjusting the size of training datasets, cost-sensitive classifiers, and snowball methods [18,19,20]. These methods may result in the loss of information in general rules and the incorrect classification of additional classes. Ultimately, they can lead to an over-matching of data and poor performance due to having too many specific rules. Traditional optimization methods can no longer solve the complex problems faced by many datasets. In recent years, people have proposed a hybrid intelligent system to improve the accuracy of data mining rather than use a separate method. The hybrid method combines the best results of various systems to improve the accuracy [21,22,23].
Particle swarm optimization (PSO) was first invented by Dr. Eberhart and Dr. Kennedy [24,25]. It is a population-based heuristic algorithm used for simulating social behavior, such as birds clustering to promising locations, in order to find accurate targets in multi-dimensional space. PSO uses groups of individuals (called particles) to perform searches as with evolutionary algorithms, and particles can be updated from each iteration to the other [26,27,28,29,30]. In order to find the optimal solution, each particle changes its search direction based on two factors: its best previous location (pbest) and all other members’ best locations (gbest) [31,32,33,34]. Shi et al. called pbest the cognitive part and gbest the social part [35].
The bacterial foraging optimization (BFO) algorithm is a bionic intelligent algorithm which was proposed by Passino in 2002 according to Escherichia coli in the human intestine [36,37]. The bacterial foraging chemotaxis process makes its local search ability stronger, but the global search ability of bacteria foraging can only be achieved by elimination and dispersal, and the global search ability is not strong enough to be limited by elimination and dispersal probability; thus it easily to falls into a local search optimal problem. In this paper, the incorporation of particle swarm optimization into an improved bacterial foraging optimization algorithm applied to the classification of imbalanced data is proposed. The borderline synthetic minority oversampling technique (Borderline-SMOTE) and Tomek link are used to pre-process imbalanced data. Thereafter, the proposed algorithm is used to classify imbalanced data.
Because PSO has a strong global search ability, individual effect, and group effect, PSO is incorporated into the improvement of the chemotaxis process of the improved BFO algorithm. The proposed algorithm improves the global searching ability and efficiency through the strong global search ability of PSO. In addition to embedding PSO into the BFO algorithm’s chemotaxis process to improve the BFO algorithm’s vulnerability to local optimization, in the improved replication operation, the crossover operator is introduced into the replication parent to increase the diversity of the population, while retaining the best individual. In the improved elimination and dispersion operation, the population evolution factor is proposed, and (1 − ) is introduced to replace the Ped in the original BFO algorithm so as to prevent the population from falling into a local optimum and achieving evolution stagnation. The purpose of this study was to improve the classification accuracy of ovarian cancer microarray data and to improve the practicability and accuracy of doctors’ judgment of ovarian cancer microarray data.
2. A Brief Description of Bacterial Foraging Optimization and Particle Swarm Optimization
In this paper, the bacterial foraging optimization algorithm is improved. Firstly, PSO is incorporated into the BFO chemotaxis process to improve the chemotaxis process. For this reason, this section introduces the basic concepts of bacterial foraging optimization and particle swarm optimization.
2.1. Bacterial Foraging Optimization
Passino introduced bacteria foraging optimization as a solution to distributed optimization and control problems. It is an evolutionary algorithm and a global random search algorithm. The BFO algorithm mainly solves the optimization problem by using four process iterative calculations: chemotaxis, swarming, reproduction, elimination, and dispersal [38]. In the chemotaxis process, there are two basic movements of E. coli in the process of foraging, namely, swimming and tumbling. Usually, in areas with poor environmental conditions (for example, toxic areas), bacteria may tumble more frequently, and in areas with a good environment, they will swim more often. Let P indicate the ith bacterium in the population of the S bacteria at the jth chemotaxis process, kth reproduction process, and lth elimination and dispersal process. Let be the cost at the location of the ith bacterium. When the bacterial population size is S and Nc is the length of the bacteria in one direction of the chemotactic operation, the chemotaxis operation of each step of the ith bacterium is expressed as
where > 0 represents the step unit of the forward swimming and represents a unit vector in the random direction vector after the tumbling. In the swarming process, in addition to searching for food in their own way, each bacterial individual receives an appeal signal from other individuals in the population; that is, the individual will swim to the center of the population and will also receive a repulsive force signal from nearby individuals to maintain a safe distance between it and other individuals. Hence, the decision-making behavior of each bacterial individual in BFO which finds food is affected by two factors. The first is its own information, that is, the purpose of individual foraging to maximize the energy acquired by the individual in unit time, and the other is information from other individuals, that is, foraging information transmitted by other bacteria in the population. The mathematical expression is described as
where denotes the penalty for the actual cost function, S is the number of bacteria, is the location of the fittest bacterium, and , , , and are different coefficients. The swarming process is minimized mathematically.
In the swarming process, the number of biologically-motivated choices is expressed as Ns. In the reproduction process, according to the strength of the foraging ability of the bacteria, the appropriate cost is selected; that is, ranks the sum of the cost of all the locations experienced by the ith bacteria in the chemotaxis operation, and the elimination ranks 50% later. The number of bacteria in the population, the reproduction process of the remaining bacteria, and the new individuals generated by themselves which are identical to themselves have the same foraging ability and the same location, and the replication operation maintains the invariance of the population size. After reproduction steps the elimination and dispersal process occurs, where is the number of steps of elimination and dispersal. These operations occur with a certain probability . When the individual bacteria meet the probability of elimination and dispersal, the individual dies and randomly generates a new individual at any location in the solution space. These new bacteria may have different bacterial foraging capabilities than the original bacteria, conducive to jumping out of the local optimal solution. A flow diagram of bacteria foraging optimization is presented in Figure 1.
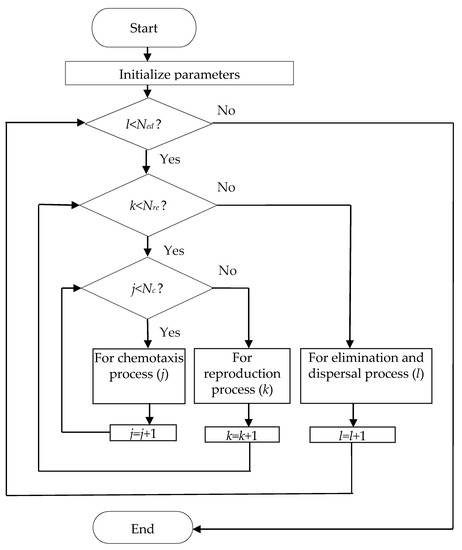
Figure 1.
A flow diagram of bacterial foraging optimization (BFO).
2.2. Particle Swarm Optimization
PSO is a bionic algorithm used for the study of birds searching for food in nature. It regards birds as a particle in space, and a bird swarm is subject to PSO [39,40]. A single particle carries corresponding information—i.e., its own velocity and location—and determines the distance and direction of its motion according to the corresponding information of the particle itself. The PSO is used to initialize a group of particles which are randomly distributed into a solution space to be searched and then iterated according to a given equation. The equation of the mature particle swarm optimization algorithm includes two optimum concepts. The first is the local optimum pbest and the other is the global optimum gbest. The local optimum is the best solution obtained by each particle in the search, and the global optimum is the best solution obtained by this particle swarm. The PSO algorithm has the characteristics of memory, using positive feedback adjustment; the principle of the algorithm is simple, the parameters are few, and the applicability is good. The formulae of PSO are Equations (4) and (5), as described.
In Equation (4), denote the velocity of the ith particle in iterations and is the inertia weight, and are learning factors, and are random numbers between [0, 1] in iteration , is the best location of the ith particle, and is the best location of fitness found by all particles in the population. In Equation (5), and denote the location of the ith particle in iterations and . A flow chart of PSO is shown in Figure 2.
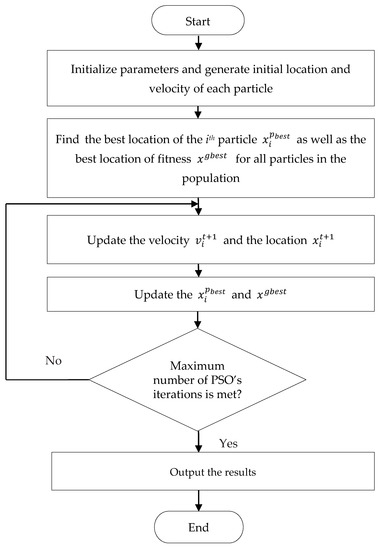
Figure 2.
A flow chart of the particle swarm optimization (PSO) algorithm.
3. The Proposed Algorithm
In this paper, the incorporation of particle swarm optimization into an improved bacterial foraging optimization algorithm applied to the classification of imbalanced data is proposed. Three datasets are used for testing the performance of the proposed algorithm. One consists of ovarian cancer microarray data, and the other two, obtained from the UCI repository, are a spam email dataset and zoo dataset. The ovarian cancer microarray data were obtained from Taiwan’s university. There are 9600 features in the microarray data of ovarian cancer, which were collected from China Medical University Hospital, with an imbalance ratio of about 1:20 [41,42]. The instances of microarray data we used included ovarian tissue, vaginal tissue, cervical tissue, and myometrium, including six benign ovarian tumors (BOT), 10 ovarian tumors (OVT), and 25 ovarian cancers (OVCA). The spam email dataset and zoo dataset were obtained from the UCI repository [43]. For the spam email dataset, there were 4601 emails with 58 features, as shown in Table 1, and the imbalance ratio was about 1:1.54. For the zoo dataset, there were 101 instances with 17 features, as shown in Table 2, and the imbalance ratio was about 1:25.

Table 1.
The 58 features of the spam email dataset.

Table 2.
The 17 features of the zoo dataset.
Figure 3 shows a flow chart of the proposed algorithm. In Figure 3, the used parameters are set first. The approaches of the Borderline-SMOTE and Tomek link are used for pre-process data. Thereafter, the improved BFO algorithm is applied to classify imbalanced data so as to solve the shortcoming of falling into a local optimum in the original BFO algorithm.
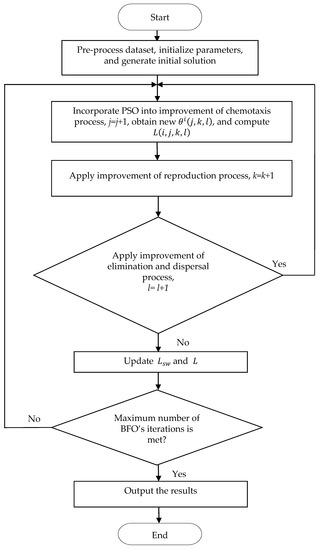
Figure 3.
A flow diagram of the proposed algorithm.
In order to over-sample the minority instances, the Borderline-SMOTE is designed in the proposed algorithm; the main idea of SMOTE is to balance classes by generating synthetic instances from the minority class [44]. For the subset of minority instances , k nearest neighbors are obtained by searching. The k nearest neighbors are defined as the smallest distance between the Euclidean distance and , and n synthetic instances are randomly selected from them which are recorded as , = 1, 2, …, n. This is done to create a new minority instance as in Equation (6) as described, where is the random number between [0, 1].
In the proposed algorithm, as a data cleaning technology, the Tomek link is effectively applied to eliminate the overlap in the sampling method [45]. The Tomek link is used to remove unnecessary overlaps between classes until the nearest neighbor pairs at the minimum distance belong to the same class. Suppose that the nearest neighbors (, ) of a pair of minimal Euclidean distances belong to different classes. represents the Euclidean distance between and . If there is no instance satisfying Equation (7), we call (, ) a pair of Tomek link.
In this paper, the parameter k used for SMOTE was set to k = 3. After preprocessing data, the solution of location was generated. Thereafter, the improved BFO algorithm was performed. Aiming at the BFO algorithm shortcoming of falling into a local optimum, we propose the incorporation of particle swarm optimization into an improved bacterial foraging optimization to solve these problems. An improved BFO proposed algorithm improves the chemotaxis process, reproduction process, and the elimination and dispersal process.
3.1. Improvement of Chemotaxis Process
The original BFO algorithm mainly searches within the process of chemotaxis. When the chemotaxis searches the target area, the swimming and tumbling operation of the chemotaxis process directly affects the effect of the algorithm. While a large swimming step makes the global search ability strong, a small swimming step makes the local search ability strong. Because of the characteristics of chemotaxis, the BFO algorithm has good local search ability because it can change direction in chemotaxis, meaning the local search accuracy is very good. However, the global search ability of bacteria can only rely on the elimination and dispersal operation process, and its global search ability is not good.
Because PSO has strong memory and global search ability, individual effect, and group effect, in this paper, the PSO is incorporated into the chemotaxis process of the original BFO so as to solve the problem of how the original BFO algorithm easily falls into local optimization. By using particles to search first and then treat particles as bacteria, the global search ability of the original BFO algorithm is improved. The purpose of this study is to find an effective algorithm which combines the advantages of PSO, including fast convergence speed, strong search ability, and the good classification effect of the BFO algorithm, to improve the accuracy of imbalanced data.
3.2. Improvement of Reproduction Process
In the reproduction process of the original BFO algorithm, half of the good bacteria () are replicated using the current bacterial position generation cost as the basis for good or bad arrangement in the bacterial population with a population size of , and the sub-population generated by replication replaces the other half of the bad bacteria in the original bacterial population.
Because each parent has one of the same offspring in the bacterial population with size after replication, the diversity of the population is reduced. In this paper, the cost of the current bacterial location is used to rank the values as good and bad, and half of the excellent bacteria S/2 are reproduced. The reproduced sub-population replaces the worse bacteria in the original bacterial population. In order to increase the diversity of the population and prevent the loss of the best individual, a hybrid operator is introduced into the parent individual (excluding the best parent individual) to cross with the best individual. The hybrid equation is [46]
where is the parent individual (excluding the best parent individual), is the best parent individual, and is the random number with entries on [0, 1].
3.3. Improvement of Elimination and Dispersal Process
The elimination–dispersal operation helps the BFO algorithm jump out of the local optimal solution and find the global optimal solution. In the elimination–dispersal process of the original BFO, elimination and dispersal is carried out according to the given fixed probability without considering the evolution of the population.
In this paper, the elimination–dispersal operation is improved by introducing the population evolution factor and elimination–dispersal is carried out according to the evolution of the population, which is conducive to the effectiveness of the algorithm and prevents the population from falling into a local optimum due to slow evolution. The formula of the population evolution factor is
where represents the optimal generation cost at the iteration and prevents the denominator from being 0. In this paper, (1 ) is used to replace as in the original BFO algorithm. When , the evolution is accelerated. At this time, the evolution degree of the population is faster and the population is in a fast and effective optimization state. Elimination–dispersal with a lower elimination–dispersal probability (1 ) can retain the current favorable location information. When 0 ≤ < 1, the evolution slows down. When the evolution degree of the population is slow, the population falls into a local optimum to a large extent. It is necessary for elimination–dispersal with a high elimination–dispersal probability (1 ) to jump out of the local optimum solution so as to prevent the population from not evolving.
In order to overcome the shortcoming of the BFO algorithm easily falling into a local optimum and uncertain orientation during the chemotaxis process, PSO is incorporated into the BFO algorithm in this paper, that is to say, PSO is added to the chemotaxis process of each individual bacterium, which is the cost of each bacterium according to PSO. For the improved chemotaxis process, PSO is performed to obtain the updated location of the The procedure of the proposed algorithm is detailed as follows.
- (1)
- The particle swarm population of size is initialized. Here, PSO is added to the chemotaxis process of each individual bacterium, and the swarm population size of PSO is the same as that of the BFO algorithm. The initial velocity and position of each particle is randomly generated. The maximum number of PSO iterations is . The BFO algorithm parameters ,, , and are set. The number of BFO iterations is .
- (2)
- The cost , defined as the classification accuracy of each particle, is calculated. The best location of the particle and the best location of the cost for all particles in the population are found. is updated and if and are improved.
- (3)
- Equation (4) is applied to update the velocity and Equation (5) is applied to update the location . In Equation (4), the velocity of each particle must be limited to the range of the set maximum velocity . If the velocity of each particle exceeds the limit, the velocity is expressed as .
- (4)
- If the set termination condition is met, it will stop; otherwise, the process goes back to step 2. The termination condition is usually to reach the best location of the cost for all particles in the population, or to exceed the set PSO’s maximum number of iterations . Through Equation (4) and Equation (5) particles treated as bacteria, PSO is completed to obtain the updated position . In other words, the PSO is performed to obtain the updated location of in the improved chemotaxis process.
- (5)
- In the swarming process, the cost of is evaluated by Equation (3).
- (6)
- In the improved reproduction process, Equation (8) is performed to increase the diversity of the population and avoid losing the best individual; in other words, the parent individual (excluding the best parent individual) crosses the best individual.
- (7)
- In the improved elimination–dispersal process, the population evolution factor is used in Equation (9). The new by PSO is generated according to (1 − ). In the improved BFO algorithm, is replaced with (1 − .
- (8)
- If the maximum number of BFO iterations is met, the algorithm is over. Finally, we output the classification accuracy results in this implementation.
The proposed algorithm is performed and cost is defined as the classification accuracy. This experiment used a classification accuracy based on the confusion matrix, which can test the performance of the classification method. The confusion matrix is shown in Table 3.

Table 3.
The confusion matrix.
TP and FP represent the true positive class and the false positive class, respectively; FN and TN represent the false negative class and the true negative class, respectively. When the predicted value is a positive example, it is recorded as P (positive). When the predicted value is a negative example, it is is recorded as N (negative). When the predicted value is the same as the actual value, it is recorded as T (true). Finally, when the predicted value is opposite to the actual value, it is is recorded as F (false). The four results of defining examples in the data set after model classification are TP: predicted positive, actual positive actual; FP: predicted positive, actual negative; TN: predicted negative, actual negative; and FN: predicted negative, actual positive. The classification accuracy calculation formula is
The receiver operating characteristic curve (ROC curve) and area under the curve (AUC) can test the performance of the classification results. This is because the ROC curve has a favorable characteristic: when the distribution of positive and negative instances in the test dataset changes, the ROC curve can remain unchanged. Class imbalance often occurs in the actual data set, i.e., there are many more negative instances than positive instances (or vice versa) and the distribution of positive and negative instances in the test data may change with time. The area under the ROC curve is calculated as the evaluation method of imbalanced data. It can comprehensively describe the performance of classifiers under different decision thresholds. The AUC calculation formula is
4. Simulation Results and Discussion
In this study, our purpose was to obtain an effective algorithm with which to improve the accuracy of imbalanced data. In order to verify the performance of the proposed algorithm, ovarian cancer microarray data, a spam email dataset and a zoo dataset are used for simulation experiments. The Borderline-SMOTE and Tomek link approaches are used for preprocess data to increase the numbers of minority classes until they are the same number as the majority class. In the simulation experiment, some parameters of the algorithm need to be determined. In this experiment, the BFO algorithm parameters were set as S = 50, = 100, = 4, = 4, = 2, = 0.25, 0.05, = 0.05, 0.05, 0.05, (i) = 0.1, and i = 1, 2,…S. The number of BFO iterations was 800. This study evaluated the results when adopting 10-fold cross validation with random partitions. The maximum number of PSO iterations was set to 5000 and the other parameters were set as inertia weight , learning factors = 1.5, and maximum velocity of each particle = 2 [47].
The parameter value of the algorithm is the key to the performance and efficiency of the algorithm. In evolutionary algorithms there are no general methods for determining the optimal parameters of the algorithm. Most parameters are selected by experience. There are many BFO and PSO parameters. Knowing how to determine the optimal BFO and PSO parameters to optimize the performance of the algorithm is a very complex optimization problem. In the parameter setting of PSO and BFO, in order to jump off the local solution to find the global solution without spending a lot of calculation time, we used empirical values.
4.1. Comparing and Analyzing the Classification Accuracy of the Proposed Algorithm and Other Methods
- (1)
- In addition to the proposed algorithm, we also employ other existing approaches for comparison. The approaches used include the support vector machine (SVM), DT, random forest (RF), KNN, and BFO. The SVM is a learning system that uses a hypothesis space of linear function in a high-dimensional feature space. DT uses partition information entropy minimization to recursively partition the dataset into smaller subdivisions and then generate a tree structure. RF is an ensemble learning method for classification that constructs multiple decision trees during training time and outputs the class that depends on the majority of the classes. KNN is a method used to classify objects based on the closest training examples in an n-dimensional pattern space. The BFO algorithm is described in Section 2.1.
- (2)
- Table 4, Table 5 and Table 6 list the classification performances of the ovarian cancer microarray data, spam email dataset, and zoo dataset, respectively. From Table 4, the average classification accuracy in the proposed algorithm for the ovarian cancer microarray data can be seen to be 93.47%. From Table 5, the average classification accuracy of the proposed algorithm for the spam email dataset can be seen to be 96.42%. As shown in Table 6, the average classification accuracy for the zoo dataset of the proposed algorithm is 99.54%. From Table 4, Table 5 and Table 6, it is clearly evident that the proposed approach has the best classification results given a fair comparison for all compared approaches. This is because the performance of the classification for the three tested datasets can be found based on intelligent information. In fact, the proposed approach has similar performance, meaning it performs well in classification accuracy.
 Table 4. The classification accuracy for microarray data of ovarian cancer. Legend: RF, random forest; SVM, support vector machine; DT, decision tree; KNN, k nearest neighbor.
Table 4. The classification accuracy for microarray data of ovarian cancer. Legend: RF, random forest; SVM, support vector machine; DT, decision tree; KNN, k nearest neighbor. Table 5. The classification accuracy for the spam email dataset.
Table 5. The classification accuracy for the spam email dataset. Table 6. The classification accuracy for the zoo dataset.
Table 6. The classification accuracy for the zoo dataset. - (3)
- In the comparison results it can be found that the classification accuracy of the original BFO method in Table 4 was 89.93%, which is not better than the proposed algorithm classification accuracy of 93.47%. In Table 5, the classification accuracy of the original BFO method can be seen to be 94.27%, which is not better than the proposed algorithm classification accuracy of 96.42%. In Table 6, the classification accuracy of the original BFO method can be seen to be 94.38%, which is not better than the proposed algorithm classification accuracy of 99.54%. Because the original BFO algorithm can change direction in the chemotaxis operation, its local search ability is better; the global search, however, can only rely on elimination and dispersal operation, and the global search ability is not very good. Hence, the classification accuracy is not better than the proposed algorithm.
- (4)
- The proposed algorithm provides a better classification effect because PSO is incorporated into the improved chemotaxis process. PSO has memory and global search abilities, so we first used particles for global search and then treat these particles as bacteria, and the chemotaxis operation improved the global search ability. The PSO algorithm introduced in this paper only uses its global operation and uses the memory of PSO to improve the bacterial search ability. In the improved reproduction operation, the crossover operator is introduced to the replica parent to increase the diversity of the population while the best individual is retained. In the improved elimination and dispersal operation, the (1 − ) replaces in the original BFO, and is introduced to prevent the population from dying and falling into a local optimum.
4.2. Analysis of ROC and AUC
In this experiment, the area below the ROC is also called the AUC and is used to evaluate the performance of the proposed approach. The value of the AUC is from 0 to 1.0, and the closer to 1.0, the better the effect of the model classifier. The value of the AUC is 0.979 for the ovarian cancer microarray data, as shown in Figure 4. The value of the AUC is 0.987 for the spam email dataset, as shown in Figure 5. The value of the AUC is 0.995 for the zoo data, as shown in Figure 6. Hence, the experimental results show that the proposed algorithm has good classification performance.
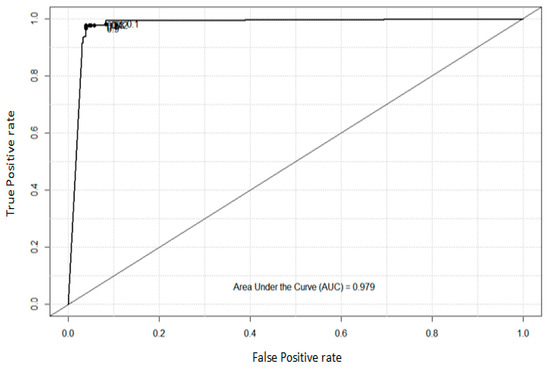
Figure 4.
The receiver operating characteristic (ROC) and the area under the curve (AUC) for the microarray data of ovarian cancer.
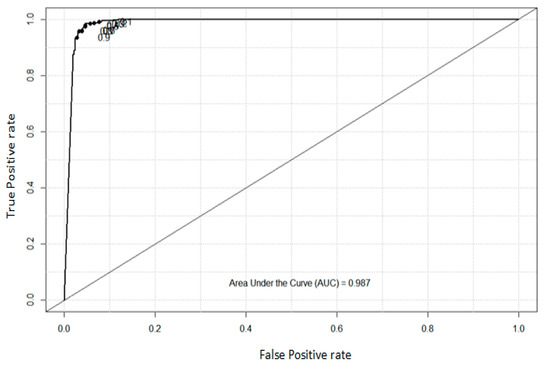
Figure 5.
The ROC and AUC for the spam email dataset.
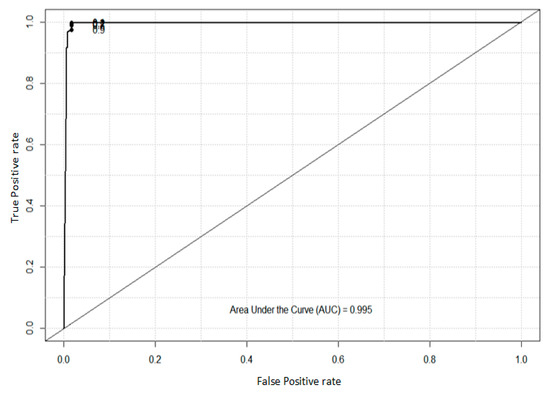
Figure 6.
The ROC and AUC for the zoo dataset.
5. Conclusions
This paper has proposed the incorporation of particle swarm optimization into an improved bacterial foraging optimization algorithm applied to the classification of imbalanced data. The Borderline-SMOTE and Tomek link approaches were used to pre-process data. Thereafter, the intelligent improved BFO was applied to the classification of imbalanced data so as to solve the shortcoming of falling into a local optimum in the original BFO algorithm. Three datasets were used for testing the performance of the proposed algorithm. The proposed algorithm includes an improved chemotaxis process, an improved reproduction process, and an improved elimination and dispersal process. In this paper, the global search ability of the BFO was improved by using particles to search and then treating particles as bacteria in the improved chemotaxis process. After the improved chemotaxis, the swarming operations, improved reproduction operations, and improved elimination and dispersal operations were performed. The average classification accuracy of the proposed algorithm for the ovarian cancer microarray data was 93.47%. The average classification accuracies of the spam email dataset and the zoo dataset of the proposed algorithm were 96.42% and 99.54%, respectively. The value of the AUC was 0.979 for the ovarian cancer microarray data, 0.987 for the spam email dataset, and 0.995 for the zoo dataset. The experimental results showed that the proposed algorithm in this research can achieve the best accuracy in the classification of imbalanced data compared with existing approaches.
In this paper, PSO was introduced into an improved bacterial foraging optimization algorithm and applied to the classification of imbalanced data. Based on the research results, we put forward the following suggestions:
- (1)
- Improvement of the algorithm’s operation: The key to implementing the optimization is the operation of the algorithm. Designing an excellent operation plays an important role in improving the performance and efficiency of the algorithm. In BFO, this will become a key area of research into BFO to improve chemotaxis and reproduction and the elimination and dispersal operation process, and to coordinate the local mining ability and global exploring ability of the processing algorithm.
- (2)
- Selection of algorithm parameters: The parameter value of the algorithm is key to the performance and efficiency of the algorithm. In evolutionary algorithms, there is no general method to determine the optimal parameters of the algorithm. At present, there are many BFO parameters. Determining the optimal parameters of BFO to optimize the performance of the algorithm itself is a complex optimization problem.
- (3)
- Combining with other algorithms: Combining the advantages of BFO and other algorithms to propose more efficient algorithms is a valuable topic in BFO research.
Author Contributions
Methodology, F.-L.Y. and C.-Y.L.; software, F.-L.Y., J.-Q.H., and J.-F.T.; formal analysis, F.-L.Y., C.-Y.L., and Z.-J.L.; investigation, F.-L.Y., C.-Y.L., and J.-F.T.; resources, C.-Y.L. and Z.-J.L.; data curation, F.-L.Y., J.-Q.H., and J.-F.T.; original draft preparation, F.-L.Y., C.-Y.L., and J.-F.T.; review and editing, F.-L.Y., C.-Y.L., and J.-F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This research was supported by the Major Education and Teaching Reform Projects in Fujian Undergraduate Colleges and Universities in 2019 under grant FBJG20190284. This work was also supported by projects under 2019-G-083.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Hu, J.J.; Yang, H.Q.; Lyu, M.R.; King, I.R.; So, A.M.C. Online Nonlinear AUC Maximization for Imbalanced Data Sets. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 882–895. [Google Scholar] [CrossRef]
- Huang, X.L.; Zou, Y.X.; Wang, Y. Cost-sensitive sparse linear regression for crowd counting with imbalanced training data. In Proceedings of the 2016 IEEE International Conference on Multimedia and Expo (ICME), Seattle, WA, USA, 11–15 July 2016. [Google Scholar]
- Padmaja, T.M.; Dhulipalla, N.; Bapi, R.S.; Krishna, P.R. Imbalanced data classification using extreme outlier elimination and sampling techniques for fraud detection. In Proceedings of the International Conference on Advanced Computing and Communications, Guwahati, India, 18–21 December 2007; pp. 511–516. [Google Scholar]
- Lin, S.W.; Ying, K.C.; Lee, C.Y.; Lee, Z.J. An intelligent algorithm with feature selection and decision rules applied to anomaly intrusion detection. Appl. Soft Comput. 2012, 12, 3285–3290. [Google Scholar] [CrossRef]
- Lee, C.Y.; Lee, Z.J. A Novel Algorithm Applied to Classify Unbalanced Data. Appl. Soft Comput. 2012, 12, 2481–2485. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network. Expert Syst. Appl. 2009, 36, 8849–8854. [Google Scholar]
- Xia, C.Q.; Han, K.; Qi, Y.; Zhang, Y.; Yu, D.J. A Self-Training Subspace Clustering Algorithm under Low-Rank Representation for Cancer Classification on Gene Expression Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 1315–1324. [Google Scholar] [CrossRef] [PubMed]
- Esfahani, M.S.; Dougherty, E.R. Incorporation of Biological Pathway Knowledge in the Construction of Priors for Optimal Bayesian Classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 202–218. [Google Scholar] [CrossRef] [PubMed]
- Sadreazami, H.; Mohammadi, A.; Asif, A.; Plataniotis, K.N. Distributed-Graph-Based Statistical Approach for Intrusion Detection in Cyber-Physical Systems. IEEE Trans. Signal Inform. Process. Netw. 2018, 4, 137–147. [Google Scholar] [CrossRef]
- Mathew, J.; Pang, C.K.; Luo, M.; Leong, W.H. Classification of imbalanced data by oversampling in kernel space of support vector machines. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4065–4076. [Google Scholar] [CrossRef]
- Zhang, J.; Bloedorn, E.; Rosen, L.; Venese, D. Learning rules from highly imbalanced data sets. In Proceedings of the Fourth IEEE International Conference on Data Mining, ICDM’04, Brighton, UK, 1–4 November 2004; Volume 1, pp. 571–574. [Google Scholar]
- Jiang, Y.; Zhou, Z.H. Editing training data for kNN classifiers with neural network ensemble. In Proceedings of the International Symposium on Neural Networks, Dalian, China, 19–21 August 2004; Volume 1, pp. 356–361. [Google Scholar]
- Tao, Q.; Wu, G.W.; Wang, F.Y.; Wang, J. Posterior probability support vector Machines for imbalanced data. IEEE Trans. Neural Netw. 2005, 16, 1561–1573. [Google Scholar] [CrossRef]
- Zhang, J.; Mani, I. kNN approach to imbalanced data distributions: A case study involving information extraction. In Proceedings of the ICML’2003 Workshop on Learning from Imbalanced Datasets, Washington, DC, USA, 21 August 2003. [Google Scholar]
- Elaidi, H.; Elhaddar, Y.; Benabbou, Z.; Abbar, H. An idea of a clustering algorithm using support vector machines based on binary decision tree. In Proceedings of the 2018 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 2–4 April 2018; pp. 1–5. [Google Scholar]
- Ye, D.; Chen, Z. A rough set based minority class oriented learning algorithm for highly imbalanced data sets. In Proceedings of the IEEE International Conference on Granular Computing, Hangzhou, China, 26–28 August 2008; pp. 736–739. [Google Scholar]
- Yang, X.; Song, Q.; Cao, A. Clustering nonlinearly separable and imbalanced data set. In Proceedings of the 2004 2nd International IEEE Conference on Intelligent Systems, Varna, Bulgaria, 22–24 June 2004; Volume 2, pp. 491–496. [Google Scholar]
- Lu, Y.; Guo, H.; Feldkamp, L. Robust neural learning from imbalanced data samples. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks, Anchorage, AK, USA, 4–9 May 1998; Volume 3, pp. 1816–1821. [Google Scholar]
- Wang, J.; Jean, J. Resolve multifont character confusion with neural network. Pattern Recognit. 1993, 26, 173–187. [Google Scholar] [CrossRef]
- Searle, S.R. Linear Models for Unbalanced Data; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Wang, J.; Miyazaki, M.; Kameda, H.; Li, J. Improving performance of parallel transaction processing systems by balancing data load on line. In Proceedings of the Seventh International Conference on Parallel and Distributed Systems, Taipei, Taiwan, 4–7 December 2000; pp. 331–338. [Google Scholar]
- Crepinsek, M.; Liu, S.H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: Common pitfalls and guidelines to avoid them. Appl. Soft Comput. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- De Corte, A.; Sörensen, K. Optimisation of gravity-fed water distribution network design: A critical review. Eur. J. Oper. Res. 2013, 228, 1–10. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’ 95), Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Jia, J.Y.; Zhao, A.W.; Guan, S.A. Forecasting Based on High-Order Fuzzy-Fluctuation Trends and Particle Swarm Optimization Machine Learning. Symmetry 2017, 9, 124. [Google Scholar] [CrossRef]
- Xue, H.X.; Bai, Y.P.; Hu, H.P.; Xu, T.; Liang, H.J. A Novel Hybrid Model Based on TVIW-PSO-GSA Algorithm and Support Vector Machine for Classification Problems. IEEE Access 2019, 7, 27789–27801. [Google Scholar] [CrossRef]
- Kim, J.J.; Lee, J.J. Trajectory Optimization with Particle Swarm Optimization for Manipulator Motion Planning. IEEE Trans. Ind. Inform. 2015, 11, 620–631. [Google Scholar] [CrossRef]
- Liu, H.M.; Yan, X.S.; Wu, Q.H. An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion. Symmetry 2019, 11, 1291. [Google Scholar] [CrossRef]
- Salleh, I.; Belkourchia, Y.; Azrar, L. Optimization of the shape parameter of RBF based on the PSO algorithm to solve nonlinear stochastic differential equation. In Proceedings of the 2019 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019. [Google Scholar]
- Medoued, A.; Lebaroud, A.; Laifa, A.; Sayad, D. Feature form extraction and optimization of induction machine faults using PSO technique. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, Istanbul, Turkey, 2–4 October 2013. [Google Scholar]
- Yeom, C.U.; Kwak, K.C. Incremental Granular Model Improvement Using Particle Swarm Optimization. Symmetry 2019, 11, 390. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.W.; Song, J.Y. Distance-Based Intelligent Particle Swarm Optimization for Optimal Design of Permanent Magnet Synchronous Machine. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.N.; Gu, T.L. Set-Based Discrete Particle Swarm Optimization Based on Decomposition for Permutation-Based Multiobjective Combinatorial Optimization Problems. IEEE Trans. Cybern. 2018, 48, 2139–2153. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. Proceeding of the 1998 IEEE International Conference on Evolutionary Computation, World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar]
- Abraham, A.; Biswas, A.; Dasgupta, S. Analysis of reproduction operator in bacterial foraging optimization algorithm. In Proceedings of the IEEE World Congress on Computational Intelligence, Hong Kong, China, 1–6 June 2008; pp. 1476–1483. [Google Scholar]
- Bidyadhar, S.I.; Raseswari, P. Bacterial Foraging Optimization Approach to Parameter Extraction of a Photovoltaic Module. IEEE Trans. Sustain. Energy 2018, 9, 381–389. [Google Scholar]
- Noguchi, T.; Togashi, S.; Nakamoto, R. Based maximum power point tracking method for multiple photovoltaic and converter module system. IEEE Trans. Ind. Electron. 2002, 49, 217–222. [Google Scholar] [CrossRef]
- Raza, A.; Yousaf, Z.; Jamil, M. Multi-Objective Optimization of VSC Stations in Multi-Terminal VSC-HVdc Grids, Based on PSO. IEEE Access 2018, 6, 62995–63004. [Google Scholar] [CrossRef]
- Lu, S.J. Gene Expression Analysis and Regulator Pathway Exploration with the Use of Microarray Data for Ovarian Cancer. Master’s Thesis, National Taiwan University of Science and Technology, Taipei, Taiwan, 2006. [Google Scholar]
- Lee, Z.J. An integrated algorithm for gene selection and classification applied to microarray data of ovarian cancer. Int. J. Artif. Intell. Med. 2008, 42, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Blake, C.; Keogh, E.; Merz, C.J. UCI Repository of Machine learning Databases; Department of Information and Computer Science, University of California: Irvine, CA, USA, 1998; Available online: https://archive.ics.uci.edu/ml/datasets.php (accessed on 24 December 2019).
- Gosain, A.; Sardana, S. Farthest SMOTE: A modified SMOTE approach. In Computational Intelligence in Data Mining; Springer: Singapore, 2019; pp. 309–320. [Google Scholar]
- Devi, D.; Purkayastha, B. Redundancy-driven modified Tomek link based undersampling: A solution to class imbalance. Pattern Recogn. Lett. 2017, 93, 3–12. [Google Scholar] [CrossRef]
- Liu, L.; Shan, L.; Yan, J.H. An Improved BFO Algorithm for Optimising the PID Parameters of Servo System. In Proceedings of the IEEE the 30th Chinese Control and Decision Conference (2018 CCDC), Shenyang, China, 9–11 June 2018; pp. 3831–3836. [Google Scholar]
- Abd-Elazim, S.M.; Ali, E.S. A hybrid particle swarm optimization and bacterial foraging for power system stability enhancement. Complexity 2015, 21, 245–255. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).