Abstract
A new method of line shape calculations of hydrogen-like atoms in magnetized plasmas is presented. This algorithm makes it possible to solve two fundamental problems in the broadening theory: the analytical description of the radiation transition array between excited atomic states and an account of a thermal ion motion effect on the line shapes formation. The solution to the first problem is based on the semiclassical approach to dipole matrix elements calculations and the usage of the specific symmetry properties of the Coulomb field. The second one is considered in terms of the kinetic treatment of the frequency fluctuation model (FFM). As the result, one has a universal description of line shapes under the action of the dynamic of ion’s microfield. The final line shape is obtained by the convolution of the ionic line shape with the Voigt electron Doppler profile. The method is applicable formally for large values of principal quantum numbers. However, the efficiency of the results is demonstrated even for well known first members of the hydrogen Balmer series and lines. The comparison of obtained results with accurate quantum calculations is presented. The new method may be of interest for investigations of spectral line shapes of hydrogen-like ions presented in different kinds of hot ionized environments with the presence of a magnetic field, including So L and divertor tokamak plasmas.
1. Introduction
Hydrogen spectral lines are of permanent interest both from the fundamental point of view and for applications in plasma diagnostics. Since the middle of the 20th century, a significant number of works and monographs (e.g., [1,2,3,4,5,6,7,8]) have been accumulated on the spectra of hydrogen plasma. However, the effect of a magnetic field on spectral lines remains a problem in plasma diagnostics. Difficulties connected with the analysis of the Stark–Zeeman spectra relate to a hydrogen in external crossed electric and magnetic fields.
Calculation of spectral line shape in plasmas is complicated by two serious problems. The first is the complex structure of the dipole matrix elements, as well as the rapid growth of the array of radiative transitions. The second is connected with the problem of the influence of an ion thermal motion on the intensity profile. This paper shows how one can get around these difficulties. The complex expressions for the transition probabilities can be simplified by using the semiclassical approximation for coordinate matrix elements obtained by S.A. Gulyaev [9,10] and specific properties of the Wigner d-functions [11]. The thermal motion of ions can be taken into account using the FFM. It turns out that spectral line shape in a plasma with moving ions is a functional of the static profile [12].
The first attempt to provide a solution to this problem was made within the framework of the classical mechanics [13]. The perturbed motion of the electron was reduced to an independent precession of two vectors representing the combination of the angular momentum and the averaged coordinate around two different axes. The quantum approach to this problem has become possible thanks to the fundamental work of V.A. Fock [14], who showed that an electron in the Coulomb field has enhanced O(4) (instead of common O(3)) symmetry. This fact leads to the existence of two additional constant of motion , which are connected with the orbital momentum by the simple relation A rigorous quantum consideration of this problem is given in [15]. In this work, the authors used the O(4) symmetry properties of the Coulomb field to obtain the spectra of a hydrogen atom in the external electric and magnetic fields. The Hamiltonian of this system is equal to
where , and are the momentum, the coordinate and the angular momentum operators of the electron, correspondingly, Z is the charge of nuclei. This formula and every other in this paper is written in the atomic units. The perturbed part can be rewritten in another way.
where
where 1 relates to + and 2 to −.
is the specific constant of motion in the Coulomb field—the Runge–Lenz vector.
We can do this, because in the Coulomb field there is connection between the Runge–Lenz vector and the coordinate (this is valid only within the manifold of a fixed principal quantum number n):
Obviously, the vectors (3) are constants of motion in the Coulomb field. Moreover, they have the angular momentum properties. Coming to the parabolic basis, there is the connection between the parabolic quantum numbers , and projections on the single direction [16]
where are projections of (3) on the z direction (quantization axis) and m is the magnetic quantum number.
Using the angular momentum properties of vectors (3), we can express the wave functions in the representation of in terms of the parabolic states.
where is the Wigner d-function.
In (8), are the angles between vectors and . We choose the reference frame in which the direction of the magnetic field coincides with the z axis.
where is the angle between electric and magnetic fields .
The coordinate matrix elements in basis (8) has the following form
where (the intensity of radiation in the dipole approximation is proportional to the squared absolute value of the coordinate matrix element).
Accurate quantum expressions for the matrix elements in (11) were obtained by Gordon [17,18] and have a very complicated structure. They contain the hyper-geometric series which makes calculations for Rydberg atoms very cumbersome. The detailed analysis of computational complexities and ways to get around them are presented in [19]. The array of radiative transitions grows proportionally to . To carry out calculations for highly excited levels, the author of [9,10] obtained the approximation of and developed the method of the distribution of atomic transitions into special groups. These results and the usage of the specific d-functions properties allow one to simplify the complicated expression (11). The results for the () and () series are obtained in [20,21]. The basics of the approach to calculating these matrix elements and the results (see Formulas (A11)–(A16)) are presented in the Appendix A.
In the present paper, we take into account thermal velocity of ions. This problem is closely related to stochastic processes in the Coulomb-like interacting medium. Statistical aspects of the collective motion in the Coulomb field are considered in [22]. The frequency fluctuation model (FFM) consists in the dependence of the spectral line profile on the jumping ion frequency .
where is the density and is the thermal velocity of ions.
Using the FFM, the intensity can be analytically expressed as the functional of the normalized static profile [12].
A similar calculation, using the FFM, but without taking into account the influence of the magnetic field on the shape of spectral lines, is given in [23]. Moreover, this work contains the detailed analysis of the influence of the thermal ion velocity on the plasma line shapes.
The spectral lines profiles in the presence of a magnetic field were calculated by Novikov et al. [24]. They used the accurate analytical expressions for the dipole matrix elements. However, this work contains profiles only of and lines. In addition, the authors did not consider the thermal motion of ions. Application of the frequency-fluctuation model to Stark–Zeeman line shapes was demonstrated by Ferri et al. [25]. Again, this work considers only the transitions between levels with a low value of the principal quantum number n. Computer modeling, taking into account the largest possible number of effects on the shape of spectral lines, is presented in the works of Rosato et al. [26,27].
In the present paper, we derive the analytical expressions for spectral lines profiles in plasma. These formulas are convenient for simply performing calculations with them. In fact, we provide the algorithm of spectral lines shapes calculations with given parameters of plasma. The expressions for transitions with and are presented.
2. Description of the Method
Firstly, we consider the general expression for the plasma spectral line static profile.
where is the full set of all quantum numbers related to the initial and final states, is the polarization, is the distribution function of the absolute value of electric field, defines the angle between the magnetic field and an ion microfield, and is the dipole matrix element (expressions (A11)–(A13) for and (A14)–(A16) for are presented in Appendix A).
Coming up to our notation, one obtains
Here, the values with bar relate to the final state.
In the summation, there are only two terms. For example, if one calculates the radiation intensity with direction of observation parallel to magnetic field, corresponds to X and Y directions. In other words, in this example, one has to put and .
In (15), is the Dirac delta-function and is the energy shift that corresponds to the set of quantum numbers . In our case, we have
Here, we use the absolute values of the vectors (4). The fact that the system has the circular symmetry is also used, which means that there is no dependence of the energy shift and the matrix elements on the azimuthal angle.
As , one can use the Holtsmark distribution
where is the charge and is the density of ions. The detailed analysis of the Holtsmark distribution is presented in [5,12].
To take into account the thermal velocity of ions in plasmas, we use Formulas (13) and (14). One can substitute expression (15) into (14). After that, it is possible to integrate over and get rid of the delta functions.
Now, it is necessary to take into account the Doppler and the electron broadening mechanisms. To do this, one has to calculate the convolution of from (13) (with from (19)) with the Voigt profile
Expression (21) relates to the Doppler broadening [5]. Here, D is the Doppler parameter
where , c is the speed of light in vacuum, and M and are the mass and temperature of atoms, respectively.
That Lorentz distribution corresponds to the electron broadening. Generally, the calculation of the parameter is a complicated process. We use the simplified approach to the electron broadening (see [5]).
where and are the density and thermal velocity of electrons, correspondingly, and is the Debye radius in plasmas.
where is the coordinate operator, is the transition intensity, and a and b denote different states referring to levels n, . For example,
More accurate calculations for the electron broadening are discussed in [28]. Moreover, modification of this broadening theory is presented in the Appendix of [24].
Finally, we can obtain the formula for the intensity of radiation as the function of the energy shift (frequency). It is the convolution of expressions (13) and (20).
To sum up, we obtain the algorithm for plasma line shapes calculations. Expressions for the dipole matrix elements are presented in the Appendix A. We take into account Stark–Zeeman, Doppler, and electron mechanisms of broadening. Moreover, using the FFM, the effect of thermal velocity is considered. For every step of the calculation, we use analytical expressions. The approximations for the transitions intensities are derived for lines with and . The main advantage this method is the opportunity of performing calculations for any large principle numbers.
3. Results and Discussion
Specific calculations for a deuterium plasma are demonstrated in this section. To estimate the accuracy of the method, we compare the results of other groups for the and spectral lines with our algorithm.
Comparison of semiclassical (universal approach) calculations and the results of Ferri et al. [25] are presented in Figure 1. One can observe the satisfactory correspondence between two approaches. Even for low levels and , the Rydberg approximation shows a high degree of accuracy. However, there is a slight discrepancy, mainly due to the imprecision in the calculations of the Stark shift (here, ). This calculation is extremely representative because in both approaches the thermal velocity of ions is taken into account in the same way. In fact, the main difference here is the choice of expressions for the transition probabilities.
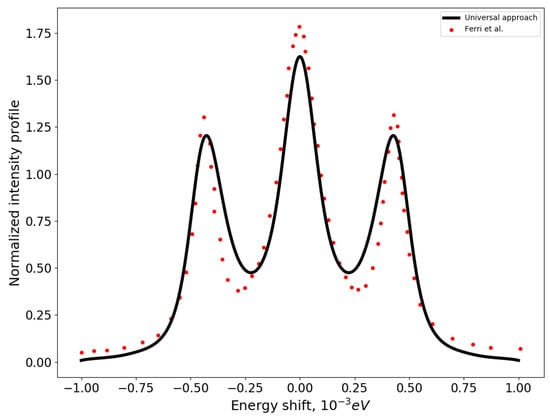
Figure 1.
Normalized intensity profile of spectral line (transition 3-2) as the function of the energy shift. The direction of observation is perpendicular to the magnetic field, eV, cm−3, T. Comparison of the semiclassical approach and an accurate calculation in [25].
One can observe a tolerable coincidence between the Rydberg approach to spectral lines in plasmas and the computer modeling in [27]. Calculations for line are presented in Figure 2. The semiclassical approach has a distinct feature: the narrowing in the center. It is connected with the widening on the sides. The reason for these little “wings” is Zeeman components. The inaccuracy of the Rydberg approximation leads to a slight decrease in the Stark shift. However, this result should be considered quite satisfactory because distance between atomic levels is equal to principle quantum number of a lower state. Generally speaking, the condition for the applicability of our approach is , but it turns out that it works well even for the Balmer series.
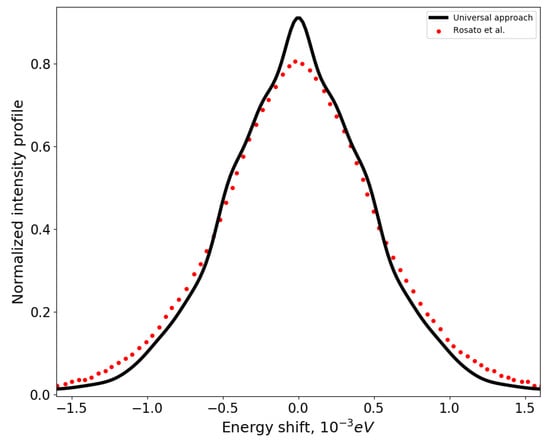
Figure 2.
Normalized intensity profile of spectral line (transition 4-2) as the function of the energy shift. Direction of observation perpendicular to magnetic field, eV, cm−3, T. Comparison of the semiclassical approach and the computer modeling in [27].
Obviously, with growth of n, the Rydberg approximation will be practically indistinguishable from the exact result. For large values of the principle quantum number, distance between atomic levels , thus it will not influence the Stark shift, as well as the electron broadening parameter (except specific cases of the interference of contributions to the electron width, the details can be found in [4]). For highly excited levels, the electron impact on the broadening can blur spectral lines. Thus, the small inexactness connected with the Rydberg approximation can all the more be neglected.
To show how the shape of the spectral line changes, Figure 3 is presented. Using the expression (27), spectral profiles are obtained for the Paschen series (the transition 4-3). It is possible to trace how the Zeeman components disappear with increasing of an ion’s temperature due to the Doppler effect and an ion thermal motion. In the first graph, two Zeeman “wings” are clearly visible. We want to underline that, in this calculation, the temperatures and concentrations of ions and electrons are different. In the fourth graph, the Zeeman components are practically blurred.
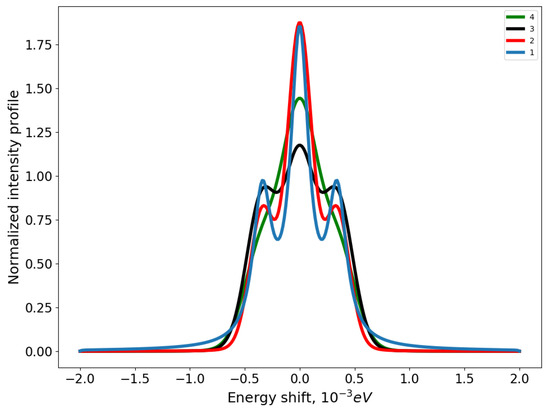
Figure 3.
Normalized intensity profile of spectral line (transition 4-3) as the function of the energy shift. Direction of observation perpendicular to magnetic field T. (1) eV, eV, cm−3, cm−3; (2) eV, eV, cm−3, cm−3; (3) eV, eV, cm−3, cm−3; (4) eV, eV, cm−3, cm−3.
In this method, we do not consider two effects connected with external magnetic field. The first one is that the environment can be spatially inhomogeneous. Therefore, this method is applicable only for comparison with local measurements, so that the temperature and density gradients cannot be large. The second effect is connected with the influence of an electron’s helical path related to the motion in an external magnetic field. Because of this, the argument of the logarithm in Formula (24) can be greatly changed. The influence of a change in the trajectories of an electron on the shape of spectral lines is described in detail in [29]. In the present paper, we focus on the problem of the great array of radiation transition. Our purpose is to show that neglecting of the big part of transitions does not strongly affect the shape of the spectral line. This can be seen by looking at Figure 1 and Figure 2. Comparison of our method with calculations of other groups clearly demonstrates that a significant part of radiative transitions does not contribute to the formation of the spectral profile. Because of that, there is a significant opportunity to simplify calculations of the spectral line shape in plasmas. This method is mainly applicable for the case when ion’s Stark broadening dominates over the electron one, in both static and impact limits for ions.
In this paper, a whole complex of problems in the theory of broadening of spectral lines in plasma is considered. However, individually, many of these topics have already been discussed previously. Semiclassical approximation for the transition probability (the intensity) is presented in [30]. Mathematical aspects of the application of the O(4) symmetry to the theory of spectral line broadening are discussed in the work [31]. However, this approach is not convenient for describing the transition array in the case of a magnetized plasma. The applicability of the FFM to plasma in the presence of a magnetic field is discussed in [32].
The presented algorithm can be a convenient tool for diagnosing helium plasma in the ITER divertor [33,34]. An example of calculation for helium is shown in Figure 4 (transition 5-4).
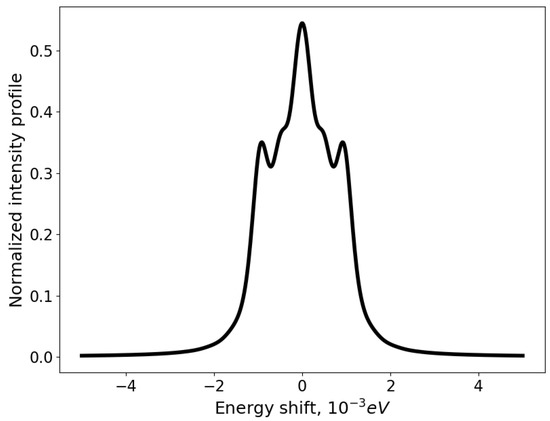
Figure 4.
Normalized intensity profile of spectral line (transition 5-4) as a function of the energy shift. Hydrogen-like Helium ion; eV, cm−3, T.
4. Conclusions
A semiclassical approach to the spectral lines in plasmas is presented. We demonstrate how one can use the analytical expressions for calculating and line shapes. Thanks to the presented method, it is possible to calculate the intensity profiles for transitions with large principle quantum numbers. Basically, this approach is suitable for the spectral line shapes of hydrogen-like ions. For calculations within the visible range, it is necessary to consider transitions with larger n. Moreover, it is shown that this approach can be used to achieve satisfactory agreement with the transitions related to the Balmer series (Figure 1 and Figure 2).
Using the FFM, one can relatively simply take into account the effect of the thermal motion of ions in the plasma on the shape of spectral lines. The FFM profile depends on the functions (14). The integrand in depends on static profile (15). The function is expressed in terms of delta-functions. It allows one do a simple integration and obtain Formula (19) for .
In [12], the authors considered a Hydrogen atom in external crossed electric and magnetic fields. They performed calculations in the specific basis (8). These states are closely related to the parabolic quantization on two different axes. Calculation of the transition probabilities in this basis leads one to Formula (11). Using the symmetry properties of the Coulomb field, the Wigner d-functions recurrence relations, and the Rydberg asymptotic formulas for the coordinate matrix elements [9,10], the simple semiclassical approximations for the dipole matrix elements in representation of states (8) are obtained in [20,21] and applied to the spectral line shape calculations. The approximations for the transitions probabilities in this basis are presented in Appendix A (see (A11)–(A16)).
To demonstrate the power of the Rydberg atom approach, Balmer series line shapes are calculated and compared with the results of other groups. The shape of line is presented in Figure 1. One can observe a good correspondence with accurate consideration from [25]. The comparison of Rydberg approach and the computer simulation [27] is presented in Figure 2. Even for the 4-2 transition, the analytical approximation shows a good correspondence with quantum calculations.
The specific calculation for the series is demonstrated in Figure 3. Using the presented algorithm, the shapes of spectral lines were calculated for various plasma parameters. This figure clearly illustrates how different mechanisms affect the shape of the spectral line.
Author Contributions
A.L.: software, writing—original draft preparation, visualization, methodology, investigation. V.L.: Conceptualization, methodology, project administration, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Dipole Matrix Elements
The detailed derivation of the semiclassical approximation of the dipole matrix elements that is the representation of states (8) is presented in [20,21]. In the Appendix, we briefly discuss the main points of calculating the transition probabilities and present the results in [20,21]. Firstly, it is necessary to consider new quantum number K
It turns out that the a radiative transition probability strongly depends on this number (A1) [9,10]. It partially solves the problem of a large array of transitions between Rydberg atomic states. It is necessary to calculate the intensity of transitions only with a certain value of K. For example, while calculating the spectral line shape of the line, one has to calculate transitions only with and . By fixing the magnetic quantum number m and K, it is possible to establish the approximate selection rules for the parabolic quantum numbers (7)
For Z matrix element (),
For X-matrix element (),
In the case of line, it is necessary to calculate the dipole matrix elements with and . Similar systems can be written for the case .
For Z matrix element (),
For X-matrix element (),
By solving systems (A2)–(A5), we can express in terms of . This leads to the reduction of the expression (11) to double sums. Moreover, as shown in [20,21], these sums are independent.
For example, the solution to the system (A2) reduces the expression (11) to the following formula
where
One can find formulas for find in [9,10]. Detailed derivation of this expression is presented in [17]. The next step is the usage of the recurrence and orthogonality relations for the Wigner d-functions [11].
In the case of both and spectral lines, these manipulations lead to the following results.
For the line
The hydrogen wave function is proportional to , , . Using well-known relations and , one can obtain
For the line,
Here, can be obtained by switching (for bar values too) and in . The same connection exists between and .
The presence of the delta-functions in Formulas (A11)–(A16) expresses the selection rule for the angular momentum. The quantum number corresponding to the angular momentum cannot change by more than 1. Moreover, the presence of delta functions partially solves the problem of the giant array of Rydberg radiative transitions.
References
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 2005; Volume 2. [Google Scholar]
- Lisitsa, V.S. Atoms in Plasmas; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012; Volume 14. [Google Scholar]
- Oks, E.A. Plasma Spectroscopy: The Influence of Microwave and Laser Fields; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012; Volume 9. [Google Scholar]
- Sobel’Man, I.I.; Vainshtein, L.A.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012; Volume 15. [Google Scholar]
- Sobel’Man, I.I. Introduction to the Theory of Atomic Spectra: International Series of Monographs in Natural Philosophy; Elsevier: Amsterdam, The Netherlands, 2016; Volume 40. [Google Scholar]
- Oks, E. Advances in X-Ray Spectroscopy of Laser Plasmas; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Oks, E. Diagnostics of Laboratory and Astrophysical Plasmas Using Spectral Lineshapes of One-, Two-, and Three-Electron Systems; World Scientific: Singapore, 2017. [Google Scholar]
- Oks, E. Stark Broadening of Hydrogen and Hydrogenlike Spectral Lines in Plasmas: The Physical Insight; Alpha Science International: Oxford, UK, 2006. [Google Scholar]
- Gulyaev, S.A. Profile of the Hn alpha. radio lines in a static ion field. Sov. Astron. AJ (Engl. Transl.) 1976, 20. Available online: http://adsabs.harvard.edu/full/1976SvA....20..573G (accessed on 20 June 2020).
- Gulyaev, S.A. Profile of the Hn beta. radio lines in a static ion field. Sov. Astron. 1978, 22. Available online: http://adsabs.harvard.edu/full/1978SvA....22..572G (accessed on 30 July 2020).
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum: Irreducible Tensors, Spherical Harmonics, Vector Coupling Coefficients, nj Symbols; World Scientific: Singapore, 2008. [Google Scholar]
- Bureeva, L.A.; Kadomtsev, M.B.; Levashova, M.G.; Lisitsa, V.S.; Calisti, A.; Talin, B.; Rosmej, F. Equivalence of the method of the kinetic equation and the fluctuating-frequency method in the theory of the broadening of spectral lines. Jetp Lett. 2010, 90, 647–650. [Google Scholar] [CrossRef]
- Born, M.; Hund, F.; Jordan, P. Vorlesungen über Atommechanik; Springer: Berlin/Heidelberg, Germany, 1925; Volume 1. [Google Scholar]
- Fock, V.A. Zur theorie des wasserstoffatoms. Z. Phys. 1935, 98, 145–154. [Google Scholar] [CrossRef]
- Demkov, Y.N.; Monozon, B.S.; Ostrovsky, V.N. Energy levels of a hydrogen atom in crossed electric and magnetic fields. Sov. Phys. JETP 1970, 30, 775–776. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Gordon, W. Zur Berechnung der Matrizen beim Wasserstoffatom. Ann. Phys. 1929, 394, 1031–1056. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of Atoms with One and Two Electrons; Pizmatgiz: Moscow, Russia, 1960. [Google Scholar]
- Dewangan, D.P. An accurate quantum expression of the z-dipole matrix element between nearby Rydberg parabolic states and the correspondence principle. J. Phys. At. Mol. Opt. Phys. 2007, 41, 015002. [Google Scholar] [CrossRef]
- Letunov, A.Y.; Lisitsa, V.S. Stark-Zeeman and Blokhincev spectra of Rydberg atoms. J. Theor. Exp. Phys. 2020, 5, 131. [Google Scholar]
- Letunov, A.Y.; Lisitsa, V.S. Spectra of a Rydberg Atom in Crossed Electric and Magnetic Fields. Universe 2020, 6, 157. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic problems in physics and astronomy. Rev. Mod. Phys. 1943, 15, 1. [Google Scholar] [CrossRef]
- Mossé, C.; Calisti, A.; Stamm, R.; Talin, B.; Bureyeva, L.A.; Lisitsa, V.S. A universal approach to Rydberg spectral line shapes in plasmas. J. Phys. At. Mol. Opt. Phys. 2004, 37, 1343. [Google Scholar] [CrossRef]
- Novikov, V.G.; Vorob’ev, V.S.; D’yachkov, L.G.; Nikiforov, A.F. Effect of a magnetic field on the radiation emitted by a nonequilibrium hydrogen and deuterium plasma. J. Exp. Theor. Phys. 2001, 92, 441–453. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Mouret, L.; Talin, B.; Gigosos, M.A.; González, M.A.; Lisitsa, V. Frequency-fluctuation model applied to Stark-Zeeman spectral line shapes in plasmas. Phys. Rev. E 2011, 84, 026407. [Google Scholar] [CrossRef] [PubMed]
- Rosato, J.; Bufferand, H.; Koubiti, M.; Marandet, Y.; Stamm, R. A table of Balmer gamma line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transf. 2015, 165, 102–107. [Google Scholar] [CrossRef]
- Rosato, J.; Marandet, Y.; Stamm, R. A new table of Balmer line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 333–337. [Google Scholar] [CrossRef]
- Seaton, M.J. Atomic data for opacity calculations. XIII. Line profiles for transitions in hydrogenic ions. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 3255. [Google Scholar] [CrossRef]
- Oks, E. Review of Recent Advances in the Analytical Theory of Stark Broadening of Hydrogenic Spectral Lines in Plasmas: Applications to Laboratory Discharges and Astrophysical Objects. Atoms 2018, 6, 50. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Stark effect of high-n hydrogen-like transitions: Quasi-contiguous approximation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 095703. [Google Scholar] [CrossRef]
- Gigosos, M.A.; González, M.Á. Comment on “A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines”. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 533–535. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogenlike Stark-broadened line shapes in plasmas. Phys. Rev. E 2013, 87, 053108. [Google Scholar] [CrossRef]
- Gorbunov, A.V.; Mukhin, E.E.; Berik, E.B.; Vukolov, K.Y.; Lisitsa, V.S.; Kukushkin, A.S.; Levashova, M.G.; Barnsley, R.; Vayakis, G.; Walsh, M.J. Laser-induced fluorescence for ITER divertor plasma. Fusion Eng. Des. 2017, 123, 695–698. [Google Scholar] [CrossRef]
- Gorbunov, A.V.; Mukhin, E.E.; Berik, E.B.; Melkumov, M.A.; Babinov, N.A.; Kurskiev, G.S.; Tolstyakov, S.Y.; Vukolov, K.Y.; Lisitsa, V.S.; Levashova, M.G.; et al. Laser-induced fluorescence of helium ions in ITER divertor. Fusion Eng. Des. 2019, 146, 2703–2706. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).