Abstract
We consider the problem of the choice of gauge in nonrelativistic strong-laser-field physics. For this purpose, we use the phase-space path-integral formalism to obtain the momentum-space matrix element of the exact time-evolution operator. With the assumption that the physical transition amplitude corresponds to transitions between eigenstates of the physical energy operator rather than the unperturbed Hamiltonian , we prove that the aforementioned momentum-space matrix elements obtained in velocity gauge and length gauge are equal. These results are applied to laser-assisted electron-ion radiative recombination (LAR). The transition amplitude comes out identical in length gauge and velocity gauge, and the expression agrees with the one conventionally obtained in length gauge. In addition to the strong-field approximation (SFA), which is the zeroth-order term of our expansion, we present explicit results for the first-order and the second-order terms, which correspond to LAR preceded by single and double scattering, respectively. Our general conclusion is that in applications to atomic processes in strong-field physics the length-gauge version of the SFA (and its higher-order corrections) should be used. Using the energy operator as the basis-defining Hamiltonian, we have shown that the resulting transition amplitude is gauge invariant and agrees with the form commonly derived in length gauge.
1. Introduction
Strong-field physics is an important area of modern science which studies the interaction of matter with strong laser fields [1,2,3,4,5,6,7,8,9,10,11]. Its development has particularly accelerated after the invention of the chirped-pulse-amplification method for the generation of ultrashort high-intensity laser pulses. The discovery of new nonlinear strong-field phenomena led to the development of attoscience [12,13,14,15,16,17]. Processes in strong laser fields can be divided into laser-assisted and laser-induced processes. The former, which can take place even without the presence of an external laser field, include laser-assisted scattering and laser-assisted electron-ion radiative recombination (LAR) [3], while examples of the latter, which are possible only in the presence of the laser field, are high-order harmonic generation (HHG) [1,2,3] and above- threshold ionization (ATI) [2,5,11]. In the present paper, we will consider the LAR process.
As the laser field in the above-mentioned processes is strong, these processes are highly nonlinear and their theoretical treatment is difficult. Various analytical and semi-analytical approximate methods have been developed for this purpose. Most popular (and successful) is the so-called strong-field approximation (SFA). The development of the SFA started with Keldysh’s seminal paper [18] (see also the subsequent papers in [19,20,21]). In this context, the papers by Faisal [22] and by Reiss [23] should also be mentioned, which are based on S-matrix theory. For further development of the SFA, see the review articles [1,2,3,4,5,6,7,8,9,10,11] and the references therein. One of the problems of the SFA is that the results depend on the choice of gauge used in the calculations. Usually one of two gauges is used: velocity or length gauge. By velocity gauge we mean the radiation gauge used in dipole approximation [24], while the length gauge is the Göppert–Mayer gauge [25].
We have recently developed a phase-space path-integral formalism for strong-field processes [26,27,28]. Using the power of the Feynman path-integral formalism [29] or, more precisely, its phase-space path-integral version [30], we presented the momentum-space matrix element of the time-evolution operator in the form of an expansion in powers of the effective interaction of the electron with the rest of the atom. The zeroth-order term of this expansion leads to the SFA, while the first-order term gives the so-called improved SFA, which, in the case of the ATI process, contains a correction due to the electron rescattering off its parent ion [2,11]. Our results were obtained in length gauge. The first goal of our present paper is to obtain such an expansion in velocity gauge.
We apply our results to the less studied (in comparison with the laser-induced HHG and ATI processes) LAR process. Electron-ion recombination in the absence of a laser field is important in plasma physics and in astrophysics [31]. In laser-assisted electron-ion radiative recombination, the incident electron may exchange energy with the laser field before it recombines with the target ion and a high-energy photon (X-ray) is radiated. The LAR process was considered in [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. Experimental analysis of the LAR process requires a set-up with three beams (the ionic target, electron, and laser beams), which must be crossed in coincidence. This is quite difficult so that experimental data are sparse. However, one should have in mind that the LAR process is the third step of the HHG process, which emphasizes its importance. In the HHG process the laser-driven electron, released in the ATI process, returns and recombines with the parent ion in the LAR process and a high-harmonic photon is emitted. In this case, the above-mentioned coincidence condition is automatically satisfied.
Various alternative formalisms have been introduced in the literature to account for the interaction of the electron in the continuum with the ionic potential. The quantitative rescattering theory (QRS) [6,54] is closely related to our improved SFA, except that it allows for more details of the actual ionic potential to enter the description. It is on the same footing as the “low-frequency approximation” [55,56], which essentially replaces the ionic potential in the Born series by the corresponding T matrix. Propagation effects of the electron in the field-affected continuum can be accounted for by the Eikonal–Volkov approximation (EVA) [57], which augments the SFA phase to include the potential. A very ambitious approach proceeds via the “analytic R matrix” (ARM) [58], which identifies a certain radius such that in the interior the dynamics are simulated exactly while outside Volkov functions are employed. Different versions of the Coulomb-corrected SFA are described in recent review article [59]. These formalisms have mostly been applied to ionization. An application to LAR should be possible but has not been carried out yet.
We will formulate our LAR problem in an arbitrary gauge. The results obtained will be presented in a form that contains the momentum-space matrix element of the time-evolution operator for an electron in an atom exposed to a laser field for which we have already found exact expressions—in velocity gauge in the current paper and in length gauge in [26,28] (see also Appendix A). In the following, we introduce a crucial step: we employ as the basis-defining Hamiltonian the (time-dependent) gauge-covariant “energy” operator , with , i.e., the sum of kinetic and potential energy, in place of the commonly used non-gauge-covariant “unperturbed” Hamiltonian . This formalizes the physical statement that the observed transitions occur between eigenstates of the energy operator rather than between eigenstates of the non-gauge-covariant Hamiltonian . Expanding then the transition amplitude in powers of the atomic potential and comparing the corresponding expressions in velocity and length gauges we will show that they are actually identical. Furthermore, we will show that each term in the expansion of the transition amplitude in powers of the atomic potential in velocity gauge is identical with the corresponding term in length gauge. Finally, we will analyze this expansion and explain the physical meaning of the zeroth-, first-, and second-order terms. In Appendix A we present expressions for the previously obtained momentum-space matrix element of the time-evolution operator in length gauge, while in Appendix B we introduce the gauge-covariant energy operator. The conventional velocity-gauge SFA for the LAR process is derived in Appendix C. We use atomic units throughout the paper.
2. Momentum-Space Matrix Element of the Time-Evolution Operator in Velocity Gauge
We suppose that the Hamiltonian of our atomic system is
where and are, respectively, the potential of the effective interaction of one electron with the rest of the atom and the atomic Hamiltonian in the absence of the laser field and in the single-active-electron approximation. The subscript “vg” stands for velocity gauge, which is the radiation gauge (or Coulomb gauge) in dipole approximation [24] (the scalar potential is and the vector potential is , ). The corresponding laser-field–electron interaction is
We consider the time-evolution operator , which corresponds to the Hamiltonian . In ionization experiments the electron-momentum distribution is recorded, and in LAR experiments the prepared incident electron beam is characterized by a particular electron momentum. Therefore, we consider the momentum-space matrix element of the time-evolution operator. For , we slice the corresponding momentum-space matrix element into time-evolution operators, each acting across an infinitesimal time slice of width , . Introducing the notation , , , , we present the momentum-space matrix element of our time-evolution operator as
Integration over all paths corresponds to summation over all histories along which a physical system can possibly evolve when going from to . Using the path-integral notation [30], we rewrite Equations (3) and (4) in the form
where is the classical canonical action for the paths , in phase space,
with the Hamiltonian
The path integral (3) or (5) is a product of infinitely many integrals. We want to find a method of evaluation of this integral using the assumption that the laser field is strong. To accomplish this we will present our path integral as a perturbative expansion in the atomic potential V. For this purpose, we introduce the Fourier transform of the potential ,
with . We use the expansion
in powers of . The sliced momentum-space matrix element of the time-evolution operator in velocity gauge can then be written as
where . The product of the integrals over gives
so that the product of the integrals over can be written as
In the product of the functions in Equation (13), the factor for gives so that . Using iteratively the remaining functions from the above product, we replace by , i.e., we replace by , , so that we finally get . Using also the relation , the first function in Equation (13) reduces to , so that we can rewrite Equation (11) as
with . In the continuum limit (, ), the sums in Equation (14) become integrals over time. Similarly, as in Appendix A of the work in [28], we obtain our final result
with and . All integrals over are eliminated and the result (10) with (14) or (15) remains exact. It is expressed as an expansion in powers of the effective interaction V of the electron with the rest of the atom in the absence of the laser field. An analogous expression, obtained using length gauge, is presented in Appendix A. In the case of long-range interactions, the asymptotic (in and out) states, which are used to define the transition amplitudes containing the above-derived matrix elements of the total time-evolution operator, should be modified [60,61,62].
3. A Gauge-Covariant Transition Amplitude for Laser-Assisted Electron-Ion Radiative Recombination
We consider the laser-assisted electron-ion radiative recombination process. In this process, the incident electron exchanges energy with the laser field before it recombines with the target ion and a high-energy photon (X-ray) is emitted. The laser field is strong, while the X-ray field is weak. We consider the X-ray field as quantized: the final state with one X-ray photon with the wave vector , energy , and unit polarization vector is described by the ket vector , which is obtained by acting with the creation operator on the initial vacuum state . The field-free Hamiltonian is
The corresponding bound and continuum eigenstates and eigenenergies of the Hamiltonian are, respectively, and and and . The total Hamiltonian is
where and , are, respectively, the vector and scalar potentials of the laser (index L) field and the X-ray (index X) field. The total wave function satisfies the Schrödinger equation
which is invariant with respect to the gauge transformation
in the sense that the transformed wave function
satisfies the same Schrödinger equation as (18), but with the transformed potentials
The transition amplitude from the initial state to the final state is defined by
where is the total time-evolution operator, which corresponds to the Hamiltonian (17) and satisfies the equation .
To further analyze the amplitude (22) we introduce the following time-evolution operator [63] (see Appendix B for a justification of this approach):
Here, the operator corresponds to the Hamiltonian and satisfies . The operator connects the eigenstates of the energy operator (A9), which is a physical quantity, and the eigenstates of the field-free Hamiltonian (interestingly, this operator also connects exact solutions of the time-dependent Schrödinger equation in the presence of an electromagnetic plane-wave field (Volkov states) in velocity and length gauges). The operator satisfies the equation
and the integral equation
This derivation is valid in the long-wavelength approximation in which the vector potential depends only on time, . In our case this holds for the considered laser field, , but for the X-ray field, in principle, we have . However, the X-ray field is weak and higher-order terms in the expansion of can be neglected. In addition, we have the matrix elements , in which only the terms of the form , , which appear for , survive. Therefore, the corrections to the interaction with the X-ray field that are due to the operators are of second order and can be neglected.
Introducing Equation (25) into (22), taking into account that and that the states and are orthogonal, we obtain
As we have explained, only the terms linear in the interaction with the X-ray field should be taken into account, so that
where the time-evolution operator corresponds to the Hamiltonian with only the laser field and we have taken into account that the initial electrons are prepared to have the momentum so that the initial electron state for satisfies [64]. Equation (27) is our final expression for the gauge-covariant transition amplitude of the LAR process. Note that the only approximation that has been introduced thus far is neglecting higher orders of the X-ray field. We did not yet specify the gauge.
4. Equivalence of the Transition Amplitudes in Velocity and Length Gauges and Expansion in Powers of the Atomic Potential
Gauge-covariant transition amplitudes are obtained only if physical quantities, represented by gauge-covariant operators like the energy operator, are used in the derivations. Derived in such a way, the transition amplitude (27) is invariant with respect to the transformations (19), (20), and (A5). Let us now choose the gauge. In length gauge we have and so that , while in velocity gauge it is , so that again , where . We have adopted the same gauge for both the laser field and the X-ray field , but we could equally well choose different gauges for the two fields. The only difference between the length- and velocity-gauge forms of Equation (27) is that in length gauge the factor is absent as the vector potential is zero so that , where the momentum-space matrix elements of the time-evolution operator in our phase-space path-integral formalism are given by Equation (A2). On the other hand, in velocity gauge we have , where the corresponding momentum-space matrix elements are given by Equation (15).
Introducing, in velocity gauge, after the operator in Equation (27), using the relations and , we obtain
The second matrix element on the r.h.s. is proportional to , where we used Equation (A4) (recall , and ). Therefore, our final result is the same in both gauges, and can be written as
with and . The zeroth-order term contains the function , which cancels the integral over and leads to
which is the same as the SFA result obtained using the S-matrix formalism and length gauge [39,40]. For the first-order term, after the substitution , denoting in the final step with , we get
The matrix element describes the three-step process in which the electron, driven by the laser field, instead of recombining directly with the ionic target, may first scatter and only subsequently, after propagation, recombine with the same ionic target. This process is denoted as the SLAR (“S” stands for “scattering”) in [39,40]. The photons emitted in the SLAR process may have higher energies than those emitted in the direct LAR process. However, as this is a first-order process, the emitted X-ray photon yield of the SLAR process is much lower than that of the zeroth-order LAR process. Examples of the SLAR spectra are presented in [39,40,46,47,48]. Finally, for the second-order term, we first make the substitution , , which gives the factor . After that, we again substitute and obtain
The matrix element describes the five-step process, which consists of the first laser-assisted scattering, electron propagation, the second laser-assisted scattering, and the second propagation followed by the recombination and emission of an X-ray photon. We denote this process as DSLAR, where “DS” stands for “double scattering”. Higher-order terms can be obtained in the same way.
In Figure 1, we present a schematic diagram of the LAR, SLAR, and DSLAR processes. The red wiggly lines represent the laser field having the polarization vector . The ion is represented “I” in a blue circle. The electron with the incident momentum is denoted by a black horizontal line with a right arrow. The X-ray photon is denoted by a violet line with an arrow (unit polarization vector and the wave vector (bold line)). The laser-field-dressed intermediate electron momenta are represented by for the SLAR process and by and for the DSLAR process. We have also displayed the Feynman diagram for the DSLAR process. In this diagram, time increases from bottom to top. The electron with the initial momentum is prepared at the time and enters the laser field having the momentum , , in the Volkov state (denoted by a circle in the diagram). After the interaction with the potential V (denoted by a square) at the time , the electron momentum is and the electron propagates (again in the Volkov state) from the time to the time , where it interacts again (for the second time) with the potential V. After the time , the electron propagates with the momentum up to the time when it finally recombines (this interaction is represented by a triangle) to the bound state and an X-ray photon with the wave vector is emitted.
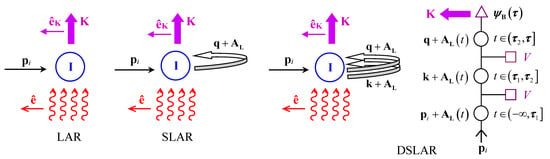
Figure 1.
Schematic diagram of laser-assisted radiative recombination (LAR) (left-hand part), LAR with rescattering (middle part—SLAR), and LAR with double scattering (right-hand part—DSLAR). For the DSLAR process the corresponding Feynman diagram is also presented.
Let us now make some comments about the application of the above result. The amplitudes (30) and (31) were considered in detail in the above-cited references [39,40,46,47,48,52,53]. The amplitude (33) is a new results and, as explained, describes a five-step process. The probability of this process is low, but in some parameter range, where the lower-order terms only give very small contributions, it may be observable. Equation (30) describes the “direct” electrons and the low-energy spectra and should agree with the exact results for laser-assisted radiative attachment. In this case, the final-state electron is bound by a short-range potential; compare with above-threshold detachment of an electron initially bound in a negative ion for which it is well known that the SFA is satisfactory [65]. Due to the influence of the long-range Coulomb potential, for electron–positive-ion LAR the agreement with exact results is probably not so good, but the direct SFA can be improved as was recently done for ATI (“atom-Volkov SFA” in [66]). As of 2002 [39], we used transition amplitudes analogous to Equation (31) and obtained numerical results for various laser-field configurations [46,47,48,53]. As far as we know, the only theory able to reproduce such results for the high-energy plateau with a cutoff in the X-ray spectra is the exactly solvable quantum model based on the effective-range theory [50,51]. Numerical results obtained using this model agree with the results obtained from our theory [39,40,46,47,48]. There are no exact calculations available for the SLAR process, but, bearing in mind the excellent agreement of our high-order SFA-based simulations of ATI and HHG with the results obtained solving the time-dependent Schrödinger equation, we expect that our SLAR results [39,40,46,47,48,53] correctly describe this process as well.
In the formalism presented in this paper, which is based on using the energy operator as the basis-defining Hamiltonian, the transition amplitude is gauge-invariant and agrees with the form normally obtained in length gauge. The question may come up how this compares with the form normally obtained in velocity gauge (using as the basis-defining Hamiltonian). Such comparisons have been carried out for the case of ATI. For photodetachment of the negative ion F by a circularly polarized laser field, there is some quantitative disagreement between the spectra calculated in the two gauges and the length-gauge result may exhibit superior agreement with the experimental data, but the differences are not very pronounced [67]. The amplitudes for ionization of the p ground state using a linearly polarized laser field, however, are qualitatively very different, and the velocity-gauge result fails to agree with a solution of the time-dependent Schrödinger equation while the length-gauge result does [65].
Finally, we comment on the pertinent qualitative differences that we expect for a laser-assisted process as we consider it here (LAR) compared with laser-induced processes (ATI, HHG, etc.), which have been more frequently investigated. Electron-ion recombination may also occur as a field-free process. This means that in LAR the incident electron may enter the field at any time and with any energy. On the other hand, for laser-induced processes, such as ATI and HHG, the ionization time and the subsequent dynamics of the liberated electron depend exclusively on the laser field. The freedom to choose the initial state of the LAR process, i.e., the fact just mentioned that the electron may enter the field at any time and with any energy, may lead to new effects (for example, a longer plateau) in comparison with the ATI and HHG processes.
5. Conclusions and Comments
Transition amplitudes for atomic processes in a strong laser field can be written in a form that contains the momentum-space matrix element of the exact time-evolution operator for an electron in interaction with the atom and the laser field. Applying the phase-space path-integral formalism of nonrelativistic quantum mechanics, we derived an exact expression for this matrix element and presented it in the form of an expansion in the effective interaction of the electron with the remainder of the atom. The result, obtained in velocity gauge, is compared with the analogous result obtained previously in length gauge. Both results are exact and, therefore, equivalent. They can be used to analyze various laser-assisted and laser-induced processes.
We applied these results to laser-assisted electron-ion radiative recombination and obtained a gauge-invariant expression for the transition amplitude of the LAR process. In the derivation, we assumed that the emitted X-ray field is weak, while for the strong external laser field we applied the long-wavelength (dipole) approximation. Introducing the above-mentioned exact momentum-space matrix element into the gauge-invariant amplitude of the LAR process, we obtained an expansion of this amplitude in the electron–atom interaction in the absence of the laser field. The lowest-order term of this expansion reproduces the well-known strong-field approximation, formulated previously in length gauge. We showed that the same result is obtained in velocity gauge provided we apply the introduced formalism based on eigenstates of the energy operator. However, if we use the conventional methodology with a non-gauge-covariant Hamiltonian we obtain an incorrect result, as is shown in Appendix C.
While the SFA for the LAR process is obtained using the zeroth-order term of our expansion, the first-order term of this expansion corresponds to the three-step SLAR process in which the electron first scatters off the ionic target and then, after propagation in the laser field, returns to and recombines with the ion and a high-energy photon is emitted. The second-order term of our expansion describes laser-assisted electron-ion radiative recombination preceded by double scattering, which is a five-step process. The Feynman diagram of this process is presented in Figure 1.
In addition, we addressed an old problem of nonrelativistic quantum mechanics applied to processes in strong fields, namely, which gauge should be used in the SFA (see, for example, [63,65,68,69,70,71], the reviews [72,73], and references therein). Our conclusion is that the SFA (in dipole approximation) is gauge-invariant and produces the results that were previously obtained in length gauge. We arrived at this conclusion starting from exact expressions using the phase-space version of Feynman’s path-integral formalism, which once more confirms its power in the application to strong-field physics.
Author Contributions
All authors contributed equally to the paper. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support by the Alexander von Humboldt Foundation and by the Ministry for Education, Science and Youth, Canton Sarajevo, Bosnia and Herzegovina.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Length-Gauge Momentum-Space Matrix Element of the Time-Evolution Operator
In [26] and in Appendix A of [28], we presented the momentum-space matrix element of the time-evolution operator of an atomic system in interaction with a strong laser field in the form of an expansion in powers of the effective interaction of the electron with the rest of the atom. This was in length gauge and the corresponding Hamiltonian was . Here, we reproduce the final result and show that it is equivalent to the velocity-gauge result which we derived in a simpler way in Section 2 of the current paper. Complications when using length gauge come from the fact that the interaction in length gauge depends on the electric-field vector which should be replaced with where . The final result is
with , , , and .
It is important to note that in the above expressions in length gauge the vector is not the vector potential of the laser field, but rather defined via the electric-field vector , so that . In length gauge, the vector potential is zero and the scalar potential is expressed via the electric-field vector. In velocity gauge, we have (as ) and the quantity really is the vector potential. The question is what we should use for the “in” and “out” states in the definition of our matrix elements. For and these states, denoted as and , respectively, are eigenstates of the laser-free Hamiltonian. However, in external fields, it is the “energy operator” that is a physical quantity rather than the field-free Hamiltonian [63]. The eigenstates of the energy operator are and , with the same eigenvalues and , respectively, as in the laser-free case. For length gauge the vector potential is zero and the factor is unity, while for velocity gauge this factor must be taken into account. Therefore, the momentum-space matrix elements in velocity gauge should be defined with . Applying this rule to the matrix element , obtained in different gauges, we get the equality
which is exactly what we have obtained in our derivations (compare Equations (15) and (A2)).
Appendix B. Gauge-Covariant Energy Operator
In order to justify the introduction of the time-evolution operator (23), in this appendix we introduce the gauge-covariant energy operator proposed by Yang [74]. An operator is called gauge covariant if it transforms unitarily under a gauge transformation (19) so that
with the unitary operator from Equation (20). A quantity represented by a gauge covariant operator is called a physical quantity [75]. From Equations (20) and (A5) it follows that under a gauge transformation the expectation values of physical quantities remain unchanged,
i.e., they are gauge invariant. The position vector and the mechanical momentum are physical quantities as
The quantity is also a physical quantity. On the other hand, the canonical momentum , the vector potential , and the total Hamiltonian of Equation (17), are not, because
Let us introduce the “energy operator” as the sum of kinetic and potential energy:
Obviously, the operator is a physical quantity, as
We now use the energy operator as the basis-defining Hamiltonian, i.e., we introduce eigenstates and eigenvalues of the energy operator by the relation
The eigenstates are related to the eigenstates of the Hamiltonian , which form a complete orthonormal basis (; is not a physical quantity), by
The corresponding time-evolution operator
where denotes the time-evolution operator of , obeys the equation
which agrees with Equation (24). Indeed, the time-evolution operator is the same as the operator of Equation (23), which occurs in the Dyson Equation (25) for the total time-evolution operator.
According to common lore, the SFA yields different expressions in different gauges. This is due to the fact that commonly the Dyson equation is based on the decomposition where the non-gauge-covariant quantity is used as the basis-defining Hamiltonian. Here we avoided this, by using the energy operator as the basis-defining Hamiltonian with the eigenfunctions (A12). In consequence, the resulting transition amplitude is gauge invariant and agrees with the form that is normally straightforwardly obtained in length gauge. A closely related gauge-covariant derivation of the ionization amplitude in the near-relativistic regime is given in [68].
Appendix C. Conventional Velocity-Gauge SFA
In velocity gauge, the scalar potential is zero, , so that the total Hamiltonian is
where
Conventionally, the velocity-gauge SFA is derived by using the Dyson equation for the total time-evolution operator
As we have explained in Appendix B, the problem with the use of the relation (A17) in deriving the SFA is the fact that is not a physical quantity. Nevertheless, we proceed inserting (A17) into (22), neglecting the terms proportional to (we assumed that the X-ray field is weak) and keeping only the term with
where with the quantization volume. Only the term proportional to contributes as we calculate the matrix element . We want to calculate the lowest-order term in the potential V. For and , the total Hamiltonian reduces to , so that the total time-evolution operator reduces to the velocity-gauge Volkov propagator for the laser field. In this approximation reduces to , where is given by Equation (30). Therefore, the SFA transition amplitude is obtained as
where the superscript “cvg” stands for conventional velocity gauge. In the derivation we used the relations and . The result (A19) is obviously different from the correct result (30). In [65], for the ATI process, it was shown, by comparison with the exact results obtained solving the time-dependent Schrödinger equation, that the conventional velocity-gauge SFA leads to incorrect results. This is particularly pronounced for the odd-parity ground states, where, in the envelope of the angle-resolved energy spectrum, dips in length gauge correspond to humps in velocity gauge and vice versa (compare Figures 1–3 in [65]). It was shown that the length-gauge SFA matches the exact numerical solution.
References
- Salières, P.; L’Huillier, A.; Antoine, P.; Lewenstein, M. Study of the spatial and temporal coherence of high-order harmonics. Adv. At. Mol. Opt. Phys. 1999, 41, 83–142. [Google Scholar]
- Becker, W.; Grasbon, F.; Kopold, R.; Milošević, D.B.; Paulus, G.G.; Walther, H. Above-threshold ionization: From classical features to quantum effects. Adv. At. Mol. Opt. Phys. 2002, 48, 35–98. [Google Scholar]
- Milošević, D.B.; Ehlotzky, F. Scattering and reaction processes in powerful laser fields. Adv. At. Mol. Opt. Phys. 2003, 49, 373–532. [Google Scholar]
- Becker, A.; Faisal, F.H.M. Intense-field many-body S-matrix theory. J. Phys. B 2005, 38, R1–R56. [Google Scholar] [CrossRef]
- Milošević, D.B.; Paulus, G.G.; Bauer, D.; Becker, W. Above-threshold ionization by few-cycle pulses. J. Phys. B 2006, 39, R203–R262. [Google Scholar] [CrossRef]
- Lin, C.D.; Le, A.T.; Chen, Z.; Morishita, T.; Lucchese, R. Strong-field rescattering physics–self-imaging of a molecule by its own electrons. J. Phys. B 2010, 43, 122001. [Google Scholar] [CrossRef]
- Agostini, P.; DiMauro, L.F. Atomic and Molecular Ionization Dynamics in Strong Laser Fields: From Optical to X-rays. Adv. At. Mol. Opt. Phys. 2012, 61, 117–158. [Google Scholar]
- Kohler, M.C.; Pfeifer, T.; Hatsagortsyan, K.Z.; Keitel, C.H. Frontiers of Atomic High-Harmonic Generation. Adv. At. Mol. Opt. Phys. 2012, 61, 159–207. [Google Scholar]
- Becker, W.; Liu, X.J.; Ho, P.J.; Eberly, J.H. Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev. Mod. Phys. 2012, 84, 1011–1043. [Google Scholar] [CrossRef]
- Popruzhenko, S.V. Keldysh theory of strong field ionization: History, applications, difficulties and perspectives. J. Phys. B 2014, 47, 204001. [Google Scholar] [CrossRef]
- Becker, W.; Goreslavski, S.P.; Milošević, D.B.; Paulus, G.G. The plateau in above-threshold ionization: The keystone of rescattering physics. J. Phys. B 2018, 51, 162002. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Salières, P.; Maquet, A.; Haessler, S.; Caillat, J.; Taïeb, R. Imaging orbitals with attosecond and Angström resolutions: Toward attochemistry? Rep. Prog. Phys. 2012, 75, 062401. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Calegari, F.; Sansone, G.; Stagira, S.; Vozzi, C.; Nisoli, M. Advances in attosecond science. J. Phys. B 2016, 49, 062001. [Google Scholar] [CrossRef]
- Cousin, S.L.; Di Palo, N.; Buades, B.; Teichmann, S.M.; Reduzzi, M.; Devetta, M.; Kheifets, A.; Sansone, G.; Biegert, J. Attosecond Streaking in the Water Window: A New Regime of Attosecond Pulse Characterization. Phys. Rev. X 2017, 7, 041030. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 1965, 20, 1307–1314, Zh. Eksp. Teor. Fiz.1964, 47, 1945–1957. [Google Scholar]
- Perelomov, A.M.; Popov, V.S.; Terent’ev, M.V. Ionization of Atoms in an alternating electric field. Sov. Phys. JETP 1966, 23, 924–934. [Google Scholar]
- Perelomov, A.M.; Popov, V.S.; Terent’ev, M.V. Ionization of Atoms in an alternating electric field. II. Sov. Phys. JETP 1967, 24, 207–216. [Google Scholar]
- Perelomov, A.M.; Popov, V.S. Ionization of Atoms in an alternating electrical field. III. Sov. Phys. JETP 1967, 25, 336–343, Zh. Eksp. Teor. Fiz.1967, 52, 514–526. [Google Scholar]
- Faisal, F.H.M. Multiple absorption of laser photons by atoms. J. Phys. B 1973, 6, L89–L92. [Google Scholar] [CrossRef]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 1980, 22, 1786–1813. [Google Scholar] [CrossRef]
- Reiss, H.R. The tunnelling model of laser-induced ionization and its failure at low frequencies. J. Phys. B 2014, 47, 204006. [Google Scholar] [CrossRef]
- Göppert-Mayer, M. Elementary processes with two quantum transitions. Ann. Phys. Leipzig 1931, 9, 273–294. [Google Scholar] [CrossRef]
- Milošević, D.B. Phase space path-integral formulation of the above-threshold ionization. J. Math. Phys. 2013, 54, 042101. [Google Scholar] [CrossRef]
- Milošević, D.B. Few-cycle-laser-pulse Induced and Assisted Processes in Atoms, Molecules, and Nanostructures. In Ultrafast Dynamics Driven by Intense Light Pulses. From Atoms to Solids, from Lasers to Intense X-rays; Kitzler, M., Gräfe, S., Eds.; Springer Series on Atomic, Optical, and Plasma Physics 86; Springer: Cham, Switzerland, 2016; pp. 27–47. [Google Scholar]
- Milošević, D.B. Semiclassical approximation for strong-laser-field processes. Phys. Rev. A 2017, 96, 023413. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 5th ed.; World Scientific: Singapore, 2009. [Google Scholar]
- Hahn, Y. Electron–ion recombination processes—An overview. Rep. Prog. Phys. 1997, 60, 691–759. [Google Scholar] [CrossRef]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Stimulated radiative recombination and X-ray generation. Phys. Rev. A 2000, 61, 023404. [Google Scholar] [CrossRef]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Bohr’s correspondence principle and X-ray generation by laser-stimulated electron-ion recombination. Phys. Rev. A 2001, 63, 055401. [Google Scholar] [CrossRef]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Laser-assisted radiative recombination and X-ray generation. Laser Phys. 2001, 11, 174–182. [Google Scholar]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Coherent phase control in laser-assisted radiative recombination and X-ray generation. J. Phys. B 2001, 34, 1221–1232. [Google Scholar] [CrossRef]
- Kuchiev, M.Y.; Ostrovsky, V.N. Multiphoton radiative recombination of electron assisted by a laser field. Phys. Rev. A 2000, 61, 033414. [Google Scholar] [CrossRef]
- Kuchiev, M.Y.; Ostrovsky, V.N. Effective ATI channels in high harmonic generation. J. Phys. B 2001, 34, 405–430. [Google Scholar] [CrossRef][Green Version]
- Leone, C.; Bivona, S.; Burlon, R.; Ferrante, G. Strong-field and plasma aspects of multiphoton radiative recombination. Phys. Rev. A 2002, 66, 051403(R). [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Rescattering effects in soft-X-ray generation by laser-assisted electron-ion recombination. Phys. Rev. A 2002, 65, 042504. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Laser-assisted electron-ion recombination: Emitted photons’ spectra and recollision effects. J. Mod. Opt. 2003, 50, 657–671. [Google Scholar] [CrossRef]
- Kamiński, J.Z.; Ehlotzky, F. Time-frequency analysis of X-ray generation by recombination in short laser pulses. Phys. Rev. A 2005, 71, 043402. [Google Scholar] [CrossRef]
- Kamiński, J.Z.; Ehlotzky, F. Generation of attosecond pulses in electron-ion recombination processes. J. Mod. Opt. 2006, 53, 7–20. [Google Scholar] [CrossRef]
- Bivona, S.; Burlon, R.; Ferrante, G.; Leone, C. Radiative recombination in a strong laser field: Low-frequency approximation. J. Opt. Soc. Am. B 2005, 22, 2076–2082. [Google Scholar] [CrossRef]
- Bivona, S.; Burlon, R.; Ferrante, G.; Leone, C. Radiative recombination in the presence of a few cycle laser pulse. Opt. Express 2006, 14, 3715–3723. [Google Scholar] [CrossRef] [PubMed]
- Bivona, S.; Burlon, R.; Leone, C. Controlling laser assisted radiative recombination with few-cycle laser pulses. Laser Phys. Lett. 2007, 4, 44–49. [Google Scholar] [CrossRef]
- Čerkić, A.; Milošević, D.B. Focal averaging and incoherent scattering in laser-assisted radiative recombination and scattering processes. Phys. Rev. A 2007, 75, 013412. [Google Scholar] [CrossRef]
- Čerkić, A.; Milošević, D.B. The role of incoherent scattering in laser-induced and laser-assisted processes. Laser Phys. 2009, 19, 783–790. [Google Scholar] [CrossRef]
- Čerkić, A.; Milošević, D.B. Few-cycle-laser-pulse-assisted electron-ion radiative recombination. Phys. Rev. A 2013, 88, 023414. [Google Scholar] [CrossRef]
- Shchedrin, G.; Volberg, A. Analytical model for laser-assisted recombination of hydrogenic atoms. J. Phys. A 2011, 44, 245301. [Google Scholar] [CrossRef]
- Zheltukhin, A.N.; Manakov, N.L.; Flegel, A.V.; Frolov, M.V. Effects of the atomic structure and interference oscillations in the electron photorecombination spectrum in a strong laser field. JETP Lett. 2011, 94, 599–605, Pis’ma Zh. Eksp. Teor. Fiz.2011, 94, 641–646. [Google Scholar] [CrossRef]
- Zheltukhin, A.N.; Flegel, A.V.; Frolov, M.V.; Manakov, N.L.; Starace, A.F. Resonant phenomena in laser-assisted radiative attachment or recombination. J. Phys. B 2012, 45, 081001. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Bicircular-laser-field-assisted electron-ion radiative recombination. Phys. Rev. A 2015, 92, 053416. [Google Scholar] [CrossRef]
- Čerkić, A.; Busuladžić, M.; Milošević, D.B. Electron-ion radiative recombination assisted by a bichromatic elliptically polarized laser field. Phys. Rev. A 2017, 95, 063401. [Google Scholar] [CrossRef]
- Morishita, T.; Le, A.-T.; Chen, Z.; Lin, C.D. Accurate Retrieval of Structural Information from Laser-Induced Photoelectron and High-Order Harmonic Spectra by Few-Cycle Laser Pulses. Phys. Rev. Lett. 2008, 100, 013903. [Google Scholar] [CrossRef] [PubMed]
- Čerkić, A.; Hasović, E.; Milošević, D.B.; Becker, W. High-order above-threshold ionization beyond the first-order Born approximation. Phys. Rev. A 2009, 79, 033413. [Google Scholar] [CrossRef]
- Milošević, D.B. Low-frequency approximation for above-threshold ionization by a laser pulse: Low-energy forward rescattering. Phys. Rev. A 2014, 90, 063423. [Google Scholar] [CrossRef]
- Smirnova, O.; Spanner, M.; Ivanov, M. Analytical solutions for strong field-driven atomic and molecular one- and two-electron continua and applications to strong-field problems. Phys. Rev. A 2008, 77, 033407. [Google Scholar] [CrossRef]
- Torlina, L.; Smirnova, O. Time-dependent analytical R-matrix approach for strong-field dynamics. I. One-electron systems. Phys. Rev. A 2012, 86, 043408. [Google Scholar] [CrossRef]
- Figueira de Morisson Faria, C.; Maxwell, A.S. It is all about phases: Ultrafast holographic photoelectron imaging. Rep. Prog. Phys. 2020, 83, 034401. [Google Scholar] [CrossRef]
- Dollard, J.D. Asymptotic convergence and the Coulomb interaction. J. Math. Phys. 1964, 5, 729–738. [Google Scholar] [CrossRef]
- Dollard, J.D. Adiabatic switching in the Schrödinger theory of scattering. J. Math. Phys. 1966, 7, 802–810. [Google Scholar] [CrossRef]
- Dollard, J.D. Screening in the Schrödinger theory of scattering. J. Math. Phys. 1968, 9, 620–624. [Google Scholar] [CrossRef]
- Becker, W.; Milošević, D.B. A gauge-covariant derivation of the strong-field approximation. Laser Phys. 2009, 8, 1621–1625. [Google Scholar] [CrossRef]
- Starace, A.F. Theory of Atomic Photoionization. In Handbuch der Physik; Mehlhorn, W., Ed.; Springer: Berlin, Germany, 1982; pp. 1–121. [Google Scholar]
- Bauer, D.; Milošević, D.B.; Becker, W. Strong-field approximation for intense-laser-atom processes: The choice of gauge. Phys. Rev. A 2005, 72, 023415. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W. Atom-Volkov strong-field approximation for above-threshold ionization. Phys. Rev. A 2019, 99, 043411. [Google Scholar] [CrossRef]
- Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Gauge dependence of the strong-field approximation: Theory vs. experiment for photodetachment of F-. Opt. Commun. 2007, 275, 116–122. [Google Scholar] [CrossRef]
- Klaiber, M.; Hatsagortsyan, K.Z.; Keitel, C.H. Gauge-invariant relativistic strong-field approximation. Phys. Rev. A 2006, 73, 053411. [Google Scholar] [CrossRef]
- Faisal, F.H.M. Gauge-invariant intense-field approximations to all orders. J. Phys. B 2007, 40, F145–F155. [Google Scholar] [CrossRef]
- Faisal, F.H.M. Gauge-equivalent intense-field approximations in velocity and length gauges to all orders. Phys. Rev. A 2007, 75, 063412. [Google Scholar] [CrossRef]
- Vanne, Y.V.; Saenz, A. Generalized gauge-invariant formulations of the strong-field approximation. Phys. Rev. A 2009, 79, 023421. [Google Scholar] [CrossRef]
- Schlicher, R.R.; Becker, W.; Bergou, J.; Scully, M.O. Interaction Hamiltonian in quantum optics or: vs. revisited. In Proceedings of the NATO Advanced Study Institute on Quantum Electrodynamics and Quantum Optics; Barut, A.O., Ed.; Plenum: New York, NY, USA, 1984; pp. 405–442. [Google Scholar]
- Bandrauk, A.D.; Fillion-Gourdeau, E.; Lorin, F. Atoms and molecules in intense laser fields: Gauge invariance of theory and models. J. Phys. B 2013, 46, 153001. [Google Scholar] [CrossRef]
- Yang, K.-H. Gauge transformations and quantum mechanics I. Gauge invariant interpretation of quantum mechanics. Ann. Phys. (N.Y.) 1976, 101, 62–96. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Diu, B.; Laloë, C. Quantum Mechanics; Hermann/Wiley: Paris, France, 1977. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).