Complexity Estimation of Cubical Tensor Represented through 3D Frequency-Ordered Hierarchical KLT
Abstract
1. Introduction
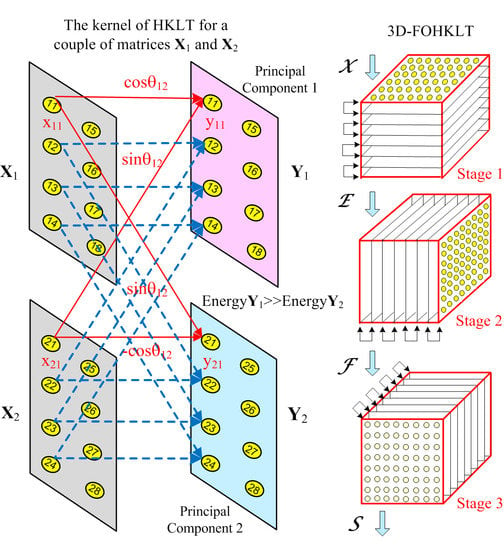
2. One-Dimensional Hierarchical Adaptive PCA/KLT Transform for a Sequence of Matrices
2.1. One-Dimensional Adaptive PCA/KLT Transform for a Sequence of Matrices
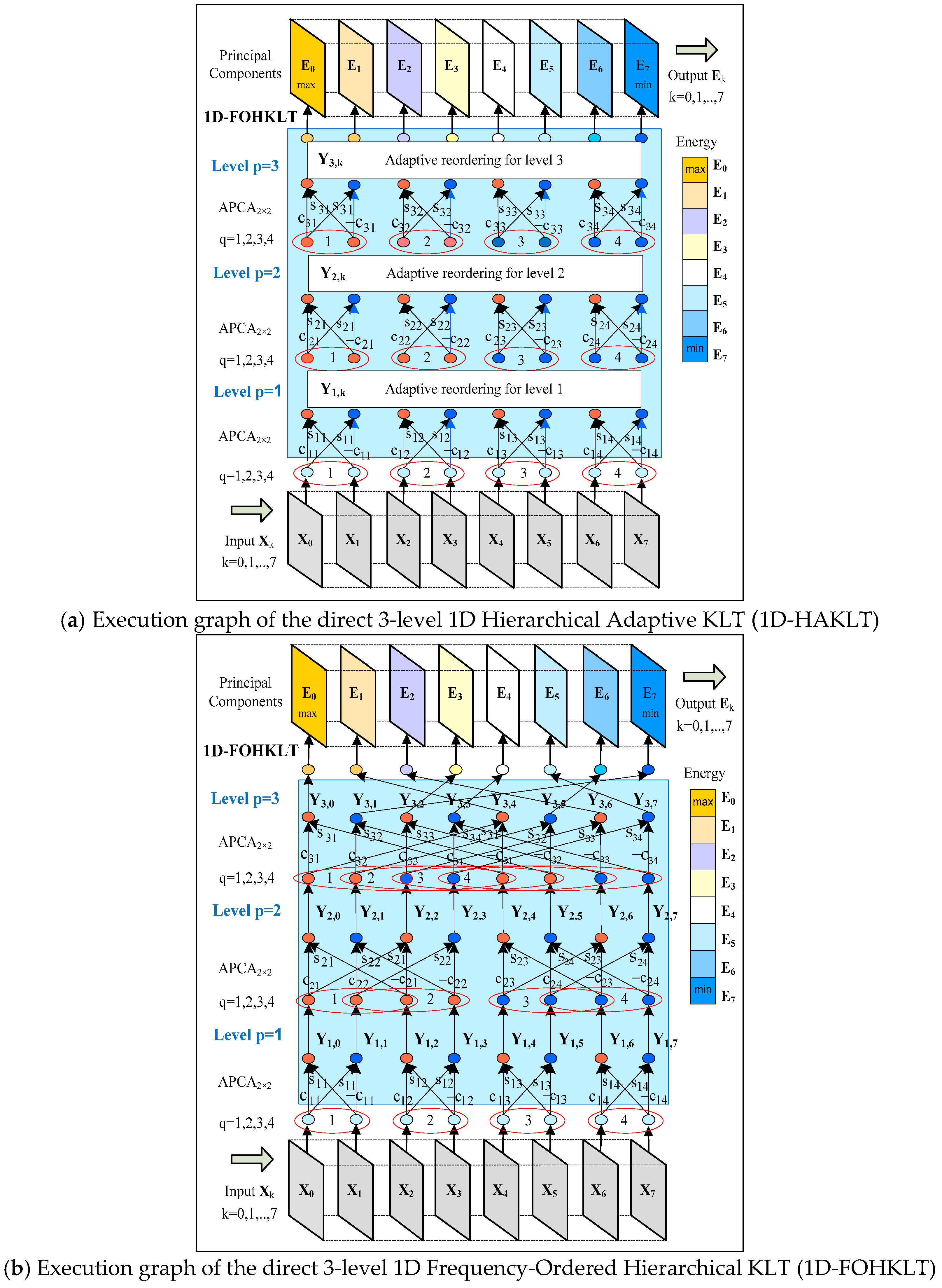
2.2. One-Dimensional Hierarchical Adaptive KLT for a Sequence of Matrices
- the binary code of the sequential decimal number k = 0, 1, …, 2n−1 of the component Yn,k is arranged inversely (i.e., ), as follows:
- the so-obtained code is transformed from Gray code into binary code , in accordance with the operations
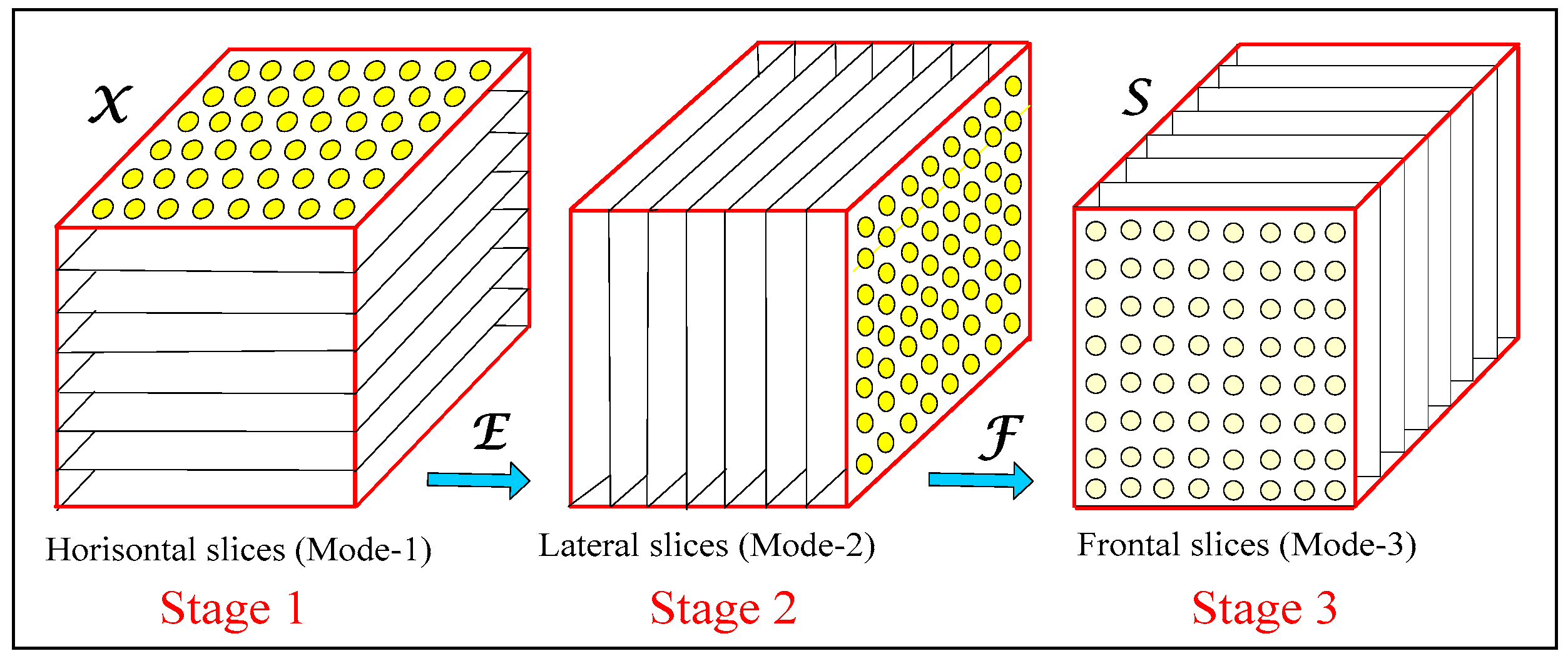
3. Decomposition of Cubical Tensor of Size N × N × N through 3D-FOHKLT
4. Algorithm 3D-FOHKLT for Cubical Tensor Representation
| Algorithm 1: Tensor representation based on the 3D-FOHKLT |
| Input: Third-order tensor of size N × N × N (N = 2n) and with elements x(i,j,k) Output: Spectral tensor of n layers, whose elements s(u,v,l) are the coefficients of the 3D-FOНKLT. 1 begin 2 Divide the tensor into horisontal slices and compose N/2 couples of matrices and of size N × N, for q = 1, 2, …, N/2; 3 for each couple of matrices and when q = 1, 2, …, N/2 and p = 1, 2, …, n, do 4 Calculate the couple of matrices and obtained through 1D-FOНKLT in accordance with Equations (7) and (8); 5 Calculate the matrices and Yn,k for k = 0, 1, …, N−1 and p = n in accordance with Equations (18)–(20); 6 Define the matrices Er for r = 0, 1, …, N−1 in the level p = n by rearranging the matrices Yn,k for k = 0, 1, …, N−1 on the basis of the vector transform , for s = 1, 2, …, N2; 7 Reshape all rearranged matrices Er into the corresponding tensor of size N × N × N. 8 end 9 Divide the tensor into lateral slices and compose N/2 couples of intermediate matrices and of size N × N, for q = 1, 2, …, N/2; 10 for each couple of matrices and when q = 1, 2, …, N/2 and p = 1, 2, …, n, do 11 Calculate the couple of matrices and transformed through 1D-FOНKLT in accordance with Equations (7) and (8); 12 Calculate the matrices and Fn,k for k = 1, 2, …, N and p = n in accordance with Equations (18)–(20); 13 Define the matrices Fr for r = 0, 1, …, N−1 in the level p = n by rearranging the matrices Fn,k for k = 0, 1, …, N−1 on the basis of the vector transform , for s = 1, 2, …, N2; 14 Reshape all rearranged matrices Fr in level p = n into the corresponding tensor of size N × N × N 15 end 16 Divide the tensor into frontal slices and compose N/2 couples of matrices and of size N × N, for q = 1, 2, …, N/2; 17 for each couple of matrices and when q = 1, 2,…, N/2 and p = 1, 2, …, n, do 18 Calculate the couple of matrices and transformed through 1D-FOНKLT in accordance with Equations (7) and (8); 19 Calculate the matrices and Sn,k for k = 1, 2, …, N and p = n in accordance with Equations (18)–(20); 20 Define the matrices Sr for r = 0, 1, …, N−1 in the level p = n by rearranging the matrices Sn,k for k = 0, 1, …, N−1 on the basis of the vector transform , for s = 1, 2, …, N2; 21 Reshape all rearranged matrices Sr in the level p = n into the spectral tensor of size N × N × N 22 end 23 Arrange the coefficients s(u,v,l) of the spectral cubical tensor layer by layer in accordance with their spatial frequencies (u,v,l) - from the lowest (0,0,0), to the highest (N−1, N−1, N−1), for u + v + l = const. 24 end |
5. Comparative Evaluation of the Computational Complexity of 3D-HAKLT and 3D-FOHKLT
5.1. Computational Complexity of 3D-HAKLT for a Cubical Tensor of Size N × N × N (N = 2n)
- The number of additions AH(n) and multiplications MH(n) needed to execute the 1D-HAKLT for a couple of matrices of size N × N in one decomposition level is
- For N/2 couples of matrices in one stage of the n-level 3D-HAKLT, these numbers are
- Then, for the three-level 3D-HAKLT is obtainedHence,
5.2. Comparison of the Computational Complexity of 3D-HAKLT and 3D-FOHKLT to H-Tucker and TT
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. One-Dimensional Frequency-Ordered Hierarchical KLT for N = 8
References
- Ji, Y.; Wang, Q.; Li, X.; Liu, J. A Survey on Tensor Techniques and Applications in Machine Learning. IEEE Access 2019, 7, 162950–162990. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; Phan, A.; Caiafa, C.; Zhou, G.; Zhao, Q.; De Lathauwer, L. Tensor Decompositions for Signal Processing Applications: From Two-Way to Multiway Component Analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Sidiropoulos, N.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.; Faloutsos, C. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Proc. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Oseledets, I. Tensor-train decomposition. Siam J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Grasedyck, L. Hierarchical Singular Value Decomposition of Tensors. Siam J. Matrix Anal. Appl. 2010, 31, 2029–2054. [Google Scholar] [CrossRef]
- Ozdemir, A.; Zare, A.; Iwen, M.; Aviyente, S. Extension of PCA to Higher Order Data Structures: An Introduction to Tensors, Tensor Decompositions, and Tensor PCA. Proc. IEEE 2018, 106, 1341–1358. [Google Scholar]
- Vasilescu, M.; Kim, E. Compositional Hierarchical Tensor Factorization: Representing Hierarchical Intrinsic and Extrinsic Causal Factors. In Proceedings of the 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD): Tensor Methods for Emerging Data Science Challenges, Anchorage, NY, USA, 4–8 August 2019; p. 9. [Google Scholar]
- Wang, P.; Lu, C. Tensor Decomposition via Simultaneous Power Iteration. In Proceedings of the 34th Intern. Conference on Machine Learning (PMLR), Sydney, Australia, 6–9 August 2017; Volume 70, pp. 3665–3673. [Google Scholar]
- Ishteva, M.; Absil, P.; Van Dooken, P. Jacoby Algorithm for the Best Low Multi-linear Rank Approximation of Symmetric Tensors. SIAM J. Matrix Anal. Appl. 2013, 34, 651–672. [Google Scholar] [CrossRef]
- Zniyed, Y.; Boyer, R.; Almeida, A.; Favier, G. A TT-based Hierarchical Framework for Decomposing High-Order Tensors. SIAM J. Sci. Comput. 2020, 42, A822–A848. [Google Scholar] [CrossRef]
- Rao, K.; Kim, D.; Hwang, J. Fast Fourier Transform: Algorithms and Applications; Springer: Dordrecht, The Netherlands, 2010; pp. 166–170. [Google Scholar]
- Kountchev, R.; Kountcheva, R. Adaptive Hierarchical KL-based Transform: Algorithms and Applications. In Computer Vision in Advanced Control Systems: Mathematical Theory; Favorskaya, M., Jain, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1, pp. 91–136. [Google Scholar]
- Lu, H.; Kpalma, K.; Ronsin, J. Motion descriptors for micro-expression recognition. In Signal Processing: Image Communication; Elsevier: Amsterdam, The Netherlands, 2018; Volume 67, pp. 108–117. [Google Scholar]
- Ahmed, N.; Rao, K. Orthogonal Transforms for Digital Signal Processing; Springer: Berlin/Heidelberg, Germany, 1975; pp. 86–91. [Google Scholar]
- Kountchev, R.; Kountcheva, R. Decorrelation of Multispectral Images, Based on Hierarchical Adaptive PCA. WSEAS Trans. Signal Proc. 2013, 9, 120–137. [Google Scholar]
- Kountchev, R.; Mironov, R.; Kountcheva, R. Hierarchical Cubical Tensor Decomposition through Low Complexity Orthogonal Transforms. Symmetry 2020, 12, 864. [Google Scholar] [CrossRef]

| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 0.23 | 0.26 | 0.36 | 0.57 | 0.91 | 1.54 | 2.68 | |
| 0.30 | 0.35 | 0.48 | 0.74 | 1.21 | 2.05 | 3.57 | |
| 0.25 | 0.33 | 0.50 | 0.80 | 1.33 | 2.28 | 4.00 | |
| 0.33 | 0.44 | 0.66 | 1.06 | 1.77 | 3.04 | 5.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kountchev, R.; Mironov, R.; Kountcheva, R. Complexity Estimation of Cubical Tensor Represented through 3D Frequency-Ordered Hierarchical KLT. Symmetry 2020, 12, 1605. https://doi.org/10.3390/sym12101605
Kountchev R, Mironov R, Kountcheva R. Complexity Estimation of Cubical Tensor Represented through 3D Frequency-Ordered Hierarchical KLT. Symmetry. 2020; 12(10):1605. https://doi.org/10.3390/sym12101605
Chicago/Turabian StyleKountchev, Roumen, Rumen Mironov, and Roumiana Kountcheva. 2020. "Complexity Estimation of Cubical Tensor Represented through 3D Frequency-Ordered Hierarchical KLT" Symmetry 12, no. 10: 1605. https://doi.org/10.3390/sym12101605
APA StyleKountchev, R., Mironov, R., & Kountcheva, R. (2020). Complexity Estimation of Cubical Tensor Represented through 3D Frequency-Ordered Hierarchical KLT. Symmetry, 12(10), 1605. https://doi.org/10.3390/sym12101605