Abstract
The well known Nakano–Nishijima–Gell-Mann (NNG) formula relates certain quantum numbers of elementary particles to their charge number. This equation, which phenomenologically introduces the quantum numbers (isospin), S (strangeness), etc., is constructed using group theory with real numbers . But, using a discrete Galois field instead of and assuring the fundamental invariance laws such as unitarity, Lorentz invariance, and gauge invariance, we derive the NNG formula deductively from Meson (two quarks) and Baryon (three quarks) representations in a unified way. Moreover, we show that quark confinement ascribes to the inevitable fractionality caused by coprimeness between half-integer (1/2) of isospin and number of composite particles (e.g., three).
1. Introduction
The standard model of particle physics has been established based on physics with real numbers (). However, problems such as the problem of infinite in gravity are yet unsolved. To avoid such problems, quantum gravity theories like superstring theory or loop quantum gravity are developing, but neither of those theories has been completed. On the other hand, the assumption that all of the physics in the universe is constructed solely of has not been proved. For instance, Yukawa considered extended wave function of elementary particles using “elementary domains” [1] and Snyder [2] and Finkelstein [3] simply considered quantization of space-time. However, these approaches are incomplete and a unified formulation is unknown. Here, we assert that a different mathematical structure, namely a world with a finite [4] and discrete space-time [5,6,7,8,9,10,11,12,13,14], is needed for the following reasons.
The description of a discrete space-time would require a discrete mathematical structure. Unitary transformation from quantum mechanics and Lorentz (Möbius) transformation from relativity requires this structure to be a number field, where addition, subtraction, multiplication, and division can be defined. The set of integers is not a field because division is not defined. For instance, fractional numbers such as are not defined. What we would consider in this paper is called a Galois field (), that is, the set of integers where two numbers differing by a multiple of a prime number p are equivalent [5,6,7,8,9,10,11,12,13,14]. has a finite, periodic, and discrete structure. Mathematical and physical justification to consider this field are as follows.
Mathematically, there is another system called p-adic numbers ( prime) that is equivalent to [15]. is regarded as the limit of p-adic integers with .
Moreover, In adele ring theory, is regarded as the limit of with [16].
So, from the viewpoint of number theory, the geometry constructed by the real numbers is only an approximation of a finite and discrete geometry [11,17]. Physics over may be obtained from physics over under the appropriate limit.
Physically, Galois fields can appear naturally in our universe from multiple perspectives. First, recent observation of microwave background radiation suggests that the world is finite and periodic (: Poincaré Dodecahedron) [4]. Second, if space-time has the Planck length as a characteristic scale, then Lorentz transformation must be discrete [18]. Theoretically, Jarnefelt estimated a huge but finite number of world coordinates as [5,7,19]. Third, the theory of quantum gravity needs to be expanded because of the difficulty of renormalizability. This problem would not appear in in the first place [5,6,13,14], so the expansion is expected to be achieved by using a discrete system. In standard particle physics theory, the existence of antiparticles depends on additional assumptions, while in the Galois field such strange assumptions are not necessary [13]. Fourth, the field theory of Galois field was investigated by Nambu in the context of recurrence time [6]. Recently, the discreteness of time is also discussed the context of time crystals [20,21,22,23,24]. So, if space-time is both finite and discrete, we have to re-examine the laws of physics [6].
In this article, we re-examine a previous model and classify hadrons by using a discrete Galois field . When we reconstruct new theories with a Galois field, these new theories must satisfy fundamental conservation laws, namely those related to unitarity, Lorentz invariance, and gauge invariance. Consequently, instead of the Nakano–Nishijima–Gell-Mann (NNG) formula (which is proposed using continuous coordinate ), we obtained the alternate formula , where Q is charge number, n is multivaluedness in Galois field, and I is total isospin. This formula is derived from Meson (two quarks) and Baryon (three quarks) representations in a unified way. The use of isospin was not investigated in detail by previous authors [5,7,8,9,10,11,12,19,25] who introduced finite geometry into the field theory. Since the NNG formula also applies to individual quarks, we apply the new formula to up-quark and down-quark, which inevitably lead to fractional numbers. Fractional numbers in Galois fields are, however, very large numbers. Therefore, isolated quarks with fractional charge can have a very large energy. We surmise that quark confinement ascribes to this fractionality in Galois field. These results may be a starting point to develop a theory without problems of infinity.
2. Galois Field
Here, we introduce the Galois fields and . A number field is a mathematical structure where addition, subtraction, multiplication and division are defined. Let be the set of integers where two numbers differing by an integral multiple of are regarded equivalent. A well-known result from number theory is that is a number field if and only if m is a prime number. This finite field is called a Galois field which is denoted by :
A Galois field is not an ordered field. But, as was made clear in Reference [25], can be partially ordered if p has the form
where x is an odd integer and is the product of the first k odd primes. So, the usual notion of magnitude (large and small) and sign (positive and negative) hold for the first elements. Therefore, we consider a prime of the form in Equation (2) which is assumed to be large enough to construct a geometry containing all coordinates in the universe.
Quantum mechanics requires complex numbers. To consider complex numbers in a Galois field, it is natural to take an analogue of the ordinary extension of real numbers to complex numbers. That is to say, the set of “complex" numbers
is a “complex" Galois field which is denoted by . For a prime p of the form − 1 (), complex conjugation is given by and since we have
The first equality holds because p is a character of the field, that is for all ; The second equality follows from Fermat’s little theorem . Note that can become negative for the non-ordered part of .
3. Lorentz Group in a Galois Field: The Coish Group
Lorentz transformation can be recovered with the Galois field introduced in the previous section [5,8,11,12]. Coordinates in Minkowski space-time are closely related to spinor structure through the Pauli matrix representation
where and
are Pauli matrices. (See Reference [26] for the case of .) The metric form is given as the determinant of X:
Let a be a 2 × 2 matrix with coefficients in . The linear transformation
is a proper Lorentz transformation if it leaves the metric form Equation (7) invariant, that is, if holds. Such matrices form the orthogonal group SL. In finite geometry, however, there also exist transformations with which reverse the sign of the metric [5].
In addition, suppose that matrices and lead to the same Lorentz transformation. Then transforms X as
Since the set of X contains the identity matrix, Equation (9) leads to . So, U is a unitary matrix of the form
Given that U is unitary, satisfies
In a Galois field, such become discrete and multivalued. That is, for a prime p of the form (such as in Equation (2)) we have
where . So, the the orthogonal group in a Galois field has multivaluedness as with a cyclotomic field, and acts as a phase factor (Figure 1). In this way, we obtain the full Coish group. The spinor group, which is a subgroup of the rotational group, has the same multivaluedness. This multivaluedness will plays an essential role for the classification of hadrons.
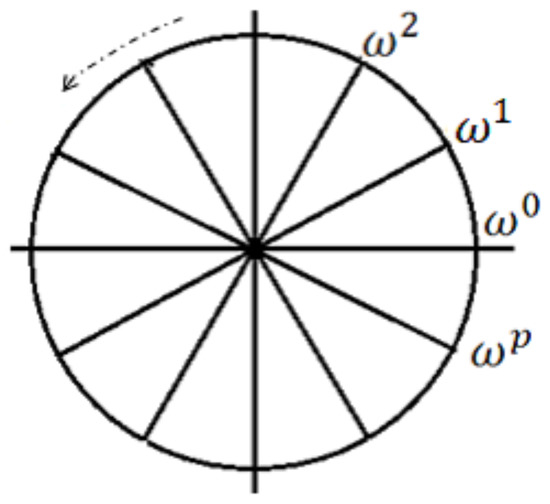
Figure 1.
Schematic representation of the discrete multivaluedness with phase factor . Each set of constitutes a cyclotomic field. When , the field has elements. A Lorentz group in a Galois field has multivaluedness such as . Regarding as a phase factor, it constitute a global gauge transformation in a Galois field.
4. Gauge Transformation in Galois Field
In this section, the charge number Q is derived with gauge transformation in Galois field in accordance with the derivation given in Reference [5]. Because of homomorphism, an orthogonal group leads a spinor group. The irreducible representation of the orthogonal group must be a matrix with elements of as its coefficients. The spinor group is a subgroup of of the two dimensional general linear homogeneous Galois group over the complex finite field . The irreducible representations of are given by Brauer and Nesbitt [27] and extended by Coish [5] as
where
Here, a is a spinor matrix which transforms a spinor
is interpreted as the multivaluedness of the representation. Next, consider the polynomial
The set can be regarded as the linearly independent set of basis for a -dimensional vector space. The action of a on is given by
So, is a matrix transforming the monomials . In particular, the phase factor transforms and . This phase factor corresponds to a gauge transformation, and Equation (13) is transformed as follows
where
Therefore, we naturally derive Equation (20) as the charge number reflecting discreteness of gauge transformation in Galois field.
5. Classification of Hadrons
Now, we can classify Hadrons in a Galois field. Coish interpreted j and k as spins and represented baryons and mesons with Equations (13) and (20). However, his model does not agree with the standard model of particle physics. So, we give a different interpretation. Instead of spins, we interpret j and k as isospin. More precisely, to encompass the multiplet structure of hadrons, it would be appropriate to interpret as the total isospin I instead of . Mesons, which are composed of particles and anti-particles, are transformed by the representation
but it is now interpreted as a representation of . Baryons, which are composed of three quarks, are transformed by another representation
of . Here, the contribution of strangeness appears as a modification of the multivaluedness n.
Mesons and baryons can be classified according to the charge number
where for mesons and for baryons.
Table 1 and Table 2, respectively, show quantum numbers and representations of mesons and baryons in a Galois field. Here, we did not use symmetry but assume the known quark contents.

Table 1.
Quantum numbers of mesons in a Galois field. Q is the charge number of baryon and are total isospins of quarks. n is derived from Equation (23).

Table 2.
Quantum numbers of baryons in a Galois field. Q is the charge number of baryon and are total isospins of quark. n is derived from Equation (23).
We derived Equation (23) equivalent to the NNG formula
where Y is the hypercharge. Figure 2 shows the classification of hadrons with n and I. Particles and anti-particles are related by CP conjugation (that is, point symmetry around the origin ) as in Reference [5]. Different values of I indicate the multiplet structure of hadrons. By comparison with the NNG formula, n includes both the isospin and the hypercharge Y. In this way, Galois fields can be used to organize the quantum number of hadrons. Similarly, as it is well known, the quantum number of leptons are related with an equation similar to the NNG formula; the origins of the weak isospin and weak hypercharge, which are properties of leptons introduced phenomenologically, may also be explained by the Galois field.
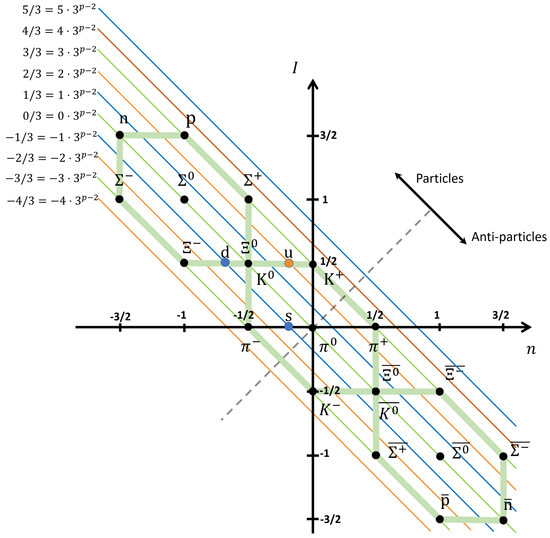
Figure 2.
Classification of hadrons with Equation (23). Our model take the n and I axis instead of Y and . We did not use symmetry but assume the same quark constituent as in the standard model of particle physics. Charge numbers such as are shown in Figure 3. Note that this figure superimposes baryons, anti-bayons, and mesons, which differ by baryon numbers. So, K0 and 0, for instance, are distinguished.
More generally, we can give a unified representation for arbitrary composit particles. First, we can give a representation of a single particle as . Likewise, a representation of particles with N ( or higher) constituents is possible with
where are half-integers, or 1, is the identity map , and maps to the conjugate group with coefficients (c.f. References [5,27]). Then, the charge number is given by where plus and minus correspond to and , respectively. This includes a representation of mesons, baryons, pentaquark, and so on, in a unified way.
6. Quark Confinement
Finally, we provide a possible approach toward quark confinement which ascribes to fractionality in Galois field.
Suppose for the moment that up-quark and down-quark can be described by the following irreducible representation of :
We expect that proton and neutron can be expressed as and , respectively. Then, the quantum numbers of proton and neutron can be written in terms of their constituent quarks as follows:
Substitute this decomposition into Equation (23) and we obtain
Then, we can solve for and
Taking the values , and as in Table 2 we obtain
which are not half-integers as in (15). Therefore, irreducible representations of quarks as in Equation (26) is not possible.
Now, suppose that we can nevertheless write the corresponding charge numbers as elements of . Then, we obtain and . Counterintuitively, these fractional quantum numbers in are very large, which can be shown as follows. The modular inverses in of an integer a in is defined by
On the other hand, from Fermat’s little theorem
we obtain
The prime given by Equation (2) contains the first odd prime , so it has the form for some . In this case, the fractional number in takes the value (see Figure 3). Therefore, fractional numbers in Galois field are large numbers of order p. Consequently, isolated quark can have, for instance a huge electromagnetic self-energy (Figure 4). In this case, quark confinement in may be a consequence of energy minimization.

Figure 3.
The values of and are shown for the primes of the form . Fractional numbers in a Galois field are large numbers proportional to p.
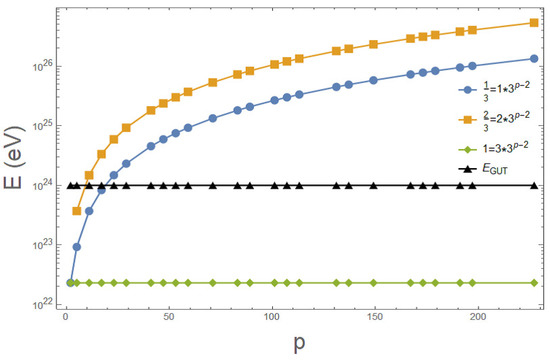
Figure 4.
Electromagnetic self-energy where Q is the charge number in Galois field, is the Coulomb constant, a is the classical electron radius, and c is the speed of light. The energy is independent of p for integral charge but increase for fractional charge. The GUT energy is shown as a rough standard.
7. Discussion and Conclusions
Finally, we summarize and discuss our results. The NNG formula is a phenomenological equation. By using a Galois field, the NNG Formula (24) is rewritten as (23). The new quantum number n, which includes isospin and hypercharge Y, arises from the multivaluedness of a linear representation of the Galois field. We also discussed quark confinement which ascribes to fractionality of Galois field. After all, these results may indicate finiteness and discreteness of the world. While such a method is unconventional, it is not inherently inconsistent under one assumption, namely that the geometry constructed by the real numbers is only an approximation of a finite and discrete geometry [11,17].
As future developments, we expect that composite particles such as pentaquarks [28,29,30] can be explained by generalizing Equation (25) to any number of particles and combining the quantum numbers n and I to a single “grand spin” as discussed in [30]. We expect that the inclusion of other flavors such as c (charm), t (top) and b (bottom) would require extension of our result to (analogous to SU(3)), , and so on, which goes in parallel to the extension of SU(2) to SU(3) or higher. Representation of particles in Figure 2 can be modified accordingly. This extention can be done based on previous studies [31] and using a method equivalent to the “enlarging lemma” [32]. Recently, with the development of quantum information, Galois fields have begun to be used to construct space-time models as error-correcting codes [33]. Further application of Galois fields is expected in the foundation of quantum physics [34] and time crystal with discrete space-time symmetry [20,21,22,23,24].
Author Contributions
Conceptualization, S.T., K.N., T.F. and T.M.; methodology, M.O., K.N., T.F. and S.T.; validation, all authors; formal analysis, K.N., M.O., T.F. and S.T.; investigation, all authors; writing, K.N., M.O., and S.T.; visualization, K.N., M.O. and S.T.; supervision, S.T.; project administration, S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank Kohkichi Konno, Masanori Yamanaka, Thomas Zeugmann, Tatsuhiko N. Ikeda, Masanori Morishita and Ryotaro Okazaki for stimulating and valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yukawa, H. Atomistics and the Divisibility of Space and Time. Prog. Theor. Phys. Suppl. 1966, 37–38, 512–523. [Google Scholar] [CrossRef][Green Version]
- Snyder, H.S. Quantized Space-Time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Finkelstein, D. Space-Time Code. Phys. Rev. 1969, 184, 1261–1271. [Google Scholar] [CrossRef]
- Luminet, J.P.; Weeks, J.R.; Riazuelo, A.; Lehoucq, R.; Uzan, J.P. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature 2003, 425, 593–595. [Google Scholar] [CrossRef] [PubMed]
- Coish, H.R. Elementary Particles in a Finite World Geometry. Phys. Rev. 1959, 114, 383–388. [Google Scholar] [CrossRef]
- Nambu, Y. Field Theory of Galois Fields. In Quantum Field Theory and Quantum Statistics; Batalin, I.A., Ed.; IOP Publishing: Bristol, UK, 1987; Volume 1, pp. 625–636, also In Broken Symmetry, World Scientific Pub Co Inc.: Singapore, 1995. [Google Scholar]
- Järnefelt, G. On the possibility of a finite model describing the universe II. The case of a relativistic free particle. Astron. Nachr. 1977, 298, 69–79. [Google Scholar] [CrossRef]
- Beltrametti, E.G.; Blasi, A.A. Rotation and Lorentz Groups in a Finite Geometry. J. Math. Phys. 1968, 9, 1027–1035. [Google Scholar] [CrossRef]
- Shapiro, I.S. Weak interactions in the theory of elementary particles with finite space. Nuclear Phys. 1960, 21, 474–491. [Google Scholar] [CrossRef]
- Joos, H. Group-Theoretical Models of Local-Field Theories. J. Math. Phys. 1964, 5, 155–164. [Google Scholar] [CrossRef]
- Ahmavaara, Y. The Structure of Space and the Formalism of Relativistic Quantum Theory. I. J. Math. Phys. 1965, 6, 87–93. [Google Scholar] [CrossRef]
- Morris, H.C. The present status of the coish model. Int. J. Theor. Phys. 1974, 9, 369–377. [Google Scholar] [CrossRef]
- Lev, F.M. Introduction to a Quantum Theory over a Galois Field. Symmetry 2010, 2, 1810–1845. [Google Scholar] [CrossRef]
- Lev, F.M. Symmetries in Foundation of Quantum Theory and Mathematics. Symmetry 2020, 12, 409. [Google Scholar] [CrossRef]
- Vladimirov, V.S.; Volovich, I.V.; Zelenov, E.I. Analysis on the Field of p-adic Numbers; World Scientific: Singapore, 1994; pp. 1–141. [Google Scholar]
- Kato, K.; Kurokawa, S.; Saito, T. Number Theory I; Iwanami-Shoten: Tokyo, Japan, 2005. (In Japanese) [Google Scholar]
- Penrose, R. The Road to Reality; Vintage: New York, NY, USA, 2004; Chapter 16. [Google Scholar]
- Amelino-Camelia, G. Doubly-Special Relativity: Facts, Myths and Some Key Open Issues. Symmetry 2010, 2, 230–271. [Google Scholar] [CrossRef]
- Järnefelt, G. Reflections on a finite approximation to Euclidean geometry. Physical and astronomical prospects. Ann. Acad. Sci. Fenn. Ser. A.I. 1951, 96, 1. [Google Scholar]
- Shapere, A.; Wilczek, F. Classical Time Crystals. Phys. Rev. Lett. 2012, 109, 160402. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Nakatsugawa, K.; Fujii, T.; Tanda, S. Quantum time crystal by decoherence: Proposal with an incommensurate charge density wave ring. Phys. Rev. B 2017, 96, 094308. [Google Scholar] [CrossRef]
- Nakatsugawa, K.; Fujii, T.; Saxena, A.; Tanda, S. Time operators and time crystals: Self-adjointness by topology change. J. Phys. A 2020, 53, 025301. [Google Scholar] [CrossRef]
- Sacha, K.; Zakrzewski, J. Time crystals: A review. Rep. Prog. Phys. 2018, 81, 016401. [Google Scholar] [CrossRef]
- Kustaanheimo, P. On the Fundamental Prime of a Finite World. Ann. Acad. Sci. Fenn. Ser. A.I. 1952, 129, 1. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: New York, NY, USA, 2005; Volume 1: Foundations. [Google Scholar]
- Brauer, R.; Nesbitt, C. On the Modular Characters of Groups. Ann. Math. 1941, 42, 556–590. [Google Scholar] [CrossRef]
- Nakano, T.; Ahn, D.S.; Ahn, J.K.; Akimune, H.; Asano, Y.; Chang, W.C.; Daté, S.; Ejiri, H.; Fujimura, H.; Fujiwara, M.; et al. Evidence for a Narrow S = +1 Baryon Resonance in Photoproduction from the Neutron. Phys. Rev. Lett. 2003, 91, 012002. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Adeva, B.; Adinolfi, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; Alvarez Cartelle, P.; et al. Search for Structure in the π± Invariant Mass Spectrum. Phys. Rev. Lett. 2016, 117, 152003. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.C.; Polyakov, M.V.; Praszałowicz, M. Possibility of the existence of charmed exotica. Phys. Rev. D 2017, 96, 014009. [Google Scholar] [CrossRef]
- Mark, J.C. On the Modular Representation of the Group GLH(3, p). Ph.D. Thesis, University of Toronto, Toronto, ON, USA, 1938. [Google Scholar]
- Kempe, J.; Bacon, D.; Lidar, D.A.; Whaley, K.B. Theory of decoherence-free fault-tolerant universal quantum computation. Phys. Rev. A 2001, 63, 042307. [Google Scholar] [CrossRef]
- Lévay, P.; Holweck, F. Finite geometric toy model of spacetime as an error correcting code. Phys. Rev. D 2019, 99, 086015. [Google Scholar] [CrossRef]
- Chang, L.N.; Lewis, Z.; Minic, D.; Takeuchi, T. Quantum systems based upon galois fields—From sub-quantum to super-quantum correlations. Int. J. Mod. Phys. A 2014, 29, 1430006. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).