A New Macro-Model of Gas Flow and Parameter Extraction for a CMOS-MEMS Vacuum Sensor
Abstract
1. Introduction
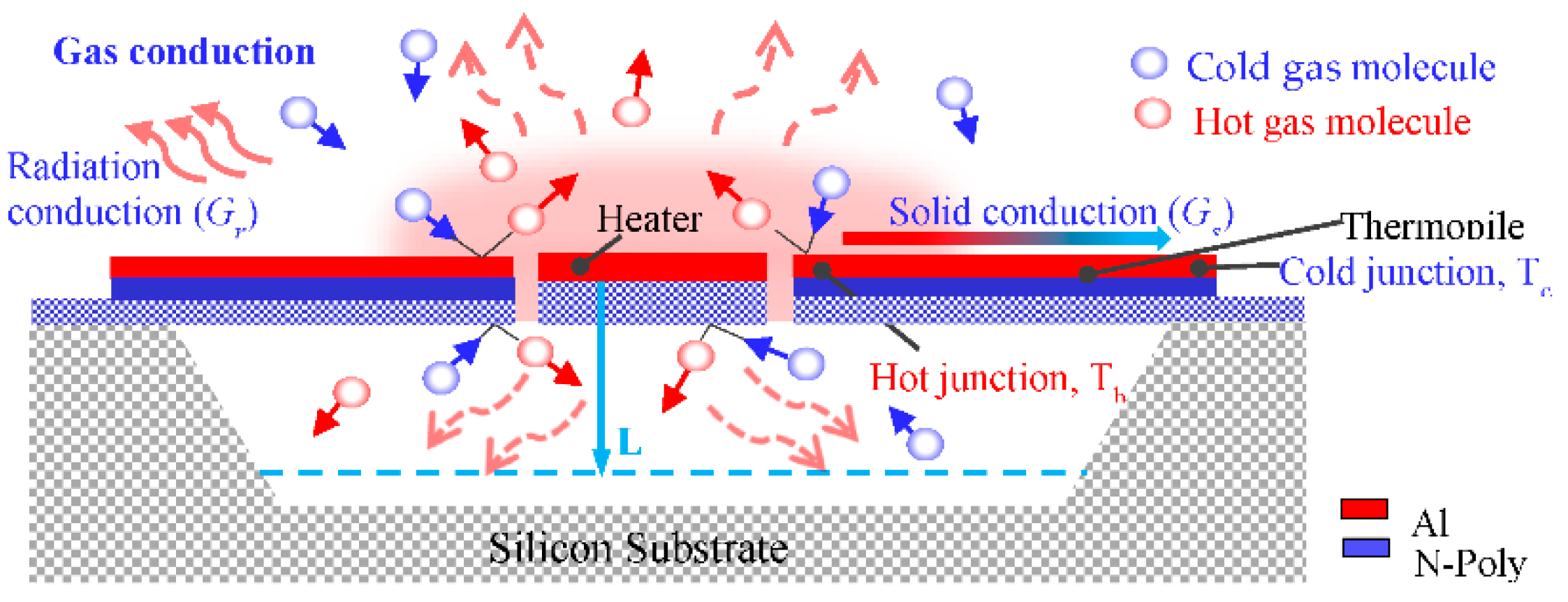
2. Working Principle of a Thermal-Type Vacuum Sensor
2.1. Working Principle
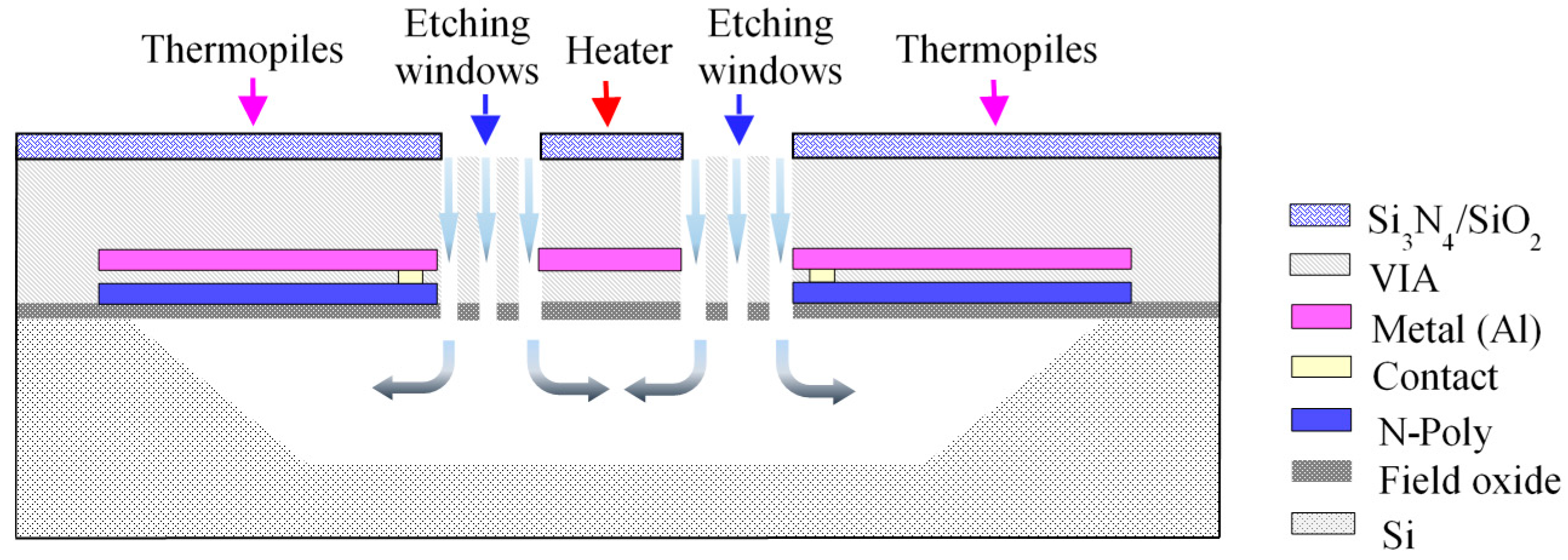
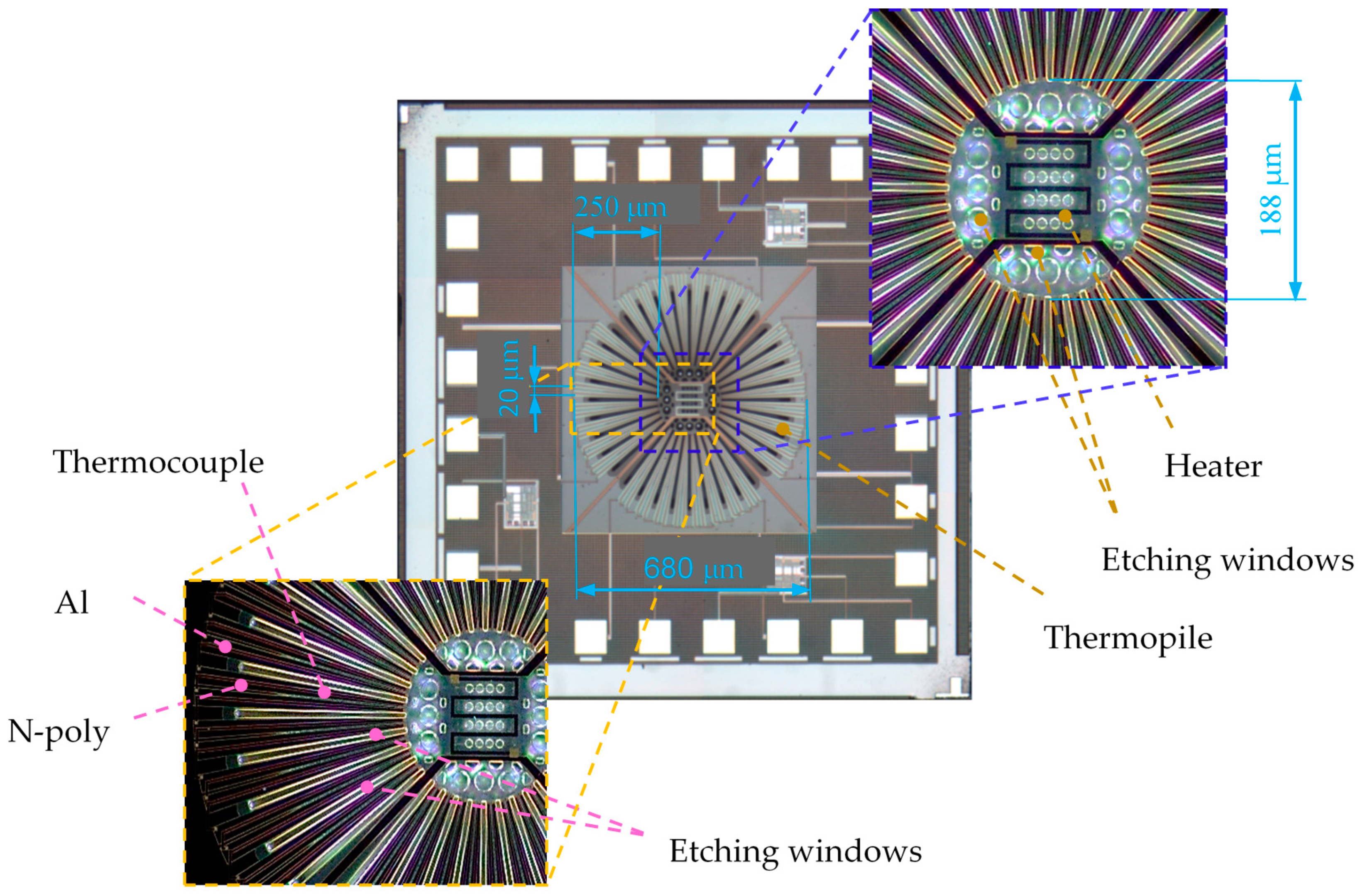
2.2. Proposed Thermal-Type Vacuum Sensor
2.3. A Simplified Theoretical Description of Heat Transfer for Thermal-Type Vacuum Sensor
3. Vacuum Measurement
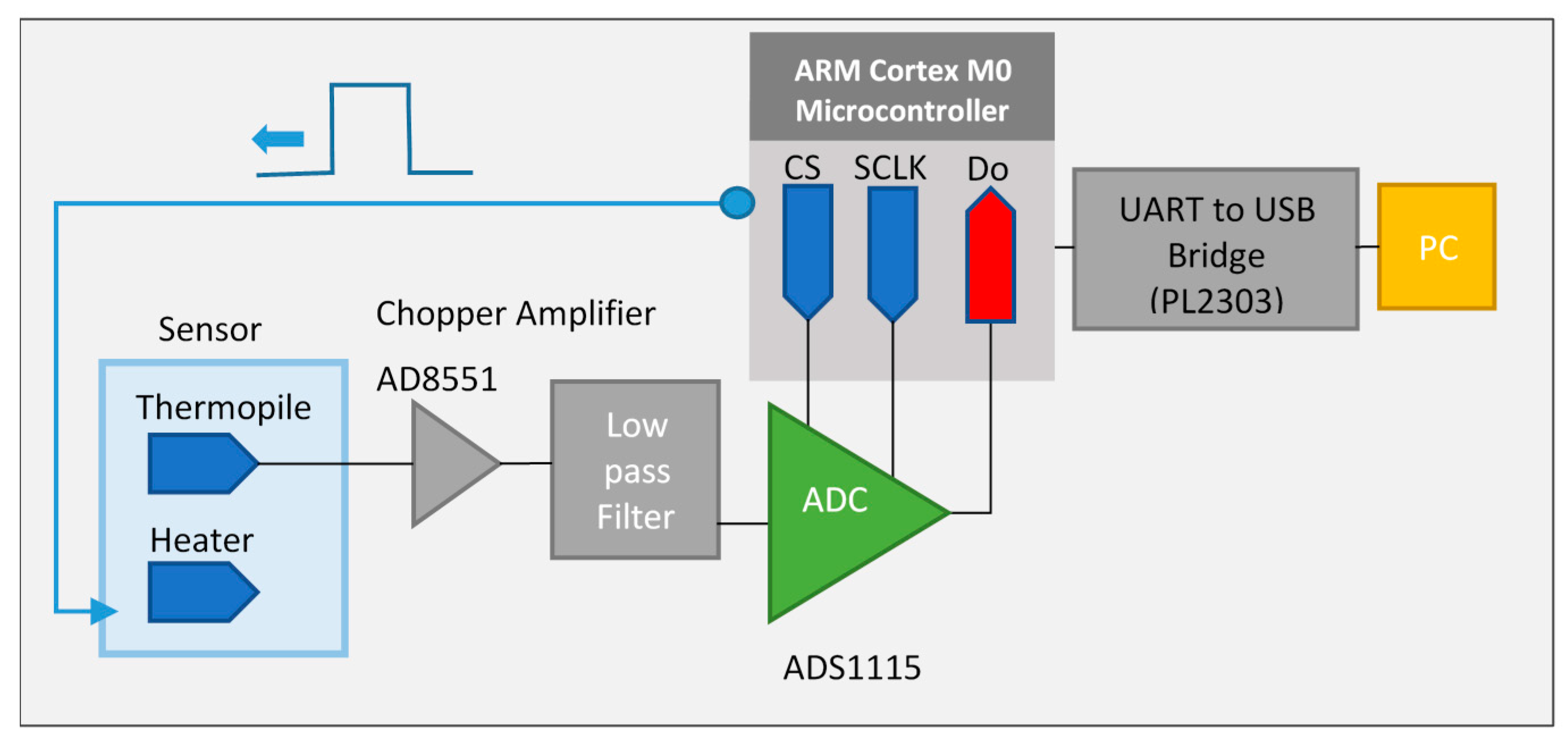
3.1. Experiment Setup
3.2. Signal Acquisition from Thermal-Type Vacuum Sensor
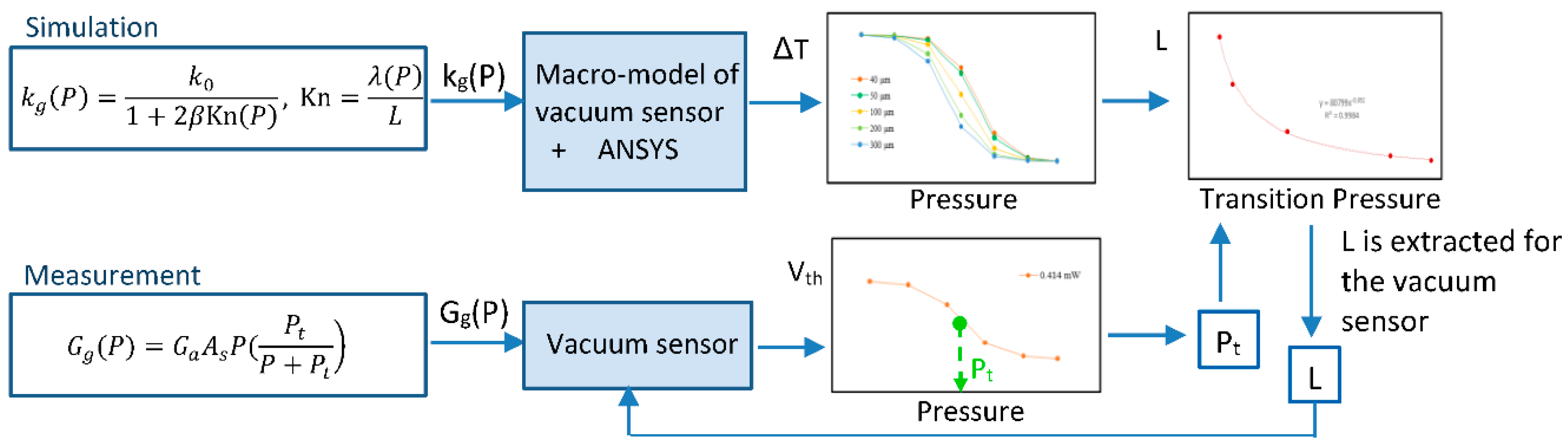
4. Building of Macro-Model of Vacuum Measurement and Verification
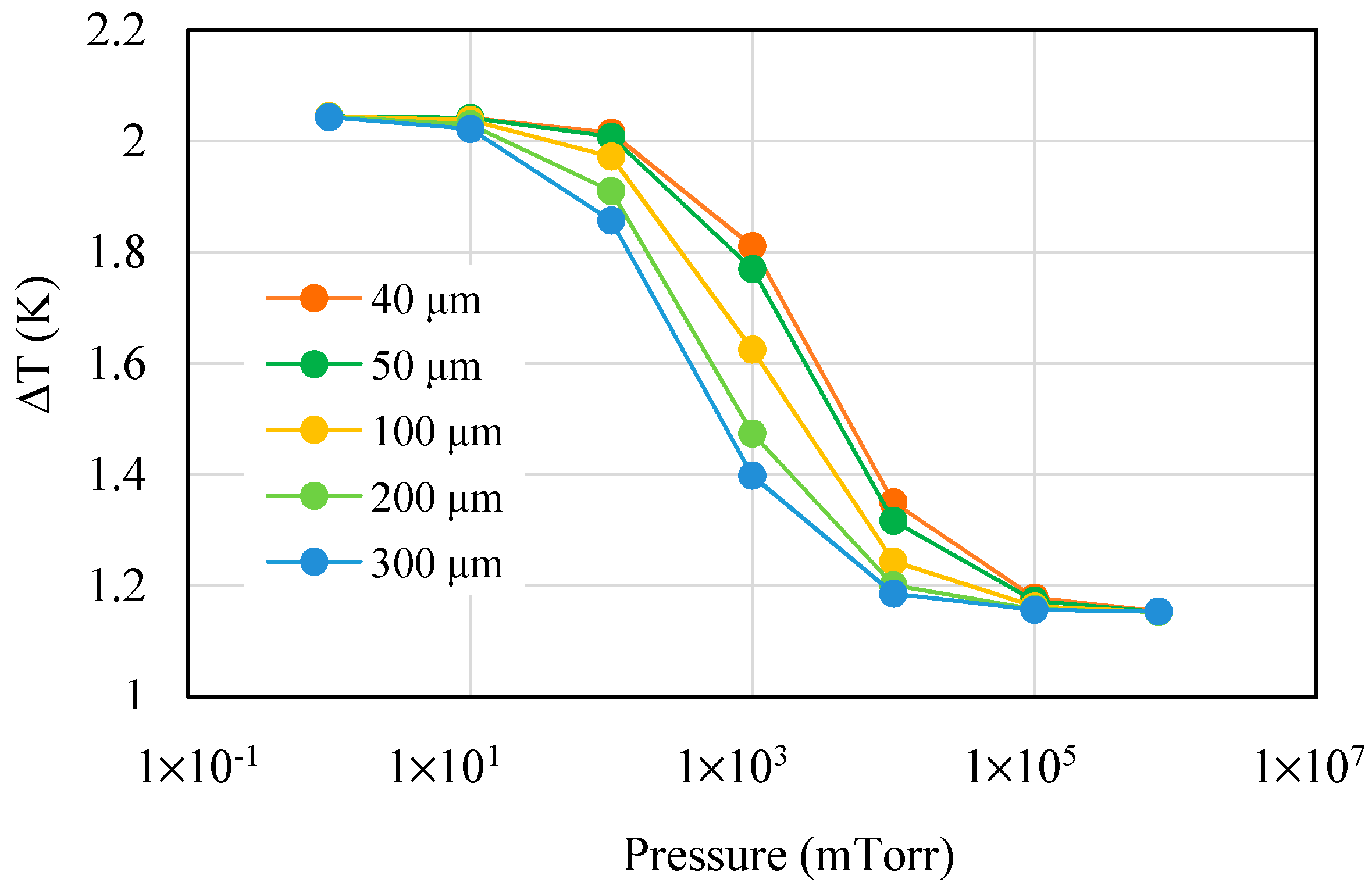
4.1. Simulation of Temperature under Different Characteristic Lengths
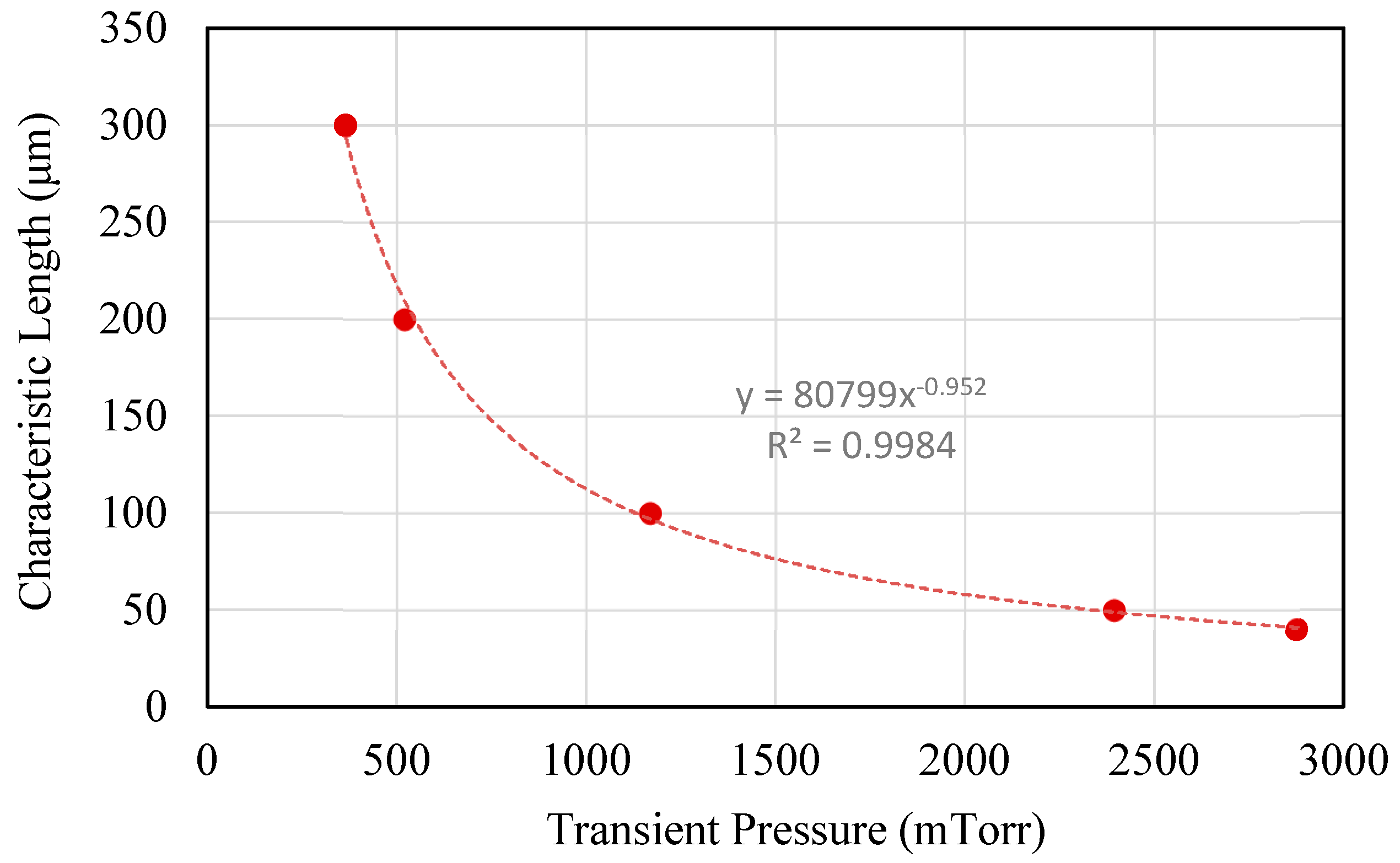
4.2. Parameter Extraction and Verification of Macro-Model
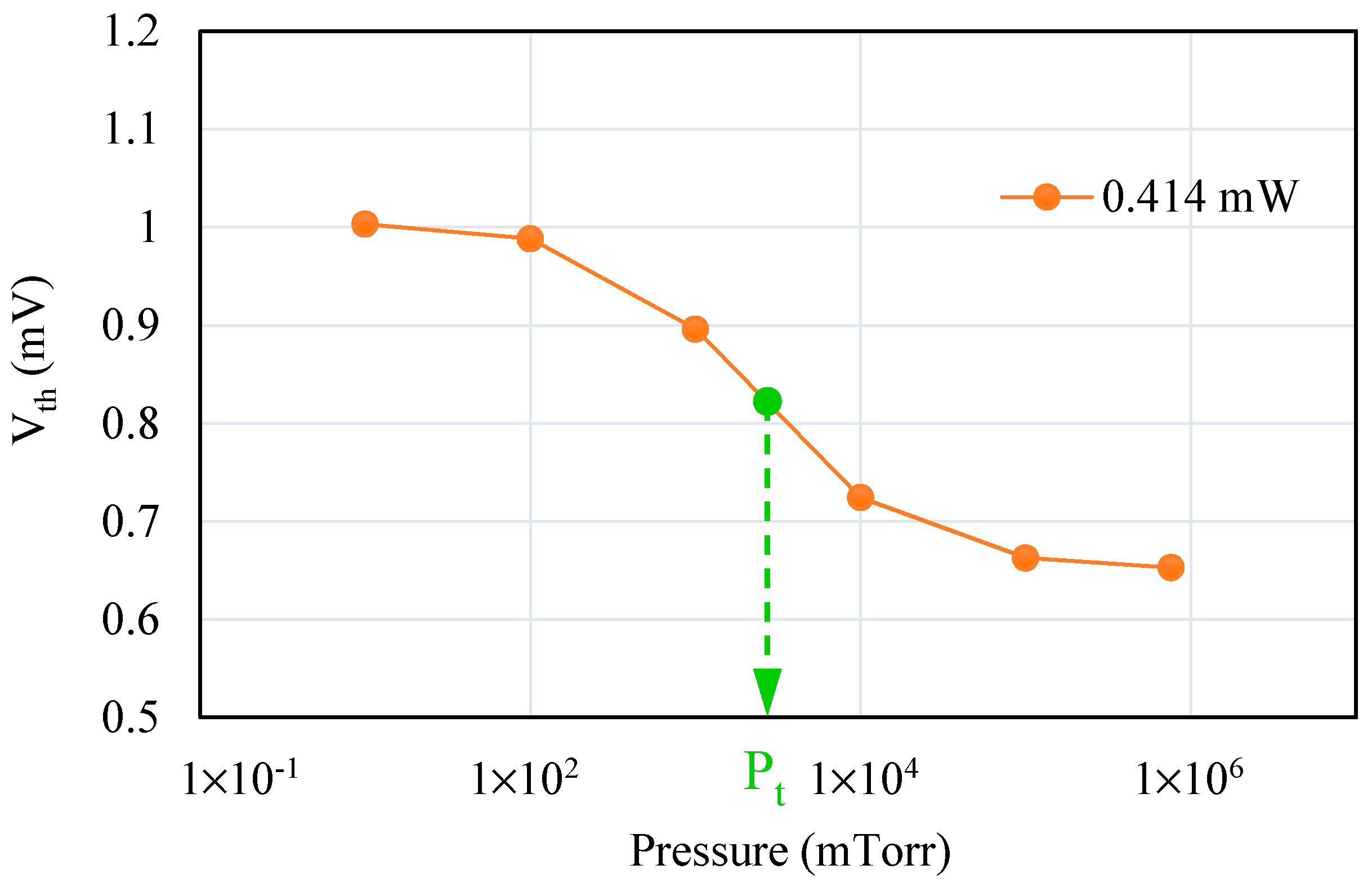
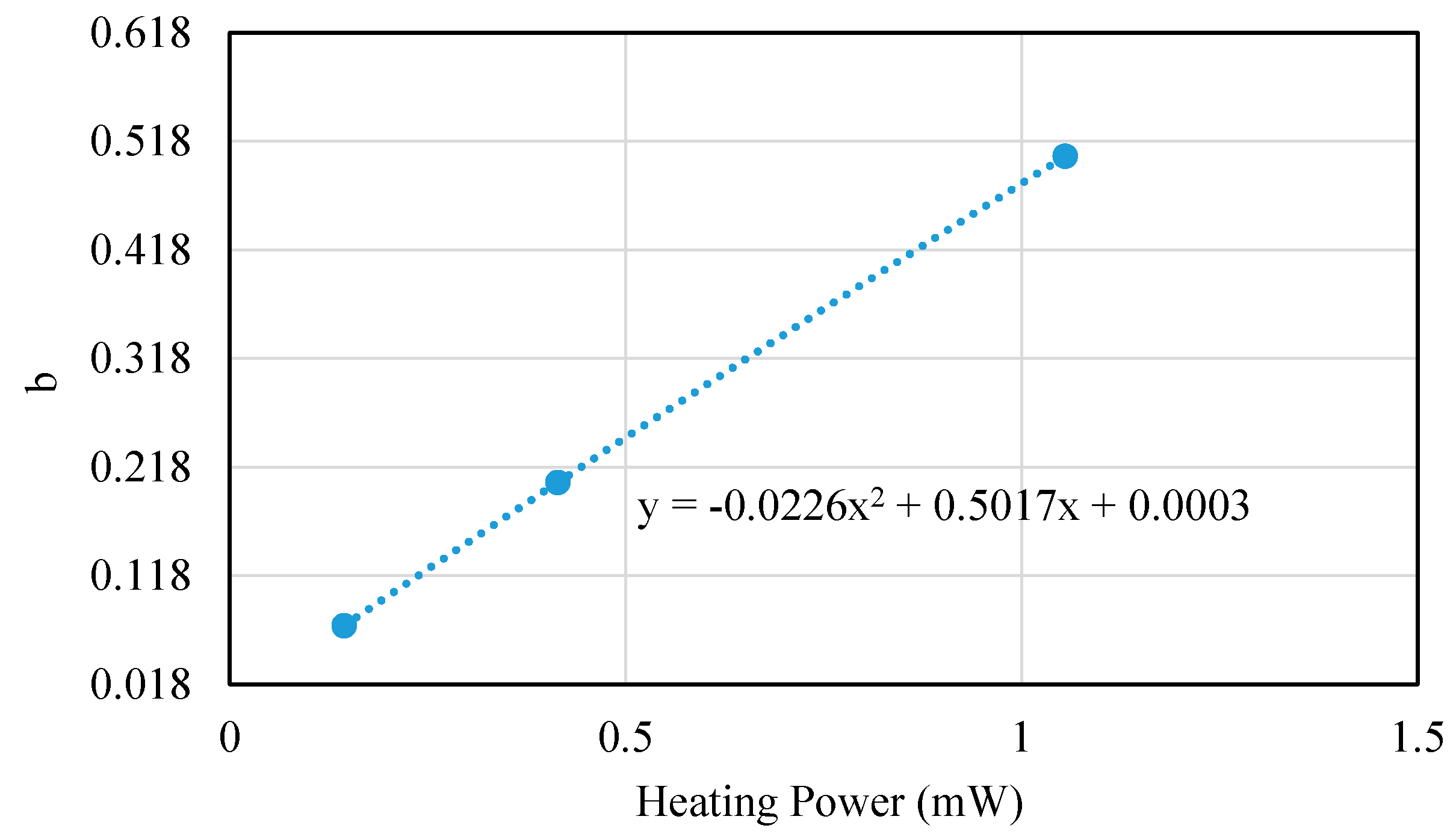
4.3. Validity of Macro-Model for Different Heating Powers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilfert, S.; Edelmann, C. Miniaturized vacuum gauges. J. Vac. Sci. Technol. A 2004, 22, 309–320. [Google Scholar] [CrossRef]
- Chen, S.J.; Wu, Y.C. Active thermoelectric vacuum sensor based on frequency modulation. Micromachines 2020, 11, 15. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.J.; Chen, B. Research on a CMOS-MEMS infrared sensor with reduced graphene oxide. Sensors 2020, 20, 4007. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Liang, P.Z.; Chen, S.J.; Cheng, Z.X. Coupled-field analysis of a silicon-thermopile-based vacuum sensor. Nanotechnol. Precis. Eng. 2008, 6, 336–342. [Google Scholar]
- Weng, P.K.; Shie, J.S. Micro-Pirani vacuum gauge. Rev. Sci. Instrum. 1994, 65, 492–499. [Google Scholar] [CrossRef]
- Shie, J.S.; Chou, B.C.; Chen, Y.M. High performance Pirani vacuum gauge. J. Vac. Sci. Technol. A 1995, 13, 2972–2979. [Google Scholar] [CrossRef]
- Chen, C.N.; Chen, C.C. Thermal Type Vacuum Gauge. U.S. Patent App. 15/070,276, 21 September 2017. [Google Scholar]
- Chen, C.N.; Huang, W.C. A CMOS-MEMS thermopile with low thermal conductance and a near-perfect emissivity in the 8–14-μm wavelength range. IEEE Electron Device Lett. 2010, 32, 96–98. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhang, Z.; Liu, S.; Luo, X. A micro-machined Pirani gauge for vacuum measurement of ultra-small sized vacuum packaging. Sens. Actuator A Phys. 2010, 161, 108–113. [Google Scholar] [CrossRef]
- Puigcorbe, J.; Vogel, D.; Michel, B.; Vila, A.; Gracia, I.; Cane, C.; Morante, J. Thermal and mechanical analysis of micromachined gas sensors. J. Micromech. Microeng. 2003, 13, 548. [Google Scholar] [CrossRef]
- Mahdavifar, A.; Aguilar, R.; Peng, Z.; Hesketh, P.J.; Findlay, M.; Stetter, J.R.; Hunter, G.W. Simulation and fabrication of an ultra-low power miniature microbridge thermal conductivity gas sensor. J. Electrochem. Soc. 2014, 161, B55. [Google Scholar] [CrossRef]
- He, F.; Huang, Q.-A.; Qin, M. A silicon directly bonded capacitive absolute pressure sensor. Sens. Actuator A Phys. 2007, 135, 507–514. [Google Scholar] [CrossRef]
- Shen, C.H.; Chen, S.J.; Guo, Y.T. A novel infrared temperature measurement with dual mode modulation of thermopile sensor. Sensors 2019, 19, 336. [Google Scholar] [CrossRef] [PubMed]
- Graf, A.; Arndt, M.; Sauer, M.; Gerlach, G. Review of micromachined thermopiles for infrared detection. Meas. Sci. Technol. 2007, 18, R59. [Google Scholar] [CrossRef]
- Van Herwaarden, A.; Sarro, P.; Meijer, H. Integrated vacuum sensor. Sens. Actuators 1985, 8, 187–196. [Google Scholar] [CrossRef]
- Van Herwaarden, A.; Sarro, P. Performance of integrated thermopile vacuum sensors. J. Phys. E 1988, 21, 1162. [Google Scholar] [CrossRef]
- Van Herwaarden, A.; Van Duyn, D.; Van Oudheusden, B.; Sarro, P. Integrated thermopile sensors. Sens. Actuator A Phys. 1990, 22, 621–630. [Google Scholar] [CrossRef]
- Folkmer, B.; Siber, A.; Bley, W.G.; Sandmaier, H.; Lang, W. Improved simulation for strongly coupled micro-electro-mechanical systems: Resonant vacuum sensor optimization. Sens. Actuator A Phys. 1999, 74, 190–192. [Google Scholar] [CrossRef]
- Todd, S.T.; Xie, H. An electrothermomechanical lumped element model of an electrothermal bimorph actuator. J. Microelectromech. Syst. 2008, 17, 213–225. [Google Scholar] [CrossRef]
- Niessner, M.; Schrag, G.; Iannacci, J.; Wachutka, G. Macromodel-based simulation and measurement of the dynamic pull-in of viscously damped RF-MEMS switches. Sens. Actuator A Phys. 2011, 172, 269–279. [Google Scholar] [CrossRef]
- Mele, L.; Rossi, T.; Riccio, M.; Iervolino, E.; Santagata, F.; Irace, A.; Breglio, G.; Creemer, J.; Sarro, P. Electro-thermal analysis of MEMS microhotplates for the optimization of temperature uniformity. Procedia Manuf. 2011, 25, 387–390. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Z. Review on macromodels of MEMS sensors and actuators. Microsyst. Technol. 2017, 23, 4319–4332. [Google Scholar] [CrossRef]
- Kaczynski, J.; Ranacher, C.; Fleury, C. Computationally efficient model for viscous damping in perforated MEMS structures. Sens. Actuator A Phys. 2020, 314, 112201. [Google Scholar] [CrossRef]
- Shah, M.A.; Lee, D.-G.; Hur, S. Design and characteristic analysis of a MEMS piezo-driven recirculating inkjet printhead using lumped element modeling. Micromachines 2019, 10, 757. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Balasubramaniam, R.; Chandra, S. Finite element analysis and experimental validation of suppression of span in optical MEMS pressure sensors. Microsyst. Technol. 2019, 25, 3691–3701. [Google Scholar] [CrossRef]
- To, A.C.; Liu, W.K.; Olson, G.B.; Belytschko, T.; Chen, W.; Shephard, M.S.; Chung, Y.W.; Ghanem, R.; Voorhees, P.W.; Seidman, D.N.; et al. Materials integrity in microsystems: A framework for a petascale predictive-science-based multiscale modeling and simulation system. Comput. Mech. 2008, 42, 485–510. [Google Scholar] [CrossRef]
- Devienne, F. Low density heat transfer. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1965; Volume 2, pp. 271–356. [Google Scholar]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Barber, R.; Emerson, D. The influence of Knudsen number on the hydrodynamic development length within parallel plate micro-channels. WIT Trans. Eng. Sci. 2002, 36, 12. [Google Scholar]
- Springer, G.S. Heat transfer in rarefied gases. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1971; Volume 7, pp. 163–218. [Google Scholar]
- Roth, A. Vacuum Technology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 17–61. [Google Scholar]
- Huang, Z.; Wang, J.; Bai, S.; Guan, J.; Zhang, F.; Tang, Z. Size Effect of Heat Transport in Microscale Gas Gap. IEEE Trans. Ind. Electron. 2017, 64, 7387–7391. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Report: A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar]
- Dongari, N.; Agrawal, A. Modeling of Navier–Stokes equations for high Knudsen number gas flows. Int. J. Heat Mass Transf. 2012, 55, 4352–4358. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, Y.; Wang, W.; Lu, M.; Sheng, G. Gas transport behaviors in shale nanopores based on multiple mechanisms and macroscale modeling. Int. J. Heat Mass Transf. 2018, 125, 845–857. [Google Scholar] [CrossRef]
- Harley, J.C.; Huang, Y.; Bau, H.H.; Zemel, J.N. Gas Flow in Micr-Channels. Gas 1994, 9, 2–1994. [Google Scholar]
- Reichenauer, G.; Heinemann, U.; Ebert, H.-P. Relationship between pore size and the gas pressure dependence of the gaseous thermal conductivity. Colloids Surf. A Physicochem. Eng. Asp. 2007, 300, 204–210. [Google Scholar] [CrossRef]
- Han, M.; Liang, X.G.; Tang, Z. Size effect on heat transfer in micro gas sensors. Sens. Actuator A Phys. 2005, 120, 397–402. [Google Scholar] [CrossRef]
- Chen, C.N. Fully quantitative characterization of CMOS–MEMS polysilicon/titanium thermopile infrared sensors. Sens. Actuators B Chem. 2012, 161, 892–900. [Google Scholar] [CrossRef]
- Chou, B.C.; Chen, Y.M.; OuYang, M.; Shie, J.-S. A sensitive Pirani vacuum sensor and the electrothermal SPICE modelling. Sens. Actuator A Phys. 1996, 53, 273–277. [Google Scholar] [CrossRef]
- Chen, C.N. Characterization of gas conductance of a thermal device with a V-groove cavity. IEEE Electron Device Lett. 2011, 33, 275–277. [Google Scholar] [CrossRef]
- Van Herwaarden, A.W. Thermal Vacuum Sensors Based on Integrated Silicon Thermopiles. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1987. [Google Scholar]
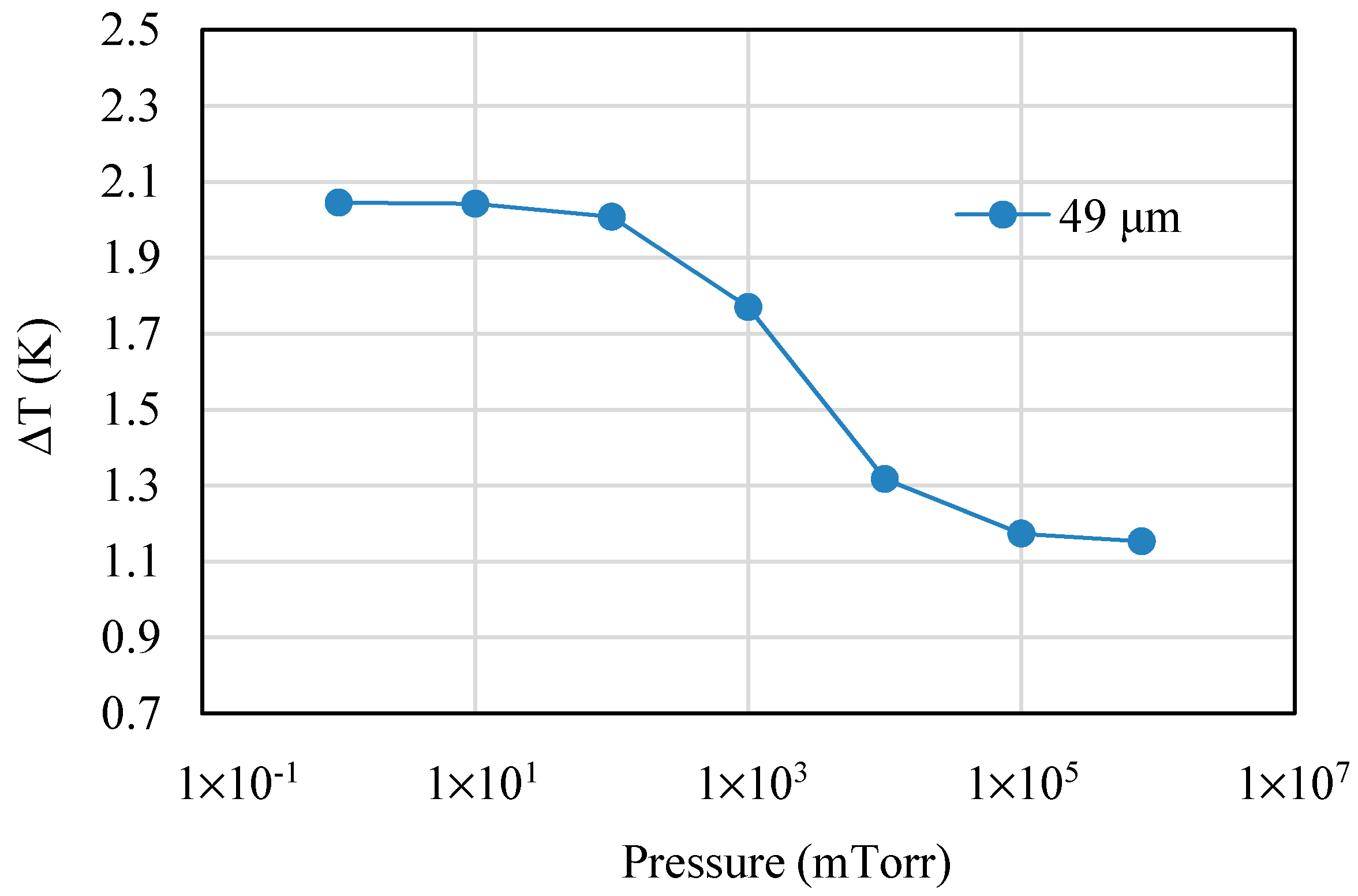
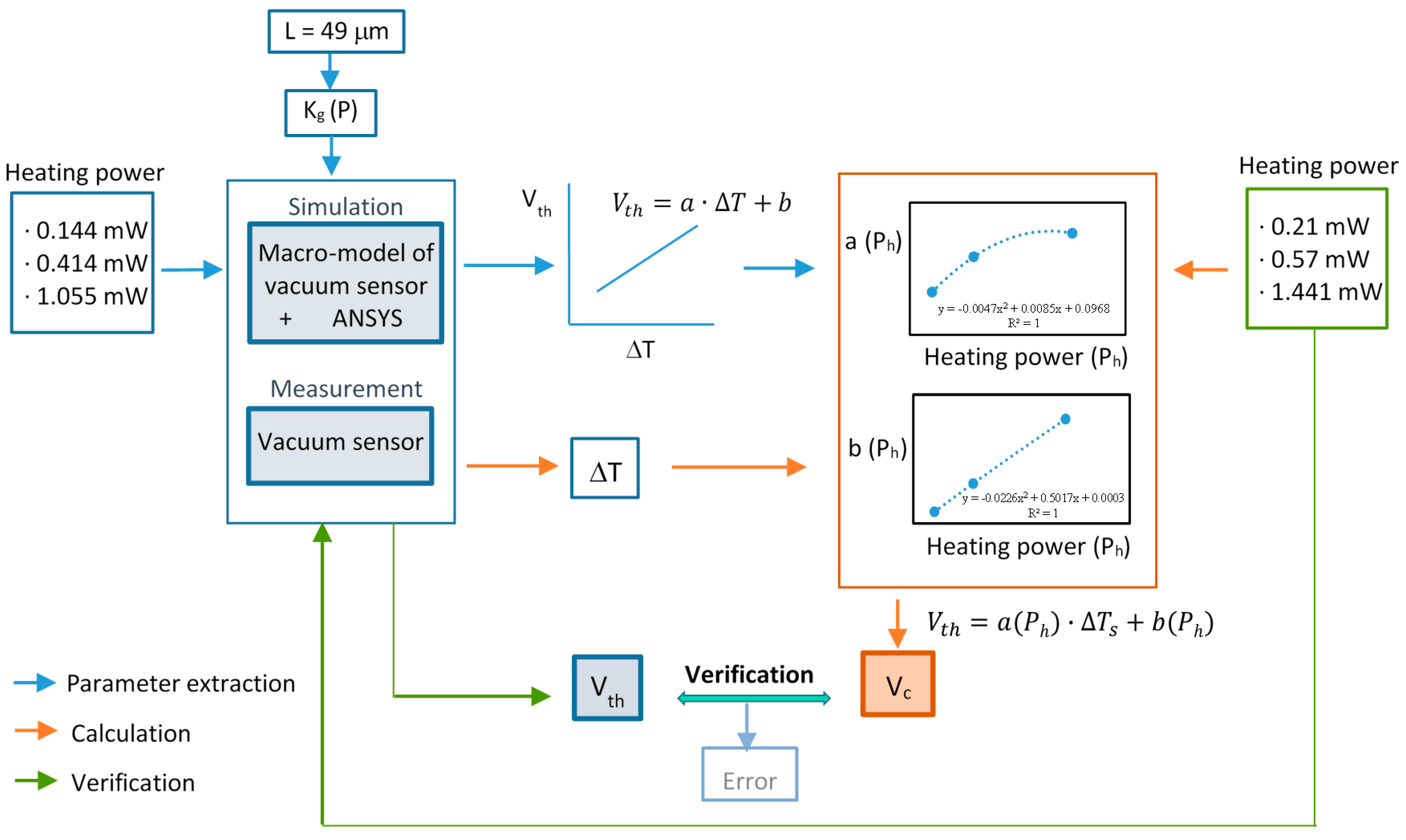

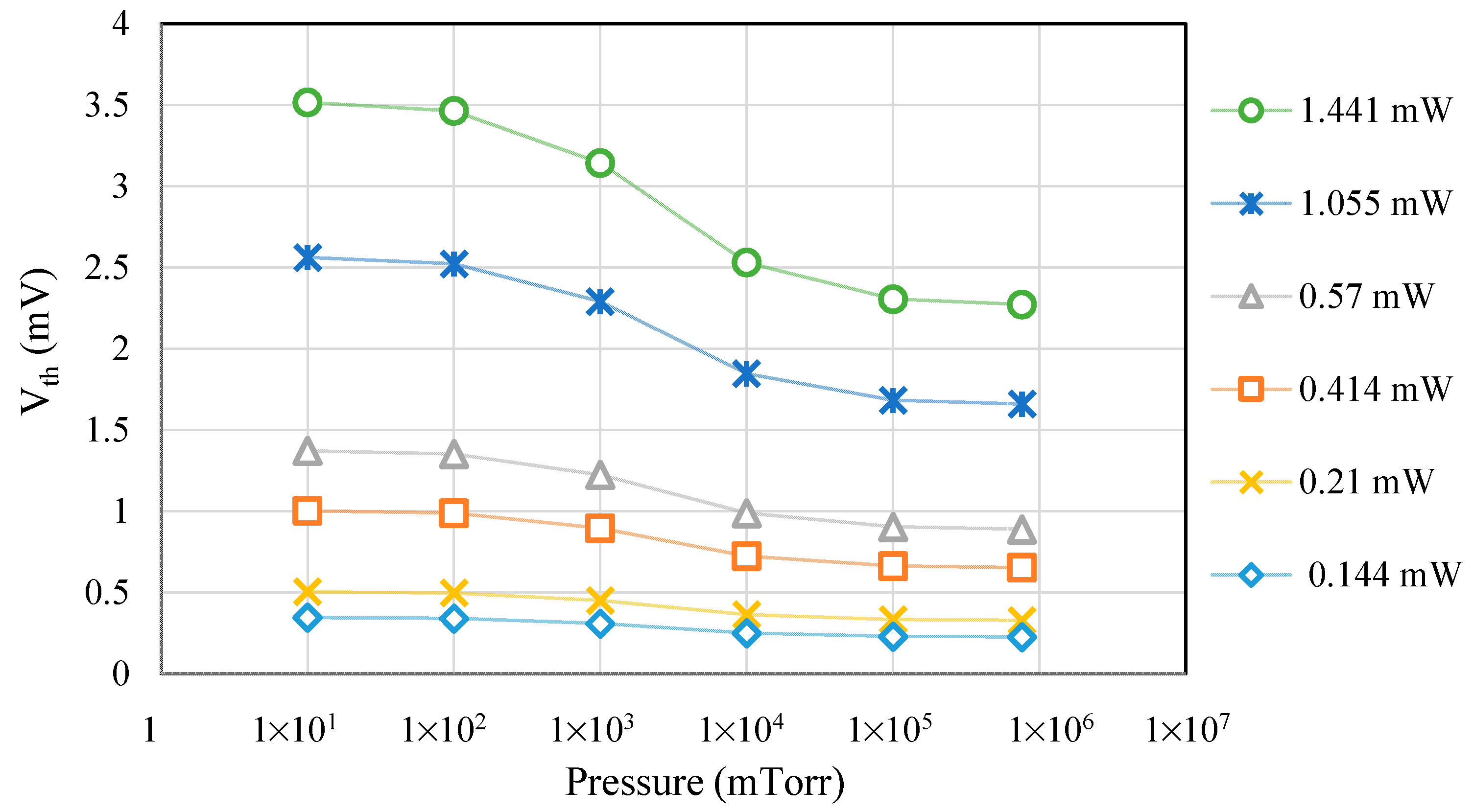
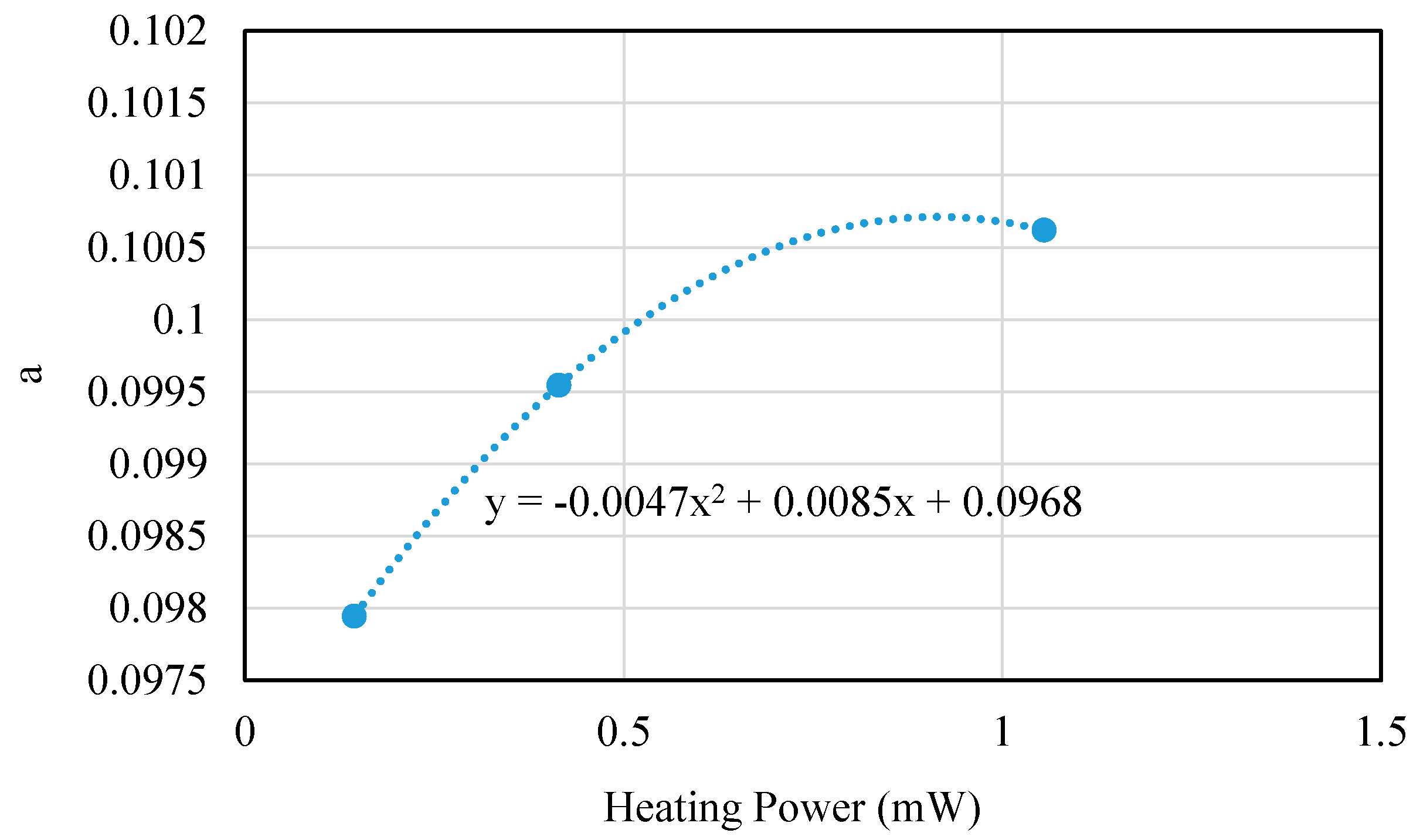
| Pressure (mTorr) | ΔTs (k) | Vc (mV) | Vth (mV) | Error (%) |
|---|---|---|---|---|
| 10 | 1.036 | 0.5049 | 0.5037 | 0.23% |
| 100 | 1.019 | 0.4983 | 0.4960 | 0.45% |
| 1000 | 0.9 | 0.4524 | 0.4506 | 0.40% |
| 10,000 | 0.67 | 0.3635 | 0.3640 | 0.13% |
| 100,000 | 0.596 | 0.3349 | 0.3329 | 0.60% |
| 760,000 | 0.585 | 0.3307 | 0.3286 | 0.64% |
| Pressure (mTorr) | ΔTs (k) | Vc (mV) | Vth (mV) | Error (%) |
|---|---|---|---|---|
| 10 | 2.811 | 1.3841 | 1.3723 | 0.86% |
| 100 | 2.765 | 1.3660 | 1.3524 | 1.00% |
| 1000 | 2.443 | 1.2394 | 1.2244 | 1.23% |
| 10,000 | 1.819 | 0.9941 | 0.9886 | 0.56% |
| 100,000 | 1.617 | 0.9147 | 0.9038 | 1.20% |
| 760,000 | 1.589 | 0.9037 | 0.8892 | 1.63% |
| Pressure (mTorr) | ΔTs (k) | Vc (mV) | Vth (mV) | Error (%) |
|---|---|---|---|---|
| 10 | 7.106 | 3.4470 | 3.5165 | 1.98% |
| 100 | 6.989 | 3.4014 | 3.4638 | 1.80% |
| 1000 | 6.176 | 3.0844 | 3.1441 | 1.90% |
| 10,000 | 4.598 | 2.4691 | 2.5311 | 2.45% |
| 100,000 | 4.087 | 2.2699 | 2.3055 | 1.54% |
| 760,000 | 4.017 | 2.2426 | 2.2729 | 1.34% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-J.; Wu, Y.-C. A New Macro-Model of Gas Flow and Parameter Extraction for a CMOS-MEMS Vacuum Sensor. Symmetry 2020, 12, 1604. https://doi.org/10.3390/sym12101604
Chen S-J, Wu Y-C. A New Macro-Model of Gas Flow and Parameter Extraction for a CMOS-MEMS Vacuum Sensor. Symmetry. 2020; 12(10):1604. https://doi.org/10.3390/sym12101604
Chicago/Turabian StyleChen, Shu-Jung, and Yung-Chuan Wu. 2020. "A New Macro-Model of Gas Flow and Parameter Extraction for a CMOS-MEMS Vacuum Sensor" Symmetry 12, no. 10: 1604. https://doi.org/10.3390/sym12101604
APA StyleChen, S.-J., & Wu, Y.-C. (2020). A New Macro-Model of Gas Flow and Parameter Extraction for a CMOS-MEMS Vacuum Sensor. Symmetry, 12(10), 1604. https://doi.org/10.3390/sym12101604






