Abstract
Tropical Algebra is used to model the dynamics of Timed Event Graphs (TEG), a particular class of Timed Discrete-Event System (TDES) in which we are interested only in synchronization and delay phenomena. Whenever this TEG has control inputs, we can use them to control the synchronization of the system to achieve some objective. Thus, this paper formulates a framework based on tropical algebra and lexicographic optimization to synchronize a TEG when dealing with many synchronization objectives that are ranked in previous priority order. We call this kind of problem the Tropical Lexicographic Synchronization Optimization (TLSO). This work develops a solution to this problem, based on Tropical Fractional Linear Programming (TFLP) and lexicographic optimization concepts. In this way, the basics of tropical algebra are determined, including essential terms to this paper, such as left and right residuations, and the following stages of the solution to the TLSO problem are explained. Therefore, this work presents a general framework based on structured algebraic models with application to TEG synchronization. By synchronization, we mean balancing and organizing events chronologically in order to achieve the desired goal. So, we are dealing with concepts closely related to symmetry ones. An illustrative numerical example is presented, which demonstrates the implementation of the proposed algorithms. The acquired results confirm the efficiency of the proposed methodology. Codes used for implementing the algorithms are listed in the appendix section of the article.
1. Introduction
Timed Event Graphs (TEGs) are used to model a wide range of Timed Discrete-Event Systems (TDES), which is a class of dynamic systems in which the change of state is governed by events [1]. Examples of model applications include manufacturing systems, production chains, queues, and urban traffic systems [2].
A powerful tool for analysis of TEGs is the so-called Tropical Algebra, which is a kind of idempotent algebraic structure which can be a semiring or a semifield depending on the application. French researchers gave the denomination as a tribute to Brazilian mathematician Imre Simon, who had a considerable influence on the development of automata and semigroup theory [3].
There are many types of tropical algebras that have applications in areas such as mathematics, engineering, and computer science. Two important examples are the Min-Plus and Max-Plus algebra. Concerning Max-Plus algebra, several results were obtained for analysis and synthesis of TDES. Among them, we highlight remarkable developments in control synthesis for such systems in the last decades (e.g., [4,5,6,7,8,9]).
The methodology used in this work addresses the synchronization problem, giving priority to TEG transitions to be synchronized, as proposed by lexicographic optimization. Each stage of the general problem is treated as a subproblem, which is solved through Tropical Fractional Linear Programming (TFLP). This optimization employs the dual iterative method, which, in turn, uses the residency operation. The original contribution of this paper is a lexicographic formulation of a TFLP problem aimed at synchronizing multiple disconnected TEGs. As references for TFLP, the reader is invited to consult [10,11], and for lexicographic optimization, the reference is [12]. More precisely, the authors propose a framework to synchronize the firing times of the transition of a TEG, considering a priority list of the pair of transitions that must be synchronized. This framework models this problem as a Lexicographic variation of a TFLP [10,11]. The authors denote the problem as a Tropical Lexicographic Synchronization Optimization (TLSO). It is important to stress that this framework can be applied in a general context. Moreover, as far as the authors’ knowledge goes, there are few works regarding linear fractional programming applications, and the authors do not find researches that deal with the insertion of lexicographic optimization in this context. Therefore, this article contributes to a formulation that unites existing concepts and relates them with a numerical example. As an illustrative application, traffic light synchronization is used as an example. In particular, this paper refers to Egmund and Olsder [13], who introduce the basics of Max-Plus algebra to deal with synchronization between phases in the traffic light system, with the purpose to generate the green waves.
This work has a theoretical impact by proposing a framework capable of synchronizing a class of models—the timed event graphs. There are few applications of this concept, for instance, manufacturing [2,14], traffic light control [13], payoff games [10], and multiprocessed systems [15,16]. The remainder of the paper is organized as follows: In Section 2, we introduce the preliminary concepts, in which the elements of tropical algebra are defined. In Section 3, the Tropical Lexicographic Synchronization Optimization is discussed, and the used tools to solve it are explained. Section 4 deals with a numerical example, which is explained while developing a study case. Finally, in the Appendix Section, we provide the listed codes implemented in ScicosLab. Note that Scicolab is a free package for mathematical computing, similar to Matlab. It can be found in http://www.scicoslab.org. The software is very convenient to work with tropical algebra since it has many of the related functions native implemented. (Version 4.4) code for the algorithm.
2. Tropical Algebra
This work is heavily based on tropical algebra. Therefore, in this section, we introduce some concepts and definitions related to this algebra. For more details on academic background, consult a historical review of Max-Plus tropical algebra [2,17,18]. “Tropical algebra” is a generic name for a family of idempotent algebraic structures, which can be a semiring or a semifield depending on the application. A special example of tropical algebra is the so-called Max-Plus Algebra. It is a particular Tropical structure act on the set with two operations, named and . Furthermore, let and be the set of column vectors with n entries in and the set of matrices with n rows and m columns in , respectively. From now on, we consider that “Max-Plus algebra” and “tropical algebra” can be used as synonyms, and this paper adopts the latter notation.
This algebra can be extended to matrices and vectors. If , , and are matrices of compatible sizes with entries in , we denote by the tropical matrix sum, in which . Furthermore, we define as the tropical matrix product, in which . In later notations, we omit the symbol ⊗ and denote the tropical product by juxtaposition, so . We use the symbol to denote . Let be a matrix of with n rows and m columns. This article denotes the Max-Plus identity matrix of appropriate order, a matrix with 0 in the diagonal and outside, by . For a square matrix A, we denote by the tropical power of A, defined recursively as and .
If A is a matrix (or a scalar) let be the matrix (or the scalar) obtained by switching the sign of its entries. If a is a vector and b is a scalar , let 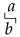 be (all the elements of a subtracted by b). Let denote the spectral radius of A, i.e., the largest eigenvalue. In Tropical Algebra, the eigenvalue defines the cycle time in a TEG and is still active research topic, with recent results, such as involving nontrivial eigenvectors [19,20]. The symbol is because
be (all the elements of a subtracted by b). Let denote the spectral radius of A, i.e., the largest eigenvalue. In Tropical Algebra, the eigenvalue defines the cycle time in a TEG and is still active research topic, with recent results, such as involving nontrivial eigenvectors [19,20]. The symbol is because 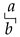 is the analog of a division in Max-Plus algebra. If , let denote the Kleene closure of A, i.e., . It is assumed from now on that the reader is familiar with the basics of this algebra, including concepts as Kleene closure [21].
is the analog of a division in Max-Plus algebra. If , let denote the Kleene closure of A, i.e., . It is assumed from now on that the reader is familiar with the basics of this algebra, including concepts as Kleene closure [21].
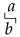 be (all the elements of a subtracted by b). Let denote the spectral radius of A, i.e., the largest eigenvalue. In Tropical Algebra, the eigenvalue defines the cycle time in a TEG and is still active research topic, with recent results, such as involving nontrivial eigenvectors [19,20]. The symbol is because
be (all the elements of a subtracted by b). Let denote the spectral radius of A, i.e., the largest eigenvalue. In Tropical Algebra, the eigenvalue defines the cycle time in a TEG and is still active research topic, with recent results, such as involving nontrivial eigenvectors [19,20]. The symbol is because 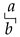 is the analog of a division in Max-Plus algebra. If , let denote the Kleene closure of A, i.e., . It is assumed from now on that the reader is familiar with the basics of this algebra, including concepts as Kleene closure [21].
is the analog of a division in Max-Plus algebra. If , let denote the Kleene closure of A, i.e., . It is assumed from now on that the reader is familiar with the basics of this algebra, including concepts as Kleene closure [21].Remark 1.
Unless stated otherwise, all operations in this paper are done in tropical algebra. So it is essential to be careful with the symbol that we use for the operations.
An important operation in tropical algebra is the residuation. The residuation works as a kind of multiplicative inverse in the matrix tropical algebra. This work defines it below:
Definition 1.
We define , —the left and right residuation of the product, respectively—as (see more details in [22])
Note that the residuations are implicitly defined by multiobjective optimization problems, since we want to optimize all the entries of the matrix X of appropriate dimension subject to the constraint or . Perhaps surprisingly, there is indeed a solution X, which is optimal in all its entries (the so-called utopical solution in optimization), and it is found by the residuations and .
Note that this is of the form of (2). Thus, notice that the previous inequality can be rewritten as
Let be the entrywise minimum between the matrices A and B. Consequently,
Therefore, we have that
Note that all the previous operations can be reversed. This implies that is the maximum possible value for the matrix X, optimal in all its entries and . This is exactly the (left) residuation: .
The general formula for computing the left residuation is . Analogously, for the right residuation, . In both cases, in the internal tropical product, we consider that .
3. Tropical Lexicographic Synchronization Programming
In general, the purpose of this research is to synchronize the transitions of the TEGs, which describes the discrete event systems. In this section, we propose a framework for establishing synchronization among the transitions of a TEG, a model for TDES. This is applicable in, for instance, traffic light systems synchronization, as is discussed further in this paper. Note that this is only one of the various possible applications of this kind, in which it is desired to have synchronization among transitions.
3.1. Motivation
As an example of application of the proposed procedure, consider a traffic light system, in which the goal is to obtain synchronization between phases at adjacent crossings, which allows green waves, a sequence of green lights in continuous crossings.
A traffic light system can be modeled as a TEG [13]. Figure 1 illustrates a TEG example in which we have two subsystems, in which each one is related to a crossing. Each transition represents a change of phases in each crossing, in which a phase corresponds to a combination of enabled green lights. We also have transitions , which represents the control of each phase. This means that we can delay the end of each phase.
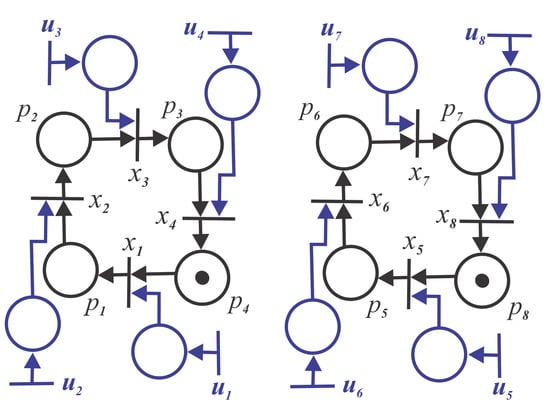
Figure 1.
Timed Event Graph (TEG) of synchronization example.
A correct synchronization of the system allows the creation of green waves. The synchronization consists on having firing times as close as possible. Thus, the problem involves choosing the firing times , which optimize the synchronization of the system, considering a priority order. Prioritization is necessary because it may not be possible to synchronize all the transitions , it is the same as synchronizing the TEG. More details are seen in the next section.
Note that the application of traffic light control is only one of the possible applications. For instance, we could consider manufacture processing and other systems that need sharing and synchronization of resources. The generic framework used to solve these described problems is proposed in the next subsections.
3.2. Formulation of the Tropical Lexicographical Synchronization Problem
Consider the Tropical linear system below, in which we have the state and input
We suppose that our policy for is , in which is a scalar and is a constant vector of the same dimension as . With this same and we can obtain a closed-loop controller , see [23]. If , it is known [8] that there are a finite K such that for all , for a constant vector of same dimension as that depends on . Let . More precisely,
For a fixed choice of , we want to choose the vector such that the entries of in steady-state () are as close as possible, i.e., they are synchronized. Unfortunately, it is not possible to have all the entries of synchronized (i.e., equal), because we may not have enough freedom in to achieve such an objective. So, we need to prioritize the synchronizations. So, it is necessary to define some elements:
- Let P be the number of pairs of transitions of the TEG that we want to synchronize.
- Let be the list of P pairs of indexes of entries of that we want to synchronize, ordered according to a decreasing defined priority. So, for instance, the pair of indexes is more important to be synchronized than the pair of indexes . Furthermore, we assume that in a pair , , i.e., we pre-specify a temporal order on the state in those indexes (the firing time comes after the firing time , or, in the best case, at the same time).
- Let . This is the synchronization index for the pair, which we want to minimize. Since the represent the firing times of the transitions for the time, represents the delay between the firing time of transition and the firing time of transition . (So, if equals to 0, the transitions happen simultaneously).
Note that, since , this is always a non-negative number. Moreover, since is in steady-state, one can see that , and therefore is independent on both k (that is why the symbol does not depend on k, although the definition seems to depend on k) and , depending only on , which in turn depends on our decision variable according to (9).
We finally conclude that a higher priority pair has an utmost priority over a lower priority pair. This implies that we have a lexicographical optimization on the indexes . Let and be the and row of the matrix M. Let be the row of M, respectively. Note that . So, our optimization problem is
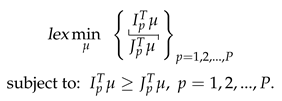
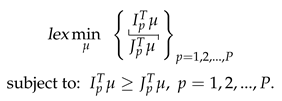
It is possible that a pair of cannot be synchronized, given the previous constraints. In Section 3.5, it is explained how this can be detected. In this case, we need to skip this pair and continue to the next one.
We define problems of this type as Tropical Lexicographic Synchronization Optimization (TLSO). Since the parameters of the problem are the matrix M, the list , and the scalar , we can denote the problem by .
3.3. Lexicographic Optimization Problem
In a general form, a Lexicographic Optimization Problem consists of solving , , subject to a constraint . Note that the objective functions are ordered so an index i has more priority than index . One procedure to solve this kind of problem consists of solving a sequence of traditional optimization problems for to :
in which is the optimal value of in the previous problem [12].
3.4. Tropical Fractional Linear Programming
We want to solve a TLSO, which is a Lexicographic Optimization Problem. We use the strategy explained in Section 3.3, which reduces lexicographic optimization problems into a sequence of traditional optimization problems. In our case, the particular traditional optimization problems are TFLP. The general form of a TFLP problem is
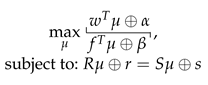 in which w, , f, , R, r, S, s are parameters. This kind of problem has been studied in [10,11], and algorithms have been proposed to solve them. The algorithm proposed in [11], in particular, relies on the ability to solve a particular case of TFLP. This particular case is called Max-Type Tropical Linear Problem (Max TLP):
in which w, , f, , R, r, S, s are parameters. This kind of problem has been studied in [10,11], and algorithms have been proposed to solve them. The algorithm proposed in [11], in particular, relies on the ability to solve a particular case of TFLP. This particular case is called Max-Type Tropical Linear Problem (Max TLP):
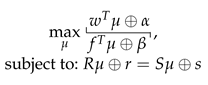
In order to guarantee that the solution for this problem is finite, the constraint of (13) must generate a set, which is upper bounded; in better words, there must exist a finite vector such that . From now on, we assume that this is true.
An algorithm to solve this problem is called Dual Method [11]. This is an iterative method that works with the following recursion:
with the initial condition . In each iteration k, the following conditions must be tested:
If these conditions are not true, the algorithm halts, and we can conclude that the feasible set of (13) is empty. Otherwise, when the algorithm converges (new equal to a previous ), it is able to find the optimal solution for the optimization problem. Note that the algorithm is independent of g. It turns out that, indeed, the solution is independent of these elements (see [11]). Any solution which is optimal for a vector is also optimal for any other . More generally, any objective function which is nondecreasing implies the same behavior. This happens because the algorithm in (14) will find a solution inside the feasible set of (13) that is maximal in any entry of [24].
When using the discussed Tropical Dual method by solving (14), we can solve the TFLP problems by converting Max-Type TFLP into Max-Type TLP problem according to Figure 2 through Charnes–Cooper conversion [25]. The complete TFLP problem is defined in (12). It is straightforward to adapt the Charnes–Cooper transformation to the tropical setting [11]. Set
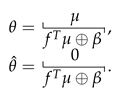
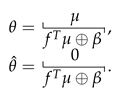
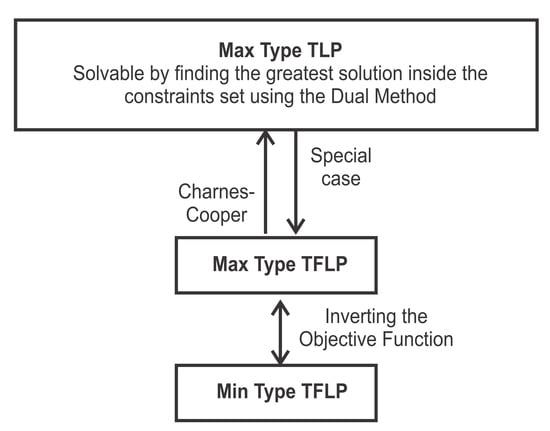
Figure 2.
Using Max-Type Tropical Linear Problem (Max TLP) to solve Tropical Fractional Linear Programming (TFLP) problems (adapted from [11]).
Then, by dividing (in tropical algebra) both sides of the affine equation on (12) by , it can be rewritten as
in which the additional equation condenses (16).
Define the vector
Let n and m be the number of rows and columns of R, respectively. With this definition, we can rewrite (17) as
Remember that is a vector of with n rows and one column, and is a vector of with one row and m columns.
This problem is a Max-type TLP as (13) and can be solved by Algorithm 1. The program’s code in the Scicoslab language is listed in Appendix A.1. Once and are obtained, in order to return to the original variable, one needs to revert (16).
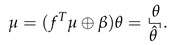
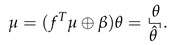
| Algorithm 1: Tropical Dual Function: TDual Algorithm |
 |
The TFLP method is implemented by the function , in which w, , f, , R, r, S, and s are parameters and it returns and , in which is the value of the optimal objective function, according to the implementation listed in Algorithm 2. The program’s code in the Scicoslab language is listed in Appendix A.2.
| Algorithm 2: Tropical Fractional Linear Programming: TFLP |
 |
3.5. Tropical Lexicographic Synchronization Programming
We solve the TLSO (10) using the general strategy proposed in Section 3.3. This implies solving a sequence of TFLPs (12), as discussed in Section 3.4. In this subsection, we describe this procedure in more detail.
First, note that the constraints in problem (10) can be rewritten as
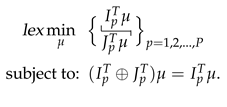
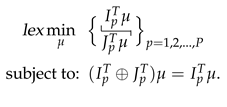
Remember that we have a list of pairs
ordered by a decreasing priority and also that . So, according to the procedure described in Section 3.3, the first problem that we need to solve is
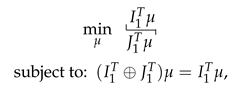 a TFLP (as in (12)) which can be solved using the procedure described in Section 3.4. After this TFLP is solved, we obtain a solution , and then we compute the first as
a TFLP (as in (12)) which can be solved using the procedure described in Section 3.4. After this TFLP is solved, we obtain a solution , and then we compute the first as
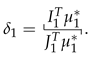
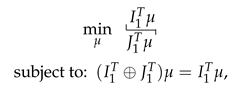
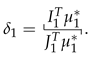
Now, the next step is to create the second problem in the sequence. We need to change the objective function to and also to add two new constraints:
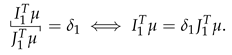
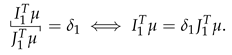
The second problem, in addition to the previous constraints and the change of objective function, is augmented by two new constraints, one to synchronize the new pair and another constraint to guarantee the previous result
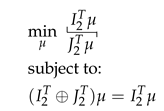
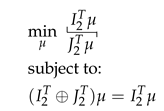
From the third problem on, up to , we have two more constraints for each new pair:
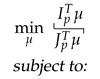
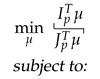
If the pair cannot be synchronized, that is, if the Algorithm 2 returns equal to empty, the pair is deleted from the list , the size P of the list is updated, and the iteration p is not increased.
The implementation of the TLSO is given by the function TLSO(A,B,L,lambda) in Algorithm 3. The program’s code in the Scicoslab language is listed in Appendix A.3, in which the parameters A and B are Max-Plus matrices. In ScicosLab the Max-Plus denomination is used instead of Tropical. L is the priority pairs list represented by a matrix with P rows and two columns, and is a scalar that is related to the period. The function TSLP returns the optimal .
It is important to stress that the TLSO is tropical homogeneous—that means, if is a solution, so is with , a scalar. Therefore, we can shift the vector that we obtain after we solve the problem, so that all its elements are non-negative.
A numerical example is developed in Section 4 to clarify the TLSO method.
| Algorithm 3: Tropical Lexicographic Synchronization Optimization: TLSO |
 |
4. Numerical Example
In this section, we develop a numerical example. We work with the TEG illustrated in Figure 1. As mentioned in the motivation Section 3.1, the illustrated TEG can model a traffic light system, which has two subsystems that refers to crossings. For more about the traffic light modeling with TEGs, see [13,26].
We suppose that the state equations are known and is given as follows:
We also suppose that the list of pairs that have a connection is known and is given as follows:
With these equations, we can write in state-space form once we define the matrices:
in which,
The matrices and have relation with the times (next state) and (current state), respectively. We execute the operation Kleene closure (see [21]) and obtain the matrix :
in which,
The matrix B is associated to control transition, thus, we obtain the matrix , as
in which,
The cycle time of the system can be obtained by calculating the eigenvalue, which results . Once the data () is ready, as a result we get the synchronizing vector from the algorithm TLSO (Algorithm 3, listed code Appendix A.3).
Obtaining matrix M: The TLSO algorithm uses the parameters , A, and B to calculate the matrix , as
in which,
Step one: The algorithm TLSO starts the search by finding an optimal synchronized vector by solving the first optimization problem for the first pair of indexes from the list .
In the first iteration (), the pair (3,7) from the list is used, we have and . In this way, (48) is the 7th line and (49) is the 3rd line of the matrix M:
In order to solve the first TFLP problem (see Section 3.4), we use , , , , , , , and .
The lexicographic algorithm calls the function TFLP (Algorithm 2) for these defined variables (w, , f, , R, r, S, s). The function returns the variables :
and (perfect synchronization between the transitions and ). In that way, we have the first vector .
Second step: At the second iteration () the pair is used, we have and , being and :
The second iteration returns from the function TFLP the result of :
and , which is the best synchronization possible in this case for this index pair.
Third step: At the third iteration (), we have the pair , in which we compute and correspondent to stages and :
Using these parameters R (58) and S (59), the third problem is solved, and the variable returns empty, which indicates that the algorithm does not converge and the synchronization is not possible. Therefore, we have to skip this phase and keep the last vector . Since there are no more pairs to synchronize, the algorithm is over.
As we explained in Section 3.5, we can shift the vector in a way that we have only non-negative values. Thus, we use , obtaining
The proposed example in this section clarifies the implementation of the lexicographic algorithm for synchronization among stages according to the previously defined list. In the first iteration, there is the perfect synchronization (). In the second iteration, the synchronization is possible with delay (). Lastly, in the third iteration, it is not possible to synchronize ( is empty).
5. Conclusions
In this work, we propose the TLSO (Tropical Lexicographic Synchronization Optimization) framework. This framework is based on TFLP (Tropical Fractional Linear Programming), which allows the formulation and solution of problems in which it is desirable to synchronize transitions of TEGs. As far as the authors’ knowledge goes, there are few practical TLFP applications in the literature. Thus, this article’s contribution is the formalization and utilization of TFLP for modeling of synchronization problems, in which we develop a numerical example of traffic light synchronization. It is important to note that if synchronization is not feasible, the method will handle it.
The research gap served by this work is the lexicographic proposition together with models resolved by TFLP for synchronization of TEGs subject to delays. The framework proposed in this research is limited to the characteristics resulting from the time events graph model, which applies to systems subjected to synchronization and delay phenomena. The study does not apply to systems where there is a dispute over resources of another nature. As future work, we propose the formulation for broader models, represented by more general TDES. Another possibility for future work is to consider an approach for closed-loop systems. The proposed lexicographic method is also suitable for other systems, such as manufacturing systems, and others in which synchronization and resource sharing are desired.
Author Contributions
Methodology development, manuscript writing and checking, A.M.M.; project supervision, methodology development and manuscript checking, V.M.G.; project supervision, methodology development and manuscript checking, C.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the CNPq (Brazilian Ministry of Science and Technology), the CAPES Foundation (Brazilian Ministry of Education), UFMG and CEFET-MG, which was greatly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DES | Discrete-Event Systems |
| TDES | Timed Discrete-Event Systems |
| TEG | Timed Event Graph |
| TFLP | Tropical Fractional Linear Programming |
| TLSO | Tropical Lexicographic Synchronization Optimization |
Appendix A. Codes of Algorithms
In this section, we list the implemented codes of algorithms in a practical free language Scicoslab. Note that all the listed codes are in Scicoslab’s language, that implements tropical algebra in its Max-Plus mode. Therefore, the bar symbol (/) implements the right residuation operation, the backslash symbol (∖) implements the left residuation operation, the plus symbol (+) implements the oplus operation (⊕), and the asterisk symbol (*) implements the otimes operation (⊗).
Appendix A.1. Code of Algorithm Tropical Dual
The program’s code that implements the Algorithm 1 TDual, in the free language Scicoslab, is listed below:
// Implementation of Algorithm1:TDual
// Tropical Dual Function
function [vnew]=TDual( E, D, e, d )
big=1000;
itmax=10000;
tol=#(0.0001);
// initialize upperbound
vprev=#(ones(size(E,2), 1)*big);
k=0;
// stop flags
converge=%F;
itok=%T;
condi=%T;
while(~converge & itok & condi)
// Recursive Equation (14)
vnew=(E∖(D*vprev+d)) &
(D∖(E*vprev+e))&vprev;
k=k+1;
// test conditions (15)
condi = and(e <= (D*vnew+d)) &
and(d <= (E*vnew+e));
converge=sum(vprev-vnew)<tol;
itok = (k < itmax);
vprev=vnew;
end;
if ~condi | ~itok
vnew=[];
end
return [vnew];
endfunction
Appendix A.2. Code of Algorithm TFLP
The program’s code that implements the Algorithm 2 TFLP, in the free language Scicoslab, is listed below:
// Implementation of Algorithm2:TFLP
// Tropical Fractional Linear Programming
function [u,delta]=TFLP(w,alfa,f,Beta,R,r,S,s)
n = size(R,1);
m = size(R,2);
epsn = full(%zeros(n,1));
epsm = full(%zeros(1,m));
// create the matrices according to (19)
E = [ R r ; f Beta ];
e = [ epsn ; %0 ];
D = [ S s ; epsm %0];
d = [ epsn; 0 ];
// calls the Dual Method to solve Max TLP in (19)
[v] = TDual( E, D, e, d );
// verify if the solution is found
ifisempty(v)
u =[];
delta = [];
else
// convert back to the original variable according to (20)
y = v(1:$-1);
z = v($);
u = y*z;
delta= (w*u+alfa)-(f*u+Beta);
end
return [u,delta];
endfunction
Appendix A.3. Code of Algorithm TLSO
The program’s code that implements the Algorithm 3 TLSO, in the free language Scicoslab, is listed below:
// Implementation of Algorithm3:TLSO
// Tropical Lexicographic Synchronization Optimization
function [u]=TLSO(A,B,L,lambda)
M=star(A-lambda)*B;
// maximum possible iterations
P=size(L,1);
p=1; // first iteration
while(p<P)
i(p) = L(p,1);
j(p) = L(p,2);
I(p,:) = M(i,:(p,:),:);
J(p,:) = M(j(p,:),:);
// iteration constraint Equation (30)
w = I(p,:);
f = J(p,:);
R = I(p,:)+J(p,:);
S = I(p,:);
// prior constraints (31)
n = p-1;
while(n>0)
R = [ R; J(n,:); I(n,:)+J(n,:)];
S = [ S; delta(n)*J(n,:);I(n,:)];
n=n-1;
end;
r = full(%zeros((p-1)*2+1,1));
s = full(%zeros((p-1)*2+1,1));
[u,delta(p)]=
TFLP(w,alpha,f,Beta,R,r,S,s);
ifisempty(u)
L(p,:) = [];
P = size(L,1);
else
ustar=u;
p=p+1;
end;
end;
return [ustar];
endfunction
References
- Baccelli, F.; Cohen, G.; Olsder, G.J.; Quadrat, J.P. Synchronization and Linearity an Algebra for Discrete Event Systems; John Wiley and Sons: New York, NY, USA, 1992. [Google Scholar]
- Hardouin, L.; Cottenceau, B.; Shang, Y.; Raisch, J. Control and State Estimation for Max-Plus Linear Systems. Found. Trends® Syst. Control 2018, 6, 1–116. [Google Scholar] [CrossRef]
- Pin, J.E. The influence of Imre Simon’s work in the theory of automata, languages and semigroups. Semigroup Forum 2019, 98, 1–8. [Google Scholar] [CrossRef]
- Amari, S.; Demongodin, I.; Loiseau, J. Control of linear min-plus systems under temporal constraints. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 7738–7743. [Google Scholar] [CrossRef]
- Amari, S.; Demongodin, I.; Loiseau, J.; Jacques, J.J.; Martinez, C. Max-plus control design for temporal constraints meeting in timed event graphs. IEEE Trans. Autom. Control. 2012, 57, 462–467. [Google Scholar] [CrossRef]
- Atto, A.M.; Martinez, C.; Amari, S. Control of discrete event systems with respect to strict duration: Supervision of an industrial manufacturing plant. Comput. Ind. Eng. 2011, 61, 1149–1159. [Google Scholar] [CrossRef]
- Kim, C.; Lee, T.E. Feedback control of cluster tools for regulating wafer delays. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1189–1199. [Google Scholar] [CrossRef]
- Gonçalves, V.M.; Maia, C.A.; Hardouin, L. On the Steady-State Control of Timed Event Graphs With Firing Date Constraints. IEEE Trans. Autom. Control 2016, 61, 2187–2202. [Google Scholar] [CrossRef]
- Majdzik, P.; Seybold, L.; Witczak, M. A max-plus algebra predictive approach to a battery assembly system control. In Proceedings of the 2014 IEEE International Symposium on Intelligent Control (ISIC), Juan Les Pins, France, 8–10 October 2014; pp. 2202–2207. [Google Scholar] [CrossRef]
- Gaubert, S.; Katz, R.; Sergeev, S. Tropical Linear-fractional programming and parametric mean payoff games. J. Symb. Comp. 2012, 47, 1447–1478. [Google Scholar] [CrossRef]
- Gonçalves, V.M.; Maia, C.A.; Hardouin, L. On tropical fractional linear programming. Linear Alg. App. 2014, 459, 384–396. [Google Scholar] [CrossRef]
- Zykina, A.V. A Lexicographic Optimization Algorithm. Autom. Remote Control 2004, 65, 363–368. [Google Scholar] [CrossRef]
- Egmund, R.J.; Olsder, G.J. The (max,+) algebra applied to synchronization of traffic light processes. WODES 1998, 26, 451–456. [Google Scholar]
- Dias, J.R.S.; Maia, C.A.; Lucena, V.F. A Computationally Efficient Method for Optimal Input-Flow Control of Timed-Event Graphs Ensuring a Given Production Rate. J. Control Autom. Electr. Syst. 2015, 26, 348–360. [Google Scholar] [CrossRef]
- Butkovic, P.; Aminu, A. Introduction to max-linear programming. IMA J. Manag. Math. 2008, 20, 233–249. [Google Scholar] [CrossRef]
- Butkovic, P.; MacCaig, M. On the integer max-linear programming problem. Discret. Appl. Math. 2014, 162, 128–141. [Google Scholar] [CrossRef]
- De Schutter, B.; van den Boom, T.; Xu, J.; Farahani, S.S. Analysis and control of max-plus linear discrete-event systems: An introduction. Discret. Event Dyn. Syst. 2020, 30, 25–54. [Google Scholar] [CrossRef]
- Komenda, J.; Lahaye, S.; Boimondb, J.L.; Boom, T. Max-plus algebra in the history of discrete event systems. Annu. Rev. Control 2018, 45, 240–249. [Google Scholar] [CrossRef]
- Umer, M.; Hayat, U.; Abbas, F. An Efficient Algorithm for Nontrivial Eigenvectors in Max-Plus Algebra. Symmetry 2019, 11, 738. [Google Scholar] [CrossRef]
- Umer, M.; Hayat, U.; Abbas, F.; Agarwal, A.; Kitanov, P. An Efficient Algorithm for Eigenvalue Problem of Latin Squares in a Bipartite Min-Max-Plus System. Symmetry 2020, 12, 311. [Google Scholar] [CrossRef]
- Cassandras, C.G.; Lafourtune, S. Introduction to Discrete Event Systems, 2nd ed.; Springer: New York, NY, USA, 2008; pp. 53–57. [Google Scholar]
- Blyth, T.; Janowitz, M. Residuation Theory; Pergamon Press: Oxford, UK, 2008; ISBN 9781483157146. [Google Scholar]
- Gonçalves, V.M.; Maia, C.A.; Hardouin, L. On max-plus linear dynamical system theory: The regulation problem. Elsevier Autom. 2017, 75, 202–209. [Google Scholar] [CrossRef]
- Gonçalves, V.M.; Maia, C.A.; Hardouin, L. Weak dual residuations applied to tropical linear equations. Linear Alg. Its App. 2014, 445, 69–84. [Google Scholar] [CrossRef][Green Version]
- Charnes, A.; Cooper, W.W. Programing with linear fractional functionals. Nav. Res. Logist. Q. 1962, 9, 181–186. [Google Scholar] [CrossRef]
- Marotta, A.M.; Maia, C.A. Modeling and Optimization of Semaphore Networks Via Linear Max-Plus Model: Application to Synchronism and Flow Control in Crossings. In Proceedings of the 47th International Conference on Computer and Industrial Engineering, Lisboa, Portugal, 11–13 October 2017; Available online: https://www.dropbox.com/sh/98wen5smashdq4m/AACHGFgY7Tcj6LzObobWWeJca/CIE47_paper_300.pdf (accessed on 27 August 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).