Abstract
In this review, we consider the time reversal T and particle-antiparticle C symmetries that, being most fundamental, can be violated at microscopic level by a weak interaction. The notable example here is from condensed matter, where strongly correlated Fermi systems like heavy-fermion metals and high superconductors exhibit C and T symmetries violation due to so-called non-Fermi liquid (NFL) behavior. In these systems, tunneling differential conductivity (or resistivity) is a very sensitive tool to experimentally test the above symmetry break. When a strongly correlated Fermi system turns out to be near the topological fermion condensation quantum phase transition (FCQPT), it exhibits the NFL properties, so that the C symmetry breaks down, making the differential tunneling conductivity to be an asymmetric function of the bias voltage V. This asymmetry does not take place in normal metals, where Landau Fermi liquid (LFL) theory holds. Under the application of magnetic field, a heavy fermion metal transits to the LFL state, and becomes symmetric function of V. These findings are in good agreement with experimental observations. We suggest that the same topological FCQPT underlies the baryon asymmetry in the Universe. We demonstrate that the most fundamental features of the nature are defined by its topological and symmetry properties.
1. Introduction
Unusual properties of strongly correlated Fermi systems are observed in superconductors with high (HTSC) and in heavy fermion (HF) metals due to a quantum phase transition (QPT) occurring at its quantum critical point (QCP) at . QPT is caused by external incentives such as chemical composition, pressure P, density x of electrons (holes), magnetic field B, etc. It is commonly accepted that QPT is the main cause of the non-Fermi liquid (NFL) behavior demonstrated by strongly correlated Fermi systems [1]. The thermodynamic, relaxation and transport properties of HF compounds had been well studied experimentally. On the other hand, the properties of HF metals (and other strongly correlated Fermi systems), that are not directly related to the density of states (DOS) or effective mass , had not yet been measured in detail. In this context, scanning tunneling microscopy and point contact spectroscopy based on Andreev reflection (AR) [2] are sensitive to both quasiparticle occupation numbers and DOS, which makes them ideal candidates for studying the effects of particle-hole symmetry violation. The measured physical characteristic in the above methods is a differential tunneling conductivity or conductance. Asymmetric part of the conductance (, where I is a tunneling current and V is a bias voltage) can be observed when a system with strongly correlated heavy fermions (like electrons and/or holes) is both in its normal and superconducting state [3,4,5,6,7,8,9]. We note that such an asymmetry does not occur in conventional metals, especially at low temperatures. Since latter systems are well described by the Landau Fermi liquid (LFL) theory, which supports the particle-hole C symmetry, the differential tunneling conductivity and the dynamic conductance become symmetric functions of bias voltage V in them [1,10,11,12].
One of the peculiar quantum phase transitions, taking place in the above systems, is so-called topological fermion condensation quantum phase transition (FCQPT). As a result of this transition, some of the fermions, comprising strongly correlated Fermi system, condense like bosons, see Refs [11,12,13] for details. These condensed fermions form fermion condensate (FC), which is responsible for many salient features, observed in the above systems. Among other things, the corresponding theoretical approach is able to describe the NFL properties of HTSC, HF metals, quantum spin liquids (for different number of spatial dimesions) as well as quasicrystals [1,11,12,13,14,15]. The same approach, being applied to the differential tunneling conductivity in HF metals, shows convincingly, that latter quantity becomes significantly asymmetric function of bias voltage V. The underlying physical mechanism is the same as in the archetypical HF metal , where external parameters put the electronic subsystem near FCQPT point in the phase diagram. The aforementioned asymmetry have been observed experimentally in HF metals both in normal and superconducting state, see, e.g., [16,17]. The asymmetry of tunneling conductivity is conveyed by the violation of both the time reversal T and the particle-antiparticle (in solids, particles, or quasiparticles, correspond to electrons, while antiparticles correspond to holes) C symmetries. The magnetic field B, being applied to a HF metal sample, returns it to the LFL state so that the corresponding T and C symmetries are restored, and [3,6,7]. One can see, therefore, that a magnetic field destroys a fermion condensate in a HF metal, restoring the normal Fermi liquid in it. This makes conductivity to be a symmetric function of V. Latter fact occurs since in normal Fermi liquids, the particle-antiparticle (C) (or particle (quasiparticle)-hole in solids) symmetry is not violated. More generally, at low temperatures both the T and the C symmetries are restored, while at elevated temperatures the NFL behavior can return, breaking the symmetries once more. The experimental observation of the flat band and a superconducting (SC) state in graphene [18] attracted sturdy attention to the band flattening, since it can lead to the bulk room- superconductivity in graphite [19]. Both band flattening and SC state emergency are consistent with recent experimental observations (and their subsequent theoretical analysis) suggesting that the flattening not only raises the critical temperature of superconducting phase transition but can as well be accompanied by asymmetric conductivity that breaks T and C symmetries [3,6,7,19,20,21,22,23,24,25].
In this review, based on experimental data and their theoretical explanation, we show that both T and C symmetries break when HF metal and/or HTSC are located near the topological FCQPT. We have also shown that latter HF compounds exhibit NFL properties in their superconducting, pseudogap and normal states. As a result, the asymmetric part of the differential tunneling conductivity is sustained throughout latter states. Since the application of magnetic field destroys the NFL properties, it also recovers the above symmetries, nullifying . This nullification is in good agreement with the recent experimental observations [18,26,27] and has been predicted theoretically in Refs. [3,6,7]. Thus, the existence of the asymmetric part is a consequence of the NFL behavior. We note that in case of triodes and diodes the asymmetric part occurs due to diametrically opposite physical reasons, since in the case of the HF metals can be destroyed by applying weak magnetic field. Therefore measurements can be viewed as a powerful and versatile tool to investigate the fundamental NFL physics of strongly correlated Fermi systems. This fact is due to the time reversal T and particle-hole C symmetries violation in the NFL phase of latter systems. We speculate that similar violations generated by topological FCQPT can take place at large scales in the Universe.
The review is organized as follows. In the following Section 2 we present short discussion of QPT and outline special properties of topological QPTs. In Section 3 the topological FCQPT is reviewed. Here we show that FCQPT leads to C and T symmetries violation. Section 4 deals with the asymmetric conductivity of HF compounds near the topological FCQPT. Here we discuss main properties of the asymmetric conductivity. In Section 5 we compare our theoretical results on the asymmetric conductivity with experimental facts collected on heavy-fermion metals and high superconductors. In Section 6 we analyze the violation of T and C symmetries in the Universe, and show that the existence of the time arrow, baryon asymmetry and the high entropy of the Universe can be accounted for, provided that the Universe undergoes the topological FCQPT. Section 7 summarizes the main results of the review and outlines the perspectives in searches for the violations of the symmetries within the framework of topological approach.
2. Quantum Phase Transitions
HF compounds are fundamental systems in the condensed matter physics that are very well studied experimentally, which until very recently have lacked theoretical explanations [1,11,12]. Many notable and yet unexplained NFL properties of HTSC, HF metals and other strongly correlated fermionic systems are likely to be due to magnetic phase transitions of quantum nature [1,28]. QPT takes place at its QCP separating the ordered phase that emerges as a result of quantum phase transition from the disordered phase. It is usually suggested that magnetic (e.g., ferromagnetic and antiferromagnetic) QPTs are responsible for the NFL behavior. The critical point of the corresponding phase transitions that we call ordinary phase transitions, can be shifted to absolute zero by varying the non-thermodynamic parameters such as chemical composition, P, B, etc. Both the ordered side of ordinary phase transition and disordered side are described within the framework of the LFL theory, supporting C and T symmetries [1,11,12,29]. As a result, one concludes that within the framework of ordinary quantum phase transition notion, it is impossible to explain the observed experimentally and the corresponding C and T violations. To still explain the observed NFL behavior, the notion of quantum and thermal fluctuations, that accompany QCP, has been proposed in Ref. [28]. This notion, unfortunately, lacked universality. Namely, being able to explain theoretically one peculiarity, this idea was not suitable to describe the whole bunch of other features in HF compounds. The only possibility to deliver the universal description of the above asymmetry as well as of the other NFL features, was to introduce the new type of QPT [1,11,12,13].
The LFL theory is based on the Landau paradigm that a Fermi liquid properties are defined by its excitations, named quasiparticles. Quasiparticles are fermions with the effective mass [29]. Within the LFL theory, the approximate constancy of the effective mass is accepted, and it is based on the fact that conventional metals are well described within the approximate constancy of . As a result, the single-particle spectrum of quasiparticles with the effective mass weakly depends on temperature T and magnetic field B. In the LFL theory, the single-particle spectrum is a variational derivative
of the system energy with respect to the quasiparticle distribution (or occupation numbers) . In turn, the spectrum (p) is related to the occupation numbers by the well-known Fermi-Dirac distribution
Here, is chemical potential. At the distribution represents the step function. The both functions are symmetrical with respect to particles and holes [29]. Taking into account that the Fermi energy of conventional metal K, we conclude that can strongly depend on T and B at very high values of T and B. Latter feature is fundamentally different from Landau supposition about quasiparticle effective mass constancy in the normal Fermi liquid. In other words, now (which in Fermi liquid approach, defines all observable properties of HF compounds) starts to depend on external stimuli like temperature, pressure and/or magnetic field [1,11,12]. Thus, to explain the observed properties of HF compounds, including the asymmetrical conductivity , we must employ a topological quantum phase transition represented by the topological FCQPT, transforming the Fermi surface into Fermi volume, and forming flat bands [1,11,12,13]. Such a topological phase transition is to be a quantum phase transition, and, as we will see in Section 3, violates C and T symmetries, while the effective mass starts to strongly depend on T and B.
3. Fermion Condensation State
Although the effect of fermion condensation had already been described in several sources (like monographs [11,12] and reviews [1,15]), here we recapitulate the basics of FC theory [1,11,12,13,14,15]. In HF compounds, the topological FCQPT is driven by external stimuli like chemical composition, pressure as well as electric, magnetic, elastic fields etc. For instance, as HF electrons (quasiparticles) concentration x reaches some critical value , the quasiparticle spectrum becomes -independent forming the so-called flat bands. This flat part does not occupy whole spectrum; it rather emerges in a segment -, where stands for initial value and is for final value of quasiparticle momentum. As the effective mass is defined by the second derivative of the spectrum, it becomes infinite (diverges) in its flat part. Beyond , the quantum phase transition (FCQPT for concreteness) occurs so that the zero-temperature quasiparticle distribution is no more step function. This implies that the quasiparticle spectrum is determined by minimization of the Landau energy functional [13] to yield
where is the chemical potential. At Equation (3) defines the occupation number , which is a minimum of the above functional . The ordinary is portrayed in Figure 1 for dimensionless (in the units of Fermi energy ) temperatures and . This Figure shows that FC breaks the C symmetry as does not have characteristic step-like shape at ; rather, it has several steps. Latter steps make the conductivity to acquire an asymmetric part. Figure 1 also shows that at increasing temperatures C asymmetry diminishes, and eventually vanishes at with being a characteristic temperature, where FC ceases to be important [1,11].
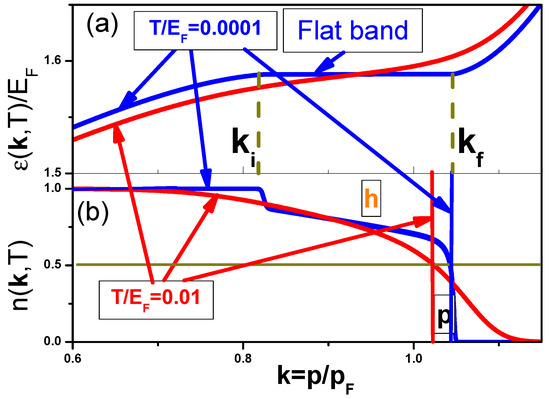
Figure 1.
Quasiparticle spectrum (a) and occupation number (b) for the FC phase vs dimensionless momentum . Reported is the case of very small ( − ) temperatures; and are Fermi momentum and energy respectively [1,6]. Vertical lines (red and blue for temperatures shown in the panels) in panel (b) correspond to where (horizontal line). In the panel (a), at (marked by dashed horizontal lines with and standing for initial and final momenta respectively) and (blue curve), is almost dispersionless and marked “Flat band”. Latter implies that the density of states in the range . The occupation number develops more asymmetry relatively to so that C invariance is broken, yielding NFL regime. To illustrate the asymmetry, the area in panel (b), where holes are “living”, is labeled “h” (in red color), while that for quasiparticles, by “p” (in black color).
Now consider how the presence of signals the violation of T and C symmetries. Suppose that we have a contact between HF and ordinary metal. Let us initially have the electronic (i.e., that of negatively charged quasiparticles) current directed from HF to an ordinary metal. Applying voltage V to the contact, we change the sign of quasiparticle charge which alters immediately the current direction. Simultaneously, one obtains exactly the above electronic current under the voltage sign change . In this case, the differential conductivity acquires an asymmetric part due to C symmetry break (Figure 1). Also, the substitution (t is time) for constant charge generates the change of current direction only. As latter direction change can be accomplished by also, it is clear that time inversion symmetry is violated if exists. Hence, if C or T symmetries are violated, nonzero appears. Concurrently, the simultaneous transform and does not change anything, which means that combined CT symmetry is preserved. It is obvious that the same consideration is true for . It should be noted that in the present case the symmetry with respect to coordinates sign flip (i.e., parity P) is not violated so that the combined general symmetry is kept intact. It is well known that partial C and T symmetries conserve for the systems of fermions, described by Landau theory. This implies that for these systems (like ordinary metals) is a symmetric function so that conductivity asymmetry is not observed in them at low T [8,10].
To derive the expression for , we first calculate the bias-dependent current flowing through the metallic contact via tunneling. This can be accomplished by the so-called Harrison method [10,30]. This method uses the fact that is a linear function of so-called Bardeen transition probability [31]. This quantity is the probability for a particle (say, an electron) to tunnel from initial state 1 to final state 2 through a layer. It is given by the expression
where is the state 2 DOS, are corresponding quasiparticle distributions with a transition matrix element . The expression for total tunneling current I reads in this case
The transition amplitude has been calculated in WKB approximation [10,30] with respect to transition amplitude t
The coefficient 2 in front of the integral (7) accounts for the two projections of the electron spin and is the chemical potential. In the above expressions, the dimensionless (so-called atomic) units have been used. As usual, e and m are the electron charge and mass, respectively. Besides that, is a quantity for a normal metal. Since temperature is low, , where is a Heaviside function.
It follows from Equation (7) that the current is due to quasiparticles with the energies so that and , , while the DOS is constant at . Thus, the LFL theory defines as a constant. This constant is obviously an even, symmetric function of the bias voltage V, i.e., . In fact, the symmetry of holds under the LFL condition of C and T symmetries conservation. This means that is symmetric function for two ordinary metals contact. Please note that in more involved evaluation of and entering Equation (5), they acquire energy dependence for so that one should insert them into the integrand of Equation (7) [32,33,34]. This has been done, for instance, in Equation (5) [34] for scanning tunneling microscope tip interacting with a magnetic adatom. This does not break the C symmetry in the LFL case. The situation becomes drastically different if HF metal is placed under the conditions, generating flat bands [13,14]. In this case, the C symmetry is also broken [1,11], the system has fermion condensate so that the DOS in the integrand of Equation (7) strengthens the tunneling spectra asymmetry as the above DOS depends strongly on , see Figure 2. This results in a strong asymmetry of relatively to . Consequently, at so that at (or ), the DOS can be expanded in power series as . It is obvious that is determined primarily by rather than , for is related to a constant value of DOS, as it is typical for the LFL theory. In this case, , where is the effective mass. At low temperatures it is given by [1,6]
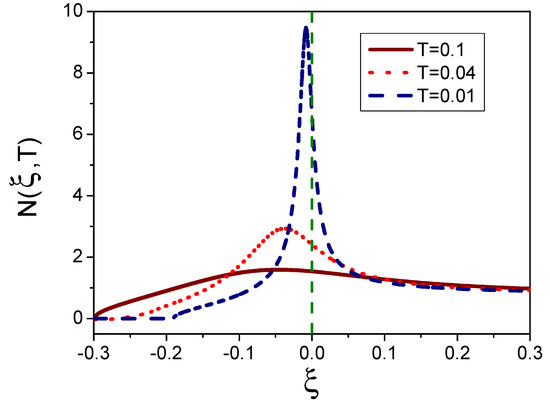
Figure 2.
Function () for three values of T (normalized to ) shown in the legend [1,6].
The quasiparticles with the spectrum and occupation number are well described by the expression (8) at , where is some threshold temperature. Latter quantity determines the situation, when all “FC traces” disappear [1]. In this case, the following inequality fulfills
In superconducting phase, does not depend on T if . Here is the temperature of phase transition, which is characterized by disappearance of superconducting gap or pseudogap. The expression for effective mass then reads [1,6]
where is the maximal superconducting gap at zero temperature.
It is noted that C symmetry break causes the T symmetry violation. Figure 1 illustrates the resulting low-temperature spectrum as well as portrays the function . It also shows that the presence of the flat band violates T symmetry. The broken C symmetry results in the difference in areas where holes (h in Figure 1) and particles (p in Figure 1) are “residing” [1]. Please note that in superconducting phase the system exhibits the asymmetrical tunneling conductivity near FCQPT and beyond the FCQPT point. This is because in this case particle-hole symmetry is still violated. Figure 3 demonstrates that this is consistent with experimental data [1,6].
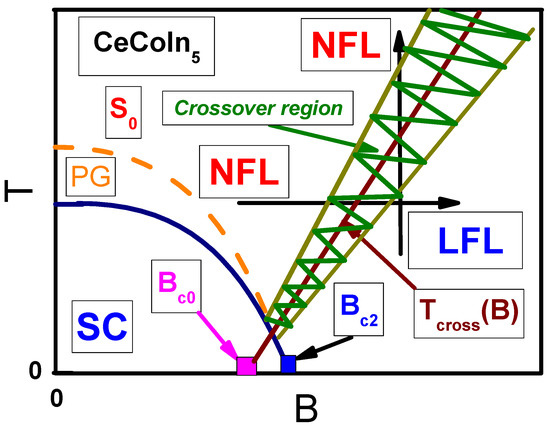
Figure 3.
Schematic phase diagram of HF compounds like the archetypical . Black arrows traversing the transition region, explain the LFL-NFL (at fixed magnetic field B, vertical) and opposite transition (at fixed temperature, horizontal) respectively. Blue solid curve demarcates the superconducting (SC) state at . Here and are, respectively, the critical field for SC state and the QCP, hidden inside SC part of the phase diagram. Flat band exists for magnetic fields . Label “PG” between yellow dashed and blue solid curves denotes the pseudogap state. The FL and NFL parts of the phase diagram are divided by shaded area (marked “Crossover region”) with the solid line inside it. A part of the line is situated inside the SC part. marks the entropy surplus, responsible for appearance.
Figure 3 shows the schematic phase diagram for . The main point is that a magnetic field induces QCP. This field, in turn, lies deep inside the superconducting part of the phase diagram [35]. It is clearly seen from Figure 3 that [36,37] so that ordinary Fermi liquid properties exist at until the superconducting phase begins to appear. Latter phase destroys normal state entropy surplus [1].
In magnetic field, the entropy leads to the transformation of the type II superconducting phase transition into the type I. The reason is that at low temperatures the entropy of SC state becomes , which is discontinuous as it should be for first order transitions [1,38]. This observation agrees with experimental results [39,40]. It not only relates to the asymmetrical conductivity but explains the entropy excess in the Universe, see Section 6. Thus, we see that the most fundamental features of the nature are defined by its topological and symmetry properties. In Figure 3, the crossover region along with line , divides the phase diagram into NFL and LFL parts, i.e., divides the diagram into two parts with different topology. Therefore, at low temperatures, these parts are separated by the first order phase transition, for the topological charge cannot change continuously [1,14,19].
4. Asymmetric Conductivity Near the Topological FCQPT
The tunneling current I between ordinary and HF metals is given by Equation (7) with one of the distribution functions of ordinary metal substituted with
Clearly, from Equations (8) and (12) that becomes finite, since particle-hole C symmetry is violated. As a result, we arrive at the equation for when the system in its normal state [1,6,7]
We recall that the factor , see Figure 1.
Tunnel conductivity remains asymmetric as a high- superconductor or a HF metal passes into the superconducting state from the normal state. The reason is that the function and the related again determine the differential conductivity. It is well-known that it is the Landau interaction, which defines the occupation number . It then becomes clear, that any weaker interaction (like pairing one) would not distort substantially. This has been shown in Refs. [1,6,7]. This implies, in turn, that at , the conductivity stays almost intact. Figure 4 shows that this theoretical result is in fairly good coincidence with experiments. Note that the effective mass has the form (10) if the metal with FC becomes superconducting. This actually determines the asymmetrical part of its conductivity.
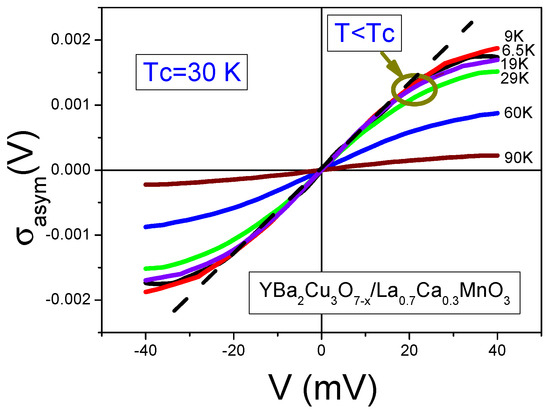
Figure 4.
Temperature dependence of the asymmetric part extracted from measurements on bilayers of the differential conductivity at different temperatures shown in the figure [41]. The dashed line shows the linear dependence of on the variable V over a wide range, see Equation (15).
Also, in superconducting case, the density of states alters, being zero inside the gap , i.e., at . This fact should be accounted for in calculations of tunneling conductance. The expression for above altered DOS reads
Here, is the superconducting gap at and E is the quasiparticle energy in the superconducting state, related to the normal state quasiparticle energy as . It follows from Equation (14) that the tunneling conductance can be asymmetric function of the bias voltage V, provided that the density of states is asymmetric with respect to the Fermi level [4] as is in the case of Fermi systems with FC, see Figure 2. As we have mentioned above, , with the coefficient does not contributing to the asymmetric conductance. Consequently, the expression for the system in its superconducting state becomes
Here, c is a constant of the order of unity. The scale entering Equation (13) is replaced by the scale in Equation (15), therefore, in that case the asymmetrical part does not depend on T when the system in its superconducting or pseudogap states. This observation is in good agreement with experimental facts, see Section 5. Similarly, as Equation (13) is valid up to , Equation (15) is valid up to [1,6,7].
5. Asymmetric Conductivity in Heavy-Fermion Metals and High Superconductors
The asymmetric conductivity can be observed when both HTSC and HF metals are shifted from their normal to superconducting phase, since and are responsible for the asymmetric part of their measured differential conductivity. As we have mentioned above, since pairing interaction (leading to superconductivity) is substantially weaker then initial Landau one, both occupation number and the density of states are almost the same as those in the normal phase [6,7,11,16]. This implies that below the conductance still remains asymmetric, which coincides with experimental data in Figure 4.
To illustrate the strength of Equations (13) and (15), we consider the temperature dependence of the asymmetric part of point contact spectra on bilayers with K [41]. The data showing that remains constant up to temperatures of and persists up to temperatures well above , see Figure 4 [1,6,7]. It is also seen from Figure 4 that starts to diminish at . These observations are in excellent agreement with the behavior described by Equations (13) and (15), and are strong evidence, supporting the FC theory [1,11,12,13,14].
In order to find out if the electron density is nonuniform in , the spectroscopic measurements have been undertaken in Ref. [42]. These measurements were augmented by tunneling microscopy at low temperatures. The manifestation of the above non-uniformity is local DOS and superconducting gap spatial fluctuations. They can serve as a consistence check for Equation (15). The inhomogeneity observed in the integrated DOS is not induced by impurities but is inherent property of the system. This is supported by observations relating the value of the integrated local DOS to the concentration x of local oxygen impurities. Spatial variations in the differential tunnel conductivity spectrum are shown in Figure 5a. Clearly, the differential tunnel conductivity is highly asymmetric in the superconducting state of . The differential tunnel conductivity shown in Figure 5a may be interpreted as measured at different values of but at the same temperature, which allows studying the dependence on . Figure 5b shows the asymmetric conductivity obtained from the data in Figure 5a. Indeed, for small values of V, is a linear function of voltage consistent with Equation (15) and the slopes of the respective straight lines of are inversely proportional to the gap size .
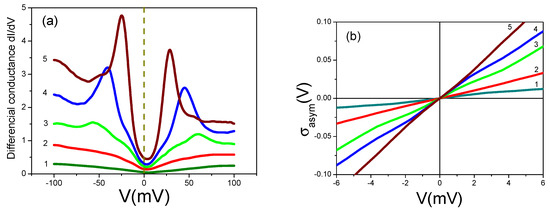
Figure 5.
Spatial variation of the spectra of the differential tunnel conductivity obtained in measurements on . (a) Lines 1 and 2 belong to regions in which the integrated local DOS is very low. Low differential conductivity and the absence of the gap are vivid features that we are dealing with a bad metal. Line 3 indicates the large gap (65 meV) with mildly pronounced peaks. The integrated value of the local DOS for curve 3 is rather small, but is larger than that for lines 1 and 2. Line 4 depicts the gap of about 40 meV, which is close to the average value of the gap. Line 5 corresponds to the maximum integrated local DOS, and depicts the smallest gap of about 25 meV, and has two well pronounced coherent peaks [42]. (b) The asymmetric part of the differential tunnel conductivity in the high- superconductor , extracted from the data exposed in Figure 5a, as a function of the voltage V (mV). The lines are numbered in accordance with the numbers of the curves in Figure 5a. Evidently, is a linear function of V, while the slope of is inversely proportional to the gap size , see Equation (15).
Both the point contact spectroscopy and the tunneling conductivity have recently been used to investigate the archetypical HF metal in its superconducting, pseudogap (PG) and normal states [16,43]. The asymmetric part shown in Figure 6a (the point contact spectroscopy [16]) and (b) (the tunneling conductivity [43]), have been extracted from experimental data collected on [16,43], and has been observed in both in its superconducting, PG and the NFL normal states. It is seen from Figure 6a that takes place in the NFL normal states at 10 K, while in the PG state at 2.6 K coincides with that of the SC states with K. As seen from Figure 6b, has similar traits. The lower the temperature (down to PG state), the more asymmetric is a conductivity. After that, the asymmetry stays almost constant down to K, thus supporting the validity of the main results presented in Section 4. As a result, we conclude that the physics of the PG state is given by the presence of the FC state, while the PG state is directly related to the SC one.
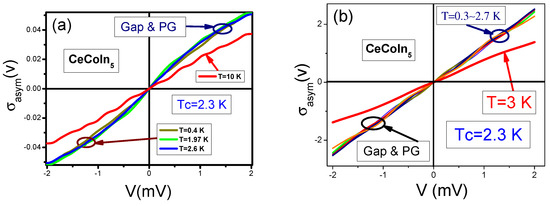
Figure 6.
The asymmetric part in . Panel (a). The asymmetric part is extracted from the experimental data [16]. It is seen that at K in both its PG state and the SC state, becomes temperature independent; K is the superconducting phase transition temperature. Panel (b). The asymmetric part is extracted from the experimental data [43]. Again, at K in its PG and SC states, and the asymmetrical part becomes temperature independent, see Equation (15). At K diminishes, as it follows from Equation (13).
At sufficiently low temperatures and under the application of magnetic field B, the LFL behavior and the C and T symmetries are restored, which makes the asymmetric part of the tunneling conductivity vanish [1,3,6,7,11]. To observe the finite asymmetry of the conductivity, the measurements must be carried out when HF metals under the consideration demonstrate the NFL behavior characterized by the particle-hole asymmetry. Latter asymmetry is the typical feature of HF metals located near the topological FCQPT. Thus, we conclude that the emergence of is the typical feature of the NFL behavior. It is seen from the schematic phase diagram of Figure 3 that under the application of magnetic field B the HF metal transits from its NFL to LFL behavior so that the asymmetric part vanishes. As has been predicted within the framework of the FC theory, is finite in the archetypical HF metal , and it disappears, provided that the metal is shifted to the LFL state by magnetic field, as it is depicted by the arrows in Figure 3 [3,6,7]. For the first time, this suppression of the asymmetrical part was observed in the HF metal (for ) in high magnetic fields of 20 T [1,44]. The asymmetric conductivity is observed in the archetypical HF metal , and attributed to the influence of Fano resonances [26]. On the other hand, the suppression of the asymmetrical part have been observed in [27], as reported in Figure 7. In that case magnetic field B is applied parallel to the magnetically hard c axis and the suppression takes place at T. We note that such a suppression can hardly be related to the elimination of the Fano resonances in magnetic fields. As a result, we can safely assume that that the asymmetry is induced by the topological FCQPT, rather than by Fano resonances. Along this way, we predict that the suppression of in can be observed at low magnetic fields T, provided that B is applied parallel to the easy magnetic axis and at K.
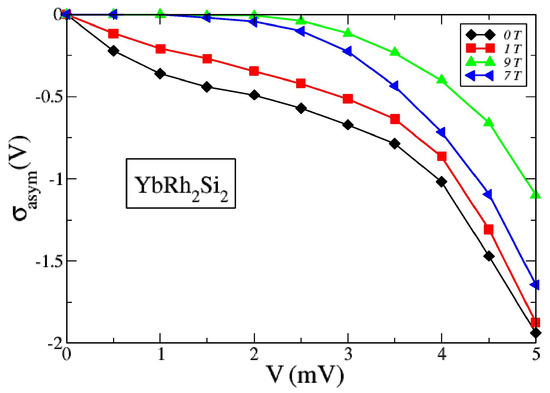
Figure 7.
The asymmetric part at different applied magnetic fields, shown in the legend. Asymmetrical part is extracted from the experimental data [27]. At T vanishes at , for at these magnetic fields the system exhibits the LFL behavior, as seen from the phase diagram in Figure 3.
The differential resistance as a function of the current I can be a hallmark of the NFL behavior and the violation of C and T symmetries, since the symmetry properties of are similar to those of . They are described by Equations (13) and (15). These observations are in accordance with experimental facts. Indeed, the differential resistance , as a function of bias current I at two different magnetic fields B measured on graphene [18], is reported in Figure 8. The asymmetric part of the differential resistance diminishes at elevated magnetic field, and vanishes at mT, as seen from Figure 8 and Figure 9. This observation is of great importance, for graphene has a perfect flat band generated by the topological FCQPT that violates the C particle-hole symmetry [18]. Notably, it has been suggested that the band flattening leads to the time-reversal symmetry breaking [12,17,24].
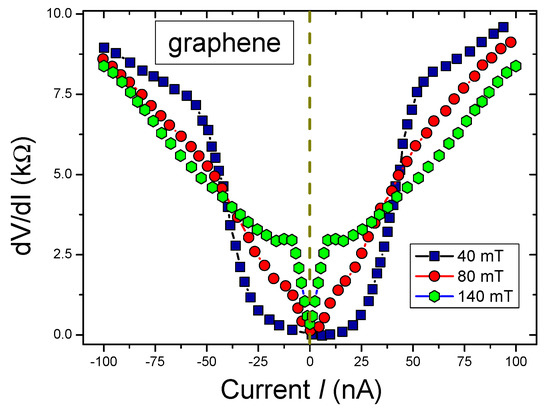
Figure 8.
Differential resistance in kiloohms vs bias current I at several magnetic fields (legend) [18]. The asymmetry in differential resistance is most pronounced at small fields mT.
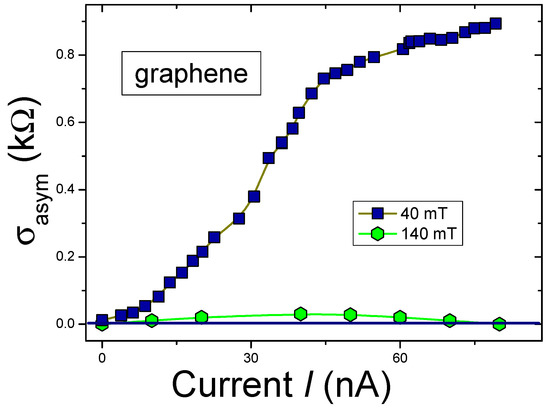
Figure 9.
The asymmetric part of the differential resistance is extracted from experimental data, obtained in measurements on graphene [18] and provided in Figure 8.
Clearly seen from Figure 9, that under the application of tiny magnetic field mT the asymmetric part of the differential resistance vanishes, since evidently the system transits to the LFL state, as seen from Figure 3. In that case we expect the resistivity to change from to under the application of magnetic fields inducing the LFL behavior. Simultaneously, the residual resistivity abruptly drops, as observed in measurements on the archetypical HF metal [35,45].
6. Violation of T and C Symmetries in the Universe
The interconnection of physics is comprised by the complicated and fundamental relations among its different branches, for instance between solid state physics and astrophysics. Latter relations, being of core importance, give an example of the intimate connection between very large and very small. As discussed in the Introduction, the demonstrated above particle-hole C symmetry violation in solids has its large-scale counterpart in the asymmetry between matter and antimatter in the early Universe. This is because the weak interaction cannot alter the baryon number that preserves the stability of a proton [46]. In this case, the FCQPT concept delivers the underlying physical mechanism for both aforementioned processes. This implies that the FC phenomenon spans from the atomic scale to that of the Universe and hence is rather general and not seldom in the nature. Since the details of matter-antimatter (baryon) asymmetry is discussed in details in [11,46,47,48,49], here we make some general remarks regarding this question.
It is well-known (see, e.g., [47,48,49]) that the relation between particles and antiparticles in the Universe is governed by so-called (or more generally ) symmetry, which is the result of successive action of charge conjugation (C), transforming a particle into antiparticle (electron into hole and vice versa in solids) and parity (P), which reverses the directions of spatial coordinates. The time inversion symmetry, T, changes t to . The overall symmetry thus transforms particles into antiparticles. The common wisdom is that during and shortly after the Big Bang, the number of particles in the Universe was approximately equal to that of antiparticles. Later on, as the temperature falls, this equality vanished, giving rise to the current, highly asymmetric state. Please note that in solids electrons and holes are so-called quasiparticles (roughly speaking, quantized elementary excitations of some ground state or vacuum); in cosmology the particles (antiparticles) correspond to baryons (antibaryons), which are the real elementary particles, with nonzero rest mass, for instance quarks and antiquarks [49].
The mapping of “very small” (quasiparticles in solids) onto “very large” (baryons in the Universe) can be best understood using a spontaneous symmetry-breaking concept. Like in solids, where the symmetries is often broken in different phase transitions (for instance in quantum phase transitions as temperature is reduced to zero or almost zero), it is believed that the Universe, during cooling down, went through a series of symmetry-breaking quantum phase transitions. One of them is the above discussed FCQPT. Under the supposition that hole in a Fermi liquid is a baryon, while the quasiparticle is an antibaryon, we can easily see the correspondence between particle-hole (in a solid) and baryon-antibaryon (in the Universe) symmetries. As already discussed, the conductivity in ordinary metals is a symmetric function of the bias voltage V, which is predicted by the LFL theory and which, in turn, is a consequence of particle-hole symmetry, “built in” in Landau’s approach to Fermi liquids. As already seen above, the latter symmetry is disrupted in solids, demonstrating NFL properties, which is the case for HF compounds and high- superconductors.
Indeed, experimental observations of low-temperature differential tunneling conductivity in high- superconductors [10] and HF metals like and [44] show that it is obviously asymmetric. Under the influence of external stimuli (like T and B), the latter asymmetry disappears. As LFL theory has many intrinsic symmetries (like particle-hole), which finally yield the symmetric conductivity, it cannot be used to explain the asymmetry, see Section 3. In this case, to describe the observed asymmetric conductivity theoretically, one should inevitably use the FC approach [46]. We note that although fundamental microscopic interaction in the FC formalism is invariant with respect to quasiparticles and holes interchange, it yields spontaneous C and T symmetries breaking at low temperatures due to the topological reconstruction of the Fermi surface [1,3,6,7,8,13,14]. This reconstruction yields the dependence of the quasiparticle spectrum in FC phase on different external stimuli [11,12], which, in turn, generate NFL anomalies in observable properties of HF metals and high- superconductors. Experiment shows that in the latter strongly correlated fermion systems, becomes strongly temperature and magnetic field dependent. Thus, is no more step function, varying gradually from 1 to 0 in the low temperature limit [1,13]. As FCQPT in solids is accompanied by the so-called flat bands formation (so that a fermion, sitting in such band, cannot propagate and hence condenses), the approach of Ref. [46] is based on this observation, valid, for instance, in HF compounds. This quantum phase transition, in turn, breaks the particle-hole symmetry, generating, inter alia, the observable asymmetric conductivity.
Similar argumentation can be utilized to gain insights into baryon-antibaryon asymmetry in the Universe. Note that it fits perfectly into the existing cosmological models. It has been proposed in Ref. [46] that the Universe was completely symmetric in its initial state. The baryon-antibaryon asymmetry has been explained in terms of macroscopic FCQPT which looks like almost the same to that in HF metals but in much larger scale. In the parameter space, the Universe gets to the FCQPT point after the initial inflation during the strong (by 10 orders of magnitude) cooling. As the result of FCQPT, the fermion condensate appeared in the Universe. Latter condensate is indeed a source of excess of matter over the antimatter. At further cooling, the Universe acquired the NFL properties, generated by the above fermion condensate. Our analysis shows, that latter condensate may be the maker of C and T symmetries break, thus distorting the particle-antiparticle balance in the Universe and the time arrow emergence. At finite temperatures baryon-antibaryon asymmetry reenters as an inherent property of the system located in the FC state. Latter property stems from Fermi surface deformation properties. Namely, it is due to the topological transformation of the Fermi sphere accompanied by deviation of the distribution function from the step function at low temperatures, as shown in Figure 1 and described in Section 3. As the temperature decreases, the system approaches the FC state with the corresponding flat band which increases the asymmetry violation [12,46]. The details rely upon the specific form of interparticle interaction. This mapping of the quasiparticles in solids to the baryons gives some hint on the origin of symmetries in the Universe as salient features of condensed matter can readily be verified experimentally as well as computed numerically and sometimes analytically.
Another interesting result, coming as a bonus of our Universe-non-Fermi Liquid analogy, is the high entropy of the Universe related to the term , see Equations (11) and (13). Latter correspondence micro (condensed matter) and macro (cosmology) physics should be further studied. This is because while in condensed matter, almost every property is accessible experimentally, in cosmology we cannot judge about its underlying physics directly. Rather, indirect methods should be used in this case. One of such indirect methods is correspondence between stellar objects and their condensed matter counterparts. As properties of the ground state (corresponding to a vacuum in the Universe that can be represented by both the dark energy and the dark matter) in solids are well understood both from ab initio calculations and experiment, the above correspondence allows us to shed light on those in cosmology and particle physics like the existence of the time arrow, the large entropy and the absence of the antimatter in the Universe.
7. Conclusions
Fundamental symmetries is a powerful method to gain information about physical system spanning from atoms in solids to the galaxies and their clusters in the Universe. Knowledge of such symmetries and conditions for their violation permit us to gain a general knowledge about physical systems without solving any equations, which are often very complicated. Quite frequently, the microscopic approach to condensed matter (e.g., computer simulations) gives only particular information about specific solids (or class of solids with identical symmetries of their crystal lattice, but still with different microscopic interatomic interactions) but not about universal features, inherent in wider class of physical systems.
Here we discuss two phenomena which are seemingly very far from each other: the asymmetric conductivity in solids with strongly correlated fermions and baryon asymmetry in the Universe. We have already shown that the asymmetric part of the tunneling conductivity/resistivity in solids arises due to the fermion condensation phenomenon in the corresponding substance. This shows that the low-temperature properties of strongly correlated fermion systems are universal, and this universality allows us to consider these strongly correlated systems, or HF compounds, as representing the new state of matter in the sense that this state do not depend on either atomic properties of HF compounds or on microscopic details of baryons in the Universe [12]. This is one of the major messages of the present short review. In addition, the universality, in turn, is due to the fact, that the considered fermion condensation phenomenon occurs due to the change of the topological class of the corresponding Fermi surface. This immediately implies the universality of both the above asymmetries as topology is one more milestone of contemporary physics—the topological class of an object can reveal a lot about its physical properties [1,11,12,13,14,19,50]. We argue here, that existing microscopic approaches,-based either on model calculations within Hubbard and Kondo models or simulations (constructed actually from more sophisticated versions of the latter models) cannot describe adequately the appearance and destruction of asymmetric conductivity in solids. We speculate that the presented FC theory, which is based on general topological and symmetry arguments, can be well considered to be a candidate to explain not only the above discussed but many other properties of seemingly different physical objects from a uniform point of view [1,11,12,13,14,19,50,51,52]. To the best of our knowledge, the effective theories of gravity, even their quantum versions, cannot explain the baryon asymmetry, the existence of time arrow, the large entropy and other yet unexplained problems of contemporary cosmology and large-scale astronomy.
Author Contributions
Designed the project and directed it, V.R.S., A.Z.M., V.A.S. and G.S.J.;Wrote the manuscript, V.R.S., A.Z.M. and V.A.S.; All authors commented on it. The manuscript reflects the contributions of all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank V. A. Khodel for stimulating discussions. This work was partly supported by U.S. DOE, Division of Chemical Sciences, Office of Basic Energy Sciences, Office of Energy Research.
Conflicts of Interest
The authors declare no competing interests.
References
- Shaginyan, V.R.; Amusia, M.Y.; Msezane, A.Z.; Popov, K.G. Scaling behavior of heavy fermion metals. Phys. Rep. 2010, 492, 31. [Google Scholar] [CrossRef]
- Andreev, A.F. The thermal conductivity of the intermediate state in superconductors. Sov. Phys. JETP 1964, 19, 1228. [Google Scholar]
- Shaginyan, V.R. Dissymmetrical tunneling in heavy-fermion metals. JETP Lett. 2005, 81, 222. [Google Scholar] [CrossRef][Green Version]
- Anderson, P.W.; Ong, N.P. Theory of asymmetric tunneling in the cuprate superconductors. J. Phys. Chem. Solids 2006, 67, 1. [Google Scholar] [CrossRef]
- Randeria, M.; Sensarma, R.; Trivedi, N.; Zhang, F. Particle-Hole Asymmetry in Doped Mott Insulators: Implications for Tunneling and Photoemission Spectroscopies. Phys. Rev. Lett. 2005, 95, 137001. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Popov, K.G. Asymmetric tunneling, Andreev reflection and dynamic conductance spectra in strongly correlated metals. Phys. Lett. A 2007, 361, 406. [Google Scholar] [CrossRef][Green Version]
- Shaginyan, V.R.; Popov, K.G.; Stephanovich, V.A.; Kirichenko, E.V. Asymmetrical tunneling in heavy fermion metals as a possible probe for their non-Fermi liquid peculiarities. J. Alloy. Compd. 2007, 442, 29. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Stephanovich, V.A.; Japaridze, G.S.; Kirichenko, E. Flat bands and strongly correlated Fermi systems. Phys. Scr. 2019, 94, 065801. [Google Scholar] [CrossRef]
- Stephanovicha, V.A.; Shaginyan, V.R.; Kirichenko, E.V. Experimental Manifestations of Fermion Condensation in Strongly Correlated Fermi Systems. Acta Phys. Pol. A 2019, 135, 1204. [Google Scholar] [CrossRef]
- Deutscher, G. Andreev Saint-James reflections: A probe of cuprate superconductors. Rev. Mod. Phys. 2005, 77, 109. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Popov, K.G.; Shaginyan, V.R.; Stephanovich, V.A. Theory of Heavy-Fermion Compounds; Springer Series in Solid-State Sciences; Springer: Heidelberg, Germany, 2015; Volume 182. [Google Scholar]
- Amusia, M.Y.; Shaginyan, V.R. Strongly Correlated Fermi Systems: A New State of Matter; Springer Tracts in Modern Physics; Springer International Publishing: Heidelberg, Germany, 2020; Volume 283. [Google Scholar]
- Khodel, V.A.; Shaginyan, V.R. Superfluidity in system with fermion condensate. JETP Lett. 1990, 51, 553. [Google Scholar]
- Volovik, G.E. A new class of normal Fermi liquids. JETP Lett. 1991, 53, 222. [Google Scholar]
- Khodel, V.A.; Shaginyan, V.R.; Khodel, V.V. New approach in the microscopic Fermi systems theory. Phys. Rep. 1994, 249, 1. [Google Scholar]
- Park, W.K.; Greene, L.H.; Sarrao, J.L.; Thompson, J.D. Andreev reflection at the normal-metal/heavy-fermion superconductor CeCoIn5 interface. Phys. Rev. B 2005, 72, 052509. [Google Scholar]
- Shaginyan, V.R.; Msezane, A.Z.; Japaridze, G.S.; Stephanovich, V.A.; Leevik, Y.S. Asymmetric Tunneling Conductance and the Non-Fermi Liquid Behavior of Strongly Correlated Fermi Systems. JETP Lett. 2018, 108, 335. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef]
- Volovik, G.E. Graphite, Graphene, and the Flat Band Superconductivity. JETP Lett. 2018, 107, 516. [Google Scholar] [CrossRef]
- Arnold, F.; Nyéki, J.; Saunders, J. Superconducting Sweet-Spot in Microcrystalline Graphite Revealed by Point-Contact Spectroscopy. JETP Lett. 2018, 107, 577. [Google Scholar] [CrossRef]
- Xu, C.; Balents, L. Topological Superconductivity in Twisted Multilayer Graphene. Phys. Rev. Lett. 2018, 121, 087001. [Google Scholar] [CrossRef]
- Peltonen, T.J.; Ojajärvi, R.; Heikkilä, T.T. Mean-field theory for superconductivity in twisted bilayer graphene. Phys. Rev. B 2018, 98, 220504. [Google Scholar] [CrossRef]
- Lian, B.; Wang, Z.; Bernevig, B.A. Twisted Bilayer Graphene: A Phonon-Driven Superconductor. Phys. Rev. Lett. 2019, 122, 257002. [Google Scholar] [CrossRef] [PubMed]
- Roy, B.; Juricic, V. Unconventional superconductivity in nearly flat bands in twisted bilayer graphene. Phys. Rev. B 2019, 99, 121407(R). [Google Scholar] [CrossRef]
- Peri, V.; Song, Z.; Bernevig, B.A.; Huber, S.D. Fragile topology and flat-band superconductivity in the strong-coupling regime. arXiv 2020, arXiv:2008.02288. [Google Scholar]
- Ernst, S.; Kirchner, S.; Krellner, C.; Geibel, C.; Zwicknagl, G.; Steglich, F.; Wirth, S. Emerging local Kondo screening and spatial coherence in the heavy-fermion metal YbRh2Si2. Nature 2011, 474, 362. [Google Scholar] [CrossRef] [PubMed]
- Seiro, S.; Jiao, L.; Kirchner, S.; Hartmann, S.; Friedemann, S.; Krellner, C.; Geibel, C.; Si, Q.; Steglich, F.; Wirth, S. Evolution of the Kondo lattice and non-Fermi liquid excitations in a heavy-fermion metal. Nat. Commun. 2018, 9, 3324. [Google Scholar] [CrossRef]
- Coleman, P. Lectures on the Physics of Highly Correlated Electron Systems VI; Mancini, F., Ed.; American Institute of Physics: New York, NY, USA, 2002; pp. 79–160. [Google Scholar]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Part 1; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Harrison, W.A. Tunneling from an Independent-Particle Point of View. Phys. Rev. 1961, 123, 85. [Google Scholar] [CrossRef]
- Bardeen, J. Tunnelling from a Many-Particle Point of View. Phys. Rev. Lett. 1961, 6, 57. [Google Scholar] [CrossRef]
- Giaever, I. Energy Gap in Superconductors Measured by Electron Tunneling. Phys. Rev. Lett. 1960, 5, 147. [Google Scholar] [CrossRef]
- Nicol, J.; Shapiro, S.; Smith, P.H. Direct Measurement of the Superconducting Energy Gap. Phys. Rev. Lett. 1960, 5, 461. [Google Scholar] [CrossRef]
- Schiller, A.; Hershfield, S. Theory of scanning tunneling spectroscopy of a magnetic adatom on a metallic surface. Phys. Rev. B 2000, 61, 9036. [Google Scholar] [CrossRef]
- Paglione, J.; Tanatar, M.A.; Hawthorn, D.G.; Boaknin, E.; Hill, R.W.; Ronning, F.; Sutherland, M.; Taillefer, L.; Petrovic, C.; Canfield, P.C. Field-Induced Quantum Critical Point in CeCoIn5. Phys. Rev. Lett. 2003, 91, 246405. [Google Scholar] [CrossRef]
- Ronning, F.; Capan, C.; Bianchi, A.; Movshovich, R.; Lacerda, A.; Hundley, M.F.; Thompson, J.D.; Pagliuso, P.G.; Sarrao, J.L. Field-tuned quantum critical point in CeCoIn5 near the superconducting upper critical field. Phys. Rev. B 2005, 71, 104528. [Google Scholar] [CrossRef]
- Ronning, F.; Capan, C.; Bauer, E.D.; Thompson, J.D.; Sarrao, J.L.; Movshovich, R. Pressure study of quantum criticality in CeCoIn5. Phys. Rev. B 2006, 73, 064519. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Stephanovich, V.A.; Kirichenko, E.V. Quasiparticles and quantum phase transition in universal low-temperature properties of heavy-fermion metals. Europhys. Lett. 2006, 76, 898. [Google Scholar] [CrossRef]
- Izawa, K.; Yamaguchi, H.; Matsuda, Y.; Shishido, H.; Settai, R.; Onuki, Y. Angular Position of Nodes in the Superconducting Gap of Quasi-2D Heavy-Fermion Superconductor CeCoIn5. Phys. Rev. Lett. 2001, 87, 057002. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, A.; Movshovich, R.; Oeschler, N.; Gegenwart, P.; Steglich, F.; Thompson, J.D.; Pagliuso, P.G.; Sarrao, J.L. First-Order Superconducting Phase Transition in CeCoIn5. Phys. Rev. Lett. 2002, 89, 137002. [Google Scholar] [CrossRef] [PubMed]
- Piano, S.; Bobba, F.; Santis, A.D.; Giubileo, F.; Scarfato, A.; Cucolo, A.M. Point Contact Spectra on YBa2Cu3O7−x/La0.7Ca0.3MnO3 bilayers. J. Phys. Conf. Ser. 2006, 43, 1123. [Google Scholar] [CrossRef]
- Pan, S.H.; O’Neal, J.P.; Badzey, R.L.; Chamon, C.; Ding, H.; Engelbrecht, J.R.; Wang, Z.; Eisaki, H.; Uchida, S.; Gupta, A.K.; et al. Microscopic electronic inhomogeneity in the high-Tc superconductor Bi2Sr2CaCu2O8+x. Nature 2001, 413, 282. [Google Scholar] [CrossRef]
- Wirth, S.; Prots, Y.; Wedel, M.; Ernst, S.; Kirchner, S.; Fisk, Z.; Thompson, J.D.; Steglich, F.; Grin, Y. Structural Investigations of CeIrIn5 and CeCoIn5 on Macroscopic and Atomic Length Scales. J. Phys. Soc. Jpn. 2014, 83, 061009. [Google Scholar] [CrossRef]
- Pristàš, G.; Reiffers, M.; Bauer, E.; Jansen, A.G.M.; Maude, D.K. Suppression of asymmetric differential resistance in the non-Fermi-liquid system YbCu5−xAlx(x = 1.3–1.75) in high magnetic fields. Phys. Rev. B 2008, 78, 235108. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Popov, K.G.; Clark, J.W.; Zverev, M.V.; Khodel, V.A. Magnetic field dependence of the residual resistivity of the heavy-fermion metal CeCoIn5. Phys. Rev. B 2012, 86, 085147. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Japaridze, G.S.; Amusia, M.Y.; Msezane, A.Z.; Popov, K.G. Baryon asymmetry resulting from a quantum phase transition in the early universe. Europhys. Lett. 2011, 94, 69001. [Google Scholar] [CrossRef][Green Version]
- Sozzi, M. Discrete Symmetries and CP Violation: From Experiment to Theory; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Branco, G.C.; Lavoura, L.; Silva, J.P. CP Violation; Clarendon Press: Oxford, UK, 1999. [Google Scholar]
- Griffiths, D. J Introduction to Elementary Particles; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Shaginyan, V.R.; Amusia, M.Y.; Msezane, A.Z.; Stephanovich, V.A.; Japaridze, G.S.; Artamonov, S.A. Fermion Condensation, T-Linear Resistivity, and Planckian Limit. JETP Lett. 2019, 110, 290. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Amusia, M.Y.; Clark, J.W.; Japaridze, G.S.; Stephanovich, V.A.; Leevik, Y.S. Thermodynamic, Dynamic, and Transport Properties of Quantum Spin Liquid in Herbertsmithite from an Experimental and Theoretical Point of View. Condens. Matter 2019, 4, 75. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Stephanovich, V.A.; Msezane, A.Z.; Japaridze, G.S.; Clark, J.W.; Amusia, M.Y.; Kirichenko, E.V. Theoretical and experimental developments in quantum spin liquid in geometrically frustrated magnets: A review. J. Mater. Sci. 2020, 55, 2257. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).