Interval Intuitionistic Fuzzy Clustering Algorithm Based on Symmetric Information Entropy

Abstract

Based on the continuous optimal aggregation operator, a novel distance measure is proposed to deal with interval intuitionistic fuzzy clustering problems. The optimal ordered weighted intuitionistic fuzzy quasi-averaging (OOWIFQ) operator and the continuous OOWIFQ operator are presented to aggregate all the values in an interval intuitionistic fuzzy number. Some of their desirable properties are also studied. The OOWIFQ operator can describe the fuzzy state of things more realistically and present the fuzzy properties more accurately. The opinions of experts are very important, the OOWIFQ operators take expert preferences into account to reduce systematic errors. Considering the hesitation of things and avoiding distortion of information, we put forward the distance measure for interval intuitionistic fuzzy numbers by using symmetric information entropy. Based on the continuous OOWIFQ operator and proposed distance measure, a new interval intuitionistic fuzzy clustering (IIFC) algorithm is proposed. The application in soil clustering shows the validity and practicability of the IIFC algorithm.

1. Introduction

Clustering is an unsupervised classification and an important way for people to understand society and nature. In recent decades, clustering has attracted extensive attention and played an important role in many fields, such as pattern recognition [1,2,3,4,5], image segmentation [6,7,8,9,10], data mining [11,12,13], etc. The traditional clustering algorithm can be divided into classification clustering method [14,15], hierarchical clustering method [16,17], density clustering method [18,19,20], grid clustering method [21,22,23,24], and model clustering method [25,26]. Traditional clustering algorithms assume that any data vector belongs to only one class. This approach can naturally cluster compact and well separated data sets. However, clusters often overlap, and some data vector parts belong to more than one cluster.

In the real world, the boundaries between many objective things are often vague. It is bound to be accompanied by ambiguity when categorizing things, which leads to fuzzy clustering analysis. Ruspini [27] put forward the concept of fuzzy partition. Many scholars proposed a variety of clustering methods, such as the method based on similarity relation [28] and fuzzy relation [29,30], the transitive closure method based on fuzzy equivalence relation [31,32], the maximum tree method based on fuzzy graph theory [33] and dynamic programming [34].

In recent years, considering the degree of hesitation between things, the research of intuitionistic fuzzy sets and interval intuitionistic fuzzy sets have become a hot topic. The facts show that intuitionistic fuzzy sets and interval intuitionistic fuzzy sets can describe and portray the ambiguous nature of the objective world more delicately. However, most of the interval intuitionistic fuzzy clustering algorithms only consider a certain value in the interval, which makes the information missing and distorted. In addition, in the clustering algorithm the preference of decision maker is not taken into account, which may easily cause the result to be inconsistent with the expected result. From the current literatures, there are a few researches on the interval intuitionistic fuzzy set clustering algorithm, and their research have important practical significance. The proposed distance measure considers all the information in the continuous interval. The distortion and loss of information are avoided. Aiming at the shortcomings of existing algorithms and combining with the distance measure based on symmetric information entropy, an interval intuitionistic fuzzy clustering algorithm with preference is proposed. The algorithm considers not only the preference of the decision maker, but also all the values of the interval. The algorithm is applied to the soil clustering to provide guidance for scientific fertilization.

The rest of this paper is organized as follows. Section 2 introduces some basic knowledge of intuitionistic fuzzy sets and relevant aggregation operators. In Section 3, a continuous optimal aggregation operator based on Chi-squared deviation is proposed. In Section 4, the new distance measure based on symmetric information entropy is proposed. The intuitionistic fuzzy clustering (IIFC) algorithm and its application are analyzed in Section 5 and Section 6, respectively. This work is concluded in the last section.

2. Preliminaries

2.1. Some Basic Concepts of Intuitionistic Fuzzy Set

Intuitionistic fuzzy set theory was developed from fuzzy set theory by Atanassov [35]. Intuitionistic fuzzy set considers membership, non-membership, and hesitation of input data. Therefore, in practical applications, intuitionistic fuzzy set has greater power to represent fuzzy and uncertain information than fuzzy set. In the following, we will briefly review some basic concepts of intuitionistic fuzzy set and introduce the distance measure of intuitionistic fuzzy sets.

Definition 1.

Let $X$ be a fixed set. A fuzzy set $\tilde{\alpha }$ is defined as [35]:

$$\tilde{\alpha }=\left\{⟨x,u_{\alpha }(x),v_{\alpha }(x)⟩\right|x\in X\}$$

(1)

where the functions $u_{\alpha }(x):X\to [0,1]$ and $v_{\alpha }(x):X\to [0,1]$ indicate the degree of membership and degree of non-membership respectively. For any $x\in X$, $0\le {\mu }_{\alpha }(x)+{\nu }_{\alpha }(x)\le 1$.

The third parameter of the intuitionistic fuzzy set $\tilde{\alpha }$ is ${\pi }_{\alpha }(x)$, called the hesitancy degree of intuitionistic fuzzy set $\alpha$, where ${\pi }_{\alpha }(x)=1-u_{\alpha }(x)-v_{\alpha }(x)$. Evidently, we can obtain $0\le {\pi }_{\alpha }(x)\le 1$. When ${\pi }_{\alpha }(x)=0$, we have ${\mu }_{\alpha }(x)+{\nu }_{\alpha }(x)=1$, the intuitionistic fuzzy set becomes the traditional fuzzy set. For convenience, $\tilde{\alpha }=(u_{\alpha },v_{\alpha })$ is called an intuitionistic fuzzy number, where $u_{\alpha }\in [0,1],v_{\alpha }\in [0,1]$ and $u_{\alpha }+v_{\alpha }\le 1.$

Definition 2.

Let $X$ be a finite set. An interval intuitionistic fuzzy set $\tilde{A}$ on $X$ is expressed as [36]:

$$\tilde{A}=\left\{⟨x,[u_A^{-}(x),u_A^{+}(x)],[v_A^{-}(x),v_A^{+}(x)]⟩\right|x\in X\}$$

(2)

where $u_A^{-}(x)\ge 0$ and $v_A^{-}(x)\ge 0$. For any $x\in X$ on $A$ satisfies the following condition: $u_A^{+}(x)+v_A^{+}(x)\le 1$. For convenience, $([u_A^{-},u_A^{+}],[v_A^{-},v_A^{+}])$ is called an interval intuitionistic fuzzy number, where $u_A^{-},v_A^{-}\ge 0$ and $u_A^{+}+v_A^{+}\le 1$.

Definition 3.

For any interval intuitionistic fuzzy numbers $\tilde{a}=([u_A^{-},u_A^{+}],[v_A^{-},v_A^{+}])$ and $\tilde{b}=([u_B^{-},u_B^{+}],[v_B^{-},v_B^{+}])$, the relationship between $\tilde{a}$ and $\tilde{b}$ is defined as follows [36]:

(a) 

If $u_A^{-}\le u_B^{-}$, $u_A^{+}\le u_B^{+}$, $v_A^{-}\ge v_B^{-}$ and $v_A^{+}\ge v_B^{+}$, then $\tilde{a}\le \tilde{b}$.

(b) 

If $u_A^{-}=u_B^{-}$, $u_A^{+}=u_B^{+}$, $v_A^{-}=v_B^{-}$ and $v_A^{+}=v_B^{+}$, then $\tilde{a}=\tilde{b}$.

2.2. Continuous Aggregation Operators

On a continuous interval, Yager [37] proposed a continuous ordered weighted average operator (C-OWA) based on the OWA operator as follows:

Definition 4.

A C-OWA operator is a mapping $F:\mathsf{\Gamma }\to R^{+}$ associated with a basic unit-interval monotonic function Q, such that

$$F_Q[a,b]={\displaystyle {\int }_0^1[b-x(b-a)]dQ(x)}$$

(3)

where $\mathsf{\Gamma }$ is the set of all positive interval numbers, and $R^{+}$ is the positive real number set. $Q$ is the basic unit-interval monotonic (BUM) function, and satisfies $Q(0)=0$, $Q(1)=1$ and $Q(x)\le Q(y)$ for any $x\le y$, $x,y\in [0,1]$.

Based on the idea of geometric mean, Yager and Xu [38] proposed the continuous ordered weighted geometric (C-OWG) operator:

Definition 5.

A C-OWG operator is a mapping $G:\mathsf{\Gamma }\to R^{+}$ associated with a BUM function $Q$, satisfying

$$G_Q([a,b])=b\cdot {(\frac{a}{b})}^{{\displaystyle {\int }_0^1(d\frac{Q(x)}{dx}xdx)}}$$

(4)

In 2008, Chen [39] et al. proposed the following continuous ordered weighted harmonic (C-OWH) operators based on the harmonic mean and the C-OWA operator:

Definition 6.

A C-OWH operator is a mapping $H:\mathsf{\Gamma }\to R^{+}$ associated with a BUM function $Q$, such that

$$H_Q([a,b])={({\displaystyle {\int }_0^1\frac{dQ(x)}{dx}[\frac{1}{b}+x(\frac{1}{a}-\frac{1}{b})]dx})}^{-1}$$

(5)

In addition, on the continuous interval number, Liu et al. [40] proposed the continuous quasi-ordered weighted averaging (C-QOWA) operators.

Definition 7.

A C-QOWA operator is a mapping $L:\mathsf{\Gamma }\to R^{+}$ associated with the BUM function $Q$, such that

$$L_Q([a,b])=f^{-1}\left\{{\displaystyle {\int }_0^1\frac{dQ(x)}{dx}[f(b)-x(f(b)-f(a))]dx}\right\}$$

(6)

where $f$ is a continuous strictly monotonic function on $[a,b]$.

3. Continuous OOWIFQ Operator for Aggregating Interval Intuitionistic Fuzzy Numbers Based on Chi-Squared Deviation

Let ${\tilde{\alpha }}_1=(u_1,v_1)$, ${\tilde{\alpha }}_2=(u_2,v_2)$, $\cdots$, ${\tilde{\alpha }}_n=(u_n,v_n)$ be $n$ intuitionistic fuzzy numbers. If the result of aggregation is $(u,v)$ and $W=(w_1,w_2\cdots ,w_n)$ is a weight vector, the total deviation between $u$ and $u_1,u_2,\cdots ,u_n$ should be as small as possible, and the total deviation between $v$ and ${\nu }_1,{\nu }_2,\cdots ,{\nu }_n$ should also be small. Therefore, the optimization model is constructed as follows:

$$\begin{array}{ll}& \min J_1,\min J_2\\ s.t& \{\begin{array}{l}{J}_1={\displaystyle \sum _{i=1}^n{\mathrm{w}}_i\frac{{(\frac{f(u_i)}{f(u)}-1)}^2}{\frac{f(u_i)}{f(u)}}}\\ J_2={\displaystyle \sum _{i=1}^n{\mathrm{w}}_i\frac{{(\frac{f(v_i)}{f(v)}-1)}^2}{\frac{f(v_i)}{f(v)}}}\end{array}\end{array}$$

(7)

where $f$ is strictly monotonic function.

From the perspective of fairness principle, assuming that decision-makers have no additional preference for the above model, the following optimization model is constructed:

$$\min J=\lambda J_1+(1-\lambda )J_2={\displaystyle \sum _{i=1}^n{\mathrm{w}}_i(\lambda (\frac{f(u_i)}{f(u)}+\frac{f(u)}{f(u_i)})+(1-\lambda )(\frac{f(v_i)}{f(v)}+\frac{f(v)}{f(v_i)})-2)}$$

(8)

Take the partial derivatives of $J$ with respect to $u$ and $v$, respectively, and we have

$$\frac{\partial J}{\partial u}=\lambda {\displaystyle \sum _{i=1}^n{w}_i(-\frac{f(u_i)}{f^2(u)}{f}^{\prime }(u)+\frac{f^{\prime }(u)}{f(u_i)})}$$

$$\frac{\partial J}{\partial v}=(1-\lambda ){\displaystyle \sum _{i=1}^n{w}_i(-\frac{f(v_i)}{f^2(v)}{f}^{\prime }(v)+\frac{f^{\prime }(v)}{f(v_i)})}$$

Since $f$ is strictly monotonic function, let $\frac{\partial J}{\partial u}=0$ and $\frac{\partial J}{\partial v}=0$, we have

$$u=f^{-1}({(\frac{{\displaystyle \sum _{i=1}^n{w}_{i}f(u_i)}}{{\displaystyle \sum _{i=1}^n\frac{w_i}{f(u_i)}}})}^{\frac{1}{2}})$$

(9)

$$v=f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m{w}_{i}f(v_i)}}{{\displaystyle \sum _{i=1}^m\frac{w_i}{f(v_i)}}})}^{\frac{1}{2}})$$

(10)

Based on the ordered weighted average operator, sorting $u$ and $v$ in descending order, the optimal ordered weighted intuitionistic fuzzy quasi-averaging (OOWIFQ) operator based on the Chi-squared deviation is derived as follows:

Definition 8.

Let ${\tilde{\alpha }}_i=(u_i,v_i)$ be an intuitionistic fuzzy number and $\widetilde{\mathsf{{\rm X}}}$ be a set of all intuitionistic fuzzy numbers. An OOWIFQ operator is a mapping $\mathrm{OOWIFQ}:{\widetilde{\mathsf{{\rm X}}}}^n\to \widetilde{\mathsf{{\rm X}}}$, defined by an associated weighting vector $w=(w_1,w_2,\cdots ,w_n)$, such that

$$\mathrm{OOWIFQ}({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\cdots ,{\tilde{\alpha }}_n)=(f^{-1}({(\frac{{\displaystyle \sum _{i=1}^n{w}_{i}f(u_{{\sigma }_i})}}{{\displaystyle \sum _{i=1}^n\frac{w_i}{f(u_{{\sigma }_i})}}})}^{\frac{1}{2}}),f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m{w}_{i}f(v_{{\epsilon }_i})}}{{\displaystyle \sum _{i=1}^m\frac{w_i}{f(v_{{\epsilon }_i})}}})}^{\frac{1}{2}}))$$

(11)

where $u_{{\sigma }_i}\ge u_{{\sigma }_{i+1}}$, $v_{{\epsilon }_i}\ge v_{{\epsilon }_{i+1}}$ is true for any $i=1,2,\cdots ,n$.

In real life, data tends to be continuous, but not discrete. Intuitionistic fuzzy number considers a value in a continuous interval, which may lose some important information and make the clustering result deviated. To overcome this shortcoming, information fusion is needed for all values on the continuous interval. Therefore, we propose a continuous OOWIFQ (C-OOWIFQ) operator based on OOWIFQ operator.

Definition 9.

Let $\tilde{\beta }=([u^{-},u^{+}],[v^{-},v^{+}])$ be an interval intuitionistic fuzzy number. A C-OOWIFQ operator is a mapping $C:\tilde{I}\to \widetilde{{\rm X}}$ associated with a BUM function $Q$, satisfying

$$\begin{array}{l}C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])\\ =(f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}}),\\ f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}}))\end{array}$$

(12)

where $\tilde{I}$ be a set of all interval intuitionistic fuzzy numbers.

Next, we will introduce the specific derivation process of Equation (13):

Let $\delta =\frac{f(u^{+})-f(u^{-})}{n}$, $\eta =\frac{f(v^{+})-f(v^{-})}{m}$, $u_j=f^{-1}(f(u^{+})-j\cdot \delta )$ and $v_i=f^{-1}(f(v^{-})+i\cdot \eta ),$ for all $i=1,2,\cdots ,m$, $j=1,2,\cdots ,n$.

(a).

When $f$ is strictly monotonic increasing, then $\delta \ge 0$, $\eta \ge 0$ holds. As a result, we have

$$f(u^{+})-j\cdot \delta \le f(u^{+})-(j-1)\cdot \delta ,f(v^{-})+(i-1)\cdot \eta \le f(v^{-})-i\cdot \eta .$$

Since $f^{-1}$ is also strictly monotonic increasing, we get

$$u_j=f^{-1}(f(u^{+})-j\cdot \delta )\le f^{-1}(f(u^{+})-(j-1)\cdot \delta )=u_{j-1}$$

(13)

$$v_{i-1}=f^{-1}(f(v^{-})+(i-1)\cdot \eta )\le f^{-1}(f(v^{-1})+i\cdot \eta )=v_i$$

(14)

(b).

On the contrary, when $f$ is strictly monotonic decreasing, then $\delta \le 0$, $\eta \le 0$ holds. It follows that

$$f(u^{+})-j\cdot \delta \le f(u^{+})-(j-1)\cdot \delta ,f(v^{-})+(i-1)\cdot \eta \le f(v^{-})-i\cdot \eta .$$

which can be further expressed as

$$u_j=f^{-1}(f(u^{+})-j\cdot \delta )\le f^{-1}(f(u^{+})-(j-1)\cdot \delta )=u_{j-1}$$

(15)

$$v_{i-1}=f^{-1}(f(v^{-})+(i-1)\cdot \eta )\le f^{-1}(f(v^{-1})+i\cdot \eta )=v_i$$

(16)

According to Equation (11), the approximation of $C_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])$ can be derived as follows:

$$\begin{array}{cc}\hfill C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])& \approx (f^{-1}({(\frac{{\displaystyle \sum _{j=1}^n{w}_{j}f(u_{{\sigma }_{(j)}})}}{{\displaystyle \sum _{j=1}^n\frac{w_j}{f(u_{{\sigma }_{(j)}})}}})}^{\frac{1}{2}})),f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m{w}_{j}f(v_{{\epsilon }_i})}}{{\displaystyle \sum _{i=1}^m\frac{w_i}{f(v_{{\epsilon }_i})}}})}^{\frac{1}{2}})\hfill \\ & =(f^{-1}({(\frac{{\displaystyle \sum _{j=1}^n{w}_{j}f(u_j)}}{{\displaystyle \sum _{j=1}^n\frac{w_j}{f(u_j)}}})}^{\frac{1}{2}})),f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m{w}_{i}f(v_i)}}{{\displaystyle \sum _{i=1}^m\frac{w_i}{f(v_i)}}})}^{\frac{1}{2}}))\hfill \end{array}$$

(17)

where $w_j$ and $w_i$ are the associated weights of the ordered weighted average operator. Using the BUM function, we can get the associated weights $w_j$ and $w_i$ as [41]

$$w_j=Q(\frac{j}{n})-Q(\frac{j-1}{n}),j=1,2,\cdots ,n.$$

(18)

$$w_i=Q(\frac{i}{m})-Q(\frac{i-1}{m}),i=1,2,\cdots ,m.$$

(19)

where ${\displaystyle \sum _{j=1}^n{w}_j=}1$ and ${\displaystyle \sum _{i=1}^m{w}_i=}1$. Accordingly, we can write $C{O}_{f,Q}$ as

$$\begin{array}{ll}\hfill C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])\approx & (f^{-1}({(\frac{{\displaystyle \sum _{j=1}^n(Q(\frac{j}{n})-Q(\frac{j-1}{n}))f(u_j)}}{{\displaystyle \sum _{j=1}^n\frac{(Q(\frac{j}{n})-Q(\frac{j-1}{n}))}{f(u_j)}}})}^{\frac{1}{2}}),\hfill \\ & f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m(Q(\frac{i}{m})-Q(\frac{i-1}{m}))f(v_i)}}{{\displaystyle \sum _{i=1}^m\frac{(Q(\frac{i}{m})-Q(\frac{i-1}{m}))}{f(v_i)}}})}^{\frac{1}{2}}))\hfill \end{array}$$

Let $\mathsf{\Delta }u=\frac{1}{n}$, $\mathsf{\Delta }v=\frac{1}{m}$, and we have

$$\begin{array}{l}C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])\\ \approx (f^{-1}({(\frac{{\displaystyle \sum _{j=1}^n(Q(j\cdot \mathsf{\Delta }u)-Q(j\cdot \mathsf{\Delta }u-\mathsf{\Delta }u))(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot j\cdot \mathsf{\Delta }u)}}{{\displaystyle \sum _{j=1}^n\frac{Q(j\cdot \mathsf{\Delta }u)-Q(j\cdot \mathsf{\Delta }u-\mathsf{\Delta }u)}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot j\cdot \mathsf{\Delta }u}}})}^{\frac{1}{2}}),\\ f^{-1}({(\frac{{\displaystyle \sum _{i=1}^m(Q(i\cdot \mathsf{\Delta }v)-Q(i\cdot \mathsf{\Delta }v-\mathsf{\Delta }v))(f(v^{+})+(f(v^{+})-f(v^{-}))\cdot i\cdot \mathsf{\Delta }v)}}{{\displaystyle \sum _{i=1}^m\frac{Q(i\cdot \mathsf{\Delta }v)-Q(i\cdot \mathsf{\Delta }v-\mathsf{\Delta }v)}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot i\cdot \mathsf{\Delta }v}}})}^{\frac{1}{2}}))\end{array}$$

Finally, let $n\to \infty ,m\to \infty$, denoted as $u=j\cdot \mathsf{\Delta }u$, $v=i\cdot \mathsf{\Delta }v$. For all $i=1,2,\cdots m$, $j=1,2,\cdots n$, we can get $u\in [0,1],v\in [0,1]$ and

$$\begin{array}{l}C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])\\ =(f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}}),\\ f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}}))\end{array}$$

(20)

Denoting $\tilde{u}=[u^{-},u^{+}]$ and $\tilde{v}=[v^{-},v^{+}]$, for convenience, we abbreviate Equation (21) as:

$$C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])=({\underset{\_}{C}}_{f,Q}(\tilde{u}),{\overline{C}}_{f,Q}(\tilde{v}))$$

(21)

The C-OOWIFQ operator has the following properties, which are proved as follows:

Property 1.

For all strictly monotonic continuous function $f$ and BUM function $Q$, $(u^{-},v^{+})\le C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])\le (u^{+},v^{-})$ holds.

Proof. 

Let us consider different cases of function $f$:

(a)

If $f$ is strictly monotonic increasing, then $f(u^{-})\le f(u^{+})$. Thus, for all $u\in [0,1]$, we have $f(u^{-})\le f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u\le f(u^{+})$. It follows that

$$f(u^{-}){\displaystyle {\int }_0^1\frac{dQ(u)}{du}}du\le {\displaystyle {\int }_0^1\frac{dQ(u)}{du}}(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)du\le f(u^{+}){\displaystyle {\int }_0^1\frac{dQ(u)}{du}}du$$

and

$$\frac{1}{f(u^{+})}{\displaystyle {\int }_0^1\frac{dQ(u)}{du}du}\le {\displaystyle {\int }_0^1\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u}}du\le \frac{1}{f(u^{-})}{\displaystyle {\int }_0^1\frac{dQ(u)}{du}}du.$$

By considering

$${\displaystyle {\int }_0^1\frac{dQ(u)}{du}du}=Q(1)-Q(0)=1,$$

the above two inequalities can be further writhen as

$$f(u^{-})\le {\displaystyle {\int }_0^1\frac{dQ(u)}{du}}(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)du\le f(u^{+})$$

and

$$\frac{1}{f(u^{+})}\le {\displaystyle {\int }_0^1\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u}}du\le \frac{1}{f(u^{-})}.$$

Accordingly, we have

$${(f(u^{-}))}^2\le \frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du}\le {(f(u^{+}))}^2.$$

Since $f^{-1}$ is also strictly monotonic increasing, it holds that

$$u^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\le u^{+}.$$

Similarly, for any $v\in [0,1]$, it can be proved that

$$v^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\le v^{+}.$$

(b)

If $f$ is strictly monotonic decreasing, then $f(u^{-})\ge f(u^{+})$. Thus, for all $u\in [0,1]$, we have $f(u^{+})\le f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u\le f(u^{-})$. Similarly, we have

$$f(u^{+})\le {\displaystyle {\int }_0^1\frac{dQ(u)}{du}}(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)du\le f(u^{-})$$

and

$$\frac{1}{f(u^{-})}\le {\displaystyle {\int }_0^1\frac{\frac{dQ(u)}{du}}{f(u^{+})-[f(u^{+})-f(u^{-})]\cdot u}}du\le \frac{1}{f(u^{+})}.$$

Because $f^{-1}$ is strictly monotonic decreasing, so

$$u^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\le u^{+}.$$

Similarly, for any $v\in [0,1]$, we have

$$v^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\le v^{+}.$$

Therefore, the Property 1 is proved. □

Property 2.

For any BUM function $Q$, if $u_1^{-}\le u_2^{-}$, $u_1^{+}\le u_2^{+}$ and $v_1^{-}\ge v_2^{-}$, $v_1^{+}\ge v_2^{+}$, then $C{O}_{f,Q}([u_1^{-},u_1^{+}],[v_1^{-},v_1^{+}])\le C{O}_{f,Q}([u_2^{-},u_2^{+}],[v_2^{-},v_2^{+}])$.

Proof. 

(a)

When $f$ function is strictly monotonic increasing, for any $u\in [0,1]$, we have

$$f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u\le f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u.$$

It follows that

$$\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u})\cdot du}\le \frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_2^{+})-(f(u_2^{+})-f(u_2^{-})0\cdot u})\cdot du}$$

Since $f^{-1}$ is also strictly monotonic increasing, so there is

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\\ \le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\end{array}$$

By similar proof processes, we can obtain

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v_1^{+})+(f(v_1^{+})-f(v_1^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v_1^{+})+(f(v_1^{+})-f(v_1^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\\ \le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v_2^{+})+(f(v_2^{+})-f(v_2^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v_2^{+})+(f(v_2^{+})-f(v_2^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\end{array}$$

(b)

When $f$ function is strictly monotonic decreasing, for any $u\in [0,1]$, we have

$$f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u\ge f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u.$$

Obviously, it holds that

$$\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u})\cdot du}\ge \frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u})\cdot du}$$

Because $f^{-1}$ is also strictly monotonic decreasing, we get

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_1^{+})-(f(u_1^{+})-f(u_1^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\\ \ge f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u_2^{+})-(f(u_2^{+})-f(u_2^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\end{array}$$

By similar proof process, we can also get

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v_1^{+})+(f(v_1^{+})-f(v_1^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v_1^{+})+(f(v_1^{+})-f(v_1^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\\ \ge f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v_2^{+})+(f(v_2^{+})-f(v_2^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v_2^{+})+(f(v_2^{+})-f(v_2^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\end{array}$$

From the above analysis, we have $C{O}_{f,Q}([u_1^{-},u_1^{+}],[v_1^{-},v_1^{+}])\le C{O}_{f,Q}([u_2^{-},u_2^{+}],[v_2^{-},v_2^{+}])$. Thus, the property is proved. □

Property 3.

For all BUM function $Q$, if $u^{-}=u^{+}=a$, $v^{-}=v^{+}=b$, then $C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])=(a,b)$.

Proof. 

Since $u^{-}=u^{+}=a$, $v^{-}=v^{+}=b$ and ${\displaystyle {\int }_0^1\frac{dQ(u)}{du}du}=1$, ${\displaystyle {\int }_0^1\frac{dQ(v)}{dv}dv}=1$ (for all $u,v\in [0,1]$), we can get

$$\begin{array}{l}\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{dx}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot x)}dx}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot x})\cdot dx}\\ =\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{dx}\cdot f(a)}dx}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(a)})\cdot dx}=\frac{f(a)\cdot {\displaystyle {\int }_0^1\frac{dQ(u)}{dx}}dx}{\frac{1}{f(a)}{\displaystyle {\int }_0^1(}\frac{dQ(u)}{du})\cdot dx}={(f(a))}^2\end{array},$$

In very similar way, we can also get

$$\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv}={(f(b))}^2.$$

So, we have $C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])=(f^{-1}{({(f(a))}^2)}^{\frac{1}{2}},f^{-1}{({(f(b))}^2)}^{\frac{1}{2}})=(a,b)$. □

Property 4.

If $Q_1(u)\le Q_2(u)$, $Q_1(v)\le Q_2(v)$ for all $u,v\in [0,1]$, then $C{O}_{f,Q_1}([u^{-},u^{+}],[v^{-},v^{+}])\le C{O}_{f,Q_2}([u^{-},u^{+}],[v^{-},v^{+}])$.

Proof. 

For all BUM function $Q$, we have:

$$\begin{array}{l}{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du\\ ={\displaystyle {\int }_0^1(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}dQ(u)\\ =(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)\cdot Q(u){|}_0^1+(f(u^{+})-f(u^{-}))\cdot {\displaystyle {\int }_0^{1}Q(u)du}\\ =f(u^{-})+(f(u^{+})-f(u^{-}))\cdot {\displaystyle {\int }_0^{1}Q(u)du}\end{array}.$$

In a similar process, the following equation can be obtained

$$\begin{array}{l}{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv\\ =f(v^{+})-(f(v^{+})-f(v^{-}))\cdot {\displaystyle {\int }_0^{1}Q(v)dv}\end{array}.$$

Moreover, we have

$$\begin{array}{l}{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du\\ ={\displaystyle {\int }_0^1(\frac{1}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u}})\cdot dQ(u)\\ =\frac{Q(u)}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u}{|}_0^1-{\displaystyle {\int }_0^1(\frac{f(u^{+})-f(u^{-})}{{(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}^2}})Q(u)du\\ =\frac{1}{f(u^{-})}-{\displaystyle {\int }_0^1(\frac{f(u^{+})-f(u^{-})}{{(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}^2}})Q(u)du\end{array}$$

and

$$\begin{array}{l}{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv\\ =\frac{1}{f(v^{+})}+{\displaystyle {\int }_0^1(\frac{f(v^{+})-f(v^{-})}{{(f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}^2}})Q(v)dv\end{array}.$$

(a)

when $f$ function is strictly monotonic increasing, then $f(u^{-})\le f(u^{+})$.

Since $Q_1(u)\le Q_2(u)$ for all $u\in [0,1]$, we have ${\displaystyle {\int }_0^1{Q}_1(u)}du\le {\displaystyle {\int }_0^1{Q}_2(u)}du$. It holds that

$$f(u^{-})+(f(u^{+})-f(u^{-}))\cdot {\displaystyle {\int }_0^1{Q}_1(u)}du\le f(u^{-})+(f(u^{+})-f(u^{-}))\cdot {\displaystyle {\int }_0^1{Q}_2(u)}du.$$

Therefore, we have

$$\begin{array}{l}\frac{1}{f(u^{-})}-{\displaystyle {\int }_0^1(\frac{f(u^{+})-f(u^{-})}{{(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}^2}})Q_1(u)du\\ \ge \frac{1}{f(u^{-})}-{\displaystyle {\int }_0^1(\frac{f(u^{+})-f(u^{-})}{{(f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}^2}})Q_2(u)du\end{array},$$

which can be written as

$${\displaystyle {\int }_0^1\frac{d{Q}_1(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du\le {\displaystyle {\int }_0^1\frac{d{Q}_2(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du$$

and

$${\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du\ge {\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du.$$

Because $f^{-1}$ is strictly monotonic increasing, so we have

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_1(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\\ \le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_2(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\end{array}.$$

In a similar process, we get

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_1(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\\ \ge f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_2(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\end{array}.$$

Thus, we have $C{O}_{f,Q_1}([u^{-},u^{+}],[v^{-},v^{+}])\le C{O}_{f,Q_2}([u^{-},u^{+}],[v^{-},v^{+}])$.

(b)

when $f$ function is strictly monotonic decreasing, then $f(u^{-})\ge f(u^{+})$. Since $Q_1(x)-Q_2(u)\le 0$, we have

$${\displaystyle {\int }_0^1\frac{d{Q}_1(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du\ge {\displaystyle {\int }_0^1\frac{d{Q}_2(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du,$$

$${\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du\le {\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du.$$

Because $f^{-1}$ is also strictly monotonic decreasing, we get

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_1(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\\ \le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_2(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\end{array}.$$

Similarly, we have

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_1(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_1(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\\ \ge f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{d{Q}_2(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{d{Q}_2(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\end{array}.$$

Therefore, we have $C{O}_{f,Q_1}([u^{-},u^{+}],[v^{-},v^{+}])\le C{O}_{f,Q_2}([u^{-},u^{+}],[v^{-},v^{+}])$.

In summary, Property 4 is proved. □

Through the above proof, the C-OOWIFQ operator has some desirable properties such as boundedness, monotonicity, identity and monotonicity about the function Q. The C-OOWIFQ operator can aggregate all points in a closed interval, and can also take into account the preferences of experts, so that the clustering of things by the C-OOWIFQ operator can be analyzed more comprehensively and effectively. The proposed IIFC algorithm improves the reliability of analysis results.

Theorem 1.

Let $([u^{-},u^{+}],[v^{-},v^{+}])$ be an interval intuitionistic fuzzy number. For any strictly monotonic function $f$ and BUM function $Q$, $C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])$ is an intuitionistic fuzzy number.

Proof. 

It is easy to know that $u^{-},v^{-}\ge 0$, $u^{+}+v^{+}\le 1$, by Property 1 we have

$$0\le u^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\le u^{+},$$

$$0\le v^{-}\le f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\le v^{+}.$$

It follows that

$$\begin{array}{l}{f}^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(u)}{du}\cdot (f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u)}du}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(u)}{du}}{f(u^{+})-(f(u^{+})-f(u^{-}))\cdot u})\cdot du})}^{\frac{1}{2}})\\ +f^{-1}({(\frac{{\displaystyle {\int }_0^1\frac{dQ(v)}{dv}\cdot (f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v)}dv}{{\displaystyle {\int }_0^1(}\frac{\frac{dQ(v)}{dv}}{f(v^{-})+(f(v^{+})-f(v^{-}))\cdot v})\cdot dv})}^{\frac{1}{2}})\le u^{+}+v^{+}\le 1\end{array}$$

Therefore, $C{O}_{f,Q}([u^{-},u^{+}],[v^{-},v^{+}])$ is an intuitionistic fuzzy number. □

4. Distance Measure of Interval Intuitionistic Fuzzy Numbers Based on Symmetric Information Entropy

Interval intuitionistic fuzzy number describes the uncertainty under the fuzzy setting. Since entropy can effectively measure uncertainty, we propose an interval intuitionistic fuzzy distance measure based on symmetric information entropy, which can be shown as follows:

Theorem 2.

Let $\tilde{a}=([u_A{}^{-},u_A{}^{+}],[v_A{}^{-},v_A{}^{+}])$ and $\tilde{b}=([u_B{}^{-},u_B{}^{+}],[v_B{}^{-},v_B{}^{+}])$ be two interval intuitionistic fuzzy numbers, then the distance measure between $\tilde{a}$ and $\tilde{b}$ is:

$$\begin{array}{cc}\hfill d(\tilde{a},\tilde{b})=\frac{1}{2\ln 2}& (|{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B)-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B){\pi }_B|\times \hfill \\ & \ln (\frac{|{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B)-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B){\pi }_B|}{|{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B)-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B){\pi }_B|}\hfill \\ & +\frac{|{\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A-{\overline{C}}_{f,Q}({\tilde{v}}_B)-{\overline{C}}_{f,Q}({\tilde{v}}_B){\pi }_B|}{|{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B)-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B){\pi }_B|})\hfill \\ & +|{\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A-{\overline{C}}_{f,Q}({\tilde{v}}_B)-{\overline{C}}_{f,Q}({\tilde{v}}_B){\pi }_B|\times \hfill \\ & \ln (\frac{|{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B)-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_B){\pi }_B|}{|{\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A-{\overline{C}}_{f,Q}({\tilde{v}}_B)-{\overline{C}}_{f,Q}({\tilde{v}}_B){\pi }_B|}\hfill \\ & +\frac{|{\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A-{\overline{C}}_{f,Q}({\tilde{v}}_B)-{\overline{C}}_{f,Q}({\tilde{v}}_B){\pi }_B|}{|{\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A-{\overline{C}}_{f,Q}({\tilde{v}}_B)-{\overline{C}}_{f,Q}({\tilde{v}}_B){\pi }_B|}))\hfill \end{array}$$

(22)

Denoting $\mathsf{\Delta }\hat{u}=|{\hat{u}}_A-{\hat{u}}_B|$, $\mathsf{\Delta }\hat{v}=|{\hat{v}}_A-{\hat{v}}_B|$, ${\hat{u}}_A={\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)+{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A){\pi }_A$,

${\hat{v}}_A={\overline{C}}_{f,Q}({\tilde{v}}_A)+{\overline{C}}_{f,Q}({\tilde{v}}_A){\pi }_A$ and ${\pi }_A=1-{\underset{\_}{C}}_{f,Q}({\tilde{u}}_A)-{\underset{\_}{C}}_{f,Q}({\tilde{v}}_A)$, Equation (22) can be abbreviated to the following formula:

$$d(\tilde{a},\tilde{b})=\frac{1}{2\ln 2}(\mathsf{\Delta }\hat{u}\ln \frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}}+\mathsf{\Delta }\hat{v}\ln \frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{v}})$$

(23)

Theorem 3.

Let $\tilde{a}=([u_A{}^{-},u_A{}^{+}],[v_A{}^{-},v_A{}^{+}])$, $\tilde{b}=([u_B{}^{-},u_B{}^{+}],[v_B{}^{-},v_B{}^{+}])$ and $\tilde{c}=([u_C{}^{-},u_C{}^{+}],[v_C{}^{-},v_C{}^{+}])$ be three interval intuitionistic fuzzy numbers, the distance measure $d$ must satisfy the following properties:

(a) 

$0\le d(\tilde{a},\tilde{b})\le 1$.

(b) 

$d(\tilde{a},\tilde{b})=1$ if and only if interval intuitionistic fuzzy numbers $\tilde{a}$ and $\tilde{b}$ reduce to $\tilde{a}=(1,0)$ and $\tilde{b}=(0,1)$ or $\tilde{a}=(0,1)$ and $\tilde{b}=(1,0)$.

(c) 

$d(\tilde{a},\tilde{b})=d(\tilde{b},\tilde{a})$.

(d) 

$\tilde{a}\le \tilde{b}\le \tilde{c}$, then $d(\tilde{a},\tilde{b})\le d(\tilde{a},\tilde{c})$ and $d(\tilde{b},\tilde{c})\le d(\tilde{a},\tilde{c})$.

Proof. 

For the proposed distance measure, four properties (a)–(d) should be satisfied, and the proof is as follows:

The partial derivative of Equation (23) is obtained as follows:

$$\begin{array}{l}\frac{\partial d(\tilde{a},\tilde{b})}{\partial \mathsf{\Delta }\hat{u}}\\ =\frac{1}{2\ln 2}(\ln \frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}}+\mathsf{\Delta }\hat{u}\frac{\mathsf{\Delta }\hat{u}}{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}\cdot \frac{\mathsf{\Delta }\hat{u}-(\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v})}{{(\mathsf{\Delta }\hat{u})}^2}+\mathsf{\Delta }\hat{v}\frac{\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}\cdot \frac{1}{\mathsf{\Delta }\hat{v}}).\\ =\frac{1}{2\ln 2}\ln (1+\frac{\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}})>0.\end{array}$$

Similarly, we get

$$\frac{\partial d(\tilde{a},\tilde{b})}{\partial \mathsf{\Delta }\hat{v}}=\frac{1}{2\ln 2}\ln (1+\frac{\mathsf{\Delta }\hat{u}}{\mathsf{\Delta }\hat{v}})>0.$$

Thus, $d(\tilde{a},\tilde{b})$ is an increasing function of independent variables $\mathsf{\Delta }\hat{u}$ and $\mathsf{\Delta }\hat{v}$.

(a)

From Equation (23), we have

$$d(\tilde{a},\tilde{b})=\frac{1}{2\ln 2}(\mathsf{\Delta }\hat{u}\ln \frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}}+\mathsf{\Delta }\hat{v}\ln \frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{v}}).$$

$\mathsf{\Delta }\hat{u}\ge 0$, $\mathsf{\Delta }\hat{v}\ge 0$, therefore we have $\frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{u}}\ge 1$ and $\frac{\mathsf{\Delta }\hat{u}+\mathsf{\Delta }\hat{v}}{\mathsf{\Delta }\hat{v}}\ge 1$. It is clear that $d(\tilde{a},\tilde{b})\ge 0$ holds. Since $d(\tilde{a},\tilde{b})$ is an increasing function of $\mathsf{\Delta }\hat{u}$ and $\mathsf{\Delta }\hat{v}$, $d(\tilde{a},\tilde{b})$ takes the maximum of 1 when $\mathsf{\Delta }\tilde{u}=\mathsf{\Delta }\tilde{v}=1$.

(b)

the proof of this property can be analyzed by the following two cases.

(i)

$d(\tilde{a},\tilde{b})$ is an increasing function of independent various $\mathsf{\Delta }\tilde{u}$ and $\mathsf{\Delta }\tilde{v}$, therefore the maximum value $d(\tilde{a},\tilde{b})=1$ is obtained when $\mathsf{\Delta }\tilde{u}=1$ and $\mathsf{\Delta }\tilde{v}=1$. From $\mathsf{\Delta }\tilde{u}=1$ and $\mathsf{\Delta }\tilde{v}=1$, we can get that $\tilde{a}=(1,0)$ and $\tilde{b}=(0,1)$ or $\tilde{a}=(0,1)$ and $\tilde{b}=(1,0)$.

(ii)

When $\tilde{a}=(1,0)$ and $\tilde{b}=(0,1)$ or $\tilde{a}=(0,1)$ and $\tilde{b}=(1,0)$, $\mathsf{\Delta }\hat{u}=\mathsf{\Delta }\hat{v}=1$ can be brought into Equation (23) to get $d(A,B)=1$.

(c)

According to Equation (23), obviously, the symmetry of distance measure is holds.

(d)

When $\tilde{a}\le \tilde{b}\le \tilde{c}$, from Definition 3, we have $u_A^{-}\le u_B^{-}\le u_C^{-}$, $u_A^{+}\le u_B^{+}\le u_C^{+}$, $v_A^{-}\ge v_B^{-}\ge v_C^{-}$ and $v_A^{+}\ge v_B^{+}\ge v_C^{+}$. Denoting $\mathsf{\Delta }{\hat{u}}_{\tilde{a},\tilde{b}}=|{\hat{u}}_A-{\hat{u}}_B|$, $\mathsf{\Delta }{\hat{v}}_{\tilde{a},\tilde{b}}=|{\hat{v}}_A-{\hat{v}}_B|$, $\mathsf{\Delta }{\hat{u}}_{\tilde{a},\tilde{c}}=|{\hat{u}}_A-{\hat{u}}_C|$ and $\mathsf{\Delta }{\hat{v}}_{\tilde{a},\tilde{c}}=|{\hat{v}}_A-{\hat{v}}_C|$, respectively. It is clear that $\mathsf{\Delta }{\tilde{u}}_{\tilde{a},\tilde{b}}\le \mathsf{\Delta }{\tilde{u}}_{\tilde{a},\tilde{c}}$ and $\mathsf{\Delta }{\tilde{v}}_{\tilde{a},\tilde{b}}\le \mathsf{\Delta }{\tilde{v}}_{\tilde{a},\tilde{c}}$. Therefore, we get $d(\tilde{a},\tilde{b})\le d(\tilde{a},\tilde{c})$. In the same way, $d(\tilde{b},\tilde{c})\le d(\tilde{a},\tilde{c})$ also holds. □

5. Interval Intuitionistic Fuzzy Clustering Algorithm

For the multiple attribute clustering problem with interval intuitionistic fuzzy information, let $m$ object sets $G=\{G_1,G_2,\cdots ,G_m\}$ and the attribute set $H=\{H_1,H_2,\cdots ,H_n\}$. In real life, sometimes the membership degree and non-membership degree of attributes for an object cannot be accurately measured. Since multiple measurements often fluctuate in a certain interval, we solve this problem well by using interval intuitionistic fuzzy numbers. Suppose the attribute matrix be $\tilde{A}={({\tilde{a}}_{ij})}_{m\times n}$, where ${\tilde{a}}_{ij}=([u_{ij}^{-},u_{ij}^{+}],[v_{ij}^{-},v_{ij}^{+}])(i=1,2,\cdots ,m,j=1,2,\cdots ,n)$. $[u_{ij}^{-},u_{ij}^{+}]$ indicates that the object $G_i$ corresponds to the attribute $H_j$ with the degree of membership between $u_{ij}^{-}$ and $u_{ij}^{+}$ and the non-membership degree between $v_{ij}^{-}$ and $v_{ij}^{+}$.

Based on the C-OOWIFQ operator and the symmetric information entropy based distance measure, we propose an interval intuitionistic fuzzy clustering (IIFC) algorithm as follows. The flow chart of IIFC algorithm is illustrated in Figure 1.

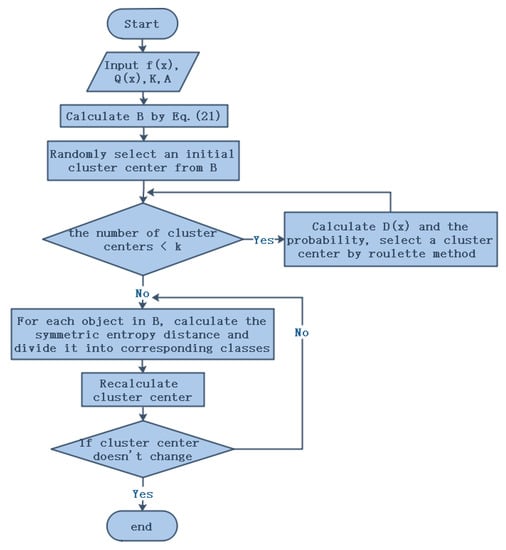
Figure 1. The flow chart of interval intuitionistic fuzzy clustering (IIFC) algorithm.

Step 1

Select an strictly monotonic function $f(x)$ and BUM function $Q(x)$, and enter the cluster number k and the sample attribute matrix $\tilde{A}={({\tilde{a}}_{ij})}_{m\times n}$, where ${\tilde{a}}_{ij}=([u_{ij}^{-},u_{ij}^{+}],[v_{ij}^{-},v_{ij}^{+}])(i=1,2,\cdots ,m,j=1,2,\cdots ,n)$.

Step 2

$b_{ij}=C{O}_{f,Q}([u_{ij}^{-},u_{ij}^{+}],[v_{ij}^{-},v_{ij}^{+}])$ is calculated by Equation (12), where $\tilde{B}={(b_{ij})}_{m\times n}$.

Step 3

Select a random sample from $\tilde{B}$ as the initial clustering center $c_1$.

Step 4

Firstly, calculate the shortest distance between each object and the existing clustering center, denoted by $D(x)$; then calculate the probability $\frac{D{(x)}^2}{{\displaystyle {\sum }_{x\in X}D{(x)}^2}}$ that each object is selected as the next cluster center. Finally, a cluster center is selected according to the roulette method.

Step 5

Repeat Step 4 until $k$ cluster centers are selected.

Step 6

For each object $x_i$ ($x_i=\{b_{i1},b_{i2},\cdots ,b_{in}\}$) in $\tilde{B}$, its symmetric entropy distance to the k cluster center is calculated by the Equation (23) and divided into the class corresponding to the cluster center with the smallest distance.

Step 7

For each category $c_i$, recalculate its cluster center $c_i=\frac{1}{\left|c_i\right|}{\displaystyle {\sum }_{x\in x_i}x}$.

Step 8

Repeat Steps 6 and 7 until the position of the cluster center does not change.

Step 9

End.

6. Numerical Example

This article focuses on the theoretical research of the algorithm. The IIFC algorithm can be applied to many fields such as data mining, image segmentation, feature extraction, and soil attribute analysis. This paper verifies the feasibility and effectiveness of the IIFC algorithm through clustering examples. The soil composition can be measured by using conventional soil agrochemical analysis method. Assume that the following experimental sample attributes are selected: total nitrogen (TN), total phosphorus (TP), organic matter (OM), available nitrogen (AN), available phosphorus (AP), and available potassium (AK). Let us suppose that fifteen soil samples are considered here, and the attribute values of these soil samples are given by using interval intuitionistic fuzzy numbers, shown in Table 1.

Table 1. The attribute values of soil sample.

No.	TN	TP	OM	AN	AP	AK
1	([0.6,0.6], [0.3,0.3])	([0.1,0.7], [0.2,0.3])	([0.1,0.5], [0.0,0.1])	([0.3,0.3], [0.1,0.4])	([0.3,0.4], [0.1,0.1])	([0.2,0.7], [0.0,0.1])
2	([0.1,0.1], [0.5,0.5])	([0.6,0.9], [0.1,0.1])	([0.1,0.1], [0.1,0.1])	([0.2,0.2], [0.1,0.2])	([0.3,0.3], [0.0,0.3])	([0.0,0.3], [0.2,0.2])
3	([0.2,0.4], [0.1,0.2])	([0.6,0.8], [0.0,0.1])	([0.0,0.7], [0.0,0.1])	([0.0,0.0], [0.1,0.1])	([0.5,0.8], [0.1,0.2])	([0.5,0.9], [0.0,0.0])
4	([0.4,0.6], [0.2,0.2])	([0.3,0.4], [0.1,0.3])	([0.5,0.6], [0.2,0.3])	([0.0,0.1], [0.1,0.1])	([0.4,0.9], [0.1,0.1])	([0.0,0.1], [0.1,0.5])
5	([0.0,0.0], [0.6,0.7])	([0.0,0.5], [0.0,0.0])	([0.0,0.1], [0.0,0.3])	([0.3,0.4], [0.1,0.2])	([0.5,0.8], [0.0,0.0])	([0.1,0.3], [0.0,0.0])
6	([0.1,0.6], [0.3,0.4])	([0.2,0.3], [0.1,0.6])	([0.0,0.8], [0.2,0.2])	([0.5,0.5], [0.3,0.5])	([0.2,0.2], [0.3,0.4])	([0.0,0.3], [0.3,0.4])
7	([0.6,0.6], [0.1,0.1])	([0.2,0.4], [0.0,0.1])	([0.1,0.2], [0.0,0.1])	([0.1,0.2], [0.2,0.3])	([0.4,0.7], [0.0,0.2])	([0.1,0.2], [0.1,0.1])
8	([0.4,0.5], [0.0,0.1])	([0.0,0.1], [0.6,0.8])	([0.1,0.9], [0.0,0.0])	([0.2,0.4], [0.3,0.6])	([0.0,0.5], [0.0,0.1])	([0.3,0.9], [0.0,0.1])
9	([0.6,0.7], [0.1,0.2])	([0.0,0.6], [0.0,0.0])	([0.3,0.8], [0.0,0.1])	([0.1,0.1], [0.3,0.6])	([0.0,0.0], [0.0,0.2])	([0.1,0.6], [0.1,0.1])
10	([0.2,0.4], [0.0,0.2])	([0.0,0.7], [0.1,0.1])	([0.2,0.2], [0.2,0.4])	([0.5,0.8], [0.0,0.1])	([0.6,0.9], [0.0,0.1])	([0.6,0.8], [0.0,0.0])
11	([0.0,0.1], [0.3,0.6])	([0.4,0.9], [0.0,0.0])	([0.1,0.1], [0.0,0.0])	([0.3,0.5], [0.1,0.5])	([0.2,0.2], [0.1,0.6])	([0.1,0.1], [0.1,0.5])
12	([0.3,0.3], [0.4,0.6])	([0.1,0.1], [0.1,0.2])	([0.5,1.0], [0.0,0.0])	([0.4,0.7], [0.1,0.1])	([0.1,0.6], [0.4,0.4])	([0.1,0.2], [0.2,0.6])
13	([0.7,0.8], [0.0,0.0])	([0.2,0.9], [0.0,0.0])	([0.1,0.5], [0.0,0.1])	([0.0,0.1], [0.5,0.8])	([0.0,0.0], [0.3,0.7])	([0.0,0.1], [0.4,0.5])
14	([0.4,0.4], [0.4,0.5])	([0.5,1.0], [0.0,0.0])	([0.7,0.8], [0.1,0.1])	([0.3,0.4], [0.1,0.6])	([0.1,0.1], [0.5,0.7])	([0.0,0.3], [0.1,0.3])
15	([0.3,0.5], [0.1,0.3])	([0.4,0.6], [0.2,0.3])	([0.2,0.6], [0.0,0.0])	([0.3,0.5], [0.1,0.2])	([0.3,0.4], [0.0,0.1])	([0.0,0.0], [0.0,0.1])

According to the steps of IIFC algorithm, the specific clustering process is analyzed as follows.

Step 1

Input the sample attribute matrix $\tilde{A}$, set $f(x)=e^x$, $Q(x)=x$, and the classification number $k=4$.

Step 2

Calculate each $b_{ij}$ with Equation (12), and the calculated result is $\tilde{B}={(b_{ij})}_{m\times n}$.

Step 3

Intuitionistic fuzzy matrix $\tilde{B}$ is calculated, shown in Table 2.

Step 4

Randomly select a sample from $\tilde{B}$ as the initial cluster center No. 1.

Step 5

Calculate the shortest distance between each object and the existing clustering center, denoted by $D(x)$; then calculate the probability that each object is selected as the next cluster center. A cluster center is selected according to the roulette method.

Step 6

Repeat Step 4 until $k$ cluster centers are selected. An initial clustering center is shown in Table 3.

Step 7

For each object $x_i$ ($x_i=\{b_{i1},b_{i2},\cdots ,b_{in}\}$) in $\tilde{B}$, the symmetric entropy distance from the $k$ cluster center is calculated by Equation (22) and divided into the class corresponding to the cluster center with the smallest distance.

Step 8

For each category $c_i$, recalculate its cluster center $c_i=\frac{1}{\left|c_i\right|}{\displaystyle {\sum }_{x\in x_i}x}$.

Table 2. Intuitionistic fuzzy matrix $\tilde{B}$.

No.	TN	TP	OM	AN	AP	AK
1	(0.60,0.30)	(0.43,0.25)	(0.31,0.05)	(0.30,0.26)	(0.35,0.10)	(0.47,0.05)
2	(0.10,0.50)	(0.76,0.10)	(0.10,0.10)	(0.20,0.15)	(0.30,0.16)	(0.16,0.20)
3	(0.30,0.15)	(0.70,0.05)	(0.39,0.05)	(0.00,0.10)	(0.66,0.15)	(0.71,0.00)
4	(0.50,0.20)	(0.35,0.20)	(0.55,0.25)	(0.05,0.10)	(0.67,0.10)	(0.05,0.31)
5	(0.00,0.65)	(0.27,0.00)	(0.05,0.16)	(0.35,0.15)	(0.66,0.00)	(0.20,0.00)
6	(0.37,0.35)	(0.25,0.37)	(0.45,0.20)	(0.50,0.40)	(0.20,0.35)	(0.16,0.35)
7	(0.60,0.10)	(0.30,0.05)	(0.15,0.05)	(0.15,0.25)	(0.56,0.10)	(0.15,0.10)
8	(0.45,0.05)	(0.05,0.70)	(0.55,0.00)	(0.30,0.46)	(0.27,0.05)	(0.63,0.05)
9	(0.65,0.15)	(0.33,0.00)	(0.57,0.05)	(0.10,0.46)	(0.00,0.10)	(0.37,0.10)
10	(0.30,0.10)	(0.39,0.10)	(0.20,0.30)	(0.66,0.05)	(0.76,0.05)	(0.70,0.00)
11	(0.05,0.46)	(0.67,0.00)	(0.10,0.00)	(0.40,0.31)	(0.20,0.37)	(0.10,0.31)
12	(0.30,0.50)	(0.10,0.15)	(0.77,0.00)	(0.56,0.10)	(0.37,0.40)	(0.15,0.41)
13	(0.75,0.00)	(0.59,0.00)	(0.31,0.05)	(0.05,0.66)	(0.00,0.51)	(0.05,0.45)
14	(0.40,0.45)	(0.77,0.00)	(0.75,0.10)	(0.35,0.37)	(0.10,0.60)	(0.16,0.20)
15	(0.40,0.20)	(0.50,0.25)	(0.41,0.00)	(0.40,0.15)	(0.35,0.05)	(0.00,0.05)

Table 3. Initial cluster center.

No.	TN	TP	OM	AN	AP	AK
1	(0.60,0.30)	(0.43,0.25)	(0.31,0.05)	(0.30,0.26)	(0.35,0.10)	(0.47,0.05)
2	(0.50,0.20)	(0.35,0.20)	(0.55,0.25)	(0.05,0.10)	(0.67,0.10)	(0.05,0.31)
3	(0.05,0.46)	(0.67,0.00)	(0.10,0.00)	(0.40,0.31)	(0.20,0.37)	(0.10,0.31)
4	(0.30,0.15)	(0.70,0.05)	(0.39,0.05)	(0.00,0.10)	(0.66,0.15)	(0.71,0.00)

After three iterations, the clustering center point no longer changes, and the final cluster center is shown in Table 4.

Table 4. The final cluster center.

No.	TN	TP	OM	AN	AK	AK
1	(0.54,0.16)	(0.32,0.25)	(0.40,0.03)	(0.25,0.31)	(0.31,0.08)	(0.32,0.07)
2	(0.54,0.18)	(0.40,0.19)	(0.44,0.17)	(0.20,0.39)	(0.29,0.32)	(0.09,0.37)
3	(0.21,0.48)	(0.57,0.06)	(0.43,0.05)	(0.38,0.23)	(0.24,0.38)	(0.14,0.28)
4	(0.20,0.30)	(0.45,0.05)	(0.21,0.17)	(0.34,0.10)	(0.69,0.07)	(0.54,0.00)

The sample soil was successfully divided into four categories: (a) very poor 2, 5, 11; (b) poor 4, 6, 12, 15; (c) fertility 1, 3, 8, 10; (d) very fertility 7, 9, 13, 14. The clustering results derived by IIFC algorithm are illustrated in Figure 2. By analyzing the soil composition of the sample, we can scientifically conduct effective fertilization guidance for the sample.

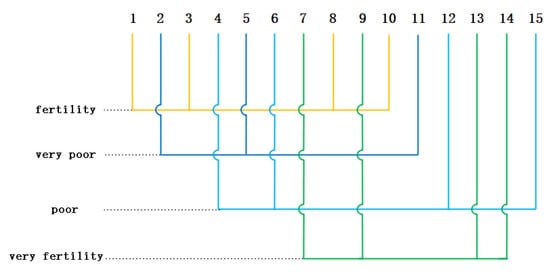
Figure 2. The clustering results derived by IIFC algorithm.

7. Conclusions

In this paper, a new continuous optimal aggregation operator based on Chi-squared deviation is proposed, which can effectively convert interval intuitionistic fuzzy number into intuitionistic fuzzy number. The distance between interval intuitionistic fuzzy numbers is calculated by constructing a new distance measure based on symmetric information entropy. The C-OOWIFQ operator and the distance measure based on symmetric information entropy are applied to deal with soil clustering. The main advantages of this paper are shown as follows:

(1)

Compared with traditional clustering and fuzzy clustering, interval intuitionistic fuzzy clustering describes the fuzzy nature of things more delicately.

(2)

The symmetric information entropy based distance measure considers all the information in the continuous interval. Thus, the distortion and loss of information are avoided, and the result is more accurate and effective.

(3)

The C-OOWIFQ takes into account the preferences of decision makers.

In addition, the IIFC algorithm can effectively solve the problem of soil clustering. In the follow-up study, we will apply the distance measure and symmetric information entropy to pattern recognition, data mining, medical diagnosis and other fields.