Abstract
In this work, we employ stochastic differential equations (SDEs) to model tree stem taper. SDE stem taper models have some theoretical advantages over the commonly employed regression-based stem taper modeling techniques, as SDE models have both simple analytic forms and a high level of accuracy. We perform fixed- and mixed-effect parameters estimation for the stem taper models by developing an approximated maximum likelihood procedure and using a data set of longitudinal measurements from 319 mountain pine trees. The symmetric Vasicek- and asymmetric Gompertz-type diffusion processes used adequately describe stem taper evolution. The proposed SDE stem taper models are compared to four regression stem taper equations and four volume equations. Overall, the best goodness-of-fit statistics are produced by the mixed-effect parameters SDEs stem taper models. All results are obtained in the Maple computer algebra system.
1. Introduction
Stem taper modeling is an attractive way to estimate tree size variables, both in forestry research and practice, due to its analytical flexibility. These types of models have been increasingly used for forest inventory and growth forecasting tools. The most difficult challenge of stem taper modeling is in modeling tree species with stems that differ from an idealized shape. This situation often leads to isolation of many tree species from stem taper modeling process.
Many types of taper modeling techniques have been proposed and applied over the years. The most traditionally used stem taper parametric equations are regression models, which are classified into segmented polynomial [1], variable exponent [2], mechanistic [3], and stochastic differential equation [4,5] methods.
In the early stages of the study of forest tree stem taper [6], a hypothesis was framed that the best-fitting form curve of the square of the diameter and the height above ground at the point of measurement is a straight-line relationship. Later, Kozak et al. [7] presented a parabolic model for which the parameters were estimated using the ordinary least squares method. Max and Burkhart [1] published segmented polynomial models to describe the evolution of squared relative diameters by relative heights. New classes of stem taper models have been derived with reference to widely accepted mechanical and biological principles [3,8]. Sloboda [4] introduced the diffusion process analogy for stem taper modeling, focused on a brief methodological discussion of the stem taper model, and theoretically demonstrated that the evolution of the stem taper can be successfully formulated as a diffusion process. Fortunately, the proposed stochastic differential equation (SDE) stem taper model has led to a very simple approximation of the stem taper dynamic and the corresponding probabilities. Petrauskas et al. [9] successful promoted the SDE stem taper model to a segmented model which uses two joining points to link three stem sections along the bole, where each section is modeled by a different type of fixed-effect parameters SDE.
Stochastic differential equations are widely used to model biological dynamical systems in which a stochasticity phenomenon plays a leading role, embracing more complex variations in the dynamics and generalizing classical ordinary differential equation models [10,11]. The analytical theory of univariate diffusion processes has been successfully utilized for modeling the growth dynamics of an even-age stand [12,13]. Over the last decade, a variety of fixed- and mixed-effect parameters diffusion processes (both symmetrical and nonsymmetrical forms) have been applied in forest tree- and stand-level growth models. Recent research has focused on developing techniques to account for between-individual variabilities in stands. Stochastic growth theories, for example, have been built around the Vasicek, Gompertz, Bertalanffy, and gamma SDEs in both univariate [14] and bivariate [15,16] forms. Multivariate diffusion processes allow us to further consider the underlying covariance structure driving the changes in the state variables; for example, a trivariate case [17], a quadrivariate Vasicek case [18], and a quadrivariate Bertalanffy case [19] have been investigated.
The main goal of this paper is to develop a segmented mixed-effect parameters SDE stem taper model that uses one joining point to link two sections, where each section is modeled by a different type of mixed-effect parameters SDE, and to describe the maximum likelihood procedure for fixed-and mixed-effect parameter estimates. Another goal is to compare the developed stem taper models with well-known regression models for prediction of diameter at any specified height and volume. In the results, we consider a possible application of the SDE stem taper modeling technique to measurements from mountain pine stands in Lithuania. All results are obtained in the Maple computer algebra system using the Statistics and VectorCalculus packages.
2. Materials and Methods
2.1. SDE Taper Framework
A large number of stem taper equations have been developed for different tree species and regions, which mathematically describe the tree diameter at an arbitrary height. Stem taper equations meet multifarious interests in forest management: first, we can calculate the stem diameter at any specified height; second, we can calculate the tree height for any specified value of stem diameter; and, finally, we can calculate the stem volume and the product volume, given specified dimensions. The estimates of specified product volume are significant in modern forest planning, for example, in evaluating the economics of different stand management regimes.
This paper focuses on two stem taper modeling frameworks, which can be classified into stochastic differential equations and regression models.
2.1.1. SDE Stem Taper Models
In this study, we determine a taper model using a univariate stochastic process , , diffusing in M different tree stems randomly chosen from a theoretical population. The SDE taper model supposes that the changes of the relative diameter according to the relative height () are expressed by the Itô-type SDE [20], where is the diameter (outside the bark) at any arbitrary height , is the diameter (at breast height, outside the bark) of the ith tree, and is the total tree height (from ground to tip) of the ith tree. Two different SDEs are used for quantifying the stem development. The first evolution model of the relative diameter by the relative height takes the Gompertz form:
where , ; is the value of the diameter at a given relative height xi; , , and are fixed-effect parameters (for all trees); is the nonrandom initial relative diameter; index B indicates a butt part of a tree stem; and , , are mutually independent standard Brownian motions. The second dynamic of the relative diameter takes the Vasicek form:
where , , and are fixed-effect parameters (identical for the entire population of trees); index T indicates a top part of a tree stem; and are mutually independent standard Brownian motions. The fixed-effect parameters , , , and govern the mathematical form of the drift curves. The volatility parameters and in the SDEs stipulate the intrinsic variability of the taper curve, as two trees i and j, , selected at random and with the same diameter at breast height and the same height (hi = hj), do not necessarily have the same stem taper curve and volume. Hence, the parameters and reflect the intrinsic variability when modeling a particular tree.
In this study, we use a segmented SDE consisting of the two different SDEs defined by Equations (1) and (2). Many regression analysis techniques have recently been used for stem taper modeling, such as linear or nonlinear fixed- and mixed-effect models or generalized additive models [21]. The mixed-effect SDE models have the ability to model the stem variability and analyze data from several individual trees simultaneously. This modeling approach describes individual stems by a common mean and variance of the global distribution, with some of the model parameters varying within the stem (called random effects), while other parameters remain invariant between stems (called fixed-effect parameters). Mixed-effect models use longitudinal data from all stems to estimate the fixed- and mixed-effect parameters. For the sake of simplicity, we assume that the parameters and are both composed of fixed parameters and are normally distributed (with 0 mean and constant variance) random variables:
In this study, the stem taper SDE with one joining point is defined, using the two different forms, by
Using Equations (3)–(6) and fixing the stem butt and top , we define four different stem taper models. The proposed SDE stem taper models use one tree-specific prior relative diameter (stem diameter measured at a stem height of 0 m).
Model 1.(Fixed effects): Equation (5),and, .
Model 2.(Fixed effects): Equation (6),and, .
Model 3.(Mixed effects): Equations (3)–(5),, , , and, .
Model 4.(Mixed effects): Equations (3), (4), and (6),,,, and,.
The diffusion process representing the solution of Equation (1) has a univariate log-normal distribution with mean, variance, and conditional probability density functions, respectively, as follows:
and index G indicates the Gompertz-form.
The diffusion process representing the solution of Equation (2) has a univariate normal distribution with mean, variance, and conditional probability density functions, respectively, as follows:
, and index V indicates the Vasicek form.
Using the mean (Equations (7) and (10)) and variance (Equations (8) and (11)) functions, we can define the mean trajectory of diameter, , variance, and p-quantile development, , for Model 1 ( and for ) and Model 3 in the following forms, respectively:
Using the mean (Equation (10)) and variance (Equation (11)) functions, we can define the mean trajectory of diameter, , variance, , and p-quantile development, , for Model 2 ( and for ) and Model 4 in the following forms, respectively:
2.1.2. SDE Parameters Estimation
In this section, we discuss the parameter estimation methods for the SDE stem taper Models 1–4. This study focuses on discretely observed longitudinal tree stem measurements without measurement noise. This assumption has a great advantage for formulating the maximum likelihood function in closed form. Maximum likelihood estimation of the fixed- and random-effect parameters in Models 1–4 is possible, due to the availability of the exact expressions for the conditional probability density functions as defined by Equations (9) and (12). Assume that the relative diameter process Yi(xi) is directly observed at discrete relative height points , composing an estimation data set where ni is the number of diameter measurements of the ith stem, . For Models 1 and 2, the log-likelihood function takes the following form:
where the conditional probability density functions, respectively, are
For the Models 3 and 4, the combined log-likelihood function for all M stems takes the following form:
where the fixed-effect parameters are denoted by the vector , and the random effects are . The conditional probability density functions, respectively, are
where the fixed-effect parameters are , and the random effects are .
As the integral in Equation (22) does not have an exact solution and no analytic expression is known, using Laplace expansion, a two-step maximization procedure can be developed for fixed and random parameters estimation. In the first optimization step, we estimate the vector for every tree after plugging the estimates of the fixed-effect parameters into the following equation:
where the function is defined as
The second optimization step estimates the vector after plugging the estimates of the random effects into the following equation:
2.1.3. Standard Errors of the Parameter Estimates of the SDE Models
The standard error measures the uncertainty of the estimated model parameters. To evaluate the asymptotic standard errors of the maximum likelihood estimators, we focused on the Fisher information matrix [22]. The approximate asymptotic variance of the approximated maximum likelihood estimators of the fixed effect parameters, , may be found by the inverse of observed Fisher information matrix. By defining the vector and the matrix , s = 1, 2, 3, 4, the observed Fisher information matrix takes the following form:
Then, the approximate asymptotic standard errors of the fixed-effect parameters are just the square roots of the diagonal terms in the variance–covariance matrix defined by the matrix :
2.1.4. Random Effects Calibration
To calibrate the random effects, , , for a new stem in Models 3 and 4, random effects are calculated using special measurements taken from a particular stem. Using new special measurements of the relative diameters at relative heights , the random effects are given by
2.2. Nonlinear Regression Stem Taper Models
Over the past few decades, forest statisticians have proposed advanced regression models for describing tree stem taper using simple functions, such as linear and more complex nonlinear functions. In developed countries, including the U.S. and Canada, the segmented polynomial model was traditionally used at the end of the twentieth century. It is obvious, however, that no single stem taper model corresponds well to longitudinal data sets for all tree species. To validate the proposed SDE stem taper models, we selected four different regression-type stem taper models of the variable form reported in forest research literature for comparison [3,23,24].
2.2.1. Segmented Polynomial
Model 5. The segmented polynomial model was derived by Max and Burkhart [1]:
where d is the diameter at any particular height h, D is the diameter at breast height, H is the total tree height, z is the relative height (), α1 and α2 are the joining points of three segments, β1–β4 are the unknown parameters to be estimated, and
2.2.2. Segmented q-Exponential
Tsallis [25] described the q-exponential function, which has been applied successfully to model complex problems in a broad range of scientific areas, such as information theory [26] and forestry [27]. The pooled segmented function obtained from the q-exponential and polynomials can be utilized to describe the changes of tree stem diameter at a specified stem height.
Model 6.A simple generalized model of stem taper can be defined, using the q-exponential function, as
where α is the joining point of two segments, β1–β9 are the unknown parameters to be estimated, and
2.2.3. Variable Exponential
Model 7.The stem taper model published by Lee et al. [24] and modified by Berhe and Arnoldsson [28] is defined as
where β1–β5 are the unknown parameters to be estimated.
Model 8.The stem taper model published by Kozak [2] is defined as
where β1–β9 are the unknown parameters to be estimated.
2.3. Nonlinear and Linear Regression Stem Volume Models
Based on review papers on compiled stem volume regression models [29], four regression models were selected and compared with techniques involving stem tapers. All models include diameter at breast height, D, and total height, H, as the independent variables, whereas the last includes a form factor.
Model 9.Schumacher and Hall [30] developed the power form stem volume model
where β1–β3 are the unknown parameters to be estimated.
Model 10.Using the q-exponential function, the stem volume can be defined in the following form [31]:
where β1–β5 are the unknown parameters to be estimated.
Model 11.Honer developed a two-parameter stem volume model [32]:
where β1 and β2 are the unknown parameters to be estimated.
Model 12.A cylindrical form factor, F, has been used for tree stem volume modeling by the Lithuanian National Forest Inventory [9]. Tree stem volume is defined as
where β1–β6 are the unknown parameters to be estimated.
2.4. Evaluation of Models to Data
A main goal of stem taper simulation as a descriptive model is to accurately predict the diameter value at a specified stem height from a set of predictors (tree diameter at breast height and total tree height). In order to interpret the performance of the statistical models on observational data, this study focuses on numerical statistics and visualization of residuals. The four statistics used to evaluate the goodness-of-fit were adjusted coefficient of determination, mean prediction error (percent prediction error, %), mean absolute prediction error (percent absolute prediction error, %), and root-mean-square error (root-mean-square error, %). The mathematical expressions of the statistics are as follows:
- Adjusted coefficient of determination:
- Mean prediction error (percent prediction error, %):
- Mean absolute prediction error (percent absolute prediction error, %):
- Root-mean-square error (root-mean-square error, %):
Here, is the total number of observations used to fit (validate) the model, M is the number of stems, ni is the number of measured diameters in the ith tree stem, and , , and are the measured, estimated, and average values, respectively, of the dependent variable (diameter, d; stem volume, v).
3. Results and Discussion
The newly developed models are nondeterministic models that consider symmetric and asymmetric diffusions of stem diameter at a particular height. Various regression models that incorporated diameter at breast height and tree height have been proposed [1,2,6,7,27,31]. However, there has been debate about the mathematical form of stem taper. Our developed models are not affected by the mathematical form of the stem taper, because we start from the evolution of the distribution [33] of the relative diameter. Another characteristic of our models is that the mixed-effect parameters SDE model deals with random growth rate for a given stem diameter and height. Such a model can express the variation in individual stem taper due to the random effects.
3.1. Estimation Results
We illustrate the proposed modeling technique by using a mountain pine tree (Pinus mugo Turra) data set. The data used for modeling consisted of measurements collected from 30 mountain pine plots located in western Lithuania (Kuršių Nerija). This tree species was planted to stop drifting sand dunes of Curonian Spit in the nineteenth to twentieth centuries. The age of sampled stands varies from 53 to 123 years. The size of round sample plot was 150 m2. Total diameter at the breast height was measured for 7002 trees, height for 702 trees, and stem diameter on each 0.5 m (longitudinal) for 319 trees. 102 trees were cut down for biomass estimation. A total of 319 trees were used. At plot establishment, the following data were recorded for every sample tree: diameter over bark at 1.30 m, tree height, and stem volume (calculated by Equation (40)). The data set was randomly divided into estimation and validation data sets. A random sample of 217 stems was selected for model estimation, and the remaining data set of 102 stems was used for model validation. The observed data set of longitudinal measurements of the diameter at a specified height are presented in Figure 1. Summary statistics for the diameter at breast height (d), the total height (h), and volume (v) for all of the stems used in the model estimation, and validation data sets, are presented in Table 1.
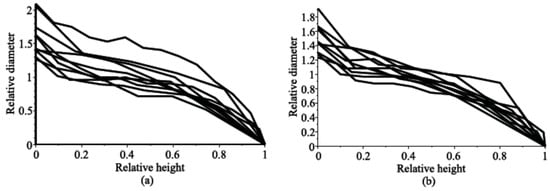
Figure 1.
Relative stem diameter plotted against relative height: (a) Measurements of 10 observed trees from the estimation data set and (b) measurements of 10 observed trees from the validation data set.

Table 1.
Summary statistics of all measured stems.
The methodology of parameter estimation, which is known as machine learning, deals with fitting the parameters to reproduce the observed data set. The approaches most commonly used in the estimation of parameters are the least squares method and the maximum likelihood procedure. The fixed- and mixed-effect parameters of the SDE stem taper Models 1–4 were estimated utilizing the maximum likelihood methodology developed in Section 2.1.2 and Section 2.1.3, and the parameters of the nonlinear regression models 5–12 were estimated by the least squares methodology [34]. For the parameters and their standard error estimates, algorithms were developed and realized using the symbolic algebra system Maple [35]. The results of parameter estimation and the standard errors for Models 1–12 are listed in Table 2.

Table 2.
Estimates of fixed-effect parameters and their standard errors (in parenthesis) for all fitted stem taper and volume models.
3.2. Comparison of Stem Taper Models
To be an applicable taper model, a model needs to predict diameter measurements at a particular height in a stem highly accurately. To evaluate taper model performance, adjusted coefficient of determination, mean prediction error (percent prediction error, %), mean absolute prediction error (percent absolute prediction error, %), and root-mean-square error (percent root-mean-square error, %) were calculated, which are presented in Table 3.

Table 3.
Statistical indices for all fitted stem taper models.
The stem taper modeling techniques presented in this study are generally grouped into SDE models and nonlinear regression models. As can be seen from Table 3, taper models 1–8 produced very similar statistical indices for both estimation and validation data sets. The stem taper SDE models (1–4) had very similar goodness-of-fit statistics (see Table 3); however, the SDE taper models used additional measurements that fixed tree diameter at stem height h = 0. Comparison of the statistical indices produced by SDE taper models (1–4) and the regression taper models (5–8) reveals that the SDE taper models were superior to the others. Random effects were calibrated, by Equation (30), using two additional stem diameters measured at a stem height of 1.0 m and 1.5 m for all stems in the validation data set. This additional information marginally improved the values of all statistical indexes.
Visualization of the residuals in Figure 2 shows that the SDE stem taper models (1–4) produced a more homogeneous residual variance than the regression stem taper models (5–8). The inclusion of random effects was found to be significant for Models 3 and 4.
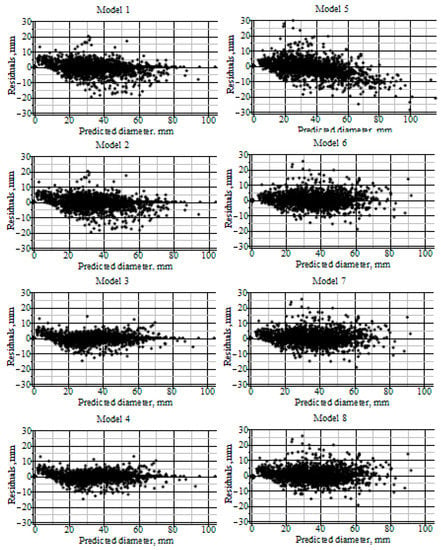
Figure 2.
Residuals of predicted diameter plotted against predicted diameter.
3.3. Comparison of Stem Volume Models
The predicted stem volume was calculated by integrating the taper equations over the height:
where di is the diameter at breast height (mm) of the ith tree, and hi is the total tree height (dcm).
The observed volume (V cm3) of each stem was computed using a truncated cone formula, up to the last section, where the final apex was calculated as a cone [31]:
where dij and Lij are the diameter (mm) and length (d cm), respectively, of the jth section j of the ith tree.
The goodness-of-fit results for all presented stem taper models and volume predictions are given in Table 4. As can be seen from the table, the statistical indices of all volume models showed subdivision into three clusters (SDE taper volume, regression taper volume, and volume models). These clusters were characterized by very similar statistical indices within each cluster, for both estimation and validation data sets. The volumes predicted using stem taper mixed-effect-parameters SDE Models 3 and 4 (extra integral by Equation (39)) showed superior goodness-of-fit statistics, compared to the others, for both estimation and validation data sets (see Table 4). However, all SDE taper models (1–4) used additional measurements, which fixed the tree diameter at stem height h = 0. Comparison of the statistical indices produced by the regression taper models (5–8; extra integral by Equation (39)) and the regression volume models (9–12) revealed that the regression volume models were superior to the regression taper models. In Models 3 and 4, the random effects calibrated by Equation (30) (using two additional stem diameter observations measured at a stem height of 1.0 m and 1.5 m for all stems in the validation data set) improved all statistical indices for the volume predictions (see Validation Data Set columns in Table 4).

Table 4.
Statistical indices for all stem volume models.
Visualizations of the residuals plotted against the predicted diameters (see Figure 3) show that volume prediction using SDE stem taper models (1–4; extra integral by Equation (33)) produced more homogeneous residual variance than the regression stem taper models (5–8; extra integral by Equation (33)) and the volume regression models (9–12). The inclusion of random effects was found to be considerable for the volume predictions of Models 3 and 4.
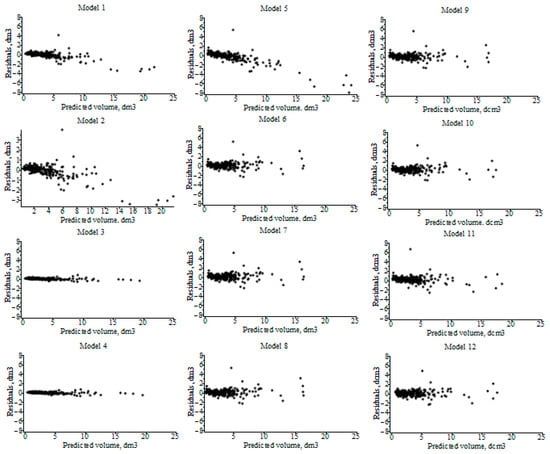
Figure 3.
Residuals of volume predictions plotted against predicted diameter.
3.4. Illustration of Tree Stem Tapers
Traditionally, stem form is described by the stem taper technique, which relates the changes in stem diameter with increasing height (i.e., from the tree stump to the tree tip). Stem taper equations can predict the diameter at any specified height, total stem volume, merchantable volume, and height at any specified stem diameter. In this study, two approaches for determining an equation-like stem taper profile were examined: stochastic differential equation models and regression equation models. All stem taper equations for both modeling techniques are visualized in Figure 4. For illustration, three stems from the validation dataset, corresponding to large, medium, and small trees, were randomly selected. Figure 4a,b shows the improved fit of mixed-effect parameters SDE stem taper Models 3 and 4 to the three randomly selected trees due to the inclusion of random effects. The better fit of the SDE stem taper models (1–4; Figure 4a,b), compared with the regression stem taper models (5–8; Figure 4c,d) can be observed by visual inspection, as the predicted stem taper curves are closer to the observed data set of stem measurements.
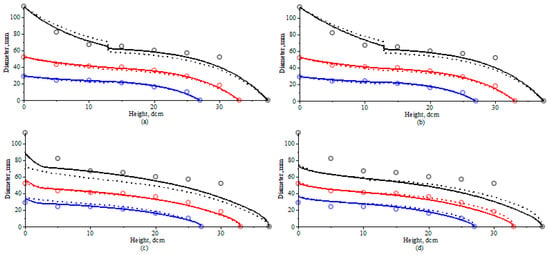
Figure 4.
Illustration of all presented stem taper equations: (a) stochastic differential equation (SDE) stem taper Models 1 and 3: mixed-effect Model 3, solid line; fixed-effect Model 1, dotted line. (b) SDE stem taper Models 2 and 4: mixed-effect Model 4, solid line; fixed-effect Model 2, dotted line. (c) Regression stem taper Models 5 and 7: Model 5, solid line; Model 7, dotted line. (d) Regression stem taper Models 6 and 8: Model 6, solid line; Model 8, dotted line. First stem, black colour; second stem, red colour; third stem, blue colour. Observed stem measurements are circles in all subfigures.
The SDE stem taper modeling technique can better interpret stem structure evolution by utilizing higher central moments of the relative diameter. Figure 5 shows the mean stem taper dynamic, as well as its 0.025 and 0.975 quantile dynamics, for three randomly selected stems from the validation data set.
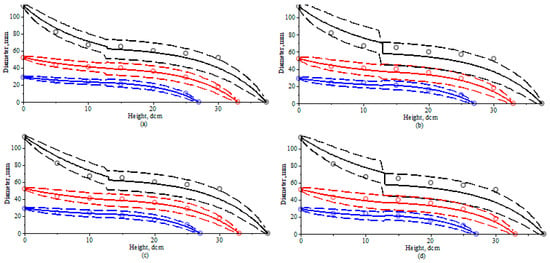
Figure 5.
SDE stem tapers curves and 0.025 and 0.975 quantiles: (a) SDE mixed-effects Model 3. (b) SDE fixed-effects Model 1. (c) SDE mixed-effects Model 4. (d) SDE fixed-effects model 2. Quantile curves are dashed for all subfigures. First stem, black colour; second stem, red colour; third stem, blue colour.
4. Conclusions
The SDE stem taper equations proposed in this paper are simple to use and provide a more accurate diameter prediction at a specified height than the most common form of regression equations as well as volume predictions. The results of our statistical analyses (see Table 2 and Table 3; Figure 2 and Figure 3) indicate that the SDE stem taper Model 3 had the overall best performance in predicting tree diameter at a specified height. However, the calibration of random effects for a new observed tree requires some additional information and provides better performance when compared with implementation of only the fixed-effect parameters SDE stem taper model. All presented regression stem taper models showed extremely similar performance in predicting tree diameter at a specified height. The results of this study also indicated that the SDE stem taper models can be used to accurately estimate the total stem volume of mountain pine trees. Future investigation will cover applications of SDE models for predicting tree biomass.
Author Contributions
Conceptualization, P.R. and E.P.; methodology, E.P.; software, P.R.; validation, M.N., E.P. and P.R.; formal analysis, P.R.; data curation, M.N. and E.P.; writing—original draft preparation, M.N., P.R. and E.P.; writing—review and editing, M.N., P.R. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are very grateful to the Lithuanian Association of Impartial Timber Scalers for the sample data set.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Max, T.A.; Burkhart, H.E. Segmented Polynomial Regression Applied to Taper Models. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Kozak, A. My Last Words on Taper Equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Garcia, O. Dynamic Modelling of Tree Form. Math. Comput. For. Nat. Res. Sci. 2015, 7, 9–15. [Google Scholar]
- Sloboda, B.; Saborowski, J. Stand Taper Form as a Stochastic Process with an Example of Application. In Proceedings of the XVII IUFRO-World Congress, Kyoto, Japan, 6–17 September 1981; pp. 137–150. [Google Scholar]
- Rupšys, P. Univariate and Bivariate Diffusion Models: Computational Aspects and Applications to Forestry. In Stochastic Differential Equations: Basics and Applications; Deangelo, T.G., Ed.; Nova Science Publisher’s: New York, NY, USA, 2018; pp. 1–77. [Google Scholar]
- Gray, H.R. Form and Taper of Forest-Tree Stems; Paper No. 32; Imperial Forestry Institute University of Oxford: Oxford, UK, 1956; p. 79. [Google Scholar]
- Kozak, A.; Mundro, D.D.; Smith, J.H.G. Taper Functions and their Application in Forest Inventory. For. Chron. 1969, 45, 278–283. [Google Scholar] [CrossRef]
- Chiba, Y. A Quantitative Analysis of Stem Form and Crown Structure: The S-Curve and its Application. Tree Physiol. 1990, 7, 169–182. [Google Scholar] [CrossRef]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Baltic For. 2013, 19, 43–151. [Google Scholar]
- Diblík, J.; Dzhalladova, I.; Růžičková, M. A Dynamical System with Random Parameters as a Mathematical Model of Real Phenomena. Symmetry 2019, 11, 1338. [Google Scholar] [CrossRef]
- Rupšys, P. The Use of Copulas to Practical Estimation of Multivariate Stochastic Differential Equation Mixed Effects Models. AIP Conf. Proc. 2015, 1684, 080011. [Google Scholar]
- Suzuki, T. Forest transition as a stochastic process. Mitt. Forstl. Bundesversuchsanstalt Wien 1971, 91, 69–86. [Google Scholar]
- Sloboda, B. Mathematische und stochastische Modelle zur Beschreibung der Dynamik von Bäumen und Beständen, insbesondere das bestandesspezifische Wachstum als stochastischer Prozeß; Habilitations-schrift, Universität-Freiburg: Freiburg, Germany, 1976; 310p. [Google Scholar]
- Rupšys, P. New insights into tree height distribution based on mixed effects univariate diffusion processes. PLoS ONE 2016, 11, e0168507. [Google Scholar] [CrossRef] [PubMed]
- Rupšys, P.; Petrauskas, E. A new paradigm in modelling the evolution of a stand via the distribution of tree sizes. Sci. Rep. 2017, 7, 15875. [Google Scholar] [CrossRef] [PubMed]
- Rupšys, P.; Petrauskas, E. Evolution of bivariate tree diameter and height distribution via stand age: Von Bertalanffy bivariate diffusion process approach. J. For. Res. Jpn. 2019, 24, 16–26. [Google Scholar] [CrossRef]
- Rupšys, P. Modeling Dynamics of Structural Components of Forest Stands Based on Trivariate Stochastic Differential Equation. Forests 2019, 10, 506. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-variate Distribution and Their Growth Models: A 4-variate Diffusion Process Approach. Forests 2017, 8, 479. [Google Scholar] [CrossRef]
- Rupšys, P. Understanding the Evolution of Tree Size Diversity within the Multivariate Nonsymmetrical Diffusion Process and Information Measures. Mathematics 2019, 7, 761. [Google Scholar] [CrossRef]
- Itô, K. On stochastic processes. Jpn. J. Math. 1942, 18, 261–301. [Google Scholar] [CrossRef]
- Bronisz, K.; Zasada, M. Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland. Forests 2019, 10, 975. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. Ser. A 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Lee, W.K.; Seo, J.H.; Son, Y.M.; Lee, K.H.; von Gadow, K. Modeling stem profiles for Pinus densiflora in Korea. For. Ecol. Manag. 2003, 72, 69–77. [Google Scholar] [CrossRef]
- Duan, A.; Zhang, S.; Zhang, X.; Zhang, J. Development of a stem taper equation and modelling the effect of stand density on taper for Chinese fir plantations in Southern China. PeerJ 2016, 4, e1929. [Google Scholar] [CrossRef]
- Tsallis, C. What are the numbers that experiments provide? Quim. Nova 1994, 17, 468. [Google Scholar]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics-an overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Development of q-exponential models for tree height, volume and stem profile. Int. J. Phys. Sci. 2010, 5, 2369–2378. [Google Scholar]
- Berhe, L.; Arnoldsson, G. Tree taper models for Cupressus lusitanica plantations in Ethiopia. South For. 2008, 70, 193–203. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. 2005, 4, 1–63. [Google Scholar]
- Schumacher, F.X.; Hall, F.S. Logarithmic expression of timber-tree volume. J. Agric. Res. 1933, 47, 719–734. [Google Scholar]
- Petrauskas, E.; Rupšys, P.; Memgaudas, R. Q-exponential Variable-form of a Steam Taper and Volume Model for Scots Pine (Pinus sylvesteris L.) in Lithuania. Baltic For. 2011, 17, 118–127. [Google Scholar]
- Honer, T.G. A new total cubic foot volume function. For. Chron. 1965, 41, 476–493. [Google Scholar] [CrossRef]
- Visalga, G.; Rupšys, P.; Petrauskas, E. Influence of Noise on Decay Predictions in Standing Trees. AIP Conf. Proc. 2017, 1895, 030006. [Google Scholar]
- Bühlmann, P.; van de Geer, S. Statistics for High-Dimensional Data: Methods, Theory and Applications; Springer: Heidelberg, Germany, 2011; 558p. [Google Scholar]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; McCarron, J.; DeMarco, P. Maple Advanced Programming Guide; Maplesoft: Ontario, ON, Canada, 2007; 388p. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).