Abstract
At present, two main magnetic confinement fusion devices exist: tokamaks and stellarators. Moreover, stellarators have been demonstrated to be a good alternative to tokamaks, due to their ability to operate in continuous mode, which eventually translates into a higher commercial profitability. In stellarators, the magnetic confinement of the plasma is achieved exclusively by the coils, thus no electric current through the plasma is needed. In particular, this article presents the Columbia Non-Neutral Torus stellarator that is located in the Automatic Control Group of Euskal Herriko Unibertsitatea (EHU). This EHU stellarator maintains symmetry in its structure due to the topology of the mesh that is formed by its coils. A cornerstone of future fusion reactors is to obtain real-time control that enables a sustained reaction. In this article, a control-oriented model for the installed magnetic confinement coils is presented. The model is based on matrices that preserve symmetry, which is defined from physical principles and then validated by different sets of experimental data. Then, based on this model, a novel predictive control suited to this particular model with symmetric objective function is implemented in the numerical simulations, and its response is compared to that of traditional controllers. Finally, this control is implemented in a real plant and the satisfactory experiment results provide validation of both the numerical model and proposed controller.
1. Introduction
In recent years, there has been an international effort to develop clean energy production technology based on fusion energy, such as =the International Thermonuclear Experimental Reactor (ITER) [1].
The energy generation involves nuclear fusion reactions, where two or more light element’s atomic nuclei, usually from deuterium and tritium (two different hydrogen isotopes), combine to form different atomic nuclei and subatomic particles. The reaction implies a net loss of mass that is transformed into energy in the form of gamma rays and kinetic energy emitted by the aforementioned particles, as shown in Equation (1) [2]. A typical deuterium–tritium reaction is supposed to be in the form:
The final objective is to achieve a state of sustained continuous nuclear fusion reaction. This objective represents a large number of scientific and technical challenges. In particular, the real-time control of the plasma by means of the confinement coils plays a key role in the performance of the process and the feasibility of the clean fusion technology. It this sense, it must be considered that the main limiting phenomenon in fusion devices is the premature reaction decay due to plasma instabilities.
Nowadays, two principal approaches coexist that try to achieve successful and commercially competitive fusion processes: inertial confinement-based and magnetic confinement-based approaches. Inertial confinement fusion attempts to achieve the reaction by compressing and heating a fuel target, and it is being studied in several U.S. facilities. Magnetic confinement attempts to achieve and maintain the reaction by using magnetically confined fuel within vacuum chambers, and it is the topology perused in ITER (International Thermonuclear Experimental Reactor), TCV (Tokamak à Configuration Variable), or JET (Joint European Torus). It is still not clear which approach will lead to the desired results.
At present, two main magnetic confinement topologies exist for fusion devices: tokamaks and stellarators. On the one hand, tokamak devices confine plasma in a toroidal region using compound magnetic fields. The principal magnetic field is usually toroidal, while a poloidal magnetic field induces a current into the plasma that acts as the secondary circuit of an electrical transformer. The poloidal field lines created around the plasma current are combined with the toroidal field producing helical field lines, which wrap around the torus, preventing the plasma displacement towards the vessel walls [3]. On the other hand, stellarators consist of a more complex helical symmetric coil system, in such a way that the plasma follows twisting magnetic beam line paths. In these kinds of devices, the magnetic confinement is fully achieved by the coils, so no induced current is needed to confine the plasma, although ohmic, non-inductive, and bootstrap currents may also be present [4]. In this sense, stellarators are a great alternative to tokamaks, with significant research progress taking place regarding the study of magnetically confined plasma physics on these devices during recent years. Additionally, the ability of stellarators to operate in continuous mode would allow higher commercial profitability.
In this context, this article studies a real-time control strategy for the coils of the EHU (Euskal Herriko Unibertsitatea)stellerator name the ultra-low-iota super elongated stellarator (ULISES), fully designed and built by the Automatic Control Group (ACG) at the Engineering Faculty of the Basque Country University (UPV/EHU) in collaboration with CIEMAT (Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas) (see Figure 1 and Figure 2). The numerical plant model will be formulated based on the symmetry of the system due to the plant topology and derived from physical principles coupled with parameter estimation. The success of the initial simulations paved the way for the real-time experimental implementation, which demonstrates the effectiveness of both the model and the control strategies [5].

Figure 1.
EHU (Euskal Herriko Unibertsitatea) stellerator located in the Automatic Control Group (ACG) at the Engineering Faculty of the Basque Country University (UPV/EHU).
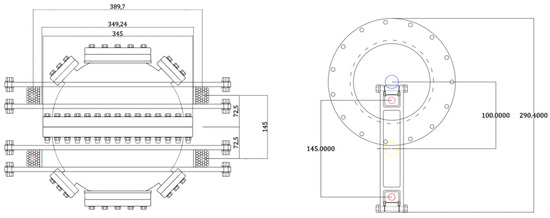
Figure 2.
Dimensions of the reaction chamber and the coils: the left the vacuum chamber and exterior coils; the right the inner coils, shown in a 90° setting for visualization purposes.
The rest of the manuscript is organized as follows. Section 2 describes three different strategies to construct the numerical models of the EHU stellarator. Section 3 describes the novel advanced predictive control laws. Section 4 presents the real-time experimental performance of the proposed controllers. Finally, concluding remarks are given in Section 5.
2. Data Acquisition System and Model Statement
In this section, three different modeling approaches are employed to obtain a reliable model of the magnetic coils system of the EHU stellarator. An analytical model obtained by means of parameter identification techniques is compared to the proposed physical equivalent system, a pure black box model, and a hybrid grey box model, in which the preliminary structure of the system is first established and then identified.
After the models have been constructed, these numerical systems will be validated experimentally. That is, real experiments will be carried out on the real plant for different study cases, so that the obtained measured output data can be compared with those of the numerical model response for the same study cases.
In order to control the EHU stellarator, a feedback loop must be provided. In this case, the feedback consists of the voltage output VOut and current I signal measurements, while the input signal VIn is also being monitored. Note that the main actuator of the system is composed of a coil system consisting of two external and two internal coils connected to a real-time fully controllable power source, as shown in Figure 1 and Figure 2. The resulting output voltage and currents are, therefore, the controlled variables, and are measured directly from the coils’ copper wires by means of physical resistance-based and Ohmic inductive sensors, respectively, providing the input for the control feedback loop through the corresponding conditioning circuits shown in Figure 3 and Figure 4 and the DAQ (Data acquisition) connected to the real-time target.
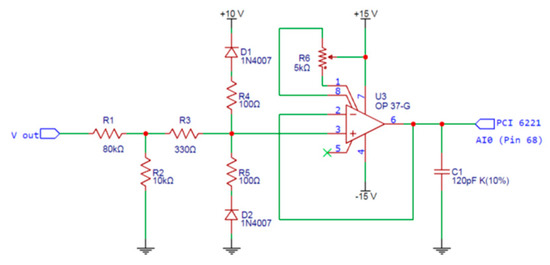
Figure 3.
Output voltage signal conditioning circuit.
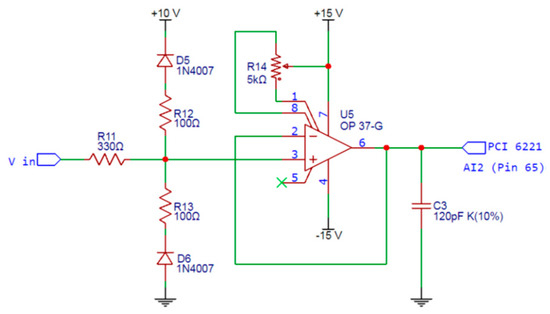
Figure 4.
Input voltage signal conditioning circuit.
For this purpose, a data acquisition system has been built. Using a National Instruments PCI-6221 instrument for data acquisition, as well as the necessary electronic components to condition the circuit, as seen in Figure 3 for the output voltage, Figure 4 for the input voltage, and Figure 5 for the output current.
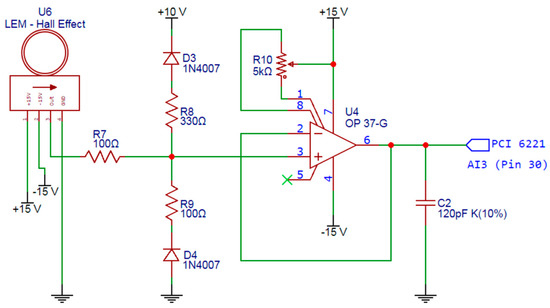
Figure 5.
Current signal conditioning circuit.
As can be seen in the figures above, the voltage output signal is driven through a voltage divider due to the high voltage values in the output point, which could destroy the PCI (Peripheral Component Interconnect) card. Additionally, all of the signals are driven through a voltage limiter, and finally through an op amp in buffer configuration before they reach the target. With this configuration, the op amp is capable of following the original signal with no attenuation, while staying below the maximum voltage value.
All the additional components are installed in order to protect the data acquisition card, while maintaining adequate signal tracking and without interference with the main circuit of the system.
2.1. Analytical Model
From the basic physical design of the ULISES described in Figure 6, an analytical plant model is created. In particular, based on the electrical elements that compose the device, a numerical model is obtained by fitting the parameters to a control-oriented space–state representation. Additionally, the parameters are defined in Table 1.
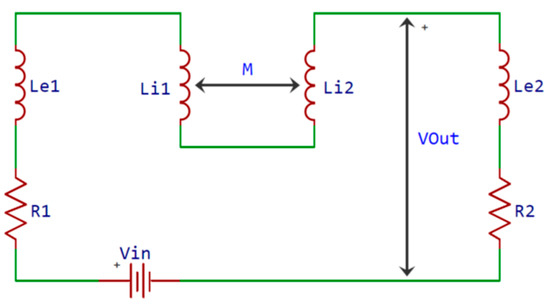
Figure 6.
Parametric electrical equivalent circuit for the coil system of the EHU stellarator.

Table 1.
Parameters of the electrical equivalent circuit of the EHU stellarator.
Merging the inductances and resistances leads to a simplified circuit with reduced parameters. These new parameters are shown in the following respective equations for the total circuit inductance and resistance:
In order to analyze the circuit behavior, the equations that govern the circuit are considered:
where I(t) represents the current through the circuit.
Note that both Kirchhoff’s laws and Ohm’s law particularized for the different lumped-parameter circuit elements are used in Equations (2)–(5).
In order to obtain a space–state representation, the following state variables are chosen, where the usual space–state variable nomenclature is employed. In this sense, note that and , the components of the state vector, have different dimensions:
Replacing Equation (4) with Equation (7), the following expression is obtained:
and the time derivative of Equation (8) leads to the expression:
Thus, all the space–state variables and their respective derivatives have been defined. Neglecting the mutual inductance, the reduced space–state model can be established, where the state variables are decoupled:
Once the analytical state–space model form is defined in Equations (10) and(11), it is necessary to identify the values of the parameters from the real experimental system. These parameters are described and defined in Figure 5 and Table 1.
For parameter identification, multiple experimental tests are performed on the real plant, collecting output data through the installed data acquisition system. Besides, an analytical solution for Equations (10) and (11) is computed to facilitate the parameter identification process:
Taking into account the expressions given in Equations (6) and (7), for each given input their resulting output will be compare with the data output from the real EHU stellarator. Bearing this objective in mind, a series of experimental tests are carried out. The experiments consisting of applying different voltage test input signals to the real system. The resulting data from the experiments are then retrieved by the instrumentation, as detailed in the previous section. Then, the values of the parameters of the space–state system are approximated by system identification.
Following this procedure for different experiments and different voltage input values, the results presented in Table 2 are achieved:

Table 2.
Parameter value identification for the electrical equivalent circuit.
Even when this identification process of the analytical model is performed based on the system physical equations, other approaches such as pure black box or grey box methods may be also used to determine the model of the system. These will be further explained in the following subsections.
2.2. Black Box Model
The black box models represent an unknown system, where only inputs and outputs are known. By analyzing these signals, a transfer function or a space–state system that represents the unknown plant may be created. However, the states of the system do not usually correspond with any physical variables of the real system [6]. In particular, considering the same input and output signals as in Section 2.1, the corresponding black box model of the EHU stellarator is:
2.3. Grey Box Model
Analogous to the black box models, grey box models represent an unknown system. However, in this case the input and output signals are known, as well as the structure of the space–state system. This means that the dimensions of the matrices and some physical restrictions on the parameters are considered during the identification [7]. However, some perturbations from higher order dynamics that were not previously taken into account in Section 2.1 are now allowed into the system. In particular, considering the same input and output signals as in Section 2.1, the corresponding grey box model of the EHU stellarator is:
2.4. Model Validation via Experimentation
In Section 2.1, Section 2.2 and Section 2.3, three different numerical models have been presented. In this section, the response of these estimated models will be compared to the experimental response of the real EHU stellarator. This comparison, as seen in Figure 7, serves to verify which one of these models is the best match for the EHU stellarator [8,9].
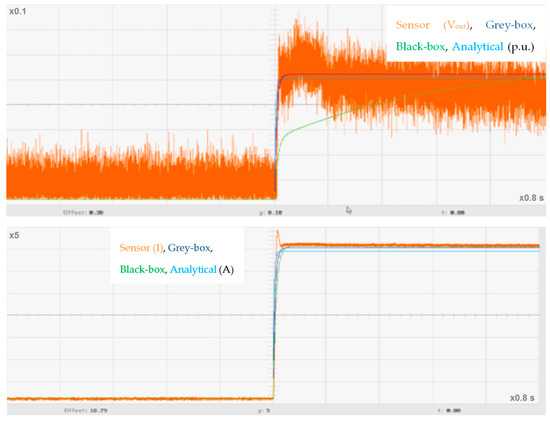
Figure 7.
Comparison of the analytical model, black box model, and the grey box model responses in real time: comparison for voltage (top) and current (bottom).
Taking into account the voltage output signal, the black box model is outperformed by both the analytical model and grey box model responses, since both of them provide an accurate estimation of the system response. On the other hand, looking into the current output signal, the analytical model shows some steady-state error. In this sense, we note that the steady-state error represents the difference between the output signal and the reference desired one once the system has reached a state where the output variations remains bounded and limited to 2%–5% of its value, where the time tends to be infinite, considering that the controlled system is stable, and thus convergent. Therefore, it may be concluded that the grey box model is the most accurate model that has been estimated for the EHU stellarator. Nevertheless, it must be considered that the differences between the grey box and the analytical model are not remarkable, while the analytical model allows identification of physical magnitudes corresponding to its different parameter components. In order to further confirm these results, the same input signal is driven to the experimental system and both the black box model and the grey box model. The results of these comparisons are shown in Figure 8.
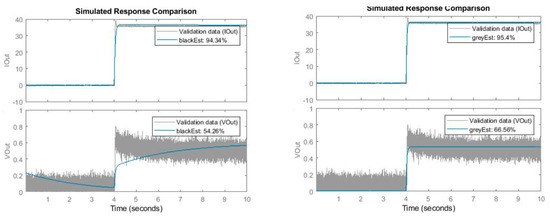
Figure 8.
Comparison between the real system and the theoretical model output signals: comparison with the black box model (left) and grey box model (right).
As can be seen in Figure 7, the proposed models yield outputs that match those of the real system with an accuracy of approximately 50%–60% for voltage output and 94%–95% for current output. The larger error in the voltage response is due to the unfiltered noise created by the magnetic fields that interfere with the instrumentation. Therefore, as the magnitude of the noise is around 200 mV, both the responses in voltage and current signals are a good match for the experimental signal output. Therefore, both the black box and the grey box models are valid, and the experimental tests also show that the grey box model presents a better match with the real system output, although the parameter representativeness is inherent to the analytical model.
3. Control Design
Once the grey system model is established and verified as the most suitable fit with the EHU stellarator, an adequate control may be designed. The main objective of the control in the platform is to ensure that the plasma inside the ULISES device chamber follows the desired trajectory so that the fusion reaction does not degenerate by regulating the coil input voltage. The control of the plasma current is indirectly achieved by controlling the input voltage, as both are directly related.
For this purpose, different controlling techniques have been tested. First, a traditionally used PID (Proportional Integral Derivative) control is implemented and tuned in order to verify whether the system can be controlled by a rather simple controller. Next, a more complex controller is developed, namely a model predictive control (MPC), in order to investigate their advantages with respect to the traditional controllers.
The development, implementation, and the system output for these controls will be explained in further detail in the following subsections.
3.1. PID Controller Implementation
PID controllers are very common, as they are simple yet effective in minimizing the error signal in addition to stabilizing the system [10]. Different methods exist to tune the controller [11,12,13]. In this particular example, the PID has been tuned using the closed-loop principle of Ziegler–Nichols, where the tuning process is subjected to the constraints of closed-loop stability and large bandwidth while maintaining disturbance rejection, and enough phase margin and gain margin to allow for disturbances and unmodelled dynamics. A proprietary tuning procedure tries to compromise between those constraints. In order to implement the resulting PID into the system, a closed-loop block diagram is designed that sends signals to the actuators and collects signals from the sensors through a DAQ NI-6221 instrument, as shown in Figure 9. Considering that only the input voltage is controlled, the output voltage signal located between the second set of coils (see Figure 6) will be used as feedback for the controllers.
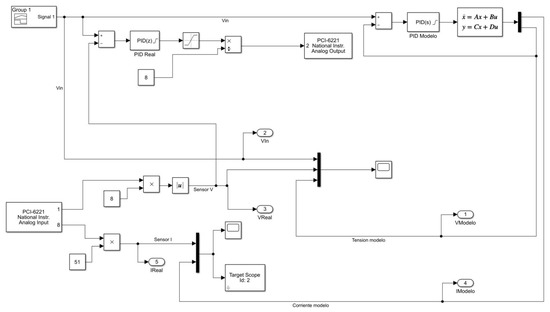
Figure 9.
PID (Proportional Integral Derivative) closed-loop block diagram.
Once the closed loop has been designed and established, a series of behavior conditions will be imposed, which the controller must fulfil [14]. For this setting, the PID parameter values will be tuned to achieve the following conditions:
- Quick response. Since the system will have to handle the confinement of a rapidly varying plasma current, the control over the coil voltage will have to be as fast as possible.
- Low overshoot. Excessive overshoot translates into a more powerful magnetic field, which can lead to unexpected behavior and ultimately cause internal damage to the device, which must be avoided.
- Minimal steady-state error. A varying signal for voltage applied to coils creates magnetic fields that can change both in direction and in magnitude. This variable magnetic field will induce a leaking voltage into the conductive materials. The leaking currents can interfere with the plasma inside the device chamber and the instrumentation signals, and can also alter the temperature conditions.
Using the robust step-response optimization algorithm for a target phase margin of 60°, the values for the PID parameters are obtained. The PID controller with the values shown in Table 3 does achieve the desired performance, as will be seen in Section 4.

Table 3.
Tuned PID parameters.
3.2. Model Predictive Control Design
Model predictive control (MPC) relies on the idea of a more complex optimization-based scheme, which takes into account the future states of the system. In a few words, using an accurate dynamic mathematical model of the real system and different measurements of the system, this controller predicts the future behavior of the system in order to grant the best control signal [15,16].
The real system has a time constant in the order of milliseconds, so that system equations (Equations (16) and (17) are discretized with a time step of that order of magnitude to obtain an acceptable difference between the continuous and the discretized optimal control profiles. However, such a small discretization time step creates a need to significantly reduce the computation time at each optimization step. The formulations discussed in this paper adopt a discretization time step of 50 ms, which is found to be sufficiently small to approximate the continuous optimal control profile. The resulting optimization problem is solved with an analytical solution equation approach using an exact Hessian approximation. Thus, given a predicted input sequence, the corresponding sequence of prediction values is generated by simulating the model forward over the prediction horizon. For notational convenience, these predicted sequences are often stacked into vectors that may be denoted by
where and denote the plasma current value and ohmic heating voltage input at time , which are predicted at time . Therefore, evolves according to the prediction model:
with an initial condition at the beginning of the prediction horizon defined as , and a control horizon, whose value is smaller than or equal to that of the prediction horizon, .
The predictive control feedback law is computed by minimizing a predicted performance cost, which is defined in terms of the predicted sequences and . In particular, the output current in compact form is rewritten as
where denotes the Ohmic heating (OH) voltage for a given reference signal at a given time. Within a prediction horizon, the control system aims to bring the internal inductance as close as possible to the reference:
The corresponding cost function that preserves symmetry is:
where the above is clearly a function of the predicted OH voltages and the positive definite weighing matrix . The optimal voltage sequence for the problem of minimizing this cost function takes into account the input restrictions as equivalent constraints on in the optimization.
Only the first element of the optimal predicted voltage sequence is input back to the plant [17]. This procedure, known as the receding horizon strategy, provides a degree of robustness to modeling errors and uncertainty, since the input at each step takes into account the current state values to compute future events. Additionally, by continually shifting the horizon to where future inputs are optimized, it attempts to compensate for the fact that this horizon is finite. Therefore, a receding horizon strategy aims to ensure that the performance of the closed-loop system is at least as good as that of the optimal prediction.
Then, a series of predictions are calculated for both the control signals and the obtained output error. After analyzing the simulation results for different prediction and control horizons, the best control of the state–space system is applied to the experimental EHU stellarator via a data acquisition card [18,19], as seen in Figure 10.
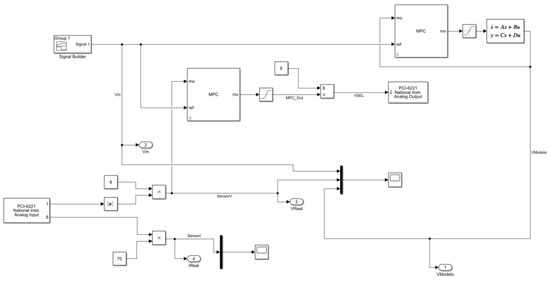
Figure 10.
Model predictive control (MPC) block diagram.
The MPC provides the following advantages compared to other type of controllers:
- Both the dynamic and static behaviors are defined and foreseen by the model.
- Both the input and output variable constraints are considered by the control algorithm.
- The use of model prediction can foresee and anticipate potential problems.
However, in order to keep up with all the calculations in order for the system to have real-time control, this controller needs a powerful calculation device, which can be an issue. Furthermore, the success of the MPC or any other model-based control relies on the accuracy of the model provided.
4. Experimental Results
In this section, the experimental results for the EHU stellarator will be presented. The output signals are obtained by implementing the PID and MPC proposed in Section 3.
4.1. PID Performance
In order to validate the response of the PID controller, the corresponding voltage control test over the real system is carried out, and its result is compared to that of the grey box model. The real performance of the control action is shown in the target PC (Personal Computer) screenshots in Figure 11.
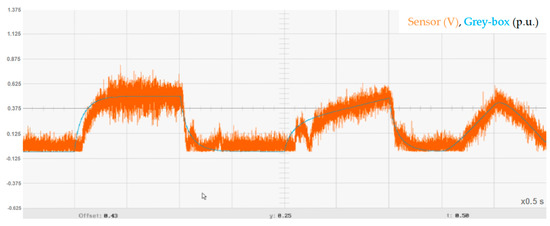
Figure 11.
Comparison of the PID controlled voltage output of the real system and the grey box model.
As shown in the voltage response, the response of the system when controlled by the PID is similar to the tracking reference, providing a fast response with insignificant overshoot.
4.2. MPC Performance
In order to implement the MPC scheme, a series of parameters must be determined. As an indicator to choose an adequate MPC controller, the performance of the estimated control models will be compared. For the values of the control and prediction horizons, initially small but increasing test values are chosen, taking into account that the control horizon is usually around half the prediction relation. The reason for this is that the computational load of the target must be sufficiently low, so as not to overrun the task execution time (TET). In this sense, the value for the control interval must ensure the capability of the target to carry out all the calculations. This means the target cannot exceed the TET, since it would no longer be a real-time system. Additionally, an appropriately sized value should be chosen to reduce computation cycles, and thus energy consumption and heat generation.
Using this procedure, the chosen values for the aforementioned MPC parameters can be observed in Table 4.

Table 4.
Tuned MPC parameters.
Then, the implementation of the MPC algorithm voltage-controlled test shoot is performed over the real system, and its results are compared with that of the grey box model, as shown in Figure 12.
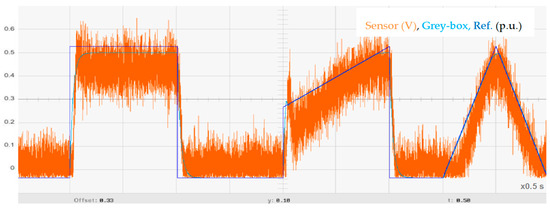
Figure 12.
Comparison of the MPC controlled voltage output of the real system and the grey box model.
The results of Figure 12 show how the measured voltage accurately follows the given set points. In this way, not only is the controller validated, but also it is shown that the grey box model accurately represents the dynamics of the real system. As can be seen in the same figure, the manipulated variable follows the tracking reference up to the point where it foresees unwanted behavior for the system, so the output signal is altered in advance.
4.3. MPC and PID Performance Comparison
Once both the PID and the MPC have been implemented and validated, these controllers can be compared in order to determinate which one offers the best performance while accomplishing the established requirements, as seen in Figure 13.
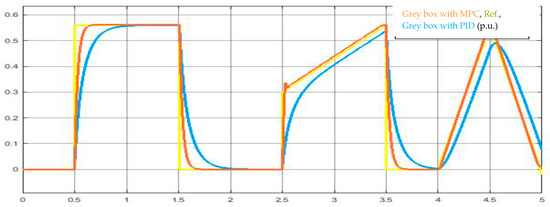
Figure 13.
Comparison of the MPC- and PID-controlled grey box model simulations.
Due to the prediction ability of the MPC, its performance is superior to that of the PID, and it fulfils all the restrictions. That is to say, it provides a quicker response than the PID, whilst providing better performance in fast-changing set point scenarios, with zero overshoot and null steady-state error.
5. Conclusions
Among the existing nuclear fusion variants around the world, stellarators have proved to be more promising than their alternatives, tokamaks. For the EHU stellarator, a series of different model estimation methods were proposed. Of these, the grey box model was the one that demonstrated the best performance, as can be inferred from Figure 7. Then, the proposed numerical model was cross-validated with the results from different experiments executed in the real EHU stellarator.
Once the grey box model was selected as the model that fits best the real plant, different real-time control laws were developed: a traditional PID and a model predictive control (MPC).
From the analysis of the real plant experimental outputs of the EHU stellarator, the MPC has been proven to provide superior performance. The ability of the MPC to predict the upcoming states or output behavior of the plant and to act accordingly, optimizing the output variable change over time, provides precise control of the system dynamics during the experiment execution. In this sense, the PID is not able to deal with dynamic changes as well as the MPC does. However, it is able to control the system because it keeps up with the reference tracking.
The control scheme proposed can be of use for other devices with a similar configuration. In particular, it could be interesting for implementation of advanced control laws as a substitute to the traditionally used PID-based control laws.
Author Contributions
All authors contributed to the modeling and implementation of the EHU stellarator. All authors conceived, developed, and implemented the control techniques. All authors analyzed and validated the results. All authors contributed to writing, review, and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Basque Government, through project IT1207-19 and by the MCIU/MINECO (Ministerio de Ciencia, Innovación y Universidades/Ministerio de Economía y Empresa) through RTI2018-094902-B-C22 (MCIU/AEI/FEDER,UE)/DPI2015-70075-R (MINECO/FEDER,EU).
Acknowledgments
The authors would like to thank the Guest Editor of the Special Issue and the referees for the thorough review of the manuscript and the useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ITER Organization. What is ITER? 2019. Available online: https://www.iter.org/proj/inafewlines (accessed on 18 December 2019).
- Wikimedia Foundation, Inc. Nuclear Fusion-Wikipedia. 2019. Available online: https://en.wikipedia.org/wiki/Nuclear_fusion (accessed on 18 December 2019).
- ITER Organization. What is a TOKAMAK? 2019. Available online: https://www.iter.org/mach/Tokamak (accessed on 18 December 2019).
- Wikimedia Foundation, Inc. Stellarator-Wikipedia. 2019. Available online: https://en.wikipedia.org/wiki/Stellarator (accessed on 18 December 2019).
- De la Sen, M.; Garrido, A.J.; Soto, J.C.; Barambones, O.; Garrido, I. Suboptimal regulation of a class of bilinear interconnected systems with finite-time sliding planning horizons. Math. Probl. Eng. 2008, 817063. [Google Scholar] [CrossRef]
- Kollár, I.; Pintelon, R.; Schouken, J. Frequency Domain System Identification Toolbox for MATLAB. IFAC Proc. Vol. 1991, 24, 1243–1247. [Google Scholar] [CrossRef]
- Li, K.; Thompson, S. Fundamental grey-box modelling. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 3648–3653. [Google Scholar]
- Garrido, I.; Garrido, A.J.; Sevillano, M.G.; Romero, J.A.; Amundarain, M.; Alberdi, M. Tokamak state-space control modeling. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008; Volume 1–4, pp. 840–847. [Google Scholar] [CrossRef]
- Garrido, A.J.; Otaola, E.; Garrido, I.; Lekube, J.; Maseda, F.J.; Liria, P.; Mader, J. Mathematical Modeling of Oscillating Water Columns Wave-Structure Interaction in Ocean Energy Plants. Math. Probl. Eng. 2015, 727982. [Google Scholar] [CrossRef]
- Heong Ang, K.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13. [Google Scholar] [CrossRef]
- De la Sen, M. On Cauchy’s Interlacing Theorem and the Stability of a Class of Linear Discrete Aggregation Models Under Eventual Linear Output Feedback Controls. Symmetry 2019, 11, 712. [Google Scholar] [CrossRef]
- Babiarz, A.; Czornik, A.; Niezabitowski, M. Output controllability of the discrete-time linear switched systems. Nonlinear Anal. Hybrid Syst. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Garrido, A.J.; Garrido, I.; Barambones, O.; Alkorta, P.; Maseda, F.J. Simple Linear Models for Plasma Control in Tokamak Reactors. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Herrera-Cáceres, C.A.; Ibeas, A. Model predictive control of cash balance in a cash concentration and disbursements system. J. Frankl. Inst. 2016, 353, 4885–4923. [Google Scholar] [CrossRef]
- Garrido, I.; Garrido, A.J.; Romero, J.A.; Carrascal, E.; Sevillano-Berasategui, M.G.; Barambones, O. Low Effort Li Nuclear Fusion Plasma Control Using Model Predictive Control Laws. Math. Probl. Eng. 2015, 527420. [Google Scholar] [CrossRef]
- Sturzenegger, D.; Morari, M.; Semeraro, V.; Gyalistras, D.; Smith, R.S. BRCM Matlab Toolbox: Model generation for model predictive building control. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Garrido, A.J.; Garrido, I.; Alberdi, M.; Amundarain, M.; Barambones, O.; Romero, J.A. Robust Control of Oscillating Water Column (OWC) Devices: Power Generation Improvement. In Proceedings of the 2013 MTS/IEEE Oceans Conference-San Diego, San Diego, CA, USA, 23–27 September 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).