Abstract
Analyses of the processes of information transfer within network structures shows that the conductivity and percolation threshold of the network depend not only on its density (average number of links per node), but also on its spatial symmetry groups and topological dimension. The results presented in this paper regarding conductivity simulation in network structures show that, for regular and random 2D and 3D networks, an increase in the number of links (density) per node reduces their percolation threshold value. At the same network density, the percolation threshold value is less for 3D than for 2D networks, whatever their structure and symmetry may be. Regardless of the type of networks and their symmetry, transition from 2D to 3D structures engenders a change of percolation threshold by a value exp{−(d − 1)} that is invariant for transition between structures, for any kind of network (d being topological dimension). It is observed that in 2D or 3D networks, which can be mutually transformed by deformation without breaking and forming new links, symmetry of similarity is observed, and the networks have the same percolation threshold. The presence of symmetry axes and corresponding number of symmetry planes in which they lie affects the percolation threshold value. For transition between orders of symmetry axes, in the presence of the corresponding planes of symmetry, an invariant exists which contributes to the percolation threshold value. Inversion centers also influence the value of the percolation threshold. Moreover, the greater the number of pairs of elements of the structure which have inversion, the more they contribute to the fraction of the percolation threshold in the presence of such a center of symmetry. However, if the center of symmetry lies in the plane of mirror symmetry separating the layers of the 3D structure, the mutual presence of this group of symmetry elements do not affect the percolation threshold value. The scientific novelty of the obtained results is that for different network structures, it was shown that the percolation threshold for the blocking of nodes problem could be represented as an additive set of invariant values, that is, as an algebraic sum, the value of the members of which is stored in the transition from one structure to another. The invariant values are network density, topological dimension, and some of the elements of symmetry (axes of symmetry and the corresponding number of symmetry planes in which they lie, centers of inversion).
1. Introduction
Issues of symmetry presence or absence play a significant role in our understanding of the influence of various system structures on the mechanisms of the processes occurring within them. In a broad sense, a symmetry (proportionality) concept can be interpreted as immutability or invariance, which manifests itself in any transformations of energy, physical structures, integrals of motion, information (etc.), which are involved in the observed process. Note that, in order to understand many processes, it is important to study not only symmetry, but also how its violation changes such processes.
Recently, there has been an increasing use of approaches and methods adopted in the theory of symmetry, in interdisciplinary research, which go beyond the traditional areas (spatial, physical, chemical, biological symmetry, symmetry of social interactions, etc.). As a rule, the main tool for studying the influence of symmetry on mechanisms of various processes is the theory of groups and models created therefrom [1,2,3].
A fundamental focus for exploring the role of symmetry in mechanisms of various processes is the study of diverse and highly complex network structures, such as social networks, data networks, transport networks, and biological structures.
With regard to topological dimensionality, the major part of the studied networks can be divided into planar (2D) and three-dimensional (3D) structures, having regular and irregular structure (networks can also be not planar and decimal-dimensional). Additionally, structures with dimensionality over 3D can be considered in some processes, for example, as studied in [4].
Ability to transmit (conductivity) or block information is one of the most important properties of network structures as a whole, and this depends on their topology. When considering the influence of the network structure on information transmission (conductivity), it is necessary to discuss not only symmetry, but also the influence of changes to the topological dimension (transition from 2D structures to 3D structures).
Note that, in addition to symmetry and dimensional properties (2D or 3D structures), network structures, regardless of their topology, comprise the parameter of network density (average number of links per node), which should be also taken into account when describing their information conductivity.
To describe the conductivity of a network structure, percolation theory, which studies the formation of connected objects in ordered and disordered structures using methods of probability theory, can be used.
One of the important applications of percolation theory is its use to study the integrity and functionality of networks [5,6]. One can also mention the work [7] in which their natural connectivity is used as a spectral measure to characterize the stability of complex networks.
To describe information transfer processes in network structures, this paper explores the possibility of using an interdisciplinary approach-based theory of space groups of symmetry, considering the effect of topological dimension and applying percolation theory.
Many studies of percolation properties of network structures exist [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. However, few of these have focused on investigating the influence of density, topological dimension, and symmetry properties on the conductivity of the network. In this regard, one study [23] exists in which the relationship between reliability of complex networks and their homological properties is investigated by comparing graph-theoretic reliability signatures and quantities derived from topological invariants. The sizes of blocked nodes in clusters are considered to be topological invariants.
2. Percolation Properties of Network Structures and their Invariance
2.1. Theoretical Methods within Percolation Theory
Materials Percolation theory (probability theory for graphs) studies solutions to node problems and link problems for networks with various regular (2D structures, such as triangular, hexagonal, and Kailey trees; and 3D structures, including hexagonal, cubic structures) and random structures. In solving the link problem, the proportion of links that need to be broken in order to split the network into at least two unlinked parts (or vice versa, the proportion of conducting links necessary for conductivity to occur) is defined. In solving the node problem, the proportion of blocked nodes at which the network splits into unlinked clusters, within which links are preserved (or vice versa, the proportion of conducting nodes necessary for conductivity to occur) is defined. The proportion of unblocked nodes (for the node problem) or unbroken links (for the link problem) necessary for conductivity to occur between two arbitrarily chosen nodes of the network is called the percolation threshold (percolation). For the same structure, values of percolation thresholds for the link problem and the node problem are different.
Using the concept of the proportion of blocked nodes or links is equivalent to the concept of probability that randomly selected nodes (or links) are in a blocked (broken) state. Therefore, it can be assumed that the percolation threshold value defines the probability of information being transmitted through the whole network if some part of its nodes (or links) is blocked (excluded), that is, if the average probability of blocking a single node (unlinking) is set.
Reaching the percolation threshold in the network corresponds to a cluster involving links between any of its arbitrary nodes. An infinite or contracting conducting cluster is formed. When transferring information through the network, it is important to consider the influence of the number and size of clusters, including blocked (or transmitting) nodes, on the conductivity of the network structure as a whole.
For finite size structures, conductivity can occur at different portions of conductive nodes (or links, see Figure 1). However, if the network size L tends towards infinity, the area of transition towards the conducting state becomes compact (see Figure 1, curve I for a small structure, curve II for an infinite network).
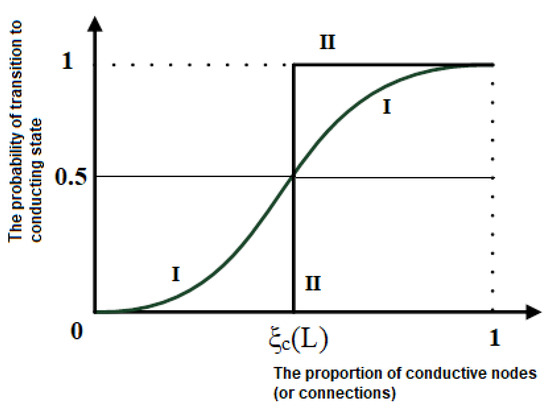
Figure 1.
Dependency of the possibility of percolation occurrence on the value of the proportion of conductive nodes (or connections).
For finite size structures, the value of the percolation threshold ξc(L) can be defined by a given value of the probability of the network transitioning to a conducting state. In Figure 1, this probability is set at 0.5. However, it can be, for example, 0.95 or 0.99 (whereupon the percolation threshold corresponds to the specified criterion of data transmission reliability).
Discussing the application of percolation theory, it should not go without mention that one of the earliest works of Sykes and Essam [8] was the first to study percolation in triangular and hexagonal 2-dimensional lattices, in which they found exact values of their percolation thresholds.
Finding exact thresholds to whole classes of lattices has more recently been done by Scullard and Ziff [9,10]. At present, precision of finding percolation thresholds numerically has risen to over 10 significant digits [11] (though be noted that for our studies precision of not more than 3 is enough).
To study percolation features of lattices, some analytical and numerical methods were applied, going as far back as the beginning of the 1960s by Frisch and Hammersley [12,13], then Stauffer [14], as well as Stanley [15] and many others; these methods are still used nowadays.
Applying percolation theory methods to study network structures, and the processes which occur within them enables us to investigate the following:
- (1)
- Find the distribution by size for clusters of blocked nodes within the network structure at a given probability of blocking the nodes.
- (2)
- Assess statistical characteristics of clusters, for example, the average size of clusters of blocked nodes within the network structure.
- (3)
- Explore how the percolation threshold value of the network structure depends on the density of the network (average number of links per node), as well as a number of other issues.
For regular structures, the total number of blocked nodes can be defined as follows [16,17,18,19,20]:
where is the number of geometric configurations of the cluster consisting of s-nodes, p is the probability of separate node blocking, s is the cluster size (number of nodes included in the cluster), and t is the cluster perimeter (number of non-blocked nodes surrounding the blocked nodes in the cluster).
is cluster distribution by size; N is the total number of nodes included in the cluster; is the average number of clusters consisting of s-nodes; is the probability of the event occurring when a randomly chosen existing node belongs to a cluster of size s; and is the total number of blocked nodes.
The complexity of the calculation lies in the fact that it requires knowing all possible configurations and perimeters. However, some asymptotic results are known for very large clusters of a number of regular structures [8,16,17,18,19,20].
To extrapolate to the case of s → ∞, it is possible to use the results obtained for small clusters. Using the extrapolation results, values of critical parameters can be obtained.
According to the analysis of analytical conductivity models for different structures (for example, see [16,17,18,19]), cluster distribution by size is subject to the power law: the number n(s) of clusters containing s blocked nodes is proportional to s−τ (), where τ is a parameter which considers the topology and spatial symmetry of the network (for example, for a square network τ = 187/91 ≈ 2.05). The power law shows that the ratio of the number of clusters of one size to the number of clusters of another size does not depend on S size, but only on the ratio of their sizes. Thus, percolation clusters are self-similar, or independent of scale, in the interval from the network step to the entire network size (invariant at scales change, i.e., preservation of proportionality, which, in fact, is a characteristic of the symmetry of properties).
It should be noted that percolation theory methods are widely used in various fields of science, not only in mathematics [21,22], physics [23,24] and computer science [25,26], descriptions of the spread of virus epidemics in networks [27,28], but also for example, in earth sciences [29,30,31], analysis of social network structures [32,33,34], and many others.
In works [35,36,37] based on Shklovsky and de Gennes’ representations of the topological structure of the connecting cluster (“skeleton and dead” ends), the following function Y(ξ, L), describing the conditional probability of flow into the network, was obtained:
where ; i is the polynomial degree, ai is the polynomial coefficients, ξ is the proportion of blocked nodes, and ξc(L) is the proportion of blocked nodes corresponding to the percolation threshold value depending on the network size L.
When describing percolation using Equation (1), the main task is to define the polynomial degree i and its coefficients. Combined use of function (1) and methods of algebraic Hodge geometry [42] and Kadanoff–Wilson similarity theory [43,44] using renormalization groups (for example see [19] enables us (in some cases) to calculate theoretical values of the percolation threshold for some regular structures [35,36,37]. According to Hodge theory, algebraic varieties (sets composed of subsets, each of which is a set of solutions to any polynomial equations) are considered. The geometric representations of algebraic varieties are shapes called Hodge cycles. Linear combinations of such geometric shapes are called algebraic cycles [45].
For regular structures, there are invariant parameters for the transition between 2D and 3D topological dimensions [19,38,39,40,41]. In particular, condition is satisfied for a link problem: , where x is the number of links per network node, d topological dimension (d is equal to 2 or 3) and is percolation threshold. Note that, for node problems, an invariant also exists: .
It can be assumed that if invariants for the transition between topological dimensions (2D and 3D) exist, then invariants corresponding to elements in symmetry groups may also exist.
2.2. Numerical Methods for Defining Percolation Thresholds
The main problem in studying percolation properties of network structures is that general analytical methods for this purpose do not yet exist, and it is only possible to study these using computer simulation methods.
Used for numerical calculations, the algorithm for defining the percolation thresholds of 2D and 3D random and regular networks includes the following steps:
- Randomly select two nodes, A and B, taking into account a restriction that there is at least one intermediate node between them.
- Set a probability of blocking a single node (for the node problem) or a link (for the link problem), and randomly block the proportion of network nodes (or links) that is equal to this probability.
- Check if there is at least one “free” path in the network (a path formed by non-excluded nodes or links) from node A to node B. If at least one of the nodes A or B is excluded, then there is no free path (number of "free" paths is 0). Otherwise, write 1.
- Increase the value of probability of blocking a single node (for the node problem) or link (for the link problem) by some value and randomly block the proportion of network nodes (or links) equal to the specified probability value. Then, define which specific network nodes were blocked.
- Go back to step 3 until all nodes of the network are moved.
- Return to item № 2 and perform items № 3–№ 5—Q times (e.g., several hundred times) from the first to the last step (in cases where the entire network is blocked), for all experiments. Find the number of times in which at least one “free” path was found (let this number be ξ). For example, say at step h = 18, in 8, 12, 19, 56, 58, 76, 80 and 89 experiments of Q, at least one “free” path was found, then number ξ(5) = 18 (8 is the total number of “free” paths). Find value ρ (h) = ξ(h)/Q for each step, where h is step number. Calculate the average size of blocked node clusters, the number of such clusters, etc. (for all N experiments at each step). The average cluster size can be defined as the ratio of the sum of all average values obtained at this clustering step (for all Q experiments) to the total number of experiments Q. For clarification, let us consider an example. Given that, for h = 6 steps, 4 clusters comprising 15 nodes were found in the 1st experiment, in the 2nd 3 clusters were found, in the 3rd 2 clusters were found, etc., and in the 100th experiment, 20 clusters were found. Then the average number of clusters with a size of 10 blocked nodes will be equal to: (4 + 3 + 2 + … + 5)/100.
- Then, go back to item № 1 and repeat once more steps № 2–№ 6 W times. For each of the W experiment values, will be found. The W index defines which of the W tests we consider.
- After the simulation, for each h step, find a value —the average value of probability of information transmission through the network as a whole using non-blocked nodes at each step (considering different possible configurations of all paths). Build graphical dependences of the average value of the probability that data or information will pass through the network as a whole on the proportion of blocked network nodes.
3. Dependence of Percolation Properties of Network Structures on Density, Symmetry Groups, and Topological Dimension
When considering the dependence of percolation properties of network structures on the network density (average number of links per node), symmetry groups, and topological dimension, we can be guided by two fundamental principles:
- (1)
- Neumann’s Principle: the symmetry elements of any physical property of a crystal (including network structures) should contain symmetry elements of their point group [46].
- (2)
- Pierre Curie’s symmetry (dissymmetry) principle [46]: at the superposition of several phenomena of different nature, each of which having own symmetry, only matching elements of symmetry of these phenomena will be preserved in the same system. This principle can be written as: , where symmetry of the cause is described by group G1, and symmetry of the consequence by group G2.
One direction for the development of these principles is the theory of similarity symmetry (A.V. Shubnikov), in which not only truly equal shapes are symmetrical, but also all shapes similar to them [47].
Note that using similarity symmetry representations—as well as Neumann’s and Curie’s principles—can be very useful in considering the dependence of percolation properties of network structures on network density, symmetry groups, and topological dimensions, as they enable us to find and assess general patterns, albeit with the minor differences of network structures.
3.1. D and 3D Networks with Regular Structures
Table 1 presents structural characteristics and values of percolation thresholds (for the node blocking problem) for some regular network structures which have 2D and 3D topological dimensions, as shown in Figure 2.

Table 1.
Characteristics and values of percolation thresholds (for the node blocking problem) of some regular network structures.
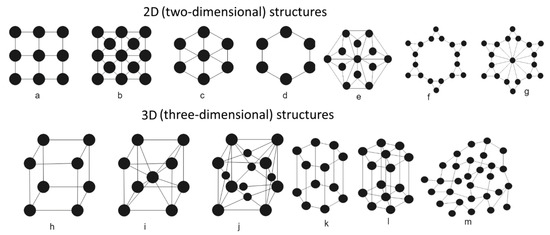
Figure 2.
Geometric representations of some regular network structures.
Note that, for regular structures (such as square, triangular and hexagonal 2D networks), percolation characteristics, such as percolation threshold values, cluster size, etc., can be calculated analytically [8,16,17,18,19,20], but for networks with irregular topology, as well as for many regular 2D and 3D structures, computer simulation methods should be used [12,13,14,15,32,33,34]. In our study, for the classification of regularity of structures, we do not use a graph theory definition, but a broader definition according to which any structures having at least some elements of symmetry are regular. For such structures as: a 3.122 network (see Table 1); centered square and hexagonal 2D networks; a centered 2D network with 3.122; a 3D hexagonal honeycomb structure; 3D parallel 3.122 structures with vertical links; 3D hexagonal and a number of others, percolation thresholds were defined using numerical simulation methods. For other structures listed in Table 1, percolation threshold values were cited from other studies.
To identify the influence of spatial symmetry and topological dimension of network structures on their percolation threshold value, it is necessary to analyze data provided in Table 1. To do this, we can use the conditional probability of network conductivity (see formula (1)). The i-polynomial degree depends on network structure topological properties (network density, spatial symmetry, dimension, etc.), which can be set in the phenomenological approach according to the description by ai. coefficients. This research proposes not to use methods of algebraic Hodge geometry [42] and Kadanoff–Wilson similarity theory [43,44] with renormalization groups (e.g., in [19]), which do not consider the spatial symmetry of the network structure. The essence of the present approach is that it is possible to express dependence of the i-polynomial degree on the conditional probability Y(ξ, L) of conductivity in the network and to define the effect of topological factors on this dependence. Using formula (1) we obtain: , where is a i-polynomial degree, ai is its coefficients, ξ is the current value of the proportion of blocked nodes, and ξc(L) is the proportion of blocked nodes corresponding to the percolation threshold value (this depends on the network size L). Taking into account the fact that near the percolation threshold, ξ ≈ ξc(L), the value of the polynomial is small and can be expanded into a series, limiting these to two terms. After the conversion, we obtain:
The right side of the Equation (2) can be a function (or functional) of several variables, each of which is associated with a certain topological property or with several properties. For example, one of the parameters can be the average number of links x (network density). In this case, formula (2) can be rewritten as: , where is the logarithm of the percolation threshold value, and is some function of x and y variables which are related to the influence of topological factors.
The described approach enables the data presented in Table 1 to be analyzed. Figure 3 shows the dependence of the natural logarithms of percolation thresholds lnP(x) versus inverse network density (1/x)—a unit divided by the average number of links per node. It can be seen from the given data that the dependences obtained have a linear form and can be approximated using linear equations.
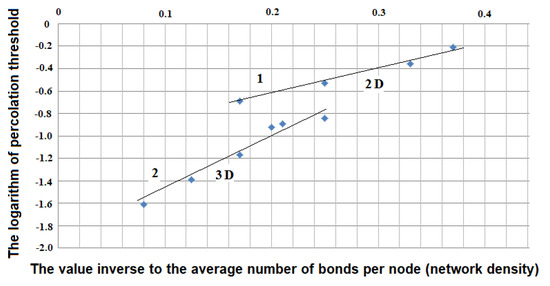
Figure 3.
Dependence of natural logarithms of percolation thresholds lnP(x) versus inverse network density (1/x) for regular structures (line 1 is for 2D topological dimension, line 2 is for 3D topological dimension).
For regular structures with a 2D topological dimension, dependence of the natural logarithm of percolation threshold value lnP(x) versus inverse network density (1/x) can be described by the equation:
with the value of numerical data and linear dependence equation correlation coefficient equal to 0.99. In this case: , and this function is an approximation of polynomial for regular 2D structures.
For regular structures with a 3D topological dimension, dependence of the natural logarithm of the percolation threshold value lnP(x) versus inverse network density (1/x) can be described by the equation:
with the value of numerical data and linear dependence equation correlation coefficient equal to 0.99. In this case: , and this function is an approximation of polynomial for regular 3D structures.
Note that, in the numerical calculations, finite-size networks with boundary nodes which do not have a full number of links were used. Therefore, such a boundary effect causes some error in the percolation threshold calculation.
The results given in Figure 3 show that increasing the number of links per node (density) reduces the percolation threshold for both 2D and 3D structures.
The specific range of inverse network density values between 0.15 to 0.25 (see Figure 3) in which the same density values correspond to different values of percolation thresholds for 2D and 3D regular structures is of particular interest. Within this range, the percolation threshold value for 3D networks is less than that for 2D networks, while the average number of links is equal.
The values of constant coefficients, , , and in Equations (3) and (4) increase at the transition from 2D to 3D regular structures: their values depend on topological dimension. An increase in the topological dimensionality by one unit decreases the value of the percolation threshold of the network and increases the possibilities of information transfer. Note that in this case there is a change in spatial symmetry groups.
It is important to study the combined effects of network density, topological dimension, and spatial symmetry on the percolation threshold value. What are the influences of each of these parameters, both individually and together?
The appearance of an additional spatial coordinate should lead to an increased number of workarounds by which information can be transmitted if some of the nodes are blocked. However, this engenders not only a change in topological dimension, but also in the spatial symmetry groups of network structures. If only one topological dimension had an effect without an influence of spatial symmetry (spatial groups of 2D and 3D networks differ in the set of symmetry elements and their multiplication operations), lines 1 and 2 in Figure 3 would be parallel, which is not the case (the lines are positioned at an angle with each other).
In order to identify exactly how the spatial symmetry groups affect the percolation properties of network structures, it is necessary to investigate 2D and 3D random networks with no symmetry properties. Having found corresponding dependences, it is possible to define the effect of the network density and topological dimension on the percolation threshold value, not taking into account spatial symmetry. When the total value of the percolation threshold is presented as a linear combination of parameters defined by topological dimension, network density, and some symmetry elements, it is possible to define the proportion which is attributable to the density and topological dimension obtained in the study of random structures. Then, it is possible to relate the remainder of the percolation threshold value to symmetry elements in the spatial groups of regular structures (for the same densities and topological dimensions as in the case of random networks) and to assess their effect on the percolation threshold.
3.2. D and 3D Random Structure Networks
The working hypothesis of this study was an assumption that some symmetry elements do not influence the percolation threshold value, while others do. In order to distinguish those symmetry elements in the spatial group which do affect the percolation threshold, it is necessary to compare data given in Figure 3 with data for 2D and 3D random networks.
Building such networks is somewhat complex and should be described separately. As an explanation within the scope of this paper, we can use the following example. Let us build a two-dimensional (2D) planar network (all nodes and their links lie in one plane without any intersection). If we create its mirror image over the developed network and pairwise connect vertical links of the original and mirror nodes, a three-dimensional (3D) structure with a mirror symmetry plane will be formed. If nodes of the original 2D planar network are connected pairwise to the nodes which do not belong to the same cell (the same element of the plane coverage), the network will no longer be planar. A planar random network cell can be determined as being a closed chain of a minimum number of nodes which, when passing through all these nodes, then returns to the starting point. At the same time, the resulting network will not have a 3D structure; its topological dimension will have a fractional value ranging between 2 and 3, depending on the proportion of non-planar links. The fractional value of the topological dimension characterizes the fractality of this structure (since it has a fractional (see Minkowski or Hausdorff) metric dimension in the Euclidean space).
To build a planar (2D) network with random number of links for each node (network density), the following algorithm is used:
- (1)
- Set the number of nodes N and number of links E.
- (2)
- Generate the S list consisting of N nodes with random coordinates (x, y).
- (3)
- Select the n0 node with the smallest x–coordinates; if there are several such nodes, then select the node with the largest y–coordinate.
- (4)
- Sort the S list of nodes by increasing distance L from node n0:
- (5)
- Combine the first three nodes from S list into the first triangle by adding edges. Passing the nodes clockwise, beginning from the edge between the first and second nodes of the list, add the edges of the triangle to the cyclical list H.
- (6)
- Sequentially process all nodes from the S list.
- Find the first raw node ni.
- In the H list, take the last edge V whose nodes na and nb together with ni form a left turn (the following condition is satisfied:
- Among the H edges, find the first edge VL which does not satisfy the left turn condition (located before the edge V to the left of it).
- Among the H edges, find the first edge VR which does not satisfy the left turn condition (located after the edge V to the right of it).
- Sequentially process the edges in the H list between VL and VR. Each of these edges together with ni node forms a new triangle by adding new edges between them.
- Remove from the H list all edges between VL and VR.
- From the first added triangle, find the edge between ni and point of the edge that is not included in the next processed triangle and add it to the H list.
- From the last added triangle, find the edge between ni and point of the edge that is not included in the previous processed triangle and add it to the H list.
- (7)
- Remove edges from the current graph until their number is equal to E. Choose edges randomly, but remove them only if there is a path between the nodes of this edge even without this edge.
Clockwise sorting of vertices:
- (1)
- Find the center of the polygon.
- (2)
- Shift all vertices so that the center is at the root of coordinates.
- (3)
- Find a reference point (for example, radius vector OA = (0, 1) see Figure 4).
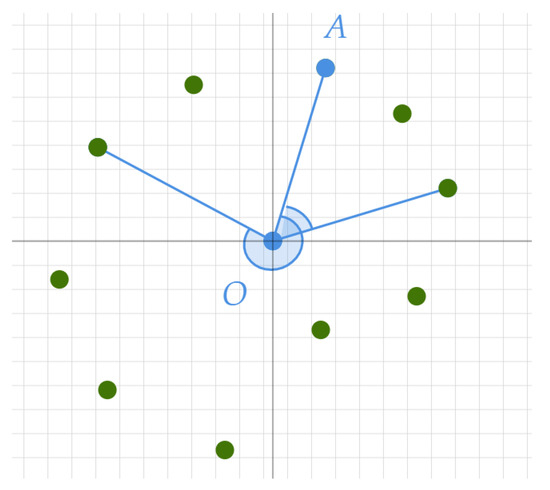 Figure 4. Vertices selection while sorting.
Figure 4. Vertices selection while sorting. - (4)
- Assess angles between vectors from the center to each vertex and OA (the angles should be within the range [0‒360)).
- (5)
- Sort the angles from smallest to largest.
Note that the only difference of algorithm for building a 3D random structure from the algorithm for planar structure is that first parallel layers of 2D random planar networks should be built. Then some of the horizontal links of these layers are randomly replaced with vertical links between adjacent layers, or some of the vertical links are added without replacing the horizontal ones.
Results of the numerical simulation and calculation of percolation threshold values for problem of blocking 2D and 3D network nodes with a random number of links at each node are given in Table 2. For numerical modelling (due to the restriction of the used computation capacities), we used networks of 100,000 nodes, as our algorithm requires considerable computation capacities.

Table 2.
Percolation threshold values for the node blocking problem of 2D and 3D random networks.
Using data for irregular structures with 2D topological dimension showed in Figure 5 and Figure 6 and in Table 2, dependence of natural logarithm of their percolation threshold value lnP(x) versus inverse network density (1/x) can be described by the following equation:
with the value of correlation coefficient of numerical data and equation equal to 0.97.
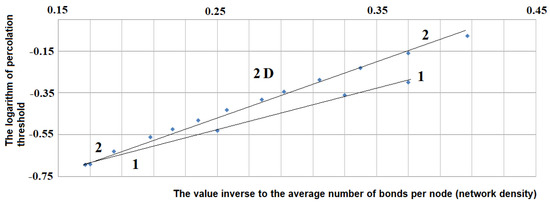
Figure 5.
Dependence of the natural logarithm of percolation threshold lnP(x) of 2D random networks versus inverse network density (1/x) in comparison with regular networks.
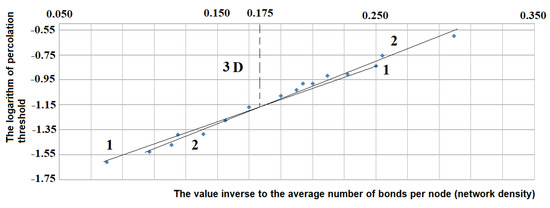
Figure 6.
Dependence of the natural logarithm of the percolation threshold lnP(x) of 3D random networks versus inverse network density (1/x) in comparison with regular networks.
Analysis of data given in Table 2 and Figure 5 shows that, for random planar (2D) structures, percolation threshold at the same network density is less than for structures with symmetry. Thus, in 2D structures, symmetry leads to increase in the required proportion of nodes at which information conductivity occurs.
For irregular structures with a 3D topological dimension, dependence of the natural logarithm of the percolation threshold lnP(x) versus inverse network density (1/x) can be described by the equation:
with the value of correlation coefficient of numerical data and the linear dependence equation equal to 0.97.
Analysis of data given in Table 2 and Figure 6 shows that, for random 3D structures, the value of the percolation threshold has an inversion point. When a network’s inverse density value is more than 0.175 (in this case, network density will be less than 5.7 links per node), the percolation threshold for the same network density will be less than for structures with symmetry, and at values lower than 0.175 (network density being more than 5.7 links per node), the situation will be inverse (see Figure 6, the inversion point is shown by the perpendicular to the horizontal axis).
In the numerical calculations, finite-size networks with boundary nodes which do not have a full number of links were used and such boundary effect causes some error in the calculation of the percolation threshold. Therefore, by comparing Equations (3) and (6), we can assume that, for transition between 2D and 3D topological dimensions, free term of these equations (, , and ) is invariant: (d − 1), where d is topological dimension.
A Comparison of the coefficients , and make it possible to suggest that invariant and , where d is the topological dimension of the structure (d is equal to 2 or 3).
In general, this is consistent with the fact [19,42,43,44,45] that there is an invariance for the percolation threshold value () depending on topological dimension (d): (or ).
Thus, regardless of the type of network, upon transition from 2D to 3D structures, the percolation threshold varies by the value of exp{−(d − 1)}, where d is the topological dimension (this value is invariant in the transition between structures for any network).
3.3. Analysis of Percolation Threshold Values for Regular 2D and 3D Structures and Selection of Components Responsible for Symmetry Elements
Let us consider the effect of network structure density, spatial symmetry groups, and topological dimension on the network percolation properties using the concept of similarity symmetry, as well as Neumann’s and Curie’s principles as mentioned above.
Defining fractions in percolation thresholds due to influence of density and topological dimension enables us to analyze the effect of spatial symmetry groups on the percolation threshold. We can do this using Neumann’s principle and Pierre Curie’s dissymmetry principle. Neumann’s principle states that symmetry elements of the physical properties of the network should include symmetry elements of their point group. Pierre Curie’s dissymmetry principle states that upon superposition of several phenomena of different nature, each of which having its own symmetry, only matching elements of symmetry of these phenomena will be preserved in the same system.
A number of network structures, although they have different spatial (geometric) symmetry groups, have the same topological dimension, density and percolation threshold (these are not specified in Table 1). Let us consider the 2D structures shown in Figure 7 below.
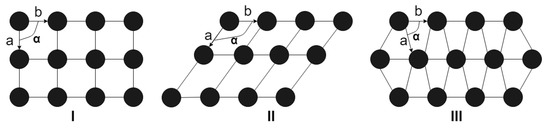
Figure 7.
Geometric structure of some 2D regular networks.
At a = b and α = π/2, for shape I in Figure 7, a tetragonal structure (square network) with a group of spatial symmetry p4mm is obtained; a ≠ b and α = π/2 is the rhombic one having a symmetry group pmm2; a ≠ b and α ≠ π/2 is monoclinic (shape II in Figure 7) with a symmetry group p112. Despite the difference in point symmetry groups (4mm, mm2, 112), these structures have one type of network, which is primitive (designated as p), sharing both the same network density and percolation threshold (equal to percolation threshold of square network, see Table 1).
In this case, we can speak about elongation or contraction (deformation without breaking and forming new links), which can describe all considered structures of the network with the highest symmetry (in this case, a square): in a certain sense, we have an affine symmetry transformation. Furthermore, we can discuss symmetry of similarity (A.V. Shubnikov), when not only truly equal figures are symmetrical, but also all those similar to them.
Some regular 3D structures, despite the difference in symmetry of point groups, also have the same network density (six links per node) and percolation threshold value. The following can be an example: a primitive (symbol—P) cubic network (according to Hermann–Mogen, full designation of the spatial symmetry group is ), primitive monoclinic () and primitive triclinic () network for which the percolation threshold value is equal to the percolation threshold of a simple (primitive) cubic network (see Table 1). In this case, we can also discuss symmetry of similarity and elongation or contraction (deformation without breaking and forming new links), which can describe all considered structures in the network with the highest symmetry and having no effect on the percolation threshold value.
Data presented in Figure 5 and Figure 6 and in Table 2 enable us to define a fraction in the percolation threshold value which is attributable to the effect of symmetry elements in the spatial groups of regular structures. To do this, it is possible to use the network densities shown in Table 1. Then, using Equations (5) and (6) for the chosen link density of regular networks, we can assess the random structure percolation threshold, not taking into account elements of spatial symmetry. Furthermore, by subtracting the obtained values from the percolation thresholds of regular structures specified in Table 1, we can find the fraction of the percolation threshold which is due to the influence of the spatial symmetry group and topological dimension. The data thus obtained are given in Table 3.

Table 3.
Fractions of percolation thresholds of 2D and 3D regular networks, resulting from the influence of spatial symmetry groups (for the node blocking problem).
When analyzing regular structures, it is worth considering not spatial groups, but rather the point groups of coverage elements (Neumann’s principle) which make up the network data. The hexagonal network (structure—a = b and α = π/3 = 60о, see shape III in Figure 7) consists of equilateral triangular elements of the coating, each of which has a perpendicular third-order symmetry axis—C3 and three symmetry planes in which the axis lies (3mm point group). For a square network, the coating element has a fourth-order symmetry axis—C4 and four symmetry planes in which the axis lies (4mm point group). Similarly, the honeycomb structure element of the coating has a sixth-order symmetry axis—C6 and six symmetry planes in which the axis lies (6 mm point group). It is easy to see that, upon transition from 3mm to 4mm, and from 4mm to 6mm, the percolation threshold value for symmetrical 2D structures changes by 0.03 units. Given that the C5 axis does not exist, and, for C2, there is no planar element to create the network, it can be assumed that transition between symmetry axes orders, in the presence of corresponding symmetry planes, also has an invariant that contributes to the percolation threshold value.
A centered square network (shape b in Figure 2) and square network (shape a in Figure 2) differ from each other by the presence of an inversion center for two pairs of nodes in the coverage element. The presence of this inversion center causes the percolation threshold between the structures to change by a value of 0.03 units (see Table 3, value of 0.05—for a square network minus 0.02—for a centered square network engenders a change to the percolation threshold value equal to 0.03).
The hexagonal network (shape c in Figure 2) can be considered as a hexagonal honeycomb structure (shape d in Figure 2) to which an inversion center for three pairs of nodes was added. The presence of this inversion center causes the percolation threshold between the structures to change by a value of 0.06 units (see Table 3, value of 0.08—for a hexagonal honeycomb network minus 0.02—for a hexagonal network engenders a change of the percolation threshold value equal to 0.06).
A centered network with 3.122 structure of (shape g in Figure 2) can be considered as a 3.122 network (shape f in Figure 2), to which an inversion center for three pairs of homogeneous groups of nodes (each including an equilateral triangle on the outer side of the general structure ring) is added. The presence of such an inversion center causes the percolation threshold to change by 0.07 units (see Table 3).
Thus, it can be concluded that the presence of inversion centers in symmetry elements of 2D structures affects the percolation threshold value. Moreover, the more pairs of structure elements have inversions, the more the fraction of the percolation threshold will be changed in the presence of such a center of symmetry.
Let us consider 3D structures. A cubic volume-centered (shape i in Figure 2) network can be considered as a cubic (shape h in Figure 2) network to which an inversion center for four pairs of nodes has been added. However, the center lies in the plane of mirror symmetry that divides the cube into two halves, which most likely negates its influence, and therefore the proportion of the percolation threshold resulting from the influence of symmetry elements is the same for these (see Table 3). This is also supported by the fact that this parameter is the same for cubic face-centered (shape j in Figure 2) networks (see Table 3) in which the inversion centers of side faces are located in the horizontal plane of the mirror symmetry. All this corresponds to Curie’s Symmetry Principle (the super-positioning of several phenomena of different natures, each of which having their own symmetry, wherein only matching elements of symmetry of these phenomena will be preserved in the same system). The presence of a plane of mirror symmetry, in which lies the center of the inversion, negates its influence, since it has the same equivalent effect.
A hexagonal network (shape l in Figure 2) can be considered as a hexagonal honeycomb structure (shape k in Figure 2) to which inversion centers for pairs of nodes located in horizontal layers are added. The presence of these inversion centers causes the percolation threshold to change by 0.02 units (see Table 3). In addition, these networks have a horizontal plane of mirror symmetry, but this has no effect, since the centers of inversion do not lie within it.
Analysis of the data presented in Table 3 shows that, in general, symmetry in 2D structures has a stronger effect on the percolation threshold than it does in 3D structures (for which this effect is very small and is within the accepted error of numerical simulation).
4. Discussion
- At the same density of links, 3D networks have smaller percolation threshold values than 2D ones. Regardless of the type of network and symmetry, at the transition from 2D to 3D structures, the percolation threshold changes to the value equal to exp{–(d − 1)}, where d = topological dimension (this value for any network is invariant at the transition between structures). Thus, an increase in topological dimension by one unit reduces the percolation threshold value of the networks and increases the potential for information transmission.
- For random planar (2D) structures, the percolation threshold value, at the same network density, is less than for 2D structures with symmetry. Thus, for 2D structures, the presence of symmetry leads to an increase in the required proportion of nodes at which information conductivity will occur.
- If 2D or 3D networks have structures which can be transformed (transformed into each other) by deformation (elongation or contraction) without breaking and forming new links, they have the same percolation threshold. There is symmetry of similarity (A.V. Shubnikov), in which not only truly equal figures are symmetrical, but also all those which are similar to them. Thus, the presence of some elements of symmetry contributes to the percolation threshold value, certain others do not.
- The presence of axes of symmetry and corresponding number of planes of symmetry in which they lie affects the percolation threshold value. A third-order axis with three planes of symmetry has an increased invariant (which is preserved for structures of any kind) of the percolation threshold by a value of 0.02 units. At the transition to a fourth-order axis with four planes of symmetry, this invariant increases by 0.03 units, and at the transition from a fourth-order axis to a sixth-order axis, it increases by 0.03 units more. Thus, the transition between the orders of the axes of symmetry, in the presence of corresponding planes of symmetry, has an invariant which contributes to the percolation threshold value.
- Percolation analyses of regular 2D structures show that the presence of inversion centers in symmetry elements reduces the percolation threshold value. Moreover, the greater the number of pairs of the structure elements which have inversion, the more the presence of such centers of symmetry contribute to the fraction of the percolation threshold. However, if the center of symmetry lies in the plane of mirror symmetry separating 3D structure layers, the mutual presence of this group of symmetry elements will not affect the percolation threshold value. This corresponds to Curie’s dissymmetry principle (upon superposition of several phenomena of different natures, each of which having its own symmetry, only matching elements of symmetry of these phenomena will be preserved in the same system), since, in this case, the center of inversion performs the same role as the plane of mirror symmetry.
- The numerical values of percolation threshold fractions (see Table 3), resulting from the influence of symmetry elements, show that, in general, the presence of spatial symmetry and density of networks has a stronger influence on the percolation threshold value in 2D structures than in 3D ones.
5. Further Activities
In this article, we studied the influence of networks spatial symmetry, topological dimension, and density on their percolation threshold with regard to the blocking of nodes problem. It was shown that for different network structures the percolation threshold for blocking nodes problem could be represented as an additive set of invariant values, that is, as an algebraic sum, the value of the members of which is stored in the transition from one structure to another. The invariant values are: network density, topological dimension, and some of the elements of symmetry (axes of symmetry and the corresponding number of symmetry planes in which they lie, the centers of inversion).
However, it should be noted that in percolation theory, the problem of blocking or breaking of links is also important. The results of this problem solution in most cases differ significantly from the solution of the blocking of nodes problem. Therefore, we consider the study of the influence of the networks spatial symmetry, topological dimension, and density on their percolation threshold for the blocking of connections to be a further and promising area of research.
In addition, when performing the simulation, it is also possible to expand the range of investigated structures.
Author Contributions
Conceptualization, D.O.Z.; Methodology, D.O.Z. and S.A.L.; Software, S.A.L.; Validation, E.G.A. and S.A.L.; Formal Analysis, E.G.A. and S.A.L.; Investigation, D.O.Z.; Resources, E.G.A.
Funding
This research was funded by Russian Foundation for Basic Research grant number 16–29–09458.
Acknowledgments
The authors express their sincere gratitude to the Russian Foundation for Basic Research for supporting this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Cracknell, A.; Bradley, C. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Gross, D.J. The role of symmetry in fundamental physics. Proc. Natl. Acad. Sci. USA 1996, 93, 14256–14259. [Google Scholar] [CrossRef] [PubMed]
- Neher, R.A.; Mecke, K.; Wagner, H. Topological estimation of percolation thresholds. J. Stat. Mech. Theory Exp. 2008, 2008, P01011. [Google Scholar] [CrossRef]
- Shang, Y. Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. Unveiling robustness and heterogeneity through percolation triggered by random-link breakdown. Phys. Rev. E 2014, 90, 032820. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.-L. Local Natural Connectivity in Complex Networks. Chin. Phys. Lett. 2011, 28, 068903. [Google Scholar] [CrossRef]
- Sykes, M.F.; Essam, J.W. Some exact critical percolation probabilities for site and bond problems in two dimensions. Phys. Rev. Lett. 1963, 10, 3–4. [Google Scholar] [CrossRef]
- Ziff, R.M.; Scullard, C.R.; Wierman, J.C.; Sedlock, M.R.A. The critical manifolds of inhomogeneous bond percolation on bow-tie and checkerboard lattices. J. Phys. A Math. Theor. 2012, 45, 494005. [Google Scholar] [CrossRef]
- Haji-Akbari, A.; Ziff, R.M. Percolation in networks with voids and bottlenecks. Phys. Rev. E 2009, 79, 021118. [Google Scholar] [CrossRef]
- Jacobsen, J.L. High-precision percolation thresholds and Potts-model critical manifolds from graph polynomials. J. Phys. A Math. Theor. 2014, 47, 135001. [Google Scholar] [CrossRef]
- Frisch, H.L.; Gordon, S.B.; Hammersley, J.M.; Vyssotsky, V.A. Monte Carlo solution of bond percolation processes in various crystal lattices. Bell Syst. Tech. J. 1962, 41, 909–920. [Google Scholar] [CrossRef]
- Frisch, H.L.; Hammersley, J.M.; Welsh, D.J.A. Monte Carlo estimates of percolation probabilities for various lattices. Phys. Rev. 1962, 126, 949–951. [Google Scholar] [CrossRef]
- Stauffer, D.; Hehl, F.W.; Ito, N. Computer Simulation and Computer Algebra; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Xu, X.; Havlin, S. Percolation of a general network of networks. Phys. Rev. E 2013, 88, 062816. [Google Scholar] [CrossRef] [PubMed]
- Grimmet, G. Percolation, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Sahimi, M. Applications of Percolation Theory; Tailor & Francis: London, UK, 1992. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Tailor & Francis: London, UK, 1992. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA; London, UK, 1988. [Google Scholar]
- Tarasevich, Y.Y. Perkolyaciya: Teoriya, Prilozheniya, Algoritmy [Percolation: Theory, Applications, Algorithms]; Yeditorial URSS: Moskow, Russia, 2012. (In Russian) [Google Scholar]
- Mizutaka, S.; Tanizawa, T. Robustness analysis of bimodal networks in the whole range of degree correlation. Phys. Rev. E 2016, 94, 022308. [Google Scholar] [CrossRef]
- De Brito, J.B.; Sampaio Filho, C.I.N.; Moreira, A.A.; Andrade, J.S. Characterizing the intrinsic correlations of scale-free networks. Int. J. Mod. Phys. C 2016, 27, 1650024. [Google Scholar] [CrossRef]
- Timonin, P.N. Statistical mechanics of high-density bond percolation. Phys. Rev. E 2018, 97, 052119. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Maletić, S.; Zhao, Y. Robustness and percolation of holes in complex networks. Phys. A Stat. Mech. Its Appl. 2018, 502, 459–468. [Google Scholar] [CrossRef]
- Bagnoli, F.; Bellini, E.; Massaro, E.; Rechtman, R. Percolation and internet science (Review). Future Internet 2019, 11, 35. [Google Scholar] [CrossRef]
- Katzav, E.; Biham, O.; Hartmann, A.K. Distribution of shortest path lengths in subcritical Erdos-Rényi networks. Phys. Rev. E 2018, 98, 012301. [Google Scholar] [CrossRef]
- Shang, Y. Modeling epidemic spread with awareness and heterogeneous transmission rates in networks. J. Biol. Phys. 2013, 39, 489–500. [Google Scholar] [CrossRef]
- Lesko, S.A.; Alyoshkin, A.S.; Filatov, V.V. Stochastic and percolating models of blocking computer networks dynamics during distribution of epidemics of evolutionary computer viruses. Rossiyskiy Tekhnologicheskiy Zhurnal (Russ. Technol. J.) 2019, 7, 7–27. (In Russian) [Google Scholar] [CrossRef]
- Hunt, A.G.; Yu, F. The fractals of percolation theory in the geosciences (Book Chapter). In Fractals: Concepts and Applications in Geosciences; CRC Press: Boca Raton, FL, USA, 2017; pp. 114–152. [Google Scholar]
- Berkowitz, B.; Ewing, R.P. Percolation theory and network modeling applications in soil physics. Surv. Geophys. 1998, 19, 23–72. [Google Scholar] [CrossRef]
- Rubie, D.C.; Jacobson, S.A. Mechanisms and Geochemical Models of Core Formation (Book Chapter). In Deep Earth: Physics and Chemistry of the Lower Mantle and Core; John Wiley & Sons, Inc.: New York, NY, USA, 2016; pp. 181–190. [Google Scholar]
- Zhukov, D.; Khvatova, T.; Lesko, S.; Zaltsman, A. Managing social networks: Applying the Percolation theory methodology to understand individuals’ attitudes and moods. Technol. Forecast. Soc. Chang. 2018, 123, 234–245. [Google Scholar] [CrossRef]
- Zhukov, D.O.; Khvatova, T.Y.; Lesko, S.A.; Zaltsman, A.D. The influence of the connections density on clusterisation and percolation threshold during information distribution in social networks. Informatika Primeneniya (Inform. Appl.) 2018, 12, 90–97. [Google Scholar]
- Khvatova, T.Y.; Zaltsman, A.D.; Zhukov, D.O. Information processes in social networks: Percolation and stochastic dynamics. In Proceedings of the CEUR Workshop Proceedings 2nd International Scientific Conference “Convergent Cognitive Information Technologies”, Convergent 2017, Moscow, Russia, 24–26 November 2017; Volume 2064, pp. 277–288. [Google Scholar]
- Gallyamov, S.R. A passing threshold of a simple cubic lattice in the site problem of Bethe lattice model. Vestnik Udmurtskogo Universiteta Matematika Mekhanika Komp’yuternye Nauki 2008, 3, 109–115. (In Russian) [Google Scholar] [CrossRef]
- Gallyamov, S.R.; Mel’chukov, S.A.E. On one method of calculationg percolation thresholds for square and diamond lattices in the percolation problem of knots. Vestnik Udmurtskogo Universiteta Matematika Mekhanika Komp’yuternye Nauki. 2009, 4, 33–44. (In Russian) [Google Scholar] [CrossRef]
- Gallyamov, S.R.; Mel’chukov, S.A.E. Hodge’s idea in percolation percolation threshold estimation by the unit cell. Vestnik Udmurtskogo Universiteta Matematika Mekhanika Komp’yuternye Nauki. 2011, 4, 60–79. (In Russian) [Google Scholar] [CrossRef]
- Frisch, H.L.; Hammersley, J.M. Percolation Processes and Related Topics. J. Soc. Ind. Appl. Math. 1963, 11, 894–918. [Google Scholar] [CrossRef]
- Galam, S.; Mauger, A. Universal formulas for percolation thresholds. Phys. Rev. E 1996, 53, 2177–2181. [Google Scholar] [CrossRef]
- Galam, S.; Mauger, A. Topology invariance in percolation thresholds. Eur. Phys. J. B 1998, 1, 255–258. [Google Scholar] [CrossRef]
- Wierman, J.C. Accuracy of universal formulas for percolation thresholds based on dimension and coordination number. Phys. Rev. E 2002, 66, 027105. [Google Scholar] [CrossRef]
- Hodge, W.V.D. The Theory and Applications of Harmonic Integrals; Cambridge University Press: London, UK, 1959. [Google Scholar]
- Kadanoff, L.P.; Jotze, W.; Hamblen, D.; Hecht, R.; Lewis, E.A.S.; Palciauskas, V.V.; Rayl, M.; Swift, J.; Aspres, D.; Kane, J. Static Phenomena Near Critical Points: Theory and Experiment. Rev. Mod. Phys. 1967, 39, 395–431. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization group and critical phenomena. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Krasnov, V.A. Algebraic cycles on a real algebraic GM-manifold and their applications. Russ. Acad. Sci. Izvestiya Math. 1994, 43, 141–160. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Clarendon Press: Oxford, UK, 1967; 322p. [Google Scholar]
- Shubnikov, A.V. Symmetry in Science and Art; Plenum Press: New York, NY, USA, 1974; 420p. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).