Bernoulli’s Problem for the Infinity-Laplacian Near a Set with Positive Reach

Abstract

We consider the exterior as well as the interior free-boundary Bernoulli problem associated with the infinity-Laplacian under a non-autonomous boundary condition. Recall that the Bernoulli problem involves two domains: one is given, the other is unknown. Concerning the exterior problem we assume that the given domain has a positive reach, and prove an existence and uniqueness result together with an explicit representation of the solution. Concerning the interior problem, we obtain a similar result under the assumption that the complement of the given domain has a positive reach. In particular, for the interior problem we show that uniqueness holds in contrast to the usual problem associated to the Laplace operator.

1. Introduction

Bernoulli’s exterior problem consists in finding a couple $(u,\Omega )$ where $\Omega$ is a bounded domain ($=$ an open, connected set) in ${\mathbb{R}}^N$ containing a given compact set K, and u is a solution of

$$\left\{\begin{array}{cc}\Delta u=0\hfill & \mathrm{in}\Omega \backslash K;\hfill \\ u=1\hfill & \mathrm{on}\partial K;\hfill \\ u=0,|\nabla u|=a\hfill & \mathrm{on}\partial \Omega ,\hfill \end{array}\right.$$

(1)

where a is a constant. Similarly, Bernoulli’s interior problem consists in finding $(v,\Omega )$ such that the closure $\overline{\Omega }$ is included in a given, bounded domain ${\Omega }_0$, and v satisfies

$$\left\{\begin{array}{cc}\Delta v=0\hfill & \mathrm{in}{\Omega }_0\backslash \overline{\Omega };\hfill \\ v=0\hfill & \mathrm{on}\partial {\Omega }_0;\hfill \\ v=1,|\nabla v|=a\hfill & \mathrm{on}\partial \Omega .\hfill \end{array}\right.$$

(2)

Both problems have been widely investigated, and several generalizations have been taken into consideration: see, for instance, [1,2,3,4,5,6,7,8,9] and the references therein. In particular, in [10,11,12] the Laplace operator is replaced by the infinity-Laplacian. Roughly speaking, the infinity-Laplacian is the operator ${\Delta }_{\infty }u=u_{ij}{u}_i{u}_j$, where the subscripts $i,j$ denote differentiation with respect to $x_i,x_j$, and the sum over repeated indices is understood. If $\nabla u\ne 0$ we may also write ${\Delta }_{\infty }u=u_{\nu \nu }{u}_{\nu }^2$ where the subscript $\nu$ denotes differentiation in the direction of $\nu =\nabla u/|\nabla u|$. However, the (viscosity) solution of the associated boundary-value problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }u=0\hfill & \mathrm{in}\Omega \subset {\mathbb{R}}^N;\hfill \\ u=\phi \hfill & \mathrm{on}\partial \Omega ,\hfill \end{array}\right.$$

(3)

where $\phi$ denotes the prescribed boundary values, fails to have second derivatives in general. Furthermore, quoting ([13], p. 238): “since the equation is not in divergence form, we cannot expect a notion of weak solution”. In fact, solutions are usually intended in the viscosity sense: a thorough presentation of the concept is found in [14]. For the present purposes it suffices to recall the following.

Definition 1.

Let Ω be a bounded domain in ${\mathbb{R}}^N$. A viscosity solution of problem (3) is a function $u\in C^0\left(\overline{\Omega }\right)$ agreeing with φ on $\partial \Omega$ and satisfying both of the following conditions at each interior point $x_0\in \Omega$: $\left(a\right)$ for every function φ of class $C^2$ in a neighborhood of $x_0$ such that the difference $\phi \left(x\right)-u\left(x\right)$ has a local minimum at $x_0$, the inequality ${\phi }_{ij}\left(x_0\right){\phi }_i\left(x_0\right){\phi }_j\left(x_0\right)\ge 0$ is satisfied; $\left(b\right)$ for every function ψ of class $C^2$ in a neighborhood of $x_0$ such that the difference $\psi \left(x\right)-u\left(x\right)$ has a local maximum at $x_0$, the inequality ${\psi }_{ij}\left(x_0\right){\psi }_i\left(x_0\right){\psi }_j\left(x_0\right)\le 0$ holds. It is worth noticing that if u does not allow the difference $\phi \left(x\right)-u\left(x\right)$ to have a local minimum at $x_0$ for any $C^2$-function φ (think about $u\left(x\right)=|x-x_0|$), then condition $\left(a\right)$ is trivially satisfied, and a similar remark holds for $\left(b\right)$.

Example 1.

Let $\Omega =B_R\left(0\right)$ and $K=\left\{0\right\}$. The function $u\left(x\right)=1-\frac{1}{R}\left|x\right|$ is the unique solution of ${\Delta }_{\infty }u=0$ in $\Omega \backslash K$ satisfying $u\left(0\right)=1$ and $u=0$ on $\partial \Omega$ (the assertion follows by letting $t_0=R$ in Lemma 3). In particular, the origin is not a removable singularity as in the case of the Laplacian.

The equation ${\Delta }_{\infty }u=0$, whose (viscosity) solutions are called infinity-harmonic, appears as the Euler-Lagrange equation of the minimal Lipschitz extension problem (see [15,16]). The name of infinity-harmonic is due to the fact that the solution of the boundary-value problem (3) can be seen as the limit, as $p\to +\infty$, of the p-harmonic functions coinciding with u along the boundary. As usual, by a p-harmonic function we mean a weak solution of ${\Delta }_{p}u=0$, where ${\Delta }_{p}u={\mathrm{div}\left(\right|\nabla u|}^{p-2}\nabla u)$ is the p-Laplace operator. Such an asymptotic representation also holds for the Bernoulli problem (see [12]). Nevertheless, when the domain is let to vary, the behavior of the infinity-harmonic functions may differ substantially from the one of the p-harmonic with finite p:

Example 2.

Choose $p\in (1,+\infty )$ and denote by $v_{R,p}$ the weak solution of ${\Delta }_{p}v=0$ in the annulus $B_1\left(0\right)\backslash {\overline{B}}_R\left(0\right)\subset {\mathbb{R}}^N$, $N\ge 2$, $R\in (0,1)$, satisfying $v_{R,p}\left(x\right)=0$ when $\left|x\right|=1$, and $v_{R,p}\left(x\right)=1$ when $\left|x\right|=R$. Let us focus on the boundary gradient $|\nabla v_{R,p}|$ along the inner boundary $\partial B_R\left(0\right)$. A straightforward computation shows that

$$|\nabla v_{R,p}\left(x\right)|=\frac{1}{R^{\frac{N-1}{p-1}}{\int }_R^1{r}^{-\frac{N-1}{p-1}}dr}forx\in \partial B_R\left(0\right),$$

where the integral is elementary but takes two different expressions according to $p=N$ or $p\ne N$. If the inner radius R tends to zero, the right-hand side tends to $+\infty$ (more on this subject is found in ([4], Section 3) for the special case $p=2$). By contrast, the infinity-harmonic function $v_{R,\infty }\left(x\right)={(1-R)}^{-1}(1-|x\left|\right)$ attaining the same boundary values as $v_{R,p}$ satisfies

$$|\nabla v_{R,\infty }{\left(x\right)|=(1-R)}^{-1}forx\in \partial B_R\left(0\right).$$

Now, the right-hand side decreases and tends to 1 as $R\to 0$. This difference reflects on the results obtained in the present paper for the interior Bernoulli problem: see Theorem 3 and the comments thereafter.

Concerning Bernoulli’s exterior problem, in the paper [12], Manfredi, Petrosyan and Shahgholian proved the result quoted below. Denote by

$$d_X\left(x\right)=\underset{y\in X}{min}|x-y|$$

the (Lipschitz continuous) distance function from a closed, nonempty subset $X\subset {\mathbb{R}}^N$, and let $X+B_r\left(0\right)$ stand for the Minkowski sum

$$X+B_r\left(0\right)=\{x\in {\mathbb{R}}^N\mid d_X\left(x\right)<r\},$$

also called the tubular neighborhood of X of radius r.

Theorem 1

(cf. ([12], Theorem 3.3)). If the compact, nonempty subset $K\subset {\mathbb{R}}^N$ is convex then for every $a>0$ there exists a unique solution of Bernoulli’s problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }u=0\hfill & in\Omega \backslash K;\hfill \\ u=1\hfill & on\partial K;\hfill \\ u=0,|\nabla u|=a\hfill & on\partial \Omega .\hfill \end{array}\right.$$

(4)

The solution is given by $u\left(x\right)=1-a{d}_K\left(x\right)$ and $\Omega =K+B_{1/a}\left(0\right)$.

In the present paper the result is extended in several directions. First, the convexity assumption on K is relaxed and replaced with the weaker assumption that K is a set with positive reach according to the following definition:

Definition 2.

Let $X\ne \varnothing$ be a closed subset of ${\mathbb{R}}^N$. Following [17] we will use the notation

$$\begin{array}{cc}\hfill U\left(r\right)& =\{x\in {\mathbb{R}}^N\mid 0<d_X\left(x\right)<r\},r\in (0,+\infty ];\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill Y\left(r\right)& =\{x\in {\mathbb{R}}^N\mid d_X\left(x\right)\ge r\},r\in (0,+\infty ).\hfill \end{array}$$

(6)

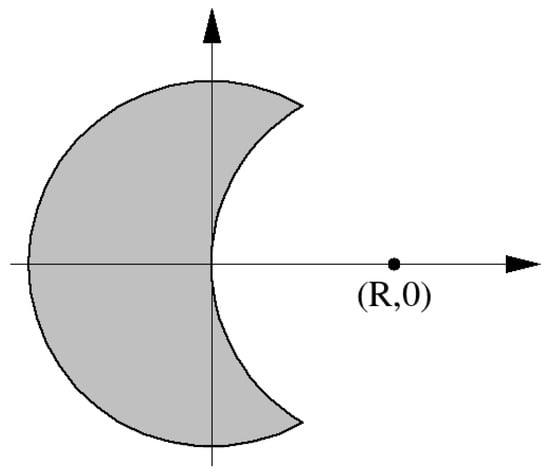
If for some $x\in {\mathbb{R}}^N$ there exists a unique $y\in X$ such that $|x-y|=d_X\left(x\right)$, then we say that y is the projection of x onto X, and we write $y={\pi }_X\left(x\right)$. A closed, nonempty set $X\subset {\mathbb{R}}^N$ is a set with positive reach if there exists $r_0\in (0,+\infty ]$ such that for all $x\in U\left(r_0\right)$ there exists a unique $y\in X$ such that $|x-y|=d_X\left(x\right)$. The largest possible value of $r_0\le +\infty$ is called the reach of X and is denoted by $\mathrm{reach}\left(X\right)$ (see Figure 1).

Figure 1. The half-moon $X={\overline{B}}_R(0,0)\backslash B_R(R,0)\subset {\mathbb{R}}^2$ satisfies $\mathrm{reach}\left(X\right)=R$. The point $x=(R,0)$ has infinitely many nearest points $y\in X$.

A further extension lies in the fact that the Neumann condition in (4) is replaced here with the non-autonomous condition

$$|\nabla u\left(x\right)|=q\left(d_K\left(x\right)\right)\mathrm{on}\partial \Omega ,$$

(7)

where $q\left(t\right)$ is a prescribed function that is required not to decrease too fast. In particular, $q\left(t\right)$ is allowed to be a constant, hence condition (7) includes the Neumann condition in (4) as a special case. To be more precise, in Theorem 2 we consider Bernoulli’s exterior problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }u=0\hfill & \mathrm{in}\Omega \backslash K;\hfill \\ u=1\hfill & \mathrm{on}\partial K;\hfill \\ u=0,|\nabla u\left(x\right)|=q\left(d_K\left(x\right)\right)\hfill & \mathrm{on}\partial \Omega ,\hfill \end{array}\right.$$

(8)

where the domain $\Omega$ is required to have a differentiable boundary and to satisfy

$$d_K\left(x\right)\le \mathrm{reach}\left(K\right)\mathrm{for}\mathrm{all}x\in \overline{\Omega }.$$

(9)

The boundary gradient of u occurring in (8) is well defined: indeed, since $\Omega$ has a differentiable boundary, the infinity-harmonic function attaining constant values at the boundary is differentiable up to $\partial \Omega$ (see [18]). Contrary to what one may expect, if we allow q to be any function of the distance $d_K\left(x\right)$ then problem (8) may well admit a solution $(u,\Omega )$ although $\Omega$ is not given by $\Omega =K+B_r\left(0\right)$, as the following example shows.

Example 3.

Let $K={\overline{B}}_1\left(0\right)\subset {\mathbb{R}}^2$, and let Ω be an ellipse in canonical position. Denote by $a,b$ the semi-axes of Ω, with $1<a<b$. Clearly, Ω does not have the form $\Omega =K+B_r\left(0\right)$: nevertheless, let us construct a function $q\left(t\right)$ such that Bernoulli’s problem (8) is solvable. Recall that the boundary-value problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }u=0\hfill & in\Omega \backslash K;\hfill \\ u=1\hfill & on\partial K;\hfill \\ u=0\hfill & on\partial \Omega ,\hfill \end{array}\right.$$

(10)

admits a unique solution u (see, for instance, ([15], Section 5)). Since problem (10) is invariant under reflections with respect to the coordinate axes, and by uniqueness, the equality $u(x_1,x_2)=u(\pm x_1,\pm x_2)$ holds for every $(x_1,x_2)\in \overline{\Omega }\backslash B_1\left(0\right)$ and for every choice of the sign in front of the variables $x_1$ and $x_2$ in the right-hand side. Consequently, we also have $|\nabla u(x_1,x_2)|=|\nabla u(\pm x_1,\pm x_2)|$ for every $(x_1,x_2)\in \partial \Omega$, and we are allowed to define $q\left(t\right)$ as follows: for each $t\in [a,b]$ we first pick $(x_1,x_2)\in \partial \Omega$ such that $d_K(x_1,x_2)=t$, then we let

$$q\left(t\right)=|\nabla u(x_1,x_2)|.$$

Since the boundary gradient possesses the symmetry property mentioned before, the definition of $q\left(t\right)$ does not depend on the particular choice of $(x_1,x_2)\in \partial \Omega$ as long as $d_K(x_1,x_2)=t$, and therefore the definition is well posed. However, then Bernoulli’s problem (8) with this choice of q is solvable, although for every $r>0$ we have $\Omega \ne K+B_r\left(0\right)$.

We prove that if $q\left(t\right)$ does not decrease too fast, for instance if the product $tq\left(t\right)$ is strictly increasing, then problem (8) is solvable if and only if $\Omega =K+B_{t_0}\left(0\right)$ for a convenient $t_0\le \mathrm{reach}\left(K\right)$, and the solution $u=u_{K,t_0}$ has the form (12):

Theorem 2 (On Bernoulli’s exterior problem).

Let $K\ne \varnothing$ be a compact, connected subset of ${\mathbb{R}}^N$, $N\ge 2$, with positive reach $r_0=\mathrm{reach}\left(K\right)\in (0,+\infty ]$, and let $q\left(t\right)$ be any real-valued function of one real variable.

(i)

For every $t_0\in (0,r_0)$ the domain $\Omega =K+B_{t_0}\left(0\right)$ has a differentiable boundary. If

$$t_{0}q\left(t_0\right)=1$$

(11)

then Bernoulli’s exterior problem (8) admits the solution $(u,\Omega )$ where $u=u_{K,t_0}$ is given by

$$u_{K,t_0}\left(x\right)=1-\frac{1}{t_0}{d}_K\left(x\right).$$

(12)

In the special case when $r_0<+\infty$, if the value $t_0=r_0$ satisfies (11) and the domain $\Omega =K+B_{t_0}\left(0\right)$ has a differentiable boundary, then problem (8) admits the same solution as before.

(ii)

Suppose that Equation (11) possesses a unique (finite) solution $t_0\in (0,r_0]$. In case $t_0=r_0$, suppose that the domain $\Omega =K+B_{t_0}\left(0\right)$ has a differentiable boundary. If the inequality $(tq\left(t\right)-1)(t-t_0)\ge 0$ holds for every finite $t\in (0,r_0]$, then the solution $(u,\Omega )$ given in (i) is unique in the class of all domains $\Omega \supset K$ satisfying (9) and with a differentiable boundary.

(iii)

If q is continuous, and if Equation (11) does not possess any solution in $(0,r_0]$, then problem (8) is unsolvable in the class mentioned above.

Observe that if Equation (11) has a solution $t_0\in (0,r_0)$, and the product $tq\left(t\right)$ is strictly increasing, then assertions (i) and (ii) apply. To see that Theorem 2 implies Theorem 1, recall that any compact, convex set $K\ne \varnothing$ is connected and satisfies $\mathrm{reach}\left(K\right)=+\infty$ (see ([17], Corollary 4.6) or ([19], p. 433)), hence (9) always holds. Furthermore the constant function $q\left(t\right)=a>0$ clearly makes the product $tq\left(t\right)$ strictly increasing. Hence Claim (i) (existence) and Claim (ii) (uniqueness) of Theorem 2 imply the statement in Theorem 1. Theorem 2 also extends ([11], Theorem 1.4), where problem (8) is considered in the special case when $K={\overline{B}}_{R_0}\left(0\right)$.

Next we consider the Bernoulli interior problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }v=0\hfill & \mathrm{in}{\Omega }_0\backslash \overline{\Omega };\hfill \\ v=0\hfill & \mathrm{on}\partial {\Omega }_0;\hfill \\ v=1,|\nabla v\left(x\right)|=q\left(d_{\partial {\Omega }_0}\left(x\right)\right)\hfill & \mathrm{on}\partial \Omega ,\hfill \end{array}\right.$$

(13)

where the complement $X={\Omega }_0^c$ of the given bounded domain ${\Omega }_0$ is assumed to be a set with positive reach $r_0=\mathrm{reach}\left(X\right)$. For instance, ${\Omega }_0$ cannot be a square in ${\mathbb{R}}^2$. The unknown domain $\Omega \subset \subset {\Omega }_0$, instead, is searched for in the class of all domains having a differentiable boundary and containing all points out of reach, i.e., $\Omega$ must satisfy the inclusion

$$Y\left(r_0\right)\subset \Omega$$

(14)

where $Y\left(r_0\right)$ is defined according to (6). For instance, if ${\Omega }_0=B_R\left(0\right)$ then $r_0=R$ and every domain $\Omega \subset \subset {\Omega }_0$ containing the origin satisfies (14).

Theorem 3 (On Bernoulli’s interior problem).

Let ${\Omega }_0\ne \varnothing$ be a bounded domain of ${\mathbb{R}}^N$, $N\ge 2$, whose complement $X={\Omega }_0^c$ is a set with positive reach. Define $r_0=\mathrm{reach}\left(X\right)\in (0,+\infty )$, and let $q\left(t\right)$ be any real-valued function of one real variable.

(i)

For every $t_0\in (0,r_0)$ satisfying (11), Bernoulli’s interior problem (13) admits the solution $(v,\Omega )$ where $\Omega =\{x\in {\Omega }_0\mid d_X\left(x\right)>t_0\}$ and $v=v_{X,t_0}$ is given by

$$v_{X,t_0}\left(x\right)=\frac{1}{t_0}{d}_X\left(x\right).$$

(15)

Furthermore, if the value $t_0=r_0$ satisfies (11) then problem (13) admits the same solution as before provided that Ω is not empty and has a differentiable boundary.

(ii)

If Equation (11) possesses a unique solution $t_0\in (0,r_0)$, and if $(tq\left(t\right)-1)(t-t_0)\ge 0$ for every $t\in (0,r_0)$, then the solution given in (i) is unique in the class of all domains $\Omega \subset \subset {\Omega }_0$ satisfying (14) and with a differentiable boundary.

(iii)

If q is continuous, and if Equation (11) does not possess any solution in $(0,r_0)$, then problem (13) is unsolvable in the class mentioned above.

As before, if Equation (11) has a solution $t_0\in (0,r_0)$ and the product $tq\left(t\right)$ is strictly increasing, then assertions (i) and (ii) apply. A corresponding result for the Laplace operator is illustrated in ([20], Theorem 4.1) and in the subsequent ([20], Example (1), p. 108). Remarkably, the monotonicity condition required there for the standard Laplacian (namely, $tq\left(t\right)$ non-increasing) excludes the case $q\left(t\right)=$ constant and is opposite to the one in Theorem 3. It is also to be recalled that the usual interior Bernoulli problem (2) lacks uniqueness of the solution. By contrast, if the Laplacian in (2) is replaced with the infinity-Laplacian, or equivalently if $q\left(t\right)=a$ (constant) in (13), with $a>1/r_0$, then the assumptions in Claim (i) and Claim (ii) of Theorem 3 are satisfied, and existence and uniqueness follow. These differences between $\Delta$ and ${\Delta }_{\infty }$ are related to the different behavior of the radial solutions which was put into evidence in Example 2.

The proofs of both Theorem 2 and Theorem 3 are given in Section 4, using Jensen’s comparison principle ([16], Theorem 3.11). The explicit construction of prospective solutions is done in Section 3, and it is based on some fundamental properties of the distance function, which are in their turn recalled in the next section. The method of proof was introduced in [20] in connection with the Laplacian, and it is a refinement of the approach in [21]. Further applications are found in [11,22,23,24,25,26].

2. Basic Properties of the Distance Function

The function $d_X\left(x\right)$ measures the distance from the running point $x\in {\mathbb{R}}^N$ to a given nonempty closed subset $X\subset {\mathbb{R}}^N$. The properties of $d_X\left(x\right)$ needed to prove Theorem 2 and Theorem 3 are found in [17,19,27] (see also [28]). Here we collect the main statements under a unified notation, and give precise references to the sources. We start with the notion of proximal normal and proximal smoothness.

Definition 3.

(Cf. ([27], Definitions 3.6.3 and 3.6.5), and ([17], pp. 119–120)). Let $X\ne \varnothing$ be a proper subset of ${\mathbb{R}}^N$.

(i)

A unit vector $\nu \in {\mathbb{R}}^N$ is a perpendicular, or a proximal normal, shortly a P-normal, to X at $y\in \partial X$ if there exists $r\in (0,+\infty )$ such that $B_r(y+r\nu )\cap X=\varnothing$.

(ii)

Any vector $\zeta \ne 0$ is also a P-normal at y if the unit vector $\nu ={\left|\zeta \right|}^{-1}\zeta$ is a P-normal at y in the sense given above. In this case we say that ζ is realized by an r-ball, where r is as before.

(iii)

Finally, the set X is proximally smooth with radius $r_0\in (0,+\infty )$ if for every $y\in \partial X$ and for every unit P-normal ν (if there exist any) at y we have $B_{r_0}(y+r_0\nu )\cap X=\varnothing$. Equivalently, X is proximally smooth with radius $r_0$ if every P-normal $\zeta \ne 0$ is realized by an $r_0$-ball.

From the definition it is clear that if X is proximally smooth with radius $r_0$ then X is also proximally smooth with radius r for every $r\in (0,r_0)$. Proximal smoothness can be considered equivalent to positive reach in the following sense:

Proposition 1.

Let $X\ne \varnothing$ be a closed, proper subset of ${\mathbb{R}}^N$.

(i)

If X is proximally smooth with radius $r_0$ then X is a set with positive reach and $r_0\le \mathrm{reach}\left(X\right)$.

(ii)

If X is a set with positive reach then for every finite $r\in (0,\mathrm{reach}(X\left)\right]$ the function $d_X$ belongs to the class $C^1\left(U\left(r\right)\right)$ and X is proximally smooth with radius r.

Proof. 

$\left(i\right)$ Suppose that X is proximally smooth with radius $r_0$, and define $U\left(r_0\right)$ according to (5). Let us check that every point $x\in U\left(r_0\right)$ has a unique projection onto X. Take $x\in U\left(r_0\right)$, define $r=d_X\left(x\right)\in (0,r_0)$ and suppose, contrary to the claim, that there exist $y_1,y_2\in \partial X$ such that $y_1\ne y_2$ and $|x-y_i|=r$ for $i=1,2$. By the definition of r, the open ball $B_r\left(x\right)$ does not intersect X, hence the unit vector ${\nu }_i={|x-y_i|}^{-1}(x-y_i)$ is a perpendicular to $\partial X$ at $y_i$ for $i=1,2$. Since X is proximally smooth with radius $r_0$ by assumption, the ball $B=B_{r_0}(y_1+r_0{\nu }_1)$ does not intersect X as well. However B contains $B_r\left(x\right)$ together with all boundary points of $B_r\left(x\right)$ excepted $y_1$. In particular, B contains the point $y_2\in \partial X$. However, since X is closed, we have $y_2\in X$ which shows that B does intersect X: a contradiction. Hence every point $x\in U\left(r_0\right)$ must have a unique projection onto X and Claim $\left(i\right)$ follows.

$\left(ii\right)$ Assume that X is a set with positive reach and choose a finite $r\in (0,\mathrm{reach}(X\left)\right]$. By Definition 2, every $x\in U\left(r\right)$ has a unique projection onto X. Since the projection ${\pi }_X\left(x\right)$ is well defined for all $x\in U\left(r\right)$, by Claim $\left(5\right)$ of ([19], Theorem 4.8) the distance function $d_X$ belongs to the class $C^1\left(U\left(r\right)\right)$. By ([17], Theorem 4.1 (a),(d)), this is equivalent to say that every P-normal $\zeta \ne 0$ is realized by an r-ball, hence X is proximally smooth with radius r. □

Claim (ii) of Proposition 1 implies that if X is a set with positive reach then for every $r\in (0,\mathrm{reach}(X\left)\right)$ the set $X+B_r\left(0\right)$ has a $C^1$ boundary (in fact $C^{1,1}$: see ([19], Theorem 4.8, Claim (9))). The last assertion fails, in general, when $r=\mathrm{reach}\left(X\right)$:

Example 4.

The closed, unbounded set $X={\mathbb{R}}^N\backslash B_1\left(0\right)$ satisfies $\mathrm{reach}\left(X\right)=1$. $\left(i\right)$ The corresponding set $X+B_1\left(0\right)$ equals the punctured space ${\mathbb{R}}^N\backslash \left\{0\right\}$ and does not have a differentiable boundary. $\left(ii\right)$ For every $r\in (0,1]$ the set $Y\left(r\right)$ defined in (6) satisfies $Y\left(r\right)=\{x\in {\mathbb{R}}^N\mid |x|\le 1-r\}$, and therefore $\mathrm{reach}\left(Y\right(r\left)\right)=+\infty$ (see Corollary 1 for a general statement).

We now recall equality (17), which is essential for our purposes.

Lemma 1.

Let $X\ne \varnothing$ be a closed, proper subset of ${\mathbb{R}}^N$ with positive reach. For every finite $r\in (0,\mathrm{reach}(X\left)\right]$ define $U\left(r\right)$ and $Y\left(r\right)$ as in (5) , (6) , and take $x_0\in U\left(r\right)$.

(i)

The projection ${\pi }_X\left(x_0\right)$ is uniquely determined.

(ii)

The distance function $d_X$, which is differentiable at $x_0$ by Proposition 1 $\left(ii\right)$, satisfies

$$\nabla d_X\left(x_0\right)=\frac{x_0-{\pi }_X\left(x_0\right)}{|x_0-{\pi }_X\left(x_0\right)|}.$$

(16)

(iii)

The set $Y\left(r\right)$ is not empty, and the following equality holds:

$$d_X\left(x_0\right)+d_{Y\left(r\right)}\left(x_0\right)=r.$$

(17)

(iv)

The projection ${\pi }_{Y\left(r\right)}\left(x_0\right)$ is uniquely determined, and the three points ${\pi }_X\left(x_0\right)$, $x_0$, ${\pi }_{Y\left(r\right)}\left(x_0\right)$ are aligned.

(v)

For every x on the segment whose endpoints are ${\pi }_X\left(x_0\right)$ and ${\pi }_{Y\left(r\right)}\left(x_0\right)$ we have

$$d_X\left(x\right)=|{\pi }_X\left(x_0\right)-x|.$$

(18)

Proof. 

$\left(i\right)$ The projection ${\pi }_X\left(x\right)$ is uniquely defined for all $x\in U\left(r\right)$ because X is a set with positive reach.

$\left(ii\right)$ Formula (16) is found, for instance, in ([27], Corollary 3.4.5 $\left(i\right)$) as well as in ([29], Theorem 1).

$\left(iii\right)$ We first use part $\left(ii\right)$ of Proposition 1 to see that X is proximally smooth with radius r. Then we follow the proof of ([27], Theorem 3.6.7): in particular, formula (3.52) in [27] corresponds to (17) above.

$\left(iv\right)$ Choose $y\in Y\left(r\right)$ such that $|x_0-y|=d_{Y\left(r\right)}\left(x_0\right)$. From (17) and the triangle inequality we get

$$|{\pi }_X\left(x_0\right)-y|\le |{\pi }_X\left(x_0\right)-x_0|+|x_0-y|=r.$$

However by definition (6) we also have $r\le |{\pi }_X\left(x_0\right)-y|$, hence the triangle inequality holds with equality, and therefore the projection ${\pi }_{Y\left(r\right)}\left(x_0\right)=y$ is uniquely determined and the three points ${\pi }_X\left(x_0\right),x_0,{\pi }_{Y\left(r\right)}\left(x_0\right)$ are aligned, as claimed.

$\left(v\right)$ Observe that for every x on the segment whose endpoints are ${\pi }_X\left(x_0\right)$ and ${\pi }_{Y\left(r\right)}\left(x_0\right)$ we obviously have $d_X\left(x\right)\le |{\pi }_X\left(x_0\right)-x|$, with equality at $x=x_0$. Let us check that the equality also holds for $x\ne x_0$. Suppose, by contradiction, that there is $y\in X$ such that $|y-x|<|{\pi }_X\left(x_0\right)-x|$. By the definition (6) of $Y\left(r\right)$, the point ${\pi }_{Y\left(r\right)}\left(x_0\right)$ satisfies $r\le |y-{\pi }_{Y\left(r\right)}\left(x_0\right)|$. This and the triangle inequality imply

$$r\le |y-x|+|x-{\pi }_{Y\left(r\right)}\left(x_0\right)|<|{\pi }_X\left(x_0\right)-x|+|x-{\pi }_{Y\left(r\right)}\left(x_0\right)|.$$

Since both $x_0$ and x lie on the segment whose endpoints are ${\pi }_X\left(x_0\right)$ and ${\pi }_{Y\left(r\right)}\left(x_0\right)$, we may replace the right-hand side with $|{\pi }_X\left(x_0\right)-x_0|+|x_0-{\pi }_{Y\left(r\right)}\left(x_0\right)|$. Thus, the inequality above becomes

$$r<|{\pi }_X\left(x_0\right)-x_0|+|x_0-{\pi }_{Y\left(r\right)}\left(x_0\right)|=d_X\left(x_0\right)+d_{Y\left(r\right)}\left(x_0\right),$$

which contradicts (17). Claim (v) follows, and the proof is complete. □

Corollary 1.

Let $X\ne \varnothing$ be a closed, proper subset of ${\mathbb{R}}^N$ with positive reach. For every finite $r\in (0,\mathrm{reach}(X\left)\right]$ the set $Y\left(r\right)$ given by (6) is also a set with positive reach, and $\mathrm{reach}\left(Y\right(r\left)\right)\ge r$.

Proof. 

The set $Y\left(r\right)$ is not empty by Lemma 1 (iii). In view of Definition 2, let us check that every point in $V\left(r\right)=\{x\in {\mathbb{R}}^N\mid 0<d_{Y\left(r\right)}\left(x\right)<r\}$ has a unique projection onto $Y\left(r\right)$. This follows from Lemma 1 (iv) provided we show that $V\left(r\right)\subset U\left(r\right)$. We note in passing that the reverse inclusion $(\supset )$ follows immediately from (17). To prove that $V\left(r\right)\subset U\left(r\right)$ we expand $R^N=X\cup U\left(r\right)\cup Y\left(r\right)$ and observe that $Y\left(r\right)\cap V\left(r\right)=\varnothing$, hence $V\left(r\right)\subset X\cup U\left(r\right)$. It remains to verify that $X\cap V\left(r\right)=\varnothing$. To this aim, observe that for every $x\in X$ and $y\in Y\left(r\right)$ we have $|x-y|\ge d_X\left(y\right)\ge r$, hence $d_{Y\left(r\right)}\left(x\right)\ge r$ and the conclusion follows. □

We conclude with a lemma that is needed in the proof of Claim $\left(i\right)$ of both Theorem 2 and Theorem 3, to manage the extremal case when $t_0=\mathrm{reach}\left(X\right)<+\infty$.

Lemma 2.

Let $X\ne \varnothing$ be a closed, proper subset of ${\mathbb{R}}^N$, $N\ge 2$, with positive reach $r_0<+\infty$. If the open set $\Omega =X+B_{r_0}\left(0\right)$ has a differentiable boundary, then the distance function $d_X$ is differentiable at every $x_0\in \partial \Omega$, and (16) holds.

Proof. 

The lemma follows from ([27], Corollary 3.4.5 $\left(i\right)$), as well as from ([29], Theorem 1) after having shown that every $x_0\in \partial \Omega$ has a unique projection onto X. To simplify the notation, without loss of generality let $x_0=0$ and suppose that the inner normal to $\partial \Omega$ at 0 is the unit vector $e_N=(0,\dots ,0,1)$. We claim that the projection ${\pi }_X\left(0\right)$ is uniquely determined, and it is given by ${\pi }_X\left(0\right)=r_0{e}_N$. Let $\overline{y}$ be any point on X that realizes $|\overline{y}|=r_0$. By definition of distance we have

$$r_0=d_X\left(x\right)\le |x-\overline{y}|\mathrm{for}\mathrm{every}x\in \partial \Omega .$$

By assumption, in a neighborhood $\mathcal{U}$ of $x_0=0$ the boundary $\partial \Omega$ is the graph of a differentiable function $x_N=x_N(x_1,\dots ,x_{N-1})$ such that $\nabla x_N\left(0\right)=0$, and the intersection $\mathcal{U}\cap \Omega$ lies above that graph. Letting $x^{\prime }=(x_1,\dots ,x_{N-1})$ and ${\overline{y}}^{\prime }=({\overline{y}}_1,\dots ,{\overline{y}}_{N-1})$ we may write

$$r_0^2\le {|x^{\prime }-{\overline{y}}^{\prime }|}^2+{(x_N\left(x^{\prime }\right)-{\overline{y}}_N)}^2$$

in a neighborhood of $x^{\prime }=0$, with equality at the origin. Hence the right-hand side (say $f\left(x^{\prime }\right)$) is minimal at $x^{\prime }=0$ and therefore its gradient $\nabla f\left(0\right)=-2{\overline{y}}^{\prime }$ must vanish. However, then the only possible value for $\overline{y}$ is $\overline{y}=r_0{e}_N$, and therefore the projection ${\pi }_X\left(0\right)$ is uniquely determined, as claimed. □

3. Solutions in Parallel Sets

The proofs of Theorem 2 and Theorem 3 are based on a comparison with the particular solutions $u_{K,t_0}$ and $v_{X,t_0}$ that are constructed below.

Lemma 3.

If $K\ne \varnothing$ is a compact, connected set in ${\mathbb{R}}^N$ with positive reach $r_0\in (0,+\infty ]$, then for every finite $t_0\in (0,r_0]$ the function $u=u_{K,t_0}$ in (12) is the unique solution of the boundary-value problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }u=0\hfill & inU\left(t_0\right);\hfill \\ u=1\hfill & on\partial K;\hfill \\ u\left(x\right)=0\hfill & whenever{d}_K\left(x\right)=t_0,\hfill \end{array}\right.$$

(19)

where $U\left(t_0\right)$ is defined by letting $X=K$ in (5).

Proof. 

The uniqueness of the solution of (19) follows from the comparison principle in ([16], Theorem 3.11). The boundary conditions are easily verified. Let us check that the equality

$${\Delta }_{\infty }{u}_{K,t_0}\left(x_0\right)=0$$

(20)

holds in the viscosity sense whenever $x_0\in U\left(t_0\right)$. Since K is a set with positive reach, by Proposition 1 $\left(ii\right)$ and by (16) the distance function $d_K$ is differentiable at $x_0$ and its gradient is the unit vector $-\nu$ given by $-\nu =|x_0-{\pi }_K\left(x_0\right){|}^{-1}(x_0-{\pi }_K\left(x_0\right))$. Consequently the function $u_{K,t_0}$ defined in (12) is also differentiable at $x_0$, and by differentiation we find

$$\nabla u_{K,t_0}\left(x_0\right)=\nu /t_0.$$

(21)

Concerning the second derivatives, since $u_{K,t_0}$ may fail to be of class $C^2$ in a neighborhood of $x_0$ we investigate its restriction to the line ℓ passing through $x_0$ and directed by $\nu$. Define the set $Y\left(t_0\right)$ by letting $X=K$ and $r=t_0$ in (6), and notice that by Lemma 1 (iv) the three points ${\pi }_K\left(x_0\right)$, $x_0$, ${\pi }_{Y\left(t_0\right)}\left(x_0\right)$ are aligned, hence the line ℓ passes through all of them. Using Claim (v) of Lemma 1 we may write

$$u_{K,t_0}\left(x\right)=1-\frac{1}{t_0}|x-{\pi }_K\left(x_0\right)|\mathrm{for}\mathrm{every}x\in \ell \cap U\left(t_0\right).$$

Hence ${\left(u_{K,t_0}\right)}_{\nu \nu }\left(x_0\right)=0$. Consequently, every smooth function $\phi$ such that the difference $\phi \left(x\right)-u_{K,t_0}\left(x\right)$ has a local minimum at $x_0$ must satisfy $\nabla \phi \left(x_0\right)=\nabla u_{K,t_0}\left(x_0\right)=\nu /t_0$ (by (21)) as well as ${\phi }_{ij}\left(x_0\right){\phi }_i\left(x_0\right){\phi }_j\left(x_0\right)={\phi }_{\nu \nu }\left(x_0\right){\phi }_{\nu }^2\left(x_0\right)\ge 0$. Similarly, any smooth function $\psi$ such that the difference $\psi \left(x\right)-u_{K,t_0}\left(x\right)$ has a local maximum at $x_0$ satisfies $\nabla \psi \left(x_0\right)=\nabla u_{K,t_0}\left(x_0\right)$ and ${\psi }_{\nu \nu }\left(x_0\right){\psi }_{\nu }^2\left(x_0\right)\le 0$. By Definition 1, equality (20) holds in the viscosity sense, as claimed. □

Lemma 4.

Let ${\Omega }_0\ne \varnothing$ be a bounded domain of ${\mathbb{R}}^N$, $N\ge 2$, whose complement $X={\Omega }_0^c$ is a set with positive reach, and define $r_0=\mathrm{reach}\left(X\right)\in (0,+\infty )$. For every $t_0\in (0,r_0]$ the function $v=v_{X,t_0}$ in (15) is the unique solution of the boundary-value problem

$$\left\{\begin{array}{cc}{\Delta }_{\infty }v=0\hfill & inU\left(t_0\right);\hfill \\ v\left(x\right)=1\hfill & whenever{d}_X\left(x\right)=t_0;\hfill \\ v=0\hfill & on\partial {\Omega }_0;\hfill \end{array}\right.$$

where $U\left(t_0\right)$ is defined as in (5).

Proof. 

The argument is similar to the proof of Lemma 3. In the present case, for $x_0\in U\left(t_0\right)$ we find

$$\nabla v_{X,t_0}\left(x_0\right)=\nu /t_0$$

(22)

where the unit vector $\nu$ is given by $\nu =|x_0-{\pi }_X\left(x_0\right){|}^{-1}(x_0-{\pi }_X\left(x_0\right))$. We may write $v_{X,t_0}\left(x\right)=\frac{1}{t_0}|x-{\pi }_X\left(x_0\right)|$ for every $x\in \ell \cap U\left(t_0\right)$, where ℓ is the line passing through $x_0$ and directed by $\nu$, and the proof proceeds as before. □

4. Proofs of Theorem 2 and Theorem 3

Proof of Theorem 2.

Claim (i). The boundary of the domain $\Omega =K+B_{t_0}\left(0\right)$ is differentiable for $t_0\in (0,r_0)$ because $\partial \Omega$ is a level surface of the function $d_K$, which is of class $C^1$ by Proposition 1 (ii) and has a nonvanishing gradient by (16). Let $u=u_{K,t_0}$ be given by (12). From Lemma 3 we know that $u_{K,t_0}$ is the unique solution of the boundary-value problem (19). To prove that the couple $(u_{K,t_0},\Omega )$ is a solution of Bernoulli’s exterior problem (8) it remains to check that the last condition there, namely condition (7), is satisfied for every $x\in \partial \Omega$. Observe that (7) reduces to $|\nabla u_{K,t_0}\left(x\right)|=q\left(t_0\right)$ for $x\in \partial \Omega$, i.e. for x satisfying $d_K\left(x\right)=t_0$. However, since $t_0$ is a solution of (11), we have to check that $|\nabla u_{K,t_0}\left(x\right)|=1/t_0$. In the case when $t_0<r_0$, we know that the distance function $d_K$ is differentiable along $\partial \Omega$ and therefore (21) holds. If, instead, $t_0=\mathrm{reach}\left(K\right)<+\infty$, then $\Omega$ has a differentiable boundary by assumption, and (21) follows from Lemma 2. From (21) we get $|\nabla u_{K,t_0}\left(x\right)|=1/t_0$, as expected.

To prove Claim (ii), suppose that Bernoulli’s exterior problem (8) admits a solution $(u,\Omega )$ where $\Omega$ is a bounded domain satisfying the assumptions. Define

$$t_1=\underset{z\in \partial \Omega }{min}{d}_K\left(z\right),t_2=\underset{z\in \partial \Omega }{max}{d}_K\left(z\right).$$

Assume, contrary to the claim, that $t_1<t_2$. Define the parallel sets ${\Omega }_i=K+B_{t_i}\left(0\right)$, $i=1,2$, and consider the functions $u_i\left(x\right)=u_{K,t_i}\left(x\right)$ given by (12). Observe that ${\Omega }_1\subset \Omega \subset {\Omega }_2$. Since $u\ge 0$ on $\partial \Omega$ as well as on $\partial K$, by the comparison principle ([16], Theorem 3.11) it follows that $u\ge 0$ on $\partial {\Omega }_1\subset \overline{\Omega }\backslash K$. However, then

$$0\le u_1\le u\mathrm{in}{\Omega }_1\backslash K.$$

(23)

Similarly, since $u_2\ge 0$ along the boundary $\partial \Omega \subset {\overline{\Omega }}_2\backslash K$, we obtain

$$u\le u_2\le 1\mathrm{in}\Omega \backslash K.$$

Let us consider a point $P_1\in \partial {\Omega }_1\cap \partial \Omega$, i.e., a point on $\partial \Omega$ such that $d_K\left(P_1\right)=t_1$. By (9) we also have $t_1<t_2\le \mathrm{reach}\left(K\right)$, hence the boundary $\partial {\Omega }_1$, which is the level set $\{d_K\left(x\right)=t_1\}$ of the continuously differentiable function $d_K\left(x\right)$, is differentiable at $P_1$ and it is tangent to $\partial \Omega$ there. Since $u_1\left(P_1\right)=u\left(P_1\right)=0$, and by (23), we deduce

$$t_1^{-1}=|\nabla u_1\left(P_1\right)|\le |\nabla u\left(P_1\right)|=q\left(t_1\right),$$

(24)

where the last equality comes from (7). Thus, we have $t_{1}q\left(t_1\right)\ge 1$. Since Equation (11) has a unique solution $t_0$ by assumption, and the inequality $(tq\left(t\right)-1)(t-t_0)\ge 0$ holds for all finite $t\in (0,r_0]$, we deduce $t_1\ge t_0$. Now we argue at a point $P_2\in \partial {\Omega }_2\cap \partial \Omega$. Notice that the function $d_K$ may fail to be differentiable at $P_2$ in case $t_2=\mathrm{reach}\left(K\right)<+\infty$: indeed, although $\Omega$ has a differentiable boundary, we have not proven that $\Omega$ is a parallel set to K, yet, and therefore Lemma 2 is not applicable. To overcome this difficulty we let $X=K$ and $r=t_2$ in (17) and obtain $d_K\left(x\right)=t_2-d_{\partial {\Omega }_2}\left(x\right)\ge t_2-|x-P_2|$ for all $x\in {\Omega }_2\backslash K$. Hence writing $t_2$ in place of $t_0$ in (12) we get

$$\begin{array}{cc}\hfill u\left(x\right)\le u_2\left(x\right)& \le 1-\frac{1}{t_2}(t_2-|x-P_2\left|\right)\hfill \\ \hfill & =\frac{1}{t_2}|x-P_2|\mathrm{for}\mathrm{all}x\in \Omega \backslash K.\hfill \end{array}$$

Hence the gradient of u, which exists by assumption, must satisfy the estimate

$$q\left(t_2\right)=|\nabla u\left(P_2\right)|\le t_2^{-1}$$

(25)

and consequently $t_2\le t_0\le t_1$, contradicting the assumption $t_1<t_2$. Hence we must have $t_1=t_2$, and Claim (ii) is followed by uniqueness (Lemma 3).

To prove Claim (iii) we suppose, by contradiction, that problem (8) is solvable, and show that Equation (11) has a solution $t_0\in (0,r_0]$, in contrast with the assumption. We follow the same argument as before. In the case when $t_1<t_2$ we arrive again at (24) and (25), hence the difference $tq\left(t\right)-1$ is non-negative at $t_1$ and non-positive at $t_2$: a contradiction arises because q is continuous. If, instead, $t_1=t_2$, then we may write $\Omega =K+B_{t_0}\left(0\right)$ where $t_0$ denotes the common value of $t_1,t_2$. By uniqueness (Lemma 3), the alleged solution u must coincide with the function $u_{K,t_0}$ in (12). Since $\Omega$ has a differentiable boundary, $u_{K,t_0}$ is differentiable along $\partial \Omega$ (by Lemma 2) and (21) holds. Hence $q\left(t_0\right)=|\nabla u\left(x\right)|=|\nabla u_{K,t_0}\left(x\right)|=1/t_0$ for $x\in \partial \Omega$, which shows that Equation (11) still has a solution $t_0\in (0,r_0]$. The proof is complete. □

Proof of Theorem 3.

The argument is similar to the proof of Theorem 2, with minor differences. In particular, in the proof of Claim (i) we use Lemma 4 and (22) to show that the couple $(v_{X,t_0},\Omega )$ is a solution of problem (13). The conclusion also holds in case $t_0=r_0$ by Lemma 2 because the two sets $X+B_{r_0}\left(0\right)$ and $\Omega =\{x\in {\Omega }_0\mid d_X\left(x\right)>r_0\}$ have the same boundary. To prove Claim (ii), denote by $(v,\Omega )$ a solution of (13) and let

$$t_1=\underset{z\in \partial \Omega }{min}{d}_X\left(z\right),t_2=\underset{z\in \partial \Omega }{max}{d}_X\left(z\right).$$

Define ${\Omega }_i=\{x\in {\Omega }_0\mid d_X\left(x\right)>t_i\}$ and $v_i=v_{X,t_i}$ for $i=1,2$. Let us check that $U\left(t_1\right)\subset {\Omega }_0\backslash \overline{\Omega }$, or equivalently $\overline{\Omega }\subset Y\left(t_1\right)$, where $U\left(t_1\right)$ and $Y\left(t_1\right)$ are defined according to (5),(6). Suppose, by contradiction, that there exists $x_0\in \overline{\Omega }\cap U\left(t_1\right)$. The segment joining $x_0$ to ${\pi }_X\left(x_0\right)$ must intersect the boundary $\partial \Omega$ at some point z (possibly $z=x_0$). By Lemma 1 (v) we have $d_X\left(z\right)=|z-{\pi }_X\left(x_0\right)|\le d_X\left(x_0\right)<t_1$, but this contradicts the definition of $t_1$. Now let us check that ${\Omega }_0\backslash \overline{\Omega }\subset U\left(t_2\right)$, which is equivalent to $Y\left(t_2\right)\subset \overline{\Omega }$. Suppose, by contradiction, that there exists $x_0\in Y\left(t_2\right)\backslash \overline{\Omega }$. Now the set $Y\left(r_0\right)$ comes into play. Recall that $Y\left(r_0\right)$ is a set with positive reach by Corollary 1. By (14), the segment joining $x_0$ to ${\pi }_{Y\left(r_0\right)}\left(x_0\right)$ must intersect the boundary $\partial \Omega$ at some point $z\ne x_0$, and we have $d_{Y\left(r_0\right)}\left(z\right)=|z-{\pi }_{Y\left(r_0\right)}\left(x_0\right)|<d_{Y\left(r_0\right)}\left(x_0\right)$. Using (17), the last inequality leads to $d_X\left(x_0\right)<d_X\left(z\right)$. However we also have $t_2\le d_X\left(x_0\right)$ because $x_0\in Y\left(t_2\right)$, hence we get $t_2<d_X\left(z\right)$ in contrast with the definition of $t_2$. In summary, we have

$$U\left(t_1\right)\subset {\Omega }_0\backslash \overline{\Omega }\subset U\left(t_2\right)$$

and by comparison we get

$$v_2\le v\mathrm{in}{\Omega }_0\backslash \overline{\Omega },v\le v_1\mathrm{in}U\left(t_1\right).$$

(26)

Now choose $P_i\in \partial \Omega$ such that $d_X\left(P_i\right)=t_i$ for $i=1,2$. Assume, by contradiction, that $t_1<t_2$. By (26) we obtain

$$q\left(t_2\right)=|\nabla v\left(P_2\right)|\le |\nabla v_2\left(P_2\right)\left|\right|\nabla v_1\left(P_1\right)|\le |\nabla v\left(P_1\right)|=q\left(t_1\right).$$

For this purpose, note that $v_i$ is differentiable at $P_i$, $i=1,2$, because $t_2<r_0$ as a consequence of assumption (14). Finally, using (22), we arrive at

$$t_{2}q\left(t_2\right)\le 1\le t_{1}q\left(t_1\right),$$

and the proof of Claim (ii), as well as the proof of Claim (iii) proceeds as before. □