Abstract
The paper presents a possibility to use a new PVM-VSI (Preference Vector Method computed in Vector Space of Increments) method in making decisions that demand that different variants should be considered, while being evaluated with respect to different criteria. Hence, knowledge about them is a must, and that knowledge is not necessarily available quantitatively, whereas the very evaluation should be relatively objective; that is, independent from the decision maker’s preferences or opinions. The paper presents the use of the PVM-VSI method in support decisions related to urban development—to rank projects submitted for implementation within the framework of a citizen budget. The ranking will make it feasible to determine which of the submitted projects will have the dominant influence on the town’s sustainable development, and, subsequently, which ones should be presented to citizens as the better ones out of the projects submitted, and to compare the method mentioned with methods used in similar decision-making problems in the past: Fuzzy AHP (Analytic Hierarchy Process), Fuzzy TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), and Fuzzy PROMETHEE (Preference Ranking Organization METHod for Enrichment of Evaluation).
1. Introduction
Managing a contemporary town with a view to achieving its sustainable development requires that the urban authorities should have to account for a number of interdependencies between factors influencing or affecting the outcome of decisions being made [1]. Thus, they have to account for economic, social, and environmental factors [2]. Hence, in their decision making they will have to be knowledgeable in urban planning, spatial development, technology, ecology, sociology, and social psychology, among others. Such knowledge is also needed when new tools, such as a participatory budget, are about to be implemented.
A participatory budget, often also called a “citizen budget” (CB), is a decision-making process involving citizens in the life of their town. In such a CB scheme, citizens co-create their town’s budget, by making joint decisions concerning allocation of a certain portion of the public budget [3]. A portion of public funds set out by the town authorities is allocated to implement those projects that take into consideration the needs that residents of a given quarter, street, or estate have. The implementation of such projects entails a risk, as it neglects the outcome of selected CB projects to be completed for the town’s sustainable development. Therefore, in order for the CB projects to account for sustainability, citizens should be informed which of the submitted projects are best in regard to the sustainable development of their town, quarter, or estate. A decision-making problem arises, which in order to be solved, needs comprehensive knowledge from a number of areas. It is advisable that the emerging decision-making issue be presented to experts who will evaluate the CB projects submitted. To that end, the experts should use available tools, for instance the known methodology MCDA (multi-criteria decision analysis), AHP (Analytic Hierarchy Process) [4,5], PROMETHEE (Preference Ranking Organization METHod for Enrichment of Evaluation) [6], TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) [7], or their variants operating on fuzzy numbers [8] employed successfully to solve similar decision-making problems [9,10,11]. Such fuzzy approaches to decision making are particularly important in decision-making problems where uncertainty arises [12,13,14].
The methodological contribution of this paper is to propose and verify a new MCDA method, called PVM-VSI (Preference Vector Method computed in Vector Space of Increments), based on vector calculations. This method, by studying deviations of variant evaluations, allows one to perceive the decision maker’s uncertainty in the decision making process and account for it in the final evaluative outcome. In practical terms, we verify the proposed method in a decision-making problem to select and evaluate citizen budget projects in a specific city in Poland. The selection was based on a sustainability assessment of the individual variants with the use of PVM-VSI. The obtained results were compared with the results of three other methods, i.e., Fuzzy AHP [15], Fuzzy TOPSIS [16,17], and NEAT F-PROMETHEE (New Easy Approach To Fuzzy PROMETHEE) [18,19].
The rest of the paper is organized as follows. Section 2 presents examples of applications of the MCDA method in assisting solutions to decision-making problems related to urban development. Section 3 describes the PVM-VSI method, applied to assign ranks to projects submitted within the framework of a participatory budget. In Section 4, a decision-making problem related to drawing up a rank of CB projects is described. Section 5 shows research results produced by the PVM-VSI method. Section 6 is devoted to research in which the Fuzzy AHP, Fuzzy TOPSIS, and NEAT F-PROMETHEE methods are used, with a view to comparing outcomes obtained by means of the methods with the PVM-VSI method applied. In addition, Section 6 presents global sensitivity and uncertainty analyses of the solution obtained using the PVM-VSI method. The paper is rounded off with conclusions from the research.
2. Literature
Multi-criteria methods are widely used in solving decision-making problems related to sustainable urban development. The reference literature has examples of the MCDA method used in solving decision-making problems involving participation of funds [10], or similar ones related to a choice of urban developmental priorities, such as allocation of urban land use [20], as well as the extent of land use zones in an urban planning scenario [21].
Another group of decision-making problems where MCDA methods are applied are public area development. The literature often quotes examples of MCDA methods used in issues concerning the selection of a new hospital site [15], hospitals or joint-venture medical institutions [22], places for new emergency services to be erected [23], places to house a new firefighting station [24], or the selection of the very project for construction of that type [9].
MCDA methods were also used in assisting urban development not related directly to emergency services, but of importance to the standard of living of residents in a given region where that project is to be implemented. These construction investments were related to environmental protection and commerce: selection of a landfill place [25], selection of a healthcare waste disposal facility [26], a wastewater treatment plant [27], a wind farm [28], and a shopping center [29]. A considerable group is made up of construction projects related to transport facilities, where MCDA methods were used to assist decision makers in their decisions, such as selection of a strategy (concept) of urban logistics [11,30,31,32], an urban distribution center [33,34], or a public parking place [35].
MCDA methods most frequently used in decisions concerning urban sustainable development are: AHP used in previous studies [11,21,24,25,28,32,35], its fuzzy version (Fuzzy AHP) [9,15,21,22,23,26,29], and a fuzzy version of the TOPSIS method used in other previous studies [10,11,20,23,26,27,29,31,33,34]. Other examples of the use of decisions made in this manner by means of the ELECTRE method [24], PROMETHEE [28], ANP (Analytic Network Process), Fuzzy DEMATEL (DEcision MAking Trial and Evaluation Laboratory), Fuzzy VIKOR (Vlse Kriterijumska Optimizacija kompromisno Resenje which means multi-criteria optimization and compromise solution, in Serbian) [30], and THOWA (2-Tuple Hybrid Ordered Weighted Averaging) [34].
Often hybrid solutions are used along with MCDA methods in which the GIS (Geographical Information System) is used [15,20,25,35], or two methods are combined with a view to finding an optimal solution [11,23,24,28,29,30]. Table 1 depicts the basic characteristics of the MCDA applications in the problems related to urban development.

Table 1.
Use of Multi-criteria decision analysis methods in decision-making urban development problems.
3. Methodological Framework
The PVM-VSI method was used as a methodological framework to evaluate and rank projects submitted for participatory budgeting. The presented method is a modification and extension of the original PVM [36,37]. It is a multi-criteria method assisting a decision maker in making a decision by providing to him a rank of decision variants. The implemented modification allows the decision maker to account for uncertainty in evaluation of decision criteria. The individual steps of the PVM-VSI method are shown in Figure 1.
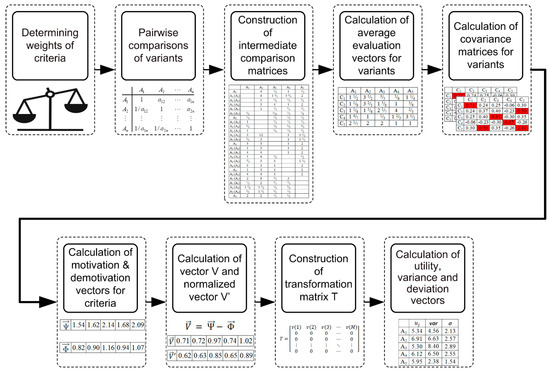
Figure 1.
Basic steps of the PVM-VSI method.
On the basis of the questionnaire addressed to respondents, comparative matrices are produced, where l is the number of criterion being compared. Entries of these matrices are , where i and j are numbers of decision variants. Information contained in those matrices is often inconsistent, which is derived from inconsistent responses. This inconsistency should be reflected in the calculation result. To that end, on the basis of the matrix , matrix is constituted. The matrix is an intermediate matrix of the comparison in reference to the variant .
In the rows of the matrix there are comparisons of the ith variant, with reference to the variant . In the columns there are successive kth decision variants.
The matrix is obtained from the following formula (1):
where is an entry of the matrix .
Matrices are normalised in order to reduce their values to compatibility, in effect to arrive at the matrix (2):
where is an entry in the matrix , while o is the number of the decision variant to which all matrices are reduced.
On the basis of the matrix , vectors of average evaluations are calculated for individual decision variants (3).
where is a vector representing the jth decision variant, whereas is an element of that vector, while N is the number of decision variants.
A matrix containing covariants is also produced for individual variants, regarding the individual criteria (4):
where is an entry of matrix .
For the calculated vectors a motivation preference vector for average value is determined (5):
where i denotes a specific criterion, is the vector element , and means the third quartile calculated with respect to the variant j.
Furthermore, a demotivation vector of preference for average values is determined (6):
where i denotes a specific criterion, is the vector element , and means the first quartile calculated with respect to the variant j.
The vector is calculated as the difference between the vectors i (7):
On the basis of that vector, the vector is determined by reducing it to a unit vector (8):
is the magnitude of the vector (9):
where i denotes a specific criterion, is an element of vector .
The vector allows determination of the transformation matrix T (10):
The matrix is always a square matrix.
Multiplying the coordinates of the vector by the matrix T yields the vector of evaluation of a given decision variant (11):
All elements of the vector , apart from the first one , equal nil. The element is the evaluation of a given decision variant and is comparative in its function. It should be noted that the best solution has the lowest value, so the issue of minimization is considered. In practice, the best option is considered to be the one over which the other variants in pairwise comparison matrices outweigh the least (compare formulas (1)–(3)).
Likewise, the matrix can be transformed, so that the output is the matrix (12):
where is an element of the matrix .
Elements of , for which i = k are variants. On that basis, the standard deviation of the evaluation of decision variants after transformation can be calculated (13):
All elements apart from the first one equal nil. The element is a standard deviation of the evaluation of a given decision variant.
Standard deviation is a measure of the variability of a given phenomenon, object, or objects. That variability can result from changes in the parameters of an object over time, measurement error, and if there are more objects, it may represent their heterogeneousness. If evaluation of objects proves to be difficult, it may stand for a degree of uncertainty of that evaluation. The method presented above, in which comparative matrices are constructed, is used to calculate a deviation standard to represent the degree of uncertainty of evaluation which the PVM method requires. The classical PVM method allows construction of a rank of decision variants. That rank, however, does not allow for a degree of uncertainty of evaluation to be accounted for. A modified method allows determination of a standard deviation for each decision variant included in the rank. Because in this method the standard deviation is at the same time a measure of uncertainty of the evaluation of decision variants, the very rank itself can be interpreted as a measure of uncertainty of its place within the rank. That uncertainty is a product of the decision maker’s uncertainty. Two decision variants that are close to one another in the rank, but characterized by a considerably large standard deviation, can thus be qualified as equivalent.
4. Decision Problem
The objective behind the research performed was to create a rank of projects submitted under a citizen budget and to make conclusive decisions as to which is best. Those projects that come up in hierarchy are more suited to influence urban sustainable development. Hence, they should be given priority by citizens and urban authorities in implementing a citizen budget. This research is meant to assist a decision maker in making their decision in a scenario where they must decide which project to select on the basis of a number of criteria. The criteria are but subjective evaluations by the decision maker in accordance with the scale adopted for the research. This may be related to how precise the evaluations by the decision maker are. Use of the PVM-VSI method is to make it easy for the decision maker to create a rank of projects and select those which will best suit the development of the town, and, indirectly, would be beneficial for the town’s people.
The decision maker evaluated by means of five criteria the same number of decision variants. The projects (variants) in the study were evaluated in accordance with the following criteria:
- C1—spatial order: a criterion on the basis of which the projects were evaluated as to their impact on sorting out the urban space and on how well the constituents of the space are harmonized;
- C2—modernization (revitalization): this criterion accounts for the impact that projects would exert on improving aesthetic assets of the town, estate, quarter, or street to which projects apply, by increasing their value in use and advantageous transformations in the area included in the project;
- C3—environmental and nature protection: a criterion that is used to evaluate projects regarding their impact on nature and the environment, surrounding greenery, inland water, and fauna management in the area concerned;
- C4—sport and tourism: a criterion used in evaluation of the impact of projects on the physical wellbeing of those who live in the area concerned, and to improve the attractiveness of the environs in the eye of tourists in the area;
- C5—culture: a criterion which is used to evaluate the projects in the sense of what bearing they have on spiritual development of people to whom the project may concern.
The criteria here were selected for the research in such a manner that they could be used in the evaluation of the variants on their impact on the economic, social, and environmental milieus included.
Five decision variants were evaluated according to the criteria presented above:
- A1: construction of a walking path along the river Warta from the East Boulevard to the Lubuski Bridge;
- A2: a swimming pool within the river Warta water current;
- A3: improvement in bicycle urban infrastructure;
- A4: integrative playground for handicapped children;
- A5: pro-eco revitalization of Słowiański Park.
These projects were the most interesting ones taken out of the pool of all projects submitted under the Citizen Budget 2018, Gorzów town. A number of projects were selected, which was dictated by the number of comparisons that would have to be drawn up; should all the submitted projects be included in the research, the duration of the very research would be extensively prolonged. The core of the research was not the selection of the most interesting projects, but a comparison of the proposed method assisting decisions with methods used so far in multi-criteria decision problems, where selection criteria are not quantified. Hence, the scope of projects could be narrowed down to a few of the most interesting projects out of the pool of all projects submitted under the 2018 CB.
5. Results
The research had nine stages. The first one was to define the weights of the individual criterion. In this case it was assumed that all criteria would have the same importance to the decision maker; thus, the criteria weights are equal. This can be interpreted as lack of weight.
Across stage two, the decision maker—taking advantage of a poll method—was asked to make pairwise comparisons of the decision variants as defined above. The variants were compared in accordance with the criteria specified above. This stage’s output produced five comparison matrices. The comparison matrix for the criterion C1 (spatial order) is presented in Table 2. The other pairwise comparison matrices are included in Appendix A.

Table 2.
Comparison matrix for variants grouped under C1 criterion – spatial order.
In the stage to follow, on the grounds of the pairwise comparison matrices, intermediate comparison matrices were constructed. The objective was to account for inconsistency of comparison matrices resulting from inconsistency in poll responses in the calculation results. An example of an intermediate comparison matrix is presented in Table 3.

Table 3.
Intermediate comparison matrices for variants grouped under C1 criterion—spatial order.
Stage four consisted of performing calculations on the basis of the matrices shown above, average evaluation vectors for the individual decision variants. The average evaluation vectors are presented in Table 4.

Table 4.
Average evaluation vectors for decision variants.
In the stages to follow, on the basis of the average evaluation vectors, a covariance matrix can be created for individual variants within the framework of individual criterion, as well as motivation and demotivation preference vectors. An example of a covariance matrix for the variant A1 is given in Table 5. Table 6 and Table 7 show motivation and demotivation vectors, respectively.

Table 5.
Covariance matrix for the variant A1.

Table 6.
Motivation preference vector.

Table 7.
Demotivation preference vector.
The successive stage was to calculate the difference between the vectors as above; that is, the vector . It is presented in Table 8.

Table 8.
Values of the vector .
In the successive step, on the basis of the vector and the value of the normalised motivation vector, the vector was determined. The values of that vector are given in Table 9.

Table 9.
Values of the vector .
With the vector known, it is possible to determine a transformation matrix T. That matrix is given in Table 10.

Table 10.
Transformation matrix T.
On the basis of the matrix vectors, average evaluations for successive decision variants and a transformation matrix of the vector of the evaluation of a given decision variant were calculated. All elements of the evaluation vector, apart from the first one, equal nil. The first one is evaluation of a given decision variant and is used to compare decision variants. The evaluations obtained by the individual decision variants are given in Table 11 and Figure 2. However, having a covariance matrix and a transformation matrix, variances can be calculated for successive decision variants, on the basis of which a standard deviation can be calculated for individual variants. Standard deviation is a value informing which area the value of evaluation calculated for a given decision variant can change in this study. Variance values (var) obtained in this study and the standard deviation values (σ) obtained from successive variants are gathered in Table 11.

Table 11.
Evaluations, values of variances, and standard deviation values obtained by individual decision variants.
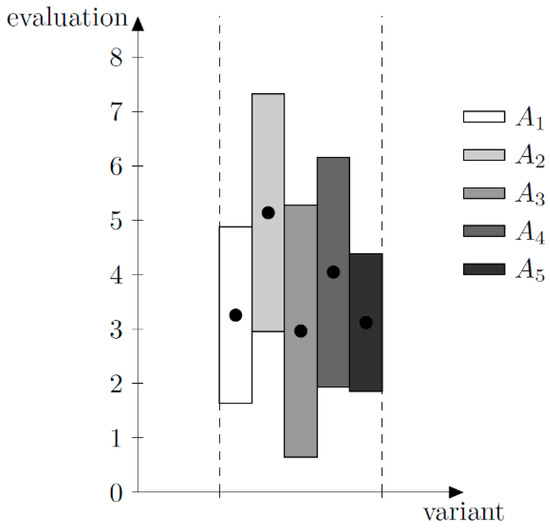
Figure 2.
Evaluations of decision variants.
6. Discussion
The obtained solution was analyzed using GSUA (global sensitivity and uncertainty analyses) [38,39] in order to determine the stability of the ranking. Additionally, the results obtained in the PVM-VSI method were compared with the results obtained in the Fuzzy AHP, Fuzzy TOPSIS, and NEAT F-PROMETHEE methods.
6.1. Global Sensitivity and Uncertainty Analyses
GSUA is a variance-based method of analyzing data and models with regard to objective function [40]. This method assigns probability distribution functions to all inputs of the model and ensures their propagation to outputs [41]. This allows determination of the meaning of input factors and to assess the interactions between the input factors of the model and its outcomes. As a result, it is possible to identify the input factors that reduce the variance of the results [39] to the greatest extent. This method is, therefore, fundamentally different from the traditional methods of sensitivity analysis.
The first element of GSUA was the uncertainty analysis. For this purpose, for all variants the possible values of the criteria were determined in the form of a pair of values: an average value and standard deviation. It can be assumed that they describe a random variable with a certain distribution. It was assumed that these variables have a normal distribution, and then 10,000 combinations of random variables were drawn, for which was determined Then, based on the calculated values of , a relative shift in the position of the variant was determined using formula (14) [40]:
where is the position of the variant in the baseline ranking shown in Table 11 and is the position in the ranking for which values were calculated on the basis of random variables. The 10,000 values of were determined, the histogram of which is shown in Figure 3.
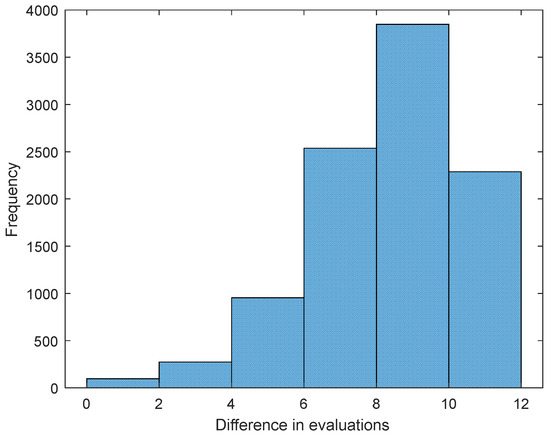
Figure 3.
Uncertainty analysis. Output: cumulative shift from the baseline ranking for five variants.
The analysis of Figure 3 coincides with the conclusions that can be drawn from the values of standard deviations σ from Table 11. Small differences in values with a large standard deviation prove that the assessments in pairwise comparison matrices are very imprecise or that the preferences of the decision maker are not very well defined. Therefore, it is not possible to determine a clear order in the ranking. In Figure 3, the maximum histogram is 8 for , while the lack of changes in the ranking is only for a very small number of randomly drawn cases. This proves the high variability of and the inability to obtain an unambiguous ranking.
In addition to the uncertainty analysis, a sensitivity analysis was carried out using the method developed by Saltelli [40,42]. In this analysis, the Monte-Carlo method was used to calculate first-order and total-effect indices for a model of k factors. The sequences of quasi-random numbers [43,44] were used to generate random values. Two studies were carried out here: (1) for criteria and (2) for criteria and variants together.
On the basis of the matrix of pairwise comparison matrices, average values and variances for the criteria were determined. These values were then used to generate random values. First-order () and total-effect () sensitivity indices, as well as their difference (), were calculated on their basis. These values are presented in Table 12.

Table 12.
First-order and total-effect indices determined for criteria.
The highest value was obtained for a criterion C3. This indicates that the greatest potential to reduce the variance of results is offered by reducing the variance of criterion C3. There are two reasons for this. The first reason is the high value of the vector coordinate corresponding to criterion C3 (Table 9). This means that the share of criterion C3 in determining is very high. The second reason is the high value of criterion C3 variance for most variants, in particular A4 and A3, as shown in Table 13. The difference has a very small positive value, which means that the criteria are not involved in any interaction with other input factors.

Table 13.
Variance evaluation vectors for decisive variants.
In a similar way, i.e., on the basis of a pairwise comparison matrix, average values and variances for criteria and variants were determined. On the basis of the determined averages and variances, random values were generated as the basis for calculating first-order () and total-effect () sensitivity indices, and their difference (). The value is shown in Table 14. Based on the value in Table 14, it is possible to determine precisely for which variants the variances of the criteria should be reduced. Comparing Table 13 and Table 14, it can be seen that the high value of coincides with the high variance values.

Table 14.
Value determined for criteria and variants.
Table 15 shows the differences . They are very close to 0, which means that there is no, or very little, interaction with other input factors.

Table 15.
Values determined for criteria and variants.
6.2. Fuzzy AHP Calculations
In this study a Fuzzy AHP method was applied, as proposed by Vahidnia [15], being an extension of AHP [4,45] in the case in which fuzzy coefficients are used by decision makers instead of precise values.
In the first stage of the study that was carried out by means of fuzzy AHP, pairwise comparison matrices obtained in Section 5 were used with respect to the five criteria with evaluation scores proposed by Saaty (crisp) but changed into fuzzy values. Fuzzy values correspond to the individual Saaty’s scale scores and they are presented in Figure 4. In order to map crisp values onto fuzzy ones, linguistic values were used, defined for both Saaty’s scale and fuzzy scale [4,15]. Mapping of crisp values onto fuzzy ones on the grounds of a linguistic scale is given in Table 16. A 1–9 scale of evaluation scores has been used to associate respective values of the left, mid, and right points of the range, within which the function is defined, to linguistic evaluations.
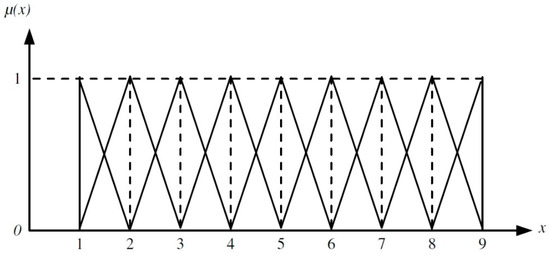
Figure 4.
A five-stage scale of linguistic evaluations and the respective fuzzy values [15].

Table 16.
Mapping crisp values onto fuzzy ones on the grounds of linguistic evaluations [15].
The pairwise comparison matrix for the criterion C1 (spatial order) obtained via changes of evaluation scores in Saaty’s scale into fuzzy values is presented in Table 17.

Table 17.
Evaluation of variants, accounting for criterion C1—a fuzzy value scale.
In stage two, on the basis of the average evaluation scores expressed as fuzzy values, evaluation was calculated for weak, intermittent, and high values. The outcome obtained for individual variants, as per each criterion, is given in Table 18.

Table 18.
Evaluation of variants, accounting for individual criterion—a fuzzy scale.
In the following stage, partial values obtained in variants for individual criteria for weak, intermittent, and high values were aggregated into a final fuzzy value. In the last stage, the final value obtained for individual weak, intermittent, and high values was subjected to defuzzification and normalization, in this way achieving the final evaluation score for each variant. On the basis of the final evaluation score, the place in the ranking for each variant is established. Table 19 has the already defuzzified aggregated vector of scale for fuzzy values, intermittent and high values, and the ranking position obtained in the research procedure, called Fuzzy AHP, via individual variants.

Table 19.
Final fuzzy evaluation scores of individual variants, defuzzified final evaluation score, and position in ranking, established via Fuzzy AHP.
6.3. Fuzzy TOPSIS Calculations
Another method used with a view to comparing results obtained by means of PVM-VSI is Fuzzy TOPSIS. In this method, fuzzy vectors achieved as a result of aggregation of pairwise comparisons and presented in Table 18 were used as input values of variant evaluations. Table 18 may, thus, be interpreted as a fuzzy decision matrix (FDM).
At the very beginning evaluation scores were normalized to achieve a normalized fuzzy decision matrix (NFDM), shown in Table 20, and a weighted normalized fuzzy decision matrix (WNFDM), which due to equal weights of the criteria, is identical with the NFDM.

Table 20.
Normalized fuzzy decision matrix for the Fuzzy TOPSIS Method.
The following stage, with research by Fuzzy TOPSIS, determines ideal and anti-ideal solutions. Values for ideal and anti-ideal solutions for individual criteria are given in Table 21.

Table 21.
Ideal and anti-ideal solutions.
Final results obtained in Fuzzy POPSIS are given in Table 22.

Table 22.
Evaluation of variants in Fuzzy TOPSIS.
6.4. NEAT F-PROMETHEE Calculations
The last method remaining to describe, and used to comparative ends, is NEAT F-PROMETHEE. In this NEAT F-PROMETHEE procedure, a V-shaped preferential function was chosen. The thresholds of this function are given in Table 23.

Table 23.
Thresholds and preference functions used in NEAT F-PROMETHEE.
A matrix of fuzzy preference relations created in NEAT F-PROMETHEE is presented in Table 24.

Table 24.
Fuzzy preference relations matrix.
Fuzzy solutions in NEAT F-PROMETHEE are given in Table 25.

Table 25.
Results of fuzzy solutions obtained in NEAT F-PROMETHEE.
The results in Table 25 were subject to defuzzification. The defuzzified outcome is given in Table 26.

Table 26.
Results in NEAT F-PROMETHEE after defuzzification.
6.5. Comparison of Obtained Ranks
The ranks obtained in the individual MCDA methods are given collectively in Table 27.

Table 27.
Ranks obtained in individual MCDA methods.
After analyzing Table 27, it can easily be noticed that the same ranks were obtained in both Fuzzy AHP, Fuzzy AHP, and NEAT F-PROMETHEE II. A slightly different ranking was obtained using the NEAT F-PROMETHEE I method. In the NEAT F-PROMETHEE I ranking, the order of variants for A1 and A4 changed, which are not comparable (using the median order—indifferentiable), while in the previously mentioned rankings, the preference was obtained . This difference is mainly due to the fact that Fuzzy AHP, Fuzzy AHP, and NEAT F-PROMETHEE II only use relations of indifference (a I b) and preference (a P b), while NEAT F-PROMETHEE I additionally includes an incomparability relation (a R b). In particular, differences between NEAT F-PROMETHEE I and II are because in the first version, the rank is constructed on the basis of crisp values i , while in the second version, a crisp version of was used. In addition, it should be noted that the NEAT F-PROMETHEE I ranking is the closest to the PVM-VSI ranking, in which the preference was obtained for variants A1 and A4. The PVM-VSI ranking overlaps with the other variants in terms of the first (A3), second (A5), and last (A2) positions. One of the reasons for this similarity may be the fact that the PVM-VSI method contains elements that are methodically similar to the other discussed methods, namely:
- Initial stages (the use of pairwise comparison matrices inter alia) are close to AHP;
- The motivating and demotivating vector of preference to a certain degree correspond methodically-wise to the values and , in the method NEAT F-PROMETHEE;
- On certain stages of the authors’ method, an approach based on vector—similar to that in the TOPSIS method—is used.
However, these authors’ methods carry out operations decisively different from the other methods concerned, for instance in the way matrices of intermittent comparisons are constructed, how transformation and covariance matrices are calculated, and calculation of multiplicative aggregation of evaluation values with transformation and average value vector matrices used. Indisputably, these authors’ methods give the decision maker a possibility to review the consistency of the solution by referring to the standard deviation. The decision maker can easily pick up variants well defined in the rank; that is, those that are characterized by the lowest deviation or lowest variability or consistency of the decision maker’s evaluation. For example, the decision problem discussed here that had the lowest standard deviation the variant A5, which took the second place in the authors’ method ranking. However, because it has lowest standard deviation, hence also the lowest differentiation of the criteria of assigned values for a given variant, it can be considered as strongly preferred.
7. Conclusions
This paper presents a new method called PVM-VSI, used to assist multicriteria decisions. The procedure used in the PVM-VSI method has been described and used to create a rank of projects submitted within the framework of a Citizen Budget, in order to point out which project in the decision makers’ opinion is more advantageous for sustainable urban development. The identical rank was made up from the existing values and successfully applied in similar decision-making problems: Fuzzy AHP, Fuzzy TOPSIS, NEAT F-PROMETHEE I, NEAT F-PROMETHEE II. The objective was to compare the results achieved by means of the new method and the results obtained by means of known and used methods in the past in assisting multicriteria decisions, in which the decision maker had to make a choice out of many variants, where the criteria were not often quantified.
The performed study showed that the presented PVM-VSI method allows use of it in solving decision problems in which many variants are subject to evaluation with many criteria considered. According to the rank obtained in the new method applied, the best project in the pool of projects submitted to the Citizen Budget is project A3—improvement of the urban bicycle infrastructure. This project was followed in the rank by: A5—pro-eco revitalization of Słowiański Park; A1—construction of a walking path along the river Warta from the East Boulevard to the Lubuski Bridge; A4—integrative playground for handicapped children; and A2—a swimming pool within the river Warta water current. Accounting for urban sustainable development, citizens can be introduced to the obtained rank so that they are aware which of the projects is recommended by experts as best serving the interests of their town.
What this paper highlights is that the new method, when applied, produces final results close to currently used methods, with a view to comparing the outcome when those methods are used in similar decision problems. In this study, project A3 proved to be the best irrespective of the used method. Also, irrespective of the applied method, the final position was taken by project A2. The proposed PVM-VSI method—as demonstrated—has extra merit. It is possible to analyze the consistency of the solution on the grounds of the standard deviation value. The decision maker has the possibility of pointing out those variants that are well defined in the rank and characterized by having the lowest deviation or the smallest variability or inconsistency of the evaluation scores. This method can play a significant role in the decision-making of problems of urban management, or more broadly, sustainable management. In such problems, we often have to deal with imprecise and subjective assessments, expressed on qualitative scales. Meanwhile, the PVM-VSI method we developed takes into account such imprecise and inconsistent assessments, at the same time examining the degree of imprecision and taking it into account in the final results. This is a completely different approach to, for example, the AHP method, in which if there is an inconsistency ratio greater than 0.1 for the examined pairwise comparison matrix, the decision maker must reassess the variants.
Author Contributions
Conceptualization, M.B. Data curation, M.K. Investigation, M.K. Methodology, M.K., P.Z., and M.B. Software, M.K. Supervision, P.Z. and M.B. Validation, P.Z. Visualization, M.B. Writing—original draft, M.K. Writing—review and editing, P.Z.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Pairwise Comparison Matrix Split into Criteria

Table A1.
Pairwise comparison matrix for variants according to criterion C1—spatial order.
Table A1.
Pairwise comparison matrix for variants according to criterion C1—spatial order.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1 | 4 | 1/3 | 1 | 1/2 |
| A2 | 1/4 | 1 | 1/3 | 1/3 | 1/2 |
| A3 | 3 | 3 | 1 | 1 | 2 |
| A4 | 1 | 3 | 1 | 1 | 2 |
| A5 | 2 | 2 | 1/2 | 1/2 | 1 |

Table A2.
Pairwise comparison matrix for variants according to criterion C2—modernization.
Table A2.
Pairwise comparison matrix for variants according to criterion C2—modernization.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1 | 3 | 2 | 1 | 1/3 |
| A2 | 1/3 | 1 | 1/3 | 1/2 | 1/4 |
| A3 | 1/2 | 3 | 1 | 1/2 | 1/2 |
| A4 | 1 | 2 | 2 | 1 | 1 |
| A5 | 3 | 4 | 2 | 1 | 1 |

Table A3.
Pairwise comparison matrix for variants according to criterion C3—environmental and nature protection.
Table A3.
Pairwise comparison matrix for variants according to criterion C3—environmental and nature protection.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1 | 2 | 3 | 3 | 1/4 |
| A2 | 1/2 | 1 | 2 | 2 | 1/4 |
| A3 | 1/3 | 1/2 | 1 | 4 | 1 |
| A4 | 1/3 | 1/2 | 1/4 | 1 | 1/3 |
| A5 | 4 | 4 | 1 | 3 | 1 |

Table A4.
Pairwise comparison matrix for variants according to criterion C4—sport and tourism.
Table A4.
Pairwise comparison matrix for variants according to criterion C4—sport and tourism.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1 | 1/2 | 1/3 | 1 | 3 |
| A2 | 2 | 1 | 1/3 | 2 | 3 |
| A3 | 3 | 3 | 1 | 3 | 4 |
| A4 | 1 | 1/2 | 1/3 | 1 | 2 |
| A5 | 1/3 | 1/3 | 1/4 | 1/2 | 1 |

Table A5.
Pairwise comparison matrix for variants according to criterion C5—culture.
Table A5.
Pairwise comparison matrix for variants according to criterion C5—culture.
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1 | 1 | 2 | 1/3 | 1/3 |
| A2 | 1 | 1 | 1 | 1/2 | 1/3 |
| A3 | 1/2 | 1 | 1 | 2 | 1/2 |
| A4 | 3 | 2 | 1/2 | 1 | 3 |
| A5 | 3 | 3 | 2 | 1/3 | 1 |
Appendix B. Symbols Used Throughout the Paper
= matrix of comparisons for the lth criterion
= element of matrix
= intermittent matrix with respect to variants
= element of matrix
= normalized matrix
= element of matrix
= vector of average evaluation score for jth decisive variant
= lth coordinate of the vector
= covariance matrix for individual variants split into individual categories,
= element of matrix
= motivating preference vector for average values;
= element of the vector
= demotivating preference vector for average values
= vector element
= vector being a subtraction product between vectors i
= vector reduced to unit form
= vector magnitude
T = transformation matrix for average values
= vectors of evaluation /usability of the jth decision variant
= evaluation of the jth decision variant
= matrix after transformation by the T matrix T
= matrix element
= standard deviation of the evaluation of the jth decision variant
References
- Pęski, W. Zarządzanie Zrównoważonym Rozwojem Miast; Wydawnictwo Arkady: Warszawa, Poland, 1999. [Google Scholar]
- Ziemba, P. Towards Strong Sustainability Management—A Generalized PROSA Method. Sustainability 2019, 11, 1555. [Google Scholar] [CrossRef]
- Kębłowski, W. Budżet Partycypacyjny: Krótka Instrukcja Obsługi; Instytut Obywatelski: Warszawa, Poland, 2013. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill International Book Co.: New York, NY, USA, 1980; ISBN 0-07-054371-2. [Google Scholar]
- Ziemba, P. Inter-Criteria Dependencies-Based Decision Support in the Sustainable wind Energy Management. Energies 2019, 12, 749. [Google Scholar] [CrossRef]
- Brans, J.P. La method PROMETHEE, Colloq d’aide a la decision. In L’ingenierie de la Decision; Elaboration D’instruments D’aide a Decision; Universite Laval: Quebec, QC, Canada, 1982. [Google Scholar]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications A State-of-the-Art Survey; Hwang, C.-L., Yoon, K., Eds.; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. ISBN 978-3-642-48318-9. [Google Scholar]
- Grzegorzewski, P. On Separability of Fuzzy Relations. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Lu, S.-T.; Tzeng, G.-H. Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Proj. Manag. 2004, 22, 573–584. [Google Scholar] [CrossRef]
- Walczak, D.; Rutkowska, A. Project rankings for participatory budget based on the fuzzy TOPSIS method. Eur. J. Oper. Res. 2017, 260, 706–714. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S. A hybrid approach integrating Affinity Diagram, AHP and fuzzy TOPSIS for sustainable city logistics planning. Appl. Math. Model. 2012, 36, 573–584. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Group Decision Making Using Intuitionistic Hesitant Fuzzy Sets. Int. J. Fuzzy Log. Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Qamar, M.A.; Hassan, N. An Approach toward a Q-Neutrosophic Soft Set and Its Application in Decision Making. Symmetry 2019, 11, 139. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Geng, Y. Multi-Criteria Decision-Making Method Based on Single-Valued Neutrosophic Schweizer–Sklar Muirhead Mean Aggregation Operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A. Hospital site selection using fuzzy AHP and its derivatives. J. Environ. Manag. 2009, 90, 3048–3056. [Google Scholar] [CrossRef]
- Chen, C.-T.; Lin, C.-T.; Huang, S.-F. A fuzzy approach for supplier evaluation and selection in supply chain management. Int. J. Prod. Econ. 2006, 102, 289–301. [Google Scholar] [CrossRef]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Online Comparison System with Certain and Uncertain Criteria Based on Multi-criteria Decision Analysis Method. In Computational Collective Intelligence; Nguyen, N.T., Papadopoulos, G.A., Jędrzejowicz, P., Trawiński, B., Vossen, G., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; pp. 579–589. [Google Scholar]
- Ziemba, P. NEAT F-PROMETHEE–A new fuzzy multiple criteria decision making method based on the adjustment of mapping trapezoidal fuzzy numbers. Expert Syst. Appl. 2018, 110, 363–380. [Google Scholar] [CrossRef]
- Ziemba, P.; Becker, J. Analysis of the Digital Divide Using Fuzzy Forecasting. Symmetry 2019, 11, 166. [Google Scholar] [CrossRef]
- Maleki, J.; Hakimpour, F.; Masoumi, Z. A Parcel-Level Model for Ranking and Allocating Urban Land-Uses. ISPRS Int. J. Geo-Inf. 2017, 6, 273. [Google Scholar] [CrossRef]
- Mosadeghi, R.; Warnken, J.; Tomlinson, R.; Mirfenderesk, H. Comparison of Fuzzy-AHP and AHP in a spatial multi-criteria decision making model for urban land-use planning. Comput. Environ. Urban Syst. 2015, 49, 54–65. [Google Scholar] [CrossRef]
- Tsai, M.-C.; Lin, C.-T. Selecting an Optimal Region by Fuzzy Group Decision Making: Empirical Evidence from Medical Investors. Group Decis. Negot. 2012, 21, 399–416. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Modam, M.M. Selecting the best zones to add new emergency services based on a hybrid fuzzy MADM method: A case study for Tehran. Saf. Sci. 2016, 85, 67–76. [Google Scholar] [CrossRef]
- Di Matteo, U.; Pezzimenti, P.M.; Astiaso Garcia, D. Methodological Proposal for Optimal Location of Emergency Operation Centers through Multi-Criteria Approach. Sustainability 2016, 8, 50. [Google Scholar] [CrossRef]
- Al-Anbari, M.A.; Thameer, M.Y.; Al-Ansari, N. Landfill Site Selection by Weighted Overlay Technique: Case Study of Al-Kufa, Iraq. Sustainability 2018, 10, 999. [Google Scholar] [CrossRef]
- Chauhan, A.; Singh, A. A hybrid multi-criteria decision making method approach for selecting a sustainable location of healthcare waste disposal facility. J. Clean. Prod. 2016, 139, 1001–1010. [Google Scholar] [CrossRef]
- Kim, Y.; Chung, E.-S.; Jun, S.-M.; Kim, S.U. Prioritizing the best sites for treated wastewater instream use in an urban watershed using fuzzy TOPSIS. Resour. Conserv. Recycl. 2013, 73, 23–32. [Google Scholar] [CrossRef]
- Wątróbski, J.; Ziemba, P.; Jankowski, J.; Zioło, M. Green Energy for a Green City—A Multi-Perspective Model Approach. Sustainability 2016, 8, 702. [Google Scholar] [CrossRef]
- Önüt, S.; Efendigil, T.; Soner Kara, S. A combined fuzzy MCDM approach for selecting shopping center site: An example from Istanbul, Turkey. Expert Syst. Appl. 2010, 37, 1973–1980. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection. Expert Syst. Appl. 2014, 41, 8112–8128. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S.; Omrani, H. Application of fuzzy TOPSIS in evaluating sustainable transportation systems. Expert Syst. Appl. 2011, 38, 12270–12280. [Google Scholar] [CrossRef]
- Shiau, T.-A.; Liu, J.-S. Developing an indicator system for local governments to evaluate transport sustainability strategies. Ecol. Indic. 2013, 34, 361–371. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S.; Goyal, S.K. A multi-criteria decision making approach for location planning for urban distribution centers under uncertainty. Math. Comput. Model. 2011, 53, 98–109. [Google Scholar] [CrossRef]
- Rao, C.; Goh, M.; Zhao, Y.; Zheng, J. Location selection of city logistics centers under sustainability. Transp. Res. Part D Transp. Environ. 2015, 36, 29–44. [Google Scholar] [CrossRef]
- Neisani Samani, Z.; Karimi, M.; Alesheikh, A.A. A Novel Approach to Site Selection: Collaborative Multi-Criteria Decision Making through Geo-Social Network (Case Study: Public Parking). ISPRS Int. J. Geo-Inf. 2018, 7, 82. [Google Scholar] [CrossRef]
- Nermend, K. Vector Calculus in Regional Development Analysis: Comparative Regional Analysis Using the Example of Poland; Contributions to Economics; Springer Science & Business Media: Heidelberg, Germany, 2009; ISBN 978-3-7908-2178-9. [Google Scholar]
- Nermend, K.; Łatuszyńska, M. Selected Issues in Experimental Economics. In Proceedings of the 2015 Computational Methods in Experimental Economics (CMEE) Conference, Międzyzdroje, Poland, 17–19 September 2015; Springer Proceedings in Business and Economics. Springer International Publishing: Cham, Switzerland, 2016. ISBN 978-3-319-28417-0. [Google Scholar]
- Ludtke, N.; Panzeri, S.; Brown, M.; Broomhead, D.S.; Knowles, J.; Montemurro, M.A.; Kell, D.B. Information-theoretic sensitivity analysis: A general method for credit assignment in complex networks. J. R. Soc. Interface 2008, 5, 223–235. [Google Scholar] [CrossRef]
- Convertino, M.; Munoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Model. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Introduction to Sensitivity Analysis. In Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 1–51. ISBN 978-0-470-72518-4. [Google Scholar]
- Servadio, J.L.; Convertino, M. Optimal information networks: Application for data-driven integrated health in populations. Sci. Adv. 2018, 4, e1701088. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Sobol, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Sobol, I.M. Uniformly distributed sequences with an additional uniform property. USSR Comput. Math. Math. Phys. 1976, 16, 236–242. [Google Scholar] [CrossRef]
- Ziemba, P.; Wątróbski, J. Selected Issues of Rank Reversal Problem in ANP Method. In Selected Issues in Experimental Economic, Proceedings of the 2015 Computational Methods in Experimental Economics (CMEE) Conference, Międzyzdroje, Poland, 17–19 September 2015; Nermend, K., Łatuszyńska, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 203–225. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).