Abstract
The diffusion subband adaptive filtering (DSAF) algorithm has attracted much attention in recent years due to its decorrelation ability for colored input signals. In this paper, a modified DSAF algorithm using the symmetry maximum correntropy criterion (MCC) with individual weighting factors is proposed and discussed to combat impulsive noise, which is denoted as the MCC-DSAF algorithm. During the iterations, the negative exponent in the Gaussian kernel of the MCC-DSAF eliminates the interference of outliers to provide a robust performance in non-Gaussian noise environments. Moreover, in order to enhance the convergence for sparse system identifications, a variant of MCC-DSAF named as improved proportionate MCC-DSAF (MCC-IPDSAF) is presented and investigated, which provides a dynamic gain assignment matrix in the MCC-DSAF to adjust the weighted values of each coefficient. Simulation results verify that the newly presented MCC-DSAF and MCC-IPDSAF algorithms are superior to the popular DSAF algorithms.
1. Introduction
Distributed estimation is required to get the interested estimated parameters from the data collected in distributed networks and sensors [1], and has been widely investigated and utilized in wireless sensor networks, target locations, environmental monitorings, medical applications, military applications, and other fields [2,3,4,5]. Diffusion strategy exchanges information between a current node and its neighbors in the networks, which makes it widely studied in distributed estimation [6]. A global solution in the network performs iterative operations when all node information is fused to the center, which requires a large amount of energy and communication resources [7]. Thus, many adaptive filtering (AF) algorithms in light of distributed estimation were reported like diffusion affine projection algorithms (DAPA) [8], diffusion least mean square algorithms (DLMS) [9], and diffusion subband adaptive filtering (SAF) algorithms (DSAF) [10]. DLMS was developed in line with the least mean square (LMS) for distributed estimation since the LMS is simple, but its convergence speed will sharply deteriorate for colored input signals. Although the DAPA and DSAF can improve the convergence when the input is colored, the complexity for DAPA is increased. DSAF is more popular because of its simple computational complexity that is similar to the DLMS [11,12,13,14,15]. However, the above mentioned algorithms are all developed based on the -norm optimization criterion, whose performance will be seriously degraded under non-Gaussian interference.
Recently, the norm optimization criterion (LOC) was used for dealing with strong impulsive noise to provide good anti-interference abilities [16]. Then, AF algorithms in line of the LOC were reported, such as the diffusion sign subband AF algorithm (DSSAF) [17], the DSSAF with enlarged cooperation (DSSAF-EC) [18], and the individual weighting factored DSSAF algorithm (IWF-DSSAF) [19]. The above mentioned algorithms are very sensitive to non-Gaussian noise, resulting in potential deterioration of their steady-state error performance, since the LOC algorithms use the sign function on the error in each iterative process. In order to ensure the reliability of signal estimation and transmission in real-life systems, it is necessary to construct a more robust method to suppress non-Gaussian noise interference.
Since the maxmimum correntropy scheme can resist the outliers, it has been used to deal with non-Gaussian noise in recent years [20]. For example, the diffusion maximum correntropy criterion (DMCC) [21,22,23,24,25] and the diffusion minimum error entropy (DMEE) algorithms [22] provide good robustness under non-Gaussian noise-interference, and have been developed over networks based on the correntropy theory. Their performance demonstrates that the computational complexity of symmetry maximum correntropy criterion (MCC)-based algorithms is less than that of minimum error entropy (MEE)-based algorithms.
Moreover, the impulse responses (IR) of many scenes are regarded as sparse [26,27,28,29,30,31], which means that the values of most IR coefficients are zero or very small, where only a small part of the IR coefficients have significant amplitude. Then, proportionate techniques [32,33] have been used to enhance the DSAF algorithms for sparse system identifications. The main idea of the proportionate adaption AF algorithms is that the proportionate assignment matrix assigns different gain to each coefficient. The large coefficients obtain large gain to provide large step-size, and vice versa. The proportionate-type scheme has been utilized in diffusion proportionate sign subband adaptive filtering (DPSSAF) [34] and its series of variants [18,19]. In this paper, the MCC [23,35,36] is adopted for constructing a new cost function in this paper, where the proposed novel algorithm is named as MCC-DSAF. The outliers in the noise make error become large, and the negative exponential term of the Gaussian kernel function in the MCC-DSAF causes the outlier to approach zero. Therefore, compared with DSSAFs, MCC-DSAF has good adaptability and stronger robustness in non-Gaussian noise environments. We also proposed an improved proportionate MCC-DSAF (MCC-IPDSAF) by giving each coefficient an independent gain. The MCC-IPDSAF not only has the ability to resist impulsive noise, but also is suitable for system identifications with different sparse characteristics. The simulated results show that the derived two algorithms have good performance if the convergence performance, steady state error and tracking behaviors are compared with popular methods.
2. The Proposed Algorithms
A smart dust network is a system that contains many sensors, robots, or other devices to build a tiny microelectromechanical systems (MEMS) to detect light, temperature, vibration, magnetism, or chemicals. Herein, an N-node smart dust network within the wireless sensor network framework is considered. At node n and time slot l, the signal arises from the linear model:
where denotes input vector, is the unknown vector with length M that we expect to estimate, and is the system noise.
2.1. Review of the DSAF Algorithm
The DSAF is implemented based on a multiband structure, which is shown Figure 1. In Figure 1, and represent N interpolations and decimations, respectively. Considering , the desired signal and inputing signal for node n are assigned to I subband signals and , where , I is the number of subbands. The subband desired vectors and subband input vectors for node n are expressed as:
for node n are handled by adaptive filter whose weight vector is , which is to generate output signal . for node n and the output signals are to get and . The subband errors are the difference between and . Using the synthesis filter bank , the fullband error is obtained. The original and decimated sequences are denoted by variables l and k respectively, where .
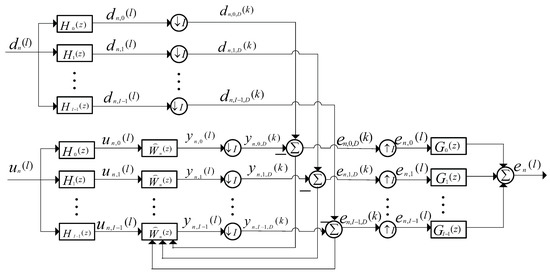
Figure 1.
The scheme of the diffusion subband adaptive filtering (DSAF) algorithm.
As we know, DSAF algorithms can be divided into two types, namely (Adapt-then-Combine) ATC and (Combine-then-Adapt) CTA [37]. In general, ATC performs better than CTA, and hence, the ATC type is employed herein.
For DSAF, its cost function for node n is
in which E denotes the expected symbol. By using ATC type in Equation (4), is minimized to obtain the updated equation of the DSAF:
where is
represents the neighbor of node n. denotes the combination coefficients of the matrix , where, and if . In other words, is zero when j is not connected to n. Otherwise, the column and row of the combination coefficients in are added to one. is a regularization parameter which prevents the denominator from being zero, is the step-size for node n. and are the intermediate estimation and estimation of for node n.
Under the Gaussian noise interference, the DSAF has a decorrelation ability for the colored input signals and enjoys a faster convergence speed than DLMS. However, for the interference of non-Gaussian noise, the error sequences in the DSAF are not stabilized due to the pulse characteristics of non-Gaussian noise, which affects the convergence characteristics of DSAF. Then, a modified DSAF algorithm based on an MCC scheme with an individual weighting factor for improving the DSAF is proposed and given the name MCC-DSAF.
2.2. The Proposed MCC-DSAF Algorithm
Correntropy between two random variables X and Y is defined as
where denotes the Mercer kernel, and is the joint probability density function. A Gaussian kernel is always used and is presented as
where is the kernel size. To use the correntropy in our algorithm, we define and . Then, the new cost function is defined as:
where denotes the kernel parameter related to the kernel size and , has a small value.
In the global network, a large amount of communication resources and energy are required and the real-time requirements of the system are high. Thus, the above problem should be well solved in the distributed network, and the global cost function should be changed into a local cost function.
For diffusion networks, local cost function can be formulated as linear-combination of local weighted correntropy, which is expressed as:
Driven by Equation (10), the increment of weight vector at instant time k is written as:
Then, the updating of the MCC-DSAF based on the gradient method can be obtained,
For the diffusion strategy, the local estimation is a linear combination of intermediate-estimation , their relationship can be expressed
In such way, is written as:
From Equation (12), the updating of the intermediate-estimation is
From Equation (13), contains more data information from neighbor nodes compared with [7,22]. According to the diffusion in [7], by replacing by in Equation (16), we have
When the error is interrupted by the pulse during the weight updating process, the negative exponential action in the Gaussian kernel function term makes the outlier close to zero, which ensures that the MCC-DSAF has good performance under non-Gaussian noise interference.
2.3. The Proposed MCC-IPDSAF Algorithm
The MCC-IPDSAF is proposed using the adaptive gain matrix in the MCC-DSAF to obtain faster convergence when the unknown system is sparse since the adaptive gain matrix can get a better balance between the convergence and steady state error. The update equation for the MCC-IPDSAF is
There are several methods for choosing to render it suitable for a sparse system [33]. As we know, the main idea of adaptive gain matrix in AFs is to obtain larger step sizes for the larger filter coefficients, which guarantees their convergence. Therefore, the MCC-IPDSAF can provide a quicker convergence compared to the MCC-DSAF in the sparse system.
denotes the adaptive gain matrix. The diagonal elements of are calculated by
where is a parameter related to system sparsity. is a regularization to prevent the denominator from being zero.
3. Performance Analysis
3.1. Data Model and Assumption
Mean square analysis of the MCC-DSAF will be performed. We define the following global variables:
where denotes the column vector, and denotes a diagonal matrix. The desired signal of the entire network , and , is an matrix.
is
Herein, the matrix is a collection of local step parameters:
where ⊗ denotes the Kronecker product. Next, is the combination coefficients matrix of :
and the matrix is defined as:
The matrix is given by
Using the global variables, the global update equation of the MCC-DSAF can be obtained,
In the analysis, we have the following assumptions:
Assumption 1.
All input regressions are independent. is independent and independent of .
Assumption 2.
Subband colored input signal is close to a white signal.
Assumption 3.
The Gaussian kernel function is independent of .
Assumption 1 is widely used in the analysis of AF algorithms. Assumption 3 does not really apply to the proposed algorithms, since is an error function. In [21,37,38,39], the variable step size is independent of . is considered as a variable step term.
The weighted error-vector for node n is expressed as:
The global weighted error-vector is:
Due to and where is the matrix whose coefficients are , and we have . Thus, we get the relationship of . Replacing with in Equation (32), then Equation (34) is modified to be:
Next, the mean square analysis for will be presented.
3.2. Convergence Analysis
The expectation is simultaneously exerted on both sides of (35), then we get
It can be seen from Assumption 3 that is independent of . Thereby, we obtain
where .
From Assumption 1, we can find that the expectation of the last term of (36) is close to zero. Therefore, (36) is rewritten as
In Equation (38), the matrix should be stable. Thus, should be stable for all n, which means that should satisfy the following equation
then,
where denotes the maximum eigenvalue of . If the norm of the weight is smaller than , we have
Next, let . Therefore, the following condition for the stability of the MCC-DSAF should satisfy
3.3. Steady-State Performance
Steady-state behavior of MCC-DSAF is studied herein. denotes any symmetric positive definite weighting matrix, denotes the weighting squared Euclidean norm . Then, considering the -Euclidean-norm on both sides of Equation (35) results in
where
and
and
We take the expectation on both sides of Equation (43) and find:
is
Herein, let . The operator is to convert a block matrix into a single-column vector. The ⊙ operator denotes the block Kronecker product. From in [40], and applying the operator to each item on the right side of (48) yields
By applying the operator to right side of Equation (48) without , the final expression is represented by matrix :
where , and applying the operator to left side of Equation (48), we get .
Finally, we have
Also, applying operator to the second term on the right side of Equation (47) yields
Thus, is
According to the above analysis, Equation (47) is obtained,
The mean square deviation (MSD) for node n is given by
Here, is defined as
where denotes the n-th column vector of , stacks the columns of its matrix into a column vector. Let in Equation (57). When k approaches infinity, the MSD for node n is
The MSD of the entire network is defined by the average of all node MSDs:
4. Simulation
The effectiveness of the proposed algorithms is verified through experimental simulation. Figure 2 shows the network topology with 20 nodes. The location coordinates for the nodes in a squared area are .
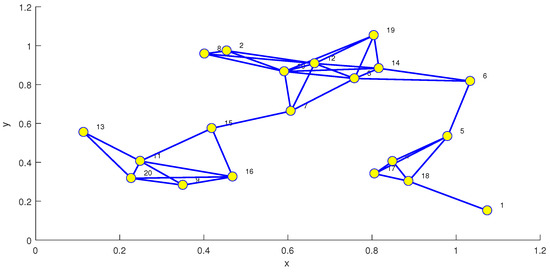
Figure 2.
Diffusion network topology with 20 nodes within a squared area of .
The combination coefficients are obtained by Metropolis criterion [11,41], where , if and if . The unknown system has a length of and the calculation of sparsity is [42,43] with . Figure 3 shows the non-Gaussian noise distribution of and for node . The normalized mean square deviation (NMSD), is used to evaluate the behaviors of the devised algorithms. The smaller the value of NMSD, the closer the estimated results are to the unknown system. In order to make it easier to compare the differences between the different algorithms, the convergence lines are run in 30 independent simulations to get the average values.
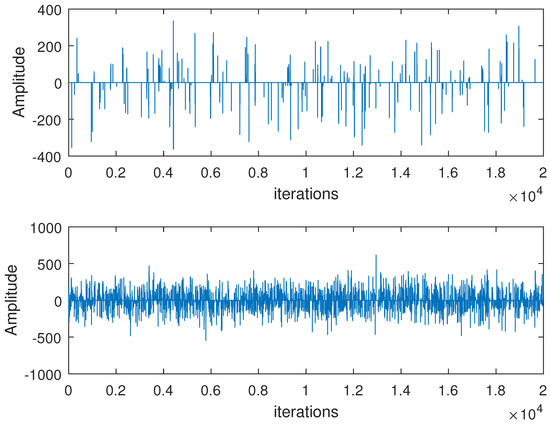
Figure 3.
The non-Gaussian noise of (up) and (down) for node .
System Identification
The algorithms use four-subband cosine modulation filter banks. White, colored and speech signals are used as input in this section. The colored signal is realized by Gaussian white noise via a first-order system with its transform function of . The variance of the input signal and the variance of the Gaussian noise are given in Figure 4. Zero-mean Gaussian noise and the impulsive noise are used to construct the measurement noise . The impulsive noise is obtained by using the Bernoulli process and the Gaussian process , which is defined as . The probability density function of the Bernoulli process is , . The signal-to-noise ratio (SNR) and signal-to-interference ratio (SIR) used in [18] are given by and , respectively. and are the variances of and . . The kernel parameter is 15, , .
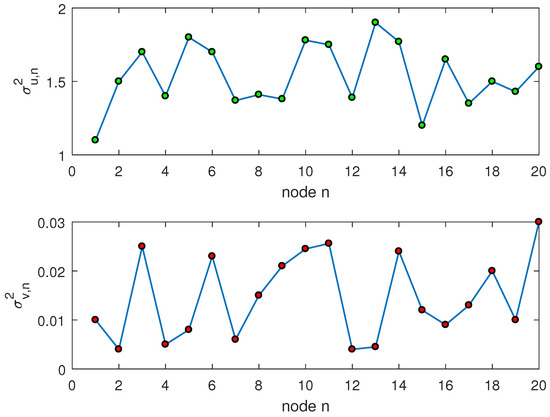
Figure 4.
The variance of input signal and Gaussian noise. (up) ; (down) .
Figure 5 gives the performance of the DSAF, MCC-DSAF, and MCC-IPDSAF for colored input signals, where . Their step-size parameters are 0.1, 0.0158 and 0.0075 to get nearly the same initial convergence. The DSAF is severely degraded under non-Gaussian noise interference. The proposed MCC-DSAF can better suppress non-Gaussian interferences. The steady-state error of MCC-IPDSAF is smaller than MCC-DSAF, which is attributed to the adaptive gain matrix that reassigns the gains to each coefficient.
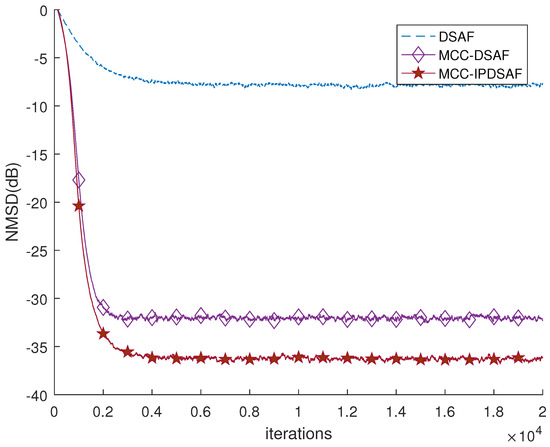
Figure 5.
The performance of DSAF, maximum correntropy criterion (MCC)-DSAF, and improved proportionate MCC-DSAF (MCC-IPDSAF) for the colored input with .
Figure 6 illustrates the performance of diffusion sign error-LMS (DSE-LMS) [44], DMCC [21], diffusion affine projection sign algorithm (DAPSA) [45], MCC-DSAF, and MCC-IPDSAF for colored input signals for . Their step-size parameters are 0.0017, 0.065, 0.11, 0.029, and 0.015. The Gaussian kernel and the DAPSA projection order is 4. DAPSA converges faster than the DSE-LMS and DMCC, but it converges slower than the proposed MCC-DSAF. MCC-DSAF’s convergence is significantly faster than DSE-LMS, DMCC, and DAPSA. It can be verified that the subband algorithms can speed-up the convergence. When the proposed MCC-IPDSAF maintains the same convergence speed with MCC-DSAF, its steady-state error is smaller than that of the MCC-DSAF.
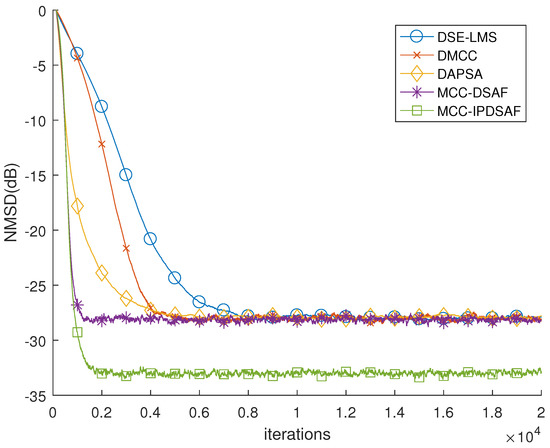
Figure 6.
The performance of DSE-LMS, diffusion maximum correntropy criterion (DMCC), DAPSA, MCC-DSAF and MCC-IPDSAF for the colored input with .
Figure 7 demonstrates the performance of DSAF, DSSAF, IWF-DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for a white input signal, where . Their step-size parameters are chosen to be 0.5, 0.14, 0.07, 0.02, 0.08, 0.055, and 0.01 for achieving the same initial convergence. DSAF shows the worst behavior. The DSSAF and IWF-DSSAF algorithms have almost the same performance as each other, and the IPDSSAF and IWF-IPDSSAF algorithms are similar, this is because IWF-DSSAF and IWF-IPDSSAF are subband variants of DSSAF and IPDSSAF, respectively, and subband splitting of white signals has almost no effect when the impulsiveness of non-Gaussian noise is not particularly large. The steady-state error of the proposed MCC-DSAF is smaller than the DSSAF and IPDSSAF because it is realized based on MCC, which can resist non-Gaussian noise. As a result, the behavior of MCC-IPDSAF is better than the other algorithms.
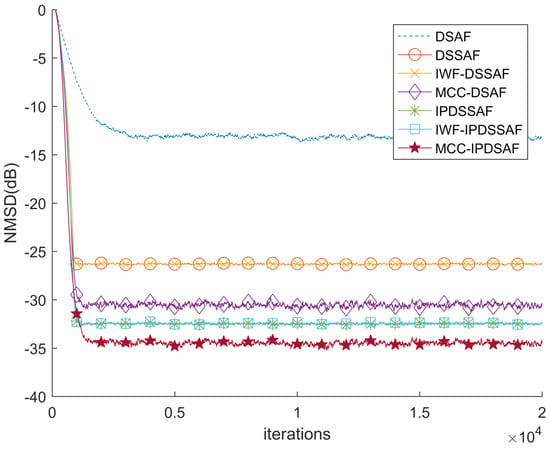
Figure 7.
The performance of the DSAF, diffusion sign subband AF algorithm (DSSAF), individual weighting factored (IWF)-DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF and MCC-IPDSAF for white input with .
Figure 8 is the performance of DSAF, DSSAF, IWF-DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for a white input signal with . Their step-size parameters are 0.25, 0.7, 0.34, 0.065, 0.4, 0.25, and 0.039, respectively. By increasing the impulsiveness of non-Gaussian noise, DSAF has completely failed, and the algorithms have similar performance to those in Figure 7.
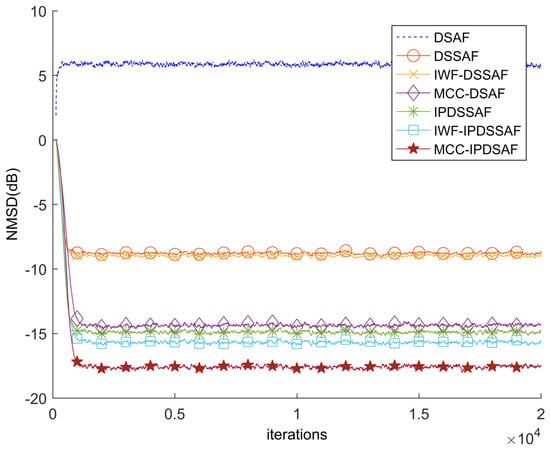
Figure 8.
The performance of DSAF, IWF-DSSAF, DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for white input with .
Figure 9 discusses the behavior of DSAF, DSSAF, IWF-DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for a colored input signal, where . The step-size parameters of these algorithms are 0.1, 0.42, 0.055, 0.0158, 0.3,0.06, and 0.0075, respectively. The DSAF has been severely degraded, while the proposed MCC-DSAF has a smaller steady-state-error than those of DSSAF, IWF-DSSAF, and IPDSSAF. Due to the advantages of adaptive gain matrix and MCC schemes, the proposed MCC-IPDSAF outperforms all other algorithms.
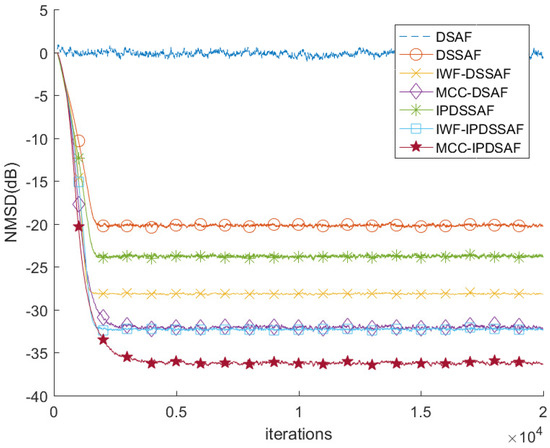
Figure 9.
The performance of IWF-DSSAF, DSSAF, DSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for the colored input with .
Figure 10 shows the performance of DSAF, DSSAF, IWF-DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for a colored input signal, where . The step size parameters of these algorithms are 0.1, 0.25, 0.06,0.021, 0.25, 0.0765, and 0.01, respectively. Compared with Figure 9, when the impulsiveness of non-Gaussian noise is increased, the steady-state error and convergence for all algorithms become worse. However, the behavior of the proposed MCC-IPDSAF algorithm is the best.
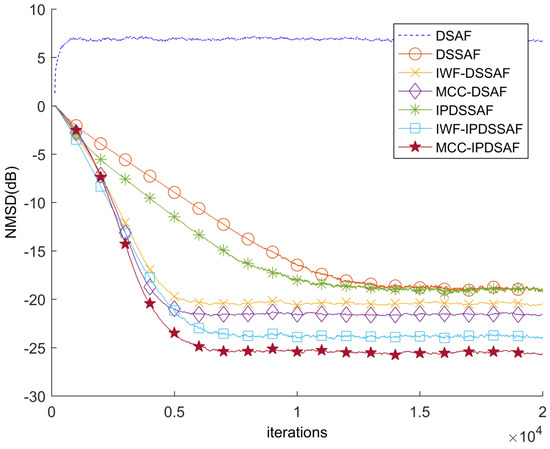
Figure 10.
The performance of DSAF, IWF-DSSAF, DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for the colored input with .
Figure 11 shows the tracking behavior of DSAF, DSSAF, IWF-DSSAF, MCC-DSAF, IPDSSAF, MCC-IPDSAF, IWF-IPDSSAF for a colored input signal, where . The unknown system changes when the iterations reach to 20,000, the proposed MCC-DSAF and MCC-IPDSAF still have good tracking performance.
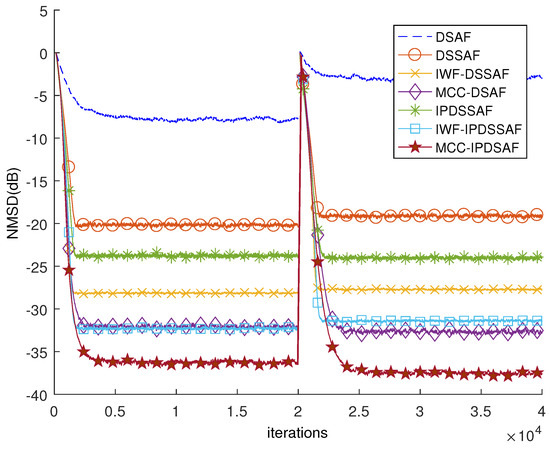
Figure 11.
The tracking performance of DSAF, IWF-DSSAF, DSSAF, MCC-DSAF, IPDSSAF, IWF-IPDSSAF, and MCC-IPDSAF for the colored input with .
Figure 12 gives a highly correlated real speech signal and the sparse channel. The real speech signal is the input, and the sampling frequency is 8 KHz, and the sample length is .
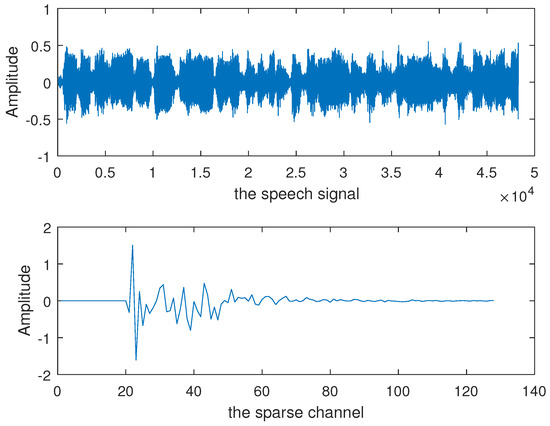
Figure 12.
The speech input signal and the sparse channel.
From Figure 13, DSAF fails to converge, while the steady state error of the proposed MCC-DSAF is better than those of the DSSAF and IWF-DSSAF for the non-Gaussian interference and speech input. The behavior of MCC-IPDSAF is superior to the other algorithms. Although the non-stationarity of speech input affects the behavior of the mentioned algorithms, the experiment result verifies the feasibility and effectiveness of the MCC-DSAF and MCC-IPDSAF algorithms.
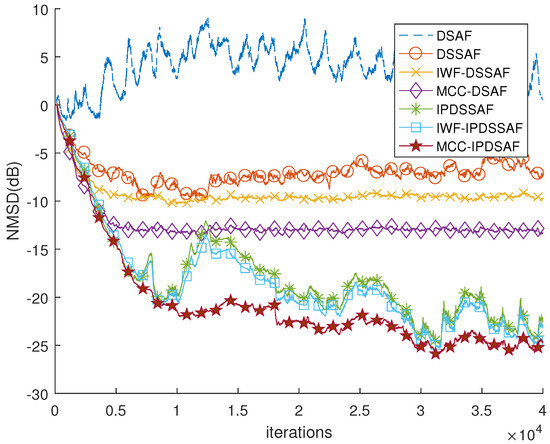
Figure 13.
The behavior of DSAF, IWF-DSSAF, DSSAF, MCC-DSAF, IWF-DSSAF, IPDSSAF, and MCC-IPDSAF for speech input with .
5. Conclusions
In this paper, the maximum correntropy criterion and an individual weighting factor have been taken to construct a new cost function within the distributed subband adaptive filtering framework, which is named MCC-DSAF. The developed MCC-DSAF has been well derived and analyzed. The proposed MCC-DSAF algorithm can not only effectively suppress non-Gaussian noise interference, but also outperforms DSSAF and IWF-DSSAF with respect to convergence and MSD. Moreover, the proportionate adaption scheme is also introduced into MCC-DSAF to get MCC-IPDSAF, which further enhances the behavior of MCC-DSAF for identifying sparse systems. The convergence analysis and the steady-state behavior of MCC-DSAF are presented. The estimation behaviors of the algorithms are verified and the simulation results demonstrate that the proposed MCC-DSAF and MCC-IPDSAF are superior to the mentioned, popular DSAF algorithms. The algorithms in this paper will provide a better effect in the fields of radar, medical, wireless sensor networks, smart dust networks, distributed channel estimations, and hydroacoustics, etc.
Author Contributions
Y.G. wrote the draft of this paper and gave the idea and basic simulation of the devised algorithm. J.L. proposed the analysis of the algorithms and constructed the figures with other algorithms. Y.L. gave the idea and the investigation of the devised algorithm. All the authors discuss the results and the analysis of the devised algorithms together, and they have read and agreed to submit the final version of the manuscript.
Funding
This paper is supported by the National Key Research and Development Program of China (2016YFE0111100), Key Research and Development Program of Heilongjiang (GX17A016), the Science and Technology innovative Talents Foundation of Harbin (2016RAXXJ044), the Natural Science Foundation of Beijing (4182077), China Postdoctoral Science Foundation (2017M620918, 2019T120134), the Fundamental Research Funds for the Central Universities (HEUCFG201829, 2072019CFG0801), and Opening Fund of Acoustics Science and Technology Laboratory (SSKF2016001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sayed, A.H. Adaptive, networks. Procs. IEEE 2014, 102, 460–497. [Google Scholar] [CrossRef]
- Rossi, L.A.; Krishnamachai, B.; Kuo, C.C.J. Distributed parameter estimation for monitoring diffusion phenomena using physical models. In Proceedings of the 2004 First Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, Santa Clara, CA, USA, 4–7 October 2004. [Google Scholar]
- Li, J.; AlRegib, G. Rate-constrained distributed estimation in wireless sensor network. IEEE Trans. Signal Process. 2007, 55, 1624–1643. [Google Scholar] [CrossRef]
- Culler, D.; Estrin, D.; Srivastava, M. Overview of sensor networks. Computer 2004, 37, 41–49. [Google Scholar] [CrossRef]
- Tu, S.Y.; Sayed, A.H. Mobile adaptive networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 649–664. [Google Scholar]
- Sayed, A.H. Adaptive, learning, and optimization over networks. Found. Trends Mach. Learn. 2014, 7, 311–801. [Google Scholar] [CrossRef]
- Chen, F.; Shi, T.; Duan, S.; Wang, L.; Wu, J. Diffusion Least Logarithmic Absolute Difference Algorithm for Distributed estimation. Signal Process. 2018, 142, 423–430. [Google Scholar] [CrossRef]
- Li, L.; He, J.; Zhang, Y. Affine projection algorithms over distributed wireless networks. J. Commun. Univ. China (Sci. Technol.) 2012, 19, 34–43. [Google Scholar]
- Lopes, C.G.; Sayed, A.H. Diffusion least-mean squares over adaptive networks: formulation and performance analysis. IEEE Trans. Signal Process. 2008, 56, 3122–3136. [Google Scholar] [CrossRef]
- Jin-gen, N.I.; Lan-shen, M.A. Distributed subband adaptive filtering algorithms. Chin. J. Electron. 2015, 43, 2222–2231. [Google Scholar]
- Seo, J.H.; Jung, S.M.; Park, P.G. A diffusion subband adaptive filtering algorithm for distributed estimation using variable step size and new combination method based on the MSD. Digit. Signal Process. 2016, 48, 361–369. [Google Scholar] [CrossRef]
- Abadi, M.S.E.; Ahmadi, M.J. Diffusion Improved Multiband-Structured Subband Adaptive Filter Algorithm with Dynamic Selection of Nodes Over Distributed Networks. IEEE Trans. Circuits Syst. 2019, 66, 507–511. [Google Scholar] [CrossRef]
- Abadi, M.S.E.; Shafiee, M.S. A family of diffusion normalized subband adaptive filter algorithms over distributed networks. Int. J. Commun. Syst. 2017, 30, 1–15. [Google Scholar]
- Abadi, M.S.E.; Shafiee, M.S. Diffusion Normalized Subband Adaptive Algorithmfor Distributed Estimation Employing Signed Regressor of Input Signal. Digit. Signal Process. 2017, 70, 73–83. [Google Scholar] [CrossRef]
- Wen, P.; Zhang, J. Widely-Linear Complex-Valued Diffusion Subband Adaptive Filter Algorithm. IEEE Trans. Signal Inf. Process. Netw. 2018, 47, 90–95. [Google Scholar] [CrossRef]
- Mathews, V.J.; Cho, S.H. Improved convergence analysis of stochastic gradient adaptive filters using the sign algorithm. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 450–454. [Google Scholar] [CrossRef]
- Ni, J. Diffusion sign subband adaptive filtering algorithm for distributed estimation. IEEE Signal Process. Lett. 2015, 11, 2029–2033. [Google Scholar] [CrossRef]
- Shi, J.; Ni, J. Diffusion sign subband adaptive filtering algorithm with enlarged cooperation and its variant. Circuits Syst. Signal Process. 2016, 36, 1714–1724. [Google Scholar] [CrossRef]
- Wang, W.Y.; Zhao, H.Q.; Liu, Q.Q. Diffusion Sign Subband Adaptive Filtering Algorithm with Individual Weighting Factors for Distributed Estimation. Circuits Syst. Signal Process. 2017, 36, 2605–2621. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Duan, J.; Zhao, H. Diffusion maximum correntropy criterion algorithms for robust distributed estimation. Digit. Signal Process. 2016, 58, 10–19. [Google Scholar] [CrossRef]
- Li, C.; Shen, P.; Liu, Y. Diffusion information theoretic learning for distributed estimation over network. IEEE Trans. Signal Process. 2013, 61, 4011–4024. [Google Scholar] [CrossRef]
- Singh, A.; Principe, J.C. Using correntropy as a cost function in linear adaptive filters. In Proceedings of the International Joint Conference, Neural Networks (IJCNN), Atlanta, GA, USA, 14–19 June 2009; pp. 2950–2955. [Google Scholar]
- Li, Y.; Jiang, Z.; Shi, W.; Han, X.; Chen, B. Blocked maximum correntropy criterion algorithm for cluster-sparse system identifi-cations. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free maximum correntropy criterion algorithm in non-Gaussian environment. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Haykin, S.; Widrom, B. Least-Mean-Square Adaptive Filters; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2017, 30, e3181. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.; Han, X.; Yin, J. Mixed norm constrained sparse APA algorithm for satellite and network echo channel estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable sparse antenna array for adaptive beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Li, Y.; Zakharov, Y. A novel block sparse reconstruction method for DOA estimation with unknown mutual coupling. IEEE Commun. Lett. 2019, 23, 1845–1848. [Google Scholar] [CrossRef]
- Jin, Z.; Li, Y.; Wang, Y. An enhanced set-membership PNLMS algorithm with a correntropy induced metric constraint for acoustic channel estimation. Entropy 2017, 19, 281. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, Y. Comparative Study of Several Sparse Adaptive Filtering Algorithms. Microcomput. Appl. 2014, 33, 1–3. [Google Scholar]
- Shi, L.; Zhao, H.Q. Two Diffusion Proportionate Sign Subband Adaptive Filtering Algorithms. Circuits Syst. Signal Process. 2017, 36, 4244–4259. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-statemean-square error analysisfor adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Wu, Q.; Li, Y.; Zakharov, Y.; Xue, W.; Shi, W. A kernel affine projection-like algorithm in reproducing kernel hilbert space. IEEE Trans. Circuits Syst. II Exp. Briefs 2019. [Google Scholar] [CrossRef]
- Ma, W.T.; Duan, J.D.; Man, W.S.; Liang, J.L.; Chen, B.D. General Mixed Norm Based Diffusion Adaptive Filtering Algorithm for Distributed Estimation over Network. IEEE Access 2017, 5, 1090–1102. [Google Scholar] [CrossRef]
- Saeed, M.O.B.; Zerguine, A.; Zummo, S.A. A variable step-size strategy for distributed estimation over adaptive networks. EURASIP J. Adv. Signal Process. 2013, 2013, 135. [Google Scholar] [CrossRef]
- Xu, X.G.; Qu, H.; Zhao, J.H.; Yan, F.Y.; Wang, W.H. Diffusion Maximum Correntropy Criterion Based Robust Spectrum Sensing in Non-Gaussian Noise Environments. Entropy 2018, 20, 246. [Google Scholar] [CrossRef]
- Tracy, D.S.; Singh, R.P. A new matrix product and its applications in partitioned matrix differentiation. Stat. Neerl. 1972, 26, 143–157. [Google Scholar] [CrossRef]
- Cattivelli, F.; Sayed, A.H. Diffusion LMS Strategies for Distributed Estimation. IEEE Trans. Signal Process. 2010, 58, 1035–1048. [Google Scholar] [CrossRef]
- Guo, Y.; Bai, Y. Robust Affine Projection Sign Adaptive Filtering Algorithm. J. Instrum. Instrum. 2017, 38, 23–32. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Ni, J.; Chen, J.; Chen, X. Diffusion sign-error LMS algorithm: Formulation and stochastic behavior analysis. Signal Process. 2016, 128, 142–149. [Google Scholar] [CrossRef]
- Ni, J.; Ma, L. Distributed affine projection algorithms against impulsive interferences. Tien Tzu Hsueh Pao/Acta Electron. Sin. 2016, 44, 1555–1560. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).