Abstract
Heat transfer analysis in an unsteady magnetohydrodynamic (MHD) flow of generalized Casson fluid over a vertical plate is analyzed. The medium is porous, accepting Darcy’s resistance. The plate is oscillating in its plane with a cosine type of oscillation. Sodium alginate (SA–NaAlg) is taken as a specific example of Casson fluid. The fractional model of SA–NaAlg fluid using the Atangana–Baleanu fractional derivative (ABFD) of the non-local and non-singular kernel has been examined. The ABFD definition was based on the Mittag–Leffler function, and promises an improved description of the dynamics of the system with the memory effects. Exact solutions in the case of ABFD are obtained via the Laplace transform and compared graphically. The influence of embedded parameters on the velocity field is sketched and discussed. A comparison of the Atangana–Baleanu fractional model with an ordinary model is made. It is observed that the velocity and temperature profile for the Atangana–Baleanu fractional model are less than that of the ordinary model. The Atangana–Baleanu fractional model reduced the velocity profile up to 45.76% and temperature profile up to 13.74% compared to an ordinary model.
1. Introduction
Due to the relevance of non-Newtonian fluids in some of the optimization processing of food items, the heat transfer phenomenon is an important research area. Non-Newtonian fluids are investigated much more, but Casson fluids among them have been investigated by a small number of researchers. This model was introduced by Casson in 1959 [1]. This fluid has great importance in many fields of industries and medicines; see for examples, Qasim and Ahmad [2], Shehzad et al. [3], and Qasim and Noreen [4]. The Casson fluid model plays a vital role in many materials such as chocolate and blood, according to Mukhopadhyay and Mandal [5]. The metachronal coordination between the beating cilia in a cylindrical tube is one of the factors under which inspiration, and some mathematical formulations, is made to analyze Casson fluid flow, according to Siddiqui et al. [6]. A system of equations for non-linear flow problems are modeled with the help of axisymmetric cylindrical coordinates. Simplification is taken place by inducting long wavelength and low Reynolds number assumptions.
The mathematical model for Casson fluid for mixed convection taking a stretching sheet was studied by Hayat et al. [7]. The velocity and temperature fields are calculated by solving partial differential equations. The homotopy analysis method is incorporated. The Atangana–Baleanu fractional derivative (ABFD) definition was based on the Mittag–Leffler function and promises an improved description of the dynamics of the system with the memory effects by Asjad et al. [8]. The mathematical model for some geological formation is often called an aquifer, which is commonly used to solve subsurface motion by a fractional-order derivative, as in Atangana and Baleanu [9]. It was an alternative to Caputo-Fabrizio [10]. A relation between the solution obtained by the Atangana–Baleanu fractional derivative and through experimental methods is highlighted. Exact solutions were obtained by integral transforms.
Aliyu et al. [11] studied the model of transmission of vector-borne diseases and cure using the Atangana–Baleanu fractional operator in a Caputo sense. They also discussed the existence and uniqueness via numerical simulations. This model was taken into consideration by the Atangana–Baleanu fractional operator in the Caputo sense (ABC) with non-singular and non-local kernels. The Picard–Lindel method is adopted. The same method is used by Koca [12].
The effectiveness of this model is seen by a huge reduction in the disease growth rate. A comparison of heat transfer enhancement in fractional nanofluids with ordinary nanofluids is made by Azhar et al. [13]. Water is taken as a base fluid mixed with fractional nanofluids. A closed form of solution for motion and temperature is calculated and graphically underlined with a higher heat enhancement rate than ordinary fluids. The influence of memory on nanofluid behavior is difficult to elaborate by classical nanofluids. This can be easy to describe by fractional nanofluids with Caputo time derivatives. Such investigations are made by Fetecau et al. [14]. Closed-form results are obtained and presented in a Wright function. Heat enhancement was found to be lower for fractional nanofluids.
The Caputo–Fabrizio and Atangana–Baleanu derivatives are those fractional derivatives that transformed the classical model to a generalized model. Comparison investigations were made by Sheikh et al. [15]. Karaagac [16] applied two step Adams Bashforth method for time fractional tricomi equation with non-local and non-singular Kernel. Furthermore, Ali et al. [17] investigated MHD flow for free convection generalized Walter’s-B fluid. The exact solution is gained by the Laplace technique. The flow is over a static vertical plate. After that, Saqib et al. [18] studied the application of Atangana–Baleanu fractional derivative to MHD channel flow. The fluid is taken through a porous medium. Abro et al. [19] investigated the MHD convection flow for Maxwell fluid as the application of the Atangana–Baleanu fractional derivative. The fluid is taken over a vertical plate in a porous medium. The same author in [20] investigated the exact solution for MHD flow of nanofluids via Atangana–Baleanu and Caputo–Fabrizio fractional derivatives. The general analytical solutions are expressed in the layout of Mittage Leffler function and generalized Mittage Leffler function. The comparison of new fractional derivative operators involving exponential and Mittag–Leffler kernels is investigated by Yavuz and Ozdemir [21]. The comparison was investigated between Caputo–Fabrizio and Atangana–Baleanu fractional derivatives. Furthermore, Imran et al. [22] investigated the comprehensive report on the MHD convective flow of Atangana–Baleanu and Caputo–Fabrizio fractional derivatives. The viscous fluid is subject to generalized boundary conditions. Abro and Khan [23] examined the study of Atangana–Baleanu fractional derivatives for the MHD flow of fractional Newtonian fluid embedded in a porous medium. Electrically conducting viscous fluid is considered in their study.
The flow of generalized second-grade fluid between parallel plates with the Riemann–Liouville fractional derivative model was investigated by Wenchang and Mingyu [24]. They acquired the exact analytical solution using the Laplace transform and Fourier transform. The flow of second-order fluid induced by a plate moving impulsively with fractional anomalous diffusion was investigated by Mingyu and Wenchang [25]. The Rayleigh–Stokes problem for a fractional second-grade fluid was studied by Shen et al. [26]. Fractional Laplace transforms and Fourier sine transform was employed to obtain the exact solution. Exact analytical solution for the unsteady flow of a generalized Maxwell fluid between two circular cylinders was determined via Laplace and Hankel transforms by Mahmood et al. [27]. Recently, Shen et al. [28] studied fractional Maxwell viscoelastic nanofluid for various particle shapes. A Caputo time-fractional derivative was implemented by Zhang et al. [29] to acquire the numerical and analytical solutions for the problem of the 2D flow of Maxwell fluid under a variable pressure gradian gradient. They used the separation of the variables method to acquire the analytical solution, while for numerical solution, the finite difference method was used. Aman et al. [30] studied fractional Maxwell fluid with a second-order slip effect for the exact analytical solution. Jan et al. [31] determined the solution for Brinkman-type nanofluid using an Atangana–Baleanu fractional model. Owolabi and Atangana [32] analyzed the numerical simulation of the Adams–Bash forth scheme using Atangana–Baleanu Caputo fractional derivatives. Saad et al. [33] established the numerical solutions for the fractional Fisher’s type equation with Atangana–Baleanu fractional derivatives. They employed the spectral collocation method based on Chebyshev approximations. In this research work, the spectral collocation method was implemented for the first time to solve the non-linear equation with Atangana–Baleanu derivatives. Some plenteous literature regarding Atangana–Baleanu derivatives and analytical solution can be found in Saqib et al. [34], Abro et al. [35], and Hristov [36] and the references therein.
Due to the importance of MHD in fluids, many researchers have taken MHD in their studies. In recent years, Khan and Alqahtan [37] investigated the MHD effects for nanofluids in a permeable channel with porosity. The solution is obtained by using Laplace transformation. Further, in the same year, Asif et al. [38] studied the unsteady flow of fractional fluid between two parallel walls with arbitrary wall shear stress. The influence of MHD slip flow of Casson fluid along a non-linear permeable stretching cylinder saturated in a porous medium with chemical reaction, viscous dissipation, and heat generation or absorption is investigated by Ullah et al. [39]. Khan et al. [40] investigated the MHD with heat transfer. A generalized modeling is carried out for the proposed problem by using the new idea of a fractional derivative, i.e., Atangana–Baleanu and Caputo Fabrizio. After that, this idea is used by Gul et al. [41] for the study of forced convection carbon nanotube nanofluid flow passing over a thin needle. Atangana and Alqahtani [42] studied the Caputo fractional derivative for analysis of the spread of river blindness disease. Furthermore, the idea of fractional derivatives was examined by Gomez and Atangana [43] with the power law and the Mittag–Leffler kernel applied to the non-linear Baggs–Freedman model, while Muhammad and Atangana [44] examined for dynamics of Ebola disease, and Khan et al. [45] studied the analytical solution of the hyperbolic telegraph equation, using the natural transform decomposition method. Some other related references dealing with fluid motion, heat transfer, or fractional derivatives are given in [46,47,48,49,50,51,52,53].
On the basis of the above literature, this work aims to use the Atangana–Baleanu fractional derivative (ABFD) of the non-singular and non-local kernel for SA (Sodium alginate) fluid. The Laplace transform method is used to get the exact solution, which is graphically plotted via Mathcad-15 software and discussed in detail.
2. Mathematical Framing of the Problem
Let us consider the unsteady flow of Casson fluid over a vertical plate, i.e., the plate is taken perpendicular to the , with perpendicular employed magnetic field to the flow of the fluid. The plate is oscillating, and the medium is porous. The heat flux is also taken into consideration. Thermal radiation effect is also considered. Initially, both the plate and fluid are at rest. After , the plate started oscillation in its plane. The fluid is electrically conducting there by the Maxwell equation:
By using Ohm’s law:
The magnetic field is normal to The Reynolds number is so small that the flow is laminar. Hence:
Keeping in mind the above assumptions, the governing equation of momentum and energy are given as (Khalid et al. [46]:
where T and u represent temperature and velocity. , and are the density, dynamic viscosity, thermal expansion coefficient, heat source parameter, magnetic parameter, porosity parameter, gravitation acceleration, heat capacity, thermal conductivity, heat flux, and Casson fluid parameter. Following Makinde and Mhone [47] and Cogley et al. [48], the fluid used is thin with a low density and radiative heat flux given by .
The physical boundary conditions are:
For non-dementalization, the following dimensionless variables are introduced.
By using Equation (4), the dimensionless form of Equations (1)–(3) are: (asterisk * is omitted for convenience):
where:
where and represent the magnetic, porosity, Prandtl number, Grashof number, mean radiation absorption, and radiation parameter, respectively.
With the intention of converting the ordinal time derivative to the Atangana–Baleanu fractional time derivative, Equations (5) and (6) reduced to:
The Atangana–Baleanu fractional time derivative is defined as:
where is the normalization function, and .
where is the Mittag–Leffler function. After Laplace transform, Equation (13) becomes:
where is represent the Laplace transform operator.
3. Problem Solution, Skin Friction, and Nusselt Number
Taking the Laplace transform of Equations (8) and (9) and by using Equation (7), we get:
where:
Note that in Equations (15) and (16), the bar on and shows the Laplace transformed function. After taking the Laplace inverse, we get:
where:
where:
Here, is the Wright function, and is defined as:
Then, the velocity profile becomes:
where:
is the Mittag–Leffler function.
Note that for deep understanding of ABFD, on may refer to the excellent articles [35,53]. However, for the detailed solution procedure of the problem, one can refer to research works [15,18,20,23,31].
4. Skin Friction and Nusselt Number
Expressions for Nusselt number and skin friction are calculated from Equations (14) and (15) by using the relation from Khan et al. [49]:
5. Discussion
To study the influence of many embedded parameters on temperature and velocity, the graphs are plotted by using the Mathcad-15 software. Figure 1 shows the physical sketch of the problem. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 are prepared to highlight the influence of time-fractional parameter on fluid flow and temperature. The time-fractional parameter controls the velocity as well as the temperature profile. Sodium alginate (SA–NaAlg) is taken as a specific example of Casson fluid. The physical sketch of the problem is provided in Figure 1.
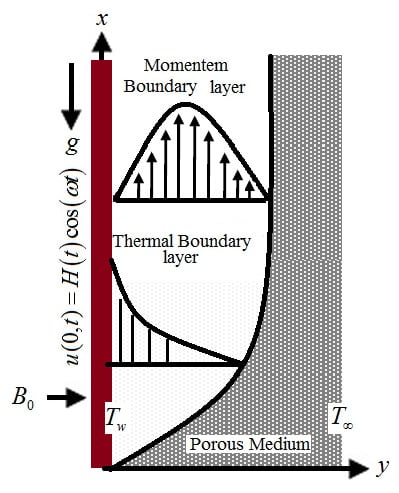
Figure 1.
Physical sketch of the problem with the coordinates system.
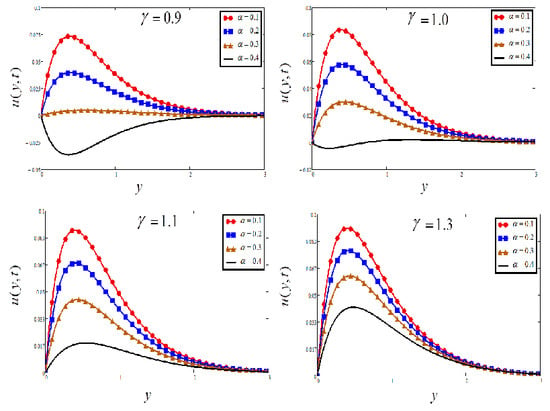
Figure 2.
Plots of velocity for four different when , and .
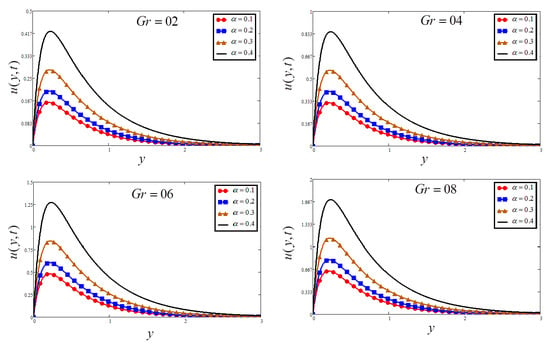
Figure 3.
Plots of velocity for four different when , and .
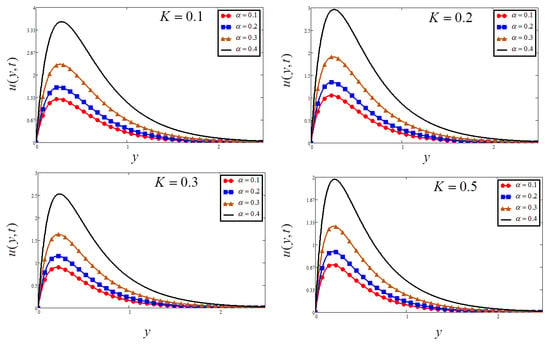
Figure 4.
Plots of velocity for four different when ., and .
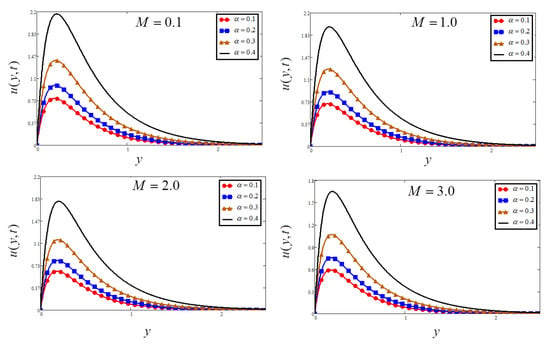
Figure 5.
Plots of velocity for four different values when , , and .
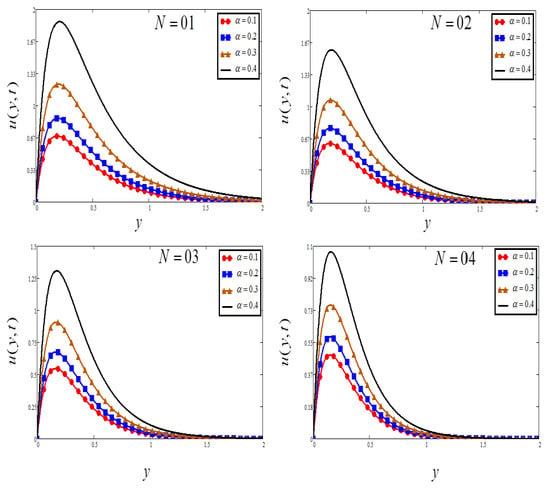
Figure 6.
Plots of velocity for four different values when , and .
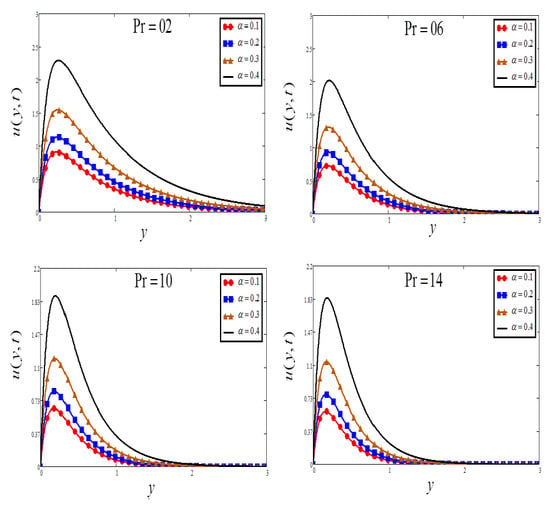
Figure 7.
Plots of velocity for four different values when , , and .
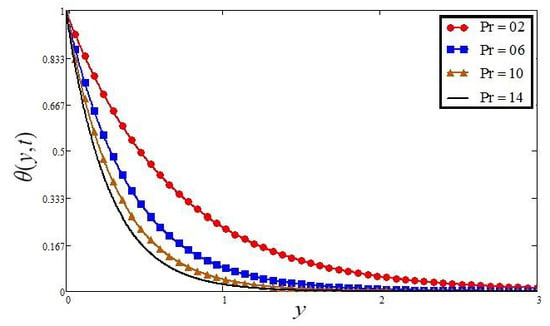
Figure 8.
Plots of temperature for four different values when and .
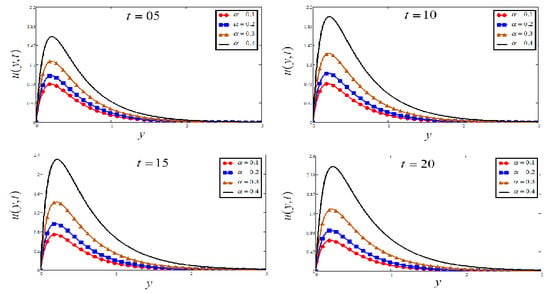
Figure 9.
Plots of velocity for four different values when , and .
Figure 2 is plotted for the influence of Casson parameter on velocity, which shows that if the value of the Casson parameter is increased, the fluid velocity increases. This is because of the circumstance that with a large value of , the yield stress falls through, and the boundary layer thickness reduces. Figure 3 investigates the impact of Grashof number on velocity. The greater value leads to an increase in the velocity of the fluid. Physically, the increase of leads to an increase in the bouncy force, and as a result, the velocity of the fluid increases.
The effect of porosity parameter against the velocity profile is investigated in Figure 4. To increase the value of the porosity parameter , first we need to decrease the flow of fluid. Physically, the resistance of the porous medium is depressed, which raises the momentum development of the flow regime, and finally accelerates the velocity of the fluid. Figure 5 shows the influence of on flow of the fluid; the rise in decreases the flow of fluid. It is physically true because the increase of means to increase the frictional force (Lorentz force), which leads to a decrease in the velocity of the fluid.
The influence of radiation parameter is highlighted in Figure 6. For the higher value of , the fluid velocity decreases. Physically, the increase in radiation parameter means the release of heat energy from the flow region, and so the fluid temperature decreases as the thermal boundary layer thickness become thinner. Figure 7 and Figure 8 illustrate the influence of Prandtl number on velocity and temperature respectively, the increase of causing a decrease in the temperature and as a result a decrease in the fluid velocity. The small degree of thermal diffusion causes expanding in velocity boundary layer width. controls the comparative thickness of the momentum and thermal boundary layers in the heat transfer problems. Subsequently, can be applied to develop the percentage of cooling.
Figure 9 and Figure 10 illustrate the outcome of time on temperature and velocity profiles. Figure 11 investigates the effect of time fraction derivative parameter on temperature. It is investigated that the time-fractional derivative parameter controls the temperature profile.
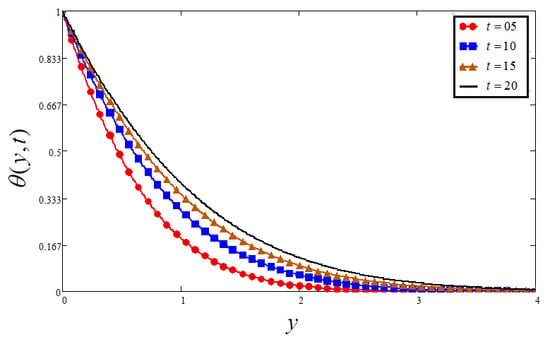
Figure 10.
Plots of temperature for four different values when , and .
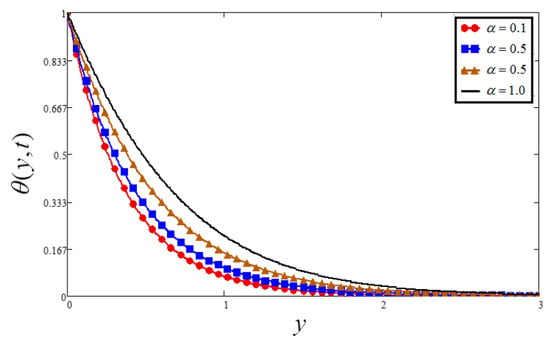
Figure 11.
Plots of temperature for four different values when , and .
A comparison of the Atangana–Baleanu fractional model with an ordinary model is investigated in Figure 12 and Figure 13 for velocity and temperature, respectively. For both cases, it is detected that the temperature and velocity profile for the Atangana–Baleanu fractional model is less than that of the ordinary model.
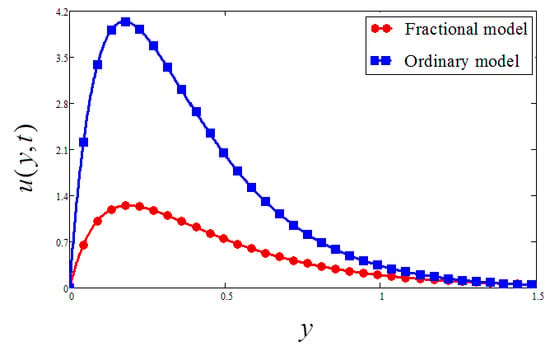
Figure 12.
Comparison of fractional SA fluid and ordinary SA fluid (velocity) when , and .
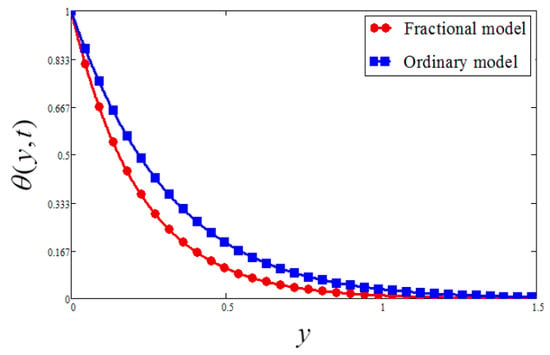
Figure 13.
Comparison of fractional SA fluid and ordinary SA fluid (temperature) when , , and .
Note that all these graphs of velocity are plotted for the phase angle equal to 90 degrees, and this value cosine is zero; therefore, all the graphs of velocity (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, Figure 9, Figure 12) have a unique pattern of velocity. That is, at the plate surface y = 0, the fluid is at rest or there is no motion in the fluid, and for large values of the independent variable y, the fluid velocity decays, and as y approaches infinity (further bigger values of y), the fluid motion disappears and velocity tends to zero. This physical pattern of the graphs of velocity agrees with the imposed condition on velocity given in Equation (6). Similarly, the unique style of all the graphs of temperature, that is temperature at y = 0, is 1, and far away from the plate surface; that is, for larger values of y, the temperature decays and tends to zero as y tends to infinity.
Table 1 and Table 2 are plotted to show the variation of different parameters on Nusselt number and skin fraction. Table 1 clarified that the Nusselt number is increased when and and are increased, while an increase in fractional derivative parameter and decreased the Nusselt number. The behavior of the present results is identical with the published results of Khan et al. [49] and Ali et al. [50]. Table 2 shows the impact of the deferent parameter on skin fraction. It is observed that , and have a positive (increasing) impact on the skin fraction, while , and and show a negative (decreasing) impact on the skin fraction. This behavior of skin fraction against different parameters is identical with the published results of Mackolil and Mahanthesh [51].

Table 1.
Variation of Nusselt number.

Table 2.
Variation of skin-friction.
6. Conclusions
In this attempt, the exact solution for the heat transfer analysis in unsteady MHD flow of fractional SA fluid past a vertical flat plate is obtained. Generalized Casson fluid model is obtained using the Atangana–Baleanu fractional derivative (ABFD) of the non-local and non-singular kernel. The exact solution for velocity and temperature are obtained by applying the Laplace transform method, and then, the influence of various embedded parameters are presented graphically. Some important outcomes are:
- ➣
- Velocity rises for a large value of , and
- ➣
- Velocity reduces for a large value of , and .
- ➣
- Temperature is increased by increasing and , while decreasing with the increase of .
- ➣
- The temperature and velocity of the fractional fluid model converge faster compared to an ordinary fluid model.
- ➣
- The Atangana–Baleanu fractional model reduced the velocity profile up to 45.76% and temperature profile up to 13.74% compared to an ordinary model.
Suggestions for future research work.
- ➣
- The researchers extend this work for different kind of nanofluids.
- ➣
- The authors also can take this model in different geometries.
Author Contributions
A.K., D.K., and I.K. modeled the problem; M.T., I.U., and A.M.A. solved the problem. P.T. and K.S.N. computed the results and wrote the main manuscript text. All authors reviewed the manuscript.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Casson, N. A flow equation for the pigment oil suspensions of the printing ink type. In Rheology of Disperse Systems; Pergamon Press: New York, NY, USA, 1959; Volume 84, p. e102. [Google Scholar]
- Qasim, M.; Ahmad, B. Numerical solution for the Blasius flow in Casson fluid with viscous dissipation and convective boundary conditions. Heat Transf. Res. 2015, 46, 689–697. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, T.; Qasim, M.; Asghar, S. Effects of mass transfer on MHD flow of Casson fluid with chemical reaction and suction. Braz. J. Chem. Eng. 2013, 30, 187–195. [Google Scholar] [CrossRef]
- Qasim, M.; Noreen, S. Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation. Eur. Phys. J. Plus 2014, 129, 7. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mandal, I.C. Boundary layer flow and heat transfer of a Casson fluid past a symmetric porous wedge with surface heat flux. Chin. Phys. B 2014, 23, 044702. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Farooq, A.A.; Rana, M.A. A mathematical model for the flow of a Casson fluid due to metachronal beating of cilia in a tube. Sci. World J. 2015, 2015, 487819. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Shehzad, S.A.; Alsaedi, A.; Alhothuali, M.S. Mixed convection stagnation point flow of Casson fluid with convective boundary conditions. Chin. Phys. Lett. 2012, 29, 114704. [Google Scholar] [CrossRef]
- Asjad, M.I.; Miraj, F.; Khan, I. Soret effects on simultaneous heat and mass transfer in MHD viscous fluid through a porous medium with uniform heat flux and Atangana-Baleanu fractional derivative approach. Eur. Phys. J. Plus 2018, 133, 224. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143, D4016005. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. The Caputo-Fabrizio fractional derivative applied to a singular perturbation problem. Int. J. Math. Model. Numer. Optim. 2019, 9, 241–253. [Google Scholar]
- Aliyu, A.I.; Inc, M.; Yusuf, A.; Baleanu, D. A fractional model of vertical transmission and cure of vector-borne diseases pertaining to the Atangana–Baleanu fractional derivatives. Chaos Solitons Fractals 2018, 116, 268–277. [Google Scholar] [CrossRef]
- Koca, I. Modelling the spread of Ebola virus with Atangana-Baleanu fractional operators. Eur. Phys. J. Plus 2018, 133, 100. [Google Scholar] [CrossRef]
- Azhar, W.A.; Vieru, D.; Fetecau, C. Free convection flow of some fractional nanofluids over a moving vertical plate with uniform heat flux and heat source. Phys. Fluids 2017, 29, 082001. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D.; Azhar, W. Natural convection flow of fractional nanofluids over an isothermal vertical plate with thermal radiation. Appl. Sci. 2017, 7, 247. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Khan, I.; Gohar, M.; Saqib, M. On the applications of nanofluids to enhance the performance of solar collectors: A comparative analysis of Atangana–Baleanu and Caputo–Fabrizio fractional models. Eur. Phy. J. Plus 2017, 132, 540. [Google Scholar] [CrossRef]
- Karaagac, B. Two step Adams Bashforth method for time fractional Tricomi equation with non-local and non-singular Kernel. Chaos Solitons Fractals 2019, 128, 234–241. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC-based-CNT’s nanofluid through a porous medium. Chaos Solitons Fractals 2018, 116, 79–85. [Google Scholar] [CrossRef]
- Abro, K.A.; Khan, I.; Tassaddiq, A. Application of Atangana-Baleanu fractional derivative to convection flow of MHD Maxwell fluid in a porous medium over a vertical plate. Math. Model. Nat. Phenom. 2018, 13, 1. [Google Scholar] [CrossRef]
- Abro, K.A.; Khan, I.; Nisar, K.S.; Alsagri, A.S. Efects of carbon nanotubes on Magnetohydrodynamic flow of methanol based nanofluids via Atangana-Baleanu and Caputo-fabrizio fractional derivatives. Therm. Sci. 2019, 23, 883–898. [Google Scholar]
- Yavuz, M.; Özdemir, N. Comparing the new fractional derivative operators involving exponential and Mittag-Leffler kernel. Discret. Contin. Dyn. Syst. S 2019, 13, 995–1006. [Google Scholar] [CrossRef]
- Imran, M.A.; Aleem, M.; Riaz, M.B.; Ali, R.; Khan, I. A comprehensive report on convective flow of fractional (ABC) and (CF) MHD viscous fluid subject to generalized boundary conditions. Chaos Solitons Fractals 2019, 118, 274–289. [Google Scholar] [CrossRef]
- Abro, K.A.; Khan, I. MHD flow of fractional Newtonian fluid embedded in a porous medium via Atangana-Baleanu fractional derivatives. Discret. Contin. Dyn. Syst. S 2019. [Google Scholar] [CrossRef]
- Wenchang, T.; Mingyu, X. Unsteady flows of a generalized second grade fluid with the fractional derivative model between two parallel plates. Acta Mech. 2004, 20, 471–476. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. Theoretical analysis of the velocity field, stress field and vortex sheet of generalized second order fluid with fractional anomalous diffusion. Sci. China Ser. A Math. 2001, 44, 1387–1399. [Google Scholar] [CrossRef]
- Shen, F.; Tan, W.; Zhao, Y.; Masuoka, T. The Rayleigh–Stokes problem for a heated generalized second grade fluid with fractional derivative model. Nonlinear Anal. Real World Appl. 2006, 7, 1072–1080. [Google Scholar] [CrossRef]
- Mahmood, A.; Parveen, S.; Ara, A.; Khan, N.A. Exact analytic solutions for the unsteady flow of a non-Newtonian fluid between two cylinders with fractional derivative model. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3309–3319. [Google Scholar] [CrossRef]
- Shen, M.; Chen, S.; Liu, F. Unsteady MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid with Cattaneo heat flux and different particle shapes. Chin. J. Phys. 2018, 56, 1199–1211. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Liu, F.; Bai, Y. Analytical and numerical solutions of the unsteady 2D flow of MHD fractional Maxwell fluid induced by variable pressure gradient. Comput. Math. Appl. 2018, 75, 965–980. [Google Scholar] [CrossRef]
- Aman, S.; Al-Mdallal, Q.; Khan, I. Heat transfer and second order slip effect on MHD flow of fractional Maxwell fluid in a porous medium. J. King Saud Univ. Sci. 2018. [Google Scholar] [CrossRef]
- Jan, S.A.A.; Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M.; Gohar, M. Engine oil based generalized brinkman-type nano-liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana-Baleanu fractional model. Numer. Methods Part. Differ. Equ. 2018, 34, 1472–1488. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023111. [Google Scholar] [CrossRef] [PubMed]
- Saad, K.M.; Khader, M.M.; Gómez-Aguilar, J.F.; Baleanu, D. Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023116. [Google Scholar] [CrossRef] [PubMed]
- Saqib, M.; Khan, I.; Shafie, S. New Direction of Atangana–Baleanu Fractional Derivative with Mittag-Leffler Kernel for Non-Newtonian Channel Flow. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 253–268. [Google Scholar]
- Abro, K.A.; Chandio, A.D.; Abro, I.A.; Khan, I. Dual thermal analysis of magnetohydrodynamic flow of nanofluids via modern approaches of Caputo–Fabrizio and Atangana–Baleanu fractional derivatives embedded in porous medium. J. Therm. Anal. Calorim. 2019, 135, 2197–2207. [Google Scholar] [CrossRef]
- Hristov, J. On the Atangana–Baleanu Derivative and Its Relation to the Fading Memory Concept: The Diffusion Equation Formulation. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 175–193. [Google Scholar]
- Khan, I.; Alqahtani, A.M. MHD Nanofluids in a Permeable Channel with Porosity. Symmetry 2019, 11, 378. [Google Scholar] [CrossRef]
- Asif, M.; Ul Haq, S.; Islam, S.; Abdullah Alkanhal, T.; Khan, Z.A.; Khan, I.; Nisar, K.S. Unsteady Flow of Fractional Fluid between Two Parallel Walls with Arbitrary Wall Shear Stress Using Caputo–Fabrizio Derivative. Symmetry 2019, 11, 449. [Google Scholar] [CrossRef]
- Ullah, I.; Abdullah Alkanhal, T.; Shafie, S.; Nisar, K.S.; Khan, I.; Makinde, O.D. MHD Slip Flow of Casson Fluid along a Nonlinear Permeable Stretching Cylinder Saturated in a Porous Medium with Chemical Reaction, Viscous Dissipation, and Heat Generation/Absorption. Symmetry 2019, 11, 531. [Google Scholar] [CrossRef]
- Khan, A.; Ali Abro, K.; Tassaddiq, A.; Khan, I. Atangana–Baleanu and Caputo Fabrizio analysis of fractional derivatives for heat and mass transfer of second grade fluids over a vertical plate: A comparative study. Entropy 2017, 19, 279. [Google Scholar] [CrossRef]
- Gul, T.; Khan, M.A.; Noman, W.; Khan, I.; Abdullah Alkanhal, T.; Tlili, I. Fractional order forced convection carbon nanotube nanofluid flow passing over a thin needle. Symmetry 2019, 11, 312. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R. Modelling the spread of river blindness disease via the Caputo fractional derivative and the beta-derivative. Entropy 2016, 18, 40. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Atangana, A. Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal Fract. 2019, 2, 10. [Google Scholar] [CrossRef]
- Muhammad Altaf, K.; Atangana, A. Dynamics of Ebola Disease in the Framework of Different Fractional Derivatives. Entropy 2019, 21, 303. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics 2019, 8, 1015. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef]
- Makinde, O.D.; Mhone, P.Y. Heat transfer to MHD oscillatory flow in a channel filled with porous medium. Rom. J. Phys. 2015, 931, 9–10. [Google Scholar]
- Cogley, A.C.; Gilles, S.E.; Vincenti, W.G. Differential approximation for radiative transfer in a nongrey gas near equilibrium. AIAA J. 1968, 6, 551–553. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; ul Karim, F.; Imran, M. MHD flow of Sodium Alginate-based Casson type nanofluid passing through a porous medium with Newtonian heating. Sci. Rep. 2018, 8, 8645. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Solutions with Wright function for time fractional free convection flow of Casson fluid. Arab. J. Sci. Eng. 2017, 42, 2565–2572. [Google Scholar] [CrossRef]
- Mackolil, J.; Mahanthesh, B. Exact and Statistical computations of radiated flow of Nano and Casson fluids under heat and mass flux conditions. J. Comput. Des. Eng. 2019. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Atangana, A.; Dumitru, B. New fractional derivatives with nonlocal and non-sin- gular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).