Abstract
Saline soil in seasonally frozen soil areas has caused tremendous damage to engineering and the ecological environment. The unfrozen water is the main factor affecting the properties of saline soil in seasonally frozen soil area and therefore needs to be studied. However, due to the high cost of laboratory measurement of the unfrozen water content, this study focuses on using an adaptive network fuzzy inference system (ANFIS) and a back propagation neural network (BPNN) to predict the unfrozen water content of saline soil in the Zhenlai area, Western Jilin. The data for the constructed model is obtained by nuclear magnetic resonance (NMR) testing. The initial water content (W0), salt content (S), and temperature (T) are used as input parameters for predicting the unfrozen water content (Wu). The results of the ANFIS and BPNN models are compared. The results show that although both methods are suitable for predicting the unfrozen water content of saline soil in the Zhenlai area, western Jilin, the prediction accuracy of the ANFIS model is higher.
1. Introduction
Seasonally frozen soil has an extensive spread all over the world [1]. In recent years, due to the continuous development of economic construction, humans have improved the development speed of seasonally frozen soil areas. In this process, because of the lack of knowledge of the seasonally frozen soil, various engineering and environmental problems have arisen. The problem has turned into a key element restricting the environment and development.
The western area of Jilin is located in the southwest of the Songnen Plain. This area is not only a seasonally frozen soil area but also one of the three soda alkali soil distribution areas in the world [2,3]. The frozen soil has caused complex engineering problems, such as subgrade pumping, pavement frost heave, structural damage to buildings, and so on [4,5,6,7]. At the same time, the salinization of frozen soil has caused the degradation of agricultural arable land and pasture, aggravating the deterioration of the ecological environment and causing the frequent occurrence of natural disasters in Jilin Province [8,9,10].
In most cases, the problems caused by frozen soil and salinization are related to unfrozen water. When the soil is frozen, not all water is frozen, and some liquid water always remains in the frozen soil, i.e., unfrozen water [11]. This unfrozen water is a very important part of the frozen soil. It migrates and redistributes during freezing, and its presence is a central issue in freezing and melting.
During the process of soil freezing, the water in the saline soil will migrate upwards (frozen process from top to bottom) as the temperature decreases, and the dissolved salts in the water will be transported upward together. In this process, due to the interaction of the temperature field, hydraulic field, and stress field, water and salt migration will occur, leading to soil frost heave and soil salinization [6,12]. The unfrozen water in the soil is the source of water migration, and the amount of water migration (unfrozen water content) at different temperatures is different. Therefore, in order to control the increase of the saline soil area, reduce the harm to projects, and improve the ecological environment of Jilin Province, it is necessary to study the saline soil in Western Jilin Province. The unfrozen water content is a key physical parameter of frozen soil and salinized soil. The prediction and analysis of unfrozen water content will provide theoretical support for water and salt migration and is of great significance to the study of frozen soil and its salinization [12,13].
At present, the common unfrozen water content measurement methods include the calorimetric method [14], the thermometry method [15], the time domain reflectometry (TDR) method [16,17], and the nuclear magnetic resonance (NMR) method [18,19]. The principle of calorimetry and thermometry is simple, and the precision is high, but the operation and the calculation are complicated. The TDR method has the advantages of fast testing speed, cheap price, being portable, and so on. However, it is not easy to get accurate permittivity measurements from the soil. The NMR method has the characteristics of being direct and non-destructive, suffering low external interference and having a short single test time. It is a quick, precise, non-destructive method for testing the unfrozen water content of soil [20].
The artificial neural network (ANN), as a multivariate nonlinear regression method, is suitable for solving nonlinear problems and can be used for the inverse mode of radiation transmission calculations. The artificial neural network was applied to civil engineering as early as 1989 [21], and then began to be widely welcomed in the fields of civil engineering, structural engineering, geotechnical environmental engineering, water resources engineering, and engineering geology. It is often used to solve problems such as concrete expansion prediction [22], saline soil frost heave prediction [23], soft rock strength prediction [24], composite material, and plastic hardening constitutive model identification, and so on [25,26,27]. The back propagation neural network (BPNN) is a sort of ANN which is widely applied at present.
The fuzzy inference system (FIS) is also applicable to the solution of nonlinear problems. In 1965, the “fuzzy set” concept was born. So far, the fuzzy inference system has been widely used in many fields, such as artificial intelligence, industrial control, image recognition, and satellite and missile systems. Fuzzy control numerical simulation analysis was applied to the structural seismic response by Fujitani and Midorikawa et al. [28]. Ghassem Habibagahi established the settlement prediction model of a rockfill dam [29]. All of these have achieved good results.
The intention of this study is to measure the unfrozen water content (Wu) of saline soil in the Zhenlai area of Western Jilin by NMR, under different temperature (T), salt content (S) and initial water content (W0). There is currently little research on the prediction of the unfrozen water content of saline soil. In this study, BPNN and adaptive network fuzzy inference system (ANFIS) prediction models of the unfrozen water content are established, and the best prediction model is selected. The prediction models are established and calculated using MATLAB software.
2. Test of Unfrozen Water Content
An NMR instrument was used in this test. The principle of NMR is as follows: The samples contain hydrogen nuclei with different physical and chemical states. These hydrogen nuclei produce different relaxation times after interference by radio frequency signals. The unfrozen water content is determined by measuring the relationship between signal intensity and the temperature, water content, and mineralogy of the soil particles [30,31].
2.1. Samples Preparation
Samples were prepared with 40 cm deep saline soil. The saline soil was from the Zhenlai research area in Western Jilin, China (Figure 1). The sample was configured at room temperature, and the steps were as follows:
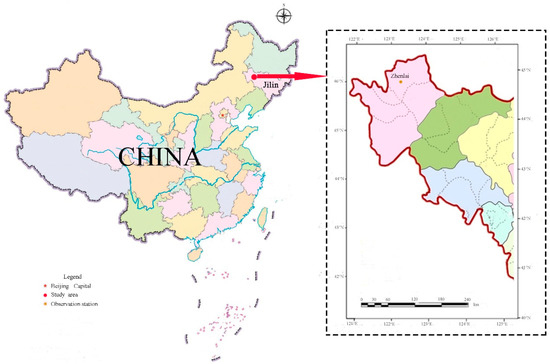
Figure 1.
Location of sampling points in the study area.
- The physical and chemical properties of the saline soil samples were tested;
- Salt was removed from the saline soil samples with deionized distilled water;
- The samples were prepared using deionized distilled water and soluble salt (a salt mixture of sodium sulfate and sodium carbonate, with a ratio of 2.8:1). After the salt in the saline soil was washed out, the sample was prepared according to the preset salt content and water content (Table 1);
 Table 1. Salt content and initial water content of samples.
Table 1. Salt content and initial water content of samples. - After the samples were well prepared, the samples were placed in a sealed fresh-keeping bag for 24 h, so that the solution was evenly distributed in the samples;
- The sample was prepared to the following size: 25 mm in diameter with a height of 50 mm, and about 70 g in weight.
2.2. Test Result
The testing of the unfrozen water content was divided into two processes: Freezing and melting. Fist, the unfrozen water content during the freezing process was measured, and then the water content during the melting process was measured. Taking into account the actual ambient temperature in the study area, in this experimentation, the freezing process temperature was set from high to low as follows: −0.2 °C, −0.5 °C, −1 °C, −3 °C, −5 °C, −10 °C, −15 °C, −20 °C. The melting process was set to the same temperature as the freezing process, but with the opposite order.
2.2.1. Varied Initial Water Content and Fixed Salt Content
For Samples 2 and 4, the content of salt (S) is the same and the initial water content (W0) is different (Figure 2). During the freezing process, the sample went through three stages. This trend of change is consistent with those introduced in the literature [32,33,34].
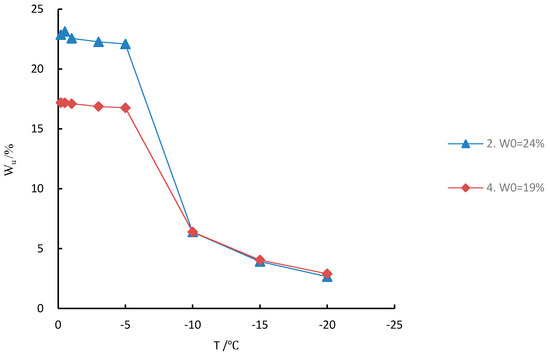
Figure 2.
Relationship between unfrozen water content and negative temperature.
The unfrozen water content (Wu) decreases with decreasing temperature until it gradually stabilizes. When the temperature is from −0.2 °C to −5 °C, the process is in the first stage (the high-temperature stage). In this stage, the water in the sample does not completely change phase. The content of unfrozen water is stable and is greater than 16%. When the temperature ranges from −10 °C to −5 °C, the process is in the second stage (mutation stage). The unfrozen water in the samples begins to crystallize into ice, and its content decreases rapidly with the decrease of temperature. When the temperature ranges from −20 °C to −10 °C, the process is in the third stage (stable stage). At this stage, the content of unfrozen water gradually tends to be stable with the drop of temperature.
This shows that, firstly, the larger the water content, the thicker the water film around the soil particles and the higher the content of unfrozen water. With the same salt content, the greater the initial water content, the greater the unfrozen water content. Thus, they are directly proportional to each other. In the first and second stages, the unfrozen water content of sample 2 is higher than that of sample 4. Secondly, when the samples are in the third stage, with the lower temperature, the water films water on the soil particles surfaces are less likely to freeze.
2.2.2. Fixed Initial Water Content and Varied Salt Content
For samples 1, 2, and 3, the initial water content (W0) is in the same, and the salt content (S) is different (Figure 3).
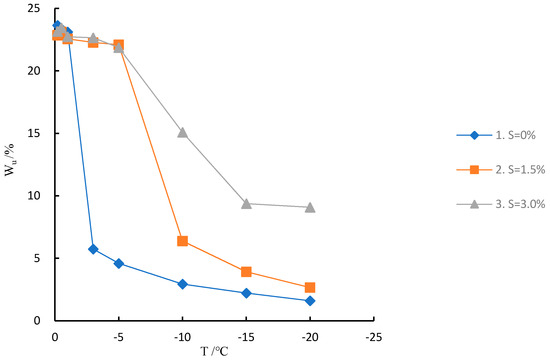
Figure 3.
Relationship between unfrozen water content and negative temperature.
The unfrozen water content increases with increasing salt content. In particular, when the temperature is −20 °C, the content of unfrozen water in sample 1 (salt content is zero) is only 1.6%, while the content of unfrozen water in sample 3 (salt content is 3%) is up to 9.08%. The higher the salt content of samples, the lower the freezing point. When the temperature is −1 °C, the content of unfrozen water in sample 1 drops sharply. The unfrozen water contents of other samples dropped sharply at below −3 °C.
This shows that the soluble salt reduces the freezing point of the sample and increases the unfrozen water content of the sample. There is a positive correlation between the content of soluble salt and the content of unfrozen water.
2.2.3. Freezing and Melting Process
For samples 2, 3, and 4, the freeze-melt process has some influence on the unfrozen water content (Figure 4).
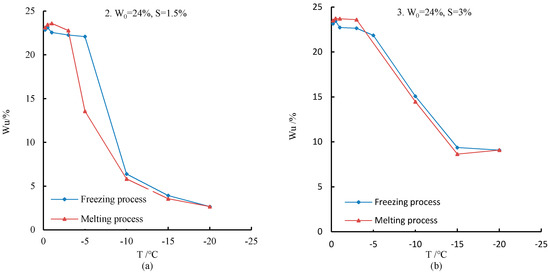
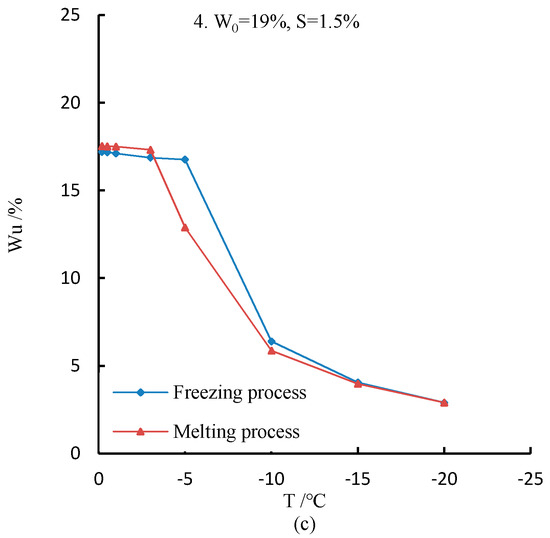
Figure 4.
Effect of freezing and melting processes on unfrozen water content: (a) Unfrozen water content curve of sample 2; (b) unfrozen water content curve of sample 3; (b) unfrozen water content curve of sample 4.
It can be clearly seen through the observation curve that during the freezing process, the unfrozen water content decreases with decreasing temperature; in the melting process, the unfrozen water content increases with increasing temperature. Above the freezing point temperature, for samples 2, 3, and 4, the unfrozen water content during the melting process was always larger than that during the freezing process.
Below the freezing point temperature, for samples 2, 3, and 4, the unfrozen water content during the freezing process was always larger than that during the melting process. Moreover, with the change of temperature, the unfrozen water content curve (Figure 4) of the sample displays a hysteresis phenomenon.
This shows that the curve of the unfrozen water content is associated with the freezing temperature. The content of unfrozen water during the processes of freezing and melting is different.
3. Numerical Simulation
According to the above discussion, in the Zhenlai research area of Western Jilin Province, the unfrozen water content (Wu) of saline soil is mainly affected by initial water content (W0), salinity (S), temperature (T), and so on. Therefore, the relationship between them can be expressed by Equation (1).
Wu = f(W0, S, T),
In this study, 32 groups of experimental data on the freezing process were selected for numerical simulation (Table 2). Among them, 26 groups of data were used for training, and 6 groups of data were used for testing. The initial water content (W0), salinity (S), and temperature (T) were taken as input variables, and unfrozen water content (Wu) was taken as the output variables. The range of their change is shown in Table 3.

Table 2.
Unfrozen water content during the freezing process.

Table 3.
Range of variables relevant to the saline soil in Western Jilin.
The 32 sets of data needed to be normalized before the model was built. The data normalization processing expressions are shown in Equation (2).
where represents the standard deviation of the data, is the sample data, is the maximum value in the sample data before normalization, and is the minimum value in the sample data before normalization [23].
3.1. Numerical Simulation Based on a BP Neural Network
Artificial neural networks (ANN) can perform functions such as classification, clustering, fitting, prediction, and compression [35]. After years of development, from ANNs have been derived a diversity of algorithms. Among them, the back propagation neural network (BPNN) is a kind of ANN. The BPNN has many advantages. It has hard non-linear mapping, self-adaptive, and self-learning capabilities. The number of neurons in each layer of the network can be installed arbitrarily according to the specific circumstances. Therefore, it is now widely used in various fields. The BPNN is a feedforward type network. It contains an input layer, one or more hidden layers, and an output layer [35].
3.1.1. Determining the Network Structure
At present, the structure of the three-layers BP neural network is stable and is most frequently applied. In this study, three-layers of BPNN was selected to predict the unfrozen water content of saline soil. The topology is as shown in Figure 5. Our BP neural network model has three input parameters and one output parameter. The values of these parameters were all obtained by experiments. The 32 groups of experimental data were divided into two groups; 26 groups were selected as training samples and 6 groups were used as test samples.
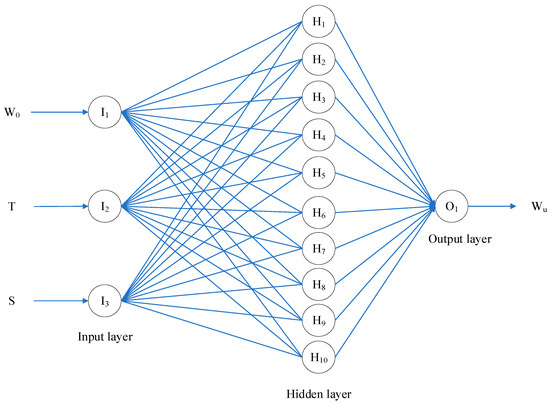
Figure 5.
The topological structure of the three layers of a backpropagation (BP) neural network.
3.1.2. Input Layer and Output Layer
The number of input layer nodes should be determined by the actual situation. It is usually the vector dimension of the training sample, which is the dimension of the input vector. The number of output layer nodes also needs to be determined according to the actual application. In the classification problem, if there are n categories, then the number of output layer nodes is generally n; in the fitting problem, the number of nodes is determined by the spatial dimension of the output of the fitting function [36].
In this study, the input value of the input layer is the value of the input parameter. The data of the input layer is first passed to the hidden layer, and the output value of the hidden layer is obtained under the action of the activation function as shown by Equations (3) and (4):
where represents the hidden layer output value, represents the activation function, (the S-type function was selected in this study), is the hidden layer input value, is the value of the input layer ith unit, is the weight of the ith unit of the input layer to the jth unit of the hidden layer, and is the offset value of the input layer to the hidden layer [23,37].
The output data of the hidden layer is passed to the output layer, and the final output data can then be obtained.
3.1.3. Number of Hidden Layer Nodes
In this study, a three-layer BP neural network was selected. Thus, there is only one hidden layer. The determination of the hidden layer neurons number is a greatly significant part of the neural network design. Here, the range of the number of nodes in the hidden layer is determined by the Equation (5):
where m represents the input neurons number, n represents the output neurons number, and c represents a constant ranging in value from 1 to 10 [22,35]. Here, the number of hidden layer neurons ranges from 3 to 12.
In the interest of determining the optimal network, the quantity of neurons is determined by the mean squared error (MSE) and the correlation coefficient (R2). The MSE is expressed by Equation (6), and R2 is expressed by Equation (7).
where N represents the number of samples, represents the predicted value of unfrozen water content, and represents the experimental value of unfrozen water content.
The number of neurons is determined from the minimum MSE and the maximum R2. This was used as the standard for choosing the hidden layer number. Figure 6 shows that when the R2 value is maximal, the number of neurons is 9. Figure 7 shows that when the MSE is minimal, the number of neurons is 9, too. Therefore, the number of hidden neurons selected for the predictive model was 9.
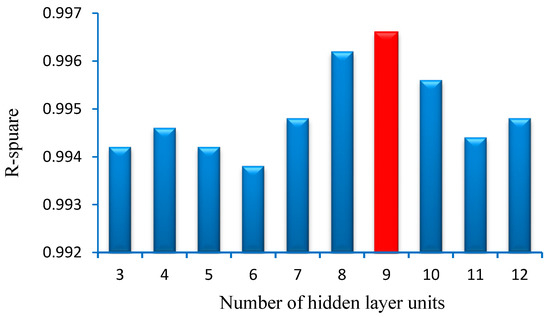
Figure 6.
R-square value of the training data when the number of hidden layer unit changes.
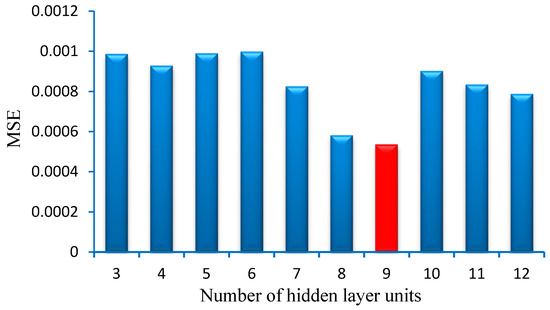
Figure 7.
Mean squared error (MSE) value of the training data when the number of hidden layer units changes.
3.1.4. Implementation Process
The BP neural network prediction model was implemented using the MATLAB software. The function ‘Newff’ was used to create the neural network. “Tansig” and “logsig” represented the transfer functions of the BPNN. The implementation steps were as follows:
- Sample data were normalized, as shown in Equation (2);
- Sample data were classified;
- The BP neural network was established;
- Training was performed;
- After the training was completed, testing was carried out;
- Error analysis and result prediction were performed.
3.2. Numerical Simulation Based on an Adaptive Fuzzy Neural Inference System (FIS)
The FIS can also be called a fuzzy system. It is a reasoning system based on fuzzy set theory and fuzzy reasoning, and has the function of dealing with fuzzy information. The fuzzy inference system takes the fuzzy theory as its main computing tool and does not rely on the mathematical model of the controlled object, so it can achieve a more complex nonlinear mapping. The input and output of the system are accurate values. Compared with the traditional method, the fuzzy inference system uses the experience of human expert control, and has the advantage of high prediction accuracy for nonlinear and complex objects. At present, fuzzy inference systems are applied very widely [23,36].
3.2.1. The Fuzzy Inference System
The FIS is static nonlinear mapping between input and output. It is chiefly composed of fuzzification, a fuzzy rule base, the fuzzy reasoning method, de-fuzzification, and so on. The basic working process is as follows: The fuzzification module converts an accurate input into a fuzzy set. Under the constraint of the rule base, the fuzzy inference module produces fuzzy conclusions. The fuzzy conclusion is converted to an accurate output by the de-fuzzification module [23,36]. The basic structure of a FIS is shown in Figure 8.
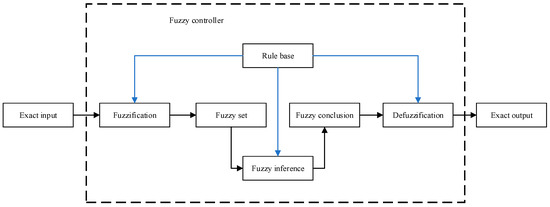
Figure 8.
Functional structure of a fuzzy inference system.
3.2.2. The Adaptive Network-Based Fuzzy Inference System (ANFIS)
The ANFIS is made up of “IF-THEN” rules that obey fuzzy logic rules. The learning algorithms are adjusted by the parameters of the logical inference system. In this study, a fuzzy neural inference system based on the Takagi-Sugeno type [38] was selected. Through the system, 32 groups of experimental data were trained and tested, and the prediction model of the unfrozen water content in the saline soil in Western Jilin was finally established. The model structure is shown in Figure 9.
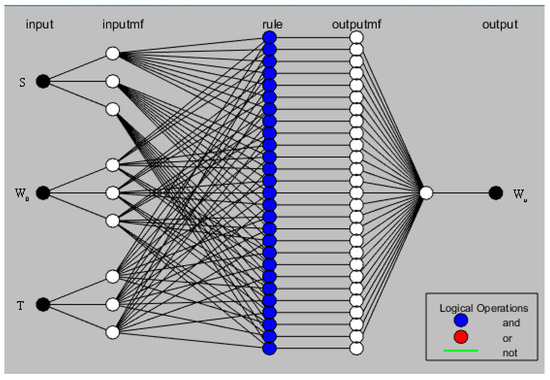
Figure 9.
Network structure of the fuzzy neural system.
It can be seen from Figure 9 that this ANFIS requires the following five layers to realize the establishment and calculation of the model.
First layer: This layer is the input layer, which passes the training data and test data to the next layer. The number of nodes in this layer is the dimension of the input vector.
Second layer: This layer is the membership function layer of the input data. The function of this layer is the fuzzified input data. The membership function value , is shown by Equation (8)
where n represents the dimension of input vectors, mi represents the number of fuzzy divisions of xi and Ai represents a fuzzy set. The fuzzy set [39] is defined as: For a given universe X, a mapping OA:X → [0, 1] is able to determine a fuzzy set A in X. OA is called the membership function of the fuzzy set A.
If the bell-type function is used as the membership function, then it takes the form in Equation (9)
where bij represents the center of the membership function and ∅i represents the width of the membership function.
Third layer: This layer is a fuzzy layer, and each node represents a fuzzy rule. The data will be fuzzified at this layer. Each rule has a corresponding credible degree (), as given by Equation (10).
Fourth layer: The layer is the output layer of fuzzy rules, and the output is normalized as shown by Equation (11)
Fifth layer: This layer is the output layer. It converts the output data of the previous layer into clear and precise values; that is, the defuzzification of the data is calculated as shown by Equation (12)
where dij represents the central value of the membership function.
In the FIS, there are many possible membership functions, such as bell type, Gaussian type, ladder type, trigonometric type and so on. In this study, the bell membership function was used because it performed best during the training process. In this study, 27 “IF-THEN” rules were chosen to form the fuzzy rule base. At the same time, the “and method” containing two operators and the prod method was employed. The composition rules of fuzzy reasoning employed the maximum-minimum regular in this predictive model. In the de-fuzzification module, the model employed the weighted average (wtaver) method. In addition, the model production method chosen was the grid segmentation method (Grid partition). The data used for the model training and testing were the same as the those used for the BP neural network. It was also necessary to normalize the data. In this paper, the MATLAB software was applied to establish and calculate the model.
4. Results and Discussion
In this study, in order to predict the unfrozen water content of the saline soil in Zhenlai, Jilin, based on the experimental data, BPNN and ANFIS methods were applied, and prediction models were established. Finally, the results were obtained.
Figure 10 displays the experimental results and model prediction results in the training phase of the BPNN model and the ANFIS model. In Figure 10, in the training phase, the predicted results from the BPNN model, and the ANFIS model are very close to the experimental results. This shows that, although there is a certain error, the two prediction models can predict the content of unfrozen water better at the training stage.
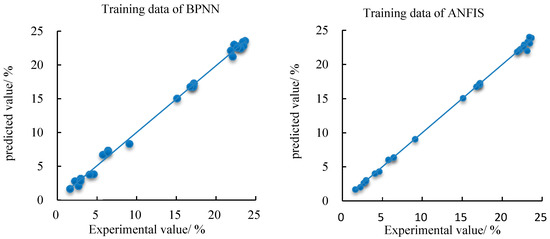
Figure 10.
Comparison between experimental and predicted Wu values for the backpropagation neural network (BPNN) and adaptive network-based fuzzy inference system (ANFIS) models.
Table 4 gives the prediction data obtained by applying the BPNN and ANFIS methods for training. The 26 sets of training data were obtained by nuclear magnetic resonance experiments. In Table 4, the mean absolute percentage errors of BPNN and ANFIS are 6.05% and 1.72%, respectively; the maximum relative errors of BPNN and ANFIS are 26.01% and 7.84%, respectively. It can be seen that the error of the ANFIS is smaller than the error of the BPNN. The relative error (RE) and the mean absolute percentage error (MAPE) were calculated using Equations (13) and (14) respectively.
where N represents the number of samples, represents the predicted value of the unfrozen water content, and represents and the experimental value of the unfrozen water content.

Table 4.
The training results from applying BPNN and ANFIS.
In the testing stage, the respective predicted results from the BPNN model and the ANFIS model were fitted with the experimental results; the fitting results are shown in Figure 11. Figure 11a shows the prediction results of the BPNN model are fitted to the experimental results. The change trend of the two curves between data 1 and 5 is basically the same, but the change trend of the two curves from data point 5 to data point 6 is different. This shows that for the data 6, there is a certain gap between the predicted results and the experimental results. Figure 11b shows the prediction results of the ANFIS model are fitted to the experimental results. From data 1 to data 6, the change trends of the two curves are basically the same. Therefore, we can see from Figure 11, that for the prediction of the unfrozen water content, the error of the BPNN model is greater than that of the ANFIS model.
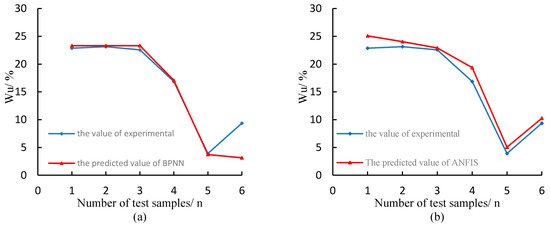
Figure 11.
Forecasting curves of test samples: (a) The prediction results of the BPNN model are fitted to the experimental results; (b) the prediction results of the ANFIS model are fitted to the experimental results.
Table 5 gives the prediction data obtained by applying the BPNN and ANFIS methods for testing. The six sets of testing data were obtained by nuclear magnetic resonance experiments. In Table 5, when the BPNN predicts the content of unfrozen water, the relative error of the first five test values is ideal. Only the relative error of the last test value is relatively large, reaching 66.43%. ANFIS predicts the content of unfrozen water with a relative error range of 1.54% to 28.51%, which is acceptable. Calculating from the data in Table 5, we see that the mean absolute percentage errors of BPNN and ANFIS are 13.10% and 11.31%, respectively. Although the mean absolute percentage errors of both are ideal, the mean absolute percentage error of ANFIS is smaller than that of BPNN.

Table 5.
The testing results of applying BPNN and ANFIS.
In order to further compare the accuracy of the BPNN model and that of the ANFIS model in the prediction of the unfrozen water content of saline soil in Zhenlai, Jilin, two parameters were employed for evaluation purposes. They are the mean square error (MSE) and correlation coefficient (R2). The calculation formulae are given by Equations (6) and (7).
When the mean square error is near to 0, the correlation coefficient approaches 1, the more the model’s training effect is better, and the prediction result is more accurate. Table 6 shows the values of the two parameters during the training and testing stages.

Table 6.
Wu statistical values for the BPNN and AHFIS models.
The mean square errors of the BPNN in the training and testing stages are 5.366 × 10−4 and 1.36 × 10−2, respectively, and the correlation coefficients are 0.9965 and 0.9444, respectively. Likewise, in the training and testing stage, the mean square errors of the ANFIS model are 1.704 × 10−4 and 4.833 × 10−3, respectively, and the correlation coefficients are 0.9988 and 0.9897 respectively (Table 6). It can be seen that the MSE and the MAPE of the ANFIS are smaller than those of the BPNN, and the R2 of the ANFIS is larger than that of the BPNN.
In this paper, the k-fold cross-validation method (k = 1, 2, …, 5) is used to compare the applicability of the unfrozen water content prediction model (BPNN model and ANFIS model). Based on four statistical indicators: R-square, p-value, MSE and MAPE, the BPNN model and ANFIS model were evaluated quantitatively. The evaluation results are shown in Table 7 and Table 8.

Table 7.
Evaluation index of cross-validation of unfrozen water content prediction models (training phase).

Table 8.
Evaluation index of cross-validation of unfrozen water content prediction models (testing phase).
Table 7 shows the cross-validation evaluation indicators for the unfrozen water content prediction model during the training phase. The average value () of the mean square errors for the BPNN and ANFIS in the training stages were 9.26 × 10−4 and 8.30 × 10−4, respectively, the average value () of the mean absolute percentage errors were 7.21 and 7.15, respectively, and the average value of the correlation coefficients were 0.9940 and 0.9940, respectively. The p-values of both models in the 5-fold cross-validation are smaller than 0.05. Therefore, according to the four evaluation indicators of cross-validation, both models performed well during the training phase, but ANFIS was slightly better.
Table 8 shows the cross-validation evaluation indicators for the unfrozen water content prediction model during the testing phase. The average value () of the mean square errors for the BPNN and ANFIS in the testing stages were 4.51 × 10−2 and 2.40 × 10−2, respectively, the average value () of the mean absolute percentage errors were 35.73 and 26.13, respectively, and the average value of the correlation coefficients were 0.7643 and 0.8339, respectively. In the two models, the and of ANFIS are the smallest, and the average value of the correlation coefficient is the largest. When k is 2, the p-value of BPNN is 0.0972, and when k is 4, the p-value of ANFIS is 0.1457. The p-values were slightly greater than 0.05, only 0.0472 and 0.0957 higher, respectively, in addition, the p-values of both models in the 5-fold cross-validation are smaller than 0.05. Therefore, during the testing phase, the predictive performance of ANFIS is better than that of BPNN.
In conclusion, the BPNN model is less accurate than the ANFIS model for predicting the unfrozen water content of saline soil of the Zhenlai area in the western Jilin Province. The ANFIS model can more accurately reflect the relationship between the unfrozen water content and its influencing elements, like the temperature, salinity, and initial moisture content of saline soil in Zhenlai, Jilin.
5. Conclusions
In this study, the NMR method was used to test saline soil from the Zhenlai area in Western Jilin Province under different conditions, such as varied temperature, salt content, and initial moisture content, and the unfrozen water content was obtained. Based on the experimental information, prediction models of the unfrozen water content were established using the BPNN model and the ANFIS model. In the course of training and testing, the data used by the two models were the same. Our conclusions are as follows:
- During the freezing process, the saline soil mainly experienced three stages: High temperature, mutation, and stability. When the content of salt was fixed, the greater the initial water content, the greater the content of unfrozen water. The content of unfrozen water decreased with decreasing temperature and eventually tended to stabilize.
- During the freezing process, the salt content was inversely proportional to the freezing point, and the ice point was reduced with increasing of salt content. As the temperature decreased, the content of unfrozen water was high in the samples with high salt content.
- In the process of freezing and melting, the content of unfrozen water decreased with decreasing temperature and increased with increasing temperature. At temperatures below freezing point, the unfrozen water content during the freezing process was always greater than that during the melting process, and the unfrozen water content showed as hysteresis phenomenon.
- The comparison shows that both BPNN and ANFIS prediction models can predict the unfrozen water content well. However, the accuracy of the two models was evaluated by way of their mean square error, mean absolute percentage error, and correlation coefficient. The ANFIS model had greater accuracy than did the BPNN. The ANFIS prediction model is more suitable for predicting the unfrozen water content in saline soil areas of Western Jilin.
- The research shows that the ANFIS can be utilized for predicting unfrozen water content, and the model will be further applied to studying water and salt migration in frozen soil. The research results will contribute to soil and water conservation, soil improvement, and engineering construction in the saline soil area of Western Jilin, which is conducive to the restoration of the ecological environment and the sustainable development of economy and construction.
Author Contributions
Q.W. and Y.L. contributed to data analysis and manuscript writing. Q.W. proposed the main structure of this study. X.Z., S.S., C.N., and Y.S. provided useful advice and revised the manuscript. All authors read and approved the final manuscript.
Funding
This research was funded by the study presented in this paper from the State Key Program of the National Natural Science Foundation of China (Grant No. 41430642), the Special Fund for Major Scientific Instruments of the National Natural Science Foundation of China (Grant No. 41627801), and the National Natural Science Foundation of China (Grant No. 41372267).
Acknowledgments
Thanks to anonymous reviewers and editors for their valuable feedback on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andersland, O.B.; Ladanyi, B. An Introduction to Frozen Ground Engineering; ASCE & John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Liu, H.Q.; Xu, J.W.; Wu, X.Q. Present situation and tendency of saline-alkali soil in west Jilin Province. J. Geogr. Sci. 2001, 11, 321–328. [Google Scholar]
- Wang, C.Y.; Wu, Z.J.; Shi, Y.L.; Wang, R.Y. The Resource of Saline Soil in the Northeast China. Chin. J. Soil Sci. 2004, 35, 643–647. [Google Scholar]
- Bao, S.C.; Wang, Q.; Wang, W.H.; Wang, Z.J. Influence of freezing-thawing process on dispersibility of cohesive soil in western Jilin seasonal frozen region. J. Heilongjiang Hydraul. Eng. Coll. 2014, 5, 155–160. [Google Scholar]
- Zhang, X.D.; Wang, Q.; Li, P.F.; Wang, R.Y. Research on Soil Dispersion of Qian’an Soil Forest. J. Northeast. Univ. (Nat. Sci.) 2015, 36, 1643–1647. [Google Scholar]
- Niu, C.C.; Wang, Q.; Wang, W.H.; Zhang, Y.G.; Ye, C. Research on Moisture Migration Experiment of Seasonally Frozen Zone Saline Soil. Adv. Mater. Res. 2015, 1065–1069, 168–171. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wang, Q.; Wang, G.; Wang, W.H.; Chen, H.; Zhang, Z.Q. A study on the coupled model of hydrothermal-salt for saturated freezing salinized soil. Math. Probl. Eng. 2017, 2017, 4918461. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Ma, H.W.; Liu, Q.; Zhu, W.; Zhang, T.X. Development and Drives of Land Salinization in Songnen Plain. Geol. Resour. 2007, 16, 120–124. [Google Scholar]
- Bao, S.C.; Wang, Q.; Bao, X.H.; Wang, Z.J. Characters of saline-alkali soil in western Jilin and biological treatment. J. Pure Appl. Microbiol. 2013, 7, 809–812. [Google Scholar]
- Wang, Q.; Liu, Y.F.; Liu, S.W. Evolution Law of Material Properties Under Multi Field Effect of Saline Soil in Western Jilin Province. J. Jilin Univ. (Earth Sci. Ed.) 2017, 47, 807–817. [Google Scholar]
- Baker, J.M. Water Relations in Frozen Soil. Encycl. Soil Sci. 2006, 1, 1858–1859. [Google Scholar]
- Zhang, X.D.; Liu, S.W.; Wang, Q.; Wang, G.; Liu, Y.F. Experimental investigation of water migration characteristics for saline soil. Pol. J. Environ. Stud. 2019, 28, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wang, Q.; Yu, T.W.; Wang, G.; Wang, W.H. Numerical study on the multifield mathematical coupled model of hydraulic-thermal-salt-mechanical in saturated freezing saline soil. Int. J. Geomech. 2018, 18, 04018064. [Google Scholar] [CrossRef]
- Kolaian, J.H.; Low, P.F. Calorimetric determination of unfrozen water in montmorillonite pastes. Soil Sci. 1963, 95, 376–384. [Google Scholar] [CrossRef]
- Williams, P.J. Unfrozen water content of frozen soils and soil moisture suction. Géotechnique 1964, 14, 231–246. [Google Scholar] [CrossRef]
- Zegelin, S.J.; White, I.; Jenkins, D.R. Improved field probes for soil water content and electrical conductivity measurement using time domain reflectometry. Water Resour. Res. 1989, 25, 2367–2376. [Google Scholar] [CrossRef]
- Azmatch, T.F.; Sego, D.C.; Arenson, L.U.; Biggar, K.W. Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils. Cold Reg. Sci. Technol. 2012, 83–84, 103–109. [Google Scholar] [CrossRef]
- Wen, Z.; Feng, W.; Deng, Y.; Wang, D.; Fan, Z.; Zhou, C. Experimental study on unfrozen water content and soil matric potential of qinghai-tibetan silty clay. Environ. Earth Sci. 2012, 66, 1467–1476. [Google Scholar] [CrossRef]
- Watanabe, K.; Wake, T. Measurement of unfrozen water content and relative permittivity of frozen unsaturated soil using NMR and TDR. Cold Reg. Sci. Technol. 2009, 59, 34–41. [Google Scholar] [CrossRef]
- Long, T.; Wei, C.F.; Tian, H.H.; Zhou, J.Z.; Wei, H.Z. Experimental study of unfrozen water content of frozen soils by low-field nuclear magnetic resonance. Rock Soil Mech. 2015, 36, 1566–1572. [Google Scholar]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput. Aided Civ. Infrastruct. Eng. 2010, 16, 126–142. [Google Scholar] [CrossRef]
- Wang, B.; Man, T.; Jin, H. Prediction of expansion behavior of self-stressing concrete by artificial neural networks and fuzzy inference systems. Construct. Build. Mater. 2015, 84, 184–191. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wang, Q.; Huo, Z.S.; Yu, T.W.; Wang, G.; Liu, T.B.; Wang, W.H. Prediction of frost-heaving behavior of saline soil in western jilin province, china, by neural network methods. Math. Probl. Eng. 2017, 2017, 7689415. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Armaghani, D.J.; Momeni, E. Prediction of the unconfined compressive strength of soft rocks: A pso-based ann approach. Bull. Eng. Geol. Environ. 2014, 74, 745–757. [Google Scholar] [CrossRef]
- Brown, D.A.; Murthy, P.L.N. Computational simulation of composite play micromechanics using artificial neural networks. Microcomput. Civ. Eng. 1991, 6, 87–97. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Panagiotopoulos, P.D. Generalised hardening plasticity approximated via anisotropic elasticity: A neural network approach. Comput. Methods Appl. Mechan. Eng. 1995, 125, 123–139. [Google Scholar] [CrossRef]
- Bi, Z.; Ma, J.; Pan, X.; Wang, J.; Shi, Y. ANFIS-Based modeling for photovoltaic characteristics estimation. Symmetry 2016, 8, 96. [Google Scholar] [CrossRef]
- Fujitani, H.; Midorikawa, M.; Iiba, M.; Kitagawa, Y.; Miyoshi, T.; Kawamura, H. Seismic response control tests and simulations by fuzzy optimal logic of building structures. Eng. Struct. 1998, 20, 164–175. [Google Scholar] [CrossRef]
- Habibagahi, G. Post-construction settlement of rockfill dams analyzed via adaptive network-based fuzzy inference systems. Comput. Geotech. 2002, 29, 211–233. [Google Scholar] [CrossRef]
- Watanabe, K.; Mizoguchi, M. Amount of unfrozen water in frozen porous media saturated with solution. Cold Reg. Sci. Technol. 2002, 34, 103–110. [Google Scholar] [CrossRef]
- Dongyang, L.I.; Liu, B.; Liu, N.; Yongjun, M.A.; Wang, L. A method to save the determining time of unfrozen water within frozen soil by nuclear magnetic resonance. J. Glaciol. Geocryol. 2014, 36, 1502–1507. [Google Scholar]
- Bittelli, M.; Flury, M.; Campbell, G.S. A thermodielectric analyzer to measure the freezing and moisture characteristic of porous media. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Wang, L.X.; Hu, Q.L.; Ling, X.Z.; Cai, D.S.; Xu, X.Y. Test study on unfrozen water content and thermal parameters of qinghai-tibet railway frozen silty clay. J. Harbin Inst. Technol. 2017, 39, 1660–1663. [Google Scholar]
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Permafrost Physics; The Science Publishing Company: Beijing, China, 2001. [Google Scholar]
- Fu, H.X. Application Design of MATLAB Neural Network; Machine Press: Beijing, China, 2010. [Google Scholar]
- Zhao, Z.; Xu, Y. Introduction to Fuzzy Theory and Neural Networks and Their Application; Tsinghua University Press: Beijing, China, 1996. [Google Scholar]
- Firat, M.; Gungor, M. Generalized regression neural networks and feed forward neural networks for prediction of scour depth around bridge piers. Adv. Eng. Softw. 2009, 40, 731–737. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).