Abstract
A black hole in a Schwarzschild spacetime is considered. A transformation is proposed that describes the relationship between the coordinate systems exterior and interior to an event horizon. The application of this transformation permits considerations of the (a)symmetry of a range of phenomena taking place on both sides of the event horizon. The paper investigates two distinct problems of a uniformly accelerated particle. In one of these, although the equations of motion are the same in the regions on both sides, the solutions turn out to be very different. This manifests the differences of the properties of these two ranges.
1. Introduction
Outside the horizon of a black hole the Killing vector is time-like and it becomes space-like inside the horizon—this means that energy conservation is broken (see e.g., [1]). Such a conversion of the Killing vector results in a lot of interesting phenomena, with the Hawking radiation and the information paradox being the most prominent among them [2,3]. The status of these two outcomes arising from the presence of the event horizon is, in a sense, similar: both appeared mainly due to the work of Hawking and both of them are still debated [4]. More recent studies have considered a range of interesting questions. One of the latest was the supposition that black holes (BH) do indeed have hair [5]; another interesting outcome was the claim that the volume of a BH may be infinite [6]. In view of the argument that there is not enough space inside a black hole to store arbitrarily large amounts of information, this discovery turns out to be a contribution that is strictly associated with the problem of information stored and lost within an event horizon [7]. Following a proposal by Unruh [8] of development of gravity analogues, condensed, soft matter or photonic black hole-like systems that develop an event horizon have been experimentally realized [9]. A recent experiment has led to a Kerr-like BH, including an ergosphere, not just an event horizon, opening up the possibility of experimental observations of the Penrose effect [10].
The interior of a black hole itself has been the subject of fewer but more diverse considerations. Hamilton et al. [11] presented a discussion on the question of (spectroscopic) vision inside the horizon of a Schwarzschild BH. In another approach Hamilton and Leslie [12] considered the exterior and interior of a BH within a so-called river model that was based on the use of a Painleve-Gullstrand co-moving frame. It is well-known that the static spacetime outside a BH’s horizon turns out to be dynamic inside the outer horizon in the situation when two horizons are formed. Such a dynamic interior of a BH may be viewed as a cosmological model [13].
The aim of this paper is to study the properties of the interior of a Schwarzschild BH, i.e., which is isotropic and static outside the horizon. The investigations are presented from a special perspective. One finds a formal, specific symmetry between the exterior and interior ranges, even though the properties of these two regions are found to be completely different. We illustrate the differences using two problems that are related to the behavior of a test particle uniformly accelerated outside and inside the horizon. In the first example, the particle moves radially outside the horizon; inside the horizon, corresponding motion takes place along a homogeneity axis (see below). It is found then that although the equations of motion are the same in both regions the solutions differ significantly. In the other example, a test particle follows a circular trajectory belonging to the photon sphere [14] and inside the horizon the test particle moves along a photon sphere analogue.
The paper is organized as follows. In Section 2, we present a transformation between coordinate systems outside and inside the horizon of the Schwarzschild black hole. Section 3 is devoted to a thorough investigation of the problem of uniformly accelerated motion along a straight line: radially outside the horizon, and along the homogeneity direction inside the horizon. In Section 4, we consider the case of uniform acceleration for motion along a circle on a photon sphere outside horizon and its analogue inside the horizon. A discussion and final remarks are provided in the last section.
2. Systems of Co-Ordinates in Space-Time with a Horizon
Arbitrary co-ordinate system constitute a diffeomorphism from an open set U of the space-time M into an open set U′ of the real Euclidean flat space , where is the dimension of M:
We will consider a spherically symmetric spacetime with a black hole defined by a horizon. The horizon , which is a global property of such a spacetime, divides into an exterior and an interior :
On (which is static) one can introduce a coordinate system which in spherical coordinates on takes the form:
where and is a (gravitational) radius of the horizon . The metric on in this framework has the form
This is the well-known Schwarzschild space-time with , and is a unit metric on .
On one can introduce the following coordinate system:
where . The metric on in this coordinate system has the following form (see [11])
Hence, on , there are two coordinate systems with two metrics and . The transformation between these two systems of coordinates has the form:
where is given by the matrix:
It acts as follows:
and
where and .
There are two Killing vectors manifesting symmetry properties in the exterior and interior of the horizon. In , there is a time-like one, representing energy conservation due to the static character of the spacetime and a space-like one, reflecting angular momentum conservation. In , there is a space-like one, reflecting -momentum conservation due to homogeneity along the -axis and another space-like one, representing angular momentum conservation.
The exterior of the Schwarzschild black hole, is a static spacetime and its interior, is a dynamic spacetime. One can introduce a class of static observers in the former and a class of resting observers in the latter case. The velocity vector of such observers has only a temporal non-vanishing coordinate . It appears natural to label them as:
- (a)
- t-observersoutside the horizon and
- (b)
- T-observersinside the horizon.
3. Uniformly Accelerated Motion along Straight Line
In this section we will consider the problem of a uniformly accelerated test particle in the exterior and interior of the horizon. The motion of such a test particle will be confined to the and hyperplanes, respectively. So, one can discuss the case of a 1 + 1 dimensional spacetime
such that
- (a)
- Outside the horizon, and is a function of spatial coordinate
- (b)
- Inside the horizon, and is a function of temporal coordinate .
The components of the velocity vector
of the test particle, will depend on in the case (a) and on in case (b).
An acceleration vector field for is:
and one obtains the following equations for its components:
- (a)
- outside the horizonand
- (b)
- inside the horizon
Hence, one finds that these two pairs of equations are transformed into each other under the interchange of the temporal and spatial coordinates, and as emphasized in the former section (see Equation (9)). Uniform acceleration is defined by the condition:
where The equations for the world line of the test particle are then derived, as follows.
- (a)
- Outside the horizon
Thus, the world line of the uniformly accelerated particle is given in the case of a static metric by the integral curve of the vector field:
where E is an integration constant.
- (b)
- Inside the horizon
In this case of a dynamic spacetime the world line of the test particle is given, as follows:
Applying the fact that inside the horizon
one finds that the world line equations for the outer and inner horizon regions, Equations (22) and (23) and Equations (25) and (26) take the same form:
Here, we will examine the following point: how does the speed of a uniformly accelerated test particle change with respect to the static observers? In general a relative velocity four-vector of , as measured by another observer characterized by velocity at the same event is given by (see [15])
where is the scalar product of the two velocity four-vectors, and , . Velocity is orthogonal to , , i.e., is a space-like vector,
Then, the squared speed is given as:
3.1. Black Hole Exterior
In the exterior of the Schwarzschild black hole the spacetime is static and static observers denoted as t-o are characterized by their velocity vector (see Equation (11)). Such an observer measures the speed of a nearby passing uniformly accelerated (ua) test particle,
Hence, for , and , one applies the procedure described above to find:
Using Equations (28) and (29), we obtain
This case of a uniformly accelerated test particle initially at rest, is illustrated in Figure 1.
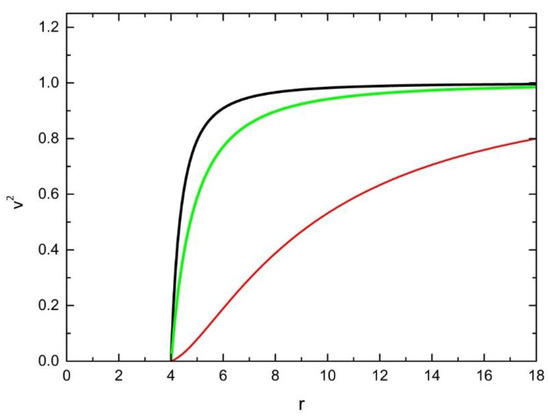
Figure 1.
Squared speed (Equation (35)) of a uniformly accelerated test particle initially at rest at (in this case ) escaping radially from the gravitational field for different values of α = 0.1 (red), α = 0.5 (green), α = 1 (black).
3.2. Black Hole Interior
Inside the horizon, . A class of resting (or co-moving, see below) observers is determined by (12)
Using Equations (26), (32), and (36), one obtains the squared speed of the uniformly accelerated test particle inside the horizon:
Using the relation inside the horizon, one can express the squared speed as a function of a temporal coordinate, . In Figure 2, the squared speed of the uniformly accelerated test particle initially at rest is illustrated by applying expression (37). The speed initially increases, reaches some (non-universal) maximal value and finally decreases to zero at the ultimate singularity, .
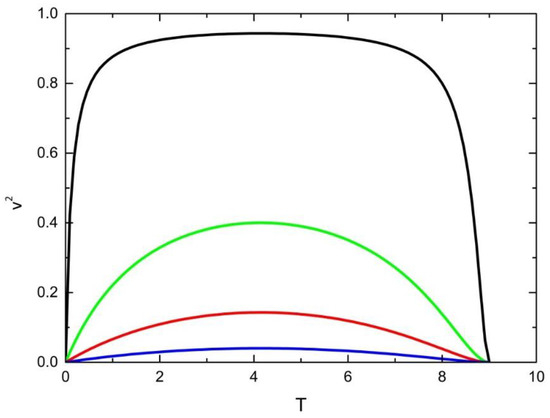
Figure 2.
Squared speed (Equation (37)) of a test particle initially, at rest (in this case ) uniformly accelerated along homogeneity axis (=t) for different values of α = 0.05 (blue), α = 0.1 (red), α = 0.2 (green), α = 1 (black).
4. Uniform Acceleration on a Photon Sphere and on Its Analogue inside the Horizon
A photon sphere outside the horizon, , has a radius, . It consists of null geodesic circles, , . Its analogue inside the horizon, , consists of planar null geodesics having two non-vanishing components, . However, in this case, the radius, of such a “sphere” diminishes from to 0. We shall consider the problem of a uniformly accelerated test particle on a circle belonging to the photon sphere and on a “circle” belonging to the photon sphere analogue.
4.1. Black Hole Exterior
In a case of a test particle moving outside the horizon along a circle of radius the velocity vector is two-component
where without loss of generality, we have considered a circle in an equatorial plane, . An acceleration vector field in the case of motion with constant speed is found to be (see [14]).
Applying a normalization condition, , one finds that the acceleration of a photon sphere, , turns out to be speed independent [14]
Hence, in this case, one can consider a generalization of the twin-paradox and other features, such as specific non-geodesic motion [16].
4.2. Black Hole Interior
Motion along a photon sphere analogue in this case, is as follows.
The two-component velocity vector of a test particle takes the form:
and its components will be -dependent. An acceleration vector field is found to be two-component,
and its components are:
Uniform acceleration is defined by the condition (see Equation (13))
The equations for the world line of the test particle are then derived as follows. Applying Equations (43)–(45), one finds,
Thus, the world line of the test particle uniformly accelerated on a sphere of ever diminishing radius, is given by an integral curve of the vector field :
where C is an integration constant. Here, we are interested in the following question (see above): how does the speed of a uniformly accelerated test particle change with respect to the static (resting) observers? Similarly, as in the former section, the speed is measured by (resting) T-observers, Equation (36). In this case, one finds:
The meaning of the result (49) is: the speed of the uniformly accelerated test particle, of total acceleration tends to the speed of light as the ultimate singularity, approaches, as .
5. Discussion and Final Remarks
In order to investigate the properties of the interior of a Schwarzschild black hole one can apply a specific symmetry to the coordinate systems of its exterior and interior. The meaning of such a symmetry is that the radial and temporal coordinates interchange their roles. This symmetry may be regarded as a justification of the fact that one can apply a Schwarzschild system of coordinates, both outside as well as inside the horizon. It is an almost trivial notion, but it is important to remember the existence of a singularity in this system, which is the horizon itself.
In the case of radial motion outside the horizon and motion along the direction of homogeneity inside the horizon, one finds that the equations of motion on both sides of the horizon obey the symmetry: they are transformed into each other under transformation (7–10). This is because the motion takes place in the hyper-planes and that are transformed into each other under . However, the properties of the solutions are very different. Outside the horizon, a radially accelerated particle departs with ever increasing speed (if the acceleration is larger than some critical value). The speed of a test particle uniformly accelerated along the homogeneity axis inside the horizon, whose equation of motion is the same as the one outside the horizon, initially increases but then decreases to zero when approaching the ultimate singularity. This means that transformation does not lead to particular physical consequences (at least in this case).
In the case of circular motion on a photon sphere and “circular” motion on a photon sphere analogue, outside and inside the horizon, respectively, the equations of motion are (rather obviously) different. Apart from the fact of the existence of a photon sphere and its analogue inside the horizon, there are no features that are in common for accelerated motion of a test particle in such orbits. The radial acceleration during circular motion of the test particle on the photon sphere is independent of its speed (which is a well-known result); the speed of a test particle following accelerated motion along a circle belonging to the photon sphere analogue (of ever decreasing radius) increases to the speed of light when approaching the ultimate singularity.
Having in mind an (intimate) symmetry between the exterior and interior of the Schwarzschild black hole, leading in the simplest case to the same equation of motion, one may wonder how it arises that the properties of the solutions are so different. The answer is: it is because and , spatial (radial) and temporal coordinates, respectively, outside the horizon interchange their roles, becoming temporal and spatial (in the direction of homogeneity) coordinates inside the horizon. Such an exchange of roles has a deeper consequence: outside the horizon, spacetime is spherically symmetric and static and inside the horizon it is no longer static, it is dynamically changing (i.e., an “anisotropic cosmology”, see [13]), but homogeneous along one of its spatial directions.
It should be noted that our discussion has been presented within a specific system of coordinates, namely Schwarzschild coordinates outside the horizon, revealing a singularity, namely the horizon itself. One may ask then: what is the significance of these results? The answer is as follows.
When considering the case of uniformly accelerated motion along a straight line (Section 3), one finds acceleration vectors outside, Equations (16) and (17) and inside, Equations (18) and (19) the horizon. These quantities (being vectors) may be transformed in a covariant way to another (arbitrary) coordinate system, e.g., a Kruskal-Szekeres coordinate system (see e.g., [1]), one free of singularities. Transformation between Schwarzschild, and Kruskal-Szekeres, coordinates,
enables us to confirm that symmetry of the equations of motion Equations (16)–(19) found in the former system is also preserved in the latter one.
The condition of a uniform acceleration, (20) is in fact independent of coordinate system (as it refers to a scalar product, i.e., a squared acceleration vector). The world line itself is characterized by velocity vectors, outside, Equations (22) and (23) and inside, Equations (25) and (26) the horizon; this characteristic, velocity vector, is also transformed in a covariant way to other systems of coordinates.
A physical quantity illustrating the properties of the interior of a Schwarzschild black hole, such as the (squared) speed of a uniformly accelerated test particle, as measured by a resting T-observer inside the horizon is expressed in terms of a scalar product, Equations (30)–(32) and (37); hence, it is independent of the coordinate system.
The case of a test particle following a circular orbit and its analogue inside the horizon may be analyzed in a similar manner leading to a similar outcome. The conclusion that the squared speed inside the horizon of an accelerated test particle tends to the value of the speed of light at the ultimate singularity is obviously a coordinate independent result.
One should underline however that the choice of the specific system of coordinates allows for one to (easily) solve Equation (21), leading to the explicit form Equations (28) and (29); solving the equation of motion in another coordinate system may not be such an easy task.
Author Contributions
P.G.: The idea of (a)symmetry, uniform acceleration, calculations; A.A.: Conceptual discussions, manuscript preparation and editing; F.F.: Numerical support, preparations of illustrations; A.R.: Discussing and developing the concepts of uniformly accelerated test particles as viewed by resting observers, calculations.
Funding
Department of Quantum Technologies, Wroclaw University of Science and Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hartle, J.B. Gravity; Addison Wesley: Boston, MA, USA, 2003; Chapter 12; p. 13. [Google Scholar]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black holes: Complementarity or firewalls? J. High Energy Phys. 2013, 62, 1–19. [Google Scholar] [CrossRef]
- Hawking, S.W.; Perry, M.; Strominger, A. Soft Hair on Black Holes. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef] [PubMed]
- Christodoulou, M.; Rovelli, C. How big is a black hole? Phys. Rev. D 2015, 91, 1–7. [Google Scholar] [CrossRef]
- Mathur, S. A model with no firewall. arXiv, 2015; arXiv:1506.04342. [Google Scholar]
- Unruh, W.G. Experimental Black-Hole Evaporation? Phys. Rev. Lett. 1981, 46, 1351–1353. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Gerace, D.; Carusotto, I.; Sanvitto, D.; Galopin, E.; Lemaître, A.; Sagnes, I.; Bloch, J.; Amo, A. Acoustic Black Hole in a Stationary Hydrodynamic Flow of Microcavity Polaritons. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [PubMed]
- Vocke, D.; Maitland, C.; Prain, A.; Biancalana, F.; Marino, F.; Faccio, D. Rotating black hole geometries in a two-dimensional photon superfluid. Optica 2018, in press. [Google Scholar]
- Hamilton, A.J.S.; Polhemus, G. Stereoscopic visualization in curved spacetime: Seeing deep inside a black hole. New J. Phys. 2010, 12, 123027–123052. [Google Scholar] [CrossRef]
- Hamilton, A.J.S.; Lisle, J.P. The river model of black holes. Am. J. Phys. 2008, 76, 519–532. [Google Scholar] [CrossRef]
- Doran, R.; Lobo, F.S.N.; Crawford, P. Interior of a Schwarzschild black hole revisited. Found. Phys. 2008, 38, 160–187. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Bajtlik, S.; Kluzniak, W. The twin paradox on the photon sphere. Phys. Rev. A 2007, 75. [Google Scholar] [CrossRef]
- Bolos, V.J. Intrinsic Definitions of “Relative Velocity” in General Relativity. Comm. Math. Phys. 2007, 273, 217–236. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Bajtlik, S. Adding to the paradox: The accelerated twin is older. arXiv, 2009; arXiv:0905.2428v1 2009. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).