Abstract
Nowadays, more and more applications are dependent on storage and management of semi-structured information. For scientific research and knowledge-based decision-making, such data often needs to be published, e.g., medical data is released to implement a computer-assisted clinical decision support system. Since this data contains individuals’ privacy, they must be appropriately anonymized before to be released. However, the existing anonymization method based on l-diversity for hierarchical data may cause serious similarity attacks, and cannot protect data privacy very well. In this paper, we utilize fuzzy sets to divide levels for sensitive numerical and categorical attribute values uniformly (a categorical attribute value can be converted into a numerical attribute value according to its frequency of occurrences), and then transform the value levels to sensitivity levels. The privacy model (, k)-anonymity for hierarchical data with multi-level sensitivity is proposed. Furthermore, we design a privacy-preserving approach to achieve this privacy model. Experiment results demonstrate that our approach is obviously superior to existing anonymous approach in hierarchical data in terms of utility and security.
1. Introduction
Hospitals and other organizations often need to publish data, e.g., medical data or census data, for the purposes of scientific research and knowledge-based decision-making [1,2,3,4,5,6,7,8,9,10]. To avoid the leakage of individual privacy, explicit identifying information is removed when data is released. However, individual privacy still could be leaked by linking other public data [11]. Privacy-preserving data publishing provides methods and tools for publishing useful information while preserving individual privacy [12]. In recent years, the problem of privacy-preserving data publishing has been studied extensively. The existing privacy protection methods mainly focus on relational data, and many mature privacy models are proposed, such as k-anonymity [11], l-diversity [13], (α, k)-anonymity [14] and t-closeness [15]. However, data often has a complicated structure in the real world. With the advent of document-oriented databases (e.g., MongoDB) and the wide use of markup languages (e.g., XML), hierarchical data has become ubiquitous [16]. To avoid the leakage of individual privacy, the hierarchical data must be properly anonymized before it is released. At present, there are few researches on privacy protection for hierarchical data. Ozalp et al. [16] proposed l-diversity anonymous methods for hierarchical data. An example for hierarchical data is given in Figure 1. The schema for education data is obtained from Sabanci University [16] and the examples appearing in this paper are related to the schema. Figure 1a represents a student’s record, which fits the education schema shown in Figure 1b. The student is born in 1990 and majors in Computer Science. He took two courses, CS201 and CS305. For CS201, his evaluations are submitted for two instructors. For CS305, he submitted an evaluation and showed he bought a database book. The labels of vertices are all quasi-identifiers (QIs) of the student and the corresponding sensitive information is remarked in the side of every vertex. Quasi-identifier is a set of attributes that can potentially identify an individual [11]. Assume that an attacker knows some QIs of a victim, and his goal is to reason the sensitive information of the victim. In [16], they used suppression and generalization [11] to make the anonymous hierarchical dataset satisfy l-diversity, which ensures the frequency of every sensitive value for the union-compatible vertices (belonging to the same vertex in schema) in an equivalence class is not more than 1/l. The constraint also can guarantee that every equivalence class contains at least l hierarchical data records. An equivalence class in an anonymous hierarchical dataset is a set of records with the same values for the QIs. However, the method does not consider the sensitivity of different sensitive attribute values, which lead to similarity attacks [15]. For example, an equivalence class contains three hierarchical data records and its class representative is shown in Figure 2, which satisfies 3-diversity. The sensitive values of their cumulative GPAs are 0.31, 0.15 and 0.09, respectively, where GPA is the grade point average. An attacker knows a victim in the equivalence class by linking with some QIs of the victim. Although the attacker does not infer the victim’s specific sensitive value, he can know that the victim’s academic performance is low with 100% probability and the victim’s privacy is leaked. Similarly, the attacker can confirm that the grade of the victim in the course CS201 is very low according to the value {D, D+, D−}. Also, the attacker can infer that the victim is very dissatisfied with the DB Prof. by the value {0, 1/10, 2/10}. To avoid similarity attack, we propose a multi-level privacy-preserving approach in hierarchical data based on fuzzy sets.
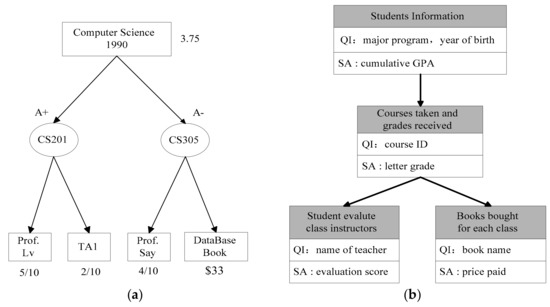
Figure 1.
An example for hierarchical data: (a) A student’s record; (b) Schema for education data.
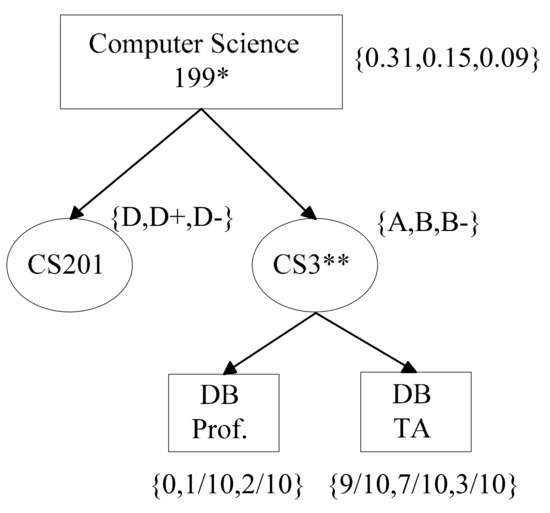
Figure 2.
A class representative satisfying 3-diviersity.
The contributions of this paper are summarized as follows:
- We utilize the fuzzy set theory to obtain the sensitivity levels for sensitive numerical and categorical attribute values, and present the privacy model (, k)-anonymity for hierarchical data with multi-level sensitivity. This model can solve the similarity attack, and provide reasonable privacy protection for sensitive value in different sensitivity level.
- We improve the privacy-preserving approach in hierarchical data to obtain the anonymous data that satisfies (, k)-anonymity.
- We do experiments to compare our approach with the existing anonymous method ClusTree proposed in [16]. Experiment results demonstrate that our approach is superior to ClusTree in terms of utility and security.
2. Related Work
In this section, we review the related work about privacy preserving data publishing for relational data and hierarchical data.
2.1. Preserving Privacy for Publishing Relational Data
The first privacy model, proposed by Samarati and Sweeney [11] in 1998, is k-anonymity for relational data, which requires that every record in a table is indistinguishable from at least k-1 other records with respect to QI. There exist many anonymization methods to implement k-anonymity, such as bottom-up generalization, top-down specialization and anonymity by clustering technique [17,18,19]. k-anonymity can protect against identity disclosure, but cannot prevent attribute disclosure. Therefore, l-diversity has been proposed [13]. It requires that every equivalence class contains at least l different sensitive values. There are numerous methods for achieving l-diversity [20,21]. Furthermore, Wong et al. [14] extended k-anonymity to (α, k)-anonymity to limit the confidence of the implications from the QI to a sensitive value to within α in order to protect the sensitive information from being inferred by strong implications, and proposed a bottom-up generalization algorithm to achieve (α, k)-anonymity. Li et al. [15] pointed out that l-diversity does not prevent skewness attack and similarity attack, so they introduced t-closeness model, which requires that the distribution of a sensitive attribute in any equivalence class is close to the distribution of the attribute in the overall table. They also revised the Incognito algorithm [17], which is a top-down generalization method proposed for k-anonymity, to achieve t-closeness. However, t-closeness still does not prevent similarity attacks. Han et al. [22] considered the difference of sensitivity for sensitive values, and proposed multi-level l-diversity model for numerical sensitive attribute. Furthermore, Jin et al. [23] presented the (αi, k)-anonymity privacy preservation based on sensibility grading. However, the levels are artificially assigned. Some researches proposed fuzzy based methods for privacy preserving [24,25]. They used fuzzy sets to transform sensitive values to semantic values and published the data with fuzzy sensitive information, which decreases the utility of sensitive information and still does not resist similarity attacks.
2.2. Preserving Privacy for Publishing Hierarchical Data
There are several studies about preserving privacy for publishing hierarchical or tree-structured data. Yang and Li [26] found that the dependencies between nodes in the XML data information may result in privacy leakage. They formally defined these dependencies as XML constraints, and designed an algorithm to sanitize XML documents by considering these constraints such that no privacy is leaked. However, their attack model is too weak. Our adversarial model assumes that the attacker has some information about the victim. Landberg et al. [27] proposed δ-dependency and extended the anatomy method in relational data to hierarchical data. But the dissection method will damage the original semantic structure of hierarchical data, and the generalization in sensitive attributes will affect the effectiveness of hierarchical data. Nergiz et al. [28] extended k-anonymity methods to a multi-relational database, and proposed multi-relational k-anonymity. Firstly, hierarchical data will be converted to multiple relational data tables, which related to each other by primary key or foreign key, then performed k-anonymity separately on each relational data. However, converting hierarchical data into relational data is not a simple matter, and will produce large amounts of data redundancy, which made the executive efficiency of algorithm extremely low. It will also lose a lot of structural information. Gkountouna and Terrovitistis [29] proposed the k(m, n)-anonymity for tree-structured data. By using generalization and structure decomposition methods, they ensured that the number of matching records not less than k when the attacker knows up to m nodes in a tree and to n structural relations between these nodes. But the method cannot resist the attack with stronger background knowledge. In addition, they used structural decomposition that destroys the structural information of the hierarchical data. Ozalp et al. [16] extended l-diversity to hierarchical data. They utilized generalization and suppression to anonymize the hierarchical data, and make the hierarchical records in an equivalence class to be indistinguishable in terms of the QIs and structure and the sensitive values for the union-compatible vertices in an equivalence class satisfies the requirements of l-diversity. This method is very scalable for the general anonymous method of hierarchical data. However, this method does not consider the different sensitivity of sensitive attribute values in anonymous hierarchical data, so the anonymous hierarchical data still does not resist similarity attack. In this paper, we use fuzzy set theory to partition rank for sensitive values of union-compatible vertices, and propose a multi-level privacy-preserving approach in hierarchical data to solve similarity attacks.
3. Problem Descriptions
In this section, we describe the attack model, give some fundamental definitions, and introduce our privacy protection model.
3.1. Attack Model
We assume that an attacker knows a victim’s QI information, which contains any combination of QI values in the same or different vertices of the victim’s record. Also, the attacker can obtain some structural links. For example, the victim took two courses, and purchased only a book for course CS201. In addition, the attacker has some negative knowledge, e.g., the victim did not take CS305. Our anonymization approach can ensure that an attacker, who has this background knowledge about a victim, does not infer any sensitive value of the victim is in some level with the probability, which is greater than a given threshold.
3.2. Basic Definitions in Hierarchical Data
In this subsection, we give some basic definitions for hierarchical data [16]. Let T be a graph with n vertices. We say that T is a rooted tree if and only if (1) T is a directed acyclic graph with n-1 edges; (2) for every vertex (except root vertex), there is a single path from the root vertex to it in T; (3) there exists an edge v → ci if ci ∈ children(v), where children(v) is the children of vertex v. Such tree is denoted by T(V, E), where V and E are the sets of vertices and edges in the tree, respectively.
A hierarchical data record satisfies the following conditions: (1) it follows a rooted tree structure; (2) each vertex v has two j-tuples (j ≥ 0), vQIt and vQI, which contains the names of QI attributes and the values of corresponding QIs, respectively; (3) each vertex v also has two m-tuples (0 ≤ m ≤ 1), vSAt and vSA, which contains the name of sensitive attribute and the value of corresponding sensitive attribute, respectively; (4) assume that |vQI| + |vSA| ≥ 1 to eliminate empty vertices. For a vertex v of a hierarchical data record, vQI is the label of v and vSA is next to v. For Figure 1, vQIt = {major program, year of birth}, vSat = {GPA}, vQI = {Computer Science, 1990}, and vSA = {3.75}.
Definition 1 (Union-Compatibility)
[16]. Two vertices v and v′ are union-compatible if and only if vQIt = v′QIt and vSAt = v′SAt.
Definition 2 (QI-isomorphism)
[16]. Let T1(V1, E1) and T2(V2, E2) are two hierarchical data records. T1(V1, E1) is isomorphic to T2(V2, E2) if and only if there exists a bijection f: V1 → V2, such that:
- (1)
- For x, y ∈ V1, there exists an edge ei ∈ E2 from f(x) to f(y) if and only if there exists an edge ej ∈ E1 from x to y.
- (2)
- f(r1) = r2, where r1 ∈ V1 and r2 ∈ V2 be the roots of T1(V1, E1) and T2(V2, E2), respectively.
- (3)
- For all pairs (x, x′), where x ∈ V1 and x′ = f(x), x and x′ are union-compatible and xQI = x′QI.
Definition 3 (Equivalence Class of Hierarchical Records)
[16]. Let Q = {T1,T2,...,Tk} is a collection of k hierarchical data records. We say Q is an equivalence class, if for , Ti and Tj are QI-isomorphic.
Definition 4 (Class Representative)
[16]. Let Q = {T1,T2,...,Tk} be an equivalence class in hierarchical data, and fi (1 ≤ i ≤ k-1) be a bijection that maps T1′s vertices to Ti+1′s vertices as in QI-isomorphism. is the class representative for Q if is QI-isomorphic to T1 with a bijection function f and , vSA = {f(v)SA, f1(f(v))SA,..., fk−1(f(v))SA}.
Let X = {x1, x2, ..., xo} be a multiset of values from the domain of a sensitive attribute A. X satisfies l-diversity if , p(xi) ≤ 1/l, where p(xi) is the frequency of si in X. For an equivalence class Q in hierarchical data, is the class representative for Q. If for , vSA satisfies l-diversity, then satisfies l-diversity. Given a hierarchical data D, an anonymous hierarchical data D* satisfies l-diversity, if the class representative of any equivalence class in D* satisfies l-diversity. The l-diversity hierarchical data does not prevent similarity attack, since it does not consider the different sensitivity of sensitive attribute values.
3.3. Privacy Model
For every sensitive attribute, including numerical and categorical attributes, we partition sensitive values to five levels: low, very low, middle, very high and high (for some sensitive attributes, e.g., a student’s grade in a course, the levels have been divided, and we do not need to handle it), and transform these value levels to corresponding sensitivity levels.
Let U be a universe of discourse. A mapping μA: U → [0, 1] is called a membership function on U, where the set A, which consists of μA(u) (u ∈ U), is a fuzzy set on U, and μA(u) is the membership degree of u to A [30,31,32]. The trapezoidal distribution [33] is used to give the membership functions for fuzzy sets low, very low, middle, very high and high, denoted by A1, A2, A3, A4, and A5, respectively. Let U be the domain of a numerical attribute (for categorical attribute, a numerical attribute can be obtained according to the frequency of every value), and min and max be the minimum and maximum values in U, respectively. The five fuzzy sets have values in the range [min, a2], [a1, a3], [a2, a4], [a3, a5] and [a4, max], respectively, where a3 = (min + max)/2, a1 = min + (a3-min)/3, a2 = min + 2(a3-min)/3, a4 = a3 + (max-a3)/3, a5 = a3 + 2(max-a3)/3. That is, a1, a2, a3, a4 and a5 uniformly divide the interval [min, max]. The membership functions for Ai (i = 1, 2, ..., 5) are shown as follows.
For any u ∈ U, argmax{uAi(u)|i ∈ {1, 2, 3, 4, 5}} is the level which u belongs to. We transform the value level to sensitivity level. For some sensitive attributes, the higher the value level is, the larger the sensitivity level is, e.g., income; but it is reversed for other sensitive attributes, e.g., student’s cumulative GPA. For a numerical attribute, we divide the five levels from 1 to 5 for sensitivity. Level 5 is the highest and level 1 is the lowest. The higher sensitivity level is, the stronger privacy protection will be given.
For example, for an equivalence class Q in a hierarchical data, we assume that the sensitive attribute of the root vertex in the class representative of Q is the cumulative GPA, whose value is {0.8, 1.6, 2.3, 2.7, 3.5, 3.9}, where the domain of the cumulative GPA is [0, 4]. We can obtain the min = 0, max = 4, a3 = 2, a1 = 2/3, a2 = 4/3, a4 = 8/3 and a5 = 10/3. The membership degree of ui to Aj are shown in Table 1, where ui ∈ {0.8, 1.6, 2.3, 2.7, 3.5, 3.9} and Aj ∈ {low, very low, middle, very high, high}. We can know that 0.8, 1.6, 2.3, 2.7, 3.5 and 3.9 are belong to low, very low, middle, very high, high and high, respectively. Their sensitivity levels are 5, 4, 3, 2, 1 and 1, respectively.

Table 1.
The membership degree of ui to Aj.
In fact, for every sensitive value a numerical attribute A, we can confirm quickly its value level by using the membership functions. As shown in Figure 3, the [min, max] is the domain of A, a1, a2, a3, a4 and a5 equally divide the [min, max]. p1, p2, p3 and p4 are the points of intersection of membership functions and , and , and , and and , respectively. The ranges of low, very low, middle, very high and high are [min, p1], [p1, p2], [p2, p3], [p3, p4] and [p4, max], respectively.
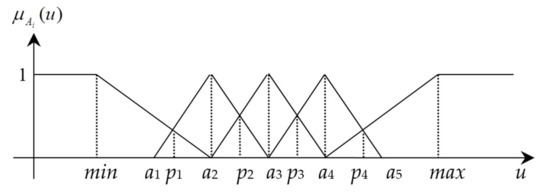
Figure 3.
The membership functions for five value levels.
For example, for the cumulative GPA and evaluation score for a teacher, the domains are [0, 4] and [0, 1], respectively. Their value levels and sensitivity levels are shown in Table 2. The letter grade of a course has been divided five levels.

Table 2.
The value levels and sensitivity levels for sensitive attributes.
For a categorical attribute, e.g., disease, according to the frequency of every value, we obtain an attribute Frequency. The values of Frequency can be divided into 5 levels including low, very low, middle, very high and high. For the disease HIV, it is more sensitive than flu, and the frequency of HIV is less than one of flu. Therefore, we divide the values of disease into 5 sensitivity levels according to the value levels of Frequency. The lower the value level is, the larger the sensitivity level is.
Definition 5 ((, k)-anonymity in Hierarchical Data).
Given a hierarchical data H, a published anonymous hierarchical data H′ satisfies (, k)-anonymity if every equivalence class Q in H′ satisfies (, k)-anonymity. That is, Q contains at least k hierarchical data records, and for every vertex v in the class representative of Q, the frequency of the values in vSA which belong to the sensitivity level i is less than or equal to , where .
4. The Anonymization Method
In this section, we introduce our anonymous method, which is divided into two parts. The first step is to realize the anonymization of two hierarchical data records or class representatives, and the second step is to anonymize the entire hierarchical data by using a clustering method.
The anonymization for two hierarchical data records is shown in Algorithm 1. The input is arbitrary two hierarchical data records T1 and T2. Without loss of generality, we assume that T1 has fewer subtrees than T2. The output is the information loss of anonymizing the two records.
We first check the root nodes of T1 and T2, stored in variables a and b, respectively, whether satisfy the anonymous constraint check_cons(a, b), shown as follows:
where is identical to (, k)-anonymity, i.e., for any an vertex v in the class representative, the number of the values in vSA, which lie in sensitivity level i, is less than or equal to k*. If check_cons(a, b) is 0, tree(a) and tree(b) are suppressed, where tree(ai) (ai ∈ {a, b}) denotes the subtree rooted ai; otherwise, the values in QI of a and b are generalized. Let subtrees(a) and subtrees(b) represent the set of subtrees under a and b, respectively. There are three cases: (1) subtrees(a) = ∅ and subtrees(b) = ∅, which indicates that a and b are leaves of hierarchical records, i.e., no vertex need to be processed, and algorithm returns the total cost in tree(a) and tree(b); (2) subtrees(a) = ∅ and subtrees(b) ≠ ∅, and we suppress all vertices under b to keep the structural consistency, and return the total cost; (3) subtrees(a) ≠ ∅ and subtrees(b) ≠ ∅, the subtrees under a and b need to be further processed. To minimize the information loss caused by anonymization, the subtrees under the a and b need to be optimally matched. Let subtrees(a) = {U1, U2, ..., Um} and subtrees(b) = {V1, V2, ..., Vn} For every subtrees Ui of a, we find the subtrees Vj of b with minimum MLevAnonytree(Ui, Vj), as shown in lines 12–23. For every pair (i, j) in pairs, we call MLevAnonytree(Ui, Vj) to generalize them. In lines 26 and 27, we suppress the unpaired subtrees of b if they exist.
| Algorithm 1. MLevAnonytree(T1, T2) |
| Input: Two hierarchical data records T1 and T2 Output: Anonymous information loss 1 a ← root(T1); b ← root(T2); 2 if check_condition(a, b) then 3 suppress tree(a) and tree(b); 4 return cost(tree(a)) + cost(tree(b)); 5 for i = 1 to |aQI| do 6 replace aQI[i] and bQI[i] with their generalized value; 7 if subtrees(a) = ∅ and subtrees(b) = ∅ then 8 return cost(tree(a)) + cost(tree(b)); 9 if subtrees(a) = ∅ and subtrees(b) ≠ ∅ then 10 suppress all vertices under b; 11 return cost(tree(a)) + cost(tree(b)); 12 pairs ← ∅; 13 for i = 1 to m do 14 min_cost ← ∞; 15 paired_index ← ∅; 16 for j = 1 to n do 17 if j ∈ pairs then 18 continue; 19 x ← Ui; y ← Vj; 20 loss ← MLevAnonytree(x, y); 21 if loss < min_cost then 22 min_cost ← loss; paired_index ← j; 23 pairs.append(i, paired_index); 24 for (i, j) ∈ pairs do 25 MLevAnonytree (Ui, Vj); 26 if there are unpaired subtrees in b then suppress them; 27 return cost(tree(a)) + cost(tree(b)); |
An anonymous example of two hierarchical data records is shown in Figure 4, where Figure 4a–c are two raw hierarchical data records, with their anonymous results identical to (, 2)-anonymity, and their class representative, respectively.
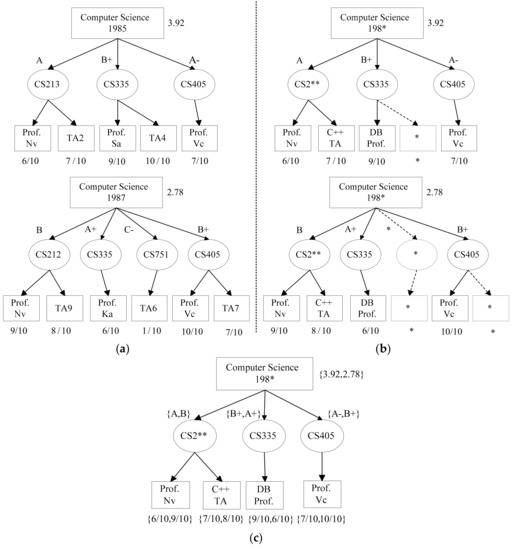
Figure 4.
An anonymous example: (a) Two raw hierarchical data records; (b) The anonymous results; (c) Class representative of results.
Now, we give the clustering algorithm for anonymizing the entire hierarchical data, as shown in Algorithm 2. The input is a hierarchical data H and privacy parameters and k. The output is the anonymous data H′ satisfies (, k)-anonymity. In lines 2–16, when the number of records in H is equal or larger than k, the algorithm creates an equivalence class from H. The first record is randomly picked in an equivalence class Q. For any residual record Ti in H, we compute the information loss by adding Ti to Q, and then sort H in ascending order according to the information loss. We select other k-1 records from the first 50 records to decrease the runtime of algorithm. In lines 17 and 18, when the number of records in H is less than k, the algorithm suppresses the all records in H.
| Algorithm 2. MLevCluTree(H, , k) |
| Input: A hierarchical data H = {T1, T2, ..., Tn}, and privacy parameters , k; Output: anonymous dataset H′ which satisfies (, k)-anonymity 1 H′ ← ∅; 2 while H ≥ k do 3 pick randomly a record x from H; H ← H-x; 4 initialize Q with x and Crep ← x; 5 Q_cost ← ∅; 6 for i = 1 to |H| do 7 loss ← MLevAnonytree(copy(x), copy(Ti)); 8 Q_cost.append(loss); 9 use Q_cost to sort H in ascending order; 10 cand_set ← H[1:50]; 11 for j = 2 to k do 12 y′ ← argminy ∈ cand_set(MLevAnonytree(copy(Crep), copy(y))); 13 H ← H- y′; cand_set ← cand_set- y′; Q ← Q ∪ y′; 14 update Crep; 15 H′←H′∪Q; 16 if H ≠ ∅ then 17 suppress all records in H; 18 return H′; |
5. Experimental Results
The objective of these experiments is to evaluate the performance of the proposed algorithm with respect to data utility, security and efficiency by comparing with existing anonymous approach Clutree [16] in hierarchical data which achieves l-diversity. The algorithms are implemented in Python, and ran on a computer with a four-core 3.4 GHz CPU and 8 GB RAM running Windows 7. We experimented on two synthetic datasets, which are obtained by the authors in [16]. They were modeled synthetically based on the real information of graduates from Sabanci University in Turkey. The synthetic dataset A has two levels (h = 2), in the order of (major program, year of birth) → courses, which contains 1000 students and nearly 20 courses per student. The synthetic data set B has three levels (h = 3), in the order of (major program, year of birth) → courses → teachers, in which there are 1000 students, every student studies nearly 20 courses, and every course has one to two teachers.
5.1. Evaluation Metrics
We evaluate data utility, security and efficiency of our method by using LM cost [16,28], dissimilarity degree of the equivalence class [22] and the execution time, respectively.
For a hierarchical data record T, the cost of T is computed as follows:
where Ω and Ψ are the sets of vertices which are not suppressed and suppressed, respectively, |ωQI| is the number of QI attributes in ω, and LM′(q) = (|uq| − 1)/(|u| − 1) is the information loss of generalizing q to uq. The larger information loss is, the lower utility is. LM cost is an important index to evaluate the utility of the anonymous method.
The equivalence class dissimilarity is proposed in [22] for relational data, and we extend it to hierarchical data. Let Q be an equivalence class and its class representative be Crep. v is a vertex in Crep, m is the number of sensitive values in v, and z is the number of sensitivity levels. The dissimilarity degree of v is defined as:
where mij is the distance between the sensitivity levels of the ith and jth sensitive values, and zij is the distance between the ith and jth sensitivity levels. The dissimilarity degree of Q is
where N is the number of vertices of Crep. The larger Degree(Q) is, the larger the difference between the sensitive values is, the stronger the ability to resist attacks is and the higher the security is.
5.2. Experimental Analysis
We compare our algorithm MLevCluTree with Clustree in [16] with respect to data utility, security and efficiency. Because l-diversity can ensure there are at least l hierarchical data records in an equivalence class, we set k = l. k is varied from 2 to 6. The value of each point is the mean value on 10 experiments.
The average information loss of a hierarchical data record for algorithms MLevClusTree and Clustree is shown in Figure 5. From the two figures, we can see that the information loss increases when k increases. Because k increases, an equivalence class contains more hierarchical data records, and the possibility of providing more general values for every QI attributes increases. Therefore, the information loss increases. For the dataset B with h = 3, because more vertices for a hierarchical data record are needed to generalize, the information loss is higher than that of the dataset B with h = 2. Although MLevClusTree considers that multiple sensitive values lie in the same level, different sensitivity levels are evaluated with different constraints. So the information loss for our MLevClusTree is less than one for Clustree, i.e., the utility of MLevClusTree is better than that of Clustree.
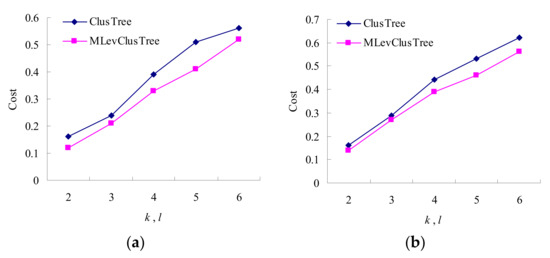
Figure 5.
Information loss on two datasets: (a) Dataset A with h = 2; (b) Dataset B with h = 3.
The security of our MLevClusTree and Clustree is evaluated by the dissimilarity degree of equivalence class, and the results are shown in Figure 6. The ordinate denotes the average dissimilarity degree of an equivalence class. For an equivalence class, we can use Equation (7) to obtain its dissimilarity degree. Therefore, the results of dataset A with h = 2 and dataset B with h = 3 are not significantly different. As k increases, there are more sensitive values in different sensitivity levels, and the dissimilarity degree of a vertex in the class representative of an equivalence class increases. So the average dissimilarity degree of an equivalence class increases. From Figure 6, we can see that the average dissimilarity degree of an equivalence class for our MLevClusTree is higher than that for Clustree, since our approach restricts the proportion of sensitive values in different sensitivity levels. Therefore, our approach enhances the ability to resist similarity attacks and improves the data security.
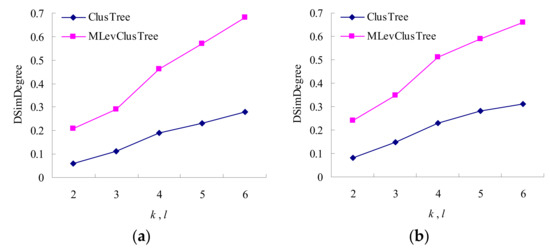
Figure 6.
Dissimilarity degree of equivalence class on two datasets: (a) Dataset A with h = 2; (b) Dataset B with h = 3.
Finally, we evaluate the efficiency of our algorithm by the execution time. The experimental results are shown in Figure 7. We can see that the execution time of two algorithms increases with the increment of k. For every equivalence class Q in hierarchical data, the first hierarchical data record is randomly selected and we do not need to compute. For every other record in the equivalence class, we need to scan partial hierarchical data to find the record whose distance to current Q is approximately minimum. When k increases, the size of an equivalence class increases. Thus, the runtime increases. Also, we can see that the time for dataset B is more than that for dataset A, because the hierarchical data with more levels needs more time to find the record whose distance to current Q is approximately minimum. From Figure 7, we know that our MLevClusTree is slightly higher than that of ClusTree when k increases, since for every equivalence class MLevClusTree needs to decide whether the number of sensitive values in every sensitivity level exceeds the given threshold.
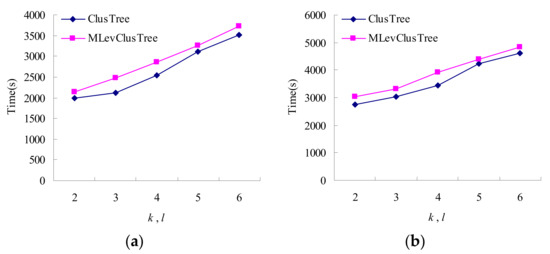
Figure 7.
Execution time on two synthetic datasets: (a) Dataset A with h = 2; (b) Dataset B with h = 3.
From these experimental results, we can see that our MlevClusTree provides stronger privacy protection and has lower information loss, although it takes more time. It is acceptable because the anonymized process is offline.
6. Conclusions
Hierarchical data has become ubiquitous with the advent of document-oriented databases and the wide use of markup languages. However, this data contains privacy information, and so must be appropriately anonymized before it is to be published for scientific research and decision-making. To prevent similarity attacks in hierarchical data, in this paper, we use fuzzy set theory to partition sensitive values for a sensitive numerical or categorical attribute uniformly into five levels by converting the categorical attribute values into the numerical attribute values, and then map the five value levels to five sensitivity levels. According to these sensitivity levels, we propose privacy model (, k)-anonymity for hierarchical data with multi-level sensitivity and design a privacy-preserving approach to achieve (, k)-anonymity. Experimental results show that the average dissimilarity degree of these equivalence classes in anonymized hierarchical data obtained by our approach is higher than that for existing anonymous approaches in hierarchical data. Thus, our approach can effectively resist similarity attacks. Also, our approach causes less information loss and so improves the utility of anonymized hierarchical data.
Author Contributions
J.W. (Jinyan Wang), G.C. and X.L. put forward privacy model and the anonymization method, G.C. implemented the anonymization method with Python, J.W. (Jinyan Wang) and X.L. wrote the original manuscript and C.L. and J.W. (Jingli Wu) improved the writing.
Funding
This paper was supported by the National Natural Science Foundation of China (Nos. 61502111, 61763003, 61672176, 61762015, 61562007, 61662008), Guangxi Natural Science Foundation (Nos. 2016GXNSFAA380192, 2015GXNSFBA139246), Guangxi “Bagui Scholar” Teams for Innovation and Research Project, Guangxi Special Project of Science and Technology Base and Talents (AD16380008), and Guangxi Collaborative Innovation Center of Multisource Information Integration and Intelligent Processing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K. Development of TOPSIS method to solve complicated decision-making problems—An overview on developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Li, Z.; Sun, D.; Zeng, H. Intuitionistic Fuzzy Multiple Attribute Decision-Making Model Based on Weighted Induced Distance Measure and Its Application to Investment Selection. Symmetry 2018, 10, 261. [Google Scholar] [CrossRef]
- Li, D.; He, J.; Cheng, P.; Wang, J.; Zhang, H. A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making. Symmetry 2018, 10, 223. [Google Scholar] [CrossRef]
- Ma, X.; Zhan, J.; Ali, M.I.; Mehmood, N. A survey of decision making methods based on two classes of hybrid soft set models. Artif. Intell. Rev. 2018, 49, 511–529. [Google Scholar] [CrossRef]
- Zhan, J.; Xu, W. Two types of coverings based multigranulation rough fuzzy sets and applications to decision making. Artif. Intell. Rev. 2018. [Google Scholar] [CrossRef]
- Zhan, J.; Liu, Q.; Herawan, T. A novel soft rough set: Soft rough hemirings and its multicriteria group decision making. Appl. Soft Comput. 2017, 54, 393–402. [Google Scholar] [CrossRef]
- Hu, C.K.; Liu, F.B.; Hu, C.F. A Hybrid Fuzzy DEA/AHP Methodology for Ranking Units in a Fuzzy Environment. Symmetry 2017, 9, 273. [Google Scholar] [CrossRef]
- Kang, J.; Han, J.; Park, J.H. Design of IP Camera Access Control Protocol by Utilizing Hierarchical Group Key. Symmetry 2015, 7, 1567–1586. [Google Scholar] [CrossRef]
- Lee, G. Hierarchical Clustering Using One-Class Support Vector Machines. Symmetry 2015, 7, 1164–1175. [Google Scholar] [CrossRef]
- Samarati, P.; Sweeney, L. Generalizing data to provide anonymity when disclosing information. In Proceedings of the ACM Symposium on Principles of Database Systems, Seattle, WA, USA, 1–3 June 1998; p. 188. [Google Scholar]
- Fung, B.C.M.; Wang, K.; Chen, R.; Yu, P.S. Privacy-preserving data publishing: A survey of recent development. ACM Comput. Surv. 2010, 42, 14. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J.; Venkitasubramaniam, M. l-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov Data 2007, 1, 3. [Google Scholar] [CrossRef]
- Wong, C.R.; Li, J.; Fu, A.; Wang, K. (α, k)-anonymity: An enhanced k-anonymity model for privacy preserving data publishing. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 754–759. [Google Scholar]
- Li, N.; Li, T.; Venkatasubramanian, S. t-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 106–115. [Google Scholar]
- Ozalp, I.; Gursoy, M.E.; Nergiz, M.E.; Saygin, Y. Privacy-preserving publishing of hierarchical data. ACM Trans. Priv. Secur. 2016, 19, 7. [Google Scholar] [CrossRef]
- Lefevre, K.; Dewitt, D.J.; Ramakrishnan, R. Incognito: Efficient full-domain k-anonymity. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; pp. 49–60. [Google Scholar]
- Fung, B.C.M.; Wang, K.; Yu, P.S. Top-down specialization for information and privacy preservation. In Proceedings of the 21st International Conference on Data Engineering, Tokoyo, Japan, 5–8 April 2005; pp. 205–216. [Google Scholar]
- Aggarwal, G.; Feder, T.; Kenthapadi, K.; Khuller, S.; Panigrahy, R.; Thomas, D.; Zhu, A. Achieving anonymity via clustering. ACM Trans. Algorithms 2010, 6, 49. [Google Scholar] [CrossRef]
- Ghinita, G.; Karras, P.; Kalnis, P.; Mamoulis, N. A framework for efficient data anonymization under privacy and accuracy constraints. ACM Trans. Database Syst. 2009, 32, 9. [Google Scholar] [CrossRef]
- Wang, J.; Du, K.; Luo, X.; Li, X. Two privacy-preserving approaches for data publishing with identity reservation. Knowl. Inf. Syst. 2018. [Google Scholar] [CrossRef]
- Han, J.; Yu, J.; Yu, H.; Jia, J. A multi-level l-diversity model for numerical sensitive attributes. J. Comput. Res. Dev. 2011, 48, 147–158. [Google Scholar]
- Jin, H.; Zhang, Z.; Liu, S.; Ju, S. (αi, k)-anonymity Privacy Preservation Based on Sensitivity Grading. Comput. Eng. 2011, 37, 12–17. [Google Scholar]
- Wang, Q.; Yang, C.; Liu, H. Fuzzy based methods for privacy preserving. Appl. Res. Comput. 2013, 30, 518–520. [Google Scholar]
- Kumari, V.V.; Rao, S.S.; Raju, K.; Ramana, K.V.; Avadhani, B.V.S. Fuzzy based approach for privacy preserving publication of data. Int. J. Comput. Sci. Netw. Secur. 2008, 8, 115–121. [Google Scholar]
- Yang, X.; Li, C. Secure XML publishing without information leakage in the presence of data inference. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; pp. 96–107. [Google Scholar]
- Landberg, A.H.; Nguyen, K.; Pardede, E.; Rahayu, J.W. δ-dependency for privacy-preserving XML data publishing. J. Biomed. Inform. 2014, 50, 77–94. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nergiz, M.E.; Clifton, C.; Nergiz, A.E. Multirelational k-anonymity. IEEE Trans. Knowl. Data Eng. 2009, 21, 1104–1117. [Google Scholar] [CrossRef]
- Gkountouna, O.; Terrovitis, M. Anonymizing collections of tree-structured data. IEEE Trans. Knowl. Data Eng. 2015, 27, 2034–2048. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Jorba, L.; Adillon, R. Interval Fuzzy Segments. Symmetry 2018, 10, 309. [Google Scholar] [CrossRef]
- Bi, L.; Dai, S.; Hu, B. Complex Fuzzy Geometric Aggregation Operators. Symmetry 2018, 10, 251. [Google Scholar] [CrossRef]
- Klir, G.J.; Clair, U.S.; Yuan, B. Fuzzy Set Theory: Foundations and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).