Abstract
Since non-automatic rigging requires heavy human involvements, and various automatic rigging algorithms are less efficient in terms of computational efficiency, especially for current curve-based skin deformation methods, identifying the iso-parametric curves and creating the animation skeleton requires tedious and time-consuming manual work. Although several automatic rigging methods have been developed, but they do not aim at curve-based models. To tackle this issue, this paper proposes a new rigging algorithm for automatic generation of dynamic skin deformation to quickly identify iso-parametric curves and create an animation skeleton in a few milliseconds, which can be seamlessly used in curve-based skin deformation methods to make the rigging process fast enough for highly efficient computer animation applications.
1. Introduction
Skin deformation techniques remain an essential and standardized part of many character animation applications these days including academia and industry practices. The usefulness of a skin deformation technique is generally measures in terms of three major characteristics: efficiency, realism, and easiness. Over years, researchers have developed a variety of skin deformation techniques to improve them. These skin deformation techniques can be roughly classified into geometric skin deformation, example-based skin deformation, and physics-based skin deformation.
Geometric skin deformation approaches directly bind skin deformation with the underlying skeleton movement without taking any underlying physics into consideration. Despite their simplicity and efficiency, they cannot produce highly realistic skin deformation without non-trivial additional efforts.
Example-based skin deformation approaches interpolate a set of given example poses to improve realism or produce certain skin deformation effects that cannot be easily produced by geometric skinning approaches. Therefore, example-based skin deformation approaches are often used together with geometric skinning. In order to achieve satisfactory realism, sufficient example skin shapes are required. In addition, how to optimally design or obtain such a set of example poses is still considered as a widely open research problem. For example, how many example poses are sufficient for high quality skinning of a specific 3D model; and where those example poses should be positioned in the deformation space.
Physics-based skin deformation approaches introduce physics rules or musculoskeletal systems to drive and simulate the movement of the skin surface, which probably have produced more physically-realistic skin deformation results to date. The limitations of Physics-based skin deformation approaches are: (1) numerical calculations such as finite element simulations require specialized knowledge and skills, making them less easy to learn and use, (2) manual operations such as mesh generation of finite elements and specification of boundary conditions are involved leading to more pre-processing time, (3) large computer memory requirements and high computational cost making them more difficult to achieve high efficiency. Model reduction can be used to reduce the data size or dimension and obtain an approximation of lower accuracy in significantly less time but more complicated implementation.
Animation quality of virtual characters is determined by efficiency and realism of skin deformations. Automatic rigging can raise the efficiency, and data-driven and physics-based skinning techniques can improve the realism. In existing literature, a rigging process includes generating and placing a skeleton inside a skin mesh and relating skin shape changes to the skeleton movements.
The above discussions indicate that geometric, example-based, and physics-based skin deformation approaches have their own strengths and limitations. How to maximize their strengths and minimize their limitations to achieve more realistic and efficient skin deformations easily requires further investigations. Besides, rigging is usually done by hand, especially for current curve-based skin deformation methods, identifying the iso-parametric curves and create the animation skeleton need tedious and time-consuming manual work. Although several automatic rigging methods have been developed, but not aim at curve-based models.
To tackle this issue, this paper proposes a new rigging algorithm to quickly identify iso-parametric curves and create an animation skeleton in a few milliseconds, which can be seamlessly used in physically curve-based skin deformation methods to make the rigging process fast enough for highly efficient computer animation applications.
Since modelling of skin surfaces and their deformations can be simplified as those of the curves defining skin surfaces. When physics-based approaches are used to deal with skin deformations, such a simplification can significantly reduce computer resource and raise computational efficiency.
The above issue is addressed by the authors of [1], through proposing a finite difference solution of curve-based dynamic skin deformations. In the paper, curves are extracted manually from the reconstructed skin deformation models, which is tedious and time-consuming. In order to tackle this problem, this paper will develop a new approach to automatically identify curves, create animation skeleton, and combine them with the finite difference solution of curve-based skin deformations [1] to achieve automatic, realistic, and efficient character animation. Specifically, this paper will develop:
(1) an automatic and quick vertex identification algorithm which quickly identifies all the vertices at iso-paramteric curves on the example skin meshes at two extreme poses for following physics-based skin deformation calculations. (2) an automatic and highly efficient rigging algorithm which quickly creates a new skeleton and embeds it in the two example skin meshes through shape matching with a template skeleton. (3) integration of curve-based presentations, automatic rigging, ODE-based simulation to achieve good realism, high efficiency for skin deformation with small data size.
The paper is structured below. First, the existing work is reviewed in Section 2, and an overview of the developed animation technique is given in Section 3. Then, identifying iso-parametric curves is investigated in Section 4, and creating animation skeleton is developed in Section 5. After that, ODE-based dynamic skin deformation experimental results are given in Section 6. Finally, the paper is concluded and future work is discussed in Section 7.
2. Related Work
Automatic rigging, Generation and placement of an animation skeleton, is developed to avoid tedious and time-consuming manual rigging. Here, an animation skeleton typically consisting of bones and joints is used to drive the movements and deformations of skin meshes, while a curve skeleton is defined as the medial axis [2] or a curve connecting the centers of closed curves on a skin mesh.
Existing automatic rigging methods can be roughly classified into four different categories: skeleton embedding, single shape-based skeleton extraction, motion-based skeleton extraction, and combination of skeleton embedding and extraction. Skeleton embedding methods require optimally embedding pre-designed skeletons to skin meshes, which is often achieved through optimization [3]. However, its main disadvantage is the requirement for pre-designed skeletons. The authors of [4] introduced one approach to address the problem that retargeting is hard for nonhuman characters, with locomotion bound to the sensing volume; and pose mappings are ambiguous with difficult dynamic motion control. Single shape-based skeleton extraction methods obtain skeletons from a single static pose [2,5]. Since only one static pose is used, such down-sampling based approaches may fail when converting a curve skeleton into its corresponding animation skeleton. Motion-based skeleton extraction methods use motion data or multiple example poses to determine the skeleton and joint locations, and overcome the disadvantage of single shape-based skeleton extraction [6,7]. The combination of skeleton embedding and extraction tackles the disadvantage of single shape-based skeleton extraction by locating a suitable template skeleton in the extracted curve skeleton through classification rules, derived from the general characteristics of each character class [8]. These methods mostly are not computationally efficient in general. For example, on a typical off-the-shelf computer, they often require at least a few seconds to complete automatic rigging for a model with several thousand vertices and tens of minutes (or even hours) for a model with tens of thousands of vertices. The authors of [9] presented one way to control characters for real-time animation, avoiding the rigging-skinning pipeline for arbitrary motion mapping. And [10] introduced one fast method to rapidly combine available sparse motion capture data with existing mesh sequences to produce a large variety of new animations.
Geometric skin deformation methods Linear Blend Skinning (LBS) also called skeleton subspace deformation (SSD) is the most well-known geometric skinning algorithm [11] due to its efficiency and simplicity. However, its limitations include collapsing elbow, candy-wrapper effects, and failure of secondary deformation [12]. The authors of [13] proposed one approach to address the deformation of B-spline surfaces while constraining the volume enclosed by the surface. The authors of [14] presented a novel framework to treat shapes in the setting of Riemannian geometry. A novel skinning algorithm based on linear combination of dual quaternions is presented in [15] to tackle some serious drawbacks of linear blend skinning. By introducing an extra scalar weight function per bone, a simple modification of the linear blend skinning (LBS) formulation was presented in [16] that enables stretching and twisting without changing the existing skeleton rig or bone weights. To remedy the problems like collapsing elbow and candy wrapper joint, curve skeletons along with the joint-based skeletons was used in [17] to animate the skin shape. The authors of [18] choose to pre-compute optimized center of rotation for each vertex, and use these centers to interpolate rigid transformations. The authors of [19] firstly provide one pure geometric method which could handle skin contact and muscle bulge problem in real-time, but fails to address deep self-intersections. To solve this problem, [20] use new composition operators enabling blending effects and local self-contact between implicit surfaces, as well as a tangential relaxation scheme derived from the as-rigid-as possible energy to solve the tracking problem. As above mentioned, in recent years, various geometric skinning methods have been proposed to overcome these limitations. But, in spite of its high efficiency, geometric skinning is still less capable of creating highly realistic skin deformations.
Example-based skin deformation methods is employed to address the realism issue of geometric skinning, by learning deformation dynamics from a set of given examples [21]. An automated framework was presented in [22] to fit the parameters of a deformation model using a set of examples consisting of skeleton configurations paired with the deformed geometry as static meshes. One parallel deformation method using the GPU fragment processors was developed by the authors of [23]. Joint weights for each vertex are automatically calculated from sample poses, thereby reducing manual effort and enhancing the quality of WPSD (Weighted Pose Space Deformation) as well as SSD (Skeletal Subspace Deformation). One data-driven technique for synthesizing skin deformation from skeletal motion was presented by the authors of [24]. Eulerian representation of skin was proposed in [25] to simulate thin hyperelastic skin that can stretch and slide over underlying body structures such as muscles, bones, and tendons. One automated algorithm, called Smooth Skinning Decomposition with Rigid Bones (SSDR), was introduced in [26] to extract the linear blend skinning (LBS) from a set of example poses. It outperforms the state-of-the-art skinning decomposition schemes in terms of accuracy and applicability. One major disadvantage of example-based skin deformation methods is the design of a sufficient set of example skin shapes in order to produce realistic skin deformations, which is often a non-trivial task in practice.
Physics-based skin deformation methods try to simulate the underlying physics to create more realistic skin deformations. The authors of [27] propose a method to simulate human beings based on anatomy concepts. In [28], volume preserving method was presented to avoid extra bulge or wrinkle. A comprehensive biomechanical model of the human upper body was developed in [29] that uses a coupled finite element model with the appropriate constitutive behavior to simulate biomechanically realistic flesh deformations and investigates an associated physics-based animation controller. A physically based simulation system for skeleton-driven deformable body characters is developed in [30] that gives a well-coordinated combination of a reduced deformable body model with nonlinear finite elements, a linear-time algorithm for skeleton dynamics, and explicit integration can boost simulation speed. An efficient algorithm based on a novel discretization of corotational elasticity over a hexahedral lattice is examined in [31] to achieve near-interactive simulation of skeleton driven, high resolution elasticity models, but it still need several seconds per animation frame. The authors of [32] formulate the equations of motions in the subspace of deformations defined by animator’s rig, bringing the benefits of physics-based simulation to enhance the realism of traditional animation pipelines, but need tens of seconds when simulate one normal character model. A closed-form skinning method is proposed in [33] to generate higher quality deformations than both linear and dual quaternion skinning through optimize skinning weights for the standard linear and dual quaternion skinning techniques and introducing joint-based deformers. Elastic animation editing with spacetime constraints was discussed in [34] that not only optimizes control forces added to a linearized dynamic model, but also optimizes material properties to better match user constraints and provide plausible and consistent motion. By minimizing quadratic deformation energy, built via a discrete Laplacian inducing linear precision on the domain boundary, a method was presented in [35] to design linear deformation subspaces, unifying linear blend skinning and generalized barycentric coordinates. A fast physically based simulation system for skeleton-driven deformable body characters is developed in [36] that gives a well-coordinated combination of a reduced deformable body model with nonlinear finite elements, a linear-time algorithm for skeleton dynamics, and explicit integration, to boost simulation speed. In [37], EigenSkin has been presented to correct SSD results, it achieves high frame rates per second, but constructing one proper error-optimal eigen displacement basis requires sufficient experience and background knowledge. Since it is not easy to model the different elastic behaviors of muscle, fat and skin using simple volumetric mesh, [38] introduce one novel multi-layer model to simulate them, but it fails handle collisions during fast motions. The authors of [39] present one computational model for geodesics in the space of thin shells and incorporate bending contributions into deformation energy. Besides, [40] develop a time- and space-discrete geodesic calculus to shoot geodesics with prescribed initial data, they all need heavy computation. The authors of [41] introduce model reduction into dynamic deformation simulations to achieve real-time performance at the cost of decreasing the computational accuracy and increasing the implementation complexity.
Curve-based methods have also been proposed for modeling and simulating 3D character models in recent years. For example, [42] proposed sweep-based human deformation. The authors of [43,44] presented a curve-based sweeping surface and dynamic skin deformation method. The authors of [45] discussed the theory, discretization, and numerics of curves which are evolving such that part of their shape, or at least their curvature as a function of arc length, remains unchanged. The authors of [46] sought congruent planar curves to generate or approximately generate a freeform surface. The authors of [1] investigated a finite difference solution to curve-based dynamic skin deformations. The authors of [47] introduce techniques for the processing of motion and animations of non-rigid shapes. Although curve-based approaches simplify physics-based skinning, analytical solutions have not yet been presented to achieve both high efficiency and good realism of physics-based skin deformations.
3. Overview
In this section, we give an overview of the proposed approach. As shown in Figure 1, the proposed approach consists of three main steps: identification of iso-parametric curves, creation of animation skeleton, and dynamic skin deformations. The purpose of identifying the iso-parametric curves has two: one is to convert polygon meshes into curve-defined models to be applied in ODE-based dynamic skin deformations discussed in Section 6, and the other is to create curve skeleton which will be changed into animation skeleton.
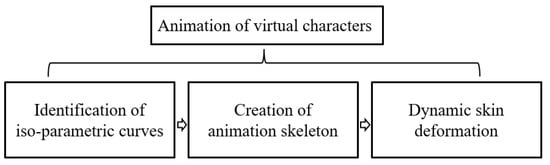
Figure 1.
Overview of the proposed approach.
Since most character models are surface polygon meshes whose deformations are similar to elastic bending of thin plates, we modify the governing equation of dynamic bending of isotropic elastic beams to develop a physics-based skin deformation model, represented by Ordinary Differential equations (ODE) on the basis of iso-parametric curves. It describes the underlying physics for skin shape creation between given examples to achieve high realistic skin deformation results with small data size and computing time.
Meanwhile, the identified iso-parametric curves naturally provide a good basis to automatically and high efficiently determine the curve skeletons of characters, using down-sampling algorithm and shape matching algorithm.
Finally, the ODE based dynamic deformation model is proposed to describe physics of curve deformations and its finite difference solution is developed to determine shape changes of the iso-parametric curves. So that the proposed dynamic skin deformation technique can create realistic deformed skin shapes for character animation efficiently with largely reduced computing time.
4. Identify Iso-Parametric Curves
Polygon character models can be divided into quad meshes and triangle meshes. Since triangle meshes can be converted into quad meshes in commercial computer graphics packages such as Maya, in this paper we investigate how to identify iso-parametric curves of quad meshes.
Assume we use a parametric variable u to denote the circumferential direction ( is an iso-parametric curve), and use v to indicate the axial direction of each of the parts of a character model, the specific goal of vertex identifier in our approach is to identify all the vertices on each iso-parametric curve, ().
The proposed iso-parametric curves identification process starts from the farthest end of the character parts such as limbs and tail, which can be manually specified or automatically identified through the analysis of curvature distribution. Specifically, several seed points are first selected to start the construction of iso-parametric curves in their circumferential directions. Then, their neighboring vertices in the axial direction are continuously added as new seed points. In this process, a vertex is visited at most once, which would lead to closed loops at the beginning and gradually open the loops especially at the connection place between different body parts.
The first step is to identify the axial and circumferential directions of each of the parts of a 3D character mesh. Figure 2 illustrates an example how this process is done. We first draw a ray starting from the vertex 2 of a cat model in the normal direction of the facet 2-17-30-11-2, which intersects another facet at a point (shown in Figure 2c). Then, we draw 10 lines, including the line 2-, at the same angle of 18°, that pass the middle point of the line 2- in the plane determined by the triangle 2--11-2, and obtain 20 intersecting points illustrated in Figure 2d. Afterwards, we calculate the centre of the 20 points and all the Euclidean distances (k = 1, 2, …, 20), among which we find the minimal and maximal Euclidean distances, and . At the end, we can calculate the difference between the minimal and maximal Euclidean distances, .
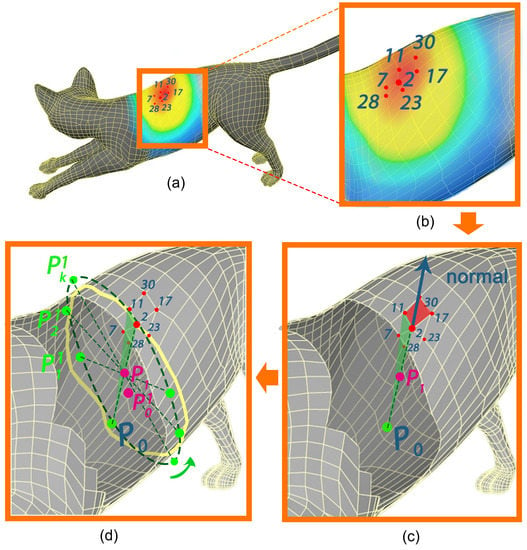
Figure 2.
Illustration of Identifying Iso-parametric Curves on example model.
Similarly, in the plane determined by the triangle 2-17--2, we do the same operations, i.e., drawing 10 lines in the plane, obtaining 20 intersecting points , calculating the minimal and maximal Euclidean distances and , and calculating the difference . If , the direction determined by the 20 intersecting points is the circumferential direction. Otherwise, the direction determined by the 20 intersecting points is the circumferential direction.
We propose an accurate method below to automatically identify the vertices on the iso-parametric curve in the circumferential direction, and use their indexes to obtain their coordinate values on the mesh.
We start with the vertex 2, and find all the edges which directly connect the vertex 2 to some of its 1-ring vertices, i.e., 2-17, 2-11, 2-28 and 2-23 as illustrated in Figure 2a. Then, we calculate the angles between these edges and the plane in the circumferential direction. The one with the minimum angle (e.g., the vertex 11 in Figure 2) is selected to connect to the vertex 2. Afterward, the same operations are performed on the new selected vertex in order to select next vertex. The process is repeated until connecting back to the vertex 2 to find all the vertices on the iso-parametric curve . Figure 3 shows the identified vertices on iso-parametric curves of a cat model (a). The computational times for the vertex identifier process are given in Table 1.
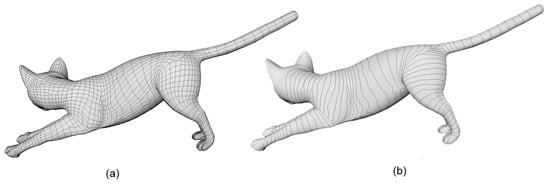
Figure 3.
Our iso-parametric curves identifying step transforms a quad mesh (a) into discrete vertices on iso-parametric curves (b).

Table 1.
Runtime breakdown of our approach when it was used to automatically process the different models. Here, VI: Vertex Identifier on iso-parametric curves, SC: Skeleton Creating, SD: Skin Deformer.
5. Creating Animation Skeleton
As discussed in the section of Related Work, locating a template animation skeleton on the extracted curve skeleton of an input 3D character model can effectively avoid the disadvantage of single shape-based skeleton extraction. To this end, we take a template animation skeleton as input, and combine it with down-sampling algorithm and our proposed shape matching algorithm to convert the obtained curve skeleton into the required animation skeleton as elaborated below.
The identified iso-parametric curves provide a very good basis to automatically and quickly determine the curve skeletons of the decomposed parts. To this end, we calculate the centres of all iso-parametric curves . The curve skeleton is obtained by connecting these centres. Then, we use the following down-sampling algorithm and shape matching algorithm to create an animation skeleton from the obtained curve skeleton and a template skeleton as discussed below.
First, we calculate the center of the points on one iso-parametric curve to obtain the curve skeletons for the limbs and the torso including neck and head. The curve skeleton of a human arm consisting of the calculated centres is shown as Figure 4a.
Figure 4.
Creation of the animation skeleton. (a) shows one curve skeleton automatically calculated by iso-parametric curves; (b) shows the minimal angle threshold between two connected line segments of a curve skeleton; (c) depicts the joints between the forearm and upper arm determined by the down-sampling algorithm; (d) indicates joints on the skin mesh at the starting pose; in (e), the double pime symbol is used to indicate the joints of the template skeleton; (f) shows the corresponding joints on the skin mesh at the ending pose; (g) is the animation skeleton automatically generated for a human hand; (h) shows some other human skeleton.
Inspired by the work of [2,5], we introduce a down-sampling algorithm, to find the joints. Here we set 20° shown in Figure 4b as the minimal angle threshold between two connected line segments of a curve skeleton. In other words, if the relative rotation between two connected line segments of a curve skeleton is greater than this threshold, a joint is specified at this point shared by the two adjacent line segments. Figure 4c depicts the joint between the forearm and upper arm determined by the down-sampling algorithm.
Also, the centers of seam-curves are denoted as the joints between the limbs and the torso labeled as 1, 2, 3 and 4. And the centers closest to the fingers and toes are labeled as 12, 15, 18 and 21 on the curve skeletons shown in Figure 4d. With the down-sampling algorithm we can identify the joints 11, 13, 14, 16, 17, 19, 20 from the curve skeletons of the limbs at the starting pose as indicated in Figure 4d.
For other joints, such as 10, which cannot be identified with the above down-sampling algorithm, we use a template skeleton and a shape matching algorithm to identify them. The shape matching algorithm is based on the matching of four feature joints 1, 2, 3, 4 generated by seam-curves and a symmetric axis from joint 6 to joint 24 in Figure 4f, and the similarity measure between the curve skeleton and the template skeleton. Once a template skeleton is selected, we first check whether the joints 3”, 4”, and 5” are on one same straight line, and the joints 1”, 2”, and 6” are on another straight line. In Figure 4e, the double pime symbol is used to indicate the joints of the template skeleton. This paper uses the human skeleton in [48], shown in Figure 4e, as a template skeleton. For this template skeleton, the joints 3”, 4”, and 5” are on one straight line, and the joints 1”, 2”, and 6” are on another straight line. The joints 5 and 6 are determined by
There are some other human skeletons like that shown in Figure 4h, the joints are not on the corresponding line segments. In order to consider such general cases, the proposed shape matching algorithm determines the joints 5” and 6” by matching the triangle 3”, 4”, 5” in Figure 4h to the triangle 3, 4, 5 in Figure 4d, and the triangle 1”, 2” 6” to the triangle 1, 2, 6. Taking the shape matching from the triangle 3”, 4”, 5” to the triangle 3, 4, 5 as an example, the coordinate values of the joint 5 is determined by the following three equations
After the joints 5 and 6 have been determined, they are connected to the curve skeleton between the joint 5 and 6 to obtain the axisymmetric axis. Then, we determine the locations of the joints 7, 8, and 9 on torso and the locations of the joints 22, 23 , 24 on neck and head according to the length similarity measure. For example, the joint 9 is determined by where is the arc length of the curve skeleton from the joint 5 to joint 6, and .
If the arms or legs are fully spreading, the down-sampling algorithm may not be applicable. In this case, the same similarity measure as that of the torso is used to identify the locations of the joints of the fully spreading limbs.
Similarly, we can automatically generate animation skeletons for other models such as a human hand in Figure 4g. In Figure 4g, the left-top hand shows the skeleton after the down-sampling algorithm, but four fingers are almost spreading, we use the template in the middle and the matching algorithm to supplement the four joints (blue) shown as the right top hand. The hand on the right bottom of Figure 4g shows the skeleton extracted by [5] is based on mesh contraction. The mesh contraction presented in [5] takes about 10 s to obtain the skeleton of the mesh with 25,000 vertices. In contrast, the proposed method takes less than 5 milliseconds to create the skeleton of the mesh with 32,185 vertices.
If there are two or more skin meshes for one model at different poses, the above algorithm can be used to obtain a skeleton for each of them for revision. If some joints obtained from different meshes are different, the joints with larger angles are used. For example, the joint 19 for the skin mesh at the starting pose shown in Figure 4d is on the iso-parametric curve , but the corresponding joint on the skin mesh at the ending pose shown in Figure 4f is on the iso-parametric curve , the joint is taken to be the joint between the forearm and upper arm since it has a larger angle. Here, the prime symbol is used to indicate the skin mesh at the ending pose.
6. ODE-Based Dynamic Skin Deformation
After automatically identifying the iso-parametric curves and creating the animation skeleton in high efficiency, we employ the curve-based skin deformation method in [1] to create the dynamic deformation model for character animation which demonstrates the proposed method can be used in curve-based skin deformation approach to create physically realistic animation high efficiently. For the sake of completeness, we introduce the physics-based skin deformation method presented in [1] briefly.
The governing equation of dynamic bending of isotropic elastic beams can be written as [1]:
where w is the deformation, x is a coordinate variable, t is a time variable, is the bending force, E is Young’s modulus, I is the second moment, is the density, and A is the cross-section area of the beam.
If the skin mesh is described with a parametric representation, the deformation will involve three components x, y, and z, the bending force will involve three components , , and , and the coordinate variable will become the parametric variable v. Accordingly, the above equation is changed into:
Since we consider physicals-base skin deformations of human character in this paper, we determine E and with Young’s modulus and Poisson ratio of human skin. If we know the skin shapes at the rest pose and the deformed pose , the deformation and deformation rate at the rest pose are zero, and the deformation at the deformed pose is the difference between the skin shape at the deformed pose and the skin shape at the rest pose . Therefore, we obtain the following constraints:
Substituting the central finite difference formula of the fourth derivative of q with respect to the parametric variable v and the first and second derivatives of q with respect to the time variable t into the above two equations, we obtain a system of linear algebra equations which can be written in the matrix form below
where n indicates the nth time integration, and m stands for the mth node of the finite difference grid.
For the undeformed skin mesh at the rest pose Figure 5a and the deformed skin mesh at the deformed pose Figure 5e, we solve the above linear algebra equations to obtain the intermediate meshes shown in (b), (c) and (d) of Figure 5.
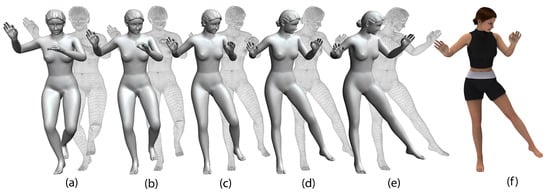
Figure 5.
The models (a) and (e) are input as examples, intermediate models (b–d) are created efficiently, (f) is the rendered model.
Given multiple poses as the input, the proposed method can also produce physically-realistic skin deformations. For example, we know the skin shapes at the three poses shown in (a), (f) and (k) of Figure 6. We use the skin shapes at (a) and (f) to create the deformed skin shapes at the pose (b), (c) and (d), and use the skin shapes at the pose (f) and (k) to create the deformed skin shapes at the poses (h), (i) and (j) of Figure 6.
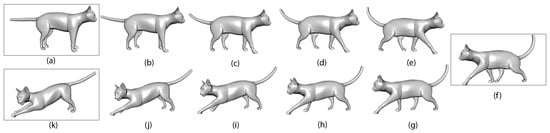
Figure 6.
(a), (f), and (k) are three input example poses, all the frames in (b–e) are in-between poses generated by the proposed approach based on (a) and (f), all the frames in (g–j) are in-between poses generated by the proposed approach based on (f) and (k).
7. Evaluation
In this section, we evaluate the proposed iso-parametric curve identification, skeleton creation, and ODE-based dynamic skin deformation.
7.1. Evaluation of Iso-Parametric Curve Identification
There are few research studies which investigate identification or extraction of iso-parametric curves. In the existing curve-based geometric modeling and deformation simulation, iso-parametric curves were manually extracted. As said in [1], even a Maya Embedded language (MEL) script were used to assist the manual extraction of iso-parametric curves, the whole extraction of a horse model with 30,134 vertices shown in Figure 7a took two hours.
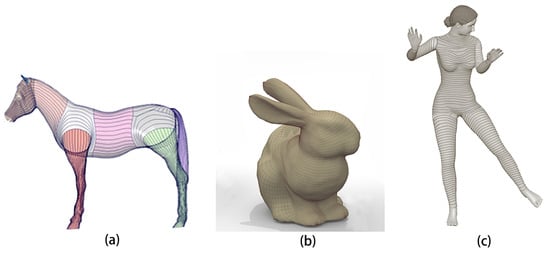
Figure 7.
Character models and extracted curves with different methods. (a) manual extraction [1], (b) skeleton-mesh co-representation [49], (c) iso-parametric curves identified by the proposed approach.
The curves defining skin surfaces are manually extracted, leading to heavy and time-consuming human involvements. The method proposed in [49] can be used to extract iso-parametric curves from a triangular mesh. However, this method: (1) requires users to manually specify the extreme points of a harmonic function to guide the conversion, (2) its computational efficiency is less optimal. For example, it requires 6.41 s to process a bunny mesh with 6966 triangles shown in Figure 7b into its polar-annular mesh representation using 100 slices on an off-the-shelf computer [49]. Our proposed iso-parametric cure identification extracts a female model with a similar vertex number shown in Figure 7c only took 2.03 milliseconds.
7.2. Evaluation of Animation Skeleton Creation
In [1,44], the animation skeleton used for calculating skin deformation is manually created. It is unsuitable for real-time animation or some applications that require high animation frame rates. In contrast, the approach proposed in this paper can generate skeleton automatically.
As shown in Figure 8a, the mesh contraction method proposed in [5] takes about 10 s to obtain the skeleton of the raptor mesh with 25,000 vertices. The method proposed in this paper takes less than 5 milliseconds to create the skeleton of the human mesh with 32,185 vertices shown in Figure 8b.
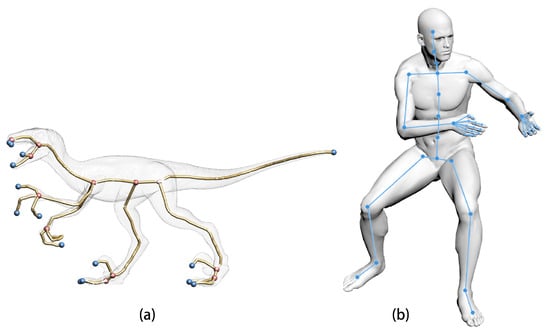
Figure 8.
Skeleton creation with different methods. (a) skeleton extraction by mesh contraction [5] , (b) skeleton generated by the proposed approach.
Only taking the meshes at one pose shown in Figure 9b,d as input, we used our proposed automatic rigging algorithm consisting of shape matching, down-sampling, and a template animation skeleton to generate the animation skeletons shown in Figure 9a,c. The animation skeletons generated by the automatic rigging method proposed in [3] are shown in Figure 9b,c. It can be observed that our method can generate comparable skeletons as [3], if not better.
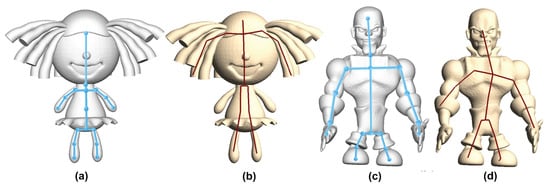
Figure 9.
Comparison results between our automatic rigging algorithm and [3]. (a) and (c) show the rigged results of the proposed method, while (b) and (d) show the rigged results by [3]. Note the skeleton in the ears of (b) actually should be the skeleton in two arms, so the skeleton in (b) may not be optimal for animation purpose.
7.3. Evaluation of ODE Dynamic Skin Deformation
The runtime time shows the proposed approach is highly efficient while producing physically realistic skin deformations. Most existing physics-based skin deformation techniques work in a discrete vertex space to obtain discrete numerical solutions of skin deformation, causing the limitations of intensive manual intervention, and heavy numerical calculations. The method in [33] generates higher quality deformations than both linear and dual quaternion skinning through skinning weights optimization, but requires at least a few minutes to precompute the deformation weights. The method in [31] still needs at least several seconds for torso and arms simulation per frame on GPU, it is still not fast enough for interactive posing.
In contrast, our method only needs few milliseconds to automatically extract iso-parametric curves, generate skeleton and achieve dynamic in-between skin deformations, as shown in Table 1, giving a runtime breakdown of the proposed approach when it is applied to generate the animation of the dancer model in Figure 5 and a cat model in Figure 6. The runtime time statistics show our approach is highly efficient while producing physically realistic skin deformations.
Figure 10 gives a comparison among the skin deformation obtained from this approach, classic linear skinning, and dual quaternion skinning. Compared these images, we can conclude that the approach combining automatic iso-parameteric curve identification and animation skeleton creation with ODE-based dynamic skin deformation generates more realistic skin deformations than classic linear skinning and dual quaternion skinning.
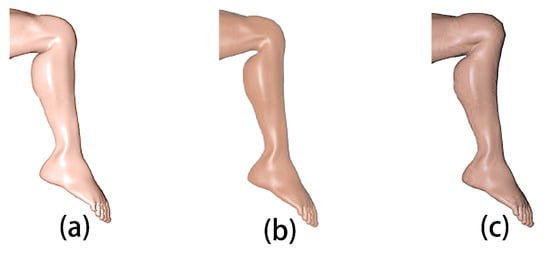
Figure 10.
Comparison among different skin deformation methods. (a) this approach, (b) classic linear skinning, (c) dual quaternion skinning.
8. Discussion and Conclusions
This paper presents an automatic rigging algorithm for ODE-based simulation of dynamic skin deformation for character animation. It includes vertex identification on iso-parametric curves, automatic skeleton creation combined with curve-based skin deformation approach. Several experiments have been conducted to demonstrate the developed approach can make the rigging process fast enough for highly efficient computer animation applications.
The method proposed in this paper is easy to learn, implement, and use. Among the three steps of the proposed approach, the iso-parametric curve identification and automatic animation skeleton creation are straightforward and easiest to implement. Although the finite difference solution of ODE-based dynamic skin deformation is a little more difficult to implement, it is still much easier than the implementation of the corresponding finite element solution.
Several improvements can be made in the future. The proposed iso-parametric curve identification is applicable to quad meshes with regular topology. Future work will investigate triangle meshes and arbitrary topologies. The proposed automatic rigging requires a template skeleton. In order to make the proposed automatic rigging applicable to various character models, different character models will be classified into different categories and a small template skeleton database with one skeleton in the database for one category of character models will be created. Besides, the proposed approach can be extended to generate detailed clothing deformations. This can be achieved by combining the proposed automatic rigging with clothing examples obtained from the SOR scheme [50].
Acknowledgments
This work is supported by the EU Horizon 2020 RISE 2017 funded project PDE-GIR 318 (H2020-MSCA-RISE-2017-778035), the National Natural Science Foundation of China (Grant no. 51475394) and Innovate UK (Knowledge Transfer Partnerships Ref: KTP010860). Shaojun Bian is also supported by Chinese Scholar Council.
Author Contributions
All authors contributed to the paper, and approved the present version to be published.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chaudhry, E.; Bian, S.; Ugail, H.; Jin, X.; You, L.; Zhang, J.J. Dynamic skin deformation using finite difference solutions for character animation. Comput. Graph. 2015, 46, 294–305. [Google Scholar] [CrossRef]
- Pan, J.; Yang, X.; Xie, X.; Willis, P.; Zhang, J.J. Automatic rigging for animation characters with 3D silhouette. Comput. Anim. Virtual Worlds 2009, 20, 121–131. [Google Scholar] [CrossRef]
- Baran, I.; Popović, J. Automatic rigging and animation of 3d characters. ACM Trans. Graph. (TOG) 2007, 26, 72. [Google Scholar] [CrossRef]
- Rhodin, H.; Tompkin, J.; Kim, K.I.; De Aguiar, E.; Pfister, H.; Seidel, H.P.; Theobalt, C. Generalizing wave gestures from sparse examples for real-time character control. ACM Trans. Graph. (TOG) 2015, 34, 181. [Google Scholar] [CrossRef]
- Au, O.K.C.; Tai, C.L.; Chu, H.K.; Cohen-Or, D.; Lee, T.Y. Skeleton extraction by mesh contraction. ACM Trans. Graph. (TOG) 2008, 27, 44. [Google Scholar] [CrossRef]
- De Aguiar, E.; Stoll, C.; Theobalt, C.; Ahmed, N.; Seidel, H.P.; Thrun, S. Performance capture from sparse multi-view video. ACM Trans. Graph. (TOG) 2008, 27, 98. [Google Scholar] [CrossRef]
- Le, B.H.; Deng, Z. Robust and accurate skeletal rigging from mesh sequences. ACM Trans. Graph. (TOG) 2014, 33, 84. [Google Scholar] [CrossRef]
- Pantuwong, N.; Sugimoto, M. A novel template-based automatic rigging algorithm for articulated-character animation. Comput. Anim. Virtual Worlds 2012, 23, 125–141. [Google Scholar] [CrossRef]
- Rhodin, H.; Tompkin, J.; In Kim, K.; Varanasi, K.; Seidel, H.P.; Theobalt, C. Interactive motion mapping for real-time character control. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2014; Volume 33, pp. 273–282. [Google Scholar]
- Vögele, A.; Hermann, M.; Krüger, B.; Klein, R. Interactive steering of mesh animations. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Lausanne, Switzerland, 29–31 July 2012; Eurographics Association: Aire-la-Ville, Switzerland, 2012; pp. 53–58. [Google Scholar]
- Magnenat-Thalmann, N.; Laperrire, R.; Thalmann, D. Joint-dependent local deformations for hand animation and object grasping. In Proceedings of the on Graphics interface88, Edmonton, AB, Canada, 6–10 June 1988. [Google Scholar]
- Lewis, J.P.; Cordner, M.; Fong, N. Pose space deformation: A unified approach to shape interpolation and skeleton-driven deformation. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 2000; pp. 165–172. [Google Scholar]
- Sauvage, B.; Hahmann, S.; Bonneau, G.P.; Elber, G. Detail preserving deformation of B-spline surfaces with volume constraint. Comput. Aided Geom. Des. 2008, 25, 678–696. [Google Scholar] [CrossRef][Green Version]
- Kilian, M.; Mitra, N.J.; Pottmann, H. Geometric modeling in shape space. ACM Trans. Graph. (TOG) 2007, 26, 64. [Google Scholar] [CrossRef]
- Kavan, L.; Collins, S.; Žára, J.; O’Sullivan, C. Geometric skinning with approximate dual quaternion blending. ACM Trans. Graph. (TOG) 2008, 27, 105. [Google Scholar] [CrossRef]
- Jacobson, A.; Sorkine, O. Stretchable and twistable bones for skeletal shape deformation. ACM Trans. Graph. (TOG) 2011, 30, 165. [Google Scholar] [CrossRef]
- Saito, S.; Zhou, Z.Y.; Kavan, L. Computational bodybuilding: Anatomically-based modeling of human bodies. ACM Trans. Graph. (TOG) 2015, 34, 41. [Google Scholar] [CrossRef]
- Le, B.H.; Hodgins, J.K. Real-time skeletal skinning with optimized centers of rotation. ACM Trans. Graph. (TOG) 2016, 35, 37. [Google Scholar] [CrossRef]
- Vaillant, R.; Barthe, L.; Guennebaud, G.; Cani, M.P.; Rohmer, D.; Wyvill, B.; Gourmel, O.; Paulin, M. Implicit skinning: Real-time skin deformation with contact modeling. ACM Trans. Graph. (TOG) 2013, 32, 125. [Google Scholar] [CrossRef]
- Vaillant, R.; Guennebaud, G.; Barthe, L.; Wyvill, B.; Cani, M.P. Robust iso-surface tracking for interactive character skinning. ACM Trans. Graph. (TOG) 2014, 33, 189. [Google Scholar] [CrossRef]
- Sloan, P.P.J.; Rose III, C.F.; Cohen, M.F. Shape by example. In Proceedings of the 2001 Symposium on Interactive 3D Graphics, Research Triangle Park, NC, USA, 19–21 March 2001; pp. 135–143. [Google Scholar]
- Mohr, A.; Gleicher, M. Building efficient, accurate character skins from examples. ACM Trans. Graph. (TOG) 2003, 22, 562–568. [Google Scholar] [CrossRef]
- Rhee, T.; Lewis, J.P.; Neumann, U. Real-Time Weighted Pose-Space Deformation on the GPU. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2006; Volume 25, pp. 439–448. [Google Scholar]
- Park, S.I.; Hodgins, J.K. Data-driven modeling of skin and muscle deformation. ACM Trans. Graph. (TOG) 2008, 27, 96. [Google Scholar] [CrossRef]
- Li, D.; Sueda, S.; Neog, D.R.; Pai, D.K. Thin skin elastodynamics. ACM Trans. Graph. (TOG) 2013, 32, 49. [Google Scholar] [CrossRef]
- Le, B.H.; Deng, Z. Smooth skinning decomposition with rigid bones. ACM Trans. Graph. (TOG) 2012, 31, 199. [Google Scholar] [CrossRef]
- Nedel, L.P.; Thalmann, D. Modeling and deformation of the human body using an anatomically-based approach. In Proceedings of the Computer Animation 98, Philadelphia, PA, USA, 8–10 June 1998; pp. 34–40. [Google Scholar]
- Angelidis, A.; Singh, K. Kinodynamic Skinning Using Volume-preserving Deformations. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, California, USA, 2–4 August 2007; Eurographics Association: Aire-la-Ville, Switzerland, 2007; pp. 129–140. [Google Scholar]
- Lee, S.H.; Sifakis, E.; Terzopoulos, D. Comprehensive biomechanical modeling and simulation of the upper body. ACM Trans. Graph. (TOG) 2009, 28, 99. [Google Scholar] [CrossRef]
- Kim, J.; Pollard, N.S. Fast simulation of skeleton-driven deformable body characters. ACM Trans. Graph. (TOG) 2011, 30, 121. [Google Scholar] [CrossRef]
- McAdams, A.; Zhu, Y.; Selle, A.; Empey, M.; Tamstorf, R.; Teran, J.; Sifakis, E. Efficient elasticity for character skinning with contact and collisions. ACM Trans. Graph. (TOG) 2011, 30, 37. [Google Scholar] [CrossRef]
- Hahn, F.; Martin, S.; Thomaszewski, B.; Sumner, R.; Coros, S.; Gross, M. Rig-space physics. ACM Trans. Graph. (TOG) 2012, 31, 72. [Google Scholar] [CrossRef]
- Kavan, L.; Sorkine, O. Elasticity-inspired deformers for character articulation. ACM Trans. Graph. (TOG) 2012, 31, 196. [Google Scholar] [CrossRef]
- Li, S.; Huang, J.; de Goes, F.; Jin, X.; Bao, H.; Desbrun, M. Space-time editing of elastic motion through material optimization and reduction. ACM Trans. Graph. (TOG) 2014, 33, 108. [Google Scholar] [CrossRef]
- Wang, Y.; Jacobson, A.; Barbič, J.; Kavan, L. Linear subspace design for real-time shape deformation. ACM Trans. Graph. (TOG) 2015, 34, 57. [Google Scholar] [CrossRef]
- Jacobson, A.; Baran, I.; Kavan, L.; Popović, J.; Sorkine, O. Fast automatic skinning transformations. ACM Trans. Graph. (TOG) 2012, 31, 77. [Google Scholar] [CrossRef]
- Kry, P.G.; Rahgoshay, C.; Rabbani, A.; Singh, K. Inverse kinodynamics: Editing and constraining kinematic approximations of dynamic motion. Comput. Graph. 2012, 36, 904–915. [Google Scholar] [CrossRef]
- Deul, C.; Bender, J. Physically-based character skinning. In Proceedings of theVirtual Reality Interactions and Physical Simulations (VRIPhys), Lille, France, 27–29 November 2013. [Google Scholar]
- Heeren, B.; Rumpf, M.; Wardetzky, M.; Wirth, B. Time-Discrete Geodesics in the Space of Shells. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2012; Volume 31, pp. 1755–1764. [Google Scholar]
- Heeren, B.; Rumpf, M.; Schröder, P.; Wardetzky, M.; Wirth, B. Exploring the geometry of the space of shells. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2014; Volume 33, pp. 247–256. [Google Scholar]
- Teng, Y.; Otaduy, M.A.; Kim, T. Simulating articulated subspace self-contact. ACM Trans. Graph. (TOG) 2014, 33, 106. [Google Scholar] [CrossRef]
- Hyun, D.E.; Yoon, S.H.; Chang, J.W.; Seong, J.K.; Kim, M.S.; Jüttler, B. Sweep-based human deformation. Vis. Comput. 2005, 21, 542–550. [Google Scholar] [CrossRef]
- You, L.; Yang, X.; Pachulski, M.; Zhang, J.J. Boundary constrained swept surfaces for modelling and animation. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 26, pp. 313–322. [Google Scholar]
- You, L.; Yang, X.; Zhang, J.J. Dynamic skin deformation with characteristic curves. Comput. Anim. Virtual Worlds 2008, 19, 433–444. [Google Scholar] [CrossRef]
- Bartoň, M.; Shi, L.; Kilian, M.; Wallner, J.; Pottmann, H. Circular arc snakes and kinematic surface generation. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2013; Volume 32, pp. 1–10. [Google Scholar]
- Bartoň, M.; Pottmann, H.; Wallner, J. Detection and reconstruction of freeform sweeps. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2014; Volume 33, pp. 23–32. [Google Scholar]
- Brandt, C.; von Tycowicz, C.; Hildebrandt, K. Geometric flows of curves in shape space for processing motion of deformable objects. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2016; Volume 35, pp. 295–305. [Google Scholar]
- Bharaj, G.; Thormählen, T.; Seidel, H.P.; Theobalt, C. Automatically rigging multi-component characters. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2012; Volume 31, pp. 755–764. [Google Scholar]
- Bærentzen, J.A.; Abdrashitov, R.; Singh, K. Interactive shape modeling using a skeleton-mesh co-representation. ACM Trans. Graph. (TOG) 2014, 33, 132. [Google Scholar] [CrossRef]
- Xu, W.; Umetani, N.; Chao, Q.; Mao, J.; Jin, X.; Tong, X. Sensitivity-optimized rigging for example-based real-time clothing synthesis. ACM Trans. Graph. 2014, 33. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).