Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives

Abstract

In this paper, the solution of fuzzy differential equations is approximated numerically using diagonally implicit multistep block method of order four. The multistep block method is well known as an efficient and accurate method for solving ordinary differential equations, hence in this paper the method will be used to solve the fuzzy initial value problems where the initial value is a symmetric triangular fuzzy interval. The triangular fuzzy number is not necessarily symmetric, however by imposing symmetry the definition of a triangular fuzzy number can be simplified. The symmetric triangular fuzzy interval is a triangular fuzzy interval that has same left and right width of membership function from the center. Due to this, the parametric form of symmetric triangular fuzzy number is simple and the performing arithmetic operations become easier. In order to interpret the fuzzy problems, Seikkala’s derivative approach is implemented. Characterization theorem is then used to translate the problems into a system of ordinary differential equations. The convergence of the introduced method is also proved. Numerical examples are given to investigate the performance of the proposed method. It is clearly shown in the results that the proposed method is comparable and reliable in solving fuzzy differential equations.

1. Introduction

Modeling of real-world problems involves ordinary differential equations (ODEs) that are not always perfect. For example, the initial value may not be known exactly and the function may contain uncertain parameters. This inexactness leads to the necessity of fuzzy differential equations (FDEs) to overcome the situation. Examples of FDEs application in real life include models such as in solid waste management systems [1], hydraulic differential servo cylinders [2], population models [3], hyperchaotic systems [4], and service composition [5].

Chang and Zadeh in [6] first introduced the fuzzy derivative concept. The concept was then extended by Dubois and Prade [7] and the authors also addressed the problem of linearity. Goetschel and Voxman [8] and Puri and Ralescu [9] studied and proposed several important definitions and theorems in the fuzzy derivative. A significant contribution for fuzzy initial value problems (FIVPs) is done by Seikkala [10] and Kaleva [11,12].

The exact solutions for certain FDEs are inconvenient and tedious to determine because of the complexity of the FDE problems. Therefore, numerical methods are used for solving the FDEs. Ma et al. in [13] contribute an important work in solving FDEs by using a numerical method. They adopted classical Euler’s method and solve the FIVPs.

Several researchers discussed predictor–corrector methods for solving FDEs [14,15,16,17]. Allahviranloo et al. in [15] developed a predictor–corrector method based on the Adams-Bashforth three-step method as a predictor and the Adams-Moulton two-step method as a corrector. The improvise method of [15] is then proposed in [14]. Shang and Guo [17] derived the predictor–corrector method based on Adams-Bashforth four-step method and the Adams-Moulton three-step method as a predictor and corrector respectively. Jayakumar [16] introduced Adams fifth order predictor–corrector method for solving FDEs by considering the Adams-Bashforth five-step method as a predictor and the Adam-Moulton four-step method as a corrector. All studies aimed to determine better accuracy and efficiency in finding solutions to FDEs.

The multistep block method is an efficient method for solving ODEs. In this method, several approximation points will be computed simultaneously on the $x$-axis in the block. Mehrkanoon et al. in [18] and Isa and Majid in [19] solved FDEs by using the 2-point fully implicit multistep block method. Diagonally implicit multistep block method is used by Zawawi et al. [20] and Ramli and Majid [21,22] for solving FDEs. Zawawi et al. proposed diagonally implicit block backward differentiation formulas, while Ramli and Majid developed an Adams-type diagonally implicit multistep block method, which considered order four for first point and order five for the second point. Fook and Ibrahim in [23] solved FDEs by using a 2-points hybrid block method.

This paper will discuss the implementation of a 2-point diagonally implicit multistep block method to solve fuzzy differential equations. The method will compute the numerical solutions at two points simultaneously using constant step size. The two formulas of the diagonally implicit block method of Adams type will have the same order for the first and second formula.

This paper is organized as follows. Some basic definitions and notations are in Section 2. Definition of FIVP in Section 3 and description of the 2-point diagonally implicit multistep block method of order four (2PDO4) will be discussed in Section 4. In the next section, the implementation of the block method for solving FIVP and its algorithm is proposed in Section 5 and Section 6 respectively. The convergence of the method is proved in Section 7. Numerical results are provided in Section 8 and conclusion of this study is at the end of the paper.

2. Preliminaries

Some basic definitions and notations that are significant for this paper will be reviewed in this section. For further details, refer [15,24,25,26] (to name a few).

Definition 1.

Let $\eta :R\to \left[0,1\right]$ is a mapping of fuzzy number with $R$ is set of all real numbers. The mapping has following properties:

1. 

$\eta$ upper semicontinuous,

2. 

$\eta$ is fuzzy convex, that is, $\eta \left(\lambda x+\left(1-\lambda \right)y\right)\ge \mathit{min}\left\{\eta \left(x\right),\eta \left(y\right)\right\}$, for all $x,y\in R, \lambda \in \left[0,1\right]$,

3. 

$\eta$ is normal, that is exist $x_0\in R$ such that $\eta \left(x_0\right)=1$,

4. 

The support of $\eta$ is $supp \eta =\left\{x\in R|\eta \left(x\right)>0\right\}$ and its closure $cl\left(supp \eta \right)$ is compact.

Consider $E$ as set of all fuzzy numbers on $R$.

Definition 2.

The $r$-level set of a fuzzy number $\eta \in E,0\le r\le 1$ and denoted by ${\left[\eta \right]}_r$, is defined as

$${\left[\eta \right]}_r=\{\begin{array}{cc}\left\{x\in R|\eta \left(x\right)>r\right\},& if 0\le r\le 1,\\ cl\left(supp \eta \right),& if r=0,\end{array}$$

and is closed and bounded interval by $\left[\underset{\_}{\eta }\left(r\right),\overline{\eta }\left(r\right)\right]$ where $\underset{\_}{\eta }\left(r\right)$ and $\overline{\eta }\left(r\right)$ denotes the left-hand endpoint and right-hand endpoint of ${\left[\eta \right]}_r$ respectively.

The summation and scalar multiplication in $E$ are defined as:

• $\eta \oplus \mu =\left(\underset{\_}{\eta }+\underset{\_}{\mu },\overline{\eta }+\overline{\mu }\right)$,
• $\lambda \odot \eta =\{\begin{array}{cc}\left(\lambda \underset{\_}{\eta }\left(r\right),\lambda \overline{\eta }\left(r\right)\right),& \lambda \ge 0,\\ \left(\lambda \overline{\eta }\left(r\right),\lambda \underset{\_}{\eta }\left(r\right)\right),& \lambda <0.\end{array}$

Given the Hausdorff distance $D:E\times E\to R_{+}\cup 0$ as the distance between two fuzzy numbers and a metric in $E$ as follows

$$D\left(\eta ,\mu \right)=\underset{r\in \left[0,1\right]}{\sup \max }\left\{\left|\underset{\_}{\eta }\left(r\right)-\underset{\_}{\mu }\left(r\right)\right|,\left|\overline{\eta }\left(r\right)-\overline{\mu }\left(r\right)\right|\right\}$$

with the following properties

• $D\left(\eta \oplus \omega ,\mu \oplus \omega \right)=D\left(\eta ,\mu \right), \forall \eta ,\mu ,\omega \in E,$
• $D\left(\lambda \odot \eta ,\lambda \odot \mu \right)=\left|\lambda \right|D\left(\eta ,\mu \right), \forall \lambda \in R,\forall \eta ,\mu \in E,$
• $D\left(\eta \oplus \mu ,\omega \oplus \sigma \right)\le D\left(\eta ,\omega \right)+D\left(\mu ,\sigma \right), \forall \eta ,\mu ,\omega ,\sigma \in E,$
• $D\left(\eta +\mu ,0\right)\le D\left(\eta ,0\right)+D\left(\mu ,0\right), \forall \eta ,\mu \in E,$
• $\left(E,D\right)$ is a complete metric space.

Let $f:R\to E$ be a fuzzy valued function.

Definition 3.

If for arbitrary fixed $t_0\in R$ and $\epsilon >0, \delta >0$ such that

$$\left|t-t_0\right|<\delta ⟹D\left(f\left(t\right),f\left(t_0\right)\right)<\epsilon$$

is said to be continuous.

Hukuhara differentiability (H-derivative) for fuzzy mappings is introduced by Puri and Ralescu in [9]. The differentiability is based on H-difference sets. Definition 4 and 5 explained the concept.

Definition 4.

Let $x,y\in E$. If there exist $z\in E$ such that $x=y\oplus z$, then $z$ is called the H-difference of $x$ and $y$, and it is denoted by $x\ominus y$. The sign “$\ominus$” stands for H-difference and note that $x\ominus y\ne x+\left(-1\right)y$.

Definition 5.

$f$ is differentiable at $t_0\in R$ if exist $f{}^{\prime }\left( t_0\right)\in E$ such that

$$\underset{h\to 0^{+}}{\mathit{lim}}\frac{f\left(t_0+h\right)\ominus f\left(t_0\right)}{h} and \underset{h\to 0^{+}}{\mathit{lim}}\frac{f\left(t_0\right)\ominus f\left(t_0-h\right)}{h}$$

exist and are equal to $f{}^{\prime }\left(t_0\right)$.

Here, the limits are taken in the metric space $\left(E,D\right)$ since we have defined $h^{-1}⨀\left(f\left(t_0\right)\ominus f\left(t_0-h\right)\right)$ and $h^{-1}⨀\left(f\left(t_0+h\right)\ominus f\left(t_0\right)\right)$.

3. Fuzzy Initial Value Problems

In this paper, we will consider first order FIVP as follows

$$y^{\prime }\left(t\right)=f\left(t,y\left(t\right)\right), y\left(t_0\right)=y_0, t\in \left[t_0,T\right]$$

(1)

where $y$ is a fuzzy function of $t$, $f\left(t,y\right)$ is a fuzzy function of crisp variable $t$ and fuzzy variable $y$, and $y^{\prime }$ is Hukuhara fuzzy derivative of $y$ with the given initial value $y\left(t_0\right)=y_0$. Let $y\left(t\right)=\left[\underset{\_}{y}\left(t\right),\overline{y}\left(t\right)\right]$, if $y\left(t\right)$ is Hukuhara differentiable then $y{}^{\prime }\left(t\right)=\left[\underset{\_}{y{}^{\prime }}\left(t\right),\overline{y}{}^{\prime }\left(t\right)\right]$, and $f\left(t,y\left(t\right)\right)=\left[\underset{\_}{f}\left(t,\underset{\_}{y}\left(t\right),\overline{y}\left(t\right)\right),\overline{f}\left(t,\underset{\_}{y}\left(t\right),\overline{y}\left(t\right)\right)\right]$.

The parametric form of $y$ is given by

$${\left[y\left(t\right)\right]}_r=\left[\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right], t\in R, r\in \left[0,1\right].$$

As referred to [21], the Seikkala derivative of a fuzzy function is defined by

$${\left[y{}^{\prime }\left(t\right)\right]}_r=\left[\underset{\_}{y{}^{\prime }}\left(t;r\right),\overline{y}{}^{\prime }\left(t;r\right)\right], t\in R, r\in \left[0,1\right]$$

provided that the equation defines a fuzzy number.

For solving (1) by using numerical methods for ODEs, it must be translated to system of ODEs. Bede in [27] proposed characterization theorems for the solutions of FDEs by using ODEs.

Theorem 1.

Let $f:\left(a,b\right)\to E$ be Hukuhara differentiable and denote ${\left[f\left(y\right)\right]}_r=\left[\underset{\_}{f}\left(y\left(t;r\right)\right),\overline{f}\left(y\left(t;r\right)\right)\right]$. Functions $\underset{\_}{f}\left(y\left(t;r\right)\right)$ and $\overline{f}\left(y\left(t;r\right)\right)$ are differentiable and based on Seikkala derivative

$${\left[f{}^{\prime }\left(y\right)\right]}_r=\left[\underset{\_}{f}{}^{\prime }\left(y\left(t;r\right)\right),\overline{f}{}^{\prime }\left(y\left(t;r\right)\right)\right], r\in \left[0,1\right].$$

Therefore (1) can be translated to the system of ODEs

$$\begin{array}{l}\underset{\_}{y^{\prime }}\left(t;r\right)=\underset{\_}{f}\left(t,\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right),\\ \overline{y}{}^{\prime }\left(t;r\right)=\overline{f}\left(t,\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right),\\ \underset{\_}{y^{\prime }}\left(t_0;r\right)={\underset{\_}{y^{\prime }}}_0\left(r\right),\\ \overline{y{}^{\prime }}\left(t_0;r\right)={\overline{y{}^{\prime }}}_0\left(r\right).\end{array}$$

(2)

Theorem 2.

Consider FIVP (1) where $f:\left[t_0,t_0+a\right]\times E\to E$ such that

1. 

${\left[f{}^{\prime }\left(t,y\right)\right]}_r=\left[\underset{\_}{f}\left(t,\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right),\overline{f}\left(t,\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right)\right]$,

2. 

$\underset{\_}{f}$ and $\overline{f}$ are equicontinuous (that is for any $\epsilon >0$ and any $\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)\in \left[t_0,t_0+a\right]\times R^2$ we have $\left|\underset{\_}{f}\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)-\underset{\_}{f}\left(t_1,{\eta }_1\left(t;r\right),{\mu }_1\left(t;r\right)\right)\right|<\epsilon$ and $\left|\overline{f}\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)-\overline{f}\left(t_1,{\eta }_1\left(t;r\right),{\mu }_1\left(t;r\right)\right)\right|<\epsilon$ for all $r\in \left[0,1\right]$ whenever $\left|\right|\left(t_1,{\eta }_1\left(t;r\right),{\mu }_1\left(t;r\right)\right)-\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)\left|\right|<\delta )$ and uniformly bounded on any bounded set,

3. 

there exist an $L>0$ such that

$\left|\underset{\_}{f}\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)-\underset{\_}{f}\left(t_1,{\eta }_1\left(t;r\right),{\mu }_1\left(t;r\right)\right)\right|\le Lmax\left\{\left|\eta -{\eta }_1\right|,\left|\mu -,{\mu }_1\right|\right\}$, $\forall r\in \left[0,1\right]$ and

$\left|\overline{f}\left(t,\eta \left(t;r\right),\mu \left(t;r\right)\right)-\overline{f}\left(t_1,{\eta }_1\left(t;r\right),{\mu }_1\left(t;r\right)\right)\right|\le Lmax\left\{\left|\eta -{\eta }_1\right|,\left|\mu -,{\mu }_1\right|\right\}$, $\forall r\in \left[0,1\right]$.

Then FIVP (1) and the system of ODEs (2) are equivalent.

4. Derivation of 2-Point Diagonally Implicit Multistep Block Method

Consider the initial value problems (IVPs) for ODEs of the form

$$y^{\prime }=f\left(x,y\right), y\left(x_0\right)=y_0, x\in \left[a,b\right]$$

(3)

where $a$ and $b$ are finite. The interval $\left[a,b\right]$ will be divided into a series of blocks. In this proposed method, each block contained two points, $y_{n+1}$ and $y_{n+2}$ which will be computed simultaneously in a block with the step size $h$ at the points $x_{n+1}$ and $x_{n+2}$ respectively as in Figure 1.

Figure 1. 2-point implicit multistep block method.

The Lagrange interpolation polynomial is applied for the derivation of predictor and corrector formulas. To obtain the predictor formulas, the set of points $\left\{\left(x_{n-2},f_{n-2}\right),\left(x_{n-1},f_{n-1}\right),\left(x_n,f_n\right)\right\}$ is interpolated and the order of the formulas is one less than the corrector formulas. The corrector formulas will use the set of interpolation points i.e., $\left\{\left(x_{n-2},f_{n-2}\right),\left(x_{n-1},f_{n-1}\right),\left(x_n,f_n\right),\left(x_{n+1},f_{n+1}\right)\right\}$ for derivation of $y_{n+1}$ and $\left\{\left(x_{n-1},f_{n-1}\right),\left(x_n,f_n\right),\left(x_{n+1},f_{n+1}\right),\left(x_{n+2},f_{n+2}\right)\right\}$ for derivation of $y_{n+2}$. The formulas of $y_{n+1}$ will used three back values $\left(x_n, x_{n-1},x_{n-2}\right)$, while the $y_{n+2}$ will used two back values i.e., $\left(x_n, x_{n-1}\right)$.

Formulas for $y_{n+1}$ and $y_{n+2}$ are derived by integrating (3) such that

$$\int y{}^{\prime }dx=\int f\left(x,y\right)dx$$

(4)

where the interval of integration for $y_{n+1}$ and $y_{n+2}$ are $\left[x_n,x_{n+1}\right]$ and $\left[x_n,x_{n+2}\right]$ respectively. These are equivalent to

$$y_{n+1}=y_n+{\int }_{x_n}^{x_{n+1}}f\left(x,y\right)dx$$

(5)

and

$$y_{n+2}=y_n+{\int }_{x_n}^{x_{n+2}}f\left(x,y\right)dx.$$

(6)

The function $f\left(x,y\right)$ in (5) and (6) is replaced by the Lagrange polynomial which interpolates the set of corresponding mentioned points. Evaluating the integral in (5) using MAPLE gives the formula for the first and second point of the block multistep method as follows:

The first point,

$$y_{n+1}=y_n+\frac{h}{24}\left(9f_{n+1}+19f_n-5f_{n-1}+f_{n-2}\right)$$

(7)

and the second point,

$$y_{n+2}=y_n+\frac{h}{3}\left(f_{n+2}+4f_{n+1}+f_n\right).$$

(8)

As referred to [28,29],

$${\displaystyle \sum }_{k=0}^j{A}_k{Y}_{n+k}=h{\displaystyle \sum }_{k=0}^j{B}_k{F}_{n+k}$$

(9)

form the general matrix of linear multistep method where $A_k$ and $B_k$ are $r$ by $r$ matrices with elements $a_{lm}$ and $b_{lm}$ for $l,m=1,2,\dots ,r$. The associated difference operator $L$ is given by

$$L\left[z\left(x\right);h\right]={\displaystyle \sum }_{k=0}^j\left[A_{k}z\left(x+h\right)-h{B}_{k}z{}^{\prime }\left(x+kh\right)\right]$$

(10)

where $z\left(x\right)$ is the exact solution and assume to be sufficiently differentiable. If $C_0=C_1=\cdots =C_q=0,C_{p+1}\ne 0$, $L$ is said to be order $p$ and $C_{p+1}$ is called the error constant.

The general form of constant $C_q$ is defined as

$$\begin{array}{ccc}{C}_0& =& {\displaystyle {\displaystyle \sum }_{k=0}^j}{A}_k,\hfill \\ C_1& =& {\displaystyle {\displaystyle \sum }_{k=0}^j}\left[k{A}_k-B_k\right],\hfill \\ ⋮& ⋮& ⋮\hfill \\ C_q& =& {\displaystyle {\displaystyle \sum }_{k=0}^j}\left[\frac{1}{q!}{k}^q{A}_k-\frac{1}{\left(q-1\right)!}{k}^{q-1}{B}_k\right], q=2,3,\dots ,p+1.\hfill \end{array}$$

(11)

To determine the order of the method, (7) and (8) is written in matrix form as follows

$$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{y}_{n+1}\\ y_{n+2}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right]\left[\begin{array}{c}{y}_{n-1}\\ y_n\end{array}\right]+h\{\left[\begin{array}{cc}\frac{9}{24}& 0\\ \frac{4}{3}& \frac{1}{3}\end{array}\right]\left[\begin{array}{c}{f}_{n+1}\\ f_{n+2}\end{array}\right]+\left[\begin{array}{cc}-\frac{5}{24}& \frac{19}{24}\\ 0& \frac{1}{3}\end{array}\right]\left[\begin{array}{c}{f}_{n-1}\\ f_n\end{array}\right]+\left[\begin{array}{cc}0& \frac{1}{24}\\ 0& 0\end{array}\right]\left[\begin{array}{c}{f}_{n-3}\\ f_{n-2}\end{array}\right]\}$$

(12)

From (12), $A_2=\left[\begin{array}{c}0\\ 0\end{array}\right], A_3=\left[\begin{array}{c}-1\\ -1\end{array}\right],A_4=\left[\begin{array}{c}1\\ 0\end{array}\right],A_5=\left[\begin{array}{c}0\\ 1\end{array}\right],B_0=\left[\begin{array}{c}0\\ 0\end{array}\right], B_1=\left[\begin{array}{c}\frac{1}{24}\\ 0\end{array}\right], B_2=\left[\begin{array}{c}-\frac{5}{24}\\ 0\end{array}\right], B_3=\left[\begin{array}{c}\frac{19}{24}\\ \frac{1}{3}\end{array}\right],B_4=\left[\begin{array}{c}\frac{9}{24}\\ \frac{4}{3}\end{array}\right]$ and $B_5=\left[\begin{array}{c}0\\ \frac{1}{3}\end{array}\right]$. Hence, by applying (11), $C_0=C_1=C_2=C_3=C_4=\left[\begin{array}{c}0\\ 0\end{array}\right]$ and $C_5=\left[\begin{array}{c}-\frac{19}{720}\\ -\frac{1}{90}\end{array}\right]$. Since $C_5\ne \left[\begin{array}{c}0\\ 0\end{array}\right]$ the method is concluded as order four and the error constant is $\left[\begin{array}{c}-\frac{19}{720}\\ -\frac{1}{90}\end{array}\right]$.

5. Implementation for Solving FIVPs

Consider the FIVP (1) and let the exact solution is denoted by $\left[\underset{\_}{Y}\left(t;r\right),\overline{Y}\left(t;r\right)\right]$ while $\left[\underset{\_}{y}\left(t;r\right),\overline{y}\left(t;r\right)\right]$ is the approximate solution. To integrate the system (2), from $t_0$ let $T>t_0$, and replace $\left[t_0,T\right]$ by

$$t_0<t_1<t_2<\cdots <t_n=T.$$

(13)

$Y_n\left(t;r\right)=\left[{\underset{\_}{Y}}_n\left(t;r\right),{\overline{Y}}_n\left(t;r\right)\right]$ denoted as the exact solution at $t_n$, with the approximate solution $y_n\left(t;r\right)=\left[{\underset{\_}{y}}_n\left(t;r\right),{\overline{y}}_n\left(t;r\right)\right]$. Given $t_n=t_0+h$ where $0\le n\le N$ and $h=\frac{T-t_0}{N}$.

The general fuzzy 2PDO4 method by considering (7) and (8) is written as

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+1};r\right)\approx \underset{\_}{Y}\left(t_n;r\right)+\frac{h}{24}[9\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)+19\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)\\ -5\underset{\_}{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)+\underset{\_}{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)],\\ \overline{Y}\left(t_{n+1};r\right)\approx \overline{Y}\left(t_n;r\right)+\frac{h}{24}[9\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)+19\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)\\ -5\overline{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)+\overline{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)],\end{array}$$

(14)

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+2};r\right)\approx \underset{\_}{Y}\left(t_n;r\right)+\frac{h}{3}[\underset{\_}{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)+4\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)],\\ \overline{Y}\left(t_{n+2};r\right)\approx \overline{Y}\left(t_n;r\right)+\frac{h}{3}[\overline{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)+4\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)],\end{array}$$

(15)

for the exact solutions and

$$\begin{array}{l}\underset{\_}{y}\left(t_{n+1};r\right)=\underset{\_}{y}\left(t_n;r\right)+\frac{h}{24}[9\underset{\_}{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)+19\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\\ -5\underset{\_}{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)+\underset{\_}{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\\ \overline{y}\left(t_{n+1};r\right)\approx \overline{y}\left(t_n;r\right)+\frac{h}{24}[9\overline{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)+19\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\\ -5\overline{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)+\overline{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\end{array}$$

(16)

$$\begin{array}{l}\underset{\_}{y}\left(t_{n+2};r\right)\approx \underset{\_}{y}\left(t_n;r\right)+\frac{h}{3}[\underset{\_}{f}\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)+4\underset{\_}{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\\ +\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)],\\ \overline{y}\left(t_{n+2};r\right)=\overline{y}\left(t_n;r\right)+\frac{h}{3}[\overline{f}\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)+4\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)],\end{array}$$

(17)

for the approximate solutions.

6. Algorithm

The following algorithm is based on using 2PDO4 method. To approximate the solution of the following FIVP

$$y^{\prime }\left(t\right)=f\left(t,y\left(t\right)\right), y\left(t_0\right)=y_0, t_0\le t\le T.$$

For $N$ as an arbitrary positive integer,

• Step 1. Let $h=\frac{T-t_0}{N}$. The initial value $y\left(t_0\right)=y_0$ is obtained from the FIVP and Runge–Kutta order four is used to determine the two starting points. Hence,

  $$\begin{array}{c}\underset{\_}{y}\left(t_0;r\right)={\underset{\_}{y}}_0, \underset{\_}{y}\left(t_1;r\right)=\underset{\_}{y_1}, \underset{\_}{y}\left(t_2;r\right)={\underset{\_}{y}}_2,\\ \overline{y}\left(t_0;r\right)={\overline{y}}_0, \overline{y}\left(t_1;r\right)={\overline{y}}_1, \overline{y}\left(t_2;r\right)={\overline{y}}_2.\end{array}$$
• Step 2. Let $n=2$.
• Step 3. Let $t_{n+1}=t_1+nh$ and $t_{n+2}=t_2+nh$.
• Step 4. Let the predictor formulas

  $$\begin{array}{l}{\underset{\_}{y}}^P\left(t_{n+1};r\right)=\underset{\_}{y}\left(t_n;r\right)+\frac{h}{12}[23\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)-16\underset{\_}{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\\ +5\underset{\_}{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\\ {\overline{y}}^P\left(t_{n+1};r\right)\approx \overline{y}\left(t_n;r\right)+\frac{h}{12}[23\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)-16\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\\ +5\overline{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\end{array}$$

  $$\begin{array}{l}{\underset{\_}{y}}^P\left(t_{n+2};r\right)=\underset{\_}{y}\left(t_n;r\right)+\frac{h}{3}[19\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)-20\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\\ +7\underset{\_}{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\\ {\overline{y}}^P\left(t_{n+2};r\right)\approx \overline{y}\left(t_n;r\right)+\frac{h}{3}[19\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)-20\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\\ +7\overline{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)].\end{array}$$
• Step 5. Let the corrector formulas

  $$\begin{array}{l}{\underset{\_}{y}}^C\left(t_{n+1};r\right)=\underset{\_}{y}\left(t_n;r\right)+\frac{h}{24}[9{\underset{\_}{f}}^P\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)+19\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\\ -5\underset{\_}{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)+\underset{\_}{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\\ {\overline{y}}^C\left(t_{n+1};r\right)\approx \overline{y}\left(t_n;r\right)+\frac{h}{24}[9{\overline{f}}^P\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)+19\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\\ -5\overline{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)+\overline{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)],\end{array}$$

  $$\begin{array}{l}{\underset{\_}{y}}^C\left(t_{n+2};r\right)\approx \underset{\_}{y}\left(t_n;r\right)+\frac{h}{3}[{\underset{\_}{f}}^P\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)+4{\underset{\_}{f}}^P\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\\ +\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)],\\ {\overline{y}}^C\left(t_{n+2};r\right)=\overline{y}\left(t_n;r\right)+\frac{h}{3}[{\overline{f}}^P\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)+4{\overline{f}}^P\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)].\end{array}$$
• $n=n+2$.
• If $n\le N-2$, go to Step 3.
• Algorithm is completed and $\left[{\underset{\_}{y}}^C\left(t_n;r\right),{\overline{y}}^C\left(t_n;r\right)\right]$ approximates $\left[\underset{\_}{Y}\left(t_n;r\right),\overline{Y}\left(t_n;r\right)\right]$.

7. Convergence

From (16) and (17)

$$\begin{array}{c}\underset{\_}{y}\left(t;h;r\right)=\left\{\left[t_0,{\underset{\_}{y}}_0\left(r\right)\right], \left[t_1,{\underset{\_}{y}}_1\left(r\right)\right],\cdots ,\left[t_N,{\underset{\_}{y}}_N\left(r\right)\right]\right\}, \\ \overline{y}\left(t;h;r\right)=\left\{\left[t_0,{\overline{y}}_0\left(r\right)\right], \left[t_1,{\overline{y}}_1\left(r\right)\right],\cdots ,\left[t_N,{\overline{y}}_N\left(r\right)\right]\right\},\end{array}$$

(18)

are the 2PDO4 method over the interval $t_0\le t\le t_N$ and approximate to $\underset{\_}{Y}\left(t;r\right)$ and $\overline{Y}\left(t;r\right)$ respectively. Given

$$\underset{h\to 0}{\lim } \underset{\_}{y}\left(t;h;r\right)=\underset{\_}{Y}\left(t;r\right), \underset{h\to 0}{\lim } \overline{y}\left(t;h;r\right)=\overline{Y}\left(t;r\right),$$

(19)

is the convergence condition for the approximates. The following lemma is considered to proof the convergence.

Lemma 1.

[9] Let ${\left\{{\mathit{w}}_{\mathit{n}}\right\}}_{\mathit{n}=\mathbf{0}}^{\mathit{N}}$ (a sequence of numbers) satisfy:

$$\left|w_{n+1}\right|\le A\left|w_n\right|+B\left|w_{n-1}\right|+C, 0\le n\le N-1$$

for some given positive constants $\mathit{A}, \mathit{B}$ and $\mathit{C}$. Then

$$\begin{array}{l}\left|w_n\right|\le \left(A^{n-1}+{\beta }_1{A}^{n-3}B+{\beta }_2{A}^{n-5}{B}^2+\cdots +{\beta }_l{B}^{\left[n/2\right]}\right)\left|w_1\right| \\ +\left(A^{n-2}B+{\gamma }_1{A}^{n-4}{B}^2+\cdots +{\gamma }_{m}A{B}^{\left[n/2\right]}\right)\left|w_0\right| \\ +\left(A^{n-2}+A^{n-3}+\cdots +1\right)C \\ +\left({\delta }_1{A}^{n-4}+{\delta }_2{A}^{n-5}+\cdots +{\delta }_{p}A+1\right)BC \\ +\left({\zeta }_1{A}^{n-6}+{\zeta }_2{A}^{n-7}+\cdots +{\zeta }_{q}A+1\right)B^{2}C \\ +\left({\lambda }_1{A}^{n-8}+{\lambda }_2{A}^{n-9}+\cdots +{\lambda }_{s}A+1\right)B^{3}C+\cdots ,n \mathrm{odd}\end{array}$$

and

$$\begin{array}{l}\left|w_n\right|\le \left(A^{n-1}+{\beta }_1{A}^{n-3}B+{\beta }_2{A}^{n-5}{B}^2+\cdots +{\beta }_l{B}^{\left[n/2\right]-1}\right)\left|w_1\right| \\ +\left(A^{n-2}B+{\gamma }_1{A}^{n-4}{B}^2+\cdots +{\gamma }_{m}A{B}^{\left[n/2\right]}\right)\left|w_0\right| \\ +\left(A^{n-2}+A^{n-3}+\cdots +1\right)C \\ +\left({\delta }_1{A}^{n-4}+{\delta }_2{A}^{n-5}+\cdots +{\delta }_{p}A+1\right)BC \\ +\left({\zeta }_1{A}^{n-6}+{\zeta }_2{A}^{n-7}+\cdots +{\zeta }_{q}A+1\right)B^{2}C \\ +\left({\lambda }_1{A}^{n-8}+{\lambda }_2{A}^{n-9}+\cdots +{\lambda }_{s}A+1\right)B^{3}C+\cdots ,n \mathrm{even}\end{array}$$

where for all $l,m,p,q$ and $s$, ${\beta }_l, {\gamma }_m, {\delta }_p, {\zeta }_q$ and ${\lambda }_s$ are constants. The proof by using mathematical induction is straightforward.

Theorem 3.

For arbitrary fixed $r,\left(r\in \left[0,1\right]\right)$, approximate solutions (16) and (17) converge to the exact solutions $\underset{\_}{Y}\left(t;r\right)$ and $\overline{Y}\left(t;r\right)$ for $\underset{\_}{Y},\overline{Y}\in C^4\left[t_0,T\right]$.

Proof. 

By applying (19), it is sufficient to show

$$\underset{h\to 0}{\lim } {\underset{\_}{y}}_N\left(r\right)=\underset{\_}{Y}\left(T;r\right), \underset{h\to 0}{\lim } {\overline{y}}_N\left(r\right)=\overline{Y}\left(T;r\right).$$

Consider the exact solutions (14) and (15), then

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+1};r\right)=\underset{\_}{Y}\left(t_n;r\right)+\frac{h}{24}[9\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)+19\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)\\ -5\underset{\_}{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)+\underset{\_}{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)]\\ -\frac{19}{720}{h}^5{\underset{\_}{Y}}^{\left(5\right)}\left({\underset{\_}{\xi }}_n\right),\\ \overline{Y}\left(t_{n+1};r\right)=\overline{Y}\left(t_n;r\right)+\frac{h}{24}[9\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)+19\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)\\ -5\overline{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)+\overline{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)]\\ -\frac{19}{720}{h}^5{\overline{Y}}^{\left(5\right)}\left({\overline{\xi }}_n\right),\end{array}$$

(20)

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+2};r\right)=\underset{\_}{Y}\left(t_n;r\right)+\frac{h}{3}[\underset{\_}{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)+4\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)]h^5-\frac{1}{90}{\underset{\_}{Y}}^{\left(5\right)}\left({\underset{\_}{\xi }}_n\right),\\ \overline{Y}\left(t_{n+2};r\right)\approx \overline{Y}\left(t_n;r\right)+\frac{h}{3}[\overline{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)+4\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)\\ +\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)]-\frac{1}{90}{h}^5{\overline{Y}}^{\left(5\right)}\left({\overline{\xi }}_n\right)\end{array}$$

(21)

where $t_n<{\underset{\_}{\xi }}_n,{\overline{\xi }}_n<t_{n+1}$. Therefore, by subtracting (20) and (16), and (21) and (17) yield

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+1};r\right)-\underset{\_}{y}\left(t_{n+1};r\right)=\underset{\_}{Y}\left(t_n;r\right)-\underset{\_}{y}\left(t_n;r\right)\\ +\frac{9h}{24}\left[\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)-\underset{\_}{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\right]\\ +\frac{19h}{24}\left[\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)-\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\right]\\ -\frac{5h}{24}\left[\underset{\_}{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)-\underset{\_}{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\right]\\ +\frac{h}{24}\left[\underset{\_}{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)-\underset{\_}{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)\right]\\ -\frac{19}{720}{h}^5{\underset{\_}{Y}}^{\left(5\right)}\left({\underset{\_}{\xi }}_n\right),\\ \overline{Y}\left(t_{n+1};r\right)-\overline{y}\left(t_{n+1};r\right)=\overline{Y}\left(t_n;r\right)-\overline{y}\left(t_n;r\right)\\ +\frac{9h}{24}\left[\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)-\overline{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\right]\\ +\frac{19h}{24}\left[\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)-\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\right]\\ -\frac{5h}{24}\left[\overline{f}\left(t_{n-1},{\underset{\_}{Y}}_{n-1}\left(r\right),{\overline{Y}}_{n-1}\left(r\right)\right)-\overline{f}\left(t_{n-1},{\underset{\_}{y}}_{n-1}\left(r\right),{\overline{y}}_{n-1}\left(r\right)\right)\right]\\ +\frac{h}{24}\left[\overline{f}\left(t_{n-2},{\underset{\_}{Y}}_{n-2}\left(r\right),{\overline{Y}}_{n-2}\left(r\right)\right)-\overline{f}\left(t_{n-2},{\underset{\_}{y}}_{n-2}\left(r\right),{\overline{y}}_{n-2}\left(r\right)\right)\right]\\ -\frac{19}{720}{h}^5{\overline{Y}}^{\left(5\right)}\left({\overline{\xi }}_n\right),\end{array}$$

(22)

and

$$\begin{array}{l}\underset{\_}{Y}\left(t_{n+2};r\right)-\underset{\_}{y}\left(t_{n+2};r\right)=\underset{\_}{Y}\left(t_n;r\right)-\underset{\_}{y}\left(t_n;r\right)\\ +\frac{h}{3}\left[\underset{\_}{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)-\underset{\_}{f}\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)\right]\\ +\frac{4h}{3}\left[\underset{\_}{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)-\underset{\_}{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\right]\\ +\frac{h}{3}\left[\underset{\_}{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)-\underset{\_}{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\right]\\ -\frac{1}{90}{h}^5{\underset{\_}{Y}}^{\left(5\right)}\left({\underset{\_}{\xi }}_n\right),\\ \overline{Y}\left(t_{n+2};r\right)-\overline{y}\left(t_{n+2};r\right)=\overline{Y}\left(t_n;r\right)-\overline{y}\left(t_n;r\right)\\ +\frac{h}{3}\left[\overline{f}\left(t_{n+2},{\underset{\_}{Y}}_{n+2}\left(r\right),{\overline{Y}}_{n+2}\left(r\right)\right)-\overline{f}\left(t_{n+2},{\underset{\_}{y}}_{n+2}\left(r\right),{\overline{y}}_{n+2}\left(r\right)\right)\right]\\ +\frac{4h}{3}\left[\overline{f}\left(t_{n+1},{\underset{\_}{Y}}_{n+1}\left(r\right),{\overline{Y}}_{n+1}\left(r\right)\right)-\overline{f}\left(t_{n+1},{\underset{\_}{y}}_{n+1}\left(r\right),{\overline{y}}_{n+1}\left(r\right)\right)\right]\\ +\frac{h}{3}\left[\overline{f}\left(t_n,{\underset{\_}{Y}}_n\left(r\right),{\overline{Y}}_n\left(r\right)\right)-\overline{f}\left(t_n,{\underset{\_}{y}}_n\left(r\right),{\overline{y}}_n\left(r\right)\right)\right]\\ -\frac{1}{90}{h}^5{\overline{Y}}^{\left(5\right)}\left({\overline{\xi }}_n\right).\end{array}$$

(23)

Denote $w_n=\underset{\_}{Y}\left(t_n;r\right)-\underset{\_}{y}\left(t_n;r\right)$ and $v_n=\overline{Y}\left(t_n;r\right)-\overline{y}\left(t_n;r\right)$. Then (22) and (23) becomes

$$\begin{array}{c}\left|w_{n+1}\right|\le \left(1+\frac{19h{L}_2}{24}\right)\left|w_n\right|+\frac{9h{L}_1}{24}\left|w_{n+1}\right|+\frac{5h{L}_3}{24}\left|w_{n-1}\right|+\frac{h{L}_4}{24}\left|w_{n-2}\right|+\frac{19}{720}{h}^5\underset{\_}{M},\\ \left|v_{n+1}\right|\le \left(1+\frac{19h{L}_6}{24}\right)\left|v_n\right|+\frac{9h{L}_5}{24}\left|v_{n+1}\right|+\frac{5h{L}_7}{24}\left|v_{n-1}\right|+\frac{h{L}_8}{24}\left|v_{n-2}\right|+\frac{19}{720}{h}^5\overline{M},\end{array}$$

(24)

and

$$\begin{array}{c}\left|w_{n+2}\right|\le \left(1+\frac{h{L}_{11}}{3}\right)\left|w_n\right|+\frac{h{L}_9}{3}\left|w_{n+2}\right|+\frac{4h{L}_{10}}{3}\left|w_{n+1}\right|+\frac{1}{90}{h}^5\underset{\_}{M},\\ \left|v_{n+2}\right|\le \left(1+\frac{h{L}_{14}}{3}\right)\left|v_n\right|+\frac{h{L}_{12}}{3}\left|v_{n+2}\right|+\frac{4h{L}_{13}}{3}\left|v_{n+1}\right|+\frac{1}{90}{h}^5\overline{M},\end{array}$$

(25)

where $\underset{\_}{M}=\underset{t_0\le t\le T}{\max }\left|{\underset{\_}{Y}}^{\left(5\right)}\left(t;r\right)\right|$ and $\overline{M}=\underset{t_0\le t\le T}{\min }\left|{\overline{Y}}^{\left(5\right)}\left(t;r\right)\right|$.

Consider the first point (24), let $L=\max \left\{L_1,\cdots ,L_8\right\}<\frac{24}{9h}$, then

$$\begin{array}{c}\left|w_{n+1}\right|\le \left(1+\frac{28hL}{24-9hL}\right)\left|w_n\right|+\frac{5hL}{24-9hL}\left|w_{n-1}\right|+\frac{hL}{24-9hL}\left|w_{n-2}\right|+\frac{19}{30\left(24-9hL\right)}{h}^5\underset{\_}{M},\\ \left|v_{n+1}\right|\le \left(1+\frac{28hL}{24-9hL}\right)\left|v_n\right|+\frac{5hL}{24-9hL}\left|v_{n-1}\right|+\frac{hL}{24-9hL}\left|v_{n-2}\right|+\frac{19}{30\left(24-9hL\right)}{h}^5\overline{M},\end{array}$$

are resulted. Let $\left|u_n\right|=\left|w_n\right|+\left|v_n\right|$, then by Lemma 1 and $w_0=v_0=0$ (also $w_1=v_1=0$):

$$\begin{array}{l}\left|u_n\right|\le \frac{{\left(1+\frac{28hL}{24-9hL}\right)}^{n-1}-1}{\frac{28hL}{24-9hL}}\times \frac{19}{30\left(24-9hL\right)}{h}^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\delta }_1{\left(1+\frac{28hL}{24-9hL}\right)}^{n-4}+{\delta }_2{\left(1+\frac{28hL}{24-9hL}\right)}^{n-5}+\cdots +{\delta }_p\left(1+\frac{28hL}{24-9hL}\right)+1\right\}\\ \times \left(\frac{5hL}{24-9hL}\right)\left(\frac{19}{30\left(24-9hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\zeta }_1{\left(1+\frac{28hL}{24-9hL}\right)}^{n-6}+{\zeta }_2{\left(1+\frac{28hL}{24-9hL}\right)}^{n-7}+\cdots +{\zeta }_q\left(1+\frac{28hL}{24-9hL}\right)+1\right\} \\ \times \left(\frac{hL}{24-9hL}\right)\left(\frac{19}{30\left(24-9hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\lambda }_1{\left(1+\frac{28hL}{24-9hL}\right)}^{n-8}+{\lambda }_2{\left(1+\frac{28hL}{24-9hL}\right)}^{n-9}+\cdots +{\lambda }_s\left(1+\frac{28hL}{24-9hL}\right)+1\right\}\\ \times {\left(\frac{5hL}{24-9hL}\right)}^2\left(\frac{19}{30\left(24-9hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\cdots \end{array}$$

are obtained. If $h\to 0$ then $w_n\to 0$ and $v_n\to 0$ which concludes the proof.

Consider the second point (25), let $L=\max \left\{L_9,\cdots ,L_{14}\right\}<\frac{3}{h}$, then

$$\begin{array}{c}\left|w_{n+2}\right|\le \frac{4hL}{3-hL}\left|w_{n+1}\right|+\left(1+\frac{2hL}{3-hL}\right)\left|w_n\right|+\frac{1}{30\left(3-hL\right)}{h}^5\underset{\_}{M},\\ \left|v_{n+2}\right|\le \frac{4hL}{3-hL}\left|v_{n+1}\right|+\left(1+\frac{2hL}{3-hL}\right)\left|v_n\right|+\frac{1}{30\left(3-hL\right)}{h}^5\overline{M},\end{array}$$

are resulted. Let $\left|u_n\right|=\left|w_n\right|+\left|v_n\right|$, then by Lemma 1 and $w_0=v_0=0$ (also $w_1=v_1=0$):

$$\begin{array}{l}\left|u_n\right|\le \frac{{\left(\frac{4hL}{3-hL}\right)}^{n-1}-1}{\frac{1+hL}{3-hL}}\times \frac{1}{30\left(3-hL\right)}{h}^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\delta }_1{\left(\frac{4hL}{3-hL}\right)}^{n-4}+{\delta }_2{\left(\frac{4hL}{3-hL}\right)}^{n-5}+\cdots +{\delta }_p\left(\frac{4hL}{3-hL}\right)+1\right\}\\ \times \left(1+\frac{2hL}{3-hL}\right)\left(\frac{1}{30\left(3-hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\zeta }_1{\left(\frac{4hL}{3-hL}\right)}^{n-6}+{\zeta }_2{\left(\frac{4hL}{3-hL}\right)}^{n-7}+\cdots +{\zeta }_q\left(\frac{4hL}{3-hL}\right)+1\right\} \\ \times {\left(1+\frac{2hL}{3-hL}\right)}^2\left(\frac{1}{30\left(3-hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\left\{{\lambda }_1{\left(\frac{4hL}{3-hL}\right)}^{n-8}+{\lambda }_2{\left(\frac{4hL}{3-hL}\right)}^{n-9}+\cdots +{\lambda }_s\left(\frac{4hL}{3-hL}\right)+1\right\}\\ \times {\left(1+\frac{2hL}{3-hL}\right)}^3\left(\frac{1}{30\left(3-hL\right)}\right)h^5\left(\underset{\_}{M}+\overline{M}\right)\\ +\cdots \end{array}$$

are obtained. If $h\to 0$ then $w_n\to 0$ and $v_n\to 0$ which concludes the proof. ☐

Remark 1.

Above theorem results that convergence order is $\mathit{O}\left({\mathit{h}}^{\mathbf{3}}\right)$.

8. Results and Discussion

To implement the 2PDO4 method, $PE{\left(CE\right)}^m$ mode is used where $P$, C and $E$ stands for predictor, corrector and evaluation of a function respectively. The $CE$ implementation is repeated $m$ times for each step and step size $h=0.1$ is considered in the numerical results.

The following FIVPs were tested to show the performance of the proposed method:

Problem 1.

(Ma et al. [13]) Consider linear FIVP:

$$y^{\prime }\left(t\right)=y\left(t\right), y\left(0\right)=\left[0.75+0.25r,1.125-0.125r\right], t,r\in \left[0,1\right].$$

Exact solution: $Y\left(t,r\right)=\left[\left(0.75+0.25r\right)e^t,\left(1.125-0.125r\right)e^t\right]$.

Problem 2.

(Pallingkinis et al. [30]) Consider linear FIVP:

$$y^{\prime }\left(t\right)=\overline{c}y\left(t\right), y\left(0\right)=\left(8/8.5/9\right), t,r\in \left[0,1\right]$$

where triangular fuzzy number $\overline{c}=\left(1/2/3\right)$.

[$\overline{c}$ is a triangular fuzzy number where the basis of the membership function of $\overline{c}$ is in the interval $\left[c_1,c_3\right]$ with the known summit $c_2$. Hence, the triangular fuzzy numbers are denoted by $\overline{c}=\left(c_1/c_2/c_3\right)$].

Exact solution: $Y\left(t,r\right)=\left[\left(8+0.5r\right)e^{\left(1+r\right)t},\left(9-0.5r\right)e^{\left(3-r\right)t}\right]$.

Problem 3.

(Ghanbari [31]) Consider nonlinear FIVP:

$$y^{\prime }\left(t\right)=2y\left(t\right)+t^2+1, y\left(0\right)=\left[r,2-r\right], t,r\in \left[0,1\right].$$

Exact solution:

$$Y\left(t,r\right)=\left[\left(r+\frac{3}{4}\right)e^{2t}-\frac{1}{4}\left(2t^2+2t+3\right),\left(\frac{11}{4}-r\right)e^{2t}-\frac{1}{4}\left(2t^2+2t+3\right)\right].$$

Problem 4.

(Dizicheh et al. [32]) Consider nonlinear FIVP:

$$y^{\prime }\left(t\right)=k_1{y}^2\left(t\right)+k_2, y\left(0\right)=\left[-0.0012+0.0012r,0.0012-0.0012r\right],$$

where $k_i>0$ for $i=1,2 t,r\in \left[0,1\right]$. Given

$$k_1\left(r\right)=\left[0.5+0.5r,1.5-0.5r\right] \mathit{and} k_2\left(r\right)=\left[0.75+0.25r,1.25-0.25r\right].$$

Exact solution:

$$Y\left(t,r\right)=\left[\frac{A\tan \left(\frac{At}{4}+{\tan }^{-1}\left(\frac{-3+3r^2}{1250A}\right)\right)}{2+2r},\frac{-\sqrt{2}B\tan \left(\frac{\sqrt{2}}{4}\left[Bt+2\sqrt{2}{\tan }^{-1}\left(\frac{3\sqrt{2}\left(-3+r\right)\left(-1+r\right)}{2500B}\right)\right]\right)}{-6+r}\right] .$$

Problem 5.

(Ma et al. [13]) Consider nonlinear FIVP:

$$y^{\prime }\left(t\right)=e^{-y^2\left(t\right)}, y\left(0\right)=\left[0.75+0.25r,1.5-0.5r\right], t,r\in \left[0,1\right].$$

The following notations are used in the tables:

• $r$: Fuzzy numbers with bounded $r$-level intervals
• $\underset{\_}{Y},\overline{Y}$: Lower and upper bounded exact solution
• $\underset{\_}{y},\overline{y}$: Lower and upper bounded approximated solution
• FCN: Total function calls
• TS: Total steps taken
• TIME: The execution time taken in seconds
• 2PDO4: 2-point diagonally implicit multistep method of order four
• ERK4: Extended Runge–Kutta-like formulae of order 4 [26]
• RK4: Runge–Kutta method of order 4 [33]
• ANN: Artificial neural network approach [34]

Absolute error is defined as $\left|Y_n\left(t;r\right)-y_n\left(t;r\right)\right|$, where $Y_n\left(t;r\right)=\left[{\underset{\_}{Y}}_n\left(t;r\right),{\overline{Y}}_n\left(t;r\right)\right]$, denoted as the exact solutions and $y_n\left(t;r\right)=\left[{\underset{\_}{y}}_n\left(t;r\right),{\overline{y}}_n\left(t;r\right)\right]$ as approximate solutions at $t_n$. The code is written in C language by using Microsoft visual C++ platform.

The numerical results of 2PDO4 compared to ERK4, RK4 and ANN are display in Table 1, Table 2, Table 3, Table 4 and Table 5 when solving Problem 1–5. Note that these results are at $t=1$ with $h=0.1$.

Table 1. Numerical results of 2PDO4, ERK4, RK4 and ANN for solving Problem 1.

	$\left|{\underset{\_}{\mathit{Y}}}_{\mathit{n}}\left(\mathit{t};\mathit{r}\right)-\underset{\_}{\mathit{y}}\left(\mathit{t};\mathit{r}\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1	ANN 1
0.0	7.112242(-7)	1.969260(-6)	1.492423(-6)	8.862866(-5)
0.1	7.349317(-7)	2.090533(-6)	1.375277(-6)	2.941706(-5)
0.2	7.586392(-7)	1.734969(-6)	1.734969(-6)	4.646277(-5)
0.3	7.823466(-7)	2.094660(-6)	1.856242(-6)	2.449152(-5)
0.4	8.060541(-7)	1.500678(-6)	1.739096(-6)	4.445810(-6)
0.5	8.297616(-7)	2.337206(-6)	1.621951(-6)	5.440010(-5)
0.6	8.534691(-7)	1.743224(-6)	1.743224(-6)	2.835439(-5)
0.7	8.771765(-7)	2.579752(-6)	1.626078(-6)	4.669132(-5)
0.8	9.008840(-7)	2.462607(-6)	1.985770(-6)	9.726296(-5)
0.9	9.245915(-7)	2.345461(-6)	2.107043(-6)	1.421725(-5)
1.0	9.482990(-7)	1.751478(-6)	1.989897(-6)	5.582846(-5)
	$\left|{\overline{Y}}_n\left(t;r\right)-{\overline{y}}_n\left(t;r\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1	ANN 1
0.0	1.066836(-6)	2.834681(-6)	2.596262(-6)	5.994298(-5)
0.1	1.054983(-6)	2.297207(-6)	2.058788(-6)	1.465839(-6)
0.2	1.043129(-6)	1.998152(-6)	2.236570(-6)	2.598870(-5)
0.3	1.031275(-6)	3.129608(-6)	2.175934(-6)	8.511551(-6)
0.4	1.019421(-6)	2.115298(-6)	2.115298(-6)	3.403441(-5)
0.5	1.007568(-6)	3.008335(-6)	2.293079(-6)	1.444274(-5)
0.6	9.957139(-7)	2.232443(-6)	2.232443(-6)	4.208012(-5)
0.7	9.838602(-7)	1.933388(-6)	2.171806(-6)	5.160297(-5)
0.8	9.720064(-7)	9.190771(-7)	1.872751(-6)	3.012583(-5)
0.9	9.601527(-7)	2.050534(-6)	2.050534(-6)	1.543513(-4)
1.0	9.482990(-7)	1.751478(-6)	1.989897(-6)	2.817154(-5)
FCN	451	451	451	-
TS	66	110	110	-
TIME	0.675	-	-	-

¹ Results of ERK4, RK4 and ANN as referred in [26].

Table 2. Numerical results of 2PDO4, ERK4 and RK4 for solving Problem 2.

	$\left|{\underset{\_}{\mathit{Y}}}_{\mathit{n}}\left(\mathit{t};\mathit{r}\right)-\underset{\_}{\mathit{y}}\left(\mathit{t};\mathit{r}\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1
0.0	7.586392(-6)	1.401183(-5)	1.591918(-5)
0.1	1.366979(-5)	2.666611(-5)	3.238815(-5)
0.2	2.357892(-5)	5.232929(-5)	4.851460(-5)
0.3	3.919819(-5)	8.186697(-5)	8.377432(-5)
0.4	6.313677(-5)	1.334720(-4)	1.296573(-4)
0.5	9.894536(-5)	2.104650(-4)	2.104650(-4)
0.6	1.513830(-4)	3.134706(-4)	3.134706(-4)
0.7	2.267426(-4)	4.676179(-4)	4.638032(-4)
0.8	3.332447(-4)	6.934862(-4)	6.858569(-4)
0.9	4.815107(-4)	9.960255(-4)	9.960255(-4)
1.0	6.851258(-4)	1.419590(-3)	1.423405(-3)
	$\left|{\overline{Y}}_n\left(t;r\right)-{\overline{y}}_n\left(t;r\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1
0.0	1.260390(-2)	2.848404(-2)	2.849930(-2)
0.1	9.798071(-3)	2.185179(-2)	2.185179(-2)
0.2	7.561266(-3)	1.664276(-2)	1.662750(-2)
0.3	5.790072(-3)	1.253006(-2)	1.257584(-2)
0.4	4.397464(-3)	9.443902(-3)	9.421014(-3)
0.5	3.310672(-3)	7.054700(-3)	7.039441(-3)
0.6	2.469226(-3)	5.211172(-3)	5.211172(-3)
0.7	1.823209(-3)	3.812939(-3)	3.805309(-3)
0.8	1.331682(-3)	2.773261(-3)	2.773261(-3)
0.9	9.613063(-4)	1.989020(-3)	1.996649(-3)
1.0	6.851258(-4)	1.419590(-3)	1.423405(-3)
FCN	451	451	451
TS	66	110	110
TIME	0.639	-	-

¹ Results of ERK4 and RK4 as referred in [26].

Table 3. Numerical results of 2PDO4 and RK4 for solving Problem 3.

	$\left|{\underset{\_}{\mathit{Y}}}_{\mathit{n}}\left(\mathit{t};\mathit{r}\right)-\underset{\_}{\mathit{y}}\left(\mathit{t};\mathit{r}\right)\right|$
$\mathit{r}$	2PDO4	RK4
0.0	6.963978(-5)	1.010956(-4)
0.1	7.770009(-5)	1.177814(-4)
0.2	8.576039(-5)	1.344671(-4)
0.3	9.382069(-5)	1.511528(-4)
0.4	1.018810(-4)	1.678386(-4)
0.5	1.099413(-4)	1.845243(-4)
0.6	1.180016(-4)	2.012100(-4)
0.7	1.260619(-4)	2.178957(-4)
0.8	1.341222(-4)	2.345815(-4)
0.9	1.421825(-4)	2.512672(-4)
1.0	1.502428(-4)	2.679529(-4)
	$\left|{\overline{Y}}_n\left(t;r\right)-{\overline{y}}_n\left(t;r\right)\right|$
$\mathit{r}$	2PDO4	RK4
0.0	2.308459(-4)	4.348102(-4)
0.1	2.227856(-4)	4.181245(-4)
0.2	2.147253(-4)	4.014387(-4)
0.3	2.066649(-4)	3.847530(-4)
0.4	1.986046(-4)	3.680673(-4)
0.5	1.905443(-4)	3.513816(-4)
0.6	1.824840(-4)	3.346958(-4)
0.7	1.744237(-4)	3.180101(-4)
0.8	1.663634(-4)	3.013244(-4)
0.9	1.583031(-4)	2.846386(-4)
1.0	1.502428(-4)	2.679529(-4)
FCN	451	451
TS	66	110
TIME	0.530	0.718

Note: Simulation results of 2PDO4 and RK4 have been obtained in the same platform.

Table 4. Numerical results of 2PDO4, ERK4 and RK4 for solving Problem 4.

	$\left|{\underset{\_}{\mathit{Y}}}_{\mathit{n}}\left(\mathit{t};\mathit{r}\right)-\underset{\_}{\mathit{y}}\left(\mathit{t};\mathit{r}\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1
0.0	2.459944(-6)	1.9100(-5)	2.6100(-5)
0.1	3.707531(-6)	2.5100(-5)	3.0000(-5)
0.2	5.461503(-6)	2.9100(-5)	3.2200(-5)
0.3	7.872724(-6)	2.9000(-5)	4.2000(-5)
0.4	1.110316(-5)	3.5000(-5)	4.8000(-5)
0.5	1.529207(-5)	3.8000(-5)	5.5000(-5)
0.6	2.047821(-5)	3.9000(-5)	6.8000(-5)
0.7	2.643397(-5)	3.5000(-5)	7.6000(-5)
0.8	3.232537(-5)	3.4000(-5)	8.9000(-5)
0.9	3.602703(-5)	1.6000(-5)	1.0400(-4)
1.0	3.275027(-5)	1.0900(-4)	2.0000(-6)
	$\left|{\overline{Y}}_n\left(t;r\right)-{\overline{y}}_n\left(t;r\right)\right|$
$\mathit{r}$	2PDO4	ERK4 1	RK4 1
0.0	6.395992(-2)	3.7712(-2)	8.7760(-3)
0.1	2.778184(-2)	1.7758(-2)	3.8480(-3)
0.2	1.248250(-2)	9.0110(-3)	1.8570(-3)
0.3	5.710280(-3)	4.8090(-3)	1.0570(-3)
0.4	2.616533(-3)	2.7230(-3)	6.4900(-4)
0.5	1.175996(-3)	1.6230(-3)	4.2000(-4)
0.6	5.009738(-4)	9.9600(-4)	3.1600(-4)
0.7	1.875370(-4)	6.3700(-4)	2.3300(-4)
0.8	4.657100(-5)	4.3100(-4)	1.8400(-4)
0.9	1.228793(-5)	2.9100(-4)	1.5000(-4)
1.0	3.275027(-5)	1.0900(-5)	2.0000(-6)
FCN	363	451	451
TS	66	110	110
TIME	0.748	-	-

¹ Results of ERK4 and RK4 as referred in [32].

Table 5. Numerical results of 2PDO4 and RK4 for solving Problem 5.

	$\underset{\_}{\mathit{y}}\left(\mathit{t},\mathit{r}\right)$
$\mathit{r}$	2PDO4	RK4
0.0	0.795170	0.795172
0.1	0.846301	0.846303
0.2	0.894275	0.894276
0.3	0.940192	0.940193
0.4	0.984968	0.984969
0.5	1.029399	1.029399
0.6	1.074198	1.074198
0.7	1.120029	1.120029
0.8	1.167520	1.167520
0.9	1.217275	1.217275
1.0	1.269868	1.269868
	${\overline{\mathit{y}}}_{\mathit{n}}\left(\mathit{t};\mathit{r}\right)$
r	2PDO4	RK4
0.0	2.017674	2.017674
0.1	1.925744	1.925744
0.2	1.836622	1.836622
0.3	1.750863	1.750863
0.4	1.668972	1.668972
0.5	1.591344	1.591344
0.6	1.518228	1.518228
0.7	1.449698	1.449698
0.8	1.385652	1.385652
0.9	1.325836	1.325836
1.0	1.269868	1.269868
FCN	451	451
TS	66	110
TIME	0.390	0.468

Note: Simulation results of 2PDO4 and RK4 has been obtained in the same platform.

From Table 1, Table 2 and Table 3, it is obvious that 2PDO4 gives better results compared to ERK4, RK4 and ANN in terms of accuracy. It is also observed that the execution times of 2PDO4 for solving Problem 3 and 5 are faster than the RK4. Table 4 shows that 2PDO4 used less number of function evaluations to obtain comparable accuracy compared to ERK4 and RK4.

For Problem 5, the exact solutions cannot be calculated analytically. Hence, we compared the approximate solutions of 2PDO4 and RK4. The approximate solutions of Problem 5 at $t=1$ with $h=0.1$ are presented in Table 5. It can be observed that 2PDO4 is applicable to solve Problem 5 with an advantage of less total steps and faster execution times compared to RK4.

It is obvious in 1−5 that 2PDO4 required less number of total steps compared to other methods. This is expected since 2PDO4 approximates the solutions at two points simultaneously.

Figure 2, Figure 3, Figure 4 and Figure 5 is a plot of the exact and approximate solutions by using 2PDO4 for Problems 1–4. It is clear in the figures that the solutions by the 2PDO4 method almost coincide with the exact solutions. While the plot of approximate solutions for Problem 5 by using 2PDO4 and RK4 is shown in Figure 6.

Figure 2. Exact solutions and approximate solutions for Problem 1 at $t=1$ with $h=0.1$.

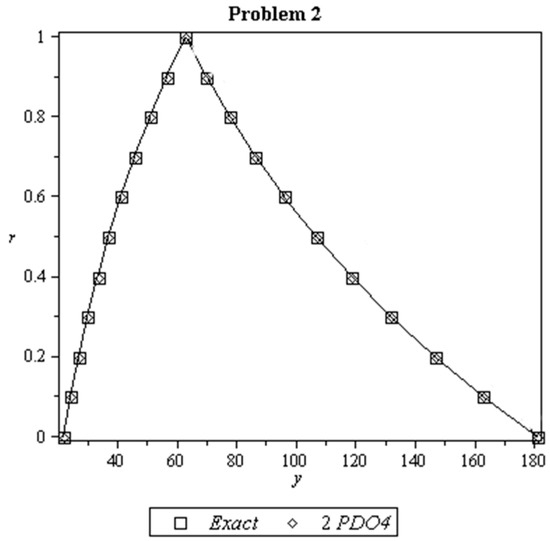
Figure 3. Exact solutions and approximate solutions for Problem 2 at $t=1$ with $h=0.1$.

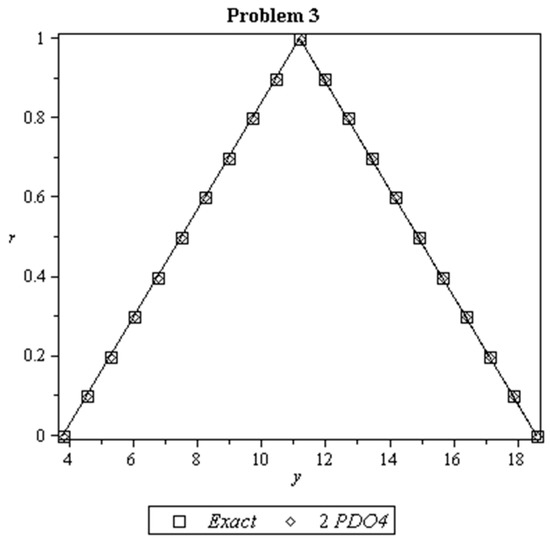
Figure 4. Exact solutions and approximate solutions for Problem 3 at $t=1$ with $h=0.1$.

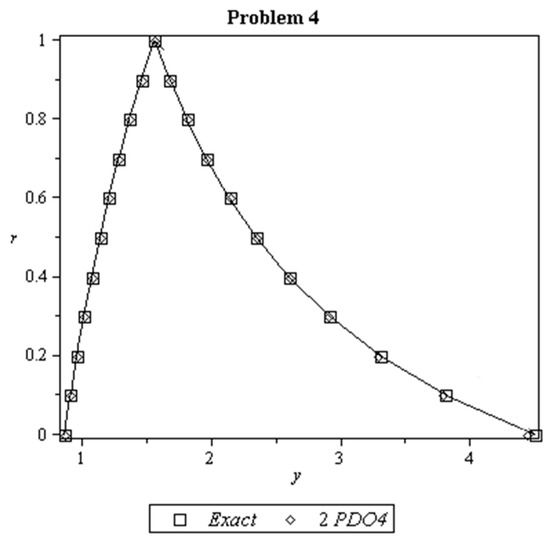
Figure 5. Exact solutions and approximate solutions for Problem 4 at $t=1$ with $h=0.1$.

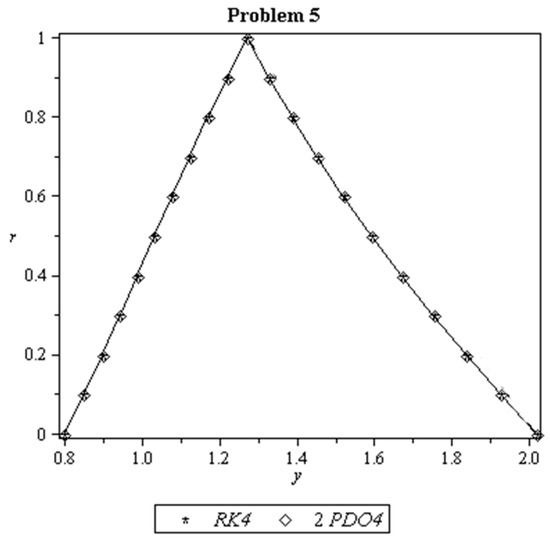
Figure 6. 2PDO4 solutions and RK4 solutions for Problem 5 at $t=1$ with $h=0.1$.

Figure 7, Figure 8, Figure 9 and Figure 10 is a plot of the absolute errors versus $r$ for lower and upper bounds of Problems 1–4. It can be seen in Figure 7, Figure 8 and Figure 9 that the errors of 2PDO4 are smaller than the comparison methods, but in Figure 10 the errors of 2PDO4 are smaller at certain points.

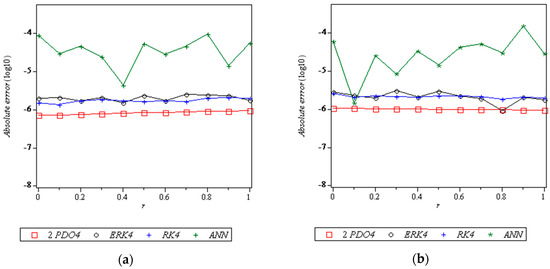
Figure 7. Graph of the numerical results when solving Problem 1: (a) Graph of absolute errors versus $r$ for lower bounds; (b) Graph of absolute errors versus $r$ for upper bounds.

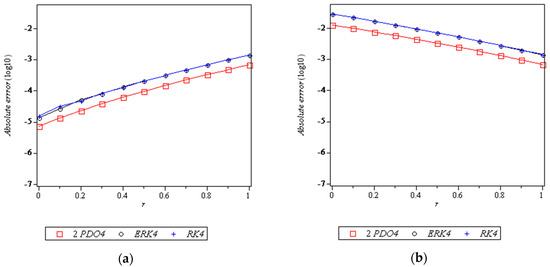
Figure 8. Graph of the numerical results when solving Problem 2: (a) Graph of absolute errors versus $r$ for lower bounds; (b) Graph of absolute errors versus $r$ for upper bounds.

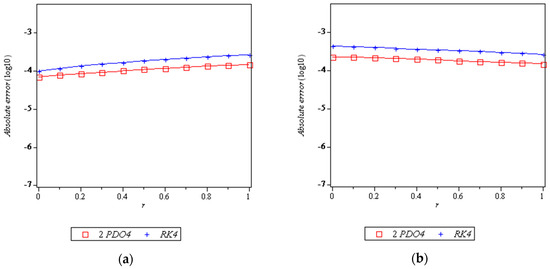
Figure 9. Graph of the numerical results when solving Problem 3: (a) Graph of absolute errors versus $r$ for lower bounds; (b) Graph of absolute errors versus $r$ for upper bounds.

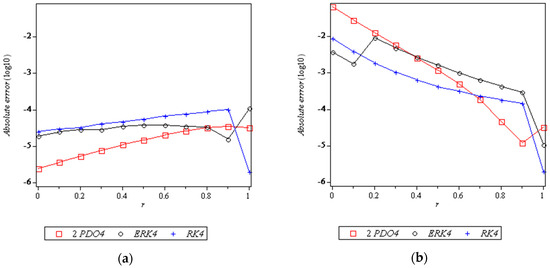
Figure 10. Graph of the numerical results when solving Problem 4: (a) Graph of absolute errors versus $r$ for lower bounds; (b) Graph of absolute errors versus for upper bounds.

9. Conclusions

In this paper, the diagonally implicit block method of order four (2PDO4) has been implemented for solving linear and nonlinear FDEs. Numerical results have shown that the proposed method gave comparable results in terms of accuracy and fewer total steps. The total functions are comparable or less compared to the existing method. The 2PDO4 is able to obtain less execution time than RK4 when solving two tested problems. Hence, the 2PDO4 method can be named in the literature as an additional and reliable method for solving FDEs.