Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives
Abstract
:1. Introduction
2. Preliminaries
- 1.
- upper semicontinuous,
- 2.
- is fuzzy convex, that is, , for all ,
- 3.
- is normal, that is exist such that ,
- 4.
- The support of is and its closure is compact.
- ,
- is a complete metric space.
3. Fuzzy Initial Value Problems
- 1.
- ,
- 2.
- and are equicontinuous (that is for any and any we have and for all whenever and uniformly bounded on any bounded set,
- 3.
- there exist an such that, and, .
4. Derivation of 2-Point Diagonally Implicit Multistep Block Method
5. Implementation for Solving FIVPs
6. Algorithm
- Step 1. Let . The initial value is obtained from the FIVP and Runge–Kutta order four is used to determine the two starting points. Hence,
- Step 2. Let .
- Step 3. Let and .
- Step 4. Let the predictor formulas
- Step 5. Let the corrector formulas
- .
- If , go to Step 3.
- Algorithm is completed and approximates .
7. Convergence
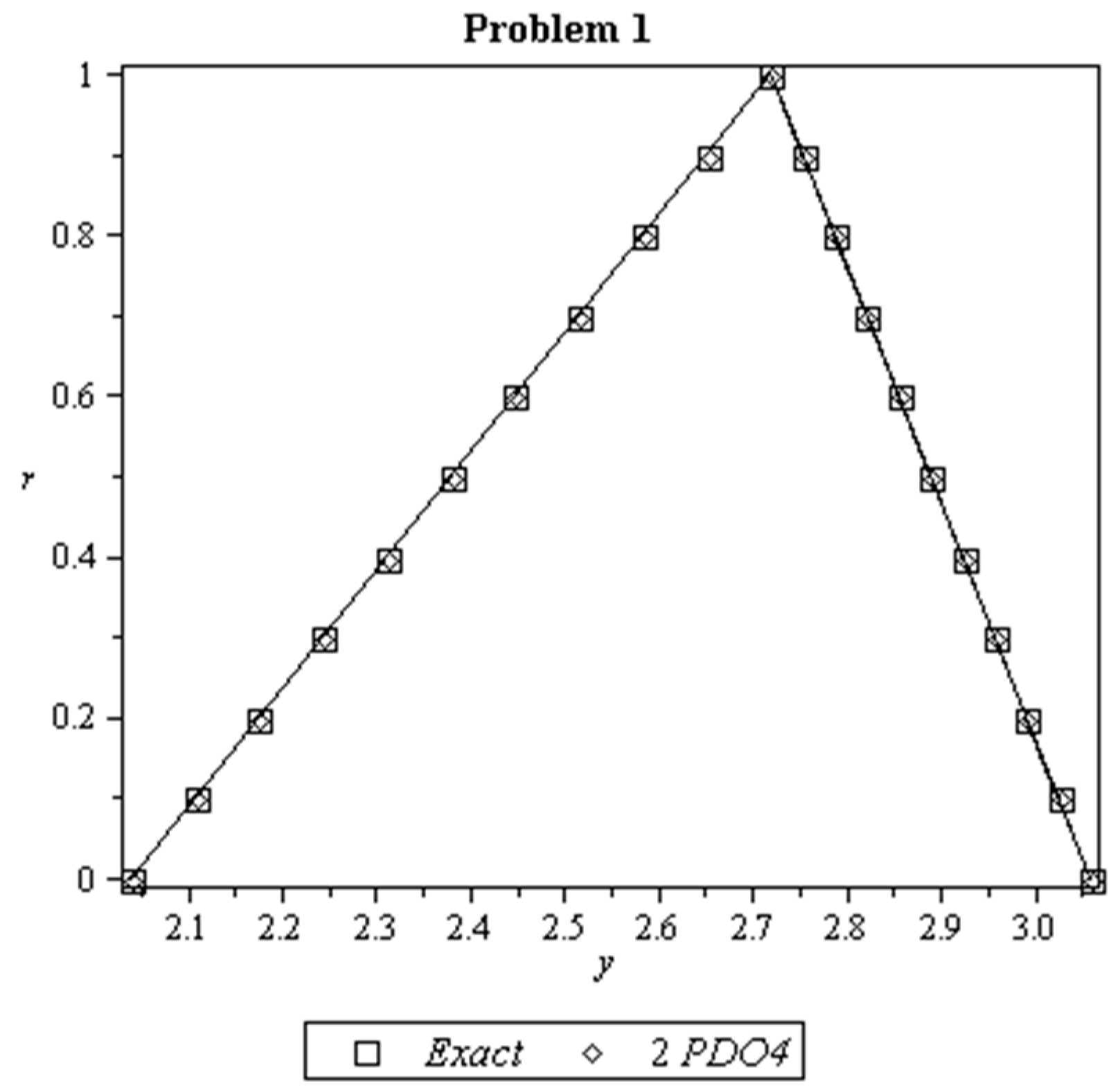
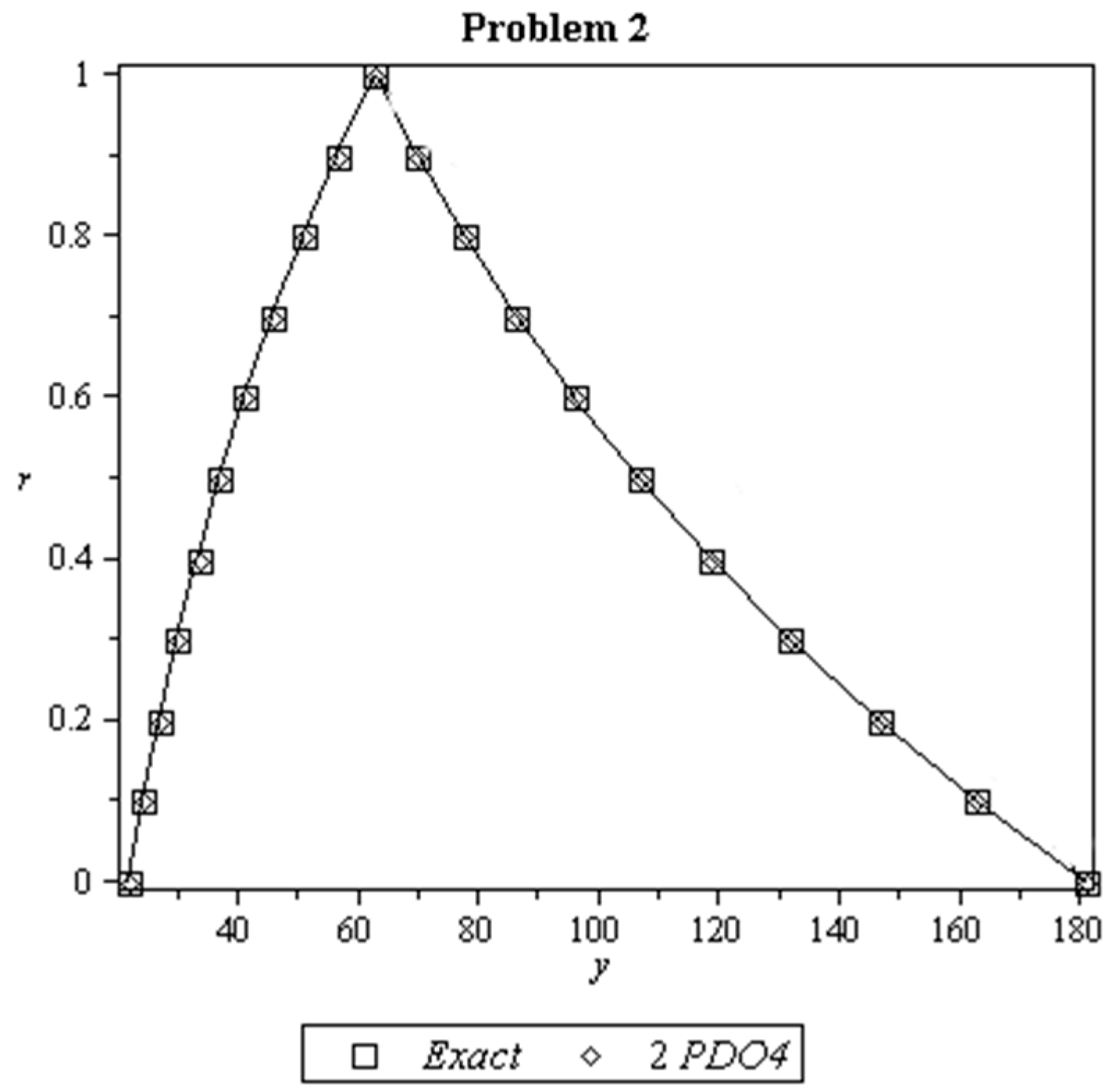
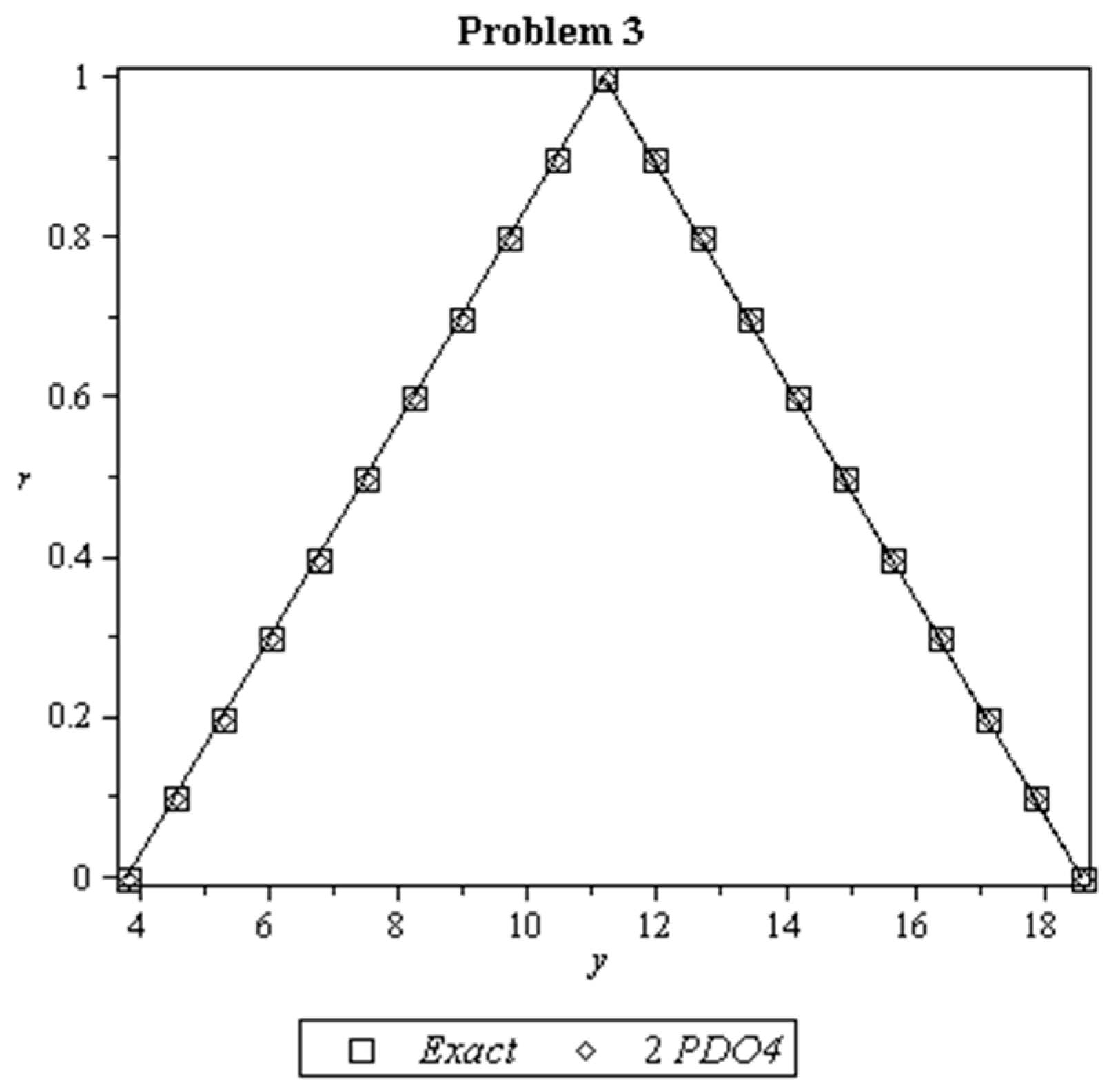
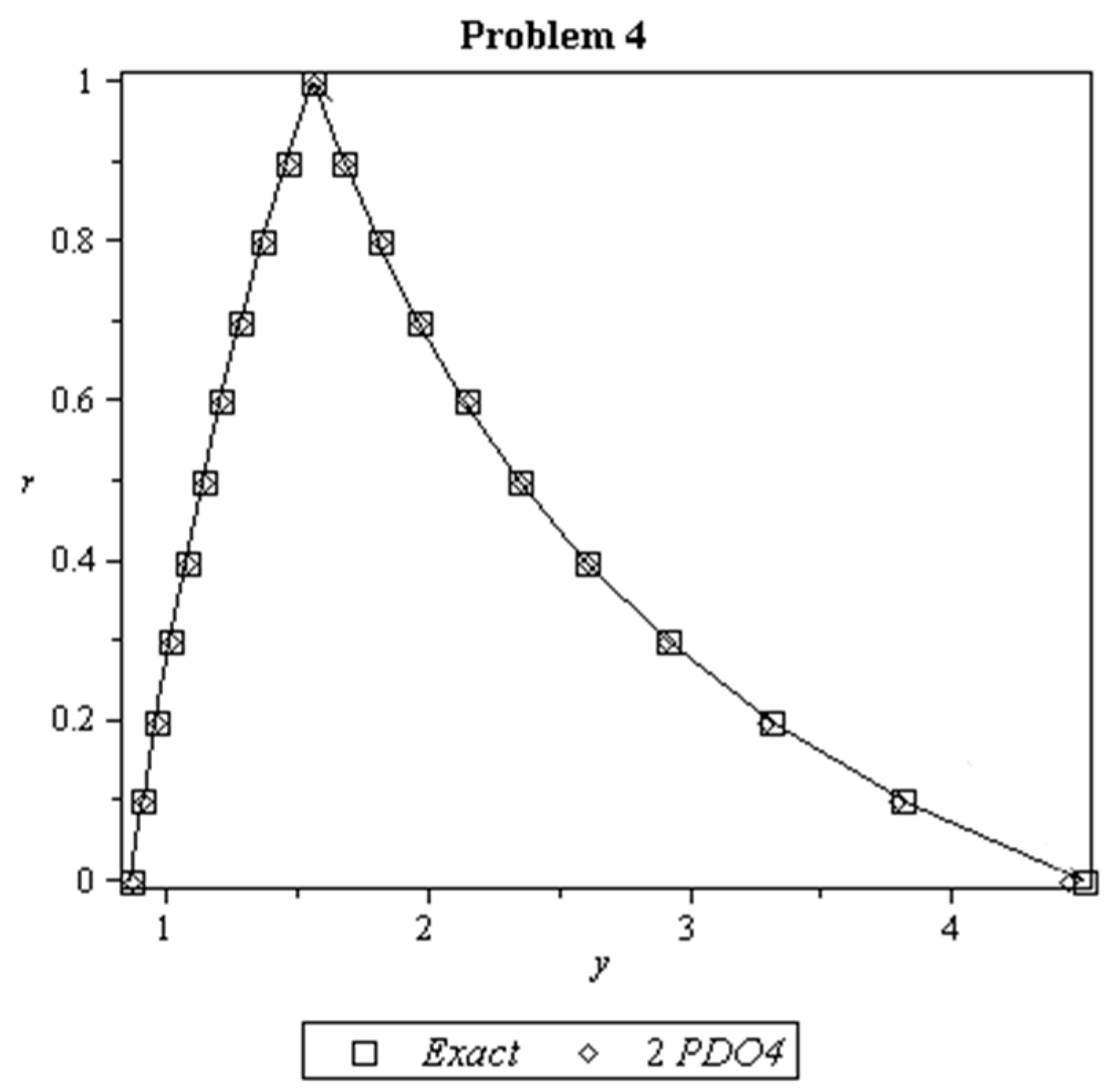
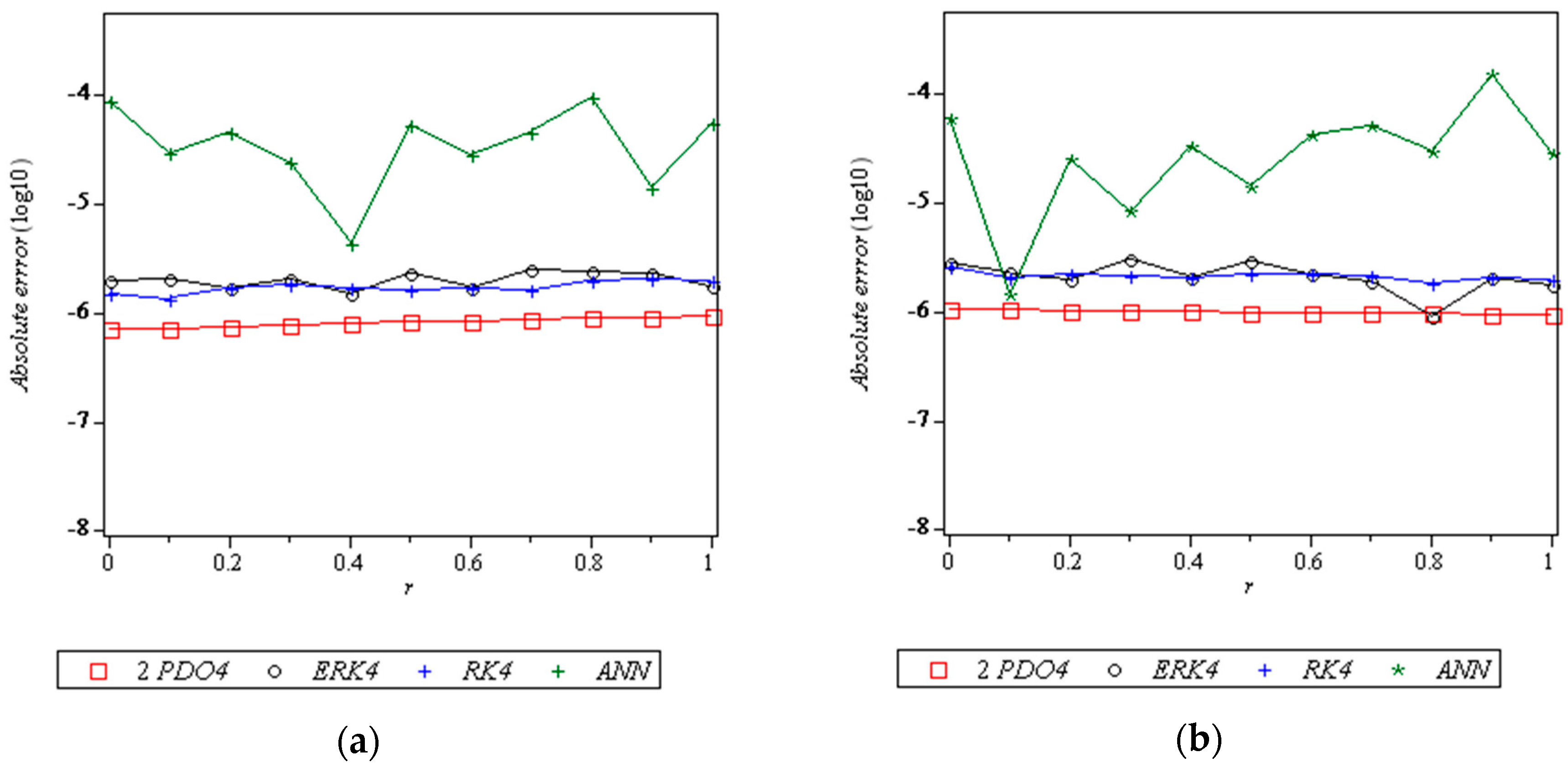
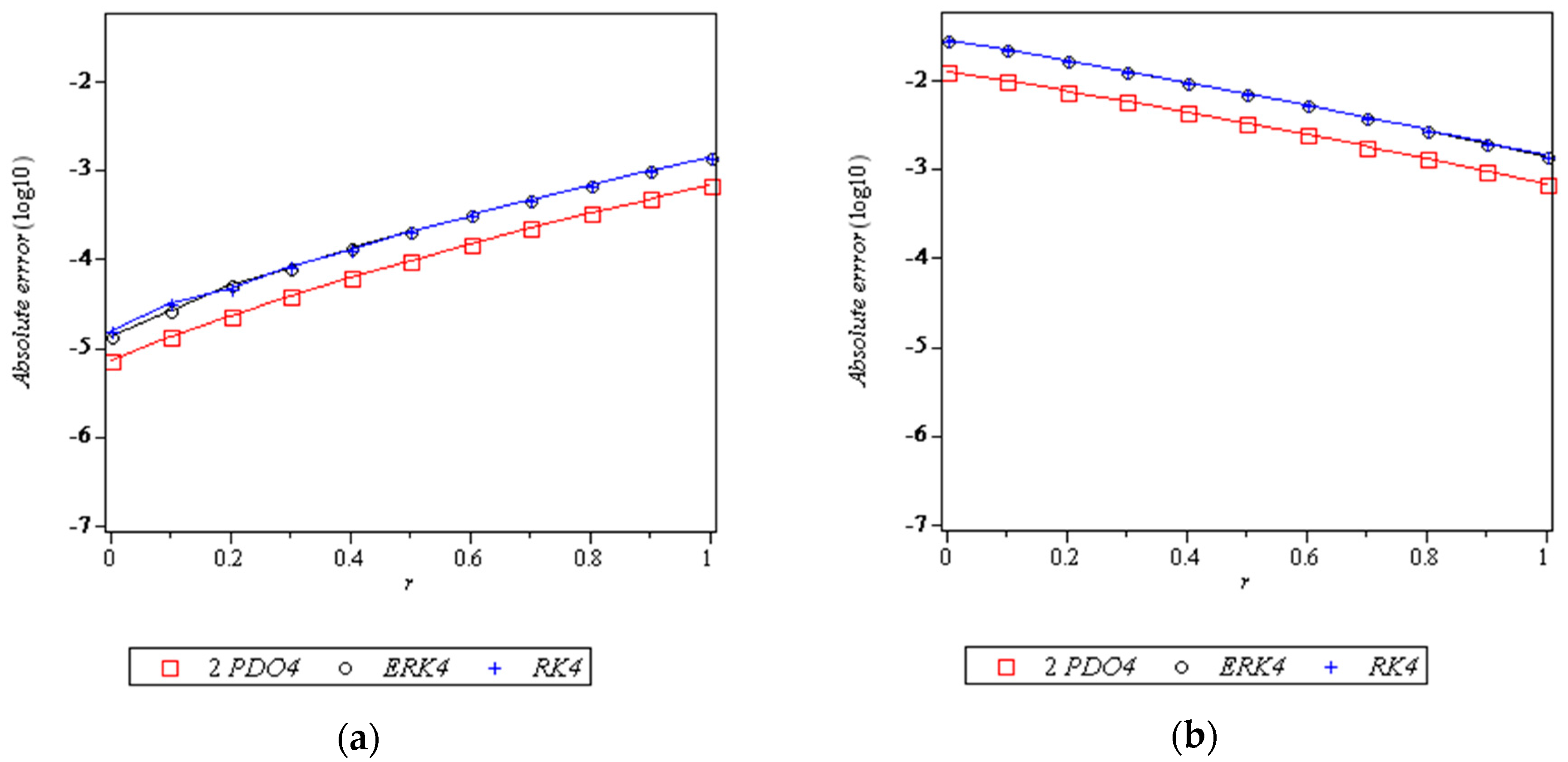
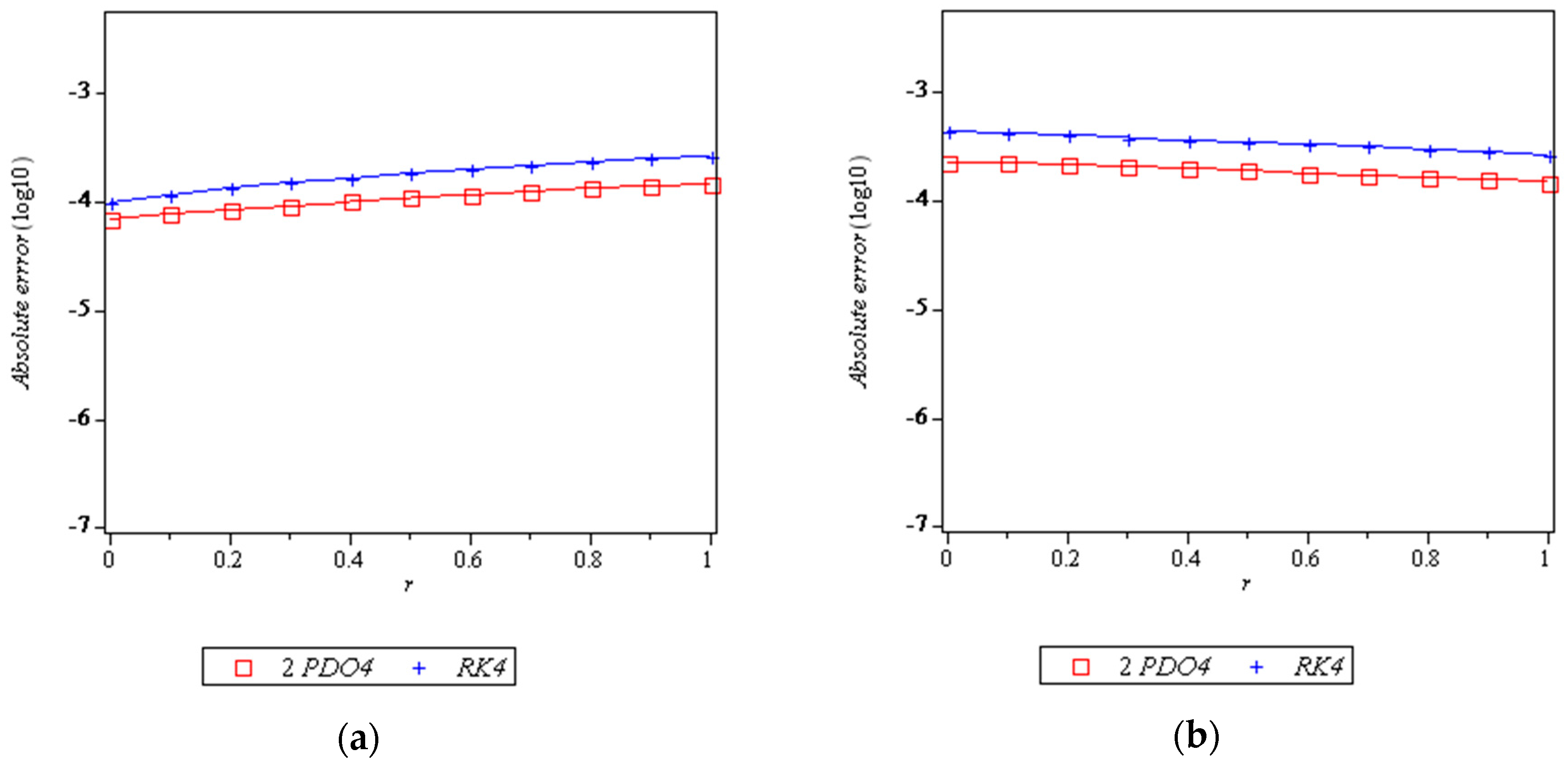
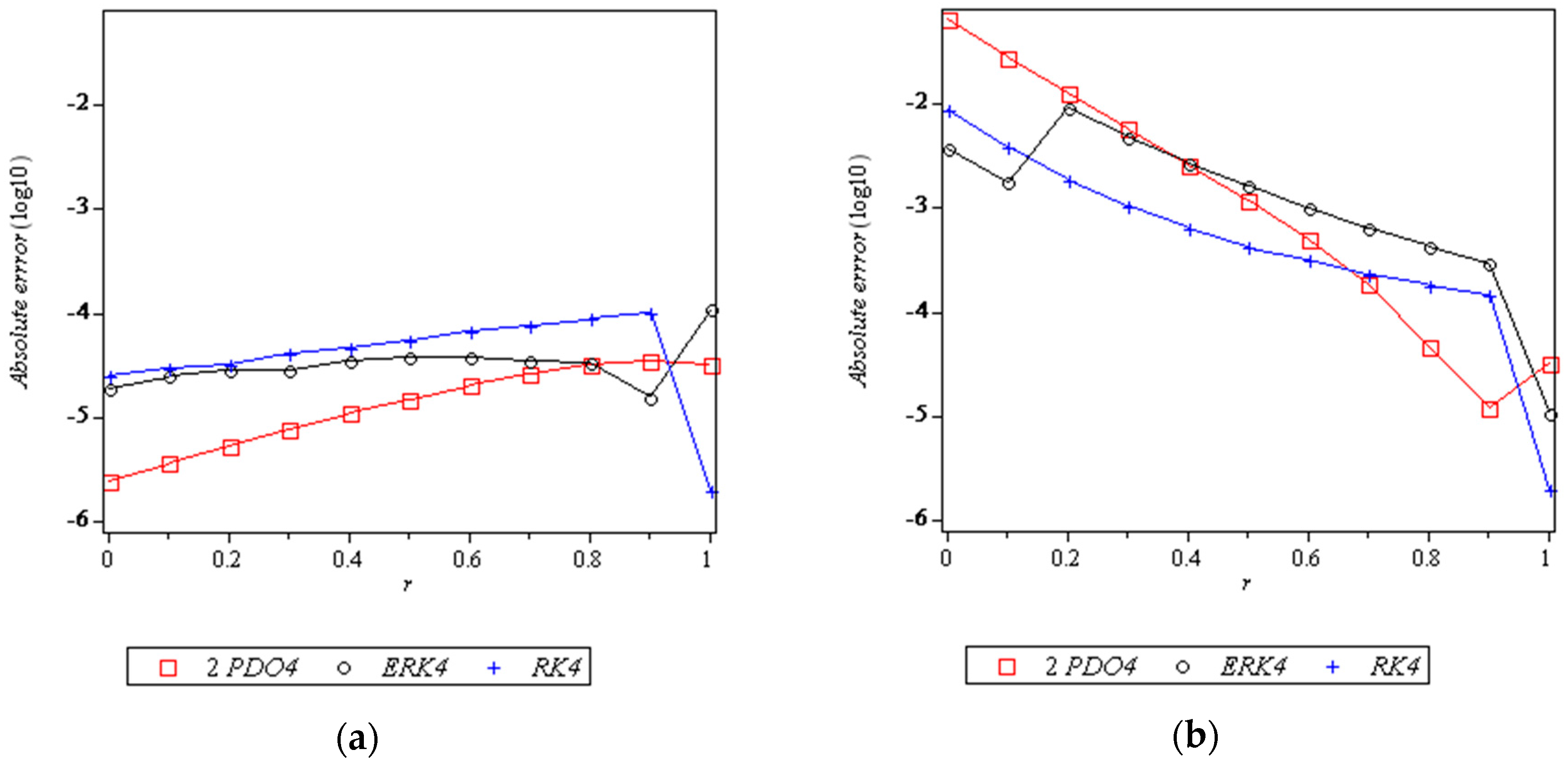
8. Results and Discussion
- : Fuzzy numbers with bounded -level intervals
- : Lower and upper bounded exact solution
- : Lower and upper bounded approximated solution
- FCN: Total function calls
- TS: Total steps taken
- TIME: The execution time taken in seconds
- 2PDO4: 2-point diagonally implicit multistep method of order four
- ERK4: Extended Runge–Kutta-like formulae of order 4 [26]
- RK4: Runge–Kutta method of order 4 [33]
- ANN: Artificial neural network approach [34]
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, H.W.; Chang, N.B. Prediction analysis of solid waste generation based on grey fuzzy dynamic modeling. Resour. Conserv. Recycl. 2000, 29, 1–18. [Google Scholar] [CrossRef]
- Bencsik, A.L.; Bede, B.; Tar, J.K.; Fodor, J. Fuzzy differential equations in modeling of hydraulic differential servo cylinders. In Proceedings of the Third Romanian-Hungarian Joint Symposium on Applied Computational Intelligence (SACI), Timisoara, Romania, 25–26 May 2006. [Google Scholar]
- Guo, M.; Xue, X.; Li, R. Impulsive functional differential inclusions and fuzzy population models. Fuzzy Sets Syst. 2003, 138, 601–615. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, X.; Yu, J. Fuzzy modeling and synchronization of hyperchaotic systems. Chaos Solitons Fractals 2005, 26, 835–843. [Google Scholar] [CrossRef]
- Ding, Z.; Shen, H.; Kandel, A. Performance analysis of service composition based on fuzzy differential equations. IEEE Trans. Fuzzy Syst. 2011, 19, 164–178. [Google Scholar] [CrossRef]
- Chang, S.S.L.; Zadeh, L.A. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 30–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Towards fuzzy differential calculus part 3: Differentiation. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Goetschel, R.; Voxman, W. Elementary fuzzy calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Differential of fuzzy functions. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Kaleva, O. The cauchy problem for fuzzy differential equations. Fuzzy Sets Syst. 1990, 35, 389–396. [Google Scholar] [CrossRef]
- Ma, M.; Friedman, M.; Kandel, A. Numerical solutions of fuzzy differential equations. Fuzzy Sets Syst. 1999, 105, 133–138. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Abbasbandy, S.; Ahmady, N.; Ahmady, E. Improved predictor-corrector method for solving fuzzy initial value problems. Inf. Sci. 2009, 179, 945–955. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ahmady, N.; Ahmady, E. Numerical solution of fuzzy differential equations by predictor-corrector method. Inf. Sci. 2007, 177, 1633–1647. [Google Scholar] [CrossRef]
- Jayakumar, T.; Raja, C.; Muthukumar, T. Numerical solution of fuzzy differential equations by Adams fifth order predictor-corrector method. Intern. J. Math. Trends Technol. 2014, 8, 33–50. [Google Scholar]
- Shang, D.; Guo, X. Adams predictor-corrector systems for solving fuzzy differential equations. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Mehrkanoon, S.; Suleiman, M.; Majid, Z.A. Block method for numerical solution of fuzzy differential equations. Int. Math. Forum 2009, 4, 2269–2280. [Google Scholar]
- Isa, S.; Majid, Z.A. Numerical solution of fuzzy differential equations by multistep block method. In Proceedings of the 7th International Conference on Research and Educations in Mathematics (ICREM7), Kuala Lumpur, Malaysia, 25–27 August 2015; pp. 113–119. [Google Scholar]
- Zawawi, I.S.M.; Ibrahim, Z.B.; Suleiman, M. Diagonally implicit block backward differentiation formulas for solving fuzzy differential equations. AIP Conf. Proc. 2013, 1522, 681–687. [Google Scholar] [CrossRef]
- Ramli, A.; Majid, Z.A. An implicit multistep block method for fuzzy differential equations. In Proceedings of the 7th International Conference on Research and Educations in Mathematics (ICREM7), Kuala Lumpur, Malaysia, 25–27 August 2015; pp. 81–87. [Google Scholar]
- Ramli, A.; Majid, Z.A. Fourth order diagonally implicit multistep block method for solving fuzzy differential equations. Int. J. Pure Appl. Math. 2016, 107, 635–660. [Google Scholar] [CrossRef]
- Fook, T.K.; Ibrahim, Z.B. Two points hybrid block method for solving first order fuzzy differential equations. J. Soft Comput. Appl. 2016, 2016, 45–53. [Google Scholar] [CrossRef]
- Ahmadian, A.; Suleiman, M.; Salahshour, S. An Operational Matrix Based on Legendre Polynomials for Solving Fuzzy Fractional-Order Differential Equations. Abstr. Appl. Anal. 2013. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Salahshour, S. A new approach for solving first order fuzzy differential equation. In Proceedings of the Information Processing and Management of Uncertainty in Knowledge-Based Systems. Applications, Dortmund, Germany, 28 June 28–2 July 2010; pp. 522–531. [Google Scholar]
- Ghazanfari, B.; Shakerami, A. Numerical solutions of fuzzy differential equations by extended Runge-Kutta-like formulae of order 4. Fuzzy Sets Syst. 2012, 189, 74–91. [Google Scholar] [CrossRef]
- Bede, B. Note on Numerical solutions of fuzzy differential equations by predictor-corrector method. Inf. Sci. 2008, 178, 1917–1922. [Google Scholar] [CrossRef]
- Fatunla, S.O. Block methods for second order ODEs. Int. J. Comput. Math. 1991, 41, 55–63. [Google Scholar] [CrossRef]
- Nasir, N.; Ibrahim, Z.B.; Suleiman, M.B.; Othman, K.I. Fifth order two-point block backward differentiation formulas for solving ordinary differential equations. Appl. Math. Sci. 2011, 5, 3505–3519. [Google Scholar]
- Pallingkinis, S.C.; Papageorgiou, G.; Famelis, I.T. Runge-Kutta methods for fuzzy differential equations. Appl. Math. Comput. 2009, 209, 97–105. [Google Scholar] [CrossRef]
- Ghanbari, M. Numerical solution of fuzzy initial value problems under generalized differentiability by HPM. Int. J. Ind. Math. 2009, 1, 19–39. [Google Scholar]
- Dizicheh, A.K.; Salahshour, S.; Ismail, F.B. A note on “Numerical solutions of fuzzy differential equations by extended Runge-Kutta-like formulae of order 4”. Fuzzy Sets Syst. 2013, 233, 96–100. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Allahviranloo, T. Numerical solution of fuzzy differential equation by Runge-Kutta method. Nonlinear Stud. 2004, 11, 117–129. [Google Scholar] [CrossRef]
- Effati, S.; Pakdaman, M. Artificial neural network approach for solving fuzzy differential equations. Inf. Sci. 2010, 180, 1434–1457. [Google Scholar] [CrossRef]
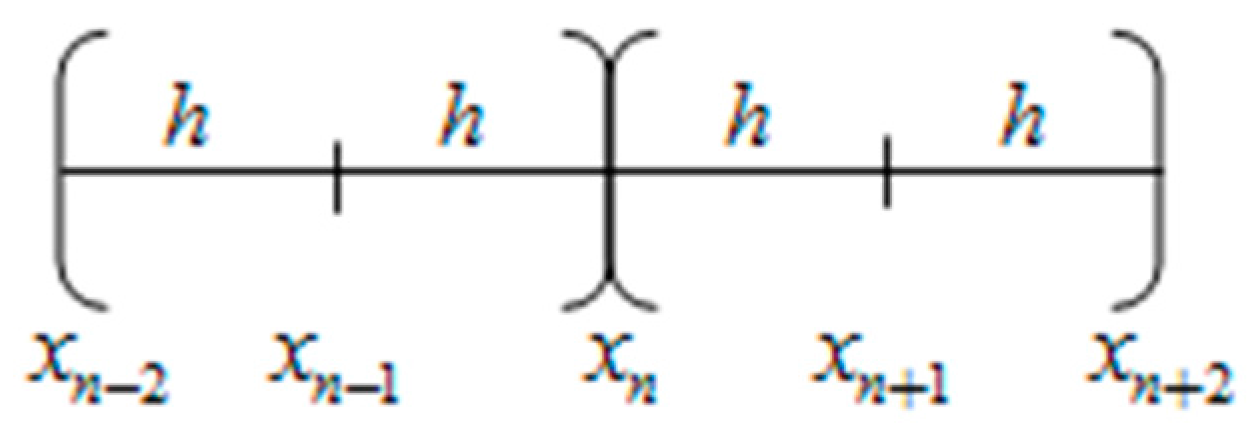

| 2PDO4 | ERK4 1 | RK4 1 | ANN 1 | |
| 0.0 | 7.112242(-7) | 1.969260(-6) | 1.492423(-6) | 8.862866(-5) |
| 0.1 | 7.349317(-7) | 2.090533(-6) | 1.375277(-6) | 2.941706(-5) |
| 0.2 | 7.586392(-7) | 1.734969(-6) | 1.734969(-6) | 4.646277(-5) |
| 0.3 | 7.823466(-7) | 2.094660(-6) | 1.856242(-6) | 2.449152(-5) |
| 0.4 | 8.060541(-7) | 1.500678(-6) | 1.739096(-6) | 4.445810(-6) |
| 0.5 | 8.297616(-7) | 2.337206(-6) | 1.621951(-6) | 5.440010(-5) |
| 0.6 | 8.534691(-7) | 1.743224(-6) | 1.743224(-6) | 2.835439(-5) |
| 0.7 | 8.771765(-7) | 2.579752(-6) | 1.626078(-6) | 4.669132(-5) |
| 0.8 | 9.008840(-7) | 2.462607(-6) | 1.985770(-6) | 9.726296(-5) |
| 0.9 | 9.245915(-7) | 2.345461(-6) | 2.107043(-6) | 1.421725(-5) |
| 1.0 | 9.482990(-7) | 1.751478(-6) | 1.989897(-6) | 5.582846(-5) |
| 2PDO4 | ERK4 1 | RK4 1 | ANN 1 | |
| 0.0 | 1.066836(-6) | 2.834681(-6) | 2.596262(-6) | 5.994298(-5) |
| 0.1 | 1.054983(-6) | 2.297207(-6) | 2.058788(-6) | 1.465839(-6) |
| 0.2 | 1.043129(-6) | 1.998152(-6) | 2.236570(-6) | 2.598870(-5) |
| 0.3 | 1.031275(-6) | 3.129608(-6) | 2.175934(-6) | 8.511551(-6) |
| 0.4 | 1.019421(-6) | 2.115298(-6) | 2.115298(-6) | 3.403441(-5) |
| 0.5 | 1.007568(-6) | 3.008335(-6) | 2.293079(-6) | 1.444274(-5) |
| 0.6 | 9.957139(-7) | 2.232443(-6) | 2.232443(-6) | 4.208012(-5) |
| 0.7 | 9.838602(-7) | 1.933388(-6) | 2.171806(-6) | 5.160297(-5) |
| 0.8 | 9.720064(-7) | 9.190771(-7) | 1.872751(-6) | 3.012583(-5) |
| 0.9 | 9.601527(-7) | 2.050534(-6) | 2.050534(-6) | 1.543513(-4) |
| 1.0 | 9.482990(-7) | 1.751478(-6) | 1.989897(-6) | 2.817154(-5) |
| FCN | 451 | 451 | 451 | - |
| TS | 66 | 110 | 110 | - |
| TIME | 0.675 | - | - | - |
| 2PDO4 | ERK4 1 | RK4 1 | |
| 0.0 | 7.586392(-6) | 1.401183(-5) | 1.591918(-5) |
| 0.1 | 1.366979(-5) | 2.666611(-5) | 3.238815(-5) |
| 0.2 | 2.357892(-5) | 5.232929(-5) | 4.851460(-5) |
| 0.3 | 3.919819(-5) | 8.186697(-5) | 8.377432(-5) |
| 0.4 | 6.313677(-5) | 1.334720(-4) | 1.296573(-4) |
| 0.5 | 9.894536(-5) | 2.104650(-4) | 2.104650(-4) |
| 0.6 | 1.513830(-4) | 3.134706(-4) | 3.134706(-4) |
| 0.7 | 2.267426(-4) | 4.676179(-4) | 4.638032(-4) |
| 0.8 | 3.332447(-4) | 6.934862(-4) | 6.858569(-4) |
| 0.9 | 4.815107(-4) | 9.960255(-4) | 9.960255(-4) |
| 1.0 | 6.851258(-4) | 1.419590(-3) | 1.423405(-3) |
| 2PDO4 | ERK4 1 | RK4 1 | |
| 0.0 | 1.260390(-2) | 2.848404(-2) | 2.849930(-2) |
| 0.1 | 9.798071(-3) | 2.185179(-2) | 2.185179(-2) |
| 0.2 | 7.561266(-3) | 1.664276(-2) | 1.662750(-2) |
| 0.3 | 5.790072(-3) | 1.253006(-2) | 1.257584(-2) |
| 0.4 | 4.397464(-3) | 9.443902(-3) | 9.421014(-3) |
| 0.5 | 3.310672(-3) | 7.054700(-3) | 7.039441(-3) |
| 0.6 | 2.469226(-3) | 5.211172(-3) | 5.211172(-3) |
| 0.7 | 1.823209(-3) | 3.812939(-3) | 3.805309(-3) |
| 0.8 | 1.331682(-3) | 2.773261(-3) | 2.773261(-3) |
| 0.9 | 9.613063(-4) | 1.989020(-3) | 1.996649(-3) |
| 1.0 | 6.851258(-4) | 1.419590(-3) | 1.423405(-3) |
| FCN | 451 | 451 | 451 |
| TS | 66 | 110 | 110 |
| TIME | 0.639 | - | - |
| 2PDO4 | RK4 | |
| 0.0 | 6.963978(-5) | 1.010956(-4) |
| 0.1 | 7.770009(-5) | 1.177814(-4) |
| 0.2 | 8.576039(-5) | 1.344671(-4) |
| 0.3 | 9.382069(-5) | 1.511528(-4) |
| 0.4 | 1.018810(-4) | 1.678386(-4) |
| 0.5 | 1.099413(-4) | 1.845243(-4) |
| 0.6 | 1.180016(-4) | 2.012100(-4) |
| 0.7 | 1.260619(-4) | 2.178957(-4) |
| 0.8 | 1.341222(-4) | 2.345815(-4) |
| 0.9 | 1.421825(-4) | 2.512672(-4) |
| 1.0 | 1.502428(-4) | 2.679529(-4) |
| 2PDO4 | RK4 | |
| 0.0 | 2.308459(-4) | 4.348102(-4) |
| 0.1 | 2.227856(-4) | 4.181245(-4) |
| 0.2 | 2.147253(-4) | 4.014387(-4) |
| 0.3 | 2.066649(-4) | 3.847530(-4) |
| 0.4 | 1.986046(-4) | 3.680673(-4) |
| 0.5 | 1.905443(-4) | 3.513816(-4) |
| 0.6 | 1.824840(-4) | 3.346958(-4) |
| 0.7 | 1.744237(-4) | 3.180101(-4) |
| 0.8 | 1.663634(-4) | 3.013244(-4) |
| 0.9 | 1.583031(-4) | 2.846386(-4) |
| 1.0 | 1.502428(-4) | 2.679529(-4) |
| FCN | 451 | 451 |
| TS | 66 | 110 |
| TIME | 0.530 | 0.718 |
| 2PDO4 | ERK4 1 | RK4 1 | |
| 0.0 | 2.459944(-6) | 1.9100(-5) | 2.6100(-5) |
| 0.1 | 3.707531(-6) | 2.5100(-5) | 3.0000(-5) |
| 0.2 | 5.461503(-6) | 2.9100(-5) | 3.2200(-5) |
| 0.3 | 7.872724(-6) | 2.9000(-5) | 4.2000(-5) |
| 0.4 | 1.110316(-5) | 3.5000(-5) | 4.8000(-5) |
| 0.5 | 1.529207(-5) | 3.8000(-5) | 5.5000(-5) |
| 0.6 | 2.047821(-5) | 3.9000(-5) | 6.8000(-5) |
| 0.7 | 2.643397(-5) | 3.5000(-5) | 7.6000(-5) |
| 0.8 | 3.232537(-5) | 3.4000(-5) | 8.9000(-5) |
| 0.9 | 3.602703(-5) | 1.6000(-5) | 1.0400(-4) |
| 1.0 | 3.275027(-5) | 1.0900(-4) | 2.0000(-6) |
| 2PDO4 | ERK4 1 | RK4 1 | |
| 0.0 | 6.395992(-2) | 3.7712(-2) | 8.7760(-3) |
| 0.1 | 2.778184(-2) | 1.7758(-2) | 3.8480(-3) |
| 0.2 | 1.248250(-2) | 9.0110(-3) | 1.8570(-3) |
| 0.3 | 5.710280(-3) | 4.8090(-3) | 1.0570(-3) |
| 0.4 | 2.616533(-3) | 2.7230(-3) | 6.4900(-4) |
| 0.5 | 1.175996(-3) | 1.6230(-3) | 4.2000(-4) |
| 0.6 | 5.009738(-4) | 9.9600(-4) | 3.1600(-4) |
| 0.7 | 1.875370(-4) | 6.3700(-4) | 2.3300(-4) |
| 0.8 | 4.657100(-5) | 4.3100(-4) | 1.8400(-4) |
| 0.9 | 1.228793(-5) | 2.9100(-4) | 1.5000(-4) |
| 1.0 | 3.275027(-5) | 1.0900(-5) | 2.0000(-6) |
| FCN | 363 | 451 | 451 |
| TS | 66 | 110 | 110 |
| TIME | 0.748 | - | - |
| 2PDO4 | RK4 | |
| 0.0 | 0.795170 | 0.795172 |
| 0.1 | 0.846301 | 0.846303 |
| 0.2 | 0.894275 | 0.894276 |
| 0.3 | 0.940192 | 0.940193 |
| 0.4 | 0.984968 | 0.984969 |
| 0.5 | 1.029399 | 1.029399 |
| 0.6 | 1.074198 | 1.074198 |
| 0.7 | 1.120029 | 1.120029 |
| 0.8 | 1.167520 | 1.167520 |
| 0.9 | 1.217275 | 1.217275 |
| 1.0 | 1.269868 | 1.269868 |
| r | 2PDO4 | RK4 |
| 0.0 | 2.017674 | 2.017674 |
| 0.1 | 1.925744 | 1.925744 |
| 0.2 | 1.836622 | 1.836622 |
| 0.3 | 1.750863 | 1.750863 |
| 0.4 | 1.668972 | 1.668972 |
| 0.5 | 1.591344 | 1.591344 |
| 0.6 | 1.518228 | 1.518228 |
| 0.7 | 1.449698 | 1.449698 |
| 0.8 | 1.385652 | 1.385652 |
| 0.9 | 1.325836 | 1.325836 |
| 1.0 | 1.269868 | 1.269868 |
| FCN | 451 | 451 |
| TS | 66 | 110 |
| TIME | 0.390 | 0.468 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isa, S.; Abdul Majid, Z.; Ismail, F.; Rabiei, F. Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives. Symmetry 2018, 10, 42. https://doi.org/10.3390/sym10020042
Isa S, Abdul Majid Z, Ismail F, Rabiei F. Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives. Symmetry. 2018; 10(2):42. https://doi.org/10.3390/sym10020042
Chicago/Turabian StyleIsa, Syahirbanun, Zanariah Abdul Majid, Fudziah Ismail, and Faranak Rabiei. 2018. "Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives" Symmetry 10, no. 2: 42. https://doi.org/10.3390/sym10020042
APA StyleIsa, S., Abdul Majid, Z., Ismail, F., & Rabiei, F. (2018). Diagonally Implicit Multistep Block Method of Order Four for Solving Fuzzy Differential Equations Using Seikkala Derivatives. Symmetry, 10(2), 42. https://doi.org/10.3390/sym10020042






