Positive Energy Condition and Conservation Laws in Kantowski-Sachs Spacetime via Noether Symmetries

Abstract

In this paper, we have investigated Noether symmetries of the Lagrangian of Kantowski–Sachs spacetime. The associated Lagrangian of the Kantowski–Sachs metric is used to derive the set of determining equations. Solving the determining equations for several values of the metric functions, it is observed that the Kantowski–Sachs spacetime admits the Noether algebra of dimensions 5, 6, 7, 8, 9, and 11. A comparison of the obtained Noether symmetries with Killing and homothetic vectors is also presented. With the help of Noether’s theorem, we have presented the expressions for conservation laws corresponding to all Noether symmetries. It is observed that the positive energy condition is satisfied for most of the obtained metrics.

1. Introduction

Einstein’s field equations (EFEs), $G_{ab}=k{T}_{ab},$ are ten-tensor equations, which describe the gravitational effects produced by a given mass in a spacetime. In these equations, the stress-energy tensor $T_{ab}$ gives the distribution of energy and momentum, k represents the gravitational constant, while $G_{ab}$ expresses the spacetime curvature and is known as the Einstein tensor. Moreover, the Einstein tensor $G_{ab}$ can be expressed as $G_{ab}=R_{ab}-\frac{R}{2}{g}_{ab},$ where $R_{ab}=$ the Ricci tensor, $g_{ab}=$ the metric tensor, and $R=$ the Ricci scalar.

The quantities $R_{ab}$ and R appearing in the EFEs are built up from $g_{ab}$ and its partial derivatives. In this way, the EFEs form a system of partial differential equations. A Lorentz metric $g_{ab}$ is regarded as an exact solution of EFEs if it is obtained by solving the EFEs exactly in closed form and is conformable to a physically realistic $T_{ab}$. Finding the exact solutions of EFEs is not an easy task unless some simplifying assumptions are employed. Therefore, only a few physically meaningful solutions of these equations are found in the literature [1]. Among the approaches followed for obtaining the exact solutions of EFEs, the most popular is to use some symmetry restrictions on the tensor $g_{ab}$. These restrictions are mathematically expressed as ${\mathcal{L}}_X{g}_{ab}=0,$ where X is called a Killing vector (KV) and $\mathcal{L}$ denotes the Lie derivative operator. It is well known that every KV corresponds to a conservation law. A large body of the literature is devoted to the investigation of KVs and corresponding conservation laws in spacetimes [1,2,3].

The symmetries of tensors other than the metric tensor are usually referred to as collineations. Some examples of collineations include curvature collineations (${\mathcal{L}}_X{R}_{bcd}^a=0$), Ricci collineations (${\mathcal{L}}_X{R}_{ab}=0$), and matter collineations (${\mathcal{L}}_X{T}_{ab}=0$). These collineations have also been thoroughly discussed [4,5,6,7,8,9].

Apart from the conventional symmetries defined above, the idea of another type of symmetry, known as Noether symmetry (NS), was given by Emmy Noether [10]. According to Noether’s theorem, if the Lagrangian of a system admits a continuous symmetry, then this symmetry corresponds to a conservation law. Consequently, if a system remains unchanged under time translation and spacial translations and rotations, this theorem yields the conservation of energy and linear and angular momenta.

The study of NS is important due to the fact that it usually provides the additional conservation laws, not given by KVs. If the Killing and Noether algebras are denoted by $K\left(M\right)$ and $N\left(M\right)$, respectively, then $K\left(M\right)\subseteq N\left(M\right)$. The NS have also a close link with homothetic vectors (HVs). In fact, if X is an HV, that is ${\mathcal{L}}_X{g}_{ab}=2\psi g_{ab};$ $\psi$ being a constant, then $X+2\psi u{\partial }_u$ is a Noether symmetry associated with $X$. Here, u is the geodesics parameter of the world line of a point particle moving in a spacetime. Conversely, if $X+2\psi u{\partial }_u$ is an NS, then X is an HV, provided that X is independent of u [11]. A Noether symmetry that is neither a KV, nor associated with an HV is known as a proper Noether symmetry.

NS and their comparison with Killing and homothetic vectors have been studied for some well-known spacetimes. A comparative study of KVs and NS for the conformally-flat Friedmann metric was provided in [12], and it was concluded that this metric admits proper NS. Considering some specific spherically-symmetric metrics, Bokhari et al. [13] conjectured that the NS of the Lagrangian provide additional conservation laws. The NS of some other physically-important spacetimes were examined by different authors. Camci [14] studied the NS of geodesic motion for the geodesic Lagrangian of the metric of G$\ddot{o}$del spacetimes. Camci and Yildirim [15] worked on the NS of the geodesic Lagrangian for some classes of pp-wave spacetimes. Hickman and Yazdan [11] studied NS in Bianchi type II spacetimes. They have shown that the Noether algebra of Bianchi type II spacetimes contain Killing, as well as homothetic vectors. Ali et al. [16,17,18] worked on the classification of different spacetimes via NS including static plane, static spherical, and static cylindrically-symmetric spacetimes. Jamil et al. [19,20] worked on the complete classification of non-static plane and non-static spherically-symmetric spacetimes via NS. Paliathanasis et al. [21] established a relation between the Lie symmetries of the Klein–Gordon equation and conformal Killing vectors of the underlying geometry, where they also stated that the resulting Lie symmetries of the conformal algebra are also NS. Tsamparlis et al. [22] stated that for dynamical system whose equations of motion are of the form ${\ddot{x}}^a+{\Gamma }_{bc}^a{\dot{x}}^b{\dot{x}}^c+f\left(x^a\right);$ $f\left(x^a\right)$ being an arbitrary function of its argument, the computation of Lie and Noether symmetries reduces to the problem of finding the special projective collineations. Recently, the Bianchi type V and non-static plane symmetric spacetimes were completely classified via their NS [23,24].

It is important to mention here that the formulation of conservation laws may not require the Lagrangian of the system. As an example, one can see the work of Ma et al. [25], who have recently established a result giving the direct formulation of conservation laws for differential equations including the heat equation, Burgers’ equation, and the Korteweg–de Vries (KdV) equation, regardless of the existence of a Lagrangian. The same authors also discussed the existence of lump solutions involving free parameters for some nonlinear partial differential equations that present Lie symmetries and that may generate associated conservation laws [26].

The Kantowski–Sachs spacetime describes a spatially-homogeneous and anisotropic universe model that admits an isometry group $G_4$ acting on homogeneous spacelike hypersurfaces. As the Kantowski–Sachs metric is of great interest and there is a great deal of information about this metric scattered throughout the literature, it would be useful to investigate the NS possessed by the Lagrangian of this metric and their relation with Killing and homothetic vectors.

For a physically-realistic spacetime, its energy density, represented by $T_{00},$ must be non-negative. This condition is usually referred to as the positive energy condition. The positive energy condition is important because if one allows both positive and negative energy regions, the empty vacuum may become unstable. In this paper, we classify the Lagrangian of the Kantowski–Sachs metric according to its NS and check the positive energy condition for the obtained models admitting different algebras of NS.

2. Determining Equations

The Kantowski–Sachs metric is given by [27]:

$$d{s}^2=d{t}^2-{\lambda }^2\left(t\right)d{r}^2-v^2\left(t\right)\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right),$$

(1)

where the functions $\lambda \left(t\right)\ne 0$ and $v\left(t\right)\ne 0$ depend on t only. The minimum KVs admitted by the above metric are:

$$\begin{array}{ccc}\hfill X_1& =& {\partial }_r,X_2={\partial }_{\varphi },\hfill \\ \hfill X_3& =& sin\varphi {\partial }_{\theta }+cot\theta cos\varphi {\partial }_{\varphi },\hfill \\ \hfill X_4& =& -cos\varphi {\partial }_{\theta }+cot\theta sin\varphi {\partial }_{\varphi }.\hfill \end{array}$$

(2)

One may use the EFEs with $k=1$ to get the following non-zero components of $T_{ab}.$

$$\begin{array}{ccc}\hfill T_{00}& =& \frac{1}{{\lambda }^3{v}^2}\left(v^{\prime 2}{\lambda }^3+2{\lambda }^{2}v{\lambda }^{\prime }{v}^{\prime }+{\lambda }^3\right),\hfill \\ \hfill T_{11}& =& -\frac{1}{v^2}\left(2v{\lambda }^2{v}^{″}+{\lambda }^2{v}^{\prime 2}+{\lambda }^2\right),\hfill \\ \hfill T_{22}& =& -\frac{v}{{\lambda }^3}\left({\lambda }^3{v}^{″}+{\lambda }^2{v}^{\prime }{\lambda }^{\prime }+v{\lambda }^2{\lambda }^{″}\right),\hfill \\ \hfill T_{33}& =& {sin}^2\theta T_{22},\hfill \end{array}$$

(3)

where the primes on metric functions denote their derivatives with respect to $t.$ The usual Lagrangian L corresponding to the Kantowski–Sachs metric (1) is given by:

$$L={\dot{t}}^2-{\lambda }^2\left(t\right){\dot{r}}^2-v^2\left(t\right)\left({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2\right),$$

(4)

where the dot represents the derivative with respect to the parameter u of the world line of a point particle moving in Kantowski–Sachs spacetime. The Lagrangian for this point particle, given in (4), represents the square of the Lagrangian for the action principle that leads to geodesics by minimizing the spacetime metric $\int ds=\sqrt{g_{ab}\frac{d{x}^a}{du}\frac{d{x}^b}{du}}du$ [28]. It may be noted that the coefficients of the quadratic terms in $\frac{d{x}^{\mu }}{du}\frac{d{x}^{\nu }}{du}$ represent the components of the metric.

A vector field $X=\eta \frac{\partial }{\partial u}+X^i\frac{\partial }{\partial x_i}$ is called an NS if the Lagrangian of a physical system remains invariant under the action of X such that the following condition holds:

$$X^{\left(1\right)}L+L\left(D\eta \right)=DF,$$

(5)

where:

$$X^{\left(1\right)}=X+X_u^i\frac{\partial }{\partial {\dot{x}}_i}$$

(6)

is the first prolongation of X such that $X_u^i=D{X}^i-{\dot{x}}_{i}D\eta$. Here, D denotes the total differential operator, given by:

$$D=\frac{\partial }{\partial u}+{\dot{x}}_i\frac{\partial }{\partial x_i}.$$

(7)

Moreover, $\eta$, $X^i$, and F all depend on the variables $(u,x_i),$ where $x_i=(t\left(u\right),r\left(u\right),\theta \left(u\right),\varphi \left(u\right)).$ The function F is known as the gauge function. Once we find the NS and corresponding gauge function, we can use Noether’s theorem to find the corresponding conservation laws in the following way:

$$I=\eta L+\left(X^i-{\dot{x}}_i\eta \right)\frac{\partial L}{\partial {\dot{x}}_i}-F.$$

(8)

We use the Lagrangian given in Equation (4) in the equation defining the NS, that is Equation (5), to get the following set of 19 equations.

$$\begin{array}{ccc}\hfill F_{,u}={\eta }_{,\varphi }={\eta }_{,\theta }={\eta }_{,r}={\eta }_{,t}& =& 0,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill 2X_{,t}^0& =& {\eta }_{,u},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill 2{\lambda }^{\prime }{X}^0+2\lambda X_{,r}^1& =& \lambda {\eta }_{,u},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill 2v^{\prime }{X}^0+2v{X}_{,\theta }^2& =& v{\eta }_{,u},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill X_{,r}^0-{\lambda }^2{X}_{,t}^1& =& 0,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill X_{,\theta }^0-v^2{X}_{,t}^2& =& 0,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill X_{,\varphi }^0-v^2{sin}^2\theta X_{,t}^3& =& 0,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\lambda }^2{X}_{,\theta }^1+v^2{X}_{,r}^2& =& 0,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\lambda }^2{X}_{,\varphi }^1+v^2{sin}^2\theta X_{,r}^3& =& 0,\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill X_{,\varphi }^2+{sin}^2\theta X_{,\theta }^3& =& 0,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill 2v^{\prime }{X}^0+2vcot\theta X^2+2v{X}_{,\varphi }^3& =& v{\eta }_{,u},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill 2X_{,u}^0& =& F_{,t},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill 2{\lambda }^2{X}_{,u}^1& =& -F_{,r},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill 2v^2{X}_{,u}^2& =& -F_{,\theta },\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill 2v^2{sin}^2\theta X_{,u}^3& =& -F_{,\varphi }.\hfill \end{array}$$

(23)

The solution of the above system of equations would give the values of the components of the vector field generating NS and the metric functions $\lambda$ and $v.$ Consequently, the corresponding Kantowski–Sachs metrics may represent the exact solutions of EFEs. We omit writing the basic calculations and present the list of metrics, their NS, Lie algebras, and the corresponding conservation laws of all symmetries in the forthcoming sections. The bounds for the positive energy condition and the singularity of the Ricci scalar are also discussed for all the obtained metrics.

3. Five Noether Symmetries

The minimal set of NS admitted by the Lagrangian of the Kantowski–Sachs metric is:

$$\begin{array}{ccc}\hfill X_0& =& {\partial }_u,X_1={\partial }_r,X_2={\partial }_{\varphi },\hfill \\ \hfill X_3& =& sin\varphi {\partial }_{\theta }+cot\theta cos\varphi {\partial }_{\varphi },\hfill \\ \hfill X_4& =& -cos\varphi {\partial }_{\theta }+cot\theta sin\varphi {\partial }_{\varphi }.\hfill \end{array}$$

(24)

Out of these five NS, four are the basic KVs of the Kantowski–Sachs metric and $X_0$ is the symmetry corresponding to the Lagrangian. Here, $X_0$ represents the translation of geodesics parameter u and $X_1$ is the translation of spatial coordinate $r.$ The generators $X_2,X_3$ and $X_4$ form a Lie subalgebra for the rotation group $SO\left(3\right).$ The values of the Kantowski–Sachs metric functions for which the corresponding Lagrangian admit the above minimal NS are given in the following Table 1:

Table 1. Exact form of metrics admitting five Noether symmetries (NS).

No.	$\mathit{\lambda }\mathbf{\left(}\mathit{t}\mathbf{\right)}$	$\mathit{v}\mathbf{\left(}\mathit{t}\mathbf{\right)}$
3a	${\lambda }^{\prime }\ne 0$	$v^{″}\ne 0$ and $v\ne cosht$
3b	$\lambda \ne sinht$	$v=cosht$
3c	${\left(\lambda {\lambda }^{\prime }\right)}^{″}\ne 0$	$v=$ const. $=\xi$
3d	$\lambda =\sqrt{a{t}^2+2bt+c}$; $a\ne 0$,	$v=$ const. $=\xi$
3e	$\lambda =\sqrt{2bt+c}$	$v=$ const. $=\xi$

The corresponding Lie algebra for generators given in Equation (24) is:

$$[X_3,X_2]=X_4, [X_2,X_4]=X_3, [X_4,X_3]=X_2, [X_i,X_j]=0, \mathrm{otherwise}.$$

Using Equation (8), the conserved forms of these NS become:

$$\begin{array}{ccc}\hfill I_0& =& -{\dot{t}}^2+{\lambda }^2\left(t\right){\dot{r}}^2+v^2\left(t\right){\dot{\theta }}^2+v^2\left(t\right){sin}^2\theta {\dot{\varphi }}^2,\hfill \\ \hfill I_1& =& -2{\lambda }^2\left(t\right){\dot{r}}^2,\hfill \\ \hfill I_2& =& -2v^2\left(t\right){sin}^2\theta \dot{\varphi },\hfill \\ \hfill I_3& =& -2v^2\left(t\right)\left(sin\varphi \dot{\theta }+cos\theta cos\varphi sin\theta \dot{\varphi }\right),\hfill \\ \hfill I_4& =& -\frac{\partial I_3}{\partial \varphi }.\hfill \end{array}$$

(25)

The energy density and the Ricci scalar for Models 3a and 3b are obtained as $T_{00}=\frac{1+v^{\prime 2}}{v^2}+\frac{2{\lambda }^{\prime }{v}^{\prime }}{v\lambda }$ and $R=-\frac{2}{v^2\lambda }\left(2v\lambda v^{″}+v^2{\lambda }^{″}+2v{v}^{\prime }{\lambda }^{\prime }+\lambda v^{\prime 2}+\lambda \right).$ One can observe that the positive energy condition is satisfied if $\frac{{\lambda }^{\prime }}{\lambda }$ and $\frac{v^{\prime }}{v}$ have the same signs. Moreover, the Ricci scalar remains non-singular for $t\to 0$.

For the remaining three models, the energy density and the Ricci scalar are given by:

$$T_{00}=\frac{1}{{\xi }^2},R=-2\left(\frac{{\lambda }^{″}}{\lambda }+\frac{1}{{\xi }^2}\right),$$

(26)

such that the energy remains positive for any arbitrary non-zero $\xi$ and the Ricci scalar is regular for any function $\lambda$.

4. Six Noether Symmetries

The Lagrangian of the following Kantowski–Sachs metric admits six NS:

$$d{s}^2=d{t}^2-{\gamma }^{2}d{r}^2-v^2\left(t\right)\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right),$$

(27)

where $\gamma$ is a non-zero constant, $v^{″}\ne 0$ and $v\ne cosht$. Out of these six NS, five are the same as given in Equation (24) and one extra Noether symmetry is given by:

$$X_5=\frac{u}{{\gamma }^2}{\partial }_r,F=-2r.$$

The conserved form for this symmetry is $I_5=-2(u\dot{r}-r)$. The corresponding non-zero commutator is $[X_0,X_5]=\frac{1}{{\gamma }^2}{X}_1$.

The metric (27) is non-conformally flat, and its energy density is obtained as $T_{00}=\frac{1+v^{\prime 2}}{v^2},$ which is always positive. The Ricci scalar is given by $R=-\frac{2}{v^2}\left(1+v^{\prime 2}+2v{v}^{″}\right)$, which has no singularity at the origin.

5. Seven Noether Symmetries

There are seven metrics whose Lagrangian admit a seven-dimensional algebra of NS. Table 2 contains all these metrics along with the two extra NS, other than the minimal NS given in (24), their Lie algebra, and the corresponding conserved quantities.

Table 2. Metrics admitting seven Noether symmetries.

No.	$\mathit{\lambda }\mathbf{\left(}\mathit{t}\mathbf{\right)}$	$\mathit{\nu }\mathbf{\left(}\mathit{t}\mathbf{\right)}$	Noether Symmetries	Invariants	Lie Algebra
7(i)	$sin\left(\beta t\right)$; $\beta \ne 0$	$\gamma \ne 0$	$X_5=cosh\left(\beta r\right){\partial }_t-cot\left(\beta t\right)sinh\left(\beta r\right){\partial }_r$	$I_5=2cosh\left(\beta r\right)\dot{t}+2cos\left(\beta t\right)sin\left(\beta t\right)sinh\left(\beta r\right)\dot{r}$	$[X_1,X_5]=\beta X_6$, $[X_1,X_6]=\beta X_5$,
			$X_6=sinh\left(\beta r\right){\partial }_t-cot\left(\beta t\right)cosh\left(\beta r\right){\partial }_r$	$I_6=\frac{1}{\beta }\frac{\partial I_5}{\partial r}$	$[X_6,X_5]=\beta X_1$.
7(ii)	$cos\left(\beta t\right)$	$\gamma \ne 0$	$X_5=cosh\left(\beta r\right){\partial }_t+tan\left(\beta t\right)sinh\left(\beta r\right){\partial }_r$	$I_5=2cosh\left(\beta r\right)\dot{t}-2cos\left(\beta t\right)sin\left(\beta t\right)sinh\left(\beta r\right)\dot{r}$	Same as in case 7(i)
			$X_6=sinh\left(\beta r\right){\partial }_t+tan\left(\beta t\right)cosh\left(\beta r\right){\partial }_r$	$I_6=\frac{1}{\beta }\frac{\partial I_5}{\partial r}$
7(iii)	$sinh\left(\beta t\right)$; $\beta \ne 0$	$\gamma \ne 0$	$X_5=cosh\left(\beta r\right){\partial }_t-coth\left(\beta t\right)sinh\left(\beta r\right){\partial }_r$	$I_5=2cosh\left(\beta r\right)\dot{t}+2cosh\left(\beta t\right)sinh\left(\beta t\right)sinh\left(\beta r\right)\dot{r}$	Same as in case 7(i)
			$X_6=sinh\left(\beta r\right){\partial }_t-coth\left(\beta t\right)cosh\left(\beta r\right){\partial }_r$	$I_6=\frac{1}{k}\frac{\partial I_5}{\partial r}$
7(iv)	$cosh\left(\beta t\right)$	$\gamma \ne 0$	$X_5=cos\left(\beta r\right){\partial }_t-tanh\left(\beta t\right)sin\left(\beta r\right){\partial }_r$	$I_5=2cos\left(\beta r\right)\dot{t}+2cosh\left(\beta t\right)sinh\left(\beta t\right)sin\left(\beta r\right)\dot{r}$	Same as in case 7(i)
			$X_6=sin\left(\beta r\right){\partial }_t+tanh\left(\beta t\right)cos\left(\beta r\right){\partial }_r$	$I_6=\frac{1}{\beta }\frac{\partial I_5}{\partial r}$
7(v)	$e^{\beta t}$	$\gamma \ne 0$	$X_5={\partial }_t-\beta r{\partial }_r$	$I_5=2\dot{t}+2\beta r{e}^{2\beta t}\dot{r}$	$[X_5,X_1]=\beta X_1$, $[X_1,X_6]=X_5$,
			$X_6=r{\partial }_t-\frac{e^{-2\beta t}}{2\beta }{\partial }_r-\frac{\beta r^2}{2}{\partial }_r$	$I_6=2r\dot{t}+\frac{\dot{r}}{\beta }+\beta r^2{e}^{2\beta t}\dot{r}$	$[X_6,X_5]=\beta X_6$
7(vi)	$c_{1}t+c_2$	$\nu =\lambda$	$X_5=\frac{u^2}{2}{\partial }_s+\frac{u(c_{1}t+c_2)}{2c_1}{\partial }_t$; $F=\frac{t(c_{1}t+2c_2)}{2c_1}$	$I_5=\frac{u^2}{2}L+\frac{u(c_{1}t+c_2)\dot{t}}{c_1}-\frac{t^2}{2}-\frac{c_{2}t}{c_1}$	$[X_0,X_5]=X_6$, $[X_0,X_6]=X_0$,
			$V_6=u{\partial }_u+\frac{c_{1}t+c_2}{2c_1}{\partial }_t$	$I_6=uL+\frac{(c_{1}t+c_2)\dot{t}}{c_1}$	$[X_6,X_5]=X_5.$
7(vii)	${(c_{1}t+c_2)}^{\frac{\alpha -2\beta }{\alpha }}$;	$c_{1}t+c_2$	$X_5=u{\partial }_u+\frac{c_{1}t+c_2}{2c_1}{\partial }_t$	$I_5=uL+\frac{(c_{1}t+c_2)\dot{t}}{c_1}$	$[X_0,X_5]=X_0$, $[X_1,X_6]=X_1$,
	$\alpha \ne 0$		$X_6=r{\partial }_r$	$I_6=-2r{(c_{1}t+c_2)}^{\frac{2(\alpha -2\beta )}{\alpha }}\dot{r}$	$[X_6,X_1]=X_5$

The metric 7(i) is non-conformally flat, whose NS other than the minimal set of NS are KVs. Here, the generators $X_1,X_5$ and $X_6$ form a Lie algebra for the rotation group $SO\left(3\right)$.

Similarly, the metric 7(ii) is non-conformally flat, and it admits seven NS, five of which are the same as given in (24), and the remaining two are KVs, represented by $X_5$ and $X_6.$

The energy density and the Ricci scalar for the models 7(i) and 7(ii) are obtained as $T_{00}=\frac{1}{{\gamma }^2}$ and $R=2\left({\beta }^2-\frac{1}{{\gamma }^2}\right).$ The positive energy condition clearly holds, and the spacetimes remain regular at the origin, as the Ricci scalar is constant.

The non-conformally-flat metric 7(iii) admits five NS as given in (24) along with two extra KVs, which are represented by $X_5$ and $X_6.$

The Weyl tensor for the metric 7(iv) has non-zero components, and hence, it is non-conformally flat. This metric possesses seven NS, out of which five are the same as given in (24) and the extra two are KVs.

The metric 7(v) is non-conformally flat, which admits two extra NS $X_5$ and $X_6$, which are KVs.

The energy density $T_{00}$ and the Ricci scalar R for the models 7(iii), 7(iv), and 7(v) are:

$$T_{00}=\frac{1}{{\gamma }^2},R=-2\left({\beta }^2+\frac{1}{{\gamma }^2}\right),$$

(28)

such that the positive energy condition is satisfied and the Ricci scalar is non-singular at the origin.

There exist two extra NS other than the minimal set of five NS for the non-conformally-flat metric 7(vi). The Noether symmetry $X_6$ corresponds to a homothetic vector $\frac{c_{1}t+c_2}{2c_1}{\partial }_t,$ with the homothetic constant $\psi =\frac{1}{2}.$ For this model, the energy density and the Ricci scalar become:

$$T_{00}=\frac{1+3c_1^2}{{(c_{1}t+c_2)}^2},R=-\frac{2(3c_1^2+1)}{{(c_{1}t+c_2)}^2}.$$

(29)

For any non-zero values of $c_1$ and $c_2$, the energy density is positive and the Ricci scalar remains non-singular at $t\to 0.$

Finally, the metric 7(vii) is non-conformally flat, which admits the minimal set of five NS along with two extra NS $X_5$ and $X_6.$ Here, $X_6$ is a KV, and $X_5$ corresponds to a homothetic vector $\frac{c_{1}t+c_2}{2c_1}{\partial }_t,$ with the homothetic constant $\psi =\frac{1}{2}.$ The energy density and Ricci scalar for this metric are given as:

$$T_{00}=\frac{\alpha +3c_1^2\alpha -4c_1^2\beta }{\alpha {(c_{1}t+c_2)}^2},R=-\frac{2(3c_1^2{\alpha }^2-6c_1^2\alpha \beta +4c_1^2{\beta }^2+{\alpha }^2)}{{\alpha }^2{(c_{1}t+c_2)}^2}.$$

(30)

For $c_2\ne 0,$ the Ricci scalar has no singularity when $t\to 0.$ The energy density may vary for different values of the constants involved in $T_{00}$. The following two graphs in Figure 1 show positive and negative energy density for some particular choices of the values of these constants.

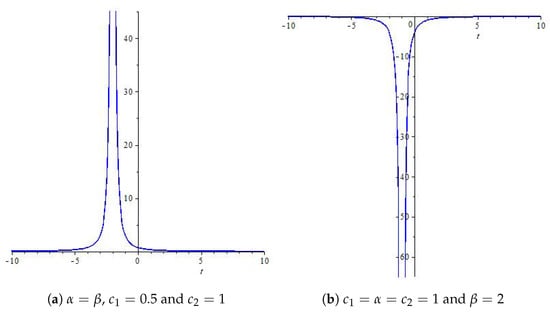
Figure 1. Graphs of $T_{00}$.

As far as the case in which the positive energy condition is not met, it could represent an accelerated phase of expansion that may possibly be attributed to the dark energy.

6. Eight Noether Symmetries

The following is only one Kantowski–Sachs metric whose Lagrangian admits eight NS:

$$d{s}^2=d{t}^2-{\gamma }^{2}d{r}^2-{(\alpha t+\beta )}^2\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right),$$

(31)

where $\alpha \ne 0$ and $\gamma \ne 0.$ The Weyl tensor for the above metric has non-vanishing components, and it is non-conformally flat. The set of eight NS for this metric contains the set of minimal five NS, given in (24), and the remaining three symmetries are:

$$\begin{array}{ccc}\hfill X_5& =& \frac{u^2}{2}{\partial }_u+\frac{u(\alpha t+\beta )}{2\alpha }{\partial }_t+\frac{ur}{2}{\partial }_r;F=\frac{t^2}{2}+\frac{\beta t}{\alpha }-\frac{r^2{\gamma }^2}{2},\hfill \\ \hfill X_6& =& \frac{u}{{\gamma }^2}{\partial }_r;F=-2r,\hfill \\ \hfill X_7& =& u{\partial }_u+\frac{\alpha t+\beta }{2\alpha }{\partial }_t+\frac{r}{2}{\partial }_r.\hfill \end{array}$$

(32)

Out of the above three NS, $X_7$ corresponds to a homothetic vector, given by $\frac{\alpha t+\beta }{2\alpha }{\partial }_t+\frac{r}{2}{\partial }_r.$ The conserved form for these symmetries and Lie algebra are listed below:

$$\begin{array}{ccc}\hfill I_5& =& \frac{u^2}{2}\left(-{\dot{t}}^2+{\gamma }^2{\dot{r}}^2+{(\alpha t+\beta )}^2({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2)\right)+\frac{u(\alpha t+\beta )\dot{t}}{\alpha }-ur{\gamma }^2\dot{r}-\frac{t^2}{2}-\frac{\beta t}{\alpha }+\frac{r^2{\gamma }^2}{2},\hfill \\ \hfill I_6& =& -2u\dot{r}+2r,\hfill \\ \hfill I_7& =& u\left(-{\dot{t}}^2+{\gamma }^2{\dot{r}}^2+{(\alpha t+\beta )}^2({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2)\right)+\frac{(\alpha t+\beta )\dot{t}}{\alpha }-r{\gamma }^2\dot{r}.\hfill \end{array}$$

(33)

$$\begin{array}{c}[X_0,X_5]=X_7, [X_0,X_7]=X_0, [X_0,X_6]=\frac{1}{{\gamma }^2}{X}_1, [X_1,X_5]=\frac{{\gamma }^2}{2}{X}_6,\\ [X_1,X_7]=\frac{1}{2}{X}_1, [X_7,X_5]=X_7, [X_7,X_6]=\frac{1}{2}{X}_6.\end{array}$$

The energy density and the Ricci scalar for Model (31) are respectively given by $T_{00}=\frac{1+{\alpha }^2}{{(\alpha t+\beta )}^2}$ and $R=-\frac{2}{{(\alpha t+\beta )}^2}.$ Here, the positive energy condition holds, and for $t\to 0$, the scalar R remains regular if $\beta \ne 0$.

7. Nine Noether Symmetries

Here, we present some Kantowski–Sachs metrics, whose Lagrangian admits nine NS.

$$\left(1\right).d{s}^2=d{t}^2-{\beta }^{2}d{r}^2-{cosh}^{2}t\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right),$$

(34)

where $\beta \ne 0.$ The Weyl tensor for the above metric vanishes, and hence, it is conformally flat. The set of NS for this metric contains the minimal set of five symmetries given in (24), and four extra NS are admitted, which are listed below:

$$\begin{array}{ccc}\hfill X_5& =& u{\partial }_r;F=-2r,\hfill \\ \hfill X_6& =& sin\theta sin\varphi {\partial }_t+tanhtcos\theta sin\varphi {\partial }_{\theta }+csc\theta tanhtcos\varphi {\partial }_{\varphi },\hfill \\ \hfill X_7& =& -sin\theta cos\varphi {\partial }_t-tanhtcos\theta cos\varphi {\partial }_{\theta }+csc\theta tanhtsin\varphi {\partial }_{\varphi },\hfill \\ \hfill X_8& =& -cos\theta {\partial }_t+tanhtsin\theta {\partial }_{\theta }.\hfill \end{array}$$

(35)

Here, $X_6,X_7$, and $X_8$ are KVs, while $X_5$ is a non-trivial Noether symmetry. The Lie algebra in this case gives:

$$\begin{array}{c}[X_0,X_5]=X_1, [X_6,X_2]=[X_4,X_8]=X_7, [X_2,X_7]=[X_3,X_8]=X_6,\\ [X_6,X_3]=[X_7,X_4]=X_8, [X_6,X_7]=X_2, [X_6,X_8]=X_3, [X_7,X_8]=X_4\end{array}$$

and the conservation laws are:

$$\begin{array}{ccc}\hfill I_5& =& -2(u{\beta }^2\dot{r}-r),\hfill \\ \hfill I_6& =& 2sin\theta sin\varphi \dot{t}-2sinhtcosht(cos\theta sin\varphi \dot{\theta }+sin\theta cos\varphi \dot{\varphi }),\hfill \\ \hfill I_7& =& -2sin\theta cos\varphi \dot{t}+2sinhtcosht(cos\theta cos\varphi \dot{\theta }-sin\theta sin\varphi \dot{\varphi }),\hfill \\ \hfill I_8& =& -2cos\theta \dot{t}-2sinhtcoshtsin\theta \dot{\theta }.\hfill \end{array}$$

(36)

The energy density and Ricci scalar for the metric (34) are respectively given by $T_{00}=1$ and $R=-6,$ such that the positive energy condition is satisfied and R is regular at the origin.

$$\left(2\right).d{s}^2=d{t}^2-{\alpha }^{2}d{r}^2-{\beta }^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(37)

where $\alpha \ne 0$ and $\beta \ne 0.$ For the above metric, the Weyl tensor has non-zero components. The extra four NS other than the minimal set of NS, given in (24), for this metric are:

$$\begin{array}{ccc}\hfill X_5& =& {\partial }_t,\hfill \\ \hfill X_6& =& -u{\partial }_t;F=-2t,\hfill \\ \hfill X_7& =& \frac{u}{{\alpha }^2}{\partial }_r;F=-2r,\hfill \\ \hfill X_8& =& r{\partial }_t+\frac{t}{{\alpha }^2}{\partial }_r.\hfill \end{array}$$

(38)

Here, $X_5$ and $X_8$ are KVs, while $X_6$ and $X_7$ are non-trivial NS. The Lie algebra and the conserved quantities are given as:

$$\begin{array}{ccc}\hfill [X_6,X_0]=& [X_8,X_1]=X_5, [X_0,X_7]=& [X_5,X_8]=\frac{1}{{\alpha }^2}{X}_1,\hfill \\ & [X_8,X_6]=X_7, [X_8,X_7]=& \frac{1}{{\alpha }^2}{X}_6\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_5& =& 2\dot{t},I_6=-2u\dot{t}+2t,I_7=-2u\dot{r}+2r,\hfill \\ \hfill I_8& =& 2r\dot{t}-2t\dot{r}.\hfill \end{array}$$

(39)

The corresponding $T_{00}$ and R for the above metric are given by $T_{00}=\frac{1}{{\beta }^2}$ and $R=-\frac{2}{{\beta }^2}$. Clearly, the energy density is positive for any value of $\beta$, and the Ricci scalar is regular at the origin.

$$\left(3\right).d{s}^2=d{t}^2-{(\alpha t+\beta )}^{2}d{r}^2-{\xi }^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(40)

where $\xi \ne 0.$ The above metric is non-conformally flat, and it admits the following four NS along with five minimal symmetries, given in Equation (24).

$$\begin{array}{ccc}\hfill X_5& =& -ucosh\left(\alpha r\right){\partial }_t+\frac{u}{\alpha t+\beta }sinh\left(\alpha r\right){\partial }_r;F=-\frac{2\beta }{\alpha }cosh\left(\alpha r\right),\hfill \\ \hfill X_6& =& -usinh\left(\alpha r\right){\partial }_t+\frac{u}{\alpha t+\beta }cosh\left(\alpha r\right){\partial }_r;F=-\frac{2\beta }{\alpha }sinh\left(\alpha r\right),\hfill \\ \hfill X_7& =& cosh\left(\alpha r\right){\partial }_t-\frac{sinh\left(\alpha r\right)}{\alpha t+\beta }{\partial }_r,\hfill \\ \hfill X_8& =& sinh\left(\alpha r\right){\partial }_t-\frac{cosh\left(\alpha r\right)}{\alpha t+\beta }{\partial }_r.\hfill \end{array}$$

(41)

From the above, one can see that $X_5$ and $X_6$ are non-trivial NS, while $X_7$ and $X_8$ are KVs. In this case, the Lie algebra becomes:

$$\begin{array}{c}[X_5,X_0]=X_7, [X_6,X_0]=X_8, [X_1,X_5]=\alpha X_6,\\ [X_1,X_6]=\alpha X_5, [X_1,X_7]=\alpha X_8, [X_1,X_8]=\alpha X_7.\end{array}$$

The conserved forms of the symmetries are given as follows:

$$\begin{array}{ccc}\hfill I_5& =& -2u\left(cosh\left(\alpha r\right)\dot{t}+(\alpha t+\beta )sinh\left(\alpha r\right)\dot{r}\right)+\frac{2\beta }{\alpha }cosh\left(\alpha r\right),\hfill \\ \hfill I_6& =& \frac{1}{\alpha }\frac{\partial I_5}{\partial r},\hfill \\ \hfill I_7& =& 2\left(cosh\left(\alpha r\right)\dot{t}+(\alpha t+\beta )sinh\left(\alpha r\right)\dot{r}\right),\hfill \\ \hfill I_8& =& \frac{1}{\alpha }\frac{\partial I_7}{\partial r}.\hfill \end{array}$$

(42)

For the above model, we have $T_{00}=\frac{1}{{\xi }^2}$ and $R=-\frac{2}{{\xi }^2}$ such that the energy density is positive and the Ricci scalar has no singularity at the origin.

8. Eleven Noether Symmetries

For $\lambda =sinht$ and $v=cosht,$ we have the following Kantowski–Sachs metric, whose Lagrangian admits eleven NS:

$$d{s}^2=d{t}^2-{sinh}^{2}td{r}^2-{cosh}^{2}t(d{\theta }^2+{sin}^2\theta d{\varphi }^2).$$

(43)

This metric has a zero Weyl tensor, and hence, it is conformally flat. The energy density and the Ricci scalar for the above model are obtained as $T_{00}=3$ and $R=-12.$ Here, the positive energy condition is clearly satisfied, and R is non-singular at the origin. The extra six NS (KVs) for the above metric are as follows:

$$\begin{array}{ccc}\hfill X_5& =& sin\theta sin\varphi (sinhr{\partial }_t-cothtcoshr{\partial }_r)+tanhtsinhr(cos\theta sin\varphi {\partial }_{\theta }+csc\theta cos\varphi {\partial }_{\varphi }),\hfill \\ \hfill X_6& =& \mathrm{same}\mathrm{as}{X}_5\mathrm{with}sinhr\leftrightarrow coshr\hfill \\ \hfill X_7& =& -sin\theta cos\varphi (sinhr{\partial }_t-cothtcoshr{\partial }_r)-tanhtsinhr(cos\theta cos\varphi {\partial }_{\theta }-csc\theta sin\varphi {\partial }_{\varphi }),\hfill \\ \hfill X_8& =& \mathrm{same}\mathrm{as}{X}_7\mathrm{with}sinhr\leftrightarrow coshr\hfill \\ \hfill X_9& =& -cos\theta (sinhr{\partial }_t-cothtcoshr{\partial }_r)+tanhtsinhrsin\theta {\partial }_{\theta },\hfill \\ \hfill X_{10}& =& \mathrm{same}\mathrm{as}{X}_9\mathrm{with}sinhr\leftrightarrow coshr\hfill \end{array}$$

(44)

One may easily simplify Equation (8) to find the expressions for the corresponding conservation laws for the above generators. The Lie algebra in this case is obtained as:

$[X_1,X_5]=X_6$,	$[X_1,X_6]=X_5$,	$[X_1,X_7]=X_8$,	$[X_1,X_8]=X_7$,	$[X_1,X_9]=X_{10}$,
$[X_1,X_{10}]=X_9$,	$[X_5,X_2]=X_7$,	$[X_6,X_2]=X_8$,	$[X_2,X_7]=X_5$,	$[X_2,X_8]=X_6$,
$[X_5,X_3]=X_9$,	$[X_6,X_3]=X_{10}$,	$[X_3,X_9]=X_5$,	$[X_3,X_{10}]=X_6$,	$[X_7,X_4]=X_9$,
$[X_8,X_4]=X_{10}$,	$[X_4,X_9]=X_7$,	$[X_4,X_{10}]=X_8$,	$[X_5,X_6]=X_1$,	$[X_7,X_5]=X_2$,
$[X_9,X_5]=X_3$,	$[X_6,X_8]=X_2$,	$[X_6,X_{10}]=X_3$,	$[X_7,X_8]=X_1$,	$[X_9,X_7]=X_4$,
$[X_8,X_{10}]=X_4$,	$[X_9,X_{10}]=X_1$,

9. Summary and Discussion

In this paper, we have classified the Lagrangian of the Kantowski–Sachs metric via its NS. The set of determining equations is obtained and then integrated in several cases. It is observed that the Kantowski–Sachs metric admits a 5-, 6-, 7-, 8-, 9-, or 11-dimensional Lie algebra of NS for different values of the metric functions. The number of non-trivial NS for this metric is shown to be one, two, or three, while the number of KVs is found to be $4,5,6,7,$ or $10.$

We have found five different metrics, each admitting the minimal set of five NS, out of which four are the minimum KVs of the Kantowski–Sachs metric and one is a non-trivial Noether symmetry, which is ${\partial }_u.$ The gauge function is trivial here.

There is only one metric (27) that admits six NS. This set of six NS contains the minimal set of five NS along with one extra Noether symmetry with the gauge function $F=-2r.$

In the case of seven-dimensional Noether algebra, we have obtained seven different metrics. For the first five metrics, 7(i)–7(v), we have six KVs and one Noether symmetry ${\partial }_u,$ with a trivial gauge function. For metric 7(vi), we have the minimal set of NS along with two extra NS, given by $X_5$ and $X_6.$ The gauge function corresponding to $X_5$ is found to be $F=\frac{t(c_{1}t+2c_2)}{2c_1}$. It can bee seen that the Noether symmetry $X_6$ for this metric corresponds to an HV $\frac{c_{1}t+c_2}{2c_1}{\partial }_t,$ with homothetic constant $\psi =\frac{1}{2}.$ Similar results are obtained for the metric 7(vii). Here, the number of KVs is five.

There exists only one metric (31) possessing eight NS, of which five are the minimal NS for the Kantowski–Sachs metric, and three extra NS are obtained, which are presented in (32). One of these three NS, denoted as $X_7,$ corresponds to an HV $\frac{\alpha t+\beta }{2\alpha }{\partial }_t+\frac{r}{2}{\partial }_r.$ The number of KVs for this metric is only four.

In the case of the nine-dimensional Lie algebra of NS, we have found three metrics (34), (37), and (40). For the metric (34), we have the minimal set of five NS along with four extra symmetries, of which three are KVs and one is a non-trivial Noether symmetry $u{\partial }_r$ with the gauge function $F=-2r.$ The number of KVs in this case is seven. For the remaining two metrics (37) and (40), we have six KVs along with three non-trivial NS.

Finally, we have only one metric (43) where the dimension of the algebra of NS is $11$. Out of eleven NS, ten are the KVs, and there is only one non-trivial Noether symmetry, given by ${\partial }_u.$

For almost all the obtained metrics, it is observed that the positive energy condition is satisfied, and the corresponding Ricci scalar has no singularity at the origin.