Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data
Abstract
1. Introduction
2. Method
3. Results
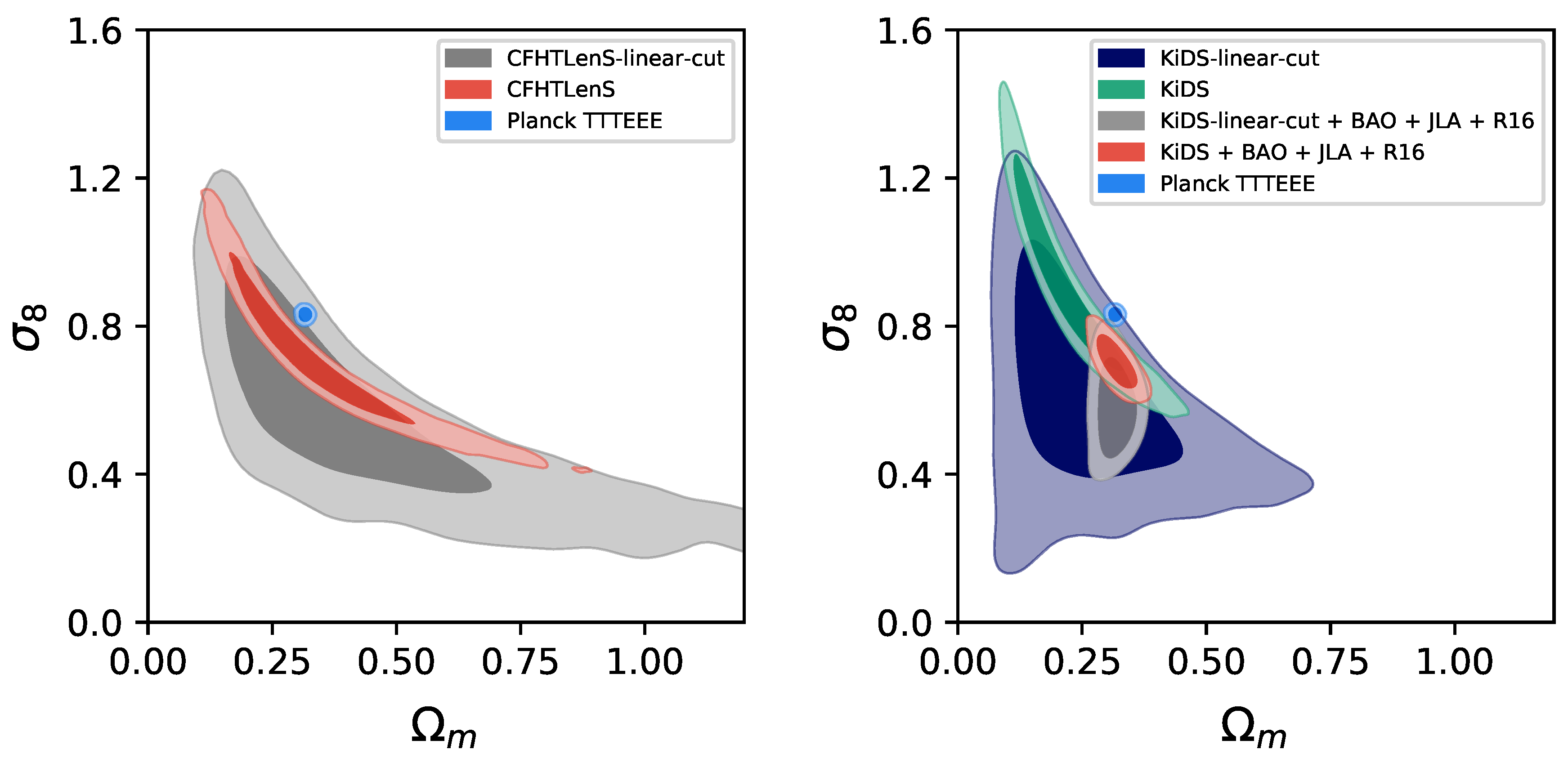
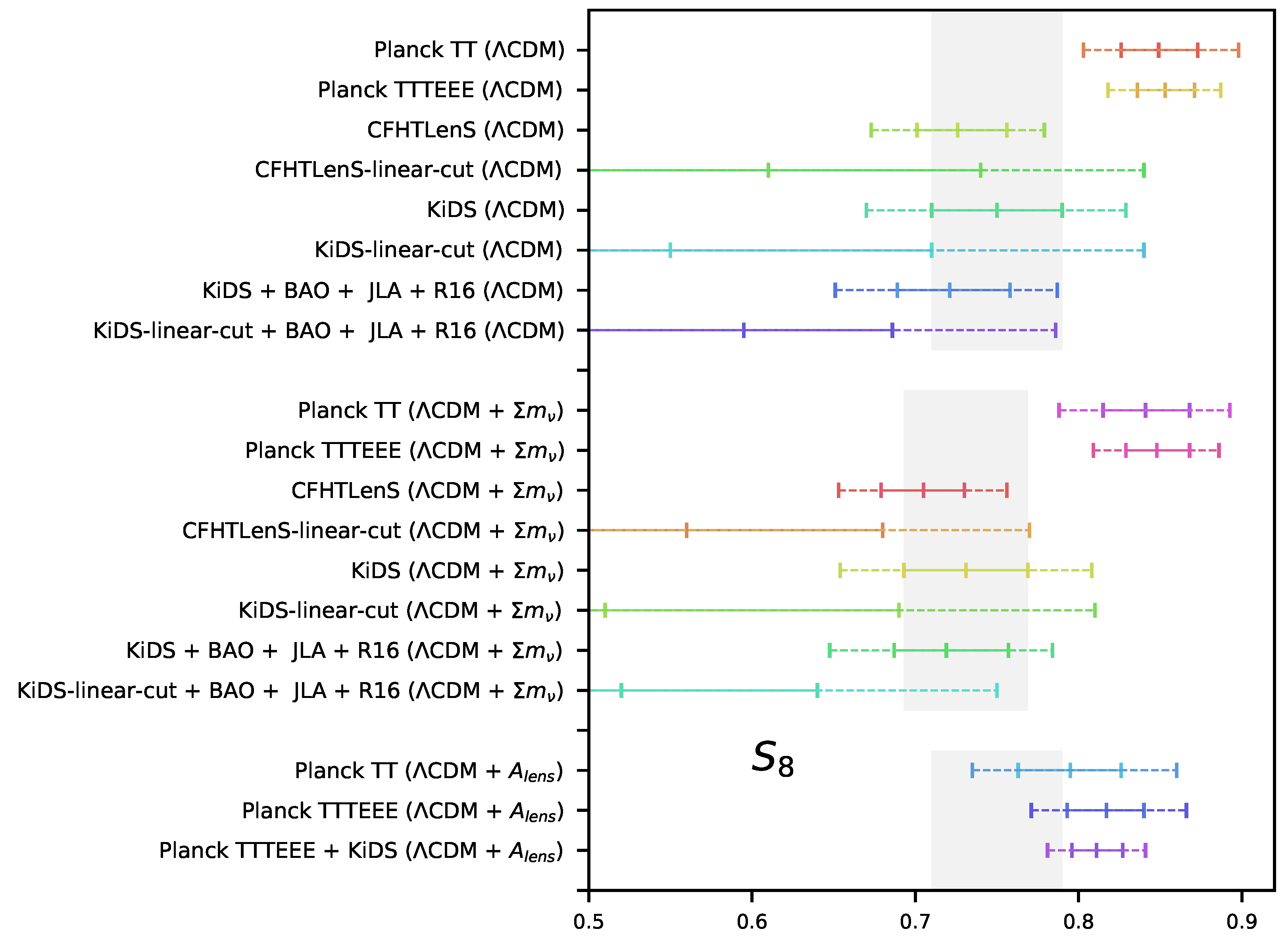
3.1. Standard Cosmological Model
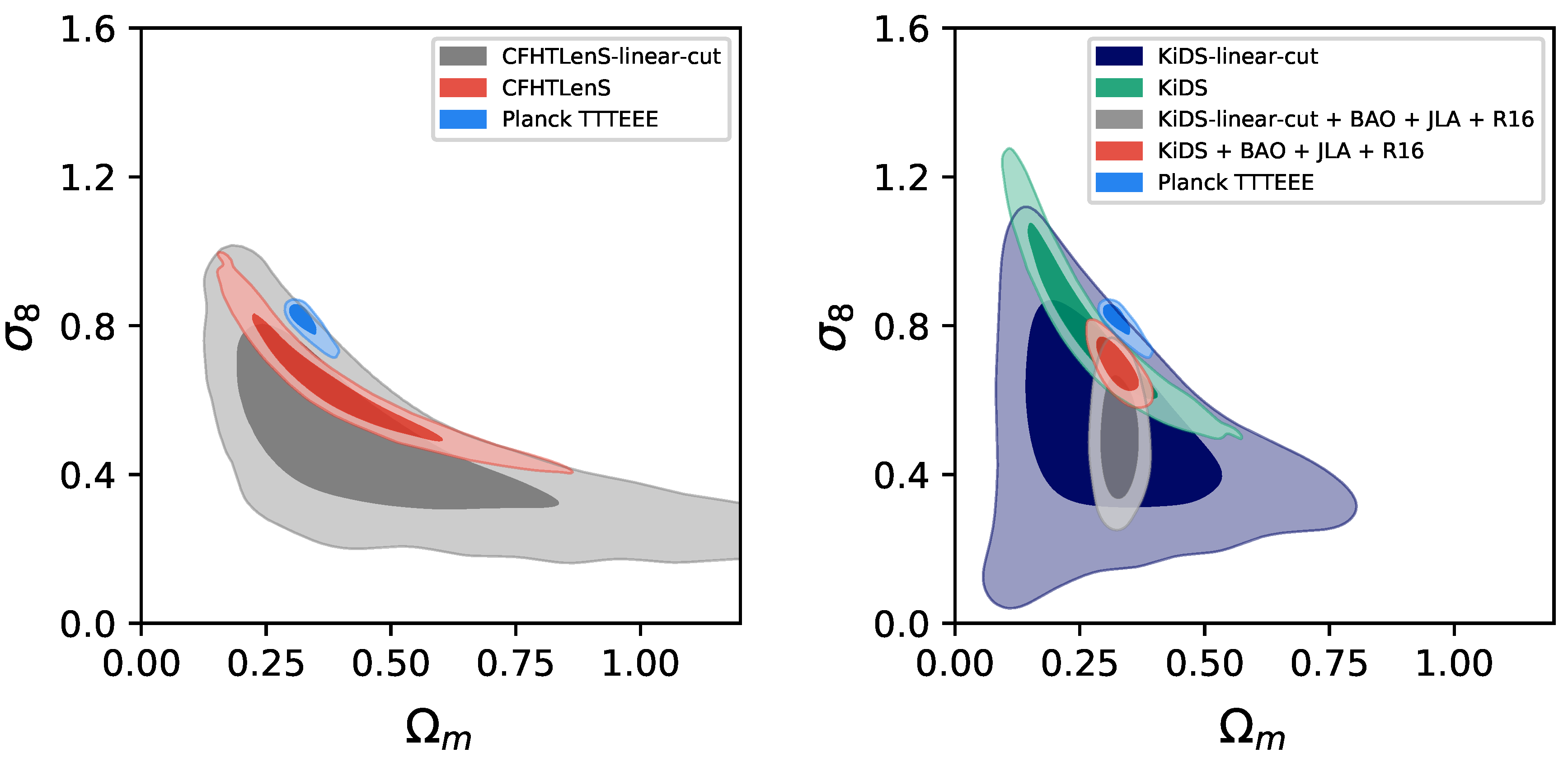
3.2. Massive Neutrinos
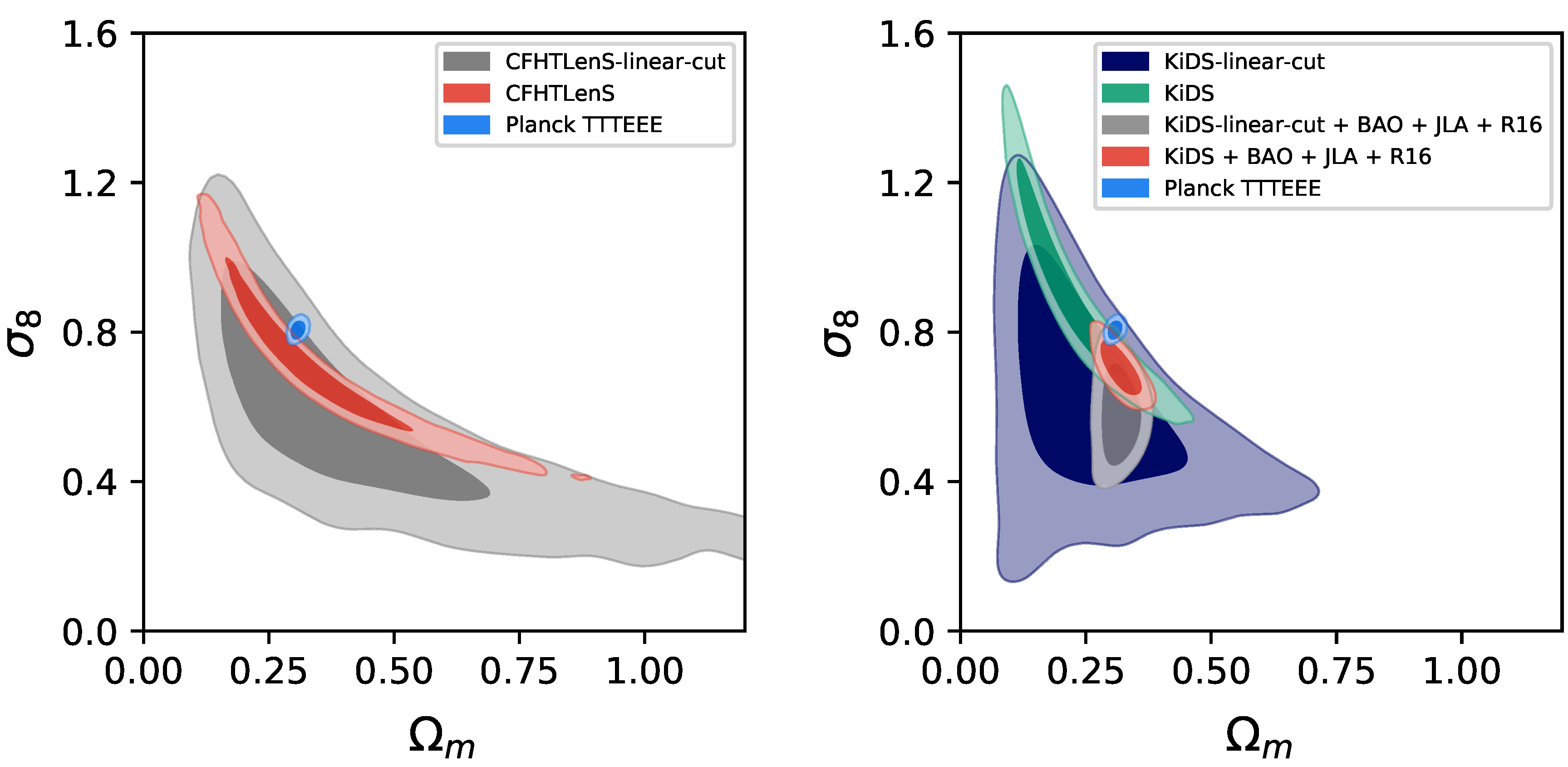
3.3. The Lensing Amplitude
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Planck TT | CFHTLenS-linear-cut | CFHTLenS | KiDS-linear-cut | KiDS | Planck TT + KiDS | Planck TT + KiDS-linear-cut |
|---|---|---|---|---|---|---|---|
| Planck TTTEEE | Planck TTTEEE + KiDS | Planck TTTEEE + KiDS-linear-cut | CFHTLenS + KiDS | CFHTLenS-linear-cut + KiDS-linear-cut | KiDS + BAO + JLA + R16 | KiDS-linear-cut + BAO + JLA + R16 | |
| Parameter | Planck TT | CFHTLenS | CFHTLenS-linear-cut | KiDS | KiDS-linear-cut | Planck TT + KiDS | Planck TT + KiDS-linear-cut |
|---|---|---|---|---|---|---|---|
| Planck TTTEEE | Planck TTTEEE + KiDS | Planck TTTEEE + KiDS-linear-cut | CFHTLenS-linear-cut + KiDS-linear-cut | KiDS + BAO + JLA + R16 | KiDS-linear-cut + BAO + JLA + R16 | ||
| Parameter | Planck TT | Planck TT + KiDS-linear-cut | Planck TTTEEE | Planck TTTEEE + KiDS | Planck TTTEEE + KiDS-linear-cut |
|---|---|---|---|---|---|
References
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. I. Overview and the cosmological legacy of Planck. arXiv, 2018; arXiv:1807.06205. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv, 2018; arXiv:1807.06209. [Google Scholar]
- Hildebrandt, H.; Viola, M.; Heymans, C.; Joudaki, S.; Kuijken, K.; Blake, C.; Erben, T.; Joachimi, B.; Klaes, D.; Miller, L.T.; et al. KiDS-450: Cosmological parameter constraints from tomographic weak gravitational lensing. arXiv, 2016; arXiv:1606.05338. [Google Scholar] [CrossRef]
- Kuijken, K.; Heymans, C.; Hildebrandt, H.; Nakajima, R.; Erben, T.; de Jong, J.T.; Viola, M.; Choi, A.; Hoekstra, H.; Miller, L.; et al. Gravitational Lensing Analysis of the Kilo Degree Survey. Mon. Not. R. Astron. Soc. 2015, 454, 3500–3532. [Google Scholar] [CrossRef]
- Fenech Conti, I.; Herbonnet, R.; Hoekstra, H.; Merten, J.; Miller, L.; Viola, M. Calibration of weak-lensing shear in the Kilo-Degree Survey. Mon. Not. R. Astron. Soc. 2017, 467, 1627–1651. [Google Scholar]
- Abbott, T.M.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark energy survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Troxel, M.A.; MacCrann, N.; Zuntz, J.; Eifler, T.F.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; et al. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Heymans, C.; Van Waerbeke, L.; Miller, L.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Simon, P.; Bonnett, C.; et al. CFHTLenS: The Canada-France-Hawaii Telescope Lensing Survey. Mon. Not. R. Astron. Soc. 2012, 427, 146–166. [Google Scholar] [CrossRef]
- Erben, T.; Hildebrandt, H.; Miller, L.; van Waerbeke, L.; Heymans, C.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Benjamin, J.; Blake, C.; et al. CFHTLenS: The Canada-France-Hawaii Telescope Lensing Survey—Imaging Data and Catalogue Products. Mon. Not. R. Astron. Soc. 2013, 433, 2545–2563. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Heymans, C.; Choi, A.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Johnson, A.; Mead, A.; Parkinson, D.; et al. CFHTLenS revisited: Assessing concordance with Planck including astrophysical systematics. Mon. Not. R. Astron. Soc. 2013, 465, stw2665. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck intermediate results-LI. Features in the cosmic microwave background temperature power spectrum and shifts in cosmological parameters. Astron. Astrophys. 2017, 607, A95. [Google Scholar] [CrossRef]
- Addison, G.E.; Huang, Y.; Watts, D.J.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Weiland, J.L. Quantifying discordance in the 2015 Planck CMB spectrum. Astrophys. J. 2016, 818, 312. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% solution: determination of the Hubble constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 2011, 732, 129. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Bucciarelli, B.; Lattanzi, M.G.; MacKenty, J.W.; Bowers, J.B.; Zheng, W.; Filippenko, A.V.; et al. Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant. Astrophys. J. 2018, 861, 126. [Google Scholar] [CrossRef]
- Kunz, M.; Nesseris, S.; Sawicki, I. Using dark energy to suppress power at small scales. Phys. Rev. D 2015, 92, 063006. [Google Scholar] [CrossRef]
- Enqvist, K.; Nadathur, S.; Sekiguchi, T.; Takahashi, T. Decaying dark matter and the tension in σ8. J. Cosmol. Astropart. Phys. 2015, 9, 067. [Google Scholar] [CrossRef]
- Hlozek, R.; Grin, D.; Marsh, D.J.; Ferreira, P.G. A search for ultralight axions using precision cosmological data. Phys. Rev. D 2015, 91, 103512. [Google Scholar] [CrossRef]
- Ichiki, K.; Yoo, C.M.; Oguri, M. Relationship between the CMB, SZ Cluster Counts, and Local Hubble Parameter Measurements in a Simple Void Model. Phys. Rev. D 2016, 93, 023529. [Google Scholar] [CrossRef]
- Dossett, J.N.; Ishak, M.; Parkinson, D.; Davis, T.M. Constraints and tensions in testing general relativity from Planck and CFHTLenS data including intrinsic alignment systematics. Phys. Rev. D 2015, 92, 023003. [Google Scholar] [CrossRef]
- Gomez-Valent, A.; Sola, J. Relaxing the σ8-tension through running vacuum in the Universe. Europhys. Lett. 2017, 120, 39001. [Google Scholar] [CrossRef]
- McCarthy, I.G.; Bird, S.; Schaye, J.; Harnois-Deraps, J.; Font, A.S.; Van Waerbeke, L. The BAHAMAS project: The CMB–large-scale structure tension and the roles of massive neutrinos and galaxy formation. Mon. Not. R. Astron. Soc. 2018, 476, 2999–3030. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological hints of modified gravity? Phys. Rev. D 2016, 93, 023513. [Google Scholar] [CrossRef]
- Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XI. CMB power spectra, likelihoods, and robustness of parameters. Astron. Astrophys. 2016, 594, A11. [Google Scholar] [CrossRef]
- Available online: https://github.com/sjoudaki/cfhtlens_revisited (accessed on 15 September 2018).
- Joudaki, S.; Blake, C.; Johnson, A.; Amon, A.; Asgari, M.; Choi, A.; Erben, T.; Glazebrook, K.; Harnois-Déraps, J.; Heymans, C.; et al. KiDS-450 + 2dFLenS: Cosmological parameter constraints from weak gravitational lensing tomography and overlapping redshift-space galaxy clustering. Mon. Not. R. Astron. Soc. 2018, 474, 4894–4924. [Google Scholar] [CrossRef]
- Troxel, M.A.; Krause, E.; Chang, C.; Eifler, T.F.; Friedrich, O.; Gruen, D.; MacCrann, N.; Chen, A.; Davis, C.; DeRose, J.; et al. Survey geometry and the internal consistency of recent cosmic shear measurements. Mon. Not. R. Astron. Soc. 2018. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon Acoustic Oscillations and the Local Hubble Constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The Clustering of the SDSS DR7 Main Galaxy Sample I: A 4 per cent Distance Measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, É.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Betoule, M.E.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Lewis, A. Efficient sampling of fast and slow cosmological parameters. Phys. Rev. D 2013, 87, 103529. [Google Scholar] [CrossRef]
- Available online: http://cosmologist.info/cosmomc/ (accessed on 15 September 2018).
- Joudaki, S.; Mead, A.; Blake, C.; Choi, A.; de Jong, J.; Erben, T.; Fenech Conti, I.; Herbonnet, R.; Heymans, C.; Hildebrandt, H.; et al. KiDS-450: Testing extensions to the standard cosmological model. Mon. Not. R. Astron. Soc. 2017, 471, 1259. [Google Scholar] [CrossRef]
- Available online: https://github.com/sjoudaki/kids450 (accessed on 15 September 2018).
- Giusarma, E.; Di Valentino, E.; Lattanzi, M.; Melchiorri, A.; Mena, O. Relic neutrinos, thermal axions, and cosmology in early 2014. Phys. Rev. D 2014, 90, 043507. [Google Scholar] [CrossRef]
- MacCrann, N.; Zuntz, J.; Bridle, S.; Jain, B.; Becker, M.R. Cosmic Discordance: Are Planck CMB and CFHTLenS weak lensing measurements out of tune? Mon. Not. R. Astron. Soc. 2015, 451, 2877–2888. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Beyond six parameters: Extending Λ CDM. Phys. Rev. D 2015, 92, 121302. [Google Scholar] [CrossRef]
- Di Valentino, E.; Giusarma, E.; Mena, O.; Melchiorri, A.; Silk, J. Cosmological limits on neutrino unknowns versus low redshift priors. Phys. Rev. D 2016, 93, 083527. [Google Scholar] [CrossRef]
- Calabrese, E.; Slosar, A.; Melchiorri, A.; Smoot, G.F.; Zahn, O. Cosmic Microwave Weak lensing data as a test for the dark universe. Phys. Rev. D 2008, 77, 123531. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining dark energy dynamics in extended parameter space. Phys. Rev. D 2017, 96, 023523. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Renzi, F.; Di Valentino, E.; Melchiorri, A. Cornering the Planck Alens anomaly with future CMB data. Phys. Rev. D 2018, 97, 123534. [Google Scholar] [CrossRef]
- Cabass, G.; Di Valentino, E.; Melchiorri, A.; Pajer, E.; Silk, J. Constraints on the running of the running of the scalar tilt from CMB anisotropies and spectral distortions. Phys. Rev. D 2016, 94, 023523. [Google Scholar] [CrossRef]
- Ooba, J.; Ratra, B.; Sugiyama, N. Planck 2015 constraints on the non-flat XCDM inflation model. arXiv, 2017; arXiv:1707.03452. [Google Scholar]
- Muñoz, J.B.; Grin, D.; Dai, L.; Kamionkowski, M.; Kovetz, E.D. Search for Compensated Isocurvature Perturbations with Planck Power Spectra. Phys. Rev. D 2016, 93, 043008. [Google Scholar] [CrossRef]
- Valiviita, J. Power Spectra Based Planck Constraints on Compensated Isocurvature, and Forecasts for LiteBIRD and CORE Space Missions. J. Cosmol. Astropart. Phys. 2017, 4, 14. [Google Scholar] [CrossRef]
- Capozzi, F.; Di Valentino, E.; Lisi, E.; Marrone, A.; Melchiorri, A.; Palazzo, A. Global constraints on absolute neutrino masses and their ordering. Phys. Rev. D 2017, 95, 096014. [Google Scholar] [CrossRef]
- Kilbinger, M.; Heymans, C.; Asgari, M.; Joudaki, S.; Schneider, P.; Simon, P.; Van Waerbeke, L.; Harnois-Déraps, J.; Hildebrandt, H.; Köhlinger, F.; et al. Precision calculations of the cosmic shear power spectrum projection. Mon. Not. R. Astron. Soc. 2017, 472, 2126–2141. [Google Scholar] [CrossRef]
| Parameter | Prior |
|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Valentino, E.; Bridle, S. Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data. Symmetry 2018, 10, 585. https://doi.org/10.3390/sym10110585
Di Valentino E, Bridle S. Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data. Symmetry. 2018; 10(11):585. https://doi.org/10.3390/sym10110585
Chicago/Turabian StyleDi Valentino, Eleonora, and Sarah Bridle. 2018. "Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data" Symmetry 10, no. 11: 585. https://doi.org/10.3390/sym10110585
APA StyleDi Valentino, E., & Bridle, S. (2018). Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data. Symmetry, 10(11), 585. https://doi.org/10.3390/sym10110585






