Abstract
Many artificial intelligence applications often require a huge amount of computing resources. As a result, cloud computing adoption rates are increasing in the artificial intelligence field. To support the demand for artificial intelligence applications and guarantee the service level agreement, cloud computing should provide not only computing resources but also fundamental mechanisms for efficient computing. In this regard, a snapshot protocol has been used to create a consistent snapshot of the global state in cloud computing environments. However, the existing snapshot protocols are not optimized in the context of artificial intelligence applications, where large-scale iterative computation is the norm. In this paper, we present a distributed snapshot protocol for efficient artificial intelligence computation in cloud computing environments. The proposed snapshot protocol is based on a distributed algorithm to run interconnected multiple nodes in a scalable fashion. Our snapshot protocol is able to deal with artificial intelligence applications, in which a large number of computing nodes are running. We reveal that our distributed snapshot protocol guarantees the correctness, safety, and liveness conditions.
PACS:
J0101
1. Introduction
Recent developments in artificial intelligence have made the innovation establish itself as an effective and attractive way to communicate between computers and machines in an intelligent manner. In fact, underneath the artificial intelligence, a large amount of computation is performed [1,2]. Meanwhile, recent advances in cloud computing and services have led to a proliferation of supporting artificial intelligence applications [3,4]. The harmony of artificial intelligence and cloud computing provides a great opportunity in that data servers and computing servers in cloud computing environments hold the data for artificial intelligence applications and process them to make decisions, respectively [5,6,7].
In addition to hardware resources, cloud computing should provide fundamental mechanisms for efficient computing. Since many artificial intelligence applications require a huge amount of computing resources, capturing the global state of resources in cloud computing environments can help reduce processing time in the presence of failure [8,9]. By capturing the global state of resources periodically, artificial intelligence applications can resume the computation from the latest snapshot, not from the beginning, while guaranteeing the service level agreement (SLA). However, capturing the global state of resources in cloud computing environments is not a trivial task since individual resources are independent units and, therefore, the snapshot protocol can only be done by passing messages due to the lack of shared memory between the nodes in the system [10,11].
Recording the global state of a system is an important paradigm and has been widely used in several aspects of distributed and cloud computing systems, such as deadlocks [12], termination detection [13], mutual exclusion [14], and consensus [15]. However, since there is no shared memory and no global clock in a cloud computing system, it is difficult to record the global state of the system efficiently. Therefore, it is important to develop snapshot protocols for recording the global state of a system in an efficient way.
In this paper, we present a distributed snapshot protocol for efficient artificial intelligence computation in cloud computing environments. The proposed snapshot protocol exploits the property of artificial intelligence applications to capture the global state of resources effectively. Note that many artificial intelligence applications exhibit iterative computation in machine learning and data mining [16,17]. With this in mind, we implement a distributed snapshot protocol by seamlessly integrating with artificial intelligence computing in cloud computing environments.
Another imperative thing to note is that the proposed distributed snapshot protocol does not require a coordinator such as a super node, which is a downside of previous research and may result in a single point of failure. Without a super node, the proposed distributed snapshot protocol allows all the nodes to play an independent role symmetrically by performing a predefined procedural method in the design and implementation. In other words, nodes are functionally equal to each other in our context. This symmetric design of the protocol is preferable in dynamic systems, including cloud computing environments, for scalability.
The remainder of the paper is organized as follows. The next section reviews related work by showing how our model differs from others in the literature. In Section 3, we describe the system model and preliminary definitions and formally define the problem. The proposed distributed snapshot algorithm for artificial intelligence computation is presented in Section 4. Section 5 presents performance evaluation with scalability settings. Finally, Section 6 concludes the paper.
2. Related Work
In this section, we summarize the related work across two perspectives in distributed systems including cloud computing: artificial intelligence computation and snapshot protocols. The basic idea of our approach is to incorporate a snapshot protocol into artificial intelligence computation seamlessly in a scalable fashion. While our analysis of the snapshot protocol assumed an independence of failures, the proposed scheme also benefits other systems for correlated failures since our protocol design takes modularity and portability into account.
2.1. Artificial Intelligence Computation
The artificial intelligence field was founded as an academic discipline in 1956 on the claim that human intelligence can be so precisely described that a machine can be made to simulate it [18]. After several waves of optimism, artificial intelligence techniques have experienced a resurgence by virtue of advances in computing power in cloud computing, big data, and practical applications. Recently, artificial intelligence and its techniques have become a significant part of our society and firms by solving many challenging problems in computer science and engineering [19].
In artificial intelligence techniques, a lot of computation is required and many of them are iteration-based [20]; the computation can be performed in large-scale computing infrastructures and cloud computing environments to reduce processing time. Since the mean time between failures (the expected time between two failures for a repairable system) of large-scale systems is quite less than that of a single machine system, fault tolerance schemes in large-scale systems have been developed. Among them, a snapshot protocol is one of the fundamental mechanisms that create a consistent snapshot of the global state of the system. Due to the lack of globally shared memory and a global clock, however, capturing a global state of distributed systems is not a trivial task [21].
For iterative computation in artificial intelligence applications, several studies have been investigated in various computation frameworks to accelerate and reduce processing time. The authors of Maiter [22] proposed a computation model called delta-based accumulative iterative computation (DAIC), which iteratively updates the vertex values by accumulating the value changes between iterations, not by the result from the previous iteration. Maiter is designed to perform the computation asynchronously to bypass the high-cost synchronous barriers in large-scale systems.
In Faiter [23], fault-tolerant mechanisms are added into the iterative computation to perform recovery with surviving data and guarantee the correctness of the computation. For load balancing upon recovery, Faiter reassigns lost data on multiple machines in the system. In HotGraph [24], the authors resolved the bottleneck problem caused by cross-partition state updates. HotGraph extracts a backbone structure that spans all the partitions of the original graph and schedules for partitions to maximize the hot graph’s effectiveness by considering locality and priority.
The authors of [25] improved the performance of the fault-tolerant framework in terms of disk and network communication. With a cost-analysis model, it can adjust the interval of checkpoints by considering the underlying computing workloads. However, these fault-tolerant frameworks for iterative computation are dependent on their computing frameworks. In other words, the checkpoint scheme can only be used in the specific framework. Therefore, the fault-tolerant scheme cannot be used in other systems. On the other hand, our snapshot protocol is designed with modularity and portability in mind.
2.2. Snapshot Protocols
The Chandy–Lamport algorithm [26] is a basic snapshot protocol with the assumption of no failures and first-in-first-out (FIFO) message communication. For the practical implementation of the snapshot protocol, the system model must consider failures and asynchronous communication [27]. In [28], a partial snapshot algorithm for a subsystem, where multiple nodes concurrently initiate the snapshot algorithm, is proposed. In Snapify [29], a snapshot algorithm for offload applications on Xeon Phi manycore processors is proposed. HotRestore [30] is a fast restore system for virtual machine clusters. HotRestore minimizes performance degradation due to large snapshot files when restoring a virtual machine cluster by mitigating the TCP backoff problem between virtual machines.
Unlike previous work, our snapshot protocol does not require a specific runtime environment or depend on a system. For example, Snapify [29] is based on remote direct memory access and is dependent on Xeon Phi manycore processors. Our proposed snapshot protocol is carefully integrated with iterative computation for artificial intelligence applications in a modular fashion. In addition, we loosen the communication model in the presence of failures.
Furthermore, most of the previous approaches are leader-based. In other words, they rely on an explicit reader to coordinate the distributed snapshot protocol. The underlying assumption of leader-based snapshot protocols is that the network topology is fully connected since they rely on broadcast or multicast primitives. As far as the message complexity is concerned, our proposed snapshot protocol differs from previous approaches in that our algorithmic design uses the one-to-one communication model and maintains a small subset of neighbor nodes, thereby reducing the message complexity.
Although one-to-one communication or unicast primitives are well studied for routing in the computer networking field, no distinguishing snapshot protocol exists other than ours (especially in cloud computing environments) to the best of our knowledge. Reducing the message complexity of the distributed snapshot protocol has been a major concern. In this regard, one possible implementation of a distributed snapshot protocol is based on the quorum system. In the quorum system, a quorum is the minimum number of votes that a distributed transaction requires to perform an operation in a distributed system [31,32].
However, one disadvantage of using the quorum system is that it sometimes needs one or more shared memory objects. Moreover, to safely calculate, the majority of the quorum system requires the following condition: ∀Q1, Q2 ∈ Q, Q1 ∩ Q2 ≠ ∅ [33,34]. Thus, a distributed snapshot protocol based on the quorum system is suitable for static systems. Since cloud computing systems are dynamic in nature, a protocol based on the quorum system requires the reorganization of quorum sets each time a node joins or departs.
3. System Model and Problem Definition
The system consists of a collection of n nodes, node1, node2, node3, ···, noden, where each node is connected by communication channels. There is no shared memory and, therefore, a node can communicate with others solely by passing messages. The message delivery model is asynchronous. When asynchronous send primitives are used, the control returns to the invoking process after the message is delivered to the buffer. Messages are delivered reliably with finite but arbitrary time delay. The network can be described as a directed graph [35], in which vertices represent the nodes and edges represent unidirectional communication channels. Let Cij denote the channel from nodei to nodej and SCij denote the state of Cij.
The state of a node at any time is defined by actions, and the contents of the node are composed of registers, stacks, local memory, distributed applications, etc. The actions performed by a node are modeled as three types of events: local events, message-sending events, and message-receiving events. In this respect, let mij, send(mij), and receive(mij) be a message sent by nodei to nodej, a sending event of mij, and a receiving event of mij, respectively. The occurrence of these events leads to transitions in the global system state. At any instant, the state of nodei (denoted by LSi) is a result of the entire sequence of events executed by nodei up to the instant. For the channel Cij, the transit state is defined as follows [36]:
transit(LSi, LSj) = {mij | send(mij) ∈ LSi ⋀ receive(mij) ∉ LSj}.
Therefore, if a snapshot protocol starts an instance to record the state of nodei and nodej, it must include transit(LSi, LSj) and transit(LSj, LSi) as well as LSi and LSj. The communication model is not restricted to the FIFO or causally ordered delivery model [37]. Furthermore, unlike previous research, we do not use broadcast primitives, which simplify the design of a snapshot protocol. In our algorithmic design, we use one-to-one communication primitives. How to accomplish the snapshot protocol safely and efficiently with the assumption of the non-FIFO model and one-to-one communication model is at the core of our contributions by collecting a consistent global state GS:
GS = {⋃iLSi, ⋃i,j SCij}.
A global state is a consistent global state if, and only if, the following conditions are met [38]:
Condition 1: send(mij) ∈ LSi ⇒ mij ∈ SCij ⊕ receive(mij) ∈ LSj,
Condition 2: send(mij) ∉ LSi ⇒ mij ∉ SCij ⋀ receive(mij) ∉ LSj.
Condition 1 states that every message mij that is recorded in LSi must be captured in the state of the channel Cij or in the collected local state of nodej. Condition 2 states that if a message mij is not recorded as a sent event in the local state of nodei, then it must be presented neither in the state of the channel Cij nor in the collected local state of nodej. The proposed snapshot protocol is able to capture a consistent global state satisfying the above conditions; the proof of the algorithm is detailed in the next section. For node failures, we consider the fail-stop model [39], where a failed node remains halted forever.
4. The Proposed Distributed Snapshot Protocol
In this section, we describe our distributed snapshot protocol for capturing a consistent global state with the assumption of the non-FIFO model and the one-to-one communication model; we then provide an illustrative example of the proposed algorithm. The correctness proof of the algorithm is also provided.
4.1. Details of the Algorithms
What makes capturing a consistent global state in distributed and cloud computing environments difficult is that each node has no global information of the system and has to communicate with other nodes without broadcast primitives due to loosely coupled environments [15]. Since each node maintains partial node information [40], it is necessary to realize a mechanism that collects local states of the nodes in the system.
There are two threads for message exchange between nodes: active (sending) thread and passive (receiving). Algorithm 1 shows the pseudocode of the proposed distributed snapshot algorithm for the active thread. Before starting a round, nodei checks whether a consistent global state is collected for failedRound (lines 16–28). If the stateNodes data structure satisfies the conditions of the GS, nodei saves the stateNodes data structure to latestSnapshot and builds the stateChannel data structure (lines 17–21). After setting the timestamp for the snapshot, nodei performs the proposeGS function (lines 23–24). These procedures are performed until either continue is true or recordedRound is equal to currentRound (line 16).
At each round, nodei updates its own local information before message exchange and performs the takeSnapshotLocal function (lines 33–35). Next, it selects a random neighbor node from its neighbor list and then sends LSi to the selected neighbor node (lines 36–38). Note that LSi includes the stateNodes data structure. If the result of the send function is true, the iteration is aborted (line 34). This guarantees that nodei adheres to the exactly-once semantic for message exchange in a round.
| Algorithm 1. The proposed distributed snapshot algorithm for nodei (sending) |
| 1: begin initialization |
| 2: sta- odes[r][j] ← null, ∀r ∈ {1 … maxround}, ∀j ∈ {1 … maxnode}; |
| 3: stateChannel[r][from][to] ← null, ∀r ∈ {1 … maxround}, ∀from,to ∈ {1 … maxnode}; |
| 4: neighborList[p] ← null, ∀p ∈ {1 … maxneighbor}; |
| 5: recordedRound ← 0; |
| 6: failedRound ← null; |
| 7: latestSnapshot ← null; |
| 8: currentRound ← 0; |
| 9: continue ← null; |
| 10: sended ← null; |
| 11: timestamp ← null; |
| 12: end |
| 13: begin before starting a round |
| 14: failedRound ← recordedRound + 1; |
| 15: continue ← true; |
| 16: while continue || recordedRound == currentRound do |
| 17: check stateNodes[failedRound][j], ∀j ∈ {1 … maxnode}; |
| 18: if stateNodes[failedRound][j] satisfies the conditions of the GS do |
| 19: latestSnapshot ← stateNodes[failedRound][j]; |
| 20: recordedRound ← failedRound; |
| 21: build stateChannel[recordedRound][from][to]; |
| 22: failedRound ← failedRound + 1; |
| 23: timestamp ← getCurrentTimestamp(); |
| 24: proposeGS(i, r, timestamp); |
| 25: else |
| 26: continue ← false; |
| 27: end if |
| 28: end |
| 29: end |
| 30: begin at each round |
| 31: sended ← false; |
| 32: currentRound ← currentRound + 1; |
| 33: updateLocalInformation(); |
| 34: while sended is false do |
| 35: stateNodes[currentRound][i] ← takeSnapshotLocal(); |
| 36: random ← selectRandomNumber(1, maxneighbor); |
| 37: neighbor ← neighborList[random]; |
| 38: sended ← send(LSi, neighbor); |
| 39: end |
| 40: end |
| 41: function updateLocalInformation(); |
| 42: stateNodes[currentRound][i] ← getlocalState(); |
| 43: stateNodes[currentRound][i].timestamp ← getCurrentTimestamp(); |
| 44: end |
Algorithm 2 shows the pseudocode of the proposed distributed snapshot algorithm for the passive thread. The role of the passive thread is to wait for messages from other nodes and update the stateNodes data structure (lines 6–8) by comparing the timestamp values of each element (lines 13–17). It is worth noting that the algorithm can be configured to push, pull, or push–pull mode. When the algorithm is configured to push mode, the send function in Algorithm 2 (line 9) is not performed. In other words, in push mode, the active thread sends the LSi and not vice versa. When the protocol is configured to pull mode, the passive thread does not receive the sending node’s stateNodes data structure; the receive function in Algorithm 2 (line 7) is not performed.
| Algorithm 2. The proposed distributed snapshot algorithm for nodei (receiving) |
| 1: begin initialization |
| 2: roundStart ← null; |
| 3: neighbor ← null; |
| 4: end |
| 5: repeat |
| 6: neighbor ← waitForMessage(); |
| 7: neighbor.stateNodes ← receive(neighbor); |
| 8: updateStateNodes(); |
| 9: send(LSi, neighbor); |
| 10: until forever; |
| 11: function updateStateNodes() |
| 12: roundStart ← recordedRound + 1; |
| 13: for each stateNodes[r][j], where roundStart < r < currentRound; |
| 14: if stateNodes[r][j].timestamp < neighbor. stateNodes[r][j].timestamp then |
| 15: stateNodes[r][j] ← neighbor. stateNodes[r][j]; |
| 16: stateNodes[r][j].timestamp ← neighbor. stateNodes[r][j].timestamp; |
| 17: end if |
| 18: end |
| 19: end |
When the push–pull mode is used, a node sends its stateNodes data structure and receives a neighbor’s stateNodes data structure. Therefore, all of the procedures of Algorithms 1 and 2 are performed. As far as the communication modes are concerned, the push–pull mode is the most effective with respect to propagating information in the system. Hence, we use the push–pull mode, and the results of this effectiveness are presented in Section 5.
Furthermore, since each node maintains a small subset of the nodes in the system, the proposed snapshot protocol is churn-resilient. In other words, our protocol is able to take a consistent global snapshot even when nodes are free to join or leave. If a snapshot protocol uses broadcast primitives, each node must know all the information of the nodes in the system. This is a major drawback of broadcast-based algorithms.
Unlike the previous algorithms, we adopt one-to-one communication primitives. Even though the proposed snapshot protocol uses one-to-one communication primitives, our algorithm guarantees the correctness, safety, and liveness conditions. Another benefit of the proposed snapshot protocol is that the message complexity can be reduced in comparison to the broadcast-based protocols. The message complexity (system-wide space complexity) of the broadcast-based protocols is O(n2) and that of the proposed distributed snapshot protocol is O(n), where n is the number of nodes in the system [12].
4.2. Illustrative Example of the Protocol
Figure 1 shows an example of executing our proposed snapshot protocol for one round with three nodes: Node A, Node B, and Node C. The size of the neighbor list is 1; that is, each node maintains one node in the system. Each element of the stateNodes data structure is in the form of three-tuple. The tuple <1, blank, 0> means the round number is 1, the node’s state is blank or null, and the timestamp value of the state is 0 or null (cf. Figure 1a). Note that to describe an instance of the proposed algorithm, the message sequence is set to A → B → C for simplicity. The actual message sequence can be different and random.
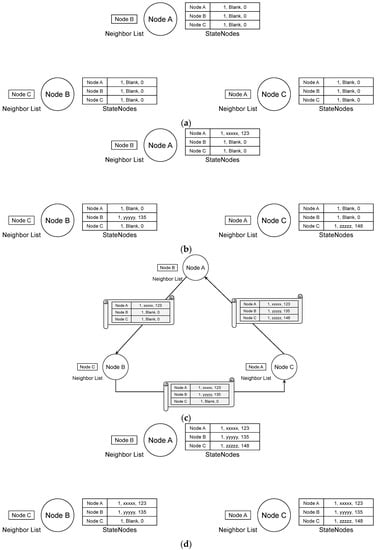
Figure 1.
An illustrative example of the proposed snapshot protocol. (a) Initial state; (b) After updating local information; (c) Message exchange; (d) Nodes’ state after one round.
Figure 1b shows the nodes’ states after updating local information. For instance, Node A’s state is <1, xxxxx, 123>. This means that the timestamp value of the state “xxxxx” is 123. Figure 1c depicts the message exchange process. Suppose Node A first sends its stateNodes data structure to Node B. After receiving Node A’s stateNodes data structure, Node B updates its stateNodes data structure according to Algorithm 2. Then, Node B sends its stateNodes data structure to Node C. Note that the message sent by Node B contains two elements for Node A and Node B.
After receiving Node B’s stateNodes data structure, Node C updates the stateNodes data structure accordingly. At this stage, Node C’s stateNodes data structure contains all the elements for three nodes. Hence, Node C can propose a consistent global state in the next round. Next, Node C sends its stateNodes data structure to Node A. By executing Algorithm 2, Node A also updates its stateNodes data structure.
Figure 1d shows the nodes’ state after the first round. In the second round, Node A and Node C will propose a consistent global state since their stateNodes data structures are collected. However, Node B is not able to propose a consistent global state because one element of the stateNodes data structure is empty. Nevertheless, Node B will be able to propose a consistent global state in the third round after performing the message exchange process in the second round.
As for the neighbor list, each element can be constructed by the peer sampling service [41], and the size of the neighbor list can be small regardless of the number of nodes in the system (e.g., 20) [12]. This configuration does not hinder the correctness of the algorithm and the probability of network partitioning is exponentially low [42]. When the size of the neighbor list is set to 20, the expected number for nodei’s information appearing in the sum of neighbor lists in the system is 20 since the peer sampling service is based on uniformity of randomness. In this regard, the probability that other nodes do not contact nodei becomes extremely low as the round number increases. Hence, all the nodes’ information will be aggregated as the round progresses. In addition, our algorithmic design of the snapshot protocol does not rely on a central authority or super node. Hence, no single point of failure or performance bottleneck exists.
It is worth noting that a round finishes after a predefined period. Because we let individual nodes include a round number of messages, they are able to maintain the stateNodes data structures for previous rounds despite the expiration of the predefined period. Furthermore, if a new node is added or an existing node is removed, the following operations are performed with the peer sampling service [41]. When a node encounters a nonexistent node, the node calls the peer sampling service and replaces the nonexistent node’s information with newly retrieved neighbor information from the peer sampling service.
For newly joined nodes, the peer sampling service is involved. That is, the peer sampling service regularly checks the newly joined nodes and pushes information of newly joined nodes to the existing nodes. Therefore, scalability can be achieved without a bottleneck or performance overheads. As for the stateNodes data structure, the size of one element of the stateNodes data structure is 3 × 64 bits (node number, round number, and timestamp) + size of a state. If we assume that the size of a state is 64 bit × 50 × 50 for a 50 × 50 matrix, the size of one stateNodes data structure is about 20 KB. When we compress the stateNodes data structure, the size is reduced by about 90% [43]. Considering the modern network bandwidth, the network will not be congested.
4.3. Intervention of the Snapshot Protocol
Figure 2 depicts the snapshot stage in an artificial intelligence computation. A user submits an artificial intelligence application to the cloud computing environment. We consider the artificial intelligence application to be iterative. For input data, the cloud initiates the process of computation. Since the artificial intelligence computation requires iterations, the output of a round feeds back to the input for the next round. Note that a round consists of data input, iteration, and data output (intermediate data).
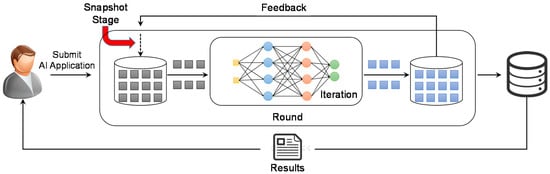
Figure 2.
The intervention of the snapshot protocol in artificial intelligence computation.
Before starting the next round, our proposed snapshot protocol fetches the state of the node and then starts the process of taking a snapshot based on the fetched data. If a node fails, the cloud retrieves the latest snapshot and the node can resume the artificial intelligence computation from the latest snapshot by provisioning a new node, thereby reducing the processing time and SLA violation. In addition, our snapshot protocol can be used in various artificial intelligence applications since our distributed snapshot protocol is not dependent on a specific workflow.
For data storage, the proposed snapshot protocol can utilize the cloud storage system. In a typical distributed system, data will be lost when a node fails. However, in a cloud computing environment, the data storage of a virtual machine is connected by a block storage service. Therefore, even though a virtual machine may fail, the data storage can be attached to a newly provisioned virtual machine. Furthermore, snapshot data can also be stored in the cloud storage system and replicated to increase the availability.
4.4. Proof of the Protocol
We prove that our proposed algorithms satisfy the following conditions:
where proposeGS(nodei, r, t) means that nodei proposes a consistent global state for round r at time t and consistentState(r) indicates that there exists a consistent global state for the round r.
Correctness: ∀i,r,t [proposeGS(nodei, r, t) ⇒ consistentState(r)],
Safety: ∀r,i ∃t [consistentState(r) ⇒ proposeGS(nodei, r, t)].
Liveness: ∀r ∃i,t [consistentState(r) ⇒ proposeGS(nodei, r, t)].
Theorem 1.
The proposed distributed snapshot protocol satisfies the correctness condition.
Proof.
The proof is by contradiction. Suppose that the proposed distributed snapshot protocol does not satisfy the correctness condition. This means that it is possible that a node proposes a consistent global state for a specific round, but no consistent global state exists for the round. Let nodei be the node that proposes a consistent global state for a round r. Based on the specification of the proposed algorithm, nodei waits for the stateNodes data structure to be aggregated before it proposes a consistent global state. Since nodei is a correct node, it does not propose a consistent global state until the stateNodes data structure is aggregated for all the nodes in the system. After aggregating the stateNodes data structure for the round r, nodei checks whether the collected states satisfy the consistent global state, that is, (1) send(mij) ∈ LSi ⇒ mij ∈ SCij ⊕ receive(mij) ∈ LSj and (2) send(mij) ∉ LSi ⇒ mij ∉ SCij ⋀ receive(mij) ∉ LSj. If Condition 1 and Condition 2 are met for the stateNodes data structure, nodei performs the proposeGS function with a timestamp value. Otherwise, nodei does not propose a consistent global state. In other words, nodei proposes a consistent global state for the round r if, and only if, there exists a consistent global state for the round r. This is a contradiction. Hence, the proposed distributed snapshot protocol satisfies the correctness condition. ☐
Theorem 2.
The proposed distributed snapshot protocol satisfies the safety condition.
Proof.
The proof is by contraposition. In logic, contraposition is an inference that says that a conditional statement is logically equivalent to its contrapositive. The contrapositive of the statement has its antecedent and consequent inverted and flipped. That is, the contrapositive of P → Q is thus Q → P. In this regard, the contraposition of the safety condition is the same as the correctness condition. Hence, the proposed distributed snapshot protocol satisfies the safety condition. ☐
Theorem 3.
The proposed distributed snapshot protocol satisfies the liveness condition.
Proof.
The proof is by induction.
Basis: There is one node in the system.
Let nodei be the node in the system. Since there is one node in the system, nodei performs the proposed algorithm in every round and updates its own local information. According to the specification of the algorithm, the updated local information of nodei is stored in the stateNodes data structure. Since the size of the stateNodes data structure is 1, checking a consistent global state is trivial. In other words, in every round, nodei updates its local information and proposes a consistent global state by checking Condition 1 and Condition 2. Because there is no message from the send() and receive() functions, the state is always consistent. Hence, the proposed distributed snapshot protocol satisfies the liveness condition when there is one node in the system.
Induction step (1): There are k nodes in the system.
Suppose the proposed distributed snapshot protocol satisfies the liveness condition when there are k nodes in the system.
Induction step (2): There are k + 1 nodes in the system.
We consider a specific round r henceforth. Based on the induction step (1), the proposed distributed snapshot protocol satisfies the liveness condition when there are k nodes in the system. When there are k + 1 nodes in the system, the same is applied to prove the liveness condition when there are k nodes in the system. Let nodek+1 be the (k + 1)th node in the system. Suppose k nodes’ stateNodes data structures are aggregated except nodek+1. Since nodek+1 is a correct node, nodek+1 follows the specification of the proposed snapshot protocol. Therefore, nodek+1 updates its local information and saves it to stateNodes. The situations where a node proposes a consistent global state are twofold. One is when nodek+1 sends its stateNodes data structure to a neighbor node. In this case, the receiving neighbor can propose a consistent global state because the receiving neighbor’s stateNodes data structure is aggregated for all the nodes. At the same time, nodek+1 also can propose a consistent global state by retrieving the receiving node’s stateNodes data structure. The other one is when nodei (nodei ≠ nodek+1) selects nodek+1 as a neighbor to target and retrieves nodek+1‘s stateNodes data structure. In this situation, both nodei and nodek+1 can propose a consistent global state for the same reason. In short, the local information of nodek+1 will be disseminated to all other nodes in the system and, eventually, all of the nodes in the system can determine whether it is a consistent global state or not. Hence, the proposed distributed snapshot protocol satisfies the liveness condition when there are k + 1 nodes. ☐
5. Performance Evaluation
In this section, we carry out performance results to demonstrate the efficiency and effectiveness of our proposed distributed snapshot protocol. For the artificial intelligence computation, we use a wine quality data set (https://archive.ics.uci.edu/ml/datasets/wine+quality) to predict wine types—red or white—and build multilayer perceptrons for classification tasks. To validate our proposed distributed snapshot protocol, the size of the data set is shrunk and, therefore, the processing time for the artificial intelligence computation is negligible. At the same time, we build an experimental environment with a discrete event simulator for scalability in terms of the number of nodes. In our experiments, we assume that there are numerous nodes in the system—from 50 to 50,000. The protocol mode is either normal or piggyback. The normal mode does not send or receive the stateNodes data structure, while the piggyback mode does. The size of the neighbor list is set to 20 unless specified otherwise. In other words, each node maintains up to 20 neighbors. The iteration for the artificial intelligence computation is set to 20. The number of rounds is set to 10. Experimental parameters and their values are listed in Table 1.

Table 1.
Experimental parameters and their values.
Figure 3 shows the number of aggregated nodes in logarithmic scale for Round 1. The numbers in the graph are averaged over the number of nodes in the system. In normal mode (cf. Figure 3a), the number of aggregated nodes increases as the number of rounds increases. However, the requisite number of rounds for checking a consistent global state is suboptimal. Note that to check a consistent global state, all the elements of the stateNodes data structure need to be aggregated. In normal mode, the requisite number of rounds is 5 when the number of nodes is 50. On the other hand, in piggyback mode, the requisite number of rounds is 2 when the number of nodes is 50 (cf. Figure 3b).
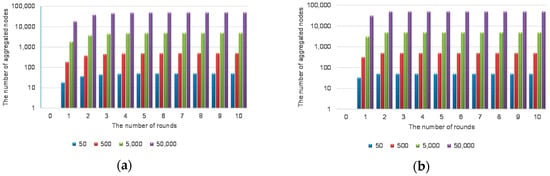
Figure 3.
The number of aggregated nodes in logarithmic scale for Round 1. (a) Normal mode; (b) Piggyback mode.
When the number of nodes is 500, the number of aggregated nodes is 499 in normal mode, even in Round 10, while the number of aggregated nodes is 500 in piggyback mode in Round 2. This means that in normal mode, no node can propose a consistent global snapshot after Round 10. On the other hand, in piggyback mode, a node can propose a consistent global snapshot after two rounds. In other words, if there exists a consistent global snapshot in round r, a node can propose a consistent global snapshot in the (r + 1)th round with the proposed distributed snapshot protocol. This result shows the effectiveness of the proposed distributed snapshot protocol.
Even when the numbers of nodes are 5000 and 50,000, the requisite number of rounds is 2 in piggyback mode. The average number of aggregated nodes for Round 1 is depicted in Figure 4. Note that the numbers are normalized between 0 and 1. We confirm that the performance of another instance of the protocol (besides Round 1) is the same. For another instance of the protocol (e.g., Round 2) the stateNodes data structure for Round 2 can also be piggybacked. Hence, the number of messages does not increase when another instance of the protocol is in progress.
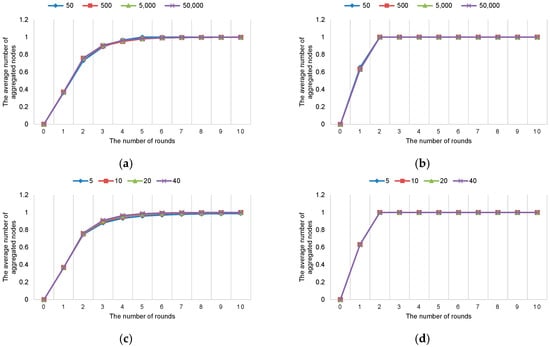
Figure 4.
The average number of aggregated nodes for Round 1. (a) Normal mode with varying number of nodes; (b) Piggyback mode with varying number of nodes; (c) Normal mode with different size of neighbor list when the number of nodes is 50,000; (d) Piggyback mode with different size of neighbor list when the number of nodes is 50,000.
To show the effect of the size of the neighbor list, we vary the size of the neighbor list when the number of nodes is 50,000 (cf. Figure 4c,d). Comparing the normal and piggyback modes, the piggyback mode outperforms the normal mode. The effect of the size of the neighbor list is negligible in piggyback mode. In normal mode, the worst performance can be found when the size of the neighbor list is 5. The reason for this is that the uniformity of randomness is relatively lower when the size of the neighbor list is small than when it is large. Nevertheless, this experiment implies that the effect of the size of the neighbor list is insignificant, since the probability of being selected from other nodes is 1 each round.
It is interesting to note that Figure 4a–d appear to be fairly symmetric. These results signify that our distributed snapshot protocol is scalable in terms of the number of nodes and maintenance of the neighbor list. More specifically, even when the number of nodes increases exponentially, the proposed protocol guarantees effectiveness and efficiency. This is a main advantage of the unstructured overlay network. Note that similar results to ours can be found in [12]. In contrast, in structured overlay networks (e.g., distributed hash table (DHT) or content addressable network (CAN)), increasing the number of nodes results in performance degradation due to lookup time and maintenance cost.
Figure 5 shows the standard deviation of the number aggregated nodes for Round 1. Note that the standard deviation is a measure to quantify the amount of variation or dispersion of a set of data values. A low standard deviation indicates that the data points tend to be close to the mean of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values. In our experiment, a low standard deviation implies more stable properties of the algorithm than a high standard deviation. The standard deviation of the piggyback mode is relatively higher than that of the normal mode. Specifically, the standard deviation of the normal mode in Round 1 is about 8, 90, 900, and 9.036 when the number of nodes is 50, 500, 5000, and 50,000, respectively. On the other hand, the standard deviation of the piggyback mode in Round 1 is about 13, 142, 1420 and 14,214 when the number of nodes is 50, 500, 5000, and 50,000, respectively. However, the standard deviation of the piggyback mode in Round 2 is 0, regardless of the number of nodes in the system.
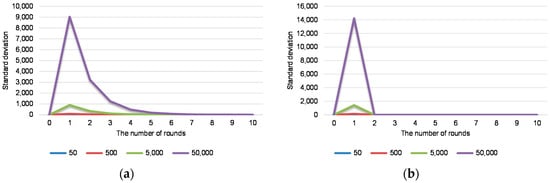
Figure 5.
The standard deviation of the number aggregated nodes for Round 1. (a) Normal mode; (b) Piggyback mode.
As far as message complexity is concerned, the number of messages in one round is n, where n is the number of nodes in the system, since the proposed distributed snapshot protocol uses the one-to-one communication model. On the other hand, previous protocols based on broadcast primitives introduce n2 messages in one round. Table 2 details the cumulative number of messages in comparison with previous protocols when the number of nodes is 50,000. As the number of nodes increases, the gap between previous protocols and our protocol goes far beyond logarithmic scale. Furthermore, unlike the broadcast-based snapshot protocol, our approach maintains a small number of neighbors in the list. This signifies the efficiency of the proposed distributed snapshot protocol.

Table 2.
The cumulative number of messages and size of received data for a node in comparison with previous protocols when the number of nodes is 50,000.
The second category of Table 2 shows the cumulative size of received data for a node when the number of nodes is 50,000. The uncompressed size of intermediate data including annotations and comments is about 2.95 KB, and its compressed size is 872 B. Each node in the broadcast-based protocol receives about 41.5 MB when the number of nodes in the system is 50,000. When the proposed protocol is used in normal mode, each node receives 872 B. On the other hand, when the piggyback mode is used in the proposed protocol, the size of the received data is the same as the broadcast-based protocol. However, in Round 1, the size of the received data of the piggyback mode is about 26.2 MB since about 37% of the stateNodes data structure is empty, on average.
There is a tradeoff between the requisite number of rounds and the size of the intermediate data for the normal mode and the piggyback mode. When the requisite number of rounds is crucial for resource management, the piggyback mode is preferred. On the other hand, if the network traffic is a great concern of the system, the normal mode is a better choice with marginal performance degradation. However, when the number of nodes is small (e.g., 100), the piggyback mode will be preferable since the size of the received data in one round for a node will be about 85.1 KB when the number of nodes is 100.
6. Conclusions
In this paper, we proposed a distributed snapshot protocol for artificial intelligence computation. Our proposed snapshot protocol differs from previous approaches in that our algorithmic design uses the one-to-one communication model and maintains a small subset of neighbor nodes, thereby reducing the message complexity. By taking advantage of the cloud computing environment, our proposed snapshot protocol is able to deal with various artificial intelligence applications that exhibit iterative behavior. The performance results show that our snapshot protocol performs well even when the number of nodes increases exponentially. With our snapshot protocol, the processing time can be reduced in the presence of failures by resuming the artificial intelligence computation from the latest snapshot, while minimizing SLA violation. The proof of the algorithm shows that our snapshot protocol satisfies the correctness, safety, and liveness conditions. Future work is to incorporate the proposed snapshot protocol into various resource management modules in cloud computing environments so that a cloud administrator can benefit from our snapshot protocol. More specifically, the proposed snapshot protocol can be used not only for artificial intelligence computation but also for general-purpose computation by virtual machines since our scheme is implemented in a modular way while preserving portability.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A3B03933370 and NRF-2015R1D1A1A01061373), and by Next-Generation Information Computing Development Program through the NRF funded by the Ministry of Science, ICT (2017M3C4A7081955).
Author Contributions
All the authors contributed equally to the work. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hassabis, D. Artificial intelligence: Chess match of the century. Nature 2017, 544, 413–414. [Google Scholar] [CrossRef]
- Moravčík, M.; Schmid, M.; Burch, N.; Lisý, V.; Morrill, D.; Bard, N.; Davis, T.; Waugh, K.; Johanson, M.; Bowling, M. Deepstack: Expert-level artificial intelligence in heads-up no-limit poker. Science 2017, 356, 508–513. [Google Scholar] [CrossRef] [PubMed]
- Cristea, D.S.; Moga, L.M.; Neculita, M.; Prentkovskis, O.; Md Nor, K.; Mardani, A. Operational shipping intelligence through distributed cloud computing. J. Bus. Econ. Manag. 2017, 18, 695–725. [Google Scholar] [CrossRef]
- Chen, G.; Wang, E.; Sun, X.; Lu, Y. An intelligent approval system for city construction based on cloud computing and big data. Int. J. Grid High Perform. Comput. 2016, 8, 57–69. [Google Scholar] [CrossRef]
- Grzonka, D.; Jakóbik, A.; Kołodziej, J.; Pllana, S. Using a multi-agent system and artificial intelligence for monitoring and improving the cloud performance and security. Futur. Gener. Comput. Syst. 2017, in press. [Google Scholar] [CrossRef]
- Jula, A.; Sundararajan, E.; Othman, Z. Cloud computing service composition: A systematic literature review. Expert Syst. Appl. 2014, 41, 3809–3824. [Google Scholar] [CrossRef]
- Khoobjou, E.; Mazinan, A.H. On hybrid intelligence-based control approach with its application to flexible robot system. Hum.-Centric Comput. Inf. Sci. 2017, 7, 5. [Google Scholar] [CrossRef]
- Shi, B.; Li, B.; Cui, L.; Zhao, J.; Li, J. Syncsnap: Synchronized Live Memory Snapshots of Virtual Machine Networks. In Proceedings of the 16th IEEE International Conference on High Performance Computing and Communications, Paris, France, 20–22 August 2014; pp. 490–497. [Google Scholar]
- Han, S.; Shen, H.; Kim, T.; Krishnamurthy, A.; Anderson, T.; Wetherall, D. Metasync: Coordinating storage across multiple file synchronization services. IEEE Int. Comput. 2016, 20, 36–44. [Google Scholar] [CrossRef]
- Qiang, W.; Jiang, C.; Ran, L.; Zou, D.; Jin, H. Cdmcr: Multi-level fault-tolerant system for distributed applications in cloud. Secur. Commun. Netw. 2016, 9, 2766–2778. [Google Scholar] [CrossRef]
- He, J.; Wu, Y.; Fu, Y.; Zhou, W. Snapshot-based data index in cloud storage systems. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; pp. 784–788. [Google Scholar]
- Lim, J.; Suh, T.; Yu, H. Unstructured deadlock detection technique with scalability and complexity-efficiency in clouds. Int. J. Commun. Syst. 2014, 27, 852–870. [Google Scholar] [CrossRef]
- Lim, J.; Chung, K.-S.; Gil, J.-M.; Suh, T.; Yu, H. An unstructured termination detection algorithm using gossip in cloud computing environments. In Proceedings of the 26th International Conference on Architecture of Computing Systems (ARCS 2013), Prague, Czech Republic, 19–22 February 2013; Kubátová, H., Hochberger, C., Daněk, M., Sick, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–12. [Google Scholar]
- Lim, J.; Chung, K.-S.; Chin, S.-H.; Yu, H.-C. A gossip-based mutual exclusion algorithm for cloud environments. In Proceedings of the 7th International Conference on Advances in Grid and Pervasive Computing, Hong Kong, China, 11–13 May 2012; Li, R., Cao, J., Bourgeois, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 31–45. [Google Scholar]
- Lim, J.; Suh, T.; Gil, J.; Yu, H. Scalable and leaderless byzantine consensus in cloud computing environments. Inf. Syst. Front. 2014, 16, 19–34. [Google Scholar] [CrossRef]
- Kavakiotis, I.; Tsave, O.; Salifoglou, A.; Maglaveras, N.; Vlahavas, I.; Chouvarda, I. Machine learning and data mining methods in diabetes research. Comput. Struct. Biotechnol. J. 2017, 15, 104–116. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Yu, Z.; Gu, F.; Li, T.; Tian, X.; Pan, Y. Deep learning in genomic and medical image data analysis: Challenges and approaches. J. Inf. Process. Syst. 2017, 13, 204–214. [Google Scholar]
- Zhuang, Y.-T.; Wu, F.; Chen, C.; Pan, Y.-H. Challenges and opportunities: From big data to knowledge in ai 2.0. Front. Inf. Technol. Electron. Eng. 2017, 18, 3–14. [Google Scholar] [CrossRef]
- Makridakis, S. The forthcoming artificial intelligence (ai) revolution: Its impact on society and firms. Futures 2017, 90, 46–60. [Google Scholar] [CrossRef]
- Maillo, J.; Ramírez, S.; Triguero, I.; Herrera, F. Knn-is: An iterative spark-based design of the k-nearest neighbors classifier for big data. Knowl.-Based Syst. 2017, 117, 3–15. [Google Scholar] [CrossRef]
- Erb, B.; Meißner, D.; Habiger, G.; Pietron, J.; Kargl, F. Consistent retrospective snapshots in distributed event-sourced systems. In Proceedings of the 2017 International Conference on Networked Systems (NetSys), Gottingen, Germany, 13–16 March 2017; pp. 1–8. [Google Scholar]
- Zhang, Y.; Gao, Q.; Gao, L.; Wang, C. Maiter: An asynchronous graph processing framework for delta-based accumulative iterative computation. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2091–2100. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, L.; Gu, Y.; Bao, Y.; Yu, G. A fault-tolerant framework for asynchronous iterative computations in cloud environments. In Proceedings of the Seventh ACM Symposium on Cloud Computing, Santa Clara, CA, USA, 5–7 October 2016; pp. 71–83. [Google Scholar]
- Zhang, Y.; Liao, X.; Jin, H.; Gu, L.; Tan, G.; Zhou, B.B. Hotgraph: Efficient asynchronous processing for real-world graphs. IEEE Trans. Comput. 2017, 66, 799–809. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Y.; Bao, Y.; Yu, G.; Gao, L. An i/o-efficient and adaptive fault-tolerant framework for distributed graph computations. Distrib. Parallel Databases 2017, 35, 177–196. [Google Scholar] [CrossRef]
- Chandy, K.M.; Lamport, L. Distributed snapshots: Determining global states of distributed systems. ACM Trans. Comput. Syst. 1985, 3, 63–75. [Google Scholar] [CrossRef]
- Egwutuoha, I.P.; Levy, D.; Selic, B.; Chen, S. A survey of fault tolerance mechanisms and checkpoint/restart implementations for high performance computing systems. J. Supercomput. 2013, 65, 1302–1326. [Google Scholar] [CrossRef]
- Kim, Y.; Araragi, T.; Nakamura, J.; Masuzawa, T. A concurrent partial snapshot algorithm for large-scale and dynamic distributed systems. IEICE Trans. Inf. Syst. 2014, 97, 65–76. [Google Scholar] [CrossRef]
- Rezaei, A.; Coviello, G.; Li, C.-H.; Chakradhar, S.; Mueller, F. Snapify: Capturing snapshots of offload applications on xeon phi manycore processors. In Proceedings of the 23rd International Symposium on High-Performance Parallel and Distributed Computing, Vancouver, BC, Canada, 23–27 June 2014; pp. 1–12. [Google Scholar]
- Cui, L.; Li, J.; Wo, T.; Li, B.; Yang, R.; Cao, Y.; Huai, J. Hotrestore: A fast restore system for virtual machine cluster. In Proceedings of the 28th Large Installation System Administration Conference (LISA14), Seattle, WA, USA, 9–14 November 2014; pp. 10–25. [Google Scholar]
- Özsu, M.T.; Valduriez, P. Distributed and parallel database systems. ACM Comput. Surv. 1996, 28, 125–128. [Google Scholar] [CrossRef]
- Corbett, J.C.; Dean, J.; Epstein, M.; Fikes, A.; Frost, C.; Furman, J.J.; Ghemawat, S.; Gubarev, A.; Heiser, C.; Hochschild, P.; et al. Spanner: Google’s globally distributed database. ACM Trans. Comput. Syst. 2013, 31, 1–22. [Google Scholar] [CrossRef]
- Ricart, G.; Agrawala, A.K. An optimal algorithm for mutual exclusion in computer networks. Commun. ACM 1981, 24, 9–17. [Google Scholar] [CrossRef]
- Maekawa, M. A √n algorithm for mutual exclusion in decentralized systems. ACM Trans. Comput. Syst. 1985, 3, 145–159. [Google Scholar] [CrossRef]
- Sriwanna, K.; Boongoen, T.; Iam-On, N. Graph clustering-based discretization of splitting and merging methods (graphs and graphm). Hum. Centric Comput. Inf. Sci. 2017, 7, 21. [Google Scholar] [CrossRef]
- Helary, J.-M. Observing global states of asynchronous distributed applications. In Proceedings of the 3rd International Workshop on Distributed Algorithms, Nice, France, 26–28 September 1989; Bermond, J.-C., Raynal, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 124–135. [Google Scholar]
- Birman, K.; Schiper, A.; Stephenson, P. Lightweight causal and atomic group multicast. ACM Trans. Comput. Syst. 1991, 9, 272–314. [Google Scholar]
- Kshemkalyani, A.D.; Raynal, M.; Singhal, M. An introduction to snapshot algorithms in distributed computing. Distrib. Syst. Eng. 1995, 2, 224. [Google Scholar] [CrossRef]
- Schneider, F.B. Byzantine generals in action: Implementing fail-stop processors. ACM Trans. Comput. Syst. 1984, 2, 145–154. [Google Scholar] [CrossRef]
- Lim, J.; Chung, K.-S.; Lee, H.; Yim, K.; Yu, H. Byzantine-resilient dual gossip membership management in clouds. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Jelasity, M.; Guerraoui, R.; Kermarrec, A.-M.; Steen, M.V. The peer sampling service: Experimental evaluation of unstructured gossip-based implementations. In Proceedings of the 5th ACM/IFIP/USENIX International Conference on Middleware, Toronto, ON, Canada, 18–22 October 2004; Springer: New York, NY, USA, 2004; pp. 79–98. [Google Scholar]
- Allavena, A.; Demers, A.; Hopcroft, J.E. Correctness of a gossip based membership protocol. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Principles of Distributed Computing, Las Vegas, NV, USA, 17–20 July 2005; pp. 292–301. [Google Scholar]
- El abbadi, N. An efficient storage format for large sparse matrices based on quadtree. Int. J. Comput. Appl. 2014, 105, 25–30. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).