Assessing the Impact of Urban Spatial Form on Land Surface Temperature Using Random Forest—Taking Beijing as a Case Study

Abstract

To examine the integrated influence of urban spatial form on the urban heat island (UHI) effect, this study selects the area within Beijing’s Fifth Ring Road as a case study. A multiscale grid system is established to quantify fourteen two- and three-dimensional morphological indicators. A Random Forest algorithm is employed to assess the relative importance of each factor. The optimal analytical scale for each key variable is then identified, and its nonlinear relationship with land surface temperature (LST) is analyzed at that scale. The main findings are as follows: (1) The Random Forest model achieves the highest predictive accuracy at a 600 m scale, significantly outperforming traditional linear models by effectively addressing multicollinearity. This suggests that machine learning offers robust technical support for UHI research. (2) Form variables exhibit distinct scale dependencies. Two-dimensional indicators dominate at medium to large scales, while three-dimensional indicators are more influential at smaller scales. Specifically, the mean building height is most significant at the 150 m scale, the standard deviation of building height at 300 m, and the impervious surface fraction at 600–1200 m. (3) Strong nonlinear effects are identified. The bare soil fraction below 0.12 intensifies surface warming; the water body fraction between 0.20 and 0.35 provides the strongest cooling; plant coverage offers maximum cooling between 0.25 and 0.45; building density cools below 0.3 buildings/hm² but contributes to warming beyond this threshold; building coverage ratio generates the greatest warming between 0.08 and 0.32; height variability provides optimal cooling between 8 m and 40 m; and mean building height shows a positive correlation with LST below 6 m but a negative one above that height.

1. Introduction

The concept of the urban heat island (UHI) was first introduced in 1833 [1] to describe the phenomenon whereby urban built-up areas exhibit higher temperatures than their rural counterparts. Currently, 55% of the global population resides in urban areas, and the United Nations’ World Urbanization Prospects projects this figure will rise to 66% by 2050 [2,3]. As urbanization accelerates, the UHI effect intensifies accordingly [4]. The Intergovernmental Panel on Climate Change (IPCC) has warned that, without substantial mitigation efforts, global warming could exceed 1.5 °C to 2 °C by the end of the century [5]. Estrada et al. analyzed 1692 major cities worldwide and found that UHIs significantly amplify global warming trends, with the largest cities experiencing the most severe temperature increases [6]. As a result, mitigating UHI impacts has become a central focus in urban climate research. Land surface temperature (LST), a sensitive indicator of climatic variation [7] emerged as a primary metric in UHI studies [8].

Urban spatial form describes the arrangement and organization of urban elements in both the horizontal plane and the vertical dimension [9]. Previous research has predominantly emphasized two-dimensional form, with surface-cover type often identified as the primary driver of the UHI effect. For instance, increases in the Normalized Difference Vegetation Index are reported to exert a significant cooling influence [10], while irregularly shaped green and blue spaces enhance local cooling [11]. A strong positive correlation between impervious-surface fraction and LST has been demonstrated, with UHI intensity rising sharply as built-up area expands [12]. As analytical grid size increases, the relationships between key factors such as building coverage, volumetric density, and urban windward surface index and LST are observed to vary substantially [13,14,15]. Low- to mid-rise clusters and large low-rise blocks have been found to exacerbate LST more than high-rise developments [16], whereas, in a global study of 2851 cities, compact mid- to high-rise forms with low floor-area ratios were shown to intensify UHIs most strongly, and dispersed high-ratio layouts to mitigate them [17]. Building density is identified as the most important determinant of LST [18], and analyses of sky view factor in Beijing indicate that taller buildings alter wind speed and heat release, thereby influencing UHI intensity [19]. At the block level, building coverage ratio, mean height, height standard deviation, and mean projected area have been determined as the primary drivers of average LST [20]. However, the relative importance of two- versus three-dimensional morphological indicators remains contested. Some studies suggest that vegetation coverage and impervious surface area are the most significant determinants of LST [21]. In contrast, other research [22,23] indicates that three-dimensional spatial indicators have a more pronounced impact on the urban heat island effect than their two-dimensional counterparts. These discrepancies underscore the complexity of the relationship between urban spatial form and LST.

Although the mechanisms by which two- and three-dimensional urban spatial morphology influence the urban thermal environment have been extensively examined, the UHI effect remains a complex, multi-causal, and multiscale phenomenon. Many studies continue to address only two- or three-dimensional form at a single scale. Prior research demonstrates that the impact of urban spatial morphology on LST is markedly scale-dependent [22] and that the relative importance of distinct morphological indicators varies with analytical scale [24]. For example, correlations between LST and key factors—such as building coverage, volumetric density, and urban windward surface index—change substantially as grid size increases [25]. Ge et al. [26] report that, at a 450 m scale, the relationship between building density and summer urban heat island intensity in Fuzhou is the strongest. Han et al. [27] find that, at an 840 m scale, all building intensity indicators exert the greatest influence on land surface temperature in Kaizhou District, Chongqing. Other studies [24] suggest that a 200 m radius is the optimal spatial scale for examining the relationship between urban block morphology and the canopy heat island effect. These variations in scale across studies indicate that the scale effect is a critical factor influencing such research and that the optimal scale differs for each factor. However, systematic multiscale analyses of the dependencies between urban form and LST are scarce, and the underlying mechanisms and relative contributions of two- versus three-dimensional forms remain insufficiently clarified. This gap underscores the need for comprehensive, in-depth research that integrates multidimensional morphology across multiple spatial scales.

The relationship between urban spatial morphology and LST is inherently complex and nonlinear, with multiple interacting factors exhibiting high collinearity. Traditional approaches—such as correlation analysis and multiple regression—produce intuitive and interpretable insights but are limited in their capacity to disentangle individual variable effects and to capture nonlinear interactions within high-dimensional datasets effectively [28]. In recent years, machine learning techniques have been increasingly applied in UHI research, highlighting the integration of advanced computational methods within environmental studies. Notable algorithms such as Random Forest [29], neural networks [30], and Categorical Boosting combined with Shapley Additive Explanations (CatBoost-SHAP) [31] have demonstrated superior performance. For instance, six machine learning models—including Adaptive Boosting (AdaBoost), Extreme Gradient Boosting (XGBoost), and Deep Neural Networks (DNNs)—have been employed to assess the influence of various landscape configuration metrics on surface temperature [32], and an artificial neural network was shown to predict LST with excellent generalization capability [33]. Machine learning effectively overcomes the expressive and predictive limitations of traditional methods by capturing nonlinear relationships between spatial patterns and LST and by mitigating multicollinearity among predictors. Random Forest (RF), in particular, has been shown to outperform conventional classification and regression techniques in complex environmental systems [34]. Compared with neural networks and XGBoost, RF affords a visual ranking of variable importance, thereby facilitating variable selection and interpretability analyses [35]. Moreover, it consistently achieves high predictive accuracy across diverse application domains [36]. Nevertheless, RF possesses notable limitations when applied to urban heat island studies. Spatial datasets often exhibit autocorrelation—such that proximate observations are statistically dependent—yet RF does not intrinsically account for spatial dependence, potentially compromising model fit and introducing bias. Additionally, its predictive reliability diminishes when extrapolating beyond the conditions represented in the training data [37]. In LST research, the model may fail to accurately forecast outcomes under extreme weather events or significant urban planning changes not reflected in the original dataset [38]. Therefore, while RF remains a robust analytical tool, its efficacy in UHI research can be enhanced by integrating strategies that address spatial autocorrelation and by combining it with complementary methods to improve generalizability and bias reduction.

In summary, the integrated effects of urban spatial form on LST are examined using the area within Beijing’s Fifth Ring Road as a case study. Grid cells are generated at five spatial scales to quantify fourteen two- and three-dimensional morphological variables. The RF algorithm is then employed to evaluate the relative importance of each variable across scales and to identify its optimal analytical scale. Finally, the nonlinear relationships between each key variable and LST are analyzed at their respective optimal scales. This methodology provides a theoretical foundation for UHI mitigation at the planning level and offers quantitative guidance for prioritizing critical morphological factors in contemporary urban renewal and future city-planning initiatives.

2. Research Area and Methodology

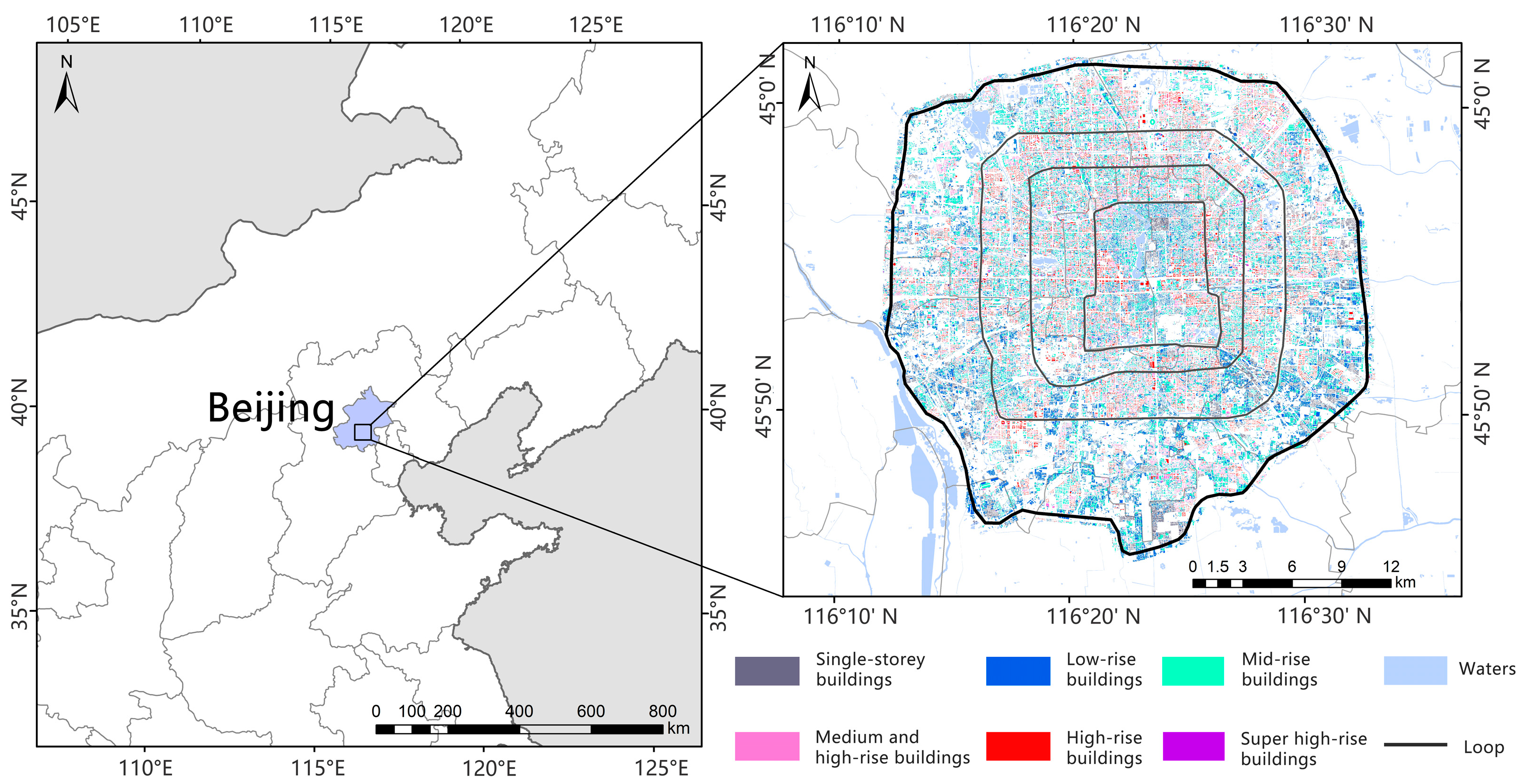
2.1. Overview of the Study Area

Beijing (39°26′–41°03′ N, 115°25′–117°30′ E) is located in the northern part of the North China Plain. It is the capital of China and a city renowned for its historical and cultural heritage. This study focuses on the central-southern part of Beijing, selecting the area within the Fifth Ring Road as the research site. This area covers 66,705 hm², accounting for 4.06% of the city’s total area (Figure 1).

As the core urban zone of Beijing, the study area features a complex and diverse spatial structure with relatively flat terrain. Building structures mainly shape their three-dimensional morphological characteristics. As a national central city and a megacity, the area suffers from a pronounced urban heat island effect. It is highly representative in terms of urban form, while the minimal impact of topography and landform makes it particularly suitable for investigating the multiscale influence of urban morphology on the heat island effect.

2.2. Data Sources

This study relies on three datasets. First, 30 m-resolution Landsat 8 OLI/TIRS imagery for Beijing, acquired on 19 July 2023, is employed. These data are pre-processed in ENVI (version 5.3) through radiometric calibration and atmospheric correction. Second, three-dimensional building distribution data are obtained via the Baidu Maps API (https://lbsyun.baidu.com), collected in June 2023 with a horizontal accuracy of approximately 3 m. Third, high-resolution Google Earth imagery is utilized to support the identification, calibration, and validation of both the Landsat 8 OLI/TIRS data and the Baidu building dataset.

2.3. Processing of Landsat 8 Data

2.3.1. Calculation of Vegetation Coverage

We first derive the Normalized Difference Vegetation Index (NDVI) for the study area using Equation (1). We then estimate plant coverage by applying Li’s [39] in Equation (2).

$$\mathrm{NDVI}={\displaystyle \frac{\mathrm{NIR}-\mathrm{R}}{\mathrm{NIR}+\mathrm{R}}}$$

(1)

$${\mathrm{P}}_{\mathrm{V}}={\displaystyle \frac{{\mathrm{NDVI}}_{\mathrm{n}}-{\mathrm{NDVI}}_{\mathrm{soil}}}{{\mathrm{NDVI}}_{\mathrm{veg}}-{\mathrm{NDVI}}_{\mathrm{soil}}}}$$

(2)

In Equation (1), $\mathrm{NIR}$ and $\mathrm{R}$ denote the reflectance values in the near-infrared and red bands, respectively. In Equation (2), ${\mathrm{NDVI}}_{\mathrm{soil}}$ represents the NDVI value of bare soil (or areas with no vegetation), ${\mathrm{NDVI}}_{\mathrm{veg}}$ represents the NDVI value of fully vegetated pixels, and ${\mathrm{NDVI}}_{\mathrm{n}}$ denotes the NDVI value of the target pixel.

2.3.2. LST Retrieval

We begin by calculating the land surface emissivity with the NDVI threshold method of Sobrino [40] (Equation (3)). Next, we derive the blackbody spectral radiance via the radiative transfer equation (Equation (4)). Finally, we convert this radiance to actual surface temperature at each pixel by applying the inverse of Planck’s law (Equation (5)).

$$\epsilon =0.004\mathrm{Pv}+0.986$$

(3)

$$\mathrm{B}\left({\mathrm{T}}_{\mathrm{s}}\right)={\displaystyle \frac{{\mathrm{L}}_{\lambda }-{\mathrm{L}}_{\mathrm{U}}-\tau (1-\epsilon ){\mathrm{L}}_{\mathrm{d}}}{\tau \epsilon }}$$

(4)

$${\mathrm{T}}_{\mathrm{s}}={\displaystyle \frac{{\mathrm{K}}_2}{\tau \ln [\frac{{\mathrm{K}}_1}{\mathrm{B}\left({\mathrm{T}}_{\mathrm{s}}\right)}+1]}}-273$$

(5)

In Equation (4), ${\mathrm{L}}_{\lambda }$ denotes the at-sensor radiance in the thermal infrared band; ${\mathrm{L}}_{\mathrm{U}}$ represents the upwelling atmospheric radiance; $\tau$ is the atmospheric transmittance; $\epsilon$ is the surface emissivity; and ${\mathrm{L}}_{\mathrm{d}}$ denotes the downwelling atmospheric radiance. In Equation (5), ${\mathrm{K}}_1$ and ${\mathrm{K}}_2$ are the band-specific calibration constants for Landsat 8 TIRS Band 10.

2.3.3. Land-Use and Land-Cover Classification

Land-cover types are classified into four categories—impervious surface, bare soil, water bodies, and plant—based on their distinct effects on the urban thermal environment and the specific conditions of the study area. To reduce random errors associated with a single-scene LST retrieval, a cloud-free, high-clarity Landsat 8 OLI/TIRS image from 19 July 2023 is selected. This date represents typical extreme heat conditions in Beijing and thus offers a representative snapshot of peak UHI characteristics [22]. Retrieved surface temperatures are validated against observations from multiple meteorological stations in Beijing, yielding strong agreement and confirming data reliability. In ENVI, the imagery is pan-sharpened to 15 m resolution, and supervised maximum-likelihood classification—guided by training samples derived from high-resolution Google Earth imagery—is applied, followed by clustering. The resultant land-cover map (Figure 2) attains an overall accuracy of 89.25%, satisfying the requirements of this study.

2.4. Calculation of Spatial Morphology Metrics

Four two-dimensional morphology metrics are selected: Patch area (PLAND), Largest Patch Index (LPI), Landscape Shannon Diversity Index (${\mathrm{SHDI}}_{\mathrm{LA}}$), and plant Coverage ($\mathrm{FVC}$). PLAND is computed by aggregating grid statistics in ArcGIS 10.8. LPI and SHDI_LA are calculated in Fragstats 4.2 using a moving-window approach. Window sizes of 90 m, 150 m, 210 m, 270 m, 330 m, 390 m, and 450 m (each corresponding to an integer multiple of the grid cell) are tested [41]. By analyzing the mean values and their stability across scales, the indices are found to stabilize at a 330 m window; this window size is therefore adopted for the final calculations.

Table 1. Calculation formulas and definitions of spatial morphology metrics.

Index Category	Spatial Morphology Index	Formula	Description
Two-Dimensional Spatial Morphology Indices	Patch area (PLAND)	$-$	Total area of each of the four patch types within each grid cell.
	Largest Patch Index (LPI)	$\mathit{LPI}={\displaystyle \frac{\mathit{max}\left({\mathit{a}}_{\mathit{ij}}\right)}{{\mathit{A}}_{\mathit{m}}}}\times 100\%$	${\mathit{a}}_{\mathrm{ij}}$ denotes the area of patch $\mathit{j}$ of class-$\mathit{i}$, and ${\mathit{A}}_{\mathit{m}}$ denotes the total area of the moving window $\mathit{m}$. The LPI indicates the intensity of disturbance from human activities.
	Landscape Shannon Diversity Index (SHDILA)	${\mathit{SHDI}}_{\mathit{LA}}=-{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{P}}_{\mathit{i}}\mathit{ln}\left({\mathit{P}}_{\mathit{i}}\right)$	${\mathit{P}}_{\mathit{i}}$ is the ratio of the total area of class-$\mathit{i}$ patches to the total area of the moving window. The ${\mathit{SHDI}}_{\mathit{LA}}$ index describes the landscape diversity of the region.
	Normalized Difference Vegetation Index (NDVI)	$\mathit{NDVI}={\displaystyle \frac{\mathit{NIR}-\mathit{R}}{\mathit{NIR}+\mathit{R}}}$	$\mathit{NIR}$ and $\mathit{R}$ denote the reflectance values in the near-infrared and red bands, respectively. The $\mathit{NDVI}$ represents the Normalized Difference Vegetation Index.
Three-Dimensional Spatial Morphology Indices	Building Diversity Index (SHDIAR)	${\mathit{SHDI}}_{\mathit{AR}}=-{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{G}}_{\mathit{i}}\mathit{ln}\left({\mathit{G}}_{\mathit{i}}\right)$	${\mathit{G}}_{\mathit{i}}$ is the ratio of the total area of class-$\mathit{i}$ buildings to the total area of the moving window. The ${\mathit{SHDI}}_{\mathit{AR}}$ index quantifies the building diversity of the region.
	Building Density (BD)	$\mathit{BD}={\displaystyle \frac{\mathit{N}}{{\mathit{A}}_{\mathit{i}}}}$	${\mathit{A}}_{\mathit{i} }$ denotes the total land area of the study region; $\mathit{N}$ denotes the total number of buildings within that region. The $\mathit{BD}$ is defined as the ratio of the number of buildings to the total land area of the region.
	Building Coverage Ratio (BCR)	$\mathit{BCR}={\displaystyle \frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{S}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}}$	${\mathit{S}}_{\mathit{i} }$ represents the footprint area of building $\mathit{i}$ within the study region. The $\mathit{BCR}$ is defined as the ratio of the total building footprint area to the total land area of the region.
	Mean Building Height (MBH)	$\mathit{MBH}={\displaystyle \frac{\sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{H}}_{\mathit{i}}}{\mathit{N}}}$	${\mathit{H}}_{\mathit{i} }$ denotes the height of building $\mathit{i}$ within the study region.
	Standard Deviation of Building Height (BHSD)	$\mathit{SDBH}=\sqrt{{\displaystyle \frac{\sum _{\mathit{i}=1}^{\mathit{n}}{({\mathit{H}}_{\mathit{i}}-\mathit{MBH})}^2}{\mathit{N}}}}$	The $\mathit{SDBH}$ reflects the dispersion and variability of building heights within the region.
	Building Crowding Degree (BCD)	$\mathit{BCD}={\displaystyle \frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{V}}_{\mathit{i}}}{\mathit{max}\left({\mathit{H}}_{\mathit{i}}\right)\times {\mathit{A}}_{\mathit{i}}}}$	${\mathit{V}}_{\mathit{i}}$ denotes the volume of building $\mathit{i}$ within the region. The $\mathit{BCD}$ is the percentage of the total volume of all buildings in the region relative to the city’s overall building volume.
	Standard Deviation of Building Volume (SDBV)	$\mathit{SDBV}=\sqrt{{\displaystyle \frac{\sum _{\mathit{i}=1}^{\mathit{n}}({\mathit{V}}_{\mathit{i}}{-\frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{V}}_{\mathit{i}}}{\mathit{N}})}^2}{\mathit{N}}}}$	The $\mathit{SDBV}$ reflects the dispersion and variability of building volumes within the region.
	Floor-Area Ratio (FAR)	$\mathit{FAR}={\displaystyle \frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{F}}_{\mathit{i}}\times {\mathit{S}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}}$	${\mathit{F}}_{\mathit{i}}$ denotes the number of storeys of building $\mathit{i}$. The $\mathit{FAR}$ indirectly reflects the residential density of the region.
	Building Shape Coefficient (BSC)	$\mathit{BSC}={\displaystyle \frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}\frac{{\mathit{P}}_{\mathit{i}}\times {\mathit{H}}_{\mathit{i}}+{\mathit{S}}_{\mathit{i}}}{{\mathit{V}}_{\mathit{i}}}}{\mathit{N}}}$	${\mathit{P}}_{\mathit{i}}$ denotes the perimeter of building $\mathit{i}$. The $\mathit{BSC}$ is one of the factors that determines urban heat loss and gain.

summarizes the computation methods and interpretations for each metric, and the processed spatial data are presented in Figure 3.

Nine three-dimensional morphology metrics are selected: Building Diversity Index (SHDI_AR), Building Density (BD), Building Coverage Ratio (BCR), Mean Building Height (MBH), Standard Deviation of Building Height (SDBH), Building Crowding Degree (BCD), Standard Deviation of Building Volume (SDBV), Floor-Area Ratio (FAR), and Building Shape Coefficient (BSC). SHDI_AR is calculated by classifying buildings into six height categories—single-storey, low-rise (2–3 storeys), mid-rise (4–6 storeys), upper-mid-rise (7–9 storeys), high-rise (10–33 storeys), and super high-rise (34+ storeys)—and applying a moving-window analysis. Following the same procedure as described for the two-dimensional metrics, a 150 m window is selected for the final computation based on its stability and representativeness. The calculation methods and interpretations for the remaining metrics are detailed in Table 1, and the processed spatial data are illustrated in Figure 4.

2.5. Raw Data Cleaning

The original dataset comprises seven two-dimensional and nine three-dimensional spatial morphology variables. In Random Forest modeling, correlation between independent variables and the dependent variable can improve predictive accuracy. However, excessive multicollinearity among independent variables may result in data redundancy, increase model complexity, and ultimately reduce algorithm performance. To mitigate these issues, pairwise correlation analysis was performed using the Pearson correlation coefficient. Variables exhibiting strong correlations with multiple other predictors were identified as redundant and subsequently excluded. After filtering, six two-dimensional spatial morphology metrics were retained for further analysis: impervious surface area (PLAND_IS), bare soil area (PLAND_BL), water body area (PLAND_WS), largest patch index (LPI), landscape diversity index (SHDI_LA), and plant coverage (PVC). Eight three-dimensional indices were retained: building diversity index (SHDI_AR), building density (BD), building coverage ratio (BCR), mean building height (MBH), standard deviation of building height (BHSD), building crowding degree (BCD), standard deviation of building volume (SDBV), and building shape coefficient (BSC).

The Pearson correlation coefficients for the fourteen spatial morphology indices are presented in Figure 5. The resulting feature set exhibits low redundancy and high explanatory power, thereby improving the stability and interpretability of the Random Forest algorithm.

2.6. Urban Heat Island Classification

Classifying LST or air temperature data facilitates clear visualization of the spatial gradients associated with the UHI effect. In this study, the mean-standard deviation method is employed to classify UHI intensity within the area enclosed by Beijing’s Fifth Ring Road. The mean value and standard deviation of LST were used as threshold points [42]. The formulas used to calculate heat island intensity are presented in

Table 2. Calculation formula for heat island intensity.

Temperature Level	Formulas	LST Range(°C)	Attribute Description
Low-temperature zone	${\mathit{T}}_{\mathit{s} } > \mu +\mathit{std}$	${\mathit{T}}_{\mathit{s}} <$42.30	Cold island zone
Sub-medium-temperature zone	$\mu +0.5\mathit{std} < {\mathit{T}}_{\mathit{s}} \le \mu +\mathit{std}$	42.30$<{ \mathit{T}}_{\mathit{s}} \le$43.74	Transition zone
Medium-temperature zone	$\mu - 0.5\mathit{std} \le { \mathit{T}}_{\mathit{s}} \le \mu +0.5\mathit{std}$	43.74$\le { \mathit{T}}_{\mathit{s}} \le$46.62
Sub-high-temperature zone	$\mu - \mathit{std} \le {\mathit{T}}_{\mathit{s}} < \mu - 0.5\mathit{std}$	46.62$\le { \mathit{T}}_{\mathit{s}} <$48.06	Heat island zone
High-temperature zone	${\mathit{T}}_{\mathit{s}} < \mu - \mathit{std}$	${\mathit{T}}_{\mathit{s}} >$48.06

, resulting in five temperature zones: high-temperature zone, sub-high-temperature zone, medium-temperature zone, sub-medium-temperature zone, and low-temperature zone.

2.7. Random Forest Model Construction

Random Forest (RF) is a machine learning algorithm originally proposed by Leo Breiman and Adele Cutler [43]. It constructs an ensemble of decision trees for prediction and classification, aggregating their outputs to enhance overall accuracy. This ensemble approach endows RF with strong noise resistance and reduced susceptibility to overfitting, while effectively addressing the multicollinearity issues that often compromise the performance of multiple linear regression models [44]. RF is well suited for multi-factor analyses of UHI effects. Previous studies have demonstrated that RF not only quantifies the relative contribution of each variable to LST more accurately than methods such as Multivariate Adaptive Regression Splines (MARS) and Generalized Additive Models (GAM), but also effectively captures nonlinear relationships between predictors and LST, offering superior explanatory power [21].

RF models were constructed in R (version 4.3.3) at five spatial resolutions: 150 m, 300 m, 600 m, 900 m, and 1200 m. This version of R is considered stable and offers broad compatibility with statistical and machine learning packages. These models are used to quantify the relative importance and scaling trends of urban morphology factors in influencing the urban heat island effect. To minimize scale-related bias, grid sizes were defined based on the original 30 m resolution of Landsat TM imagery and its integer multiples. Both two-dimensional and nine three-dimensional morphology variables were reclassified to align with these five grid scales. This uniform spatial framework ensures consistency across model inputs, enabling robust analysis of how the influence of urban form on the thermal environment varies with spatial scale.

Key RF parameters were tuned to optimize model accuracy and computational efficiency. The number of trees (ntree) influences ensemble stability and predictive accuracy, with larger values improving performance but increasing runtime. The number of variables randomly selected at each split (mtry) controls feature randomness; selecting too few variables may reduce model accuracy, whereas selecting too many can lead to overfitting. For each grid scale, the dataset was randomly divided into a training set (75%) and a test set (25%). During training, five-fold cross-validation with randomized parameter search was employed to enhance generalization and mitigate overfitting risk. Model performance was subsequently evaluated on the test set to verify stability and accuracy on unseen data. The optimal parameter combination across all scales was found to be ntree = 300 and mtry = 10, yielding consistently high predictive accuracy and predictive precision.

3. Results and Analysis

3.1. Spatial Distribution of the Urban Heat Island

Analysis of the heat-island intensity map for the Fifth Ring Road (Figure 6) shows that the low-temperature zone covers 11,185 hm², accounting for 15.60% of the total area within the Fifth Ring; the sub-medium-temperature zone covers 9001 hm², accounting for 12.56%; the medium-temperature zone covers 29,458 hm², accounting for 41.09%; the sub-high-temperature zone covers 12,122 hm², accounting for 16.91%; and the high-temperature zone covers 9915 hm², accounting for 13.83%.

From the overall spatial pattern, heat island intensity is higher in the south and lower in the north. The high-temperature zones are mainly distributed in the central and southern parts, with slightly greater intensity in the southwest than in the southeast. Cold islands are mainly found in the north.

By ring-road distribution: within the Second Ring Road, the area is 6257 hm², accounting for 9.38% of the Fifth Ring total. Of this, heat island zones cover 3181 hm²—only 14.82% of the total heat island area but 50.84% of the Second Ring area—indicating a severe local heat island effect; between the Second and Third Ring Roads, the area is 9573 hm², accounting for 14.35%. Heat island zones cover 3110.42 hm², similar to the Second Ring, but are dominated by sub-high-temperature zones. High-temperature zones decrease by 765.72 hm² compared with the Second Ring, accounting for 14.49% of the total heat island area. Between the Third and Fourth Ring Roads, the area is 8824.14 hm², accounting for 21.65%; heat island zones also cover 8824.14 hm², representing 22.47% of the total heat island area. Between the Fourth and Fifth Ring Roads, the area is 36,442.31 hm², accounting for 54.62%; heat island zones cover 10,348.99 hm², or 48.21% of the total heat island area, but only 28.40% of that ring’s area.

In summary, within the Second Ring Road, the heat island footprint is small, but intensity is high and distribution is dense; from the Second to Fourth Ring Roads, both intensity and density decline but remain substantial; although the Fourth–Fifth Ring zone has the largest heat island area, its overall temperature is relatively lower.

3.2. Distribution of the Random Forest Model

The RF model was constructed using spatial morphology indices to investigate their influence on LST. Model performance was evaluated using the variance explained on the training set and the R² on the test set, thereby assessing the combined explanatory power of two- and three-dimensional morphological variables in relation to the urban heat island effect [45]. The variance explained indicates the extent to which the predictors collectively account for LST variability, while the test-set R² reflects the model’s predictive accuracy on unseen data. Higher values for both metrics denote improved model performance.

Across all spatial scales, the RF model achieved a variance explained exceeding 75.49%, indicating that it captured the majority of LST variation. The test-set R² was greater than 76.66% at all scales, further confirming strong model fit. As summarized in

Table 3. Random forest model testing data.

Metrics	Scales
	150 m	300 m	600 m	900 m	1200 m
RMSE	0.0547	0.0506	0.0499	0.0519	0.0509
R2	0.7666	0.7990	0.8114	0.7782	0.7556
MAE	0.0421	0.0393	0.0386	0.0410	0.0402
Var explained	75.49	80.00	81.40	81.16	77.97
Mean of squared residuals	0.0031	0.0027	0.0025	0.0026	0.0036

, the highest performance was observed at the 600 m scale, with a variance explained of 81.40% and a test-set R² of 81.14%. Based on these results, the 600 m grid is selected for comprehensive analysis and prediction of heat island intensity within Beijing’s Fifth Ring Road.

3.3. Relative Importance of Spatial Morphology Factors

To assess the relative importance of each two- and three-dimensional morphology metric in explaining land surface temperature (LST), the increase in mean squared error (inMSE) was ranked across five spatial scales [46], as shown in

Table 4. Random forest relative importance calculation results.

Variable Categories	Impact Factors	Scales
		150 m	300 m	600 m	900 m	1200 m
Two-dimensional spatial morphological indices	PLAND_IS	38.97 (7)	30.34 (6)	38.35 (1)	22.62 (1)	22.89 (1)
	PLAND_BL	63.15 (2)	34.17 (4)	22.01 (4)	16.13 (3)	9.39 (6)
	PLAND_WS	62.85 (3)	35.61 (3)	20.76 (5)	12.86 (5)	18.27 (3)
	LPI	35.45 (9)	22.54 (13)	16.01 (10)	7.68 (10)	7.02 (8)
	SHDILA	41.91 (6)	25.83 (9)	17.24 (9)	8.06 (8)	5.25 (11)
	$\mathrm{PVC}$	33.48 (12)	27.38 (8)	17.26 (8)	18.60 (2)	19.43 (2)
Three-dimensional spatial morphological indices	SHDIAR	30.11 (13)	25.2 (10)	13.73 (12)	5.57 (12)	5.19 (12)
	BD	54.96 (5)	36.39 (2)	18.1 (6)	10.11 (7)	8.52 (7)
	BCR	36.29 (8)	25.01 (11)	22.88 (3)	12.53 (6)	11.09 (5)
	MBH	69.61 (1)	34.16 (5)	17.36 (7)	8.06 (9)	4.31 (13)
	BHSD	61.63 (4)	42.13 (1)	27.01 (2)	14.83 (4)	14.43 (4)
	BCD	30.03 (14)	21.52 (14)	14.06 (11)	4.64 (13)	3.33 (14)
	SDBV	35.02 (10)	29.75 (7)	13.32 (13)	6.73 (11)	5.8 (10)
	BSC	34.75 (11)	22.79 (12)	11.16 (14)	3.28 (14)	6.27 (9)

.

Among the two-dimensional indices, PLAND_IS consistently ranks first in importance from 600 m to 1200 m, indicating a stable and significant influence on LST. This finding indicates that PLAND_IS consistently exerts a stable and significant influence on LST. PLAND_WS fraction and PLAND_BL fraction also rank highly, showing that they strongly affect LST intensity. PVC ranks second only at the 900 m and 1200 m scales; at finer scales (150 m to 600 m), it falls below eighth place. This pattern reflects a clear scale dependency, suggesting that the plant’s cooling effect only becomes pronounced at larger spatial extents. Both SHDI_LA and LPI remain low in importance across all scales, indicating that their direct impact on LST is limited.

For three-dimensional indices, BHSD and BD occupy the top two ranks at the 300 m scale. They also maintain high importance at other scales, demonstrating a stable and significant effect on the heat island. MBH ranks first at the 150 m scale but declines steadily to thirteenth place as the scale increases. This trend may reflect a dual role: at microscales, taller individual buildings cast shadows and reduce local surface temperature, while at macro scales, their effect is diluted by the collective morphology of multiple structures. BCR ranks third in importance at the 600 m scale but falls behind at other scales, indicating an optimal scale for its effect. By contrast, the SHDI_AR, BCR, SDBV, and BSC all show relatively low importance, suggesting they play a minor role in explaining LST variation.

3.4. Scale-Effect Analysis of Key Factors

Key spatial morphology indices were first selected based on their ranking among the top three in importance at least once across the five spatial scales (150 m, 300 m, 600 m, 900 m, and 1200 m). From the two-dimensional set, four metrics were retained: PLAND_IS, PLAND_BL, PLAND_WS, and PVC. From the three-dimensional set, four metrics were also retained: BD, BCR, MBH, and BHSD. To assess the variation in relative importance with scale, scale-effect curves were plotted for each selected variable (Figure 7 and Figure 8).

Among the two-dimensional metrics, PLAND_IS ranks first at scales of 600 m and above, while PVC ranks second at 900 m and 1200 m. Both metrics demonstrate increasing influence on LST as scale increases, suggesting that impervious surfaces are the primary contributors to surface warming and vegetation is the dominant cooling factor, particularly at larger spatial extents. In contrast, PLAND_BL exhibits considerable fluctuation and a declining trend in importance with increasing scale. This pattern is likely due to the relatively small proportion of bare land within the study area: while isolated patches can have strong localized effects at fine scales, their influence diminishes at coarser resolutions. PLAND_WS ranks third at 150 m, 300 m, and 1200 m, but drops to fifth at 600 m and 900 m. Its importance follows a concave pattern, indicating that water bodies exert the strongest cooling effects at both very small and very large scales, whereas reduced spatial connectivity at intermediate scales may limit their thermal regulatory function.

In the three-dimensional metrics, MBH ranks first at 150 m but declines steadily to thirteenth at 1200 m. At fine scales, taller buildings cast shadows and thus strongly affect LST. At coarse scales, the collective form of many buildings dilutes this single-metric effect. Both the BHSD and BD show convex trends, peaking in importance at the 300 m scale (first and second, respectively). This finding indicates that both height variability and density are critical for temperature regulation, with 300 m as their optimal analytical scale. Notably, the BHSD consistently outranks BD at all scales, highlighting the greater influence of vertical variability over horizontal density. BCR ranks low at 150 m and 300 m, rises to third at 600 m, and remains above sixth at larger scales. This pattern suggests that BCR exerts a stable and effective moderating influence on temperature at coarse scales.

Overall, the combined importance of two-dimensional factors increases with scale, while that of three-dimensional factors decreases. This contrast shows that planar form factors become more dominant for temperature control at large scales, whereas vertical form factors have more direct effects at fine scales but are diluted as the scale expands. These results show that at small scales (150 m and 300 m), three-dimensional spatial form factors primarily influence the heat island effect, while at larger scales (900 m and 1200 m), two-dimensional spatial form factors play a more important role.

3.5. Nonlinear Relationships at Optimal Scales

Given the evident scale dependence of each morphology factor, the spatial scale at which each key variable ranked highest in importance was selected as its optimal analytical scale. The selected scales are as follows: PLAND_IS at 600 m; PVC at 900 m; PLAND_WS at 300 m; PLAND_BL at 150 m; BD at 300 m; BCR at 600 m; MBH at 150 m; and BHSD at 300 m. We then plotted each factor’s nonlinear response to LST at its optimal scale (Figure 9).

Among the two-dimensional metrics, both PLAND_IS and PLAND_BL fractions exhibit a clear positive correlation with LST. The warming effect of PLAND_IS is particularly pronounced: a 0.2 increase in impervious surface fraction results in an approximate 1 °C rise in LST, whereas the same increase in bare land fraction raises LST by only about 0.4 °C. In contrast, PVC and PLAND_WS are negatively correlated with LST. PVC demonstrates its strongest cooling effect within the 0.25–0.45 range, while PLAND_WS produces a stronger cooling effect than PVC, likely due to the high specific heat capacity and evaporative cooling properties of water bodies.

For the three-dimensional metrics, both BD and MBH exhibit threshold effects. At densities below 0.3 buildings/hm², BD is associated with a cooling effect; beyond this threshold, it contributes to warming. This pattern likely results from low-density configurations enhancing ground–air heat exchange and maintaining ventilation, whereas high-density development obstructs airflow and traps heat. MBH exhibits a cooling effect below 6 m but a pronounced warming effect above 6 m. This pattern likely arises because taller buildings inhibit horizontal wind flow, increasing temperatures; however, very tall structures also provide shading, generate wind corridors, and free up land for green spaces, which contribute to localized cooling. BCR demonstrates a positive correlation with LST across its full range, with the most pronounced warming observed between 0.08 and 0.32 coverage. High building coverage reduces surface albedo, increases solar energy absorption, and intensifies local heating. Beyond 0.32, the warming trend plateaus, suggesting that shading effects from dense structures partially offset additional heat accumulation. BHSD consistently correlates negatively with LST, with the strongest cooling observed between 8 m and 40 m. This is likely due to increased height variability promoting turbulent air exchange, which enhances ventilation and allows cooler air to penetrate deeper into the urban fabric, thereby reducing surface temperatures.

4. Discussion

4.1. Performance of the Random Forest Algorithm in the Study

The UHI prediction model developed using the RF algorithm demonstrated strong predictive performance across all spatial scales. At the 600 m grid resolution, the model achieved its highest accuracy, with an explained variance of 81.40% on the training dataset and R² of 81.14% on the validation dataset. These results confirm the algorithm’s effectiveness in modeling the relationship between spatial morphology and LST. RF is particularly well suited for handling high-dimensional, nonlinear, and collinear spatial data. The findings of this study are consistent with previous research. For instance, Oukawa et al. reported that the RF algorithm explained over 96% of the variance in both daytime and nighttime UHI conditions, significantly outperforming traditional multiple linear regression models [34]. The present study further validates the robustness of RF, which leverages an ensemble learning framework and a voting mechanism across multiple decision trees to reduce overfitting risk and enhance generalization [47]. As such, RF offers a reliable and interpretable approach for investigating the nonlinear and scale-dependent relationships between urban spatial form and the UHI effect.

As previously discussed, RF exhibits limited predictive capacity when applied to scenarios beyond the scope of the training dataset. In contrast, neural network algorithms are inspired by the structure of biological neurons in the human brain. They consist of multiple interconnected layers and learn complex patterns in data by iteratively adjusting weights and biases. Neural networks are particularly effective at handling nonlinear problems and have achieved outstanding performance in domains such as image recognition, speech processing, and natural language understanding. However, a key drawback of neural networks is their limited interpretability, which poses challenges for understanding and explaining model decisions [48]. To address this issue, future studies could consider using neural networks as feature extractors to capture high-level representations from complex input data. These extracted features could then be input into a Random Forest model for classification or regression. This hybrid approach would combine the feature learning capabilities of neural networks with the robustness and interpretability of RF, thereby enhancing both predictive performance and model transparency.

4.2. Relationships Between Spatial Morphology Factors and the LST

Among the two-dimensional indices, the fractions of PLAND_WS and PLAND_BL maintain a stable and significant influence on LST across all spatial scales. This consistency likely reflects their direct regulation of surface temperature through evaporative cooling and albedo effects, which tend to be less sensitive to changes in grid resolution [49]. Both PLAND_WS [50] and PVC [51] demonstrate increasing importance at larger scales, aligning with findings from macro-scale studies—such as those at the city or district level—that report stronger positive correlations between impervious surface extent and LST. In contrast, the SHDI_LA ranks low and is non-significant at every scale. Although some research identifies SHDI_LA as a key LST driver, this discrepancy may result from multi-factor coupling: the effects of PLAND_WS, PVC, and BD can overshadow the impact of diversity, pushing SHDI_LA’s relative importance downward.

In the three-dimensional indices, BHSD and BD consistently and significantly affect the LST [52]. Both factors serve as primary LST drivers with cross-scale applicability. MBH exerts its greatest effect at the 150 m scale—consistent with findings that height’s influence peaks at small-scale thresholds. BCR is most important at the 600 m scale, aligning with studies that report up to a 39.3% contribution of coverage ratio to block-level LST [24]. By contrast, SHDI_AR, BCD, SDBV, and BSC rank low in importance at all scales. Our study area’s relatively homogeneous mix of mid- to high-rise buildings may suppress variation in these metrics; further research in areas with more complex building forms is needed to assess their potential roles.

The dominant spatial morphology factors vary by scale. At the 150 m resolution, MBH emerges as the primary driver of LST. At 300 m, the BHSD becomes most influential, while from 600 m to 1200 m, PLAND_IS assumes the dominant role. In the context of Beijing’s Fifth Ring Road area, two-dimensional form factors exert greater influence at medium to large scales, whereas three-dimensional form factors are more impactful at finer scales. These findings are consistent with prior research [53] and further reinforce the identification of PLAND_IS, PLAND_WS, PLAND_BL, and PVC as the most important two-dimensional morphology metrics, along with BD, BCR, MBH, and BHSD as the key three-dimensional metrics shaping urban thermal environments.

Urban morphology factors and the UHI effect exhibit complex nonlinear relationships and distinct threshold behaviors, consistent with previous findings [54]. These patterns can be effectively analyzed using scale-appropriate RF models. Among the two-dimensional indices, PLAND_IS demonstrates a strong positive correlation with LST. In this study, its warming effect is nearly linear, and the per-percentage-point temperature increase is substantial. The temperature increase is substantial. This finding aligns with prior research, which has shown that impervious surfaces—such as roads and buildings—heat rapidly due to their low specific heat capacity and limited evaporative cooling, making them major contributors to UHI formation [55]. The positive relationship between PLAND_BL and LST has also been documented. Although each percentage increase in bare soil results in a smaller temperature rise than an equivalent increase in impervious surface, bare soil still contributes to urban warming. Its lack of vegetation cover and moisture buffering causes rapid heating under solar radiation [56]. The negative correlation between both PLAND_WS and PVC with LST is well established. Prior studies have shown that PLAND_WS play a key role in regulating the urban thermal environment; areas adjacent to water often exhibit lower temperatures, forming localized cold sources [57]. In this study, PLAND_WS produces its strongest cooling effect within the 0.20–0.35 range. Within this interval, the extent and spatial distribution of water bodies promote heat balance, increase evaporation, and facilitate local heat exchange, resulting in lower surface temperatures. PVC contributes to cooling primarily through evapotranspiration, which consumes latent heat and increases air humidity, thereby reducing LST and mitigating UHI intensity [58]. PVC delivers its strongest cooling effect between 0.25 and 0.45. This result aligns with other studies of urban green-space functions, which show that within this range, vegetation forms a relatively continuous and stable ecosystem, thereby maximizing its cooling and humidifying benefits [59]. It is further hypothesized that the cooling effect per percentage point of water bodies exceeds that of vegetation, owing to water’s higher specific heat capacity—a conclusion supported by comparative studies on surface thermal regulation [60]. Among the three-dimensional indices, BD demonstrates a nonlinear threshold effect on LST. When BD is below 0.3 buildings/hm², it contributes to cooling; however, above this threshold, it becomes a warming factor. Previous studies have found that moderate building density supports urban ventilation and heat exchange, thereby promoting cooling. In contrast, high-density development can impede airflow and produce a “canyon effect,” which traps heat and increases LST [61]. BCR is positively correlated with LST across its entire range, with the strongest warming observed between 0.08 and 0.32. At lower coverage levels, incremental increases in built area significantly enhance solar radiation absorption and heat accumulation. However, once BCR exceeds 0.32, the warming effect plateaus, possibly due to spatial constraints and the approach to local thermal equilibrium [62]. The BHSD is negatively correlated with LST across its entire range, with the strongest cooling effect occurring between 8 m and 40 m. This observation aligns with studies showing that moderate variations in building height can enhance air convection and heat exchange, thereby lowering temperature [63]. Buildings of varying heights create a staggered spatial layout that guides airflow into the urban interior, disrupts stable heat accumulation, and enhances ventilative cooling [64]. When MBH is below 6 m, it correlates positively with LST. Low, closed-in buildings hinder heat dissipation and do not block solar radiation effectively, causing surface warming. Once MBH exceeds 6 m, the correlation becomes negative. Taller buildings shade the ground, reducing heat absorption, and they channel airflow upward, enhancing vertical convection and accelerating heat removal, thereby lowering LST [52].

4.3. Urban Planning Strategies to Mitigate the Heat Island Effect Within Beijing’s Fifth Ring Road

This study demonstrates that effective mitigation of the UHI effect requires a comprehensive understanding of both two-dimensional and three-dimensional urban form, as well as a strategic application of each factor’s scale-dependent and nonlinear relationships with LST to maximize cooling benefits. A detailed analysis of key morphological drivers, their scale dependencies, and nonlinear responses reveals actionable insights for urban renewal and climate-adaptive planning. At small spatial scales (150 m and 300 m), three-dimensional form factors such as the standard deviation of BHSD and MBH are the most influential. Interventions at these scales should focus on manipulating building height variability to enhance turbulent airflow, promote convective heat exchange, and improve ventilation between urban and suburban areas—an approach supported by previous research [65]. This study refines the ranking of form-factor importance at each scale and highlights the mean building height’s critical role in local-scale cooling, offering a more nuanced perspective on form-thermal interactions. For medium- and large-scale interventions (600 m and above), attention should shift to two-dimensional land-use factors with high importance at these scales—namely PLAND_IS, PLAND_WS, and PCV. Planners can optimize the urban land-cover pattern by reducing impervious areas, expanding connected water features, and increasing green patches. By leveraging the nonlinear cooling effects of water and vegetation, they can create large-scale blue–green corridors and fully harness evapotranspiration and evaporative cooling to lower urban temperatures.

Two-dimensional and three-dimensional form factors interact in complex ways to influence LST. While previous multiscale studies often employed traditional linear models to identify key variables, such approaches risk overlooking nonlinear relationships and threshold effects. In contrast, the Random Forest method employed in this study captures both the scale-dependent importance and the nonlinear response curves of morphological factors, revealing that a factor’s ranking in model importance does not always correspond to its unit-level cooling effectiveness. For example, although PVC may rank higher than PLAND_WS at larger scales, the per-unit cooling effect of water bodies remains stronger due to their higher specific heat capacity.

Accordingly, urban-renewal strategies must balance practical constraints with the specific thermal behavior of each morphological factor. Planning interventions should be tailored to local conditions, integrating three-dimensional form adjustments in fine-scale projects and emphasizing two-dimensional land-use optimization at broader, regional scales. Such an integrated, multiscale approach enables more precise and climate-responsive urban design aimed at mitigating the UHI effect.

4.4. Innovations and Limitations

This study provides a detailed analysis of how urban spatial form affects LST. By quantifying nineteen two-dimensional and three-dimensional form factors across multiple grid scales and applying the RF algorithm, we reveal nonlinear patterns and scale-sensitive effects. The innovation lies in integrating horizontal and vertical urban characteristics (two-dimensional and three-dimensional form factors) and examining them across different spatial resolutions. This comprehensive approach offers urban planners new insights for addressing the UHI effect. By conducting a multiscale analysis of the relationship between urban structure and LST, this study addresses the limitations of traditional single-scale approaches and better aligns with the practical demands of diverse urban renewal projects. It captures the dynamic, scale-sensitive influence of urban morphology on thermal environments and contributes to the development of a more comprehensive evaluation framework for urban form. Through nonlinear analysis using the RF model, the research identifies optimal predictive configurations that enhance model accuracy and reveals key threshold intervals for critical morphological variables. Furthermore, applying the RF model allows for the characterization of nonlinear relationships between each factor and LST, while also identifying the optimal spatial scales for targeted interventions. These nuanced insights—extending beyond the explanatory scope of simple linear correlations—offer a more rigorous scientific foundation for informing future urban-renewal strategies aimed at mitigating the UHI effect.

However, this study has several limitations that warrant further investigation. First, the use of building data sourced from the Baidu Maps API restricted the temporal scope of the analysis to the year 2023. Future research should incorporate high-resolution remote sensing imagery and machine learning–based techniques for shadow detection and height estimation. These methods would enable more accurate, time-sensitive assessments of urban morphology and facilitate longitudinal analyses of structural changes and their thermal impacts. Second, the study area was limited to Beijing’s Fifth Ring Road, which may constrain the generalizability of the findings. Expanding the analysis to include multiple major Chinese cities would reduce site-specific bias, enhance the robustness of identified UHI drivers, and support the development of more broadly applicable urban climate adaptation strategies. Furthermore, the data used in this study are limited to a specific summer period in Beijing, which does not capture seasonal variation patterns. It is recommended that future research extend this method to multi-temporal or seasonal contexts to provide a more comprehensive understanding of spatiotemporal dynamics.

5. Conclusions

This study uses Beijing’s Fifth Ring Road area as a case study. We construct a multiscale grid framework to quantify fourteen two- and three-dimensional spatial morphology factors and apply the RF algorithm to elucidate their relative importance and nonlinear relationships with LST across scales. The main findings are as follows: (1) The RF algorithm achieves optimal accuracy at the 600 m scale. Compared with traditional linear regression, it more effectively handles multicollinearity among predictors, providing robust technical support for urban heat island research. (2) Spatial form factors exhibit pronounced scale dependency, with clear shifts in dominant drivers across scales. Two-dimensional form factors are more important at medium and large scales, while three-dimensional form factors dominate at small scales. At 150 m, MBH is the key driver. At 300 m, BHSD leads. From 600 m to 1200 m, the PLAND_IS fraction is dominant. Among them, the influence of the PLAND_IS fraction and PVC increases with scale. PLAND_WS fraction first decreases, then increases with scale. The impact of the PLAND_BL fraction and MBH decreases with scale. BHSD variability and BD show a unimodal pattern, peaking at 300 m. BCR fluctuates, peaking at 600 m. (3) Morphology factors display clear nonlinear relationships with the LST. PLAND_BL fraction below 0.12 shows a pronounced warming effect. PLAND_WS fractions between 0.20 and 0.35 produce significant cooling. PVC between 0.25 and 0.45 yields the strongest cooling. BD below 0.3 buildings/hm² cools, but warms above this threshold. BCR between 0.08 and 0.32 has the most pronounced warming effect. BHSD variability between 8 m and 40 m provides optimal cooling. MBH correlates positively with LST below 6 m and negatively above 6 m.

These findings reveal the scale-dependent and nonlinear mechanisms underlying the relationship between urban morphology and thermal environments. The results offer scientific guidance for enhancing thermal resilience and support evidence-based strategies for urban planning and renewal in megacities.