Abstract
This paper applied a Smoothed Particle Hydrodynamics (SPH) approach to solve Shallow Water Equations (SWEs) to study practical dam-break flows. The computational program is based on the open source code SWE-SPHysics, where a Monotone Upstream-centered Scheme for Conservation Laws (MUSCL) reconstruction method is used to improve the Riemann solution with Lax-Friedrichs flux. A virtual boundary particle method is applied to treat the solid boundary. The model is first tested on two benchmark collapses of water columns with the existence of downstream obstacle. Subsequently the model is applied to forecast a prototype dam-break flood, which might occur in South-Gate Gorges Reservoir area of Qinghai Province, China. It shows that the SWE-SPH modeling approach could provide a promising simulation tool for practical dam-break flows in engineering scale.
1. Introduction
The hydraulic dam plays an important role in the flood control and power generation, which brings great benefit to the national and domestic economy. However, the collapse of dam could bring catastrophic effect on the surrounding and downstream areas. Therefore, accurate and timely predictions of the dam break flow propagation have both theoretical and engineering importance to prevent the damage of property and loss of life [1]. The modeling of dam break flow in downstream areas is a benchmark shallow water problem and usually investigated by solving the shallow water equations (SWEs) using either analytical or numerical approaches. The traditional numerical approaches, based on the Finite Difference and Finite Volume method, discretize the computational domain using a series of fixed cells, but these meet big challenges in dealing with the wet-dry boundaries and complicated free surface formations [2].
The Smoothed Particle Hydrodynamics (SPH) is a robust mesh-free numerical modeling technique originated from the astrophysics [3]. SPH does not use any grid to evaluate the variable properties and derivatives but uses individual free-moving particles. The first SPH application in free surface flow was documented as early as 1994 [4]. Since then it has been increasingly explored to study various free surface flow problems, including the dam break flood [5,6]. Until now most documented SPH works have solved the Navier-Stokes (N-S) equations using either the weakly compressible SPH (WCSPH) or incompressible SPH (ISPH) solution methods. Dam break flow hazards usually influence large downstream areas and the practical interest is to interpret the macro flow features in the horizontal scale rather than the detailed flow information along the depth. It would be extremely time-consuming to solve the N-S equations with a large volume of water under these circumstances and thus the SPH solution of SWEs demonstrates its unique superiority, i.e., it can equally well disclose the flow information in the shallow area but at a much lower CPU expense.
The earliest SWE-SPH modeling philosophy could be attributed to Wang and Shen [7], who proposed the novel Lagrangian parcel concept for 1-D unsteady flows. However, this milestone work was not given sufficient attention until nearly a decade later when the potentials of SPH modeling technique were fully explored. Since then, the SWE-SPH modeling has been used in more complex 2D shallow water coastal lows [8] and flood routing with particle splitting and coalescing [9,10], with their numerical solutions being based on the variational energy principles [11]. Recently, another kind of novel SWE-SPH solver, which is based on the fundamental momentum principles, has been proposed by Chang et al. [12,13,14] for a wide range of open channel and shallow water simulations. The latest benchmark study is documented to investigate the solute transport with steep velocity and concentration gradients in an engineering environment [15]. Besides, more in-depth studies have been carried out to study the behaviors of moving object in a flood by Amicarelli et al. [16] and Albano et al. [17].
The main purpose of this work is to evaluate the potentials of the SWE-SPH modeling approach in an engineering context and the open source code SWE-SPHysics [9,10] is used as the modeling tool. The paper is structured as follows. Section 2 briefly introduces the SWE-SPH principles and open source code SPHysics. Section 3 uses two benchmark dam break flows with the existence of downstream obstacle to validate the model for numerical accuracy and efficiency. Section 4 is the practical model application to a prototype dam break scenario, which would occur in the region of South-Gate Gorges Reservoir. A comprehensive discussion is made on the dam break flood propagation features in the downstream area under different breach conditions.
2. SWE-SPH Principles and SWE-SPHysics
SWE-SPHysics [9,10] is a free open-source SPH code that was released in 2013 by the University of Manchester. It is programmed in FORTRAN language and specifically designed for the shallow water flow over large areas. The 1D version may not fully demonstrate the significant benefit of SWE-SPH modeling in the present paper so the 2D version is used in all of the case studies. For the completeness of work, a brief introduction on the SWE-SPH model principles is reviewed as follows.
SWE-SPH solves the Lagrangian form of SWEs, which are represented in the conservation of mass and momentum as:
where , is the traditional density of water and is the flow depth; is the time; is the depth-averaged velocity; is the topographic elevation; is the gravitational acceleration; and is the bed friction source term.
In SPH framework, the numerical interpolant of any function and its spatial derivative can be approximated as follows:
where the summation is carried out over all the particles within the area of compact support of the kernel function , and is the smoothing length, is the position vector of particle; denotes the approximation; is the number of particles in the support domain; is the index of particle; and are the mass and density of particle , respectively.
The SWE-SPH particles are represented by each individual water column in the horizontal (x, y) domain, and the density of reference particle is calculated by summarizing the influence of all neighboring particles within its influence range as:
For shallow flow computations the abrupt change of flow depth could lead to the stretching and overlapping of particles since the mass and volume of each particle are kept unchanged, therefore, a variable smoothing length must be used to maintain the numerical accuracy as:
where and are the initial smoothing length (twice of initial particle spacing) and flow depth, while and are the corresponding new values, respectively. represents the spatial dimensions, with = 1 for 1-D flows and = 2 for 2-D flows. Equation (6) implies that the smoothing length is also the function of particle density and thus Equation (5) is implicit, which could be solved by using the Newton–Raphson iterations [18].
Following the SWE-SPHysics User Manual [9,10], the governing Equations (1) and (2) can be efficiently solved by using the leap-frog time integration scheme based on the energy principles with a variational formulation. Since the solution process is fully explicit, the CPU usage is economic but the computational time step must observe the following Courant stability requirement as:
where is the Courant number being less than unity. Equation (7) implies that the movement of particle column within a certain time step should be only a fraction of its influence range.
Near the solid boundaries, the kernel support domain of fluid particles is truncated. The SWE-SPHysics adopts the treatment of Virtual Boundary Particle (VBP) approach. The basic principle of VBP is similar to the general mirror particle technique in the N-S SPH, but casted in a SWE formulation. The VBP does not involve in the main computation cycles but only serves as the medium to interpolate inner fluid particles to the boundary region.
3. Model Validations
This section includes model validations by two benchmark dam break flows. The first one is 2D dam break flow with a triangular hump located on the downstream channel. The second one is 3D dam break flow with a rectangular obstacle located in the downstream area. The SWE-SPH computations will be validated against the experimental data of the water surface. The complex dam break flow propagation features will also be discussed.
These two validation cases are the benchmarks widely used to study various numerical models. Before applying the present SWE-SPH model to the practical dam break flooding at South-Gate Gorges Reservoir dam, we use these laboratory cases to investigate the model accuracy and efficiency. This can also serve as the guideline for the selection of key computational parameters for practical purpose.
3.1. Dam Break Flow Interaction with a Triangular Hump
In this section, the experimental data of the dam break flow over a triangular hump in an EU CADAM project [19] is used to validate the SWE-SPHysics model for reproducing the shock waves. The detailed layout of the experiment is shown in Figure 1, where a dam is positioned 15.5 m from the upstream boundary in a 38 m long channel. 10 m downstream of the dam site, a triangular hump of 6 m wide and 0.4 m high is placed on the channel. The upstream reservoir water depth is 0.75 m and the downstream water depth behind the hump is 0.15 m. The breadth of the channel is 1.75 m and the channel bed is assumed to be rough with the Manning’s coefficient = 0.0125. Four water gauges, G4, G10, G13 and G20 are located at a distance of 4 m, 10 m, 13 m and 20 m, respectively, downstream of the dam. The water levels measured at these locations will be used to validate the model results.

Figure 1.
Schematic layout of dam break flow experiment with a triangular hump [19].
In the model setup, a particle spacing of 0.025 m is used for both the bed and inner fluid particles, and thus the total number of particles is 108,062 and 65,817, respectively. The Courant coefficient in Equation (7) is taken as = 0.4 and the time step is dynamically adjusted in the computation to achieve maximum efficiency. The total simulation time is 40 s for the entire dam break flow process. The Manning’s coefficient of n = 0.0125 is used to represent the frictional condition of the channel bed. The upstream and downstream boundary of the channel is treated as impermeable solid boundaries.
The time histories of water level at gauging points G4, G10, G13 and G20 are shown in Figure 2a–d, compared between the experimental data [19] and SWE-SPHysics simulation results. It shows that the dam break flood wave arrives at G4 at time = 1 s, causing its water level to steadily increase. With the propagation of flood flow until = 2.8 s, it reaches the upstream toe of the triangular hump and causes an abrupt increase in the water level there. This is due to the strong reflection effect of the hump at G10, where most flows are reflected back and they propagate against the upstream direction. This negative bore wave results in the second water level rise at G4 around = 13.2 s. Besides, due to the existence of tailing water between the hump and right wall, the partially overtopped flows violently interact with the original water. This leads to some reflected waves returning back over the hump crest, forming a moving hydraulic jump propagating in the upstream direction. The moving jump arrives at G10 and G4 around = 24.4 s and 27.0 s, respectively, which causes the second water level rise in the time history. On the other hand, the first reflected wave which has already arrived at the upstream boundary at time = 24.1 s, re-reflects from there and propagates downstream and then superimposes with the hydraulic jump moving in the opposite direction. The combined waves once more propagate in both directions and eventually reach G4 at = 35.4 s, resulting in the third water surface rise. To better illustrate the complicated dam break flooding wave propagation and reflection features, Figure 3a,b shows the water surface variations in the spatial and temporal domain. The results are extracted at the centreline of the numerical flume.
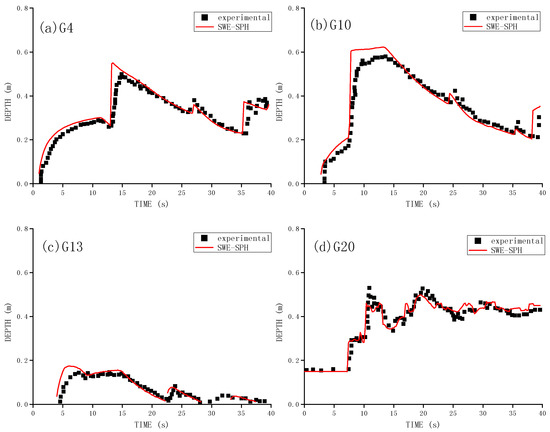
Figure 2.
Time histories of dam break flow surface profile at gauging points between experimental data [19] and SWE-SPHysics modeling results at: (a) G4; (b) G10; (c) G13 and (d) G20.
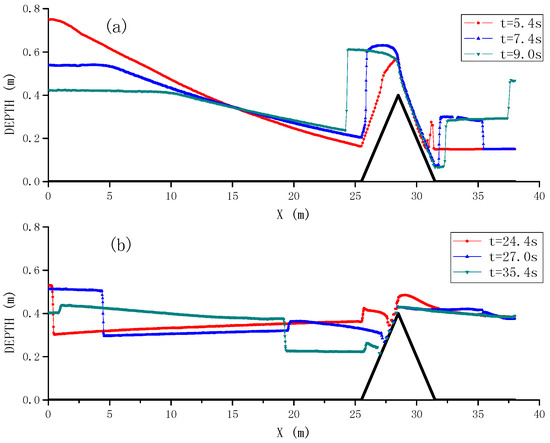
Figure 3.
Spatial and temporal evolutions of the dam break flow surface profile at time: (a) t = 5.4, 7.4 and 9.0 s; and (b) t = 24.4, 27.0 and 35.4 s.
Figure 2 also demonstrates a generally satisfactory agreement between the numerical and experimental results, although some kinds of the discrepancy are unavoidably found due to the existence of vertical acceleration in the flow, which is generated during the complex flow-structure interactions and thus violates the fundamental assumptions of SWEs. Compared with similar simulation carried out by incompressible SPH solver for 2-D N-S equations using identical spatial resolution [20], the present SWE-SPH could save an order of CPU hours. The former took nearly 20 h of CPU time while the latter only used a couple of minutes.
3.2. Dam Break Flow Interaction with a Rectangular Obstacle
In this section, a dam break flow interaction with a rectangular obstacle that partially occupies the channel is simulated by the SWE-SPH model. The simulation is based on the benchmark experiment of Kleefsman et al. [21]. The schematic setup of the water tank is shown in Figure 4, which has the dimension of 3.22 m × 1.00 m × 1.00 m. The reservoir is located on the right hand side of the domain and a sluice gate is placed at 1.288 m from the upstream boundary. The water depth in the reservoir is 0.55 m. At a distance of 1.248 m downstream of the sluice gate there is a rectangular obstacle with dimension of 0.161 m × 0.403 m × 0.161 m. To measure the flow depth, four gauging points H1–H4 are placed inside the studied area, in which H2 and H4 are located at x = 0.992 m and 2.636 m, respectively, from the origin set on the left (downstream) boundary. In the experiment the dam break was assumed to be instantaneous. Since the downstream obstacle occupies only a portion of the channel width, 3D simulations must be carried out if N-S equations are to be used, such as documented by Jian et al. [22]. On the other hand, SPH solutions from the SWEs would provide a promising tool for such a purpose. However, it should be realized that SWE-SPH computations cannot provide dynamic wave impact pressures since the fundamental governing equations are depth-averaged by assuming a hydrostatic pressure distribution.
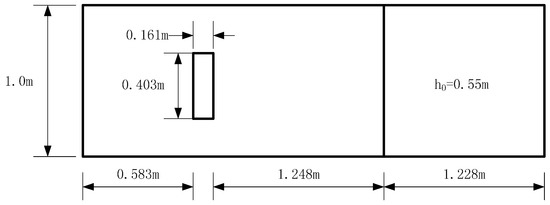
Figure 4.
Schematic layout of dam break flow experiment with a rectangular obstacle [21].
In the model setup, a particle spacing of 0.01 m is used for both the bed and fluid particles, thus resulting in a total number of 32,300 bed particles and 12,423 water particles, respectively. To address the roughness of channel bed, the Manning’s coefficient is chosen as n = 0.01 by following the recommendations of [21]. The Courant stability coefficient is taken as = 0.4 and the computational time step is automatically adjusted, which is the same as in the previous case. The total simulation time is 6 s.
Figure 5a,b shows the time history of water depth variations at gauging point H2 and H4, compared between the present SWE-SPH computations and benchmark data of Kleefsman et al. [21]. The agreement between the two is quite promising, which seems even better than the 3D WCSPH/ISPH computations carried out by Jian et al. [22]. One possible reason could be that the present channel bed is rough, while this was not taken into consideration in the 3D ISPH model. Thus, the advantage of SWEs type model is that bed roughness can be easily and explicitly reflected in the model parameters while this may not be a simple issue in N-S type models. Also the present SWE-SPH used the CPU time in minutes, while the WCSPH/ISPH of Jian et al. [22] used this in hours. The time history indicates that after the dam break flood wave reflects from the left boundary and reaches H2, the water depth there achieves the maximum value. This reflection wave continues to propagate into the reservoir area and arrive at H4 around time t = 2.76 s, leading to the first water level rise. Then this negative bore wave reflects on the reservoir wall and travels back towards the downstream, causing the second water level rise at H4 around t = 3.6 s.
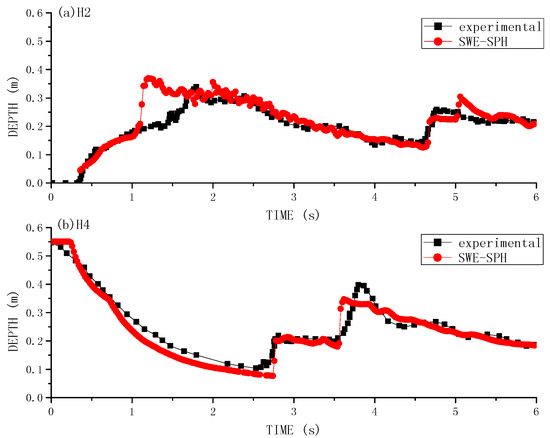
Figure 5.
Time histories of dam break flow surface profile at gauging points between experimental data [21] and SWE-SPHysics modeling results at: (a) H2; and (b) H4.
Different from the previous triangular hump which occupies the whole cross-sectional area forming a 2D problem, the present rectangular obstacle occupies only a fraction of the cross section and thus the flow pattern is highly 3-dimensional with complex flood wave diffractions and superimpositions. As shown in Figure 6a,b for the velocity field of dam break flow at two different time instants, parts of the flow overtop the obstacle crest with reflection, while most of them propagate towards the downstream region around both sides of the obstacle, as shown at time t = 0.74 s in Figure 6a. Furthermore, when the two water streams arrive at the downstream boundary, they tend to converge along the middle section of the wall and then collide to form two symmetric circulation vortices, as shown in Figure 6b at time t = 1.76 s. The vortices could stay there for a while until being diminished by the second reflection wave from the upstream reservoir area.
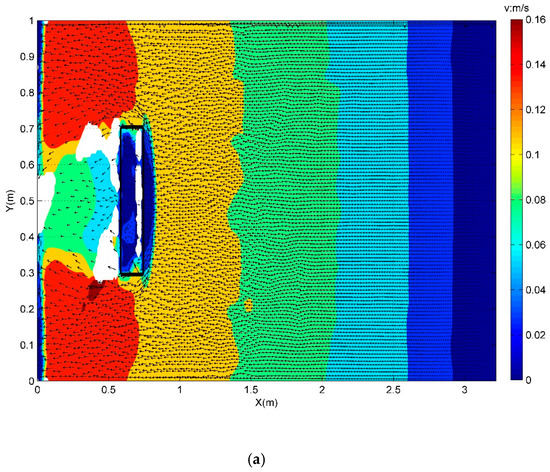
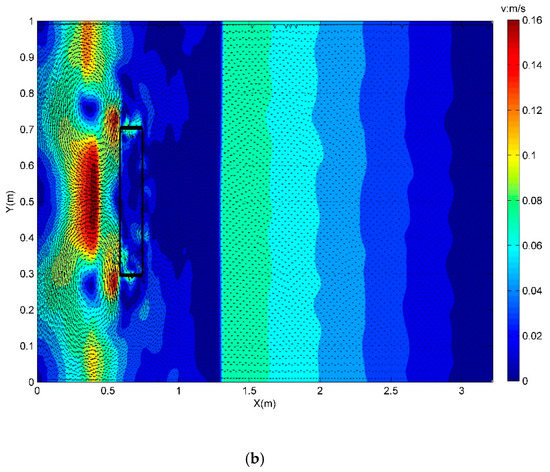
Figure 6.
Velocity fields of dam break flow at different stages: (a) t = 0.74 s; and (b) t = 1.76 s.
3.3. Sensitivity Analysis of the Model
In this section, a series of tests is carried out to study the convergence of the model, the model accuracy with other established numerical methods and the influence of particle splitting techniques on the simulation results.
3.3.1. Model Convergences with Different Particle Spacing
For the dam break flow interactions with a triangular hump [19] and a rectangular obstacle [21], additional runs were carried out by using two alternative particle spacings to check the convergence of the model. For the former [19], additional particle spacing of 0.03 m and 0.04 m are used as compared with the original 0. 025 m, whereas for the latter [21], additional particle spacing of 0.02 m and 0.03 m are used as compared with the original 0.01 m.
For the triangular case, the time histories of water level at gauging points G4, G10, G13 and G20 are shown in Figure 7a–d, compared between the three SWE-SPHysics computational results. There is almost no difference observed, which indicates the convergence of model simulations in this case. Only slight fluctuations are found in the last gauging station G20, which is within the expectations since the flow condition is rather complex there. On the other hand, for the rectangular case, the computed time histories of water level at gauging points H2 and H4 are shown in Figure 8a,b. In this case, the particle spacing of 0.03 m seems to lead to inaccurate results at H2, which is near the upstream of the obstacle. In contrast, the other two refined computations demonstrate good convergence behaviours at both gauging locations.
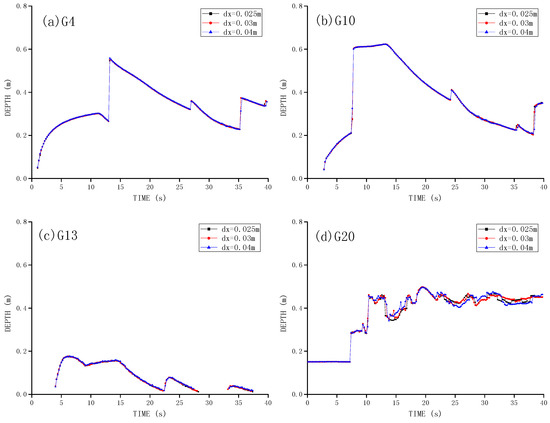
Figure 7.
Time histories of dam break flow surface profile at gauging points for three SWE-SPHysics modeling results on [19] at: (a) G4; (b) G10; (c) G13; and (d) G20.
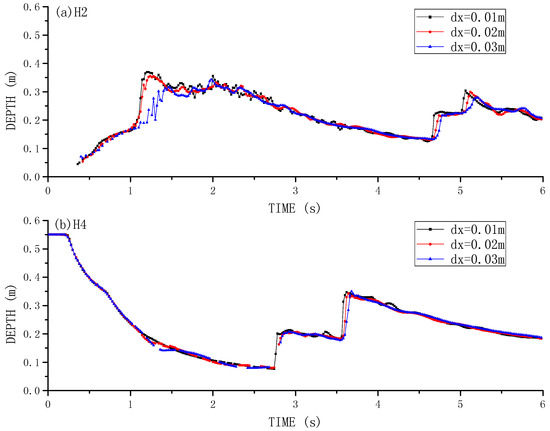
Figure 8.
Time histories of dam break flow surface profile at gauging points for three SWE-SPHysics modeling results on [21] at: (a) H2; and (b) H4.
3.3.2. Comparisons with Other Numerical Modeling Results
For the dam break flow in downstream large areas, the SWE-SPH model should be able to give the same accurate results as the other grid models or SPH models. To support this, for the dam break flow over a triangular hump [19], the present SWE-SPH computations are compared with the numerical results of Zhou et al. [23] using a high-resolution Godunov-type cut-cell scheme. For the dam break flow over a rectangular obstacle [21], the VOF results of Kleefsman et al. [21] and 3D ISPH results of Jian et al. [22] are compared.
Figure 9a–d shows the comparisons of the triangular case [19], which demonstrate that the SWE-SPH computations are generally better than the numerical results of Zhou et al. [23] especially at gauging points G10 and G13. Figure 10a,b compares the documented numerical results with the experimental data [21] and SWE-SPH computations on the rectangular case [21] at two gauging locations H2 and H4. Figure 10a includes the VOF data from [21] and Figure 10b includes the 3D ISPH data from [22]. The former discloses that the VOF results are closer to the experimental data especially for the larger water depth variations. In comparison, the latter shows that SWE-SPH achieved similar agreement as the 3D ISPH in that it better predicted the second water level jump at time t = 4.7 s while poorly predicted the first water level jump at t = 1.75 s at the observation location H2, which is near the upstream of the structure.
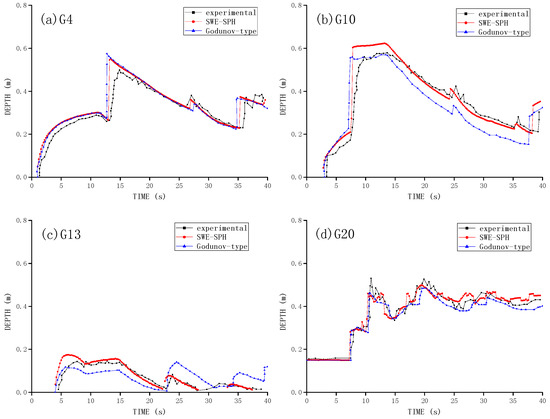
Figure 9.
Time histories of dam break flow surface profile at gauging points between Godunov cut-cell [23] and SWE-SPHysics results and experimental data [19] at: (a) G4; (b) G10; (c) G13; and (d) G20.
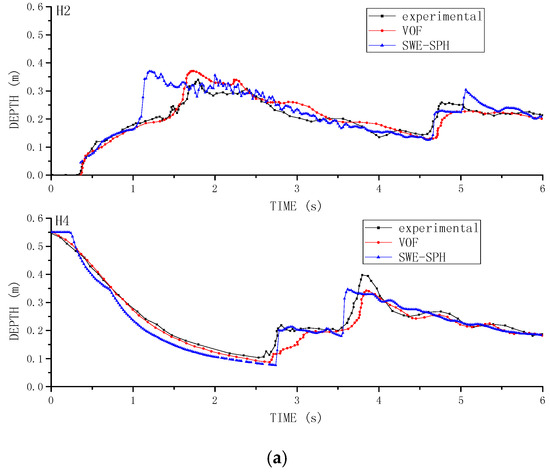
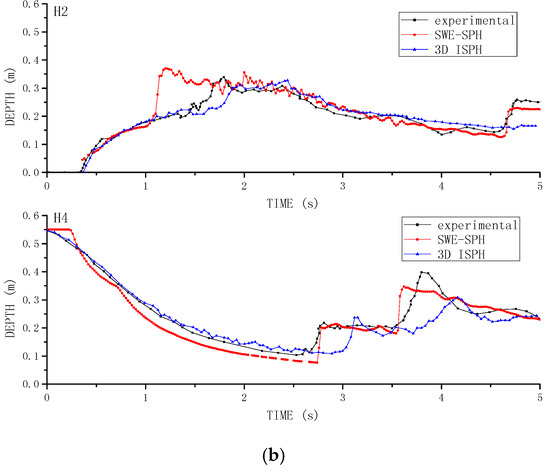
Figure 10.
Time histories of dam break flow surface profile at gauging points between SWE-SPHysics results, experimental data [21], VOF [21] and 3D ISPH [22] computations: (a) VOF data; and (b) 3D ISPH data.
3.3.3. Evaluations on the Particle Splitting Technique
The particle splitting technique as proposed by Vacondio et al. [9] proved to be an efficient approach to improve the accuracy of SWE-SPH solutions especially near the dry-wet boundary. In this section, the two controlled cases are run with and without the use of the splitting technique to examine its effect. The test case is based on the previous dam break flow with a rectangular obstacle [21]. The area of particle splitting is set somewhere upstream near the obstacle as shown in the highlighted zone in Figure 11.

Figure 11.
Area of particle splitting for dam break case [21], coordinated from (0.75, 0.2) to (0.8, 0.8).
The original run used a particle spacing of 0.02 m without the particle splitting, therefore involved 3162 particles. By using the splitting technique, the particle numbers gradually increased to 8243. Also, here another refined computation is made by using the particle spacing of 0.01 m but without the splitting, which results in a particle number of 12,423. The computational results from these numerical designs are shown in Figure 12a,b for the gauging station H2 and H4.
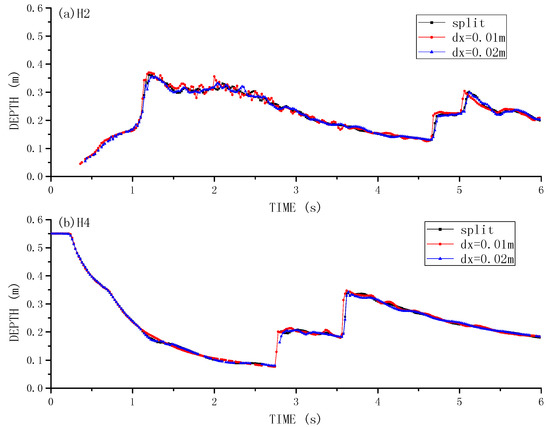
Figure 12.
Time histories of dam break flow surface profile at gauging points computed by using particle refinement and splitting technique at: (a) H2; and (b) H4.
It is shown from Figure 12 that the numerical results maintain nearly the same for all the test options, which is due to the fact that the particle resolution is refined and the model is converged. Under this situation the particle splitting seems not to contribute much to the simulation accuracies. However, it should be noted that when the particle spatial resolution is relatively rough, the particle splitting should be very useful to maintain a good accuracy especially near the wet-dry interface boundaries.
4. Model Applications in Engineering Field
The South-Gate Gorges Reservoir is situated in the northwest Valley of Huzhu County of Qinghai Province, China. It is mainly a medium-scale irrigation hydraulic works. The reservoir area is located at an elevation of 2700 m above the sea level, with a catchment area of 218 km2. The dam height measures at 37.5 m and the length of dam is 467 m. The reservoir has a storage capacity of 18.4 million m3, which serves the downstream area of 1200 km2 with a population of 240 K. Since the reservoir was initially put into operation in 1983, dam leaking has always been an issue. It is estimated that the average leaking rate is around 0.7 m3/s, which accounts for 46% of the annual run-off into the reservoir. This is not only a waste of water resources but also poses a potential threat to the safety of the dam. To partially relieve the problem, the reservoir has been operated under the designed low water level at 2760 m for most of the years. In spite of this, quite a few local collapses have been found on the left shoulder of the dam. The dimension of the collapsed caves could reach as large as 2 m in diameter. These constitute a serious threat to the safety operation of the dam. The South-Gate Gorges Reservoir and Dam are located in the upstream area of Xining, the capital of Qinghai and also many key agricultural sites, so any scale of dam break could cause significant losses to the local economy [24]. To evaluate potential dam break hazards and take relevant engineering measures to combat the disaster, it would be useful to carry out virtual dam break simulations in this area. A site photo including the reservoir, dam and immediate downstream area with points of interest is shown in Figure 13. The hydraulic dam site is located at 36°57′55.54″ North Latitude and 101°53′27.59″ East Longitude.
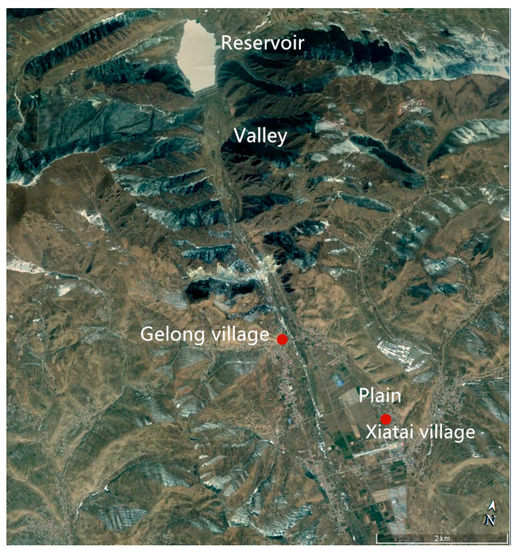
Figure 13.
Site photo of South-Gate Gorges Reservoir area (from Google earth).
For this purpose, the present SWE-SPHysics computation is made to simulate the dam break flood propagation in the downstream area by assuming an instantaneous dam collapse and the breach dimension being 100%, 80% and 60% of the total dam length, respectively. The breach is assumed to be located in the middle of the dam. By using a grid size of 30 m × 30 m, 89,168 bed particles are generated for the area of 7 km × 10 km around the reservoir. This includes the reservoir and dam, downstream valley, valley exit and subsequent plain area. Figure 14 shows the 3D topography for the SWE-SPH model input. According to the hydrological flood routing [24], the reservoir water levels are 2772.05 m, 2772.64 m and 2773.57 m, respectively, for a flood frequency of 1/2000, 1/5000 and 1/10,000. All of the following computations are made by using the 1/5000 flood frequency.
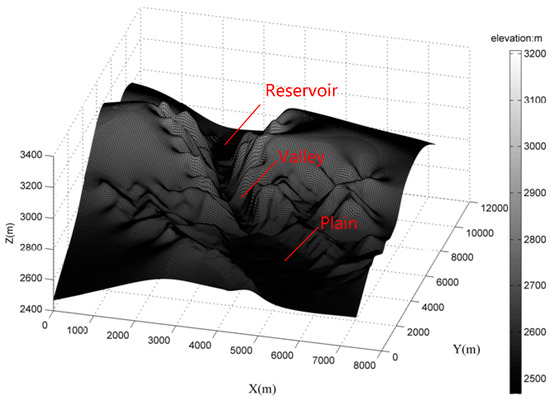
Figure 14.
3D topographic map for SWE-SPH model input.
In the SWE-SPH simulations, an initial particle spacing of 20 m is used, so totally 2664 water particles are involved in the computation. The Courant coefficient is still taken as = 0.4 with a variable time step. The bed roughness of the whole simulation area is assumed to be n = 0.024, by analyzing relevant hydrological data [24]. Due to the size limitation of the selected computational domain, the numerical simulation is only carried out to 600 s, 700 s and 800 s, respectively, for the breach width ratio of 100%, 80% and 60%. Based on SWE-SPH simulation results, the flood maps after the dam break are shown at time t = 600 s for the three different breach ratios in Figure 15a–c.

Figure 15.
Flood maps at t = 600 s after the dam break for different breach ratio conditions: (a) 60%; (b) 80%; and (c) 100%.
Figure 15 shows that after the collapse of the dam, the flood wave rapidly propagates to the downstream area, first entering into the valley and following its meandering route. Here, due to the constraint of the local topography, the flood flow assumes a higher velocity and momentum. Also the bending of the valley route causes the flood wave to be reflected at the mountains situated on lateral banks and thus generate large scale flow circulations. The Figure clearly indicates two drastic flow transitional zones inside the valley. According to the results analysis, it takes around 3.5 min, 4.8 min and 5.5 min, respectively, for the flood wave to reach the exit of valley and enter into wider downstream areas for the breach ratio 100%, 80% and 60%. After this stage the flood flows spread out into the vast plain area and therefore, the flow depth significantly decreases due to the enlargement of the flow path. Besides, Figure 15 also demonstrates a longer and wider inundation area under the condition of higher breach ratio, such as Figure 15c compared with Figure 15a. To further support the above analysis, the flow velocity fields computed at time t = 200 s, 400 s and 600 s are shown in Figure 16a–c for the breach ratio of 100%. It further evidences that the dam break flow could constitute a disastrous event with huge destructive capacity since the flow velocity near the dam break flow front can reach as large as 20 m/s thus carrying sufficient momentum and energy.
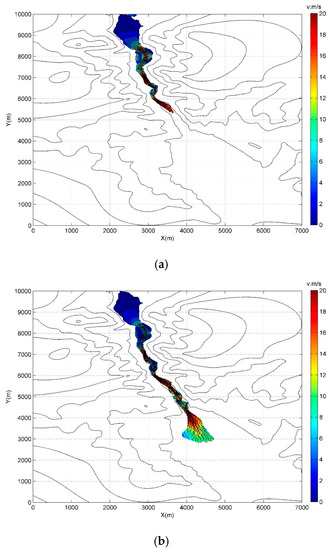
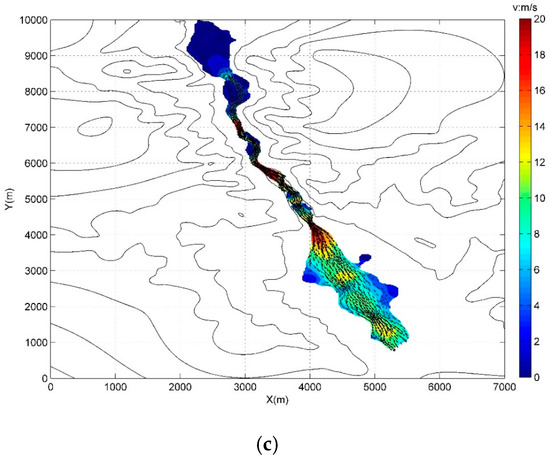
Figure 16.
Flow velocity fields under breach ratio 100% at different time instants: (a) t = 200 s; (b) t = 400 s; and (c) t = 600 s.
To further investigate the dam break flow feature, Figure 17 provides the time history of dam break flow discharges at the dam site for three different breach ratios. Generally it shows the flood discharge is highly proportional to the size of the dam breach, i.e., the discharge reaches its highest level for the breach ratio 100% and lowest for the ratio 60%, although the time appearance of peak flow discharges remains nearly the same in all cases around t = 75 s. However, it is noted that the peak flow discharge drops significantly from 350,000 m3/s to 140,000 m3/s from the full breach to 80% breach, while it only further reduces to 90,000 m3/s for the 60% breach ratio. This implies that full breach of the dam is the worst scenario in dam break disasters.
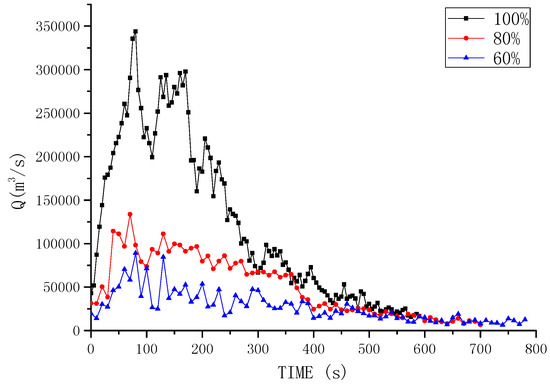
Figure 17.
Time history of dam break flow discharges at dam site for different breach ratios.
Figure 18a,b shows the spatial variations of water surface profile and flow velocity along the streamwise direction of dam break flow under three different breach ratios, where the horizontal coordinate is measured from the reservoir location. The numerical results are extracted along the middle section of the flow path. The time scale has been shifted just to synchronize the results of different breach conditions.
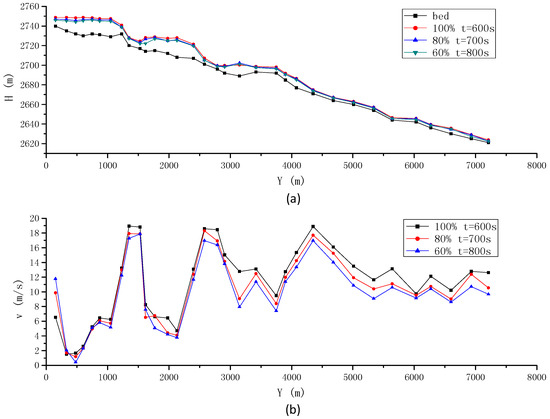
Figure 18.
Spatial variations of (a) water surface; and (b) velocity profile along the central streamwise direction of dam break flow, for different breach conditions.
Figure 18 also discloses the high correlation between the water level/flow velocity and the breach ratios, as concluded from Figure 17. That is to say, a larger ratio of breach causes a higher water surface and flow velocity. Besides, Figure 18a demonstrates two abrupt water surface drops (at 1500 m and 2750 m downstream location), which correspond to the drastic increase of flow velocity as shown in Figure 18b. These changes of flow condition occur in the valley areas, where the flood wave reflection and diffraction are triggered at the channel bend. Compared with the time-dependent flow discharges in Figure 17, the spatial water surface and velocity distributions as shown in Figure 18 demonstrate less difference for different breach conditions.
Since the above proposed dam break flow is virtual, there is neither experimental nor field data available for a comparison. Therefore a convergence analysis must be made to evaluate the accuracy of model in a numerical context. For this purpose an alternative run is made by using additional two different particle spacings, i.e., 15 m and 10 m, as against the original value of 20 m. The comparisons have been made for three different dam breach ratios, but only the full collapse case is shown here and the other two cases demonstrate almost similar behaviours. By using a particle spacing of 15 m and 10 m, there are about 4653 and 10,508 particles existing in the computational domain, respectively. The simulation is carried out to 600 s for the study area of interest. Subsequently the spatial variations of water surface and velocity profile along the streamwise direction of the downstream channel are shown in Figure 19a,b. Figure 19 clearly shows that nearly the same results have been obtained regardless of the particle spacing used. This further implies that the numerical results are converged and the model predictions are reliable.
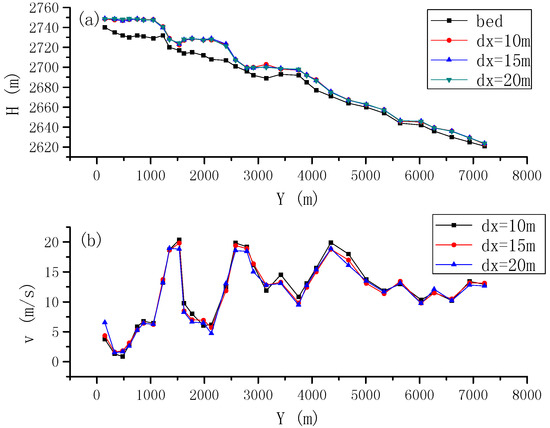
Figure 19.
Spatial variations of (a) water surface; and (b) velocity profile along the central streamwise direction of dam break flow, for different particle spacing.
In view of the CPU cost, it took about 4 min, 8 min and 22 min, respectively, for the particle spacing 20 m, 15 m and 10 m, i.e., particle number 2664, 4653 and 10,508, in the South-Gate Gorges Dam collapse simulation. This suggests that the CPU increase in SWE-SPH model is roughly proportional to the increase in particle number, rather than the increase in particle number being squared, as widely documented in the N-S type SPH works. The computations were made on the Lenovo/X240 E5-2620 V2 95 W 2.0 GHz 8 core *2 with 32 GB RAM.
To provide more practical information on the dam break flow disaster evaluations, Figure 20 shows the downstream flooding area development for the three different flood frequencies of 1/2000, 1/5000 and 1/10,000 based on the breach ratio of 60%. Finally, based on the SWE-SPH simulations, Figure 21a,b show the digital inundation photo for the two downstream sites of Gelong Village and Xiatai Village, respectively, as indicated in Figure 13, which are located 4.8 km and 6.9 km downstream of the dam site. The maximum submerge depths are 3.8 m and 2.7 m.
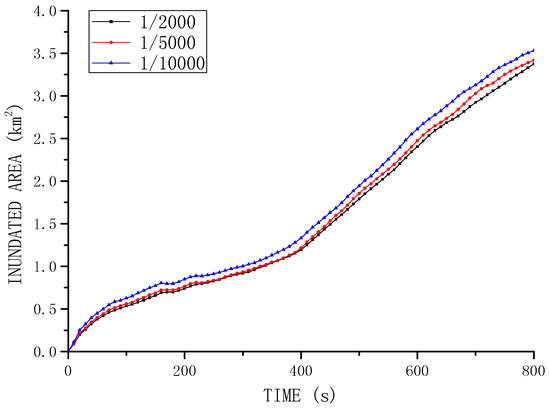
Figure 20.
Downstream flooding area development for different flood frequencies.


Figure 21.
Digital inundation photos for two key downstream sites: (a) Gelong Village; and (b) Xiatai Village.
5. Conclusions
The study demonstrates the great potentials of SWE-SPH modeling technique in practical engineering applications. Two major objectives have been achieved. By using the open source code SWE-SPHysics to two benchmark dam break flows interacting with a triangular hump and rectangular obstacle, the numerical accuracy is fully evidenced. The SWEs modeling demonstrates unique advantages of simulating either large scale flows with shallow depth, or flows with 3D characteristics where the vertical variation and impact pressure are of less interest. The model validations indicate that the SWE-SPH computations are of similar accuracy as the N-S type SPH solutions for the proposed simulation cases. Secondly, the robustness of SWE-SPH modeling technique is further demonstrated by the model prediction of a prototype dam break flow in Qinghai Province, China. The model discloses its accurate treatment of the wet-dry boundary and complex topography, so that very complicated flooding wave features such as the reflection, diffraction, superposition and vortex circulation are well reproduced. It has been proved that the SWE-SPH model could provide a promising simulation tool for shallow dam-break flows in the engineering field.
Acknowledgments
This research work is supported by the National Natural Science Foundation of China (No. 51479087), Major State Basic Research Development Program (973 program) of China (No. 2013CB036402), Chinese Ministry of Water Resources Special Funds for Scientific Research on Public Causes (No. 201501028), State Grid Qinghai Electric Power Company (No. SGTYHT/14-JS-188) and Open Research Fund Program of State Key Laboratory of Hydroscience and Engineering, Tsinghua University (No. 397SKLHSE-2015-B-02).
Author Contributions
Shenglong Gu, Xianpei Zheng and Liqun Ren made the computations and data analysis; Hongwei Xie guided the engineering project and provided the data; Jiahua Wei and Yuefei Huang drafted the manuscript; Songdong Shao made the proof reading and editing. All authors contributed to the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, A.S.; Hsu, M.H.; Chen, T.S.; Chang, T.J. An integrated inundation model for highly developed urban areas. Water Sci. Technol. 2005, 51, 221–229. [Google Scholar] [PubMed]
- Liu, G.R.; Liu, M.B. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to testing the fission hypothesis. Astrono. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; Dalrymple, R.A. Using a 3D SPH method for wave impact on a tall structure. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 63–69. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, H.T. Lagrangian simulation of one-dimensional dam-break flow. J. Hydraul. Eng. 1999, 125, 1217–1220. [Google Scholar] [CrossRef]
- De Leffe, M.; Le Touze, D.; Alessandrini, B. SPH modeling of shallow-water coastal flows. J. Hydraul. Res. 2010, 48, 118–125. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K. Accurate particle splitting for smoothed particle hydrodynamics in shallow water with shock capturing. Int. J. Numer. Methods Fluids 2012, 69, 1377–1410. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P. Shallow water SPH for flooding with dynamic particle coalescing and splitting. Adv. Water Res. 2013, 58, 10–23. [Google Scholar] [CrossRef]
- Rodriguez-Paz, M.; Bonet, J. A corrected smooth particle hydrodynamics formulation of the shallow-water equations. Comput. Struct. 2005, 83, 1396–1410. [Google Scholar] [CrossRef]
- Chang, T.J.; Kao, H.M.; Chang, K.H.; Hsu, M.H. Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. J. Hydrol. 2011, 408, 78–90. [Google Scholar] [CrossRef]
- Kao, H.M.; Chang, T.J. Numerical modeling of dambreak-induced flood and inundation using smoothed particle hydrodynamics. J. Hydrol. 2012, 448–449, 232–244. [Google Scholar] [CrossRef]
- Chang, T.J.; Chang, K.H. SPH modeling of one-dimensional nonrectangular and nonprismatic channel flows with open boundaries. J. Hydraul. Eng. 2013, 139, 1142–1149. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chang, T.J. SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 2017, 9, 132. [Google Scholar] [CrossRef]
- Amicarelli, A.; Albano, R.; Mirauda, D.; Agate, G.; Sole, A.; Guandalini, R. A smoothed particle hydrodynamics model for 3D solid body transport in free surface flows. Comput. Fluids 2015, 116, 205–228. [Google Scholar] [CrossRef]
- Albano, R.; Sole, A.; Mirauda, D.; Adamowski, J. Modelling large floating bodies in urban area flash-floods via a Smoothed Particle Hydrodynamics model. J. Hydrol. 2016, 541, 344–358. [Google Scholar] [CrossRef]
- Ata, R.; Soulaimani, A. A stabilized SPH method for inviscid shallow water flows. Int. J. Numer. Methods Fluids 2005, 47, 139–159. [Google Scholar] [CrossRef]
- Morris, M. CADAM: Concerted Action on Dambreak Modeling–Final Report; Rep. SR 571; HR Wallingford: Wallingford, UK, 2000. [Google Scholar]
- Pu, J.; Shao, S.; Huang, Y.; Hussain, K. Evaluations of SWEs and SPH numerical modelling techniques for dam break flows. Eng. Appl. Comput. Fluid Mech. 2013, 7, 544–563. [Google Scholar]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A volume-of-fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Jian, W.; Liang, D.; Shao, S.; Chen, R.; Yang, K. Smoothed Particle Hydrodynamics simulations of dam-break flows around movable structures. Int. J. Offshore Polar Eng. 2016, 26, 33–40. [Google Scholar] [CrossRef]
- Zhou, J.G.; Causon, D.M.; Mingham, C.G.; Ingram, D.M. Numerical prediction of dam-break flows in general geometries with complex bed topography. ASCE J. Hydraul. Eng. 2004, 130, 332–340. [Google Scholar] [CrossRef]
- Xie, H.; Gu, S. Dam Break Flow Simulations and Flooding Wave Analysis at South-Gate Gorges Reservoir Dam; Engineering Report; Flood Control Institute: Qinghai, China, 2017. (In Chinese) [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).