Abstract
The coupled routing and excess storage (CREST) distributed hydrological model has been applied regionally and globally for years. With the development of remote sensing, requirements for data assimilation and integration have become new challenges for the CREST model. In this paper, an improved CREST model version 3.0 (Tsinghua University and China Institute of Water Resources and Hydropower Research, Beijing, China) is proposed to enable the use of remotely-sensed data and to further improve model performance. Version 3.0 model’s runoff generation, soil moisture, and evapotranspiration based on three soil layers to make the CREST model friendly to remote sensing products such as soil moisture. A free water reservoir-based module which separates three runoff components and a four mechanism-based cell-to-cell routing module are also developed. Traditional CREST and CREST 3.0 are applied in the Ganjiang River basin, China to compare their simulation capability and applicability. Research results indicate that CREST 3.0 outperforms the traditional model and has good application prospects in data assimilation, flood forecasting, and water resources planning and management applications.
1. Introduction
1.1. Review of Distributed Hydrological Model
Hydrological models have been successfully invented and applied for decades worldwide. Based on the structures and configurations of the model, hydrological models can be categorized into three types, which include black-box, conceptual, and physically-based distributed models [1]. With the development of observation and monitoring technologies and computer sciences, distributed hydrological models have become mainstream in the academic circle of hydrology. Many distributed hydrological models, such as TOPKAPI (TOPographic Kinematic APproximation and Intergration) [2,3], DHSVM (Distributed Hydrology Soil Vegetation Model) [4], and VIC (Variable Infiltration Capacity) [5], etc., have been successfully developed and applied. Distributed models are good at simulating the behaviors of the highly complex dynamics of the hydrological system [6,7,8]. They can generate spatiotemporal distributions of different state variables of the studied catchments. These state variables typically include soil moisture, evapotranspiration, and land surface temperature, etc., and are of great significance to flood forecasting, drought monitoring, agriculture cultivation, water resources planning and management, etc. [9]. The favorable simulation functionality normally cannot be achieved by using black-box and conceptual models. Therefore, even though the model structures are very complex and the computational burden is significantly heavy [10,11,12], distributed hydrological models have still been increasingly popular and are of great importance in modern hydrological studies.
There are mainly three ways to construct a distributed hydrological model. The first is to construct the model using conceptually-based modules such as water storage capacity distribution curve method for runoff generation computation, infiltration curve method for runoff component separation, experience equation-based evapotranspiration calculation, linear reservoir method for flow concentration, etc. [13,14]. The second way is to construct the model mainly based on the partial differential equations (PDEs) that finely describe the dynamics of the hydrological processes [15]. These equations usually include the Richards equation for runoff generation computation, Darcy’s law for soil water movement and transportation, and shallow water equations (typically Saint-Venant equations) for overland flow and channel routing. The third way is to construct the model based on both of the above-mentioned methods [16].
The PDE-based methods are usually based on Newton’s law of motion, and its physical meaning is clearer than the conceptual methods. However, the application of these kinds of methods in real-world occasions is still challenging. The PDEs are complex and the analytic solution is non-existent in most cases. We have to apply numerical solution methods [17] such as finite difference, finite element, or finite volume, instead of the analytic solution methods. The numerical methods adopted to solve the PDEs are also faced with some difficulties. The spatiotemporal resolutions that are used to discretize the PDEs must obey some predefined constraints, such as Courant number criterion, to ensure the stability of the numerical methods [18]. This limitation makes the solution of PDEs with “non-harmonious” spatiotemporal resolution—such as a very small spatial resolution combined with a large computational time step—become impossible. Furthermore, the a-priori model parameters (e.g., saturated hydraulic conductivity, field capacity, wilting point, etc.) are obtained from laboratory-scale experiments and may not be effective at a larger-scale, potentially leading to scaling issues [19]. In addition, the numerical solution of PDEs with high spatiotemporal resolution is a time-consuming computation task and significantly slows down the application efficiency of the PDE-based models.
Although the physical meanings of the conceptually-based distributed hydrological models are not as strong as their PDE-based counterparts, conceptually-based distributed hydrological models still survive during the history of hydrological model development due to their simplicity, good accuracy, agile spatiotemporal resolutions, higher computational efficiency, etc. The adaptability of spatiotemporal resolutions of conceptually-based models is better than the PDE-based models to some extent. This merit enables the conceptually-based models to freely couple with retrieved remote sensing data with different and irregular spatiotemporal resolutions. For the purpose of studying climate change, the requirement of better global hydro-meteorological simulation has sharply increased. The conceptually-based models can fully adopt the useful information contained in the remote sensing retrieved big data with larger spatiotemporal resolutions, and usually perform satisfactorily in global water cycle modeling and simulation [20,21,22].
1.2. Brief Introduction of the Coupled Routing and Excess Storage (CREST) Model and Motivation of Model Improvement
The coupled routing and excess storage (CREST) model was jointly developed by the University of Oklahoma and NASA SERVIR, and is a conceptually-based distributed hydrological model developed to simulate the spatial and temporal variations of land surface, and subsurface water fluxes and storage by cell-to-cell simulation [23,24,25,26,27]. CREST’s distinguishing characteristics include: (1) distributed rainfall–runoff generation and cell-to-cell routing; (2) coupled runoff generation and routing via three feedback mechanisms; and (3) representation of sub-grid cell variability of soil moisture storage capacity and sub-grid cell routing (via linear reservoirs). The coupling between the runoff generation and routing mechanisms allows detailed and realistic treatment of hydrological variables such as soil moisture. Furthermore, the representation of soil moisture variability and routing processes at the sub-grid scale enables the CREST model to be readily scalable to multi-scale modelling research at local, regional, and global scopes [28].
The version history of the CREST model can be traced back to the original 1.x version developed by Wang and Hong in 2011 [23]. After that, the model has been continuously updated from CREST 1.6c to a modular designed 2.0 Fortran version with embedded SCE-UA (Shuffled Complex Evolution developed in the University of Arizona) automatic parameter optimization by Xue and Hong [24,25]. Recently, the Fortran version has been updated to 2.1 and has been successfully applied regionally and globally. In addition to the Fortran version, there is another CREST 2.1 implementation using MATLAB and GDAL libraries with additional input/output functionalities [26]. Versions 2.0 and 2.1 are noted as 2.x for simplicity in this paper.
The CREST 2.x has been widely applied and has been proved to be easy and effective. However, with the development of remote sensing technology, CREST 2.x is faced with some new challenges. There are many remotely-sensed products that provide a huge amount of useful and valuable spatiotemporal information of the studied area, such as soil moisture (from satellite products such as AMSR-E (Advanced Microwave Scanning Radiometer-EOS), SMAP (Soil Moisture Active Passive), SMOS (Soil Moisture and Ocean Salinity), and Sentinel-1) [29,30,31], potential and actual evapotranspiration (from satellite products such as MODIS (MODerate-resolution Imaging Spectroradiometer), AVHRR (Advanced Very High Resolution Radiometer), and FY (Fengyun)), land surface temperature (from satellite products such as MODIS), total water storage (from satellite products such as GRACE (Gravity Recovery and Climate Experiment)), etc. [32]. However, CREST 2.x has some limitations which prevent further and deeper applications of remotely-sensed products to assist model calibration, simulation, and validation. The frequently used CREST 2.x supports only one soil layer to describe the tension water storage. Using one soil layer to mimic the hydrological processes cannot be applied to all types of watersheds, and may lead to accuracy deterioration. Especially, this phenomenon may become severe when applying the CREST 2.x model globally. Additionally, one soil layer model structure or configuration cannot make use of the remotely-sensed soil moisture products to assist the model calibration and validation. The remotely-sensed soil moisture products usually describe the volume water content corresponding to 5–10 cm soil depth. However, the depth of soil layer in CREST 2.x is usually much larger than 5–10 cm. Furthermore, the runoff generated by CREST 2.x is separated into two components, including surface and subsurface runoff, based on saturated hydraulic conductivity. CREST 2.x does not consider the free water storage and ignores the runoff generation and flow concentration processes of the ground water. This limits the effectiveness of model application to watersheds in which the ground water plays an important role. The surface flow, subsurface flow, and river channel flow generated by CREST 2.x are routed down by using a three-mechanism cell-to-cell routing method. The flow concentration module of CREST 2.x does not consider the ground water routing, and may tend to under-estimate the water quantity in long-term and long computational timestep hydrological simulations.
1.3. Content of This Paper
The above-mentioned limitations of the CREST 2.x model motivate us to further develop and improve the model into a new version (3.0). In this research, we make four improvements to the traditional CREST 2.x model:
1. Separating the soil layer into three layers and considering tension water, soil moisture, and evapotranspiration computations.
2. Adding a free water storage computation module with a free water distribution curve to describe the sub-grid variations of free water storage.
3. According to free water storage, separating runoff into three components, including overland flow, interflow, and ground water.
4. Improving the flow concentration module into a four-mechanism cell-to-cell routing, including overland flow, interflow, ground water, and river channel flow routings. Based on the arrival time of each upstream grid cell to its downstream outlet grid cell, the generated runoff is routed down along the flow concentration path generated according to the eight-flow-direction method.
The improved CREST 3.0 model and the traditional 2.x model were applied in the Ganjiang River basin, China to test the characteristics of model calibration, simulation, and validation. These improvements make the CREST model easier to combine with the remotely-sensed data such as soil moisture and actual evapotranspiration to decrease the uncertainty problems in distributed hydrological model calibration and validation, and provide the possibility to improve the model simulation capability in regional and global applications.
2. Methodology
2.1. Traditional CREST Model—Version 2.x
The CREST model was initially designed to provide real-time regional and global hydrological predictions by simultaneously modeling over multi-basins with significantly cost-effective computational efficiency [23]. It is also applicable for small-to-medium-size basins at very high-resolutions [24,26]. CREST simulates the spatiotemporal variations of water fluxes and storage on a regular grid with the grid cell resolution being user-defined, thereby enabling multi-scale applications. The scalability of CREST simulations is accomplished through sub-grid-scale representation of soil moisture storage capacity (using a variable infiltration curve) and multi-scale runoff generation processes (using multi-linear reservoirs). The representation of the primary water fluxes such as infiltration and routing are physically related to the spatially variable land surface characteristics (i.e., vegetation, soil type, topography, etc.). The runoff generation process and routing scheme are coupled, thus providing more realistic interactions between lower atmospheric boundary layers, terrestrial surface, and subsurface water. The above flexible modeling features and embedded automated calibration algorithms make CREST a powerful yet cost-effective tool for distributed hydrological modeling and implementation at global, regional, basin, and small catchment scales [25].
The principles of the traditional CREST 2.x model can be found in relevant literature [23,24,26,33,34]. The brief principles and calculation processes of the CREST 2.x model are demonstrated in Figure 1 [25] and in the following paragraphs. As we can see in Figure 1a, the CREST 2.x model requires grid-based precipitation, potential evapotranspiration (PET), and watershed characteristics (such as DEM (Digital Elevation Model), flow direction, flow accumulation, slope, etc.) as forcing data or model inputs. After the canopy interception, infiltration, runoff generation, evapotranspiration (ET) computation, and cell-to-cell routing, the model generates discharge, actual ET (AET), soil moisture, runoff, etc. As demonstrated in Figure 1b, the model is composed of a variable infiltration curve-based runoff generation module, a saturated hydraulic conductivity-based runoff component separation module, a soil moisture computation module, and a cell-to-cell routing module.
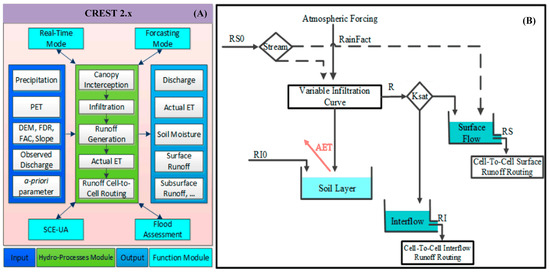
Figure 1.
(A) The framework of the coupled routing and excess storage (CREST) model version 2.x and (B) vertical profile of hydrological processes in a grid cell [25]. AET: actual evapotranspiration; PET: potential ET; FDR: flow direction; FAC: flow accumulation; SCE-UA: shuffled complex evolution developed in the University of Arizona; RS: surface runoff; RI: interflow runoff.
2.2. Improved CREST Model—Version 3.0
2.2.1. Tension Water Storage Capacity Distribution Curve-Based Runoff Generation
For each grid cell, the total runoff generated by the CREST 3.0 is computed by using a tension water storage capacity distribution curve. CREST 3.0 supposes that the runoff generation has a close relationship with the amount of net rainfall and tension water storage. The runoff does not generate until the tension water storage reaches the field capacity. Before the runoff generates, the rainfall replenishes the tension water storage after deduction of the evapotranspiration. CREST 3.0 adopts a tension water storage capacity distribution curve, which is also adopted in previous versions of CREST model, to describe the sub-grid inhomogeneity of the tension water storage capacity. The equation of the distribution curve is [23]:
where f/F represents the proportion of the pervious area of the grid cell whose tension water storage capacity is less than or equal to the value of WM’; WM’ represents the tension water capacity at a point; WMM represents the maximum value of WM’; b is a model parameter that reflects the inhomogeneity degree of the tension water storage capacity in the vadose zone. The areal mean tension water capacity, WM, can be computed as
where IM is the proportion of the impervious area of the grid cell. The total runoff, R, is generated on the pervious area of the grid cell as:
If P − KC × EM + A is less than WMM, then
R = P − KC × EM − WM + W + WM × [1 − (P − KC × EM + A)/WMM]1+b
Otherwise
where P represents precipitation; EM represents potential evapotranspiration; W represents tension water storage; KC represents model parameter used to modify the potential evapotranspiration; and A is an index indicating the saturation degree of the grid cell, and is computed as
R = P − KC × EM − WM + W
A = WMM × (1 − (1 − W/WM)1/(1+b))
2.2.2. Three Soil Layers-Based Soil Moisture and Evapotranspiration Computation
In CREST 3.0, evapotranspiration is related to potential evapotranspiration through a three-layer soil moisture module depending on parameters KC, WUM, WLM, and C. Until the storage WU of the uppermost layer is exhausted, evaporation occurs at the potential rate, equal to KC times the potential evaporation as [23]:
EU = KC × EM
Upon exhaustion of the upper layer (capacity WUM), any remaining potential evapotranspiration is applied to the lower layer, but the efficiency is modified by multiplication by the ratio of the actual storage WL to the capacity storage WLM of that layer as
EL = (KC × EM − EU) × WL/WLM
When the lower layer storage WL is reduced to a proportion C of WLM, evapotranspiration is assumed to continue, but at a further reduced rate, and the evapotranspiration ED is given by
ED = C × (KC × EM − EU) − EL
2.2.3. Free Water Reservoir-Based Separation of Three Runoff Components
The total runoff, R, is separated into three components including RS, overland runoff, RG, the ground water contribution, and RI, a contribution to interflow. The concepts of free water storage S and free water storage capacity SM are used. The latter is assumed to be distributed between zero and a point maximum SMM in a parabolic manner, over FR, that portion of the sub-grid which is currently producing runoff. The distribution curve of the SM in a grid cell is stated as [23]
where f is the portion of the sub-grid area for which the free water storage capacity is less than or equal to SM’ and EX is a model parameter that describes the inhomogeneity of the SM. The areal mean free water storage capacity SM may be used instead of SMM as a model parameter, and has the relationship
SMM = SM × (1 + EX)
Assume AU is an index indicating the free water storage of the grid cell and it is computed as
and FR is computed as
AU = SMM × (1 − (1 − S/SM)1/(1+EX))
FR = (R − IM × (P − KC × EM))/(P − KC × EM)
The interflow and ground water are computed as
where KG and KI are discharge coefficients for ground water and interflow, respectively. The overland runoff is computed as:
RG = S × KG × FR
RI = S × KI × FR
If P − KC × EM ≤ 0, then
RS = 0
Otherwise
If P − KC × EM + AU < SMM, then
RS = (P − KC × EM − SM + S + SM × (1 − (P − KC × EM + AU)/SMM)1+EX) × FR
Otherwise
RS = (P − KC × EM + S − SM) × FR
2.2.4. Four Mechanisms-Based Cell-To-Cell Routing
CREST 3.0 adopts the four mechanisms-based cell-to-cell routing method to implement flow routing of overland flow, interflow, ground water, and river channel flow. For each upstream grid cell, the arrival time from the upstream grid cell to its downstream basin outlet grid cell is accumulated along the flow path based on the flow concentration time within each grid cell. The flow path is generated based on the eight flow direction method adopted in ArcGIS software. The flow concentration time within grid cell (i, j) is computed as [23]:
where Ti,j represents the flow concentration time within grid cell (i, j); Li,j represents the distance between the centers of grid cell (i, j) and its adjacent downstream grid cell; Si,j represents the slope from grid cell (i, j) to its adjacent downstream grid cell; K is defined as the runoff velocity coefficient. The value of K varies from cell to cell and within cells depending on the following four processes that it represents: for ground water runoff, K is set to a value representative of the ground water flow velocity; for interflow runoff, K is set to a value representative of the soil saturated hydraulic conductivity; for overland runoff, K corresponds to the land surface roughness; and for river channel flow, K is a channel velocity coefficient determined by the channel roughness and hydraulic radius [23].
The interflow and ground water flow move more slowly in response to relatively small values of K. In contrast, overland flow and river channel flow move faster and correspond to larger values of K. All values of K—which control the timing of peak flow—can be provided a priori using land cover maps, soil surveys, and channel cross-sections, but typically must be optimized through calibration [23].
The overland, interflow, and ground water runoff are generated in a hill slope grid cell and flow downstream along their flow paths according to the eight flow direction method. The runoff component retains its flow movement mechanism until it encounters the stream grid cell. After the runoff comes into the stream grid cell, it will flow downstream according to the river channel routing mechanism. The total flow concentration time of the upstream grid cell is accumulated along its flow path, meanwhile considering its flow movement mechanism.
2.3. Model Calibration
The CREST 3.0 model has 15 parameters, which can be found in Table 1. The model parameters are optimized using the SCE-UA optimization method developed by Duan [35,36,37,38,39,40,41,42,43,44]. The objective function of the parameter optimization is the Nash–Sutcliffe coefficient of efficiency (NSCE). Some parameters or state variables of the CREST 3.0 model have strong physical meanings, and their values must obey some constraints including KG + KI < 1, non-negative tension water storages, and KRF ≥ KOF ≥ KIF ≥ KGF. These constraints are implemented by punishment function method. The constraints are treated as punishment terms which are added to the objective function value if the constraints are conflicted.

Table 1.
Parameters and their boundaries of the CREST 3.0 model [23].
3. Study Area and Data Description
In this study, we apply the original CREST 2.x and the improved CREST 3.0 models in daily streamflow simulation in the Ganjiang River basin, China to verify the performance of the improved model.
The Ganjiang River is a tributary of the Yangtze River and is the longest river in Jiangxi Province, China. It is located in the southeast part of China. The basin outlet is the Waizhou station, and the drainage area is 81,258 km2. The elevation of the Ganjiang River basin ranges from 11 to 1997 m, and the terrain varies significantly from hilly land to low hill. The climate of the Ganjiang River basin is mainly subtropical humid monsoon climate, and rainfall usually happens during April and June and flood frequently happens during May and July [45,46]. The DEM, slope, flow direction, and flow routing sequence maps of the Ganjiang River basin are demonstrated in Figure 2.

Figure 2.
Maps of Ganjiang River basin. (A) DEM; (B) Slope; (C) Flow direction; (D) Flow routing sequence.
This study adopts hydro-meteorological data from 2003 to 2009 to carry out daily streamflow simulation. The rainfall data adopts the TRMM (Tropical Rainfall Measuring Mission) satellite-based remote sensing product 3B42V7. The original spatiotemporal resolutions of the TRMM 3B42V7 rainfall data are 0.25° × 0.25° and 3 h. We resampled the TRMM rainfall data into spatiotemporal resolutions of 1 km × 1 km and 1 day by using the nearest-neighbor method and daily rainfall accumulation method. The potential evapotranspiration (PET) data was downloaded from the global daily potential evapotranspiration dataset of the Famine Early Warning System (FEWS) of the USGS (The United States Geological Survey) and the spatiotemporal resolutions are 1° × 1° and 1 day. The spatial resolution of the PET data was resampled into 1 km × 1 km by using the nearest-neighbor method. The daily streamflow data was obtained from Waizhou station observations.
4. Results and Discussion
4.1. Comparison of Basin Outlet Discharge Simulations between CREST 2.x and 3.0
For the purposes of comparing the simulation capability of the CREST 2.x and 3.0 models, the measured and simulated basin outlet hydrographs are compared herein. The basin outlet streamflow simulation results are demonstrated in Figure 3. As we can see in Figure 3, the performance of CREST 3.0 is overall better than the 2.x version. The low flow simulations of the CREST 2.x are significantly underestimated. In contrast, the low flow simulations of the CREST 3.0 version are much better than the 2.x model. CREST 3.0 can simulate the flow recession process and base flow of the Ganjiang River basin with satisfactory accuracy.
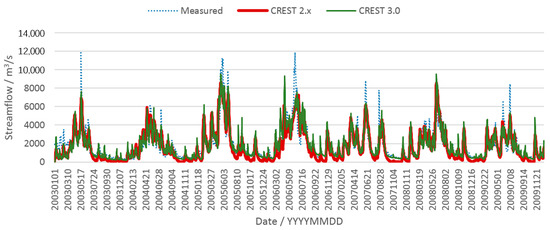
Figure 3.
Hydrographs of basin outlet of CREST 2.x and 3.0 models.
CREST 2.x only considers two runoff components, including overland flow and interflow. Without consideration and computation of ground water, CREST 2.x failed to simulate the base flow process. CREST 3.0 adds a linear reservoir-based ground water simulation module, and considers the runoff generation and flow concentration processes of the ground water. Therefore, the base flow and ground water simulations of CREST 3.0 outperform the 2.x version. The addition of the base flow simulation functionality of the improved 3.0 version is of great significance to global climate change research, global land surface modelling, water resources planning and management, etc. In these applications, the base flow plays a very important role in enclose the water cycle balance. Therefore, the 3.0 version has good application prospects in these study areas.
The scatter plots between measured and simulated basin outlet streamflow of CREST 2.x and 3.0 models are demonstrated in Figure 4. As shown in Figure 4, the simulation results of CREST 3.0 are better than the 2.x version. The distribution of the scatters of version 3.0 is more homogeneous around the regression line than version 2.x. Especially for high flow values, 2.x tends to underestimate the high discharge values. Therefore, the high flow simulations of the 2.x version are slightly worse than the 3.0 version.
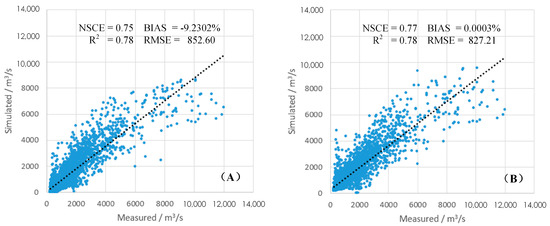
Figure 4.
Scatter plots between measured and simulated basin outlet streamflow of CREST (A) 2.x and (B) 3.0 models.
We also compared model performances of CREST 2.x and 3.0 according to Nash–Sutcliffe coefficient of efficiency (NSCE), BIAS (a statistic is biased if it is calculated in such a way that it is only systematically different from the population parameter of interest), regression R2, and root mean square error (RMSE) [47]. The error statistics of CREST 2.x and 3.0 are listed in Table 2. The NSCE of CREST 2.x and 3.0 were 0.75 and 0.77, respectively. The BIAS of CREST 2.x and 3.0 were −9.2302% and 0.0003%, respectively. The R2 of CREST 2.x and 3.0 were both 0.78. The RMSE of CREST 2.x and 3.0 were 852.60 and 827.21, respectively. These results indicate that CREST 3.0 overall outperformed the 2.x version.

Table 2.
Error statistics of CREST 2.x and 3.0. NSCE: Nash–Sutcliffe coefficient of efficiency; RMSE: root mean square error.
4.2. Comparison of Areal Mean Soil Moisture Simulations between CREST 2.x and 3.0
Figure 5 shows the areal mean soil moisture simulations of CREST 2.x and 3.0. CREST 2.x only considers one soil layer. Therefore, it generates soil moisture of the total vadose zone. CREST 3.0 separates the vadose zone into three soil layers and considers the runoff generation, soil moisture, and evapotranspiration computations of upper, lower, and deep soil layers. It can be observed that the simulated total tension water soil moisture of CREST 2.x (W) was smaller than the 3.0 generated W. This indicates that CREST 2.x may underestimate the total soil moisture of the vadose zone due to the exclusion of the deep soil layer. CREST 2.x separates runoff into overland flow and interflow according to saturated hydraulic conductivity, and can be recognized as only considering the upper and lower layer soil moisture. These soil moistures correspond to upper (WU) and lower (WL) layer soil moistures of CREST 3.0. It is demonstrated in Figure 5 that values and variation tendencies of upper (WU) and lower (WL) soil layers of CREST 3.0 seem similar to the total soil moisture (W) of CREST 2.x.
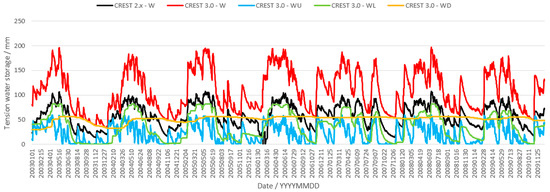
Figure 5.
Simulated tension water storage of CREST 2.x and 3.0 models. W: total soil moisture; WL: lower layer soil moisture; WU: upper layer soil moisture.
In Figure 6, we show the simulated tension water storages of CREST 2.x (W) and 3.0 (WU + WL). We can see that the W and WU + WL simulations are closer to each other. The variation tendency and absolute values are similar to each other. For high values, CREST 3.0 simulations are larger than the 2.x version. For low values, CREST 3.0 simulations are smaller than the 2.x version. For medium values, the simulations of the two models are similar to each other.
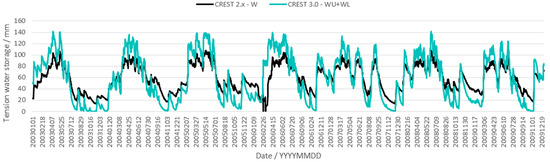
Figure 6.
Simulated tension water storages of CREST 2.x (one soil layer) and 3.0 (sum of upper and lower soil layers) models.
Figure 7 shows the scatter plot of simulated tension water storages of CREST 2.x (W) and 3.0 (WU + WL) models. The regression R2 value between the CREST 2.x and 3.0 are 0.8594, which indicates a high linear correlation relationship between W and WU + WL. The distribution of scatters is even and good. These results prove that the vadose zone total tension water storage simulations of the CREST 2.x model are similar to the sum of upper and lower soil layers tension water storage simulations of CREST 3.0.
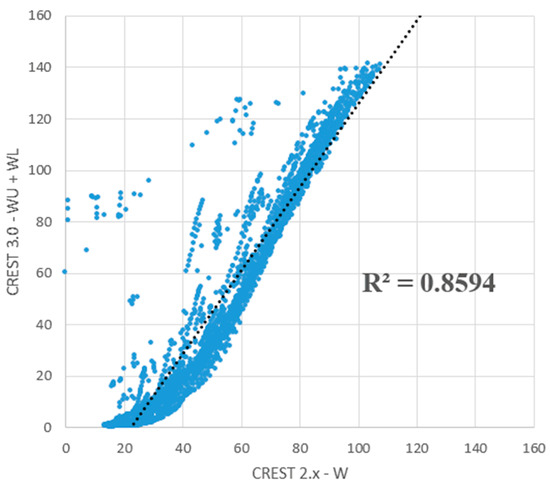
Figure 7.
Scatter plot of simulated tension water storages of CREST 2.x (one soil layer) and 3.0 (sum of upper and lower soil layers) models.
In this research, we do not have sufficient station-observed soil moisture data to further validate the effectiveness and accuracy of the model simulations. This is because the soil moisture data in China is not publicly available to researchers. As a substitute, remotely-sensed soil moisture data provided by satellites such as AMSR-E, SMOS, and SMAP become valuable in research activities. However, both station-observed and remotely-sensed soil moisture data have their own limitations when applied to real-world scenarios. The distribution of soil moisture observation stations in most areas of China is sparse, therefore, the representativeness of the station-based data is poor when interpolating to the whole basin. Remote sensing data can provide spatial distribution of the soil moisture, but the uncertainty issue of remote sensing data is severe for soil moisture variables. Therefore, it is suggested that the validation of soil moisture simulations must combine the advantages of the station observation and remotely-sensed data in future studies.
4.3. Comparison of Areal Mean Actual Evapotranspiration Simulations between CREST 2.x and 3.0
Figure 8 shows the areal mean actual evapotranspiration (AET) simulations of the CREST 2.x model. Most AET simulations are good and reasonable. However, there are some unreasonable AET peak values that we call “singular points”. These singular points are much larger than other AET simulation results, and may be unreasonable. After comparing the computed AET with remote sensing retrieved PET used in this study, we found that these singular values are even larger than observed PET values. Therefore, we confirm that the evapotranspiration computation algorithm or codes of the CREST 2.x model need to be improved, and the singular values are unreasonable.
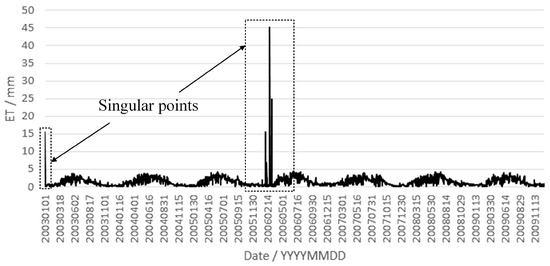
Figure 8.
Simulated evapotranspiration of CREST 2.x (including singular points).
In order to compare AET simulation results of CREST 2.x and 3.0, we exclude the above-mentioned singular values. Figure 9 demonstrates simulated evapotranspiration of CREST 2.x (excluding singular points) and 3.0 models. CREST 2.x can only generate total AET, and CREST 3.0 generates the AET of upper, lower, and deep soil layers. It can be seen the total AET of CREST 3.0 is larger than the total AET of CREST 2.x, which indicates that CREST 2.x may underestimate the total AET due to the exclusion of deep soil layer evapotranspiration. It also can be found that most AET of the upper soil layer is larger than the AET of the lower soil layer, and the AET of the deep soil layer is usually very small.
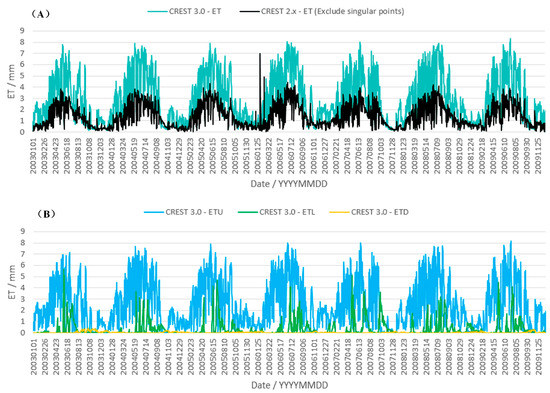
Figure 9.
Simulated evapotranspiration of CREST 2.x (excluding singular points) and 3.0 models. (A) ET of CREST 2.x and 3.0; (B) ETU, ETL, and ETD of CREST 3.0. ETU: evapotranspiration of upper soil layer; ETL: evapotranspiration of lower soil layer; ETD: evapotranspiration of deep soil layer.
Figure 10 shows the scatter plot of the simulated evapotranspiration of CREST 2.x (excluding singular points) and 3.0 models. The regression R2 between CREST 2.x and 3.0 is 0.875, which indicates a high correlation relationship. The scatter distribution is also satisfactory and even. Figure 10 indicates that the evapotranspiration of CREST 3.0 is overall larger than the 2.x version. These results indicate that the exclusion of deep soil layer tension water storage and evapotranspiration computation leads the CREST 2.x to generate lower AET compared with the CREST 3.0 model.
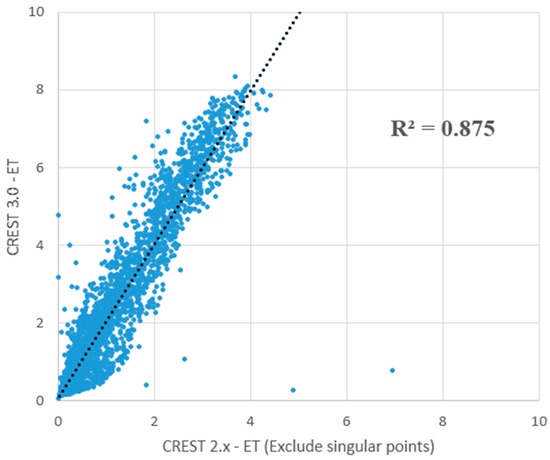
Figure 10.
Scatter plot of simulated evapotranspiration of CREST 2.x (excluding singular points) and 3.0 models.
The validation of ET simulations is much more difficult than soil moisture variables. Unlike the soil moisture, the true values of ET for different underlying surfaces (e.g., bare soil and vegetation-covered land surface) are difficult to obtain. Observed ET data are usually potential ET (PET) of the water surface, rather than actual ET (AET). Precise estimation of the relationship between PET and AET for all kinds of underlying surfaces is also very challenging. Even though the study of ET is a hot issue in remote sensing and hydrology studies, a solidly reliable ET data set or product is still difficult to obtain, and the uncertainty issue in ET estimation is severe. Considering that the station-observed ET data is not sufficient, remote sensing-generated products (e.g., MODIS MOD16, AVHRR, etc.) are better substitutes for researchers and engineers in real-world applications. Therefore, we will further validate the ET simulations by using remotely-sensed ET products in future research.
4.4. Analysis of Areal Mean Runoff Generation Area and Free Water Storage Simulations
Apart from grid-based streamflow, soil moisture, and AET, CREST 3.0 can also generate runoff generation area (FR) and free water storage (S) simulations for each grid cell. Figure 11 demonstrates simulated areal mean runoff generation area and free water storage of the CREST 3.0 model. Most of the FR are between 0.1 and 0.9. This result indicates that for large basins such as the Ganjiang River basin, the tension water storage cannot be totally saturated (FR = 1) or totally exhausted (FR = 0) for the whole basin. This conclusion is reasonable. For very large basins such as the Ganjiang River basin, the spatial distribution of rainfall intensity is usually significantly uneven and the rainfall usually cannot fall on the whole basin for long enough to saturate the whole watershed. Therefore, the areal mean FR cannot be 1. For large basins, the base flow plays an important role in drought periods. The drought season streamflow is stable and larger than 0. The free water reservoir can be supplied by base flow, and the free water storage of the whole basin cannot be totally exhausted.
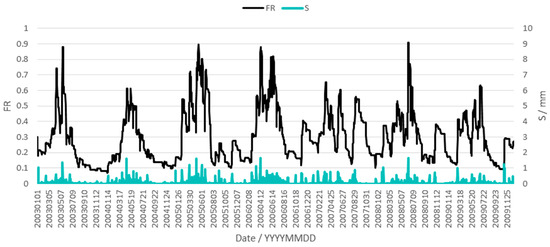
Figure 11.
Simulated areal mean runoff generation area and free water storage of the CREST 3.0 model.
The free water storage, S, reflects the quantity of runoff generated during the runoff generation process to some extent. Figure 11 shows that when FR is increasing, S is still increasing; when FR is decreasing, S is also decreasing. This result indicates that when runoff generation area, FR, is large, the generated runoff is also large. The FR and S react with the same tendency in the process of runoff generation.
5. Conclusions
In this paper, we make four improvements to the traditional CREST 2.x distributed hydrological model and propose a new version 3.0. With the addition of three soil layers-based soil moisture and evapotranspiration computations, free water reservoir-based separation of three runoff components, and four mechanisms-based cell-to-cell routing, CREST 3.0 outperforms the traditional 2.x version in simulation accuracy, output information, and application fields. CREST 3.0 is also friendlier than the 2.x version in its handling of remote sensing retrieved data such as soil moisture. Furthermore, following conclusions can be made here:
(1) CREST 3.0 resolves the high and low flow underestimation problem of the CREST 2.x model. Version 3.0 considers the overland flow, interflow, ground water flow, and river channel flow, and may be more adaptable to different kinds of watersheds and may perform better in flood forecasting applications than the 2.x version.
(2) CREST 3.0 solves the soil moisture and evapotranspiration under-estimation problem of the CREST 2.x model. The 3.0 version considers the soil moisture and evapotranspiration of upper, lower, and deep soil layers. CREST 3.0 performs better in the water quantity estimation and may perform better in water resources planning and management applications.
(3) CREST 3.0 separates the soil layer into three layers, and the depth of the upper soil layer can be configured to adapt to remote sensing retrieved soil moisture data such as AMSR-E, SMAP, SMOS, and Sentinel-1. The 3.0 version is capable of using the remotely-sensed soil moisture and AET data to assist model calibration and validation. The CREST 3.0 model is more suitable to data assimilation tasks than the 2.x version.
(4) Apart from grid-based streamflow, soil moisture, and AET, CREST 3.0 can also generate runoff generation area and free water storage for grid cells. These additional products can provide more useful information for scientific research and real-world engineering applications.
Acknowledgments
This research was funded by China Postdoctoral Science Foundation on Grant (Grant No. 2016M600096); Major International (Regional) Joint Research Project—China’s Water and Food Security under Extreme Climate Change Impact: Risk Assessment and Resilience (G0305, 7141101024); International Project (71461010701); Study of distributed flood risk forecast model and technology based on multi-source data integration and hydro meteorological coupling system (2013CB036406); Research on Key Technologies of Real Time Dynamic Control of Water Level in Flood Season of Cascade Reservoirs (KY1734); Third Sub-Project: Flood Forecasting, Controlling and Flood Prevention Aided Software Development—Flood Control Early Warning Communication System and Flood Forecasting; Controlling and Flood Prevention Aided Software Development for Poyang Lake Area of Jiangxi Province (0628-136006104242, JZ0205A432013, SLXMB200902); Construction project of Shaanxi province medium and small river hydrological monitoring and forecast system—construction of Guanzhong and north of Shaanxi flood forecast scheme (JZ0205A112015); National Key R&D Program of China (Grant No. 2016YFC0402703); IWHR Research & Development Support Program (JZ0145b222017); and Open Fund of State Key Laboratory of Remote Sensing Science (Grant No. OFSLRSS201611). The authors wish to sincerely acknowledge Xianwu Xue, Ke Zhang, Xinyi Shen, and other contributors for their excellent works of developing previous versions of CREST models. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Tesla K40 GPU used for this research. Guangyuan Kan and Yang Hong are corresponding authors.
Author Contributions
Guangyuan Kan, Yang Hong, and Jiren Li designed the model and the experiments; Guoqiang Tang, Yuan Yang, Ke Liang, Lian He, Zhansheng Li, and Youbing Hu provided the data; Liuqian Ding, Xiaoyan He, Ke Liang, and Yaokui Cui gave useful advices; Guangyuan Kan and Guoqiang Tang wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jung, D.; Choi, Y.H.; Kim, J.H. Multiobjective Automatic Parameter Calibration of a Hydrological Model. Water 2017, 9, 187. [Google Scholar] [CrossRef]
- Ciarapica, L.; Todini, E. TOPKAPI: A model for the representation of the rainfall-runoff process at different scales. Hydrol. Process. 2002, 16, 207–229. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Todini, E. Towards a comprehensive physically-based rainfall-runoff model. Hydrol. Process. 2002, 6, 859–881. [Google Scholar] [CrossRef]
- Whitaker, A.; Alila, Y.; Beckers, J.; Toews, D. Application of the distributed hydrology soil vegetation model to redfish creek, British Columbia: Model evaluation using internal catchment data. Hydrol. Process. 2003, 17, 199–224. [Google Scholar] [CrossRef]
- Yuan, F.; Xie, Z.H.; Liu, Q.; Yang, H.W.; Su, F.G.; Liang, X.; Ren, L.L. An application of the VIC-3L land surface model and remote sensing data in simulating streamflow for the Hanjiang River basin. Can. J. Remote Sens. 2004, 30, 680–690. [Google Scholar] [CrossRef]
- Oconnell, P.E.; Todini, E. Modelling of rainfall, flow and mass transport in hydrological systems: An overview. J. Hydrol. 1996, 175, 3–16. [Google Scholar] [CrossRef]
- Chen, L.J.; Wang, L.Z.; Ma, Y.; Liu, P. Overview of Ecohydrological Models and Systems at the Watershed Scale. IEEE Syst. J. 2015, 9, 1091–1099. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.A.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Dooge, J.C.L. Looking for hydrologic laws. Water Resour. Res. 1986, 22, 46–58. [Google Scholar] [CrossRef]
- Yalew, S.; van Griensven, A.; Ray, N.; Kokoszkiewicz, L.; Betrie, G.D. Distributed computation of large scale SWAT models on the Grid. Environ. Model. Softw. 2013, 41, 223–230. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhu, A.X.; Qin, C.Z. Estimation of theoretical maximum speedup ratio for parallel computing of grid-based distributed hydrological models. Comput. Geosci. 2013, 60, 58–62. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhu, A.X.; Liu, Y.B.; Zhu, T.X.; Qin, C.Z. A layered approach to parallel computing for spatially distributed hydrological modeling. Environ. Model. Softw. 2014, 51, 221–227. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Bao, H.J.; Yu, Z.B. Application of a Developed Grid-Xinanjiang Model to Chinese Watersheds for Flood Forecasting Purpose. J. Hydrol. Eng. 2009, 14, 923–934. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Yu, Z.B.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468, 47–62. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B.; Refsgaard, A. Recent developments of the Systeme Hydrologique Europeen (SHE) towards the MIKE SHE. In Modelling and Management of Sustainable Basin-scale Water Resource Systems; IAHS Publications 231; IAHS Publications: Wallingford, UK, 1995; pp. 427–434. [Google Scholar]
- Miao, Q.H.; Yang, D.W.; Yang, H.B.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- Sayari, S.; Rahimpour, M.; Zounemat-Kermani, M. Numerical modeling based on a finite element method for simulation of flow in furrow irrigation. Paddy Water Environ. 2017, 15, 879–887. [Google Scholar] [CrossRef]
- Kashiyama, K.; Okada, T. Automatic mesh generation method for shallow-water flow-analysis. Int. J. Numer. Methods Fluids 1992, 15, 1037–1057. [Google Scholar] [CrossRef]
- Bloschl, G.; Sivapalan, M. Scale issues in hydrological modeling—A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Connolly, R.D. Modelling effects of soil structure on the water balance of soil-crop systems: A review. Soil Tillage Res. 1998, 48, 1–19. [Google Scholar] [CrossRef]
- Durand, D.; Gascuel-Odoux, C.; Cordier, M.O. Parameterisation of hydrological models: A review and lessons learned from studies of an agricultural catchment (Naizin, France). Agronomie 2002, 22, 217–228. [Google Scholar] [CrossRef]
- Pietroniro, A.; Leconte, R. A review of Canadian remote sensing and hydrology, 1999–2003. Hydrol. Process. 2005, 19, 285–301. [Google Scholar] [CrossRef]
- Wang, J.; Hong, Y.; Li, L.; Gourley, J.J.; Khan, S.I.; Yilmaz, K.K.; Adler, R.F.; Policelli, F.S.; Habib, S.; Irwn, D.; et al. The coupled routing and excess storage (CREST) distributed hydrological model. Hydrol. Sci. J. 2011, 56, 84–98. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based multi-satellite precipitation analysis over the Wangchu basin of Bhutan: Are the latest satellite precipitation products 3B43V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Zhang, K. CREST User manual Version 2.1-Fortran; The University of Oklahoma (OU) HyDROS Lab: Norman, OK, USA, 2015. [Google Scholar]
- Shen, X.; Hong, Y.; Zhang, K.; Hao, Z. Refining a distributed linear reservoir routing method to improve performance of the CREST model. J. Hydrol. Eng. 2016, 22, 04016061. [Google Scholar] [CrossRef]
- Vergara, H.; Kirstetter, P.E.; Gourley, J.J.; Flamig, Z.L.; Hong, Y.; Arthur, A.; Kolar, R. Estimating a-priori kinematic wave model parameters based on regionalization for flash flood forecasting in the Conterminous United States. J. Hydrol. 2016, 541, 421–433. [Google Scholar] [CrossRef]
- The University of Oklahoma, Hydrometeorology and Remote Sensing Laboratory. 2017. Website of CREST Model. Available online: http://hydro.ou.edu/research/crest/ (accessed on 15 June 2017).
- Zhao, E.Y.; Gao, C.X.; Jiang, X.G.; Liu, Z.X. Land surface temperature retrieval from AMSR-E passive microwave data. Opt. Express 2017, 25, A940–A952. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.; Vu, T.; Veettil, A.V.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Rodiguez-Fernandez, N.J.; Sabater, J.M.; Richaume, P.; de Rosnay, P.; Kerr, Y.H.; Albergel, C.; Drusch, M.; Mecklenburg, S. SMOS near-real-time soil moisture product: Processor overview and first validation results. Hydrol. Earth Syst. Sci. 2017, 21, 5201–5216. [Google Scholar] [CrossRef]
- Felfelani, F.; Wada, Y.; Longuevergne, L.; Pokhrel, Y.N. Natural and human-induced terrestrial water storage change: A global analysis using hydrological models and GRACE. J. Hydrol. 2017, 553, 105–118. [Google Scholar] [CrossRef]
- Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite remote sensing and hydrologic modeling for flood inundation mapping in lake Victoria basin: Implications for hydrologic prediction in ungauged basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of global flood detection using satellite-based rainfall and a hydrologic model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Duan, Q. A Global Optimization Strategy for Efficient and Effective Calibration of Hydrologic Models. Ph.D. Thesis, Department of Hydrology and Water Resources, University of Arizona, Tucson, AZ, USA, 1991. [Google Scholar]
- Duan, Q.; Sorooshianz, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.; Sorooshian, S. A shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Kan, G.; Zhang, M.; Liang, K.; Wang, H.; Jiang, Y.; Li, J.; Ding, L.; He, X.; Hong, Y.; Zuo, D.; et al. Improving water quantity simulation & forecasting to solve the energy-water-food nexus issue by using heterogeneous computing accelerated global optimization method. Appl. Energy 2016. [Google Scholar] [CrossRef]
- Kan, G.; Lei, T.; Liang, K.; Li, J.; Ding, L.; He, X.; Yu, H.; Zhang, D.; Zuo, D.; Bao, Z.; et al. A multi-core CPU and many-core GPU based fast parallel shuffled complex evolution global optimization approach. IEEE Trans. Parallel Distrib. Syst. 2016, 28, 332–344. [Google Scholar] [CrossRef]
- Kan, G.; Liang, K.; Li, J.; Ding, L.; He, X.; Hu, Y.; Amo-Boateng, M. Accelerating the SCE-UA global optimization method based on multi-core CPU and many-core GPU. Adv. Meteorol. 2016, 2016, 8483728. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Li, J.; Ding, L.; Hong, Y.; Zhang, H.; Liang, K.; Zhang, M. Computer aided numerical methods for hydrological model calibration: An overview and recent development. Arch. Comput. Methods Eng. 2017. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Ding, L.; Li, J.; Hong, Y.; Zuo, D.; Ren, M.; Lei, T.; Liang, K. Fast hydrological model calibration based on the heterogeneous parallel computing accelerated shuffled complex evolution method. Eng. Optim. 2017. [Google Scholar] [CrossRef]
- Kan, G.; He, X.; Ding, L.; Li, J.; Liang, K.; Hong, Y. A heterogeneous computing accelerated SCE-UA global optimization method using OpenMP, CUDA and OpenACC. Water Sci. Technol. 2017, 76, 1640–1651. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Li, Z.; Xue, X.; Hu, Q.; Yong, B.; Hong, Y. A study of substitutability of TRMM remote sensing precipitation for gauge-based observation in Ganjiang River basin. Adv. Water Sci. 2015, 26, 340–346. (In Chinese) [Google Scholar]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM level-3 products over a midlatitude basin: Is day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).