Detailed Sponge City Planning Based on Hierarchical Fuzzy Decision-Making: A Case Study on Yangchen Lake
Abstract
:1. Introduction
2. Methods and Data Description
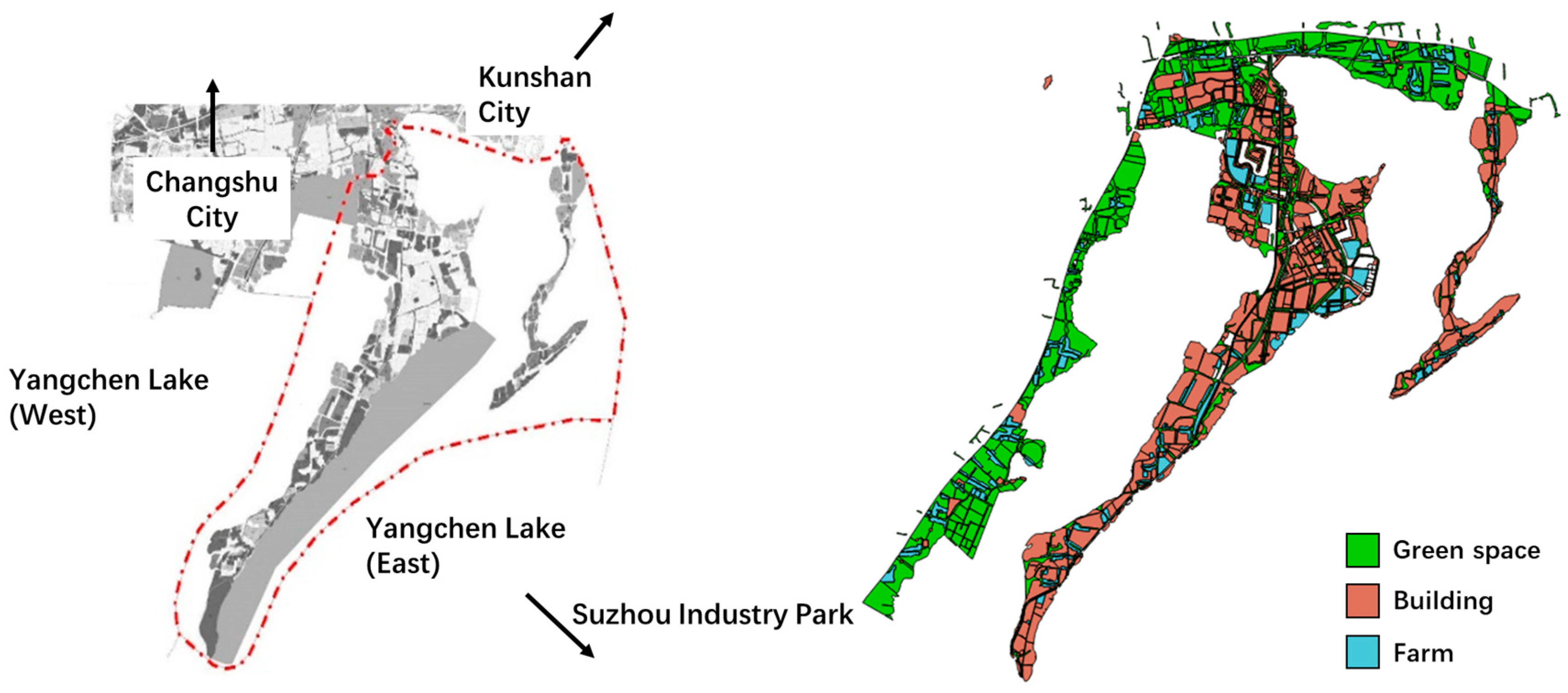
2.1. Study Description
2.2. Data Collection and Criteria Selection
2.3. Methodology
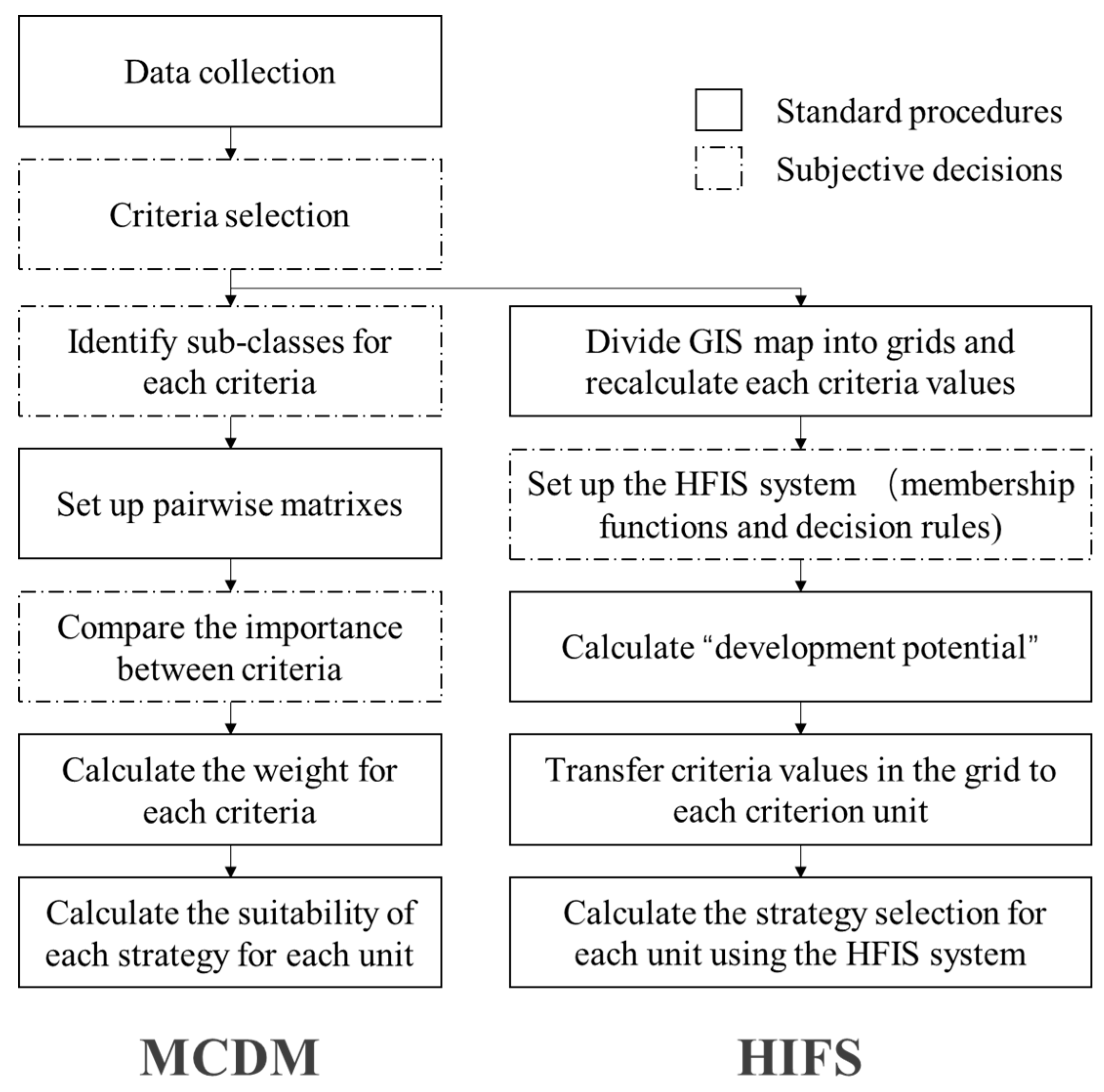
2.3.1. Multi-Criteria Decision Making with an Analytical Hierarchy Procedure
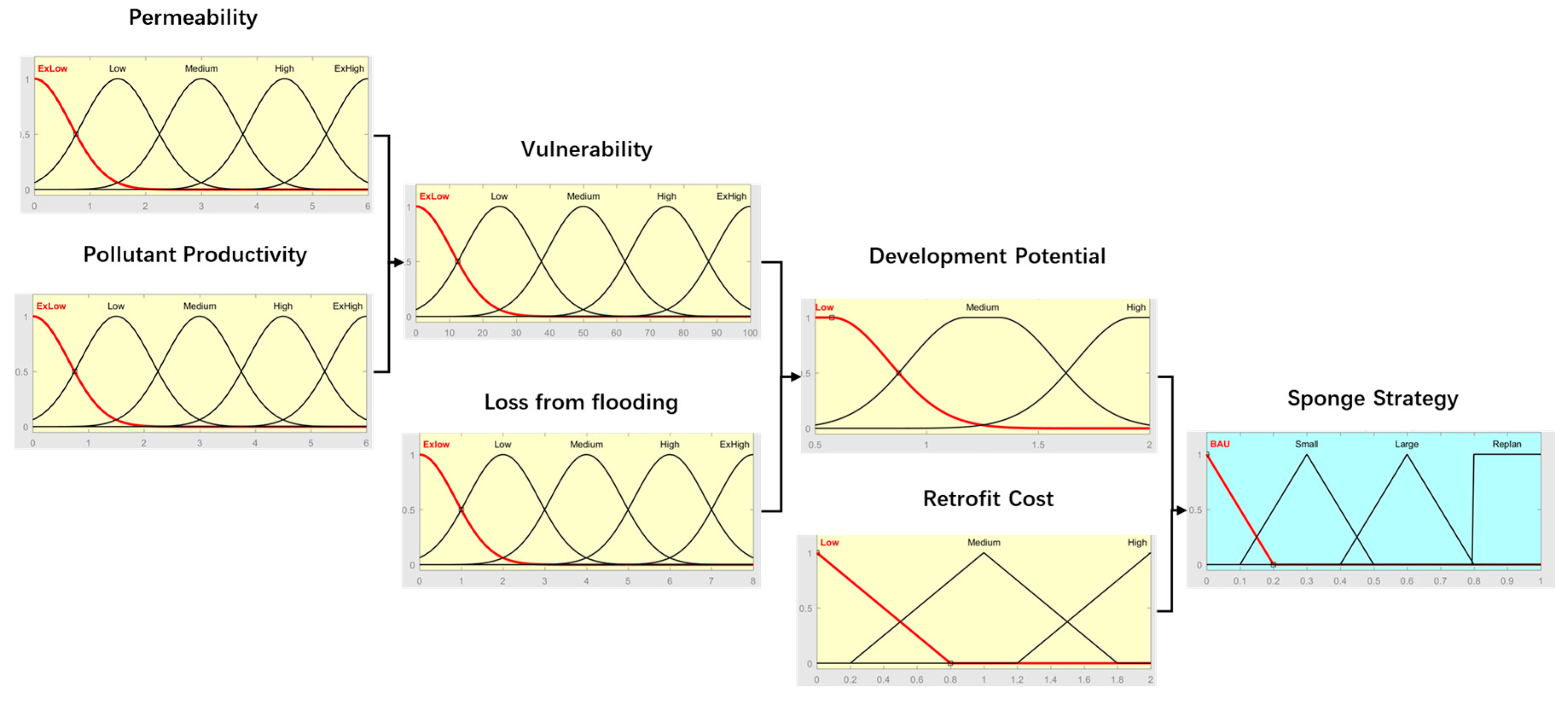
2.3.2. Hierarchical Fuzzy Inference System (HFIS) Decision Making
- IB,j is the criteria value of grid j;
- IA,i is the value of the corresponding criteria in polygon i;
- is the intersect area of grid j and polygon i;
- is the area of polygon i.
- DA,i is the development potential of polygon i;
- DB,i is the development potential of grid j;
- is the intersecting area of grid j and polygon i;
- Ai is the area of polygon i.
3. Results and Discussion
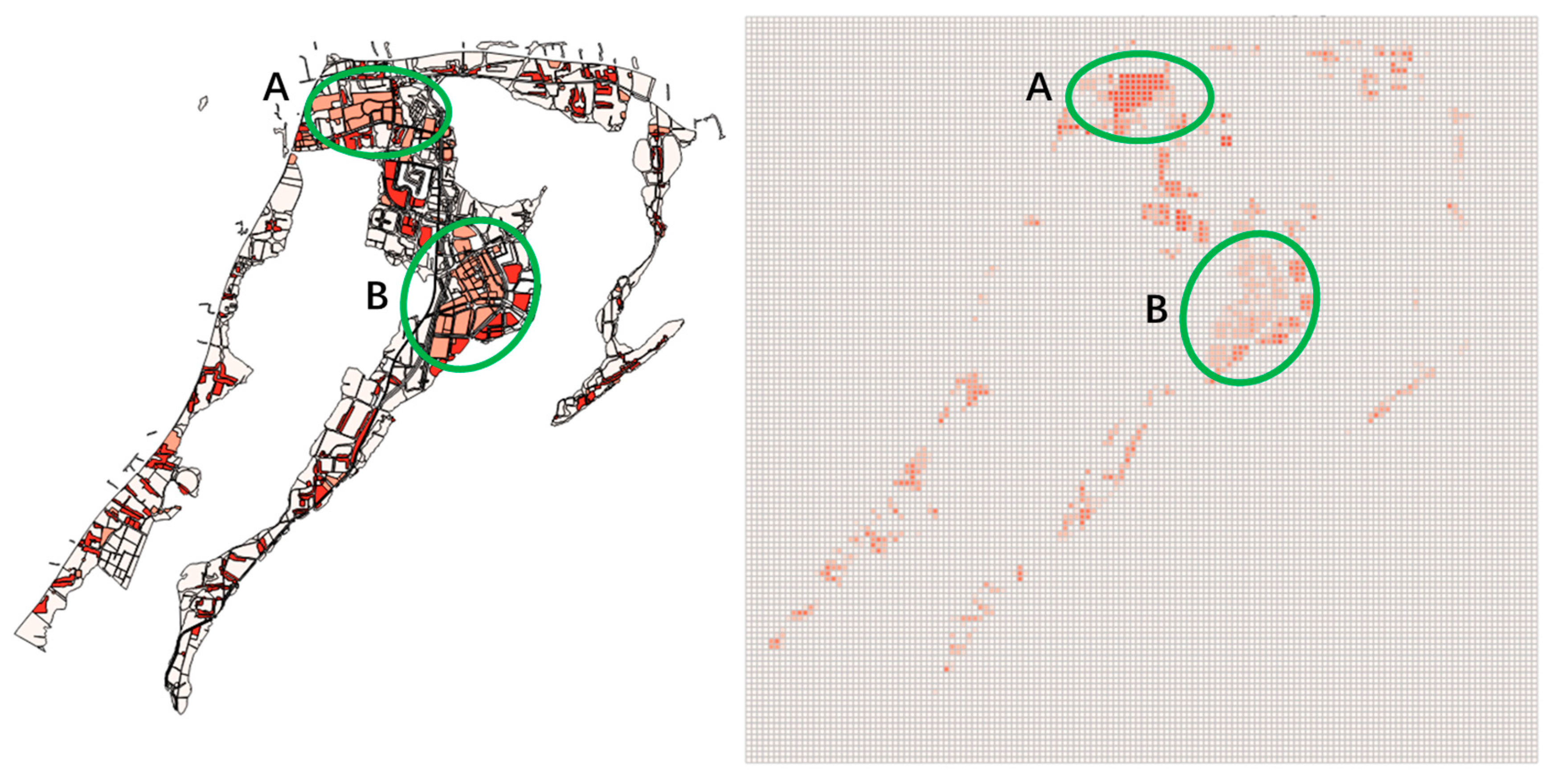
3.1. Fuzzified GIS Map
3.2. Sponge Urban Plan for Yangchen Lake Resort
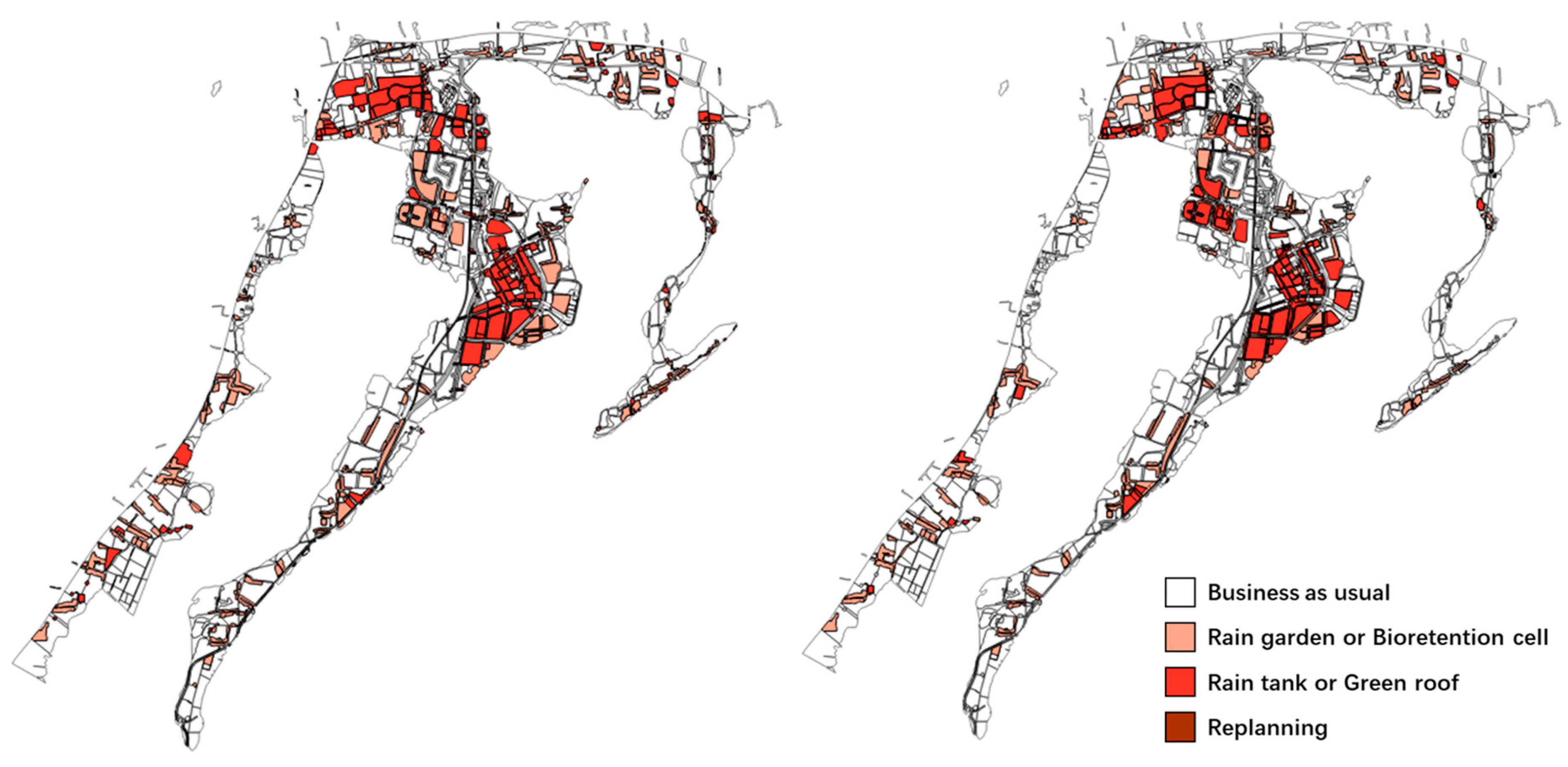
3.3. Comparison of MCDM and HFIS
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xia, J.; Zhang, Y.; Xiong, L.; He, S.; Wang, L.; Yu, Z. Opportunities and challenges of the Sponge City construction related to urban water issues in China. Sci. China Earth Sci. 2017, 60, 652–658. [Google Scholar] [CrossRef]
- Urbonas, B.; Stahre, P. Stormwater: Best Management Practices and Detention for Water Quality, Drainage, and CSO Management; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Fairlie, S. Low Impact Development: Planning and People in a Sustainable Countryside; Jon Carpenter Chipping Norton: Chipping Norton, UK, 1996. [Google Scholar]
- Wong, T.H.; Brown, R.R. The water sensitive city: Principles for practice. Water Sci. Technol. 2009, 60, 673–682. [Google Scholar] [CrossRef] [PubMed]
- Albano, R.; Mancusi, L.; Abbate, A. Improving flood risk analysis for effectively supporting the implementation of flood risk management plans: The case study of “Serio” Valley. Environ. Sci. Policy 2017, 75, 158–172. [Google Scholar] [CrossRef]
- Inam, A.; Adamowski, J.; Halbe, J.; Malard, J.; Albano, R.; Prasher, S. Coupling of a distributed stakeholder-built system dynamics socio-economic model with SAHYSMOD for sustainable soil salinity management part 1: Model development. J. Hydrol. 2017, 551. [Google Scholar] [CrossRef]
- Urich, C.; Sitzenfrei, R.; Kleidorfer, M.; Bach, P.M.; McCarthy, D.T.; Deletic, A.; Rauch, W. Evolution of urban drainage networks in DAnCE4Water. In Proceedings of the 9th International Conference on Urban Drainage Modelling, Belgrade, Serbia, 4–6 September 2012. [Google Scholar]
- Ferguson, B.C.; Brown, R.R.; Frantzeskaki, N.; de Haan, F.J.; Deletic, A. The enabling institutional context for integrated water management: Lessons from Melbourne. Water Res. 2013, 47, 7300–7314. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.W.; Lempert, R.J.; Keller, K.; Hackbarth, A.; Mijere, C.; McInerney, D.J. Robust climate policies under uncertainty: A comparison of robust decision making and info-gap methods. Risk Anal. 2012, 32, 1657–1672. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.B.; Qi, C.; Yang, Y.J. Optimal expansion of a drinking water infrastructure system with respect to carbon footprint, cost-effectiveness and water demand. J. Environ. Manag. 2012, 110, 194–206. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Paydar, Z. Evaluation of potential irrigation expansion using a spatial fuzzy multi-criteria decision framework. Environ. Model. Softw. 2012, 38, 147–157. [Google Scholar] [CrossRef]
- Jeong, J.S.; García-Moruno, L.; Hernández-Blanco, J. A site planning approach for rural buildings into a landscape using a spatial multi-criteria decision analysis methodology. Land Use Policy 2013, 32, 108–118. [Google Scholar] [CrossRef]
- Rahman, R.; Saha, S.K. Remote sensing, spatial multi criteria evaluation (SMCE) and analytical hierarchy process (AHP) in optimal cropping pattern planning for a flood prone area. J. Spat. Sci. 2008, 53, 161–177. [Google Scholar] [CrossRef]
- Van Niekerk, A.; du Plessis, D.; Boonzaaier, I.; Spocter, M.; Ferreira, S.; Loots, L.; Donaldson, R. Development of a multi-criteria spatial planning support system for growth potential modelling in the Western Cape, South Africa. Land Use Policy 2016, 50, 179–193. [Google Scholar] [CrossRef]
- Araya-Munoz, D.; Metzger, M.J.; Stuart, N.; Wilson, A.M.W.; Carvajal, D. A spatial fuzzy logic approach to urban multi-hazard impact assessment in Concepcion, Chile. Sci. Total Environ. 2017, 576, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Pourghasemi, H.R.; Moradi, H.R.; Fatemi Aghda, S.M.; Gokceoglu, C.; Pradhan, B. GIS-based landslide susceptibility mapping with probabilistic likelihood ratio and spatial multi-criteria evaluation models (North of Tehran, Iran). Arab. J. Geosci. 2013, 7, 1857–1878. [Google Scholar] [CrossRef]
- Radmehr, A.; Araghinejad, S. Flood vulnerability analysis by fuzzy spatial multi criteria decision making. Water Resour. Manag. 2015, 29, 4427–4445. [Google Scholar] [CrossRef]
- Rahman, M.R.; Shi, Z.H.; Chongfa, C. Assessing regional environmental quality by integrated use of remote sensing, GIS, and spatial multi-criteria evaluation for prioritization of environmental restoration. Environ. Monit. Assess. 2014, 186, 6993–7009. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Zadeh, L.A. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Lee, G.; Jun, K.S.; Chung, E.-S. Robust spatial flood vulnerability assessment for Han River using fuzzy TOPSIS with α-cut level set. Expert Syst. Appl. 2014, 41, 644–654. [Google Scholar] [CrossRef]
- Lee, M.-J.; Kang, J.E.; Kim, G. Application of fuzzy combination operators to flood vulnerability assessments in Seoul, Korea. Geocarto Int. 2015, 1–24. [Google Scholar] [CrossRef]
- Rezaei, F.; Safavi, H.R.; Ahmadi, A. Groundwater vulnerability assessment using fuzzy logic: A case study in the Zayandehrood aquifers, Iran. Environ Manag. 2013, 51, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Şener, E.; Şener, Ş. Evaluation of groundwater vulnerability to pollution using fuzzy analytic hierarchy process method. Environ. Earth Sci. 2015, 73, 8405–8424. [Google Scholar] [CrossRef]
- Singh, P.K.; Nair, A. Livelihood vulnerability assessment to climate variability and change using fuzzy cognitive mapping approach. Clim. Chang. 2014, 127, 475–491. [Google Scholar] [CrossRef]
- Gray, S.R.J.; Gagnon, A.S.; Gray, S.A.; O’Dwyer, B.; O’Mahony, C.; Muir, D.; Devoy, R.J.N.; Falaleeva, M.; Gault, J. Are coastal managers detecting the problem? Assessing stakeholder perception of climate vulnerability using Fuzzy Cognitive Mapping. Ocean Coast. Manag. 2014, 94, 74–89. [Google Scholar] [CrossRef]
- Navas, J.M.; Telfer, T.C.; Ross, L.G. Spatial modeling of environmental vulnerability of marine finfish aquaculture using GIS-based neuro-fuzzy techniques. Mar. Pollut. Bull. 2011, 62, 1786–1799. [Google Scholar] [CrossRef] [PubMed]
- Talebian, A.; Shafahi, Y. The treatment of uncertainty in the dynamic origin–destination estimation problem using a fuzzy approach. Trans. Plan. Technol. 2015, 38, 795–815. [Google Scholar] [CrossRef]
- Teh, L.C.; Teh, L.S. A fuzzy logic approach to marine spatial management. Environ. Manag. 2011, 47, 536–545. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, K.; Chen, X.; Zhu, W. Combining a fuzzy matter-element model with a geographic information system in eco-environmental sensitivity and distribution of land use planning. Int. J. Environ. Res. Public Health 2011, 8, 1206–1221. [Google Scholar] [CrossRef] [PubMed]
- Sivanandam, S.; Sumathi, S.; Deepa, S. Introduction to Fuzzy Logic Using Matlab; Springer: Berlin, Germany, 2007; Volume 1. [Google Scholar]
| Land Use | Permeability | Pollutant Productivity | Loss from Flooding | Retrofit Cost |
|---|---|---|---|---|
| Farm | 1 | 2 | 1 | 1 |
| Building | 0 | 1 | 2 | 2 |
| Green space | 2 | 0 | 0 | 0 |
| Goal | Weight | Criteria | Weight | Class | Weight | Strategy Weight | |||
|---|---|---|---|---|---|---|---|---|---|
| Business as Usual | Raintank Green Roof | Rain Garden Bioretention | Re-Planning | ||||||
| Development | 1.0000 | Permea-bility | 0.0553 | High | 0.0754 | 0.6692 | 0.1155 | 0.1155 | 0.0998 |
| Medium | 0.2290 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | ||||
| Low | 0.6955 | 0.0871 | 0.3854 | 0.3854 | 0.1422 | ||||
| Land use | 0.0649 | Farm | 0.6955 | 0.0886 | 0.0952 | 0.5513 | 0.2649 | ||
| Building | 0.2290 | 0.3812 | 0.4331 | 0.1030 | 0.0828 | ||||
| Park | 0.0754 | 0.6201 | 0.0708 | 0.2166 | 0.0925 | ||||
| Area (ha) | 0.0401 | 1.19–45 | 0.1140 | 0.3000 | 0.3000 | 0.3000 | 0.1000 | ||
| 0.25–1.19 | 0.4054 | 0.2500 | 0.2500 | 0.2500 | 0.2500 | ||||
| 0–0.25 | 0.4806 | 0.2857 | 0.2857 | 0.2857 | 0.1429 | ||||
| Flood loss | 0.2994 | High | 0.7514 | 0.0445 | 0.1723 | 0.1958 | 0.5874 | ||
| Medium | 0.1782 | 0.0813 | 0.3598 | 0.3598 | 0.1991 | ||||
| Low | 0.0704 | 0.3000 | 0.3000 | 0.3000 | 0.1000 | ||||
| Retrofit cost | 0.3286 | High | 0.0658 | 0.4167 | 0.0833 | 0.0833 | 0.4167 | ||
| Medium | 0.2172 | 0.3000 | 0.3000 | 0.3000 | 0.1000 | ||||
| Low | 0.7171 | 0.3125 | 0.3125 | 0.3125 | 0.0625 | ||||
| Pollution | 0.2117 | High | 0.7429 | 0.0457 | 0.1451 | 0.3494 | 0.4598 | ||
| Medium | 0.1939 | 0.0871 | 0.3854 | 0.3854 | 0.1422 | ||||
| Low | 0.0633 | 0.3313 | 0.2916 | 0.2916 | 0.0855 | ||||
| Comparison criteria | HFIS | MCDM | |
|---|---|---|---|
| Strategy Choice | Business as ususal | 49.7% | 55.6% |
| rain water tanks or green roofs | 28.7% | 22.7% | |
| the rain garden or bioretention cells | 21.6% | 21.7% | |
| Overlay area of choosing same strategy (other than BAU) | 69.7% | ||
| User-defined decisions | 34 | 141 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Fu, D.; Wang, Y.; Singh, R.P. Detailed Sponge City Planning Based on Hierarchical Fuzzy Decision-Making: A Case Study on Yangchen Lake. Water 2017, 9, 903. https://doi.org/10.3390/w9110903
Zhang J, Fu D, Wang Y, Singh RP. Detailed Sponge City Planning Based on Hierarchical Fuzzy Decision-Making: A Case Study on Yangchen Lake. Water. 2017; 9(11):903. https://doi.org/10.3390/w9110903
Chicago/Turabian StyleZhang, Junyu, Dafang Fu, Yajun Wang, and Rajendra Prasad Singh. 2017. "Detailed Sponge City Planning Based on Hierarchical Fuzzy Decision-Making: A Case Study on Yangchen Lake" Water 9, no. 11: 903. https://doi.org/10.3390/w9110903
APA StyleZhang, J., Fu, D., Wang, Y., & Singh, R. P. (2017). Detailed Sponge City Planning Based on Hierarchical Fuzzy Decision-Making: A Case Study on Yangchen Lake. Water, 9(11), 903. https://doi.org/10.3390/w9110903






