Abstract
This study proposes a bivariate distribution with Exponentiated Gumbel (BEG) marginals to estimate return levels of annual maximum daily rainfall (AMDR) in Mexico. We analyze 181 gauging stations across two contrasting climates (Coahuila, Tabasco) and compare BEG against Generalized Extreme Value (GEV), Gumbel (G), and Exponentiated Gumbel (EG). Parameters are estimated by maximum likelihood. Model selection uses AICc (primary) and BIC (tie-breaker), both computed from the same maximized log-likelihood. On a per-station basis, BEG yields the lowest AICc for 70% of samples. Differences in return levels become more pronounced at high non-exceedance probabilities. Monte Carlo reliability checks show that BEG reduces bias and mean squared error (MSE) relative to univariate fits. Using L-moments to delineate homogeneous regions and fitting all BEG pairs confirms these results. A worked example (station 5001) shows that bootstrap 95% CIs for BEG are narrower than for EG, illustrating reduced marginal-quantile uncertainty under joint estimation. Together, BEG provides a robust, dependence-aware tool for regional frequency analysis of extreme rainfall.
1. Introduction
Held and Soden [] highlighted that variations in the hydrological cycle have profound impacts on human activities, including an increased risk of flooding as well as the occurrence and severity of droughts. Floods are among the most damaging natural hazards worldwide, and their impacts have intensified due to factors such as irregular human settlements near rivers, deforestation, and continuous land-use changes.
Mexico is especially vulnerable to hydrometeorological events that cause widespread damage across its territory. Between 2007 and 2020, heavy rains, floods, and tropical cyclones affected 27.8 million people, resulting in 1173 fatalities and economic losses exceeding 24.6 billion USD []. Analyses of rainfall patterns in Mexico [,] indicate that floods caused by extreme rainfall events are likely to become more frequent and intense in the future. Given the potential consequences of underestimating or overestimating rainfall quantiles—ranging from hydraulic structure failure to unnecessarily inflated construction costs—reliable statistical tools are essential for estimating their magnitude and frequency.
Numerous at-site and regional rainfall frequency analyses have been conducted worldwide, and results consistently demonstrate that no single distribution universally fits annual maximum daily rainfall (AMDR) data. Although the Gumbel distribution (G) is widely applied, studies such as Gado et al. [] in Egypt have shown that it is not always appropriate, while in other regions it has been identified as the most suitable model [,,,,,,,,,].
In Italy, Moccia et al. [] analyzed AMDR records from 297 gauging stations and found that the Fréchet distribution (EVIII) provided the best fit. Their study also revealed significant differences in return periods and return levels compared to results from G, reversed Weibull (EVII), Pareto, Lognormal, and Gamma distributions, echoing earlier findings by Koutsoyiannis [,]. The EVI, EVII, and EVIII distributions are all special cases of the Generalized Extreme Value (GEV) distribution, which has often been identified as the best-fitting model for AMDR samples in multiple regions [,,,,,,,,,]. Similarly, the Log-Pearson Type III (LPIII) distribution has also proven effective in modeling AMDR series [,,,,,].
The Exponentiated Gumbel (EG) distribution was proposed by Nadarajah [], who demonstrated its improved performance in climate modeling compared to the EVI and GEV distributions. Escalante-Sandoval [] applied EG, exponentiated Weibull (EW), exponentiated Fréchet (EF), and their mixed forms to AMDR series from 19 Mexican stations, showing that exponentiated and mixed exponentiated distributions provide flexible and reliable alternatives for modeling extreme rainfall. More recently, Soleiman and Abdollahi [] compared the G and EG distributions, concluding—based on AIC and BIC criteria—that EG offered a more flexible fit for hydrological datasets, corroborating earlier findings by Nadarajah [].
Regional frequency analysis has also emerged as a practical approach to reduce uncertainties associated with short or incomplete rainfall records at gauged sites. In this context, multivariate joint estimation models have proven valuable, as they enhance the estimation of marginal distribution parameters and improve regional at-site estimates of return levels by incorporating information from neighboring sites within homogeneous regions. Bivariate approaches have shown promise in flood frequency analysis [,,,,,,,,].
In multivariate flood modeling, copula-based approaches remain standard because they decouple marginal behavior from the joint structure and are widely used in hydrology [,,,,,,]. By contrast, the multivariate logistic model provides a direct parametric description of dependence, avoids the need to select a copula family a priori, and can reduce modeling and computational burden while preserving the ability to capture joint behavior [,].
In this study, a bivariate distribution with Exponentiated Gumbel marginals (BEG) is proposed to improve the estimation of marginal parameters and corresponding quantiles. The performance of this model is compared with that of univariate probability distributions, namely G, GEV, and EG.
2. Materials and Methods
2.1. Study Area and Data
Mexico is characterized by a summer–rainy and winter–dry regime, except in the northwest. Annual precipitation ranges from <500 mm in the north and northwest to >2000 mm in the humid south and southeast. Two states that illustrate this climatic contrast are Coahuila, in northern Mexico, and Tabasco, in the southeast (Figure 1).
Figure 1.
Location of the study areas within Mexico.
Coahuila (151,563 km2) has a semi-warm summer and cold winter climate, with a mean annual temperature of 20 °C (min. 4 °C, max. 30 °C). Rainfall is scarce, averaging ~400 mm yr−1, concentrated in summer. Maximum daily rainfall varies between 11.3 and 453 mm.
Tabasco (25,267 km2) is predominantly warm-humid, with abundant summer rains (75.97%), year-round humid conditions (19.64%), and sub-humid summer rains (4.39%). The mean annual temperature is 27 °C (min. 18.5 °C, max. 36 °C). Rainfall occurs throughout the year, peaks from June to October, and averages 2550 mm yr−1. Maximum daily rainfall ranges from 38.8 to 816.9 mm.
The dataset consists of records from 106 rain gauge stations in Coahuila and 75 stations in Tabasco, obtained from National Water Commission (CONAGUA) []. The location of each station is detailed in Appendix A.
2.2. Delineation of Homogeneous Regions
The joint parameter estimation model requires that all samples belong to the same homogeneous region. In this study, regions were delineated using the Hosking–Wallis L-moments framework (L-CV, Tao2; L-skewness, Tao3; L-kurtosis, Tao4), []. We assessed regional homogeneity via the H statistic.
2.3. Univariate Distributions
We consider the G, GEV, and EG distributions as candidate marginals for AMDR. All parameters are estimated by MLE with standard regularity conditions; detailed formulas and log-likelihoods are compiled in Appendix B. The Rosenbrock optimization algorithm for constrained variables [] was selected for estimating the univariate parameters by the direct maximization of its corresponding log-likelihood function.
2.4. Biexponentiated Gumbel Distribution (BEG)
As already mentioned, multivariate extreme value distributions have been shown to be a reliable option for fitting hydrological variables. Yue and Wang [] compared the mixed and logistic bivariate models and concluded that the logistic model (LM) is the best option in flood frequency analysis.
As outlined by Collali et al. [], LM is denoted as follows:
where x and y denote the extreme events (e.g., annual maximum daily rainfall) gauged at a pair of neighboring sites, m is the association parameter, and
The marginals’ distributions F(x) and F(y) are specified as Exponentiated Gumbel (EG). As in the univariate case, we jointly estimate the parameters using the Rosenbrock optimization algorithm under the requisite parameter constraints []. Appendix C presents the log-likelihood formulation and the parameter-estimation procedure in detail.
2.5. Selection of Best Fit
The selection of fit between the Empirical and Theoretical distribution of the AMDR was based on the AICc and BIC goodness of fit tests.
The AIC was proposed by Akaike []:
while the BIC is []:
where represents the log-likelihood of empirical distribution, p the number of maximum-likelihood estimates of the parameters, and n the length of record.
For small n, a corrected version of AIC is proposed as []:
A distribution having least value of AICc is considered as best model; BIC is used to break ties when the difference in connected AIC (ΔAICc) is less than. Model preference is evaluated per station.
Here, AICc and BIC are computed from the same maximized log-likelihood for each candidate model.
2.6. Reliability of Estimated Quantiles
It is very important to evaluate whether the joint estimation of BEG distribution provides more accurate and reliable marginal quantiles than univariate fits. This evaluation is essential in hydrological frequency analysis, since underestimation of quantiles can increase the risk of hydraulic structure failure, while overestimation may result in unnecessarily high construction costs. To assess reliability, quantile estimates obtained from the BEG model were compared with those from univariate distributions using two statistical criteria: bias (BIAS) and mean squared error (MSE). This framework allowed us to determine not only the accuracy of the estimated quantiles but also the extent to which the joint estimation procedure enhances the transfer of information across sites, thereby improving the robustness of extreme rainfall frequency analysis.
To formalize this evaluation, the reliability of estimated quantiles was expressed in terms of bias and mean squared error, which are defined as follows:
Let be the marginal return level for the base station, where the marginal is EG, but its parameters are estimated jointly with a neighbor via the BEG likelihood.
For the number of simulated samples “”
and
When estimating quantiles is desirable to have unbiased and minimum MSE estimators.
Bivariate Bootstrap for Uncertainty Quantification (BEG)
We quantified uncertainty with a nonparametric bivariate bootstrap aligned to the BEG likelihood. Within the common period (CP), we resampled year indices as pairs (Xt, Yt) with replacement to preserve the empirical cross-site dependence; non-overlap segments (before/after the CP) were resampled independently within each station. For each bootstrap replicate (B =1000 per station–neighbor pair, unless noted), we re-estimated the BEG model (EG marginals and logistic model) by maximum likelihood and computed the base-station marginal return level 95% CIs were the percentile interval [q0.025, q0.975] across replicates.
3. Results
3.1. Quality Control Analysis
For each station, annual maximum daily rainfall values were analyzed. The data underwent a comprehensive quality control process, including outlier detection (Grubbs test, three-sigma rule), independence verification (Anderson–Mantilla–Amigó test), homogeneity assessment (Helmert, Student’s t, Cramer, Pettit, Standard Normal, Buishand, and Von Neumann tests), and trend analysis (Spearman and Mann–Kendall tests). Table 1 presents the results of this quality analysis for a selection of climatological stations in Coahuila.

Table 1.
Results of the quality control analysis for selected climatological stations in Coahuila, based on annual maximum daily rainfall data. Tests include outlier detection, independence verification, homogeneity assessment, and trend analysis.
3.2. Delineation of Homogeneous Regions
The rain gauge stations in Coahuila and Tabasco were classified into homogeneous regions by applying the L-moments delineation procedure previously described. This methodological approach yielded six regions in Coahuila and eight regions in Tabasco were ultimately retained (Appendix D), ensuring consistency with the adopted regionalization framework.
3.3. Univariate and Bivariate Frequency Analysis
The analysis of the Coahuila dataset considered all possible pairwise station combinations within each homogeneous region to evaluate the dependence structure of extreme rainfall. Appendix E illustrates a representative example for station 5001, showing the BEG model combinations applied and the corresponding return level estimates.
It is important to clarify that return levels are computed from the base-station marginal EG distribution, where its parameters are estimated jointly with the neighbor through the BEG likelihood. Thus, although BEG is bivariate, the reported return levels are univariate design values for the base station.
When extended to the complete set of stations, the procedure enabled a systematic assessment of return levels using the BEG framework. For comparison, alternative univariate models—G, GEV, and EG—were also fitted to the same station, and the resulting return levels were ranked according to goodness-of-fit statistics, including the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). Notably, in 74% of the stations in Coahuila the best fit was achieved with the BEG distribution (Table 2), highlighting its reliability for modeling extreme rainfall in this region.

Table 2.
Distribution of best-fit probability models for precipitation data in Coahuila.
A similar procedure is applied in Tabasco, where all possible station pairs within each homogeneous region were analyzed. In this case, 65% of the stations achieved the best fit with the BEG distribution (Table 3), confirming the robustness of this approach under the markedly different climatic conditions of southeastern Mexico. Among the 181 total cases analyzed across 14 regions, the BEG distribution demonstrated the highest suitability, fitting 70% of the cases. This was followed by the G (12%), EG (10%), and GEV (8%) distributions. The BEG model showed particularly strong performance in regions 4 and 6 in Coahuila, accounting for 24 and 28 best fits, respectively.

Table 3.
Distribution of best-fit probability models for precipitation data in Tabasco.
3.4. Reliability of Estimated Quantiles
A data generation procedure was performed to see whether the quantiles obtained through the bivariate joint estimation of parameters are more reliable than those obtained by its univariate counterpart.
For the EG distribution, data were generated using population parameters , and with sample sizes n = 10, 20 and 50. A total of 1000 simulated samples were considered for each n.
For the BEG distribution, quantiles were obtained by combining samples with sizes n1-n2: 10–10, 10–20, 20–20, 20–50, 50–50 and 50–100. Comparisons were performed for non-exceedance probabilities of 0.50, 0.80, 0.90. 095 0.98 and 0.99. The associated site has population parameters , and .
Results (Table 4 and Table 5) indicate that as increased relative to , both BIAS and MSE of the shorter series decreased. This demonstrates an effective transfer of information when parameters are jointly estimated, supporting the conclusion that quantiles computed using the BEG distribution are more reliable than those obtained from the univariate case. For this analysis represents the base station length, is the neighbor length/common period; larger emulates borrowing information.

Table 4.
Quantile biases obtained for the EG marginal with length .

Table 5.
Quantile MSE’s obtained for the EG marginal with length .
3.5. Bivariate Bootstrap for Uncertainty Quantification (BEG)
We quantify uncertainty via bootstrap 95% Confidence Intervals for marginal return levels under BEG (joint estimation) and EG (univariate). For BEG we use paired resampling over the common period (CP) to preserve dependence and independent resampling within non-overlap segments. Each bootstrap replicate re-estimates parameters and recomputes the return levels. We denote 95% percentile confidence intervals (CIs) as [CIL, CIU], where CIL and CIU represent the lower and upper bounds of the interval, respectively.
For the illustrative bivariate combination (station 5001-station 5146), we used a nested bootstrap (1000 base resamples × 1000 neighbor resamples). Results are presented in Table 6. Bootstrap CIs are narrower under BEG than EG, underscoring reduced quantile uncertainty via information sharing.

Table 6.
Confidence Intervals (95%) for BEG and EG Distributions at Station 5001.
These results demonstrate that the BEG distribution consistently outperforms classical models, providing the best fit in both the arid to semi-arid conditions of Coahuila and the humid tropical environment of Tabasco. This consistency across regions and evaluation metrics underscores the versatility of the BEG framework for regional frequency analysis in contrasting hydroclimatic settings.
4. Discussion
The results obtained in Coahuila and Tabasco demonstrate the advantages of adopting flexible probability models such as the Bivariate Exponentiated Gumbel (BEG) distribution for extreme rainfall analysis. In both regions, the BEG framework provided the best fit for a majority of stations—74% in Coahuila and 65% in Tabasco—when compared to the classical Gumbel, Generalized Extreme Value (GEV), and Exponentiated Gumbel distributions. This superior performance, confirmed by goodness-of-fit criteria including AIC and BIC, highlights the ability of the BEG model to capture the dependence structure of extreme events more effectively than univariate alternatives.
The simulation experiments reinforce this conclusion. By jointly estimating parameters across paired samples, the BEG approach significantly reduced bias and mean squared error in quantile estimation, particularly as one sample length increased relative to the other. This result demonstrates the effective transfer of information between series, a feature that is especially relevant in hydrological contexts where records are often short, fragmented, or incomplete. In contrast, univariate models produced higher estimation errors under identical conditions, confirming the greater robustness of BEG.
An important aspect of these findings is the consistency of the BEG performance across contrasting climatic contexts. In Coahuila, a predominantly arid to semi-arid region, rainfall extremes are generally short-lived and spatially heterogeneous, which complicates regionalization and frequency analysis. Conversely, Tabasco is located in a humid tropical environment where rainfall extremes are often more spatially extensive and influenced by large-scale atmospheric dynamics. Despite these marked hydroclimatic differences, the BEG distribution consistently outperformed traditional models, underscoring its robustness and adaptability.
The systematic evaluation of all possible station pairs within homogeneous regions further strengthens the validity of the results. This approach ensures that spatial dependence is explicitly considered, rather than assuming independence between stations—a limitation common in univariate frequency analysis. The strong performance of the BEG distribution suggests that bivariate or multivariate models may be more appropriate for regions with high spatial variability, particularly where water resource planning and hydraulic design require accurate estimation of joint extremes.
From a practical perspective, the improved fit obtained with the BEG distribution has direct implications for risk management and infrastructure design. Underestimation of return levels, especially for long return periods, can lead to inadequate sizing of hydraulic structures and increased vulnerability to extreme events. By providing more reliable estimates, the BEG framework contributes to reducing uncertainty in hydrological design, supporting more resilient adaptation strategies in the face of climate variability and change.
Finally, these results align with recent studies emphasizing the importance of moving beyond stationary univariate models in hydrology. The incorporation of flexible, bivariate approaches not only improves statistical performance but also offers a more realistic representation of rainfall extremes, particularly in regions with complex climatic dynamics. The outcomes from Coahuila and Tabasco therefore provide empirical evidence supporting the broader adoption of BEG-based regional frequency analysis in Mexico and comparable hydroclimatic contexts.
Limitations of the Proposed Model
Despite its advantages, the BEG (Bivariate Exponentiated Gumbel) distribution has several limitations that should be acknowledged. First, it assumes that both marginals follow the Exponentiated Gumbel form and that dependence between stations is adequately captured by the logistic parameter m; if either assumption is violated (e.g., heavy-tail behavior not well described by EG, or nonlinear/spatially anisotropic dependence not well represented by the logistic model), performance may degrade. Second, the method relies on the definition of homogeneous regions and on pairing gauges that are assumed to be hydrologically comparable; when regions are poorly defined or strongly affected by localized processes (orography, land use, tropical cyclones, convective cells), the “information transfer” from a long-record neighbor to a short-record base station may introduce bias rather than reduce it. Third, the framework is essentially stationary: it assumes that extremes come from a single, time-invariant process after quality control and trend screening. Long-term non-stationarity driven by climate variability or land-use change is not modeled explicitly, so extrapolated return levels at long return periods may still be optimistic or conservative. Fourth, BEG is pairwise by construction—parameters for a target station depend on the specific neighbor used in the joint fit—which means estimates can change if a different neighbor is selected, and the approach does not yet exploit more than two sites at once. Finally, while bootstrap confidence intervals help quantify uncertainty, we have not formally tested whether reductions in bias and mean squared error are statistically significant across all stations, so gains in reliability should be interpreted as practical rather than universally guaranteed.
5. Conclusions
This study applied the Bivariate Exponentiated Gumbel (BEG) distribution to extreme rainfall analysis in Coahuila and Tabasco, two Mexican states with contrasting climatic conditions. The main conclusions are as follows:
Across the stations analyzed, the BEG distribution provided the best fit in 74% of the cases in Coahuila and 65% in Tabasco, outperforming classical alternatives such as the Gumbel, Generalized Extreme Value (GEV), and Exponentiated Gumbel distributions. This performance was consistently confirmed by statistical indicators, including AIC and BIC.
Simulation experiments showed that BEG reduced bias and mean squared error when estimating quantiles, especially for short or heterogeneous samples. The joint estimation of parameters allowed effective transfer of information, resulting in more reliable quantiles than those obtained from univariate approaches.
The BEG model demonstrated strong adaptability in both arid to semi-arid conditions (Coahuila) and humid tropical conditions (Tabasco), underscoring its versatility as a tool for regional frequency analysis of extreme rainfall.
The systematic evaluation of all possible pairwise station combinations within homogeneous regions captured spatial dependence more effectively than univariate models. This methodological strength enhances the reliability of rainfall return level estimates, particularly for long return periods.
The improved accuracy of return level estimates obtained with the BEG distribution can reduce underestimation of design events, thereby contributing to safer and more resilient hydraulic infrastructure, as well as supporting climate adaptation planning in water management.
In summary, the BEG distribution proves to be a reliable and flexible alternative for regional extreme rainfall analysis in Mexico. Its demonstrated robustness suggests that it can be extended to other regions with similar hydroclimatic variability, providing a valuable tool for both scientific research and applied hydrological practice. Future research should explore the application of the BEG model under non-stationary conditions, test its performance in multivariate settings that include variables such as streamflow or temperature, and assess its potential for integration into climate change impact studies.
Funding
This research received no external funding.
Data Availability Statement
Rainfall data will be available at: https://smn.conagua.gob.mx/es/climatologia/informacion-climatologica/normales-climatologicas-por-estado (Accessed on 1 March 2025).
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEV | Bivariate Extreme Value Distribution |
| FFA | Flood Frequency Analysis |
| GEV | Generalized Extreme Value |
| Region | Homogeneous Region |
| T | Return Period |
Appendix A. Location of Climatological Stations
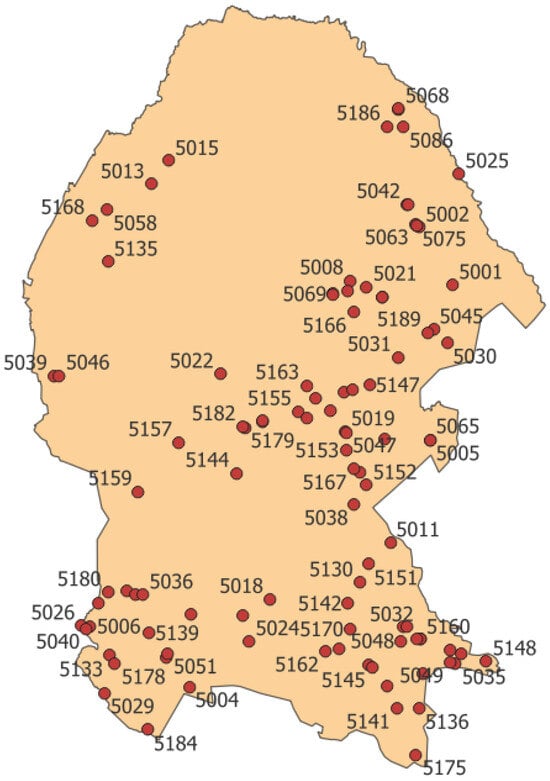
Figure A1.
Map Showing the Spatial Distribution of Rainfall Climatological Stations in the State of Coahuila, Mexico.
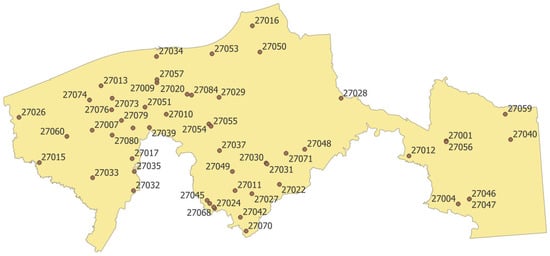
Figure A2.
Map Showing the Spatial Distribution of Rainfall Climatological Stations in the State of Tabasco, Mexico.
Appendix B. Univariate Distributions
Appendix B.1. Generalized Extreme Value (GEV)
The cumulative distribution function is:
where are the location, scale, and shape parameters, respectively.
And
The log-likelihood for the GEV distribution is:
The quantile corresponding to a given return period T is:
Appendix B.2. Gumbel (G)
Appendix B.3. Exponentiated Gumbel (EG)
Appendix C. Bivariate Joint Estimation of Parameters
The bivariate likelihood function is:
The bivariate log-likelihood function is:
This expression is used when both samples share a common length of record, however; the general form for considering different sizes is:
If marginals F(x) and F(y) are proposed to be EG distributions, the BEG log-likelihood function to maximize in the parameter estimation procedure is:
where x and y are the variables in the common period (CP) with length , r denotes to the variable x or y with length before the CP, s is the variable x or y with length after the CP; if if for j = 1, 2, 3; p = 1 and q = 1 if r or s represent to variable x; p = 2 and q = 2 if r or s characterize to variable y, m is the association parameter, and
It is very important to note that initial guesses for μ, σ, κ are taken from univariate EG fits at each station, while m is initialized near 2 to ensure valid dependence.
Appendix D. Delineation of Homogeneous Regions

Table A1.
Stations by Homogeneous Region in Coahuila.
Table A1.
Stations by Homogeneous Region in Coahuila.
| Region 1 | Region 2 | Region 3 | Region 4 | Region 5 | Region 6 |
|---|---|---|---|---|---|
| 5006 | 5003 | 5046 | 5002 | 5005 | 5001 |
| 5011 | 5135 | 5047 | 5008 | 5013 | 5004 |
| 5015 | 5139 | 5158 | 5009 | 5022 | 5007 |
| 5019 | 5160 | 5016 | 5029 | 5020 | |
| 5026 | 5170 | 5018 | 5038 | 5023 | |
| 5027 | 5021 | 5060 | 5024 | ||
| 5032 | 5028 | 5074 | 5025 | ||
| 5035 | 5030 | 5086 | 5031 | ||
| 5039 | 5033 | 5133 | 5034 | ||
| 5042 | 5058 | 5145 | 5036 | ||
| 5045 | 5063 | 5149 | 5037 | ||
| 5048 | 5066 | 5171 | 5040 | ||
| 5049 | 5069 | 5181 | 5041 | ||
| 5065 | 5144 | 5043 | |||
| 5081 | 5150 | 5044 | |||
| 5136 | 5152 | 5050 | |||
| 5140 | 5153 | 5051 | |||
| 5141 | 5156 | 5052 | |||
| 5146 | 5159 | 5068 | |||
| 5147 | 5163 | 5075 | |||
| 5148 | 5166 | 5085 | |||
| 5168 | 5167 | 5130 | |||
| 5178 | 5169 | 5142 | |||
| 5189 | 5180 | 5151 | |||
| 5182 | 5155 | ||||
| 5184 | 5157 | ||||
| 5185 | 5162 | ||||
| 5186 | 5164 | ||||
| 5174 | |||||
| 5175 | |||||
| 5176 | |||||
| 5179 | |||||
| 5188 |

Table A2.
Stations by Homogeneous Region in Tabasco.
Table A2.
Stations by Homogeneous Region in Tabasco.
| Region 1 | Region 2 | Region 3 | Region 4 | Region 5 | Region 6 | Region 7 | Region 8 |
|---|---|---|---|---|---|---|---|
| 27001 | 27014 | 27007 | 27002 | 27013 | 27016 | 27012 | 27003 |
| 27069 | 27079 | 27010 | 27011 | 27088 | 27022 | 27054 | 27004 |
| 27076 | 27083 | 27015 | 27020 | 27092 | 27055 | 27056 | 27006 |
| 27087 | 27019 | 27031 | 27065 | 27008 | |||
| 27090 | 27024 | 27038 | 27073 | 27009 | |||
| 27091 | 27030 | 27057 | 27075 | 27017 | |||
| 27093 | 27032 | 27084 | 27077 | 27018 | |||
| 27033 | 27078 | 27021 | |||||
| 27041 | 27026 | ||||||
| 27042 | 27027 | ||||||
| 27044 | 27028 | ||||||
| 27045 | 27029 | ||||||
| 27046 | 27034 | ||||||
| 27047 | 27035 | ||||||
| 27060 | 27036 | ||||||
| 27061 | 27037 | ||||||
| 27068 | 27039 | ||||||
| 27070 | 27040 | ||||||
| 27080 | 27048 | ||||||
| 27049 | |||||||
| 27050 | |||||||
| 27051 | |||||||
| 27053 | |||||||
| 27059 | |||||||
| 27071 |
Appendix E. Univariate and Bivariate Frequency Analysis

Table A3.
Schematic Example of the Information Transfer Process Between Stations.
Table A3.
Schematic Example of the Information Transfer Process Between Stations.
| Stations | ||||
|---|---|---|---|---|
| Year | 5001 | 5164 | Sample Sizes | |
| 1950 | 22.6 | |||
| 1951 | 31.6 | |||
| 1952 | 33.9 | |||
| * | ||||
| * | n1 | |||
| * | ||||
| 1979 | 41.6 | |||
| 1980 | 67.8 | |||
| 1981 | 127.0 | 74.6 | ||
| 1982 | 78.3 | 39.6 | ||
| * | ||||
| * | n2 | |||
| * | ||||
| 2011 | 63.8 | 33.9 | ||
| 2012 | 31.0 | 54.2 | ||
| 2013 | 123.3 | 45.2 | ||
* Indicates rows continuity to avoid a large Table.

Table A4.
Examples of BEG Model Combinations Applied to Station 5001 in Coahuila.
Table A4.
Examples of BEG Model Combinations Applied to Station 5001 in Coahuila.
| Station | Neighboring | Relative Sample Sizes | Bivariate Parameters | Marginal (1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | Station | n1 | n2 | n3 | μ1 | σ1 | κ1 | μ2 | σ2 | κ2 | m | AICc | BIC |
| 5001 | 5164 | 31 | 33 | 0 | 42.717 | 22.322 | 0.665 | 50.487 | 17.693 | 1.169 | 1.035 | 594.52 | 600.60 |
| 5050 | 31 | 33 | 0 | 49.948 | 27.076 | 0.904 | 41.497 | 13.665 | 0.963 | 1.206 | 594.96 | 601.04 | |
| 5034 | 0 | 64 | 3 | 48.946 | 25.585 | 0.859 | 33.873 | 12.085 | 0.754 | 1.050 | 595.18 | 601.25 | |
| 5007 | 0 | 64 | 3 | 46.609 | 24.365 | 0.743 | 34.268 | 14.238 | 1.038 | 1.206 | 600.12 | 606.19 | |
| 5036 | 0 | 64 | 3 | 45.193 | 24.354 | 0.764 | 29.507 | 12.872 | 0.784 | 1.077 | 601.52 | 607.60 | |
| 5176 | 4 | 60 | 0 | 45.173 | 23.763 | 0.799 | 29.111 | 8.768 | 0.570 | 1.023 | 602.02 | 608.10 | |
| 5174 | 31 | 31 | 2 | 49.492 | 27.230 | 0.895 | 32.670 | 15.985 | 1.006 | 1.168 | 603.76 | 609.83 | |
| 5044 | 0 | 64 | 0 | 45.153 | 26.603 | 0.791 | 26.492 | 9.730 | 0.460 | 1.090 | 605.38 | 611.46 | |
| 5051 | 0 | 64 | 3 | 43.322 | 23.935 | 0.710 | 28.491 | 11.147 | 0.661 | 1.077 | 607.07 | 613.14 | |
| 5155 | 31 | 33 | 0 | 49.925 | 27.651 | 0.921 | 45.603 | 22.941 | 1.048 | 1.110 | 608.77 | 614.85 | |
| 5175 | 23 | 41 | 0 | 43.681 | 22.319 | 0.659 | 36.422 | 16.394 | 1.171 | 1.068 | 609.05 | 615.12 | |
| 5130 | 19 | 45 | 0 | 54.461 | 31.889 | 1.204 | 22.650 | 5.653 | 0.330 | 1.135 | 613.61 | 619.69 | |
| 5040 | 20 | 41 | 3 | 48.929 | 28.383 | 0.945 | 40.417 | 22.083 | 1.170 | 1.054 | 614.29 | 620.37 | |
| 5041 | 22 | 42 | 3 | 41.680 | 21.738 | 0.638 | 29.325 | 13.178 | 1.085 | 1.082 | 615.29 | 621.37 | |
| 5031 | 0 | 64 | 0 | 48.549 | 24.788 | 0.783 | 56.045 | 19.533 | 0.786 | 1.058 | 620.77 | 626.85 | |
| 5142 | 19 | 45 | 0 | 43.428 | 22.898 | 0.699 | 30.003 | 19.932 | 1.178 | 1.039 | 632.64 | 638.71 | |
| 5025 | 29 | 32 | 3 | 43.242 | 25.017 | 0.741 | 78.291 | 28.688 | 1.002 | 1.070 | 640.02 | 646.10 | |
| 5020 | 29 | 35 | 0 | 50.048 | 27.978 | 0.937 | 54.687 | 33.128 | 0.827 | 1.049 | 644.13 | 650.21 | |
| 5085 | 37 | 27 | 0 | 47.056 | 25.731 | 0.818 | 69.494 | 39.405 | 0.881 | 1.266 | 649.00 | 655.07 | |
| 5068 | 37 | 27 | 0 | 40.618 | 22.931 | 0.656 | 85.085 | 43.273 | 1.029 | 1.015 | 653.26 | 659.34 | |

Table A5.
Example of Return Levels (mm) Estimated with the BEG Distribution for Station 5001 in Coahuila.
Table A5.
Example of Return Levels (mm) Estimated with the BEG Distribution for Station 5001 in Coahuila.
| Station | Neighboring | Return Period T (Years) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | Station | 1.1 | 2 | 5 | 10 | 20 | 50 | 100 | 500 | 1000 | 5000 | 10,000 |
| 5001 | 5164 | 27.1 | 61.3 | 95.7 | 119.6 | 143.1 | 174.0 | 197.3 | 251.3 | 274.5 | 328.5 | 351.8 |
| 5050 | 27.4 | 62.7 | 95.7 | 117.8 | 139.2 | 166.9 | 187.8 | 236.1 | 256.8 | 305.0 | 325.8 | |
| 5034 | 28.2 | 62.4 | 94.8 | 116.6 | 137.8 | 165.3 | 186.0 | 234.0 | 254.6 | 302.6 | 323.2 | |
| 5007 | 28.3 | 63.5 | 97.9 | 121.6 | 144.7 | 174.9 | 197.6 | 250.5 | 273.2 | 326.0 | 348.7 | |
| 5036 | 26.6 | 61.3 | 94.9 | 118.0 | 140.4 | 169.8 | 191.9 | 243.3 | 265.4 | 316.7 | 338.7 | |
| 5176 | 26.6 | 59.6 | 91.3 | 112.9 | 133.9 | 161.4 | 182.0 | 229.9 | 250.5 | 298.4 | 319.0 | |
| 5174 | 26.9 | 62.6 | 96.0 | 118.4 | 140.1 | 168.3 | 189.5 | 238.5 | 259.6 | 308.5 | 329.6 | |
| 5044 | 24.5 | 61.6 | 97.4 | 121.8 | 145.6 | 176.6 | 200.0 | 254.1 | 277.4 | 331.5 | 354.8 | |
| 5051 | 25.9 | 61.3 | 96.3 | 120.5 | 144.1 | 175.1 | 198.5 | 252.8 | 276.2 | 330.4 | 353.8 | |
| 5155 | 26.7 | 62.4 | 95.7 | 117.9 | 139.4 | 167.2 | 188.2 | 236.6 | 257.4 | 305.8 | 326.6 | |
| 5175 | 28.2 | 62.5 | 97.2 | 121.4 | 145.1 | 176.2 | 199.7 | 254.3 | 277.7 | 332.3 | 355.8 | |
| 5130 | 24.3 | 60.5 | 92.3 | 112.9 | 132.4 | 157.4 | 176.1 | 218.9 | 237.3 | 280.0 | 298.4 | |
| 5040 | 24.8 | 61.0 | 94.5 | 116.8 | 138.3 | 166.2 | 187.2 | 235.6 | 256.5 | 304.8 | 325.7 | |
| 5041 | 26.9 | 61.0 | 95.6 | 119.9 | 143.7 | 175.0 | 198.7 | 253.6 | 277.2 | 332.1 | 355.7 | |
| 5031 | 29.4 | 64.2 | 97.8 | 120.8 | 143.1 | 172.4 | 194.4 | 245.4 | 267.3 | 318.3 | 340.2 | |
| 5142 | 26.9 | 61.0 | 95.0 | 118.4 | 141.4 | 171.5 | 194.3 | 247.0 | 269.7 | 322.4 | 345.1 | |
| 5025 | 24.5 | 60.7 | 96.1 | 120.5 | 144.2 | 175.3 | 198.8 | 253.2 | 276.6 | 331.0 | 354.4 | |
| 5020 | 26.3 | 62.2 | 95.4 | 117.6 | 139.0 | 166.7 | 187.5 | 235.7 | 256.4 | 304.5 | 325.2 | |
| 5085 | 26.7 | 62.0 | 95.7 | 118.7 | 140.9 | 169.9 | 191.8 | 242.4 | 264.2 | 314.9 | 336.6 | |
| 5068 | 24.7 | 60.1 | 95.8 | 120.7 | 145.2 | 177.3 | 201.6 | 257.8 | 282.0 | 338.3 | 362.5 | |

Table A6.
Return Levels (mm) from Alternative Univariate Distributions (G, GEV, and EG), Ordered by Best Fit for Station 5001.
Table A6.
Return Levels (mm) from Alternative Univariate Distributions (G, GEV, and EG), Ordered by Best Fit for Station 5001.
| Station | Return Period T (Years) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | Distribution | 1.1 | 2 | 5 | 10 | 20 | 50 | 100 | 500 | 1000 | 5000 | 10,000 | AICc | BIC |
| 5001 | BEG | 27.1 | 61.3 | 95.7 | 119.6 | 143.1 | 174.0 | 197.3 | 251.3 | 274.5 | 328.5 | 351.8 | 594.524 | 600.600 |
| G | 26.4 | 62.2 | 94.8 | 116.4 | 137.1 | 163.9 | 184.0 | 230.5 | 250.4 | 296.8 | 316.7 | 638.332 | 642.453 | |
| EG | 26.7 | 60.7 | 95.5 | 119.8 | 143.8 | 175.2 | 199.0 | 254.1 | 277.9 | 333.0 | 356.8 | 639.931 | 646.008 | |
| GEV | 26.7 | 61.0 | 94.8 | 118.6 | 142.5 | 175.1 | 200.9 | 265.1 | 294.8 | 369.1 | 403.5 | 640.099 | 646.176 | |
References
- Held, I.; Soden, B. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- CENAPRED. Impacto Socioeconómico de los principales desastres ocurridos en la República Mexicana. Centro Nacional de Prevención de Desastres. Versiones del 2007 al 2020. Secretaria de Seguridad y Protección Ciudadana. Gobierno de México. Available online: http://www.cenapred.unam.mx/PublicacionesWebGobMX/buscar_buscaSubcategoria.action (accessed on 1 April 2025).
- Jáuregui, E. El Clima de la Ciudad de México; Instituto de Geografía, UNAM and Plaza-Valdés Editores: CDMX, Mexico, 2000; ISBN 978-9-6836-8090-7. [Google Scholar]
- Peralta-Hernández, A.; Balling, R.; Barba-Martínez, L. Comparative analysis of indices of extreme rainfall events: Variations and trends from southern México. Atmosfera 2009, 22, 219–228. [Google Scholar]
- Gado, T.; Salama, A.; Zeidan, B. Selection of the best probability models for daily annual maximum rainfalls in Egypt. Theor. Appl. Climatol. 2021, 144, 1267–1284. [Google Scholar] [CrossRef]
- Melice, J.; Reason, C. Return period of extreme rainfall at George, South Africa. S. Afr. J. Sci. 2007, 103, 499–501. [Google Scholar]
- Nadarajah, S.; Choi, D. Maximum daily rainfall in South Korea. J. Earth Syst. Sci. 2007, 116, 311–320. [Google Scholar] [CrossRef]
- Momin, U.; Kulkarni, P.; Horaginamani, M.; Ravichandran, M.; Patel, A.; Kousai, H. Consecutive days maximum rainfall analysis by Gumbel’s extreme value distribution for southern Telangana. Ind. J. Nat. Sci. 2011, 7, 408–412. [Google Scholar]
- Chifurira, R.; Chikobvu, D. Modelling extreme maximum annual rainfall for Zimbabwe. In Proceedings of the 56th Annual Conference of the South African Statistical Association, Grahamstown, South Africa, 27–30 October 2014; pp. 9–16. [Google Scholar]
- Manzano-Agugliaro, F.; Zapata-Sierra, A.; Rubi-Maldonado, J. Assessment of obtaining IDF curve methods for Mexico. Technol. Sci. Water. 2014, 5, 149–158. [Google Scholar]
- Vitor, R.; Rogeiro, C.; Marciano, A.; Silva, C.; Souza, A. Performance of the probability distribution models applied to heavy rainfall daily events. Sci. Agrotechnol. 2014, 38, 335–342. [Google Scholar] [CrossRef]
- Asim, M.; Nath, S. Study on rainfall probability analysis at Allahabad District of Uttar Pradesh. J. Biol. Agric. Healthc. 2015, 5, 214–222. [Google Scholar]
- Dreux, R.; Vieira, J.; Wolff, W.; Folegatti, M. Daily maximum annual rainfall statistical regionalization in Andalusia. In Proceedings of the X Congreso Internacional AEC: Clima, Sociedad, Riesgos y Ordenación del Territorio, Alicante, Spain, 5–8 October 2016; Volume 1, pp. 87–96. [Google Scholar] [CrossRef]
- Baghel, H.; Mittal, H.; Singh, P.; Yadav, K.; Jain, S. Frequency analysis of rainfall data using probability distribution models. Int. J. Curr. Microbiol. Appl. Sci. 2019, 8, 1390–1396. [Google Scholar] [CrossRef]
- Amoakowaah, M.; Kofitze, L.; Omari, A.; Ilimoan, E.; Quansah, E.; Aryee, J.; Preko, K. Estimation of the return periods of maximum rainfall and floods at the Pra river catchment, Ghana, west Africa using the Gumbel extreme value theory. Heliyon 2021, 7, e06980. [Google Scholar] [CrossRef]
- Moccia, B.; Mineo, C.; Ridolfi, E.; Russo, F.; Napolitano, F. Probability distributions of daily rainfall extremes in Lazio and Sicily, Italy, and design rainfall inferences. J. Hydrol. Reg. Stud. 2021, 33, 100771. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation. Hydrol. Sci. J. 2004, 49, 575–590. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: II. Empirical investigation of long rainfall records. Hydrol. Sci. J. 2004, 49, 591–610. [Google Scholar] [CrossRef]
- Onibon, H.; Ouarda, T.; Barbet, M.; St-Hilaire, A.; Bobee, B.; Bruneau, P. Analyse fréquentielle régionale des précipitations journalières maximales annuelles au Québec, Canada. Hydrol. Sci. J. 2004, 49, 717–735. [Google Scholar] [CrossRef]
- Villarini, G. Analyses of annual and seasonal maximum daily rainfall accumulations for Ukraine, Moldova, and Romania. Int. J. Climatol. 2012, 32, 2213–2226. [Google Scholar] [CrossRef]
- Barbosa, E.; Lucio, P.; Santos, C. Seasonal analysis of return periods for maximum daily precipitation in the Brazilian Amazon. J. Hydrometeorol. 2015, 16, 973–984. [Google Scholar] [CrossRef]
- Nguyen, T.; El Outayek, S.; Hee, S.; Van Nguyen, V. A Systematic approach to selecting the best probability models for annual maximum rainfall—A case study using data in Ontario (Canada). J. Hydrol. 2017, 553, 49–58. [Google Scholar] [CrossRef]
- Boudrissa, N.; Cheraitia, H.; Halimi, L. Maximum daily yearly rainfall in northern Algeria using generalized extreme value distributions from 1936 to 2009. Meteorol. Appl. 2017, 24, 114–119. [Google Scholar] [CrossRef]
- Alam, A.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit probability distributions and return periods for maximum monthly rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Moujahid, M.; Stour, L.; Agoumi, A.; Saidi, A. Regional approach for the analysis of annual maximum daily precipitation in northern Morocco. Weather Clim. Extrem. 2018, 21, 43–51. [Google Scholar] [CrossRef]
- Mlynski, D.; Walega, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating maximum daily precipitation in the upper Vistula basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef]
- Garcia-Marin, A.; Morbidelli, R.; Saltalippi, C.; Cifrodelli, M.; Estevez, J.; Flammini, A. On the choice of the optimal frequency analysis of annual extreme rainfall by multifractal approach. J. Hydrol. 2019, 575, 1267–1279. [Google Scholar] [CrossRef]
- Batista, M.; Coelho, G.; De Mello, C.; De Olivera, M. Spatialization of the annual maximum daily rainfall in southeastern Brazil. Eng. Agric. 2019, 39, 97–109. [Google Scholar] [CrossRef]
- Mayooran, T.; Laheetharan, A. The statistical distribution of annual maximum rainfall in Colombo District. Sri Lankan J. Appl. Stat. 2014, 15, 107–130. [Google Scholar] [CrossRef]
- Montes-Pajuelo, R.; Rodriguez-Perez, A.M.; Lopez, R.; Rodriguez, C.A. Analysis of Probability Distributions for Modelling Extreme Rainfall Events and Detecting Climate Change: Insights from Mathematical and Statistical Methods. Mathematics 2024, 12, 1093. [Google Scholar] [CrossRef]
- Kumar, R.; Bhardwaj, A. Probability analysis of return period pf daily maximum rainfall in annual data set of Ludhiana, Punjab. Indian J. Agric. Res. 2015, 49, 160–164. [Google Scholar] [CrossRef]
- Amin, M.; Rizwan, M.; Alazba, A. A best-fit probability distribution for the estimation of rainfall in northern regions of Pakistan. Open Life Sci. 2016, 11, 432–440. [Google Scholar] [CrossRef]
- Yuan, J.; Emura, K.; Farnham, C.; Alam, A. Frequency analysis of annual maximum hourly precipitation and determination of best fit probability distribution for regions in Japan. Urban Clim. 2018, 24, 276–286. [Google Scholar] [CrossRef]
- Nassif, W.; Al-Taai, O.; Mohammed, A.; Al-Shamarti, H. Estimate probability distribution of monthly maximum daily rainfall of Iraq. J. Phys. Conf. Ser. 2021, 1804, 012078. [Google Scholar] [CrossRef]
- Nadarajah, S. The exponentiated Gumbel distribution with climate application. Environmetrics 2006, 17, 13–23. [Google Scholar] [CrossRef]
- Escalante-Sandoval, C. Estimación de lluvias de diseño con distribuciones exponenciadas y exponenciadas mezcladas en la Costa de Chiapas. Ing. Hidra. Mex. 2007, 22, 103–113. [Google Scholar]
- Soleiman, K.; Abdollahi, A. The comparison between Gumbel and exponentiated Gumbel Distribution and their application in hydrological process. Adv. Mach. Learn. Artif. Intell. 2021, 2, 49–54. [Google Scholar] [CrossRef]
- Gumbel, E.J. Multivariate distributions with given margins. Rev. Fac. Cienc. Ser. A 1959, 2, 178–218. [Google Scholar]
- Gumbel, E.J. Distributions des valeurs extremes en plusiers dimensions. Publ. l’Institute Stat. l’Université Paris 1960, 9, 171–173. [Google Scholar]
- Gumbel, E.J. Multivariate extremal distributions. Bul. Int. Stat. Inst. 1960, 39, 471–475. [Google Scholar]
- Raynal, J.; Salas, D. Multivariate extreme value distributions in hydrological analyses. In Water for the Future: Hydrology in Perspective; IAHS Publication: Wallingford, UK, 1987; Volume 164, pp. 111–119. [Google Scholar]
- Escalante-Sandoval, C.; Dominguez, J. Parameter estimation for bivariate extreme value distribution by maximum entropy. Hydrol. Sci. Technol. AIH 1997, 13, 1–10. [Google Scholar]
- Yue, S. The bivariate lognormal distribution to model a multivariate flood episode. Hydrol. Process. 2000, 14, 2575–2588. [Google Scholar] [CrossRef]
- Yue, S. A bivariate gamma distribution for use in multivariate flood frequency analysis. Hydrol. Process. 2001, 15, 1033–1045. [Google Scholar] [CrossRef]
- Yue, S.; Rasmussen, P. Bivariate frequency analysis: Discussion of some useful concepts in hydrological application. Hydrol. Process. 2002, 16, 2881–2898. [Google Scholar] [CrossRef]
- Escalante-Sandoval, C. Application of bivariate extreme value distribution to flood frequency analysis: A case study of Northwestern Mexico. Nat. Hazard. 2008, 42, 37–46. [Google Scholar] [CrossRef]
- Salvadori, G.; Michele, C.D.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2007; Volume 56, ISBN 978-1-4020-4414-4. [Google Scholar]
- Zhang, L.; Singh, V.P. Copulas and Their Applications in Water Resources Engineering, 1st ed.; Cambridge University Press: Cambridge, UK, 2019; ISBN 978-1-108-56510-3. [Google Scholar]
- Coles, S.G.; Tawn, J.A. Modelling Extreme Multivariate Events. J. R. Stat. Soc. Ser. B Stat. Methodol. 1991, 53, 377–392. [Google Scholar] [CrossRef]
- Siamaki, M.; Safavi, H.; Haytham, M. Extraction of intensity-duration for short-term extreme rainfalls from daily and yearly extreme rainfalls using copula functions. Theo. App. Clim. 2024, 155, 5759–5777. [Google Scholar] [CrossRef]
- Collalti, D.; Spencer, N.; Strobl, E. Flash flood detection via copula-based intensity–duration–frequency curves: Evidence from Jamaica. Nat. Hazards Earth Syst. Sci. 2024, 4, 873–890. [Google Scholar] [CrossRef]
- Liu, S.; Dong, X. The return period analysis of heavy rainfall disasters based on copula joint statistical modeling. Geomat. Nat. Hazards Risk 2025, 16, 2483799. [Google Scholar] [CrossRef]
- Zhaocai, W.; Chao, M.; Junhao, W.; Tunhua, W. Extreme precipitation risk assessment with improved WOA-Optimized copula model under composite conditions. Theo. Appl. Clim. 2025, 156, 446. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. A comparison of two bivariate extreme value distributions. Stoch. Environ. Res. 2004, 18, 61–66. [Google Scholar] [CrossRef]
- Gumbel, E.J. Bivariate Logistic Distributions. J. Am. Stat. Assoc. 1961, 56, 335–349. [Google Scholar] [CrossRef]
- Comisión Nacional del Agua (CONAGUA). Base de datos climatológica nacional. Available online: https://smn.conagua.gob.mx/es/climatologia/informacion-climatologica/normales-climatologicas-por-estado (accessed on 1 March 2025).
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments, 1st ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-43045-6. [Google Scholar]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical identification model. IEEE Trans. Autom. Control. 1974, 6, 716–723. [Google Scholar] [CrossRef]
- Bunham, K.; Anderson, D. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).