Deciphering Relative Sea-Level Change in Chesapeake Bay: Impact of Global Mean, Regional Variation, and Local Land Subsidence, Part 1: Methodology

Abstract

The Chesapeake Bay (CB) region faces significant risks from relative sea-level change (RSLC), driven by global mean sea-level rise (GMSLR), regional sea-level rise (RSLR), and local land subsidence (LS). This study introduces a methodology to decipher RSLC trends in the CB area by integrating these components. We develop trend equations spanning 1900–2100, incorporating acceleration for GMSLR and RSLR since 1992, with linear LS estimation using tide gauge, satellite altimetry, and InSAR data. Our approach employs dynamic RSLC equations, Maclaurin series expansions, and inverse simulations to project RSLC trends through 2100. Stable RSLC rates require over 122 years of data for reliable linear trend estimation, with the Baltimore tide gauge providing the necessary long-term dataset. Similarity in monthly mean sea-level variations within a coastal region enables a new method to identify LS from short-term tide gauge data by correlating it with corresponding long-term data at Baltimore. LS is categorized into bedrock-surface subsidence (BSS) and compaction subsidence (CS), with methods proposed to map BSS contours and estimate CS. CS is further classified into primary consolidation, secondary consolidation, construction-induced, and negative subsidence to determine specific compaction types. The projection model highlights the dominant influence of GMSLR acceleration since 1992, with local LS and RSLR influenced by ocean circulation, density changes, and gravitational, rotational, and deformational (GRD) effects. This integrated approach enhances understanding and predictive reliability for RSLC trends, supporting resilience planning and infrastructure adaptation in coastal CB communities.

1. Introduction

Chesapeake Bay (CB), located in the Mid-Atlantic region, is the largest estuary in the U.S. [1]. The CB coastal region, spanning across Maryland and Virginia, is at risk of rising sea levels and land subsidence (LS) [2]. Relative sea level rises 3.24 to 6.04 mm/year at 15 tide gauges (TGs) in Figure 1 along the CB coast [3]. The projections for mean sea level (MSL) at Baltimore, MD, between 2000 and 2050 suggest a likely relative rise of 22 to 54 cm, with an average of 36 cm [4], consistent with Ezer’s (2023) estimate of 31 cm [5]. These figures underscore the critical concern of relative sea-level change (RSLC) for coastal regions, especially in areas like CB, where complex interactions among global, regional, and local processes drive significant variations in sea-level trends. These variations affect coastal infrastructure, ecosystems, and the livelihoods of communities in the region. Understanding the three processes of RSLC is essential for accurate projections and the development of effective adaptation strategies.

Global mean sea-level rise (GMSLR) is a well-documented phenomenon driven by thermal expansion of seawater and the melting of land-based ice [6]. Recent studies, such as those by [6,7,8,9,10,11,12,13,14], have provided critical insights into the acceleration and variability of GMSLR, emphasizing the importance of long-term altimetry data for quantifying these trends. While GMSLR establishes a global baseline, regional sea-level rise (RSLR) introduces significant deviations due to factors such as ocean dynamics, gravitational redistribution, sea floor deformation, and the inverse barometer effect (Gregory et al., 2019) [15]. These regional factors create spatial variability that necessitates localized analysis for regions like Chesapeake Bay.

Chesapeake Bay, in particular, faces additional challenges from LS [16], a phenomenon caused by both geological and anthropogenic processes. The interplay of glacial isostatic adjustment (GIA) [17] with human-induced activities such as groundwater withdrawal and urban development exacerbates the rate of RSLC in the region [18,19,20,21]. Our advances in subsidence categorization—differentiating bedrock-surface subsidence (BSS) from compaction subsidence (CS) and further dissecting CS into primary consolidation, secondary consolidation (PCS), construction-induced (CIS), and negative subsidence (NS)—provide new opportunities to refine RSLC analysis.

Despite significant progress, existing models often treat GMSLR, RSLR, and LS as separate entities, leading to limitations in predictive accuracy. Integrated methodologies, such as those proposed by Parris et al. (2012) [8] and refined by our approach, offer a unified framework to simulate and project RSLC by incorporating global, regional, and local contributions. These advancements are particularly valuable for Chesapeake Bay, which serves as a testbed due to its unique geological setting and anthropogenic pressures, and is broadly applicable to other coastal regions with differing geological conditions.

In this paper, Part 1 introduces a novel methodology for deciphering RSLC in Chesapeake Bay, addressing gaps in previous research by integrating comprehensive analyses of GMSLR, RSLR, and LS. The methodology builds on established frameworks, such as the RSLC equation by Gregory et al. (2019) [15] and the acceleration model by Parris et al. (2012) [8], while introducing new approaches to LS rate estimation at both long-term and short-term tide gauge locations. By applying these innovations to CB in Part 2, this work aims to enhance the understanding of RSLC dynamics and provide a robust foundation for future resilience planning in CB.

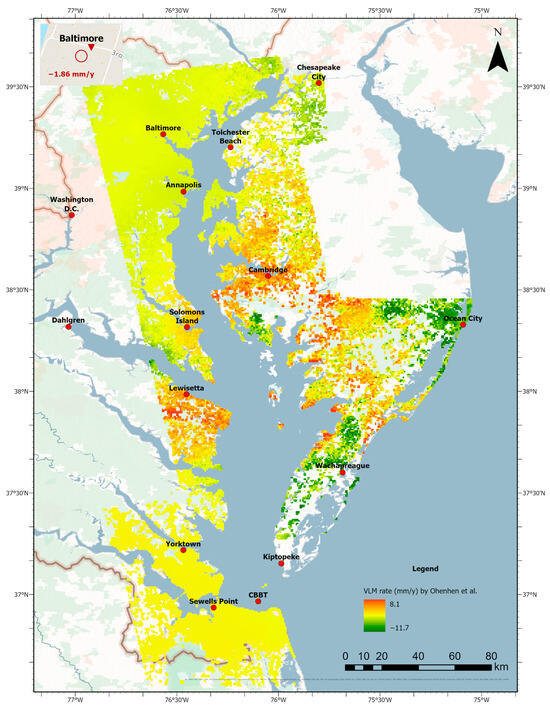
Figure 1. Fifteen tide gauges in the Chesapeake Bay area and LS of 1.86 mm/year (denoted as y in figures and tables) at tide gauge Baltimore, MD, detected from InSAR image data [22].

2. Definition of Regional Sea-Level Rise (RSLR or $\mathit{h}\mathbf{\prime }$)

This section establishes a general equation of RSLC $\Delta R$ at an ocean site in terms of “global-mean sea-level rise” (GMSLR) $h$ [15], RSLR $h^{\prime }$, and vertical land motion (VLM) $\Delta F$—or land subsidence (LS) ($-\Delta F$)—by introducing and defining $h^{\prime }$ to support analysis and simulation of tide-gauge-derived sea-level trends in the next section.

RSLC $\Delta R$ in terms of geocentric sea-level change (GSLC) and VLM $\Delta F$: Terminology for sea-level change defined by Gregory et al. [15] is employed in this paper as shown in Figure 2 to define RSLC $\Delta R$. Mean sea level (MSL) $\eta$ is located by its geodetic height $\eta$ above the reference ellipsoid (a negative value if below). Monthly mean relative sea-level data are used in this research. Sea floor $F$ is the lower boundary of the ocean, its interface with solid earth. The sea floor $F$ is the part of the surface of solid earth (whether bedrock or consolidated sediment, and lying beneath any unconsolidated sediment, e.g., [23]) that is always or sometimes submerged under sea water. Sea floor change $\Delta F$, also equally referred to as vertical land motion (VLM) $\Delta F$ or land subsidence (LS) ($-\Delta F$), occurs due to glacial isostatic adjustment (GIA), tectonics, sediment compaction, groundwater and fossil fuel withdrawals, and other non-climatic factors [14]. VLM $\Delta F$ and LS ($-\Delta F$) are used interchangeably to describe sea floor change $\Delta F$, but LS ($-\Delta F$) is employed more frequently than VLM, especially when describing methodological approaches in this two-part paper. This preference is due to the widespread use of VLM and LS in the literature.

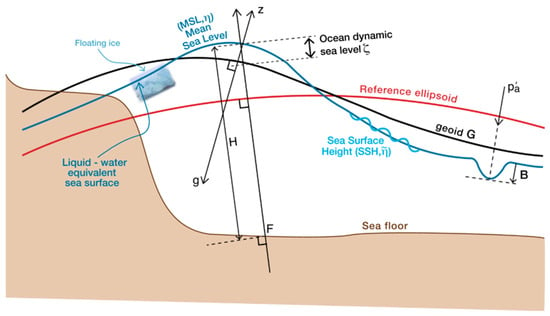
Figure 2. Relationship between surfaces relating to sea level (from [15]). The normal to the reference ellipsoid defines the vertical in the terrestrial reference frame. The normal to the geoid is the vertical coordinate ($z$) for geophysical fluid dynamics and is anti-parallel to the local effective acceleration $g$ due to gravity. The difference between these two definitions of the vertical direction is greatly exaggerated in this diagram; it is negligible in reality. The local vertical coordinates of mean sea level $\eta$, the geoid $G$, and the sea floor $F$ are relative to the reference ellipsoid, while dynamic sea level $\tilde{\zeta }$ is relative to the geoid. The local time–mean thickness of the ocean $H$ is the vertical distance between mean sea level and the sea floor. The deviation of atmospheric pressure $p_a^{\prime }$ from its global mean causes the depression $B$ in sea level by the inverse barometer effect.

The change in local mean sea level with respect to the terrestrial reference frame is called geocentric sea-level change (GSLC, $\Delta \eta$). Both the mean sea level $\eta$ and the sea floor height $F$ may change and thus alter relative sea level at an ocean point of interest. Hence, RSLC $\Delta R$ [15] is geodetically expressed as

$$\Delta R=\Delta \eta -\Delta F$$

(1)

This means RSLC $\Delta R$ represents the difference between GSLC $\Delta \eta$ and VLM $\Delta F$, i.e., RSLC $\Delta R$ at any ocean point of interest is the combination of GSLC $\Delta \eta$ and LS ($-\Delta F$). Gregory et al. (2019) [15] further relate RSLC $\Delta R$ changes in seawater thickness $\Delta H$:

$$\Delta R=\Delta H$$

(2)

GMSLR $h$: GMSLR can be simply understood as the global mean increase in seawater thickness. The increase $\Delta V$ in the ocean volume divided by the ocean surface area $A$ is termed “global-mean sea-level rise” (GMSLR) $h$ [15]. By definition, GMSLR $h$ is expressed as follows:

$$h={\displaystyle \frac{\Delta V}{A}}={\displaystyle \frac{1}{A}}\Delta \left(\int \left(\eta -F\right)\mathrm{d}A\right)={\displaystyle \frac{1}{A}}\int \Delta R\mathrm{d}A={\displaystyle \frac{1}{A}}\int \Delta H\mathrm{d}A$$

(3)

Over long, multidecadal to centennial timescales, the primary drivers of GMSLR are thermal expansion due to the heating of the ocean and the addition of water mass associated with ice mass loss from ice sheets and glaciers [14,24]. Other drivers, such as the movement of water between ocean and land (e.g., groundwater depletion and water impoundment), have a secondary impact on GMSLR, although they can become more significant over certain time periods [25].

RSLR $h^{\prime }$—a local deviation of GMSLR $h$: However, GSLC $\Delta \eta$ is not uniform across the globe [14]. At the regional level, GSLC $\Delta \eta$ can deviate significantly from GMSLR $h$ [10,14,26,27,28,29,30]. To consider this deviation, we first introduce GSLC $\Delta \eta$ as the combination of GMSLR $h$ and a deviation $h^{\prime }$ of GMSLR $h$ at any specific ocean point of interest. Thus, we can write

$$h={\displaystyle \frac{1}{A}}\Delta \left(\int \left(h+h^{\prime }-F\right)\mathrm{d}A\right)={\displaystyle \frac{1}{A}}\Delta \left(\int h\mathrm{d}A\right)+{\displaystyle \frac{1}{A}}\Delta \left(\int \left(h^{\prime }-F\right)\mathrm{d}A\right)$$

(4)

This simplifies to

$$h=h+{\displaystyle \frac{1}{A}}\Delta \left(\int \left(h^{\prime }-F\right)\mathrm{d}A\right)$$

(5)

The global mean of the deviation $h^{\prime }$ must be equal to the global mean of VLM $\Delta F$, i.e., $\left(1/A\right)\int {\Delta \mathrm{h}}^{\prime }\mathrm{d}A=\left(1/A\right)\int \Delta F\mathrm{d}A$. This is required by Equation (5) as follows:

$${\displaystyle \frac{1}{A}}\Delta \left(\int \left(h^{\prime }-F\right)\mathrm{d}A\right)=0$$

(6)

This implies that the global mean of the combination of the deviation $h^{\prime }$ and LS (−$\Delta F)$ is zero, i.e., RSLR and VLM do not contribute to GMSLR $h$. However, both contribute to GSLC $\Delta \eta$ by affecting local seawater thickness $\Delta H$ in Equation (3).

Physical understanding of RSLR $h^{\prime }$: According to [15] as shown in Figure 3, the deviation $h^{\prime }$ can be described as

$$h^{\prime }=\Delta \zeta -\Delta B+\Delta F+\Delta \Gamma$$

(7)

where $\Delta \zeta$ represents change in ocean dynamic sea level (as shown Figure 2), $\Delta B$ represents the depression in sea level by the inverse barometer effect, and $\Delta \Gamma$ represents the GRD-induced RSLC.

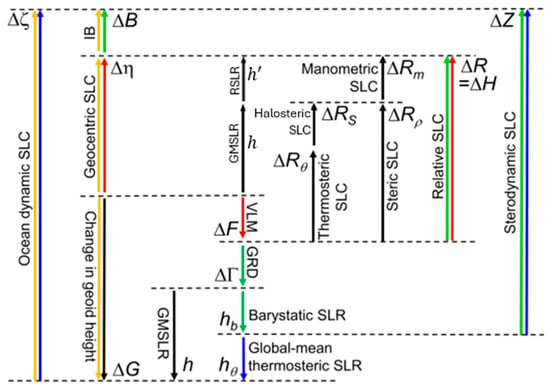
Figure 3. Schematic of relationships between sea-level change components [modified from [15] with $\Delta \eta =h+h^{\prime }$]. The lengths of the arrows do not have any significance—they are only illustrative—and the dotted horizontal lines serve only to indicate alignment. All of the quantities are differences between two states, and all except $h$, $h_{\theta },$ and $h_b$ are functions of two-dimensional geographical location, specified by latitude and longitude. Any closed circuit gives equality, in which a term has a positive sign when traversed in the direction of its arrow and a negative sign if in the opposite direction to its arrow. For example, $\Delta R-\Delta \eta +\Delta F=0$ is the circuit marked in red, $\Delta \zeta =\Delta \eta +\Delta B-\Delta G$ in orange, $\Delta Z=\Delta \zeta +h_{\theta }$ in blue, $\Delta R+\Delta B=\Delta Z+h_b+\Delta \Gamma$ in green, and $\Delta \mathsf{\Gamma }=\Delta G^{\prime }-{\Delta F}^{\prime }$ (see Equation (A1)) [15]. Additionally, RSLR $h^{\prime }$ can be inferred from the following relationships: $h^{\prime }=\Delta \zeta -$ $\Delta B+\Delta F+\Delta \Gamma$, derived from $\Delta \zeta =\Delta \eta +\Delta B-\Delta G$, $\Delta G=\Delta F+\Delta \mathsf{\Gamma }+h$, and $\Delta \eta =h+h^{\prime }$. [Notes: SLC: sea-level change; IB: inverse barometer; RSLR: regional sea-level rise; GMSLR: global-mean sea-level rise; VLM: vertical land motion (negative land subsidence, LS); GRD: changes in Earth’s gravity, Earth’s rotation (and hence centrifugal acceleration) and viscoelastic solid-Earth deformation].

In this paper, $h^{\prime }$ is referred to as regional sea-level rise (RSLR). In a region like Chesapeake Bay, its variation is generally insignificant. Therefore, we define GSLC $\Delta \eta$ at any specific ocean point of interest as the combination of GMSLR $h$ and RSLR $h^{\prime }$, a deviation of $h$, in that region.

$$\Delta \eta =h+h^{\prime }$$

(8)

We think the regional deviation $h^{\prime }$ resulted from two main factors: (1) regional variations in the ocean’s circulation (currents) and its density (temperature and salinity) [31,32]; and (2) regional effects of global gravitational, rotational, and deformational (GRD; see Appendix A) changes due to contemporary ice mass loss and the movement of water between land and ocean [14]. Changes in Earth’s GRD responses dictate the spatial distribution of water across the global ocean [15,33,34,35].

RSLR $h^{\prime }$ equation at a tide gauge: Combing Equations (1) and (8), we can estimate $h^{\prime }$ from $\Delta R$ at a tide gauge as

$$h^{\prime }=\Delta R-h+\Delta F$$

(9)

And $\Delta R$ can be addressed in terms of $h$, $h^{\prime }$, and $\Delta F$ as

$$\Delta R=h+h^{\prime }-\Delta F$$

(10)

This quantity, RSLR $h^{\prime }$ is defined throughout the ocean with Equation (9), providing a representation of the combined regional contribution to local RSLC $\Delta R$ in Equation (10) in a region such as the Chesapeake Bay area. Equations (8)–(10) clarify that the RSLR term $h^{\prime }$ causes the local GSLC at a tide gauge $\Delta \eta$ to differ from GMSLR $h$.

3. Trend Equations of RSLC

In Section 3, we further develop RSLC trend equations based on the general dynamic RSLC Equation (10) established in Section 2. These equations are then used to analyze, simulate, and project RSLC from tide gauge data and to separate the RSLC trend into its components: GMSLR, RSLR, and LS.

General trend equation of RSLC with RSLR, GMSLR, and local LS: Let $\overline{\eta }$, $\overline{F}$, and $\overline{R}$ denote trends of dynamic GSLC $\Delta \eta$, VLM $\Delta F$, and RSLC $\Delta R$, respectively. Additionally, let $\overline{h}$ and $\overline{h^{\prime }}$ denote trends of dynamic $h$ and $h^{\prime }$, respectively. The RSLR $\Delta R$ is based on monthly mean sea-level data. Both $\overline{\eta }$, and $\overline{F}$ change with time $t$ in years.

A general trend equation of RSLC derived from dynamic RSLC Equation (10) and GSLC Equation (8) is the following:

$$\overline{R}=\overline{\eta }-\overline{F}=\overline{h}+\overline{h^{\prime }}-\overline{F}$$

(11)

Equation (11) is employed in Figure 4 to conceptually illustrate relationships of RSLC at two typical locations, labeled ① and ②, with local LS, RSLR, and GMSLR in Chesapeake Bay. Notably, there is no compaction subsidence (CS) of sedimentary materials at Location ①, whereas such subsidence is present at Location ②.

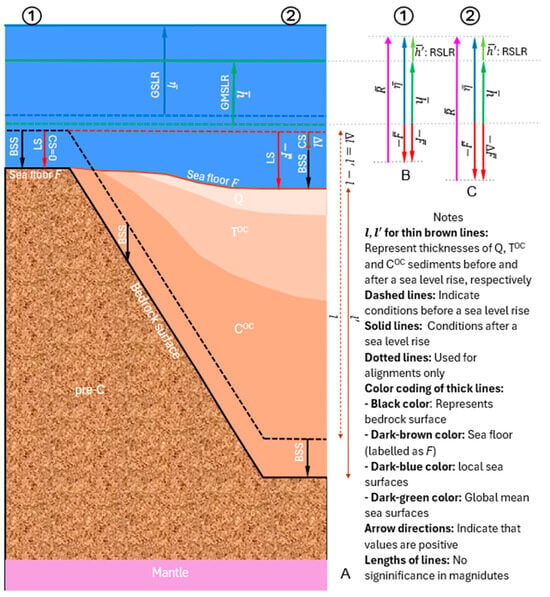
Figure 4. Conceptual relationships of GSLC (geocentric sea-level change) with RSLR (regional sea-level rise), GMSLR (global mean sea-level rise) and local LS (land subsidence) in Chesapeake Bay. (A) A profile along the coast in a region with tide gauge locations ①: bedrock (pre-C) surface as sea floor and ②: compressible Q, T, and C sediments’ surface as sea floor. (B) Relationships between trend quantities at Location ①. (C) Relationships between trend quantities at Location ②. $\overline{h^{\prime }}$ in B and C denotes the regional sea-level rise (RSLR). Shades in the navy color represent changed seawater bodies while the shade in the light blue color represents the unchanged seawater body.

RSLC trend equation: We adopt a user-focused conceptual framework similar to Parris et al. [8] and utilized by Sweet et al. [13,14]. According to this framework, sea level rose linearly from 1900 to 1992 and has risen or is projected to rise quadratically from 1992 to 2100. This acceleration since 1992 coincides with global sea-level acceleration overserved via altimetry since 1993 [12].

Using Maclaurin series, we define $\overline{\eta }\left(t\right)={\overline{\eta }}_0+{\sum }_{i=1}^{\infty }{\alpha }_i^{\eta }{t}^i$ and $\overline{F}\left(t\right)={\overline{F}}_0+{\sum }_{i=1}^{\infty }{\alpha }_i^F{t}^i$, where ${\overline{\eta }}_0$, ${\overline{F}}_0$, ${\alpha }_i^{\eta }$, and ${\alpha }_i^F$ are constants when its derivative in any order exists. Based on the definition of RSLC, we have $\overline{R}\left(t\right)=\overline{\eta }-\overline{F}={\overline{\eta }}_0-{\overline{F}}_0+{\sum }_{i=1}^{\infty }\left({\alpha }_i^{\eta }-{\alpha }_i^F\right)t^i={\overline{R}}_0+{\sum }_{i=1}^{\infty }\left({\alpha }_i^{\eta }-{\alpha }_i^F\right)t^i$, where ${\overline{\eta }}_0$, ${\overline{F}}_0$, and ${\overline{R}}_0$ are intercept constants. The rate of RSLC trend is $\dot{\overline{R}}\left(t\right)={\alpha }_1^{\eta }-{\alpha }_1^F+{\sum }_{i=2}^{\infty }\left({\alpha }_i^{\eta }-{\alpha }_i^F\right)t^{i-1}={\overline{R}}_c+{\dot{\overline{R}}}_n$, where ${\overline{R}}_c={{\alpha }_1^{\eta }-\alpha }_1^F$ which is called the linear constat of RSLC trend and ${\dot{\overline{R}}}_n={\sum }_{i=2}^{\infty }\left({\alpha }_i^{\eta }-{\alpha }_i^F\right)t^{i-1}$ which can be called the non-linear rate of RSLC trend as in [36]. If $\overline{\eta }$ is quadratic after $t_0$ and $\overline{F}$ linear, ${\dot{\overline{R}}}_n= {\alpha }_2^{\eta }t$, we have

$$\overline{R}\left(t\right)={\overline{R}}_0+{\overline{R}}_{c}t, t\le t_0$$

(12)

$$\overline{R}\left(t\right)={\overline{R}}_0+{\overline{R}}_{c}t+0.5{\alpha }_2^{\eta }{\left(t-t_0\right)}^2, t\ge t_0$$

(13)

where ${\alpha }_2^{\eta }$ denotes the acceleration of the RSLC trend. Equations (12) and (13) represent a complete RSLC trend formulation with two phases, following Parris et al.’s framework, by defining $1900\le t\le 2100$ and $t_0=1992$. The two equations can be applied to any long-term tide gauges for identifying RSL ${\overline{R}}_0$ in 1900, RSLC rate ${\overline{R}}_c$, and RSLR acceleration ${\alpha }_2^{\eta }$ through inverse simulation. However, a less than 0.01 mm/year stability of linear RSLC trend rate ${\overline{R}}_c$ requires a data timescale of at least 122 years when Equations (12) and (13) are independently applied to a long-term tide gauge (see Section 4.1). Only the tide gauge of Baltimore, served 122 years since 1902 in the study area, meets this requirement.

Parris et al.’s GMSLR trend equation: Parris et al. (2012) [8] suggested trend of GMSLR $\overline{h}$ as

$$\overline{h}\left(t\right)={\overline{h}}_0+{\alpha }_1^{h}t, t\le t_0$$

(14)

$$\overline{h}\left(t\right)={\overline{h}}_0+{\alpha }_1^{h}t+0.5{\alpha }_2^h{\left(t-t_0\right)}^2, t\ge t_0$$

(15)

where ${\overline{h}}_0$, ${\alpha }_1^h$, and ${\alpha }_2^h$ are constants, representing GMSL in 1900, linear GMSLR rate, and GMSLR acceleration since 1992, respectively, $1990\le t\le 2100$, and $t_0=1992$. Sweet et al. (2017, 2022) [13,14] utilized Equation (12). Dangendorf et al. (2017) [11] found ${\alpha }_1^h$ be 1.1 ± 0.3 mm/year between 1902 and 1990 [11] from global tide gauge data. Nerem et al. found ${\alpha }_2^h$ to be 0.084 ± 0.025 mm/year² [12] from altimetry global mean sea-level data with ${\alpha }_1^h$ of 1.70 mm/year between 1900 and 2009 and 1955 and 2000 [7,37], respectively. Part 2 will show that a ${\alpha }_2^h$ value of 0.120 ± 0.025 mm/year² is derived from altimetry global mean sea-level data by using the ${\alpha }_1^h$ value of 1.1 ± 0.3 mm/year. It futher suggests using 1.1 ± 0.3 mm/year as a linear GMSLR trend rate and 0.120 ± 0.025 mm/year² as GMSLR acceleration in Parris et al.’s framework.

RSLR trend equation based on Parris et al.’s framework: The trend of $h^{\prime }$ can be written as

$$\overline{h^{\prime }}\left(t\right)={\overline{h^{\prime }}}_0+{\alpha }_1^{h^{\prime }}t, t\le t_0$$

(16)

$$\overline{h^{\prime }}\left(t\right)={\overline{h^{\prime }}}_0+{\alpha }_1^{h^{\prime }}t+0.5{\alpha }_2^{h^{\prime }}{\left(t-t_0\right)}^2, t\ge t_0$$

(17)

where ${\overline{h^{\prime }}}_0$, ${\alpha }_1^{h^{\prime }}$, and ${\alpha }_2^{h^{\prime }}$ are constants, representing regional sea level in 1900, linear RSLR rate, and RSLR acceleration since 1992, respectively, $1990\le t\le 2100$, and $t_0=1992$. The linear RSLR rate ${\alpha }_1^{h^{\prime }}$ can be found using Equation (14):

$${\alpha }_1^{h^{\prime }}={\overline{R}}_c-{\alpha }_1^h+{\alpha }_1^F$$

(18)

If a stable RSLC rate ${\overline{R}}_c$ can be found from a long-term tide gauge such as tide gauge Baltimore through inverse simulation by using Equations (12) and (13), the LS rate ${\alpha }_1^F$ can be determined from GPS measurement or Interferometric Synthetic Aperture Radar (InSAR) data, and the GMSLR rate ${\alpha }_1^h$ of 1.1 ± 0.3 mm/year [11] is employed.

RSLC trend equation in terms of RSLR, GMSLR, and local LS based on Parris et al.’s framework: Associating Equations (12) and (13) with a combination of Equations (14) and (15) as well as (16) and (17) yields

$$\overline{R}\left(t\right)=\left({\overline{h}}_0+{\overline{h^{\prime }}}_0-{\overline{F}}_0\right)+\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{\alpha }_1^F\right)t, 1900\le t\le 1992$$

(19)

$$\begin{gathered} \overline{R}\left(t\right)=\left({\overline{h}}_0+{\overline{h^{\prime }}}_0-{\overline{F}}_0\right)+\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{\alpha }_1^F\right)t+0.5\left({\alpha }_2^h+{\alpha }_2^{h^{\prime }}\right){\left(t-t_0\right)}^2, \\ 1992\le t\le 2100 \end{gathered}$$

(20)

where ${\overline{h}}_0+{\overline{h^{\prime }}}_0-{\overline{F}}_0{={\overline{\eta }}_0-{\overline{F}}_0=\overline{R}}_0$ in Equations (12) and (13), i.e., intercept of RSLC trend; ${\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{\alpha }_1^F={{\alpha }_1^{\eta }-\alpha }_1^F={\overline{R}}_c$ in Equations (12) and (13), i.e., linear constant rate of RSLC trend; and ${\alpha }_2^h+{\alpha }_2^{h^{\prime }}={\alpha }_2^{\eta }$, i.e., acceleration of RSLC trend in Equation (13). ${\alpha }_1^{h^{\prime }},$ a linear component of RSLR, and ${\alpha }_2^{h^{\prime }}$, the quadratic acceleration of RSLR, can be estimated from ${\overline{R}}_c$ and ${\alpha }_2^{\eta }$ values derived from local tide gauge data by using Equations (12) and (13), ${\alpha }_1^h$ values such as 1.1 ± 0.3 mm/year [11], and ${\alpha }_2^h$ values from global altimetric sea level data such as 0.084 ± 0.025 mm/year² [12]. An average ${\alpha }_2^h$ value of 0.0991 mm/year² is found by using the ${\alpha }_1^h$ value of 1.1 ± 0.3 mm/year in Part 2 of this paper. The linear part of Equations (12) and (13) can be changed to piecewise forms if needed.

The variation in the RSLC linear constant ${\overline{R}}_c$ with data timescales (hereafter T), ranging from 3.0 to 123.7 years, is analyzed using NOAA tide gauge data from the New York Battery tide gauge, which has the longest data timescale in the U.S. at 168 years.

In summary, a best estimate of the linear GLMSL trend since 1990 from global tide gauge data can be used to determine its acceleration since 1992 through quadratic fitting of satellite altimetry global sea-level data. These two quadratic parameters can then be incorporated into RSLC trend simulations from a single long-term tide gauge record and used for RSLC trend projections.

4. Methodology for Estimating LS Using Short-Term Tide Gauge Data

4.1. Reference Tide Station in the Study Area—Tide Gauge Baltimore

Finding a constant LS rate ($-\dot{\overline{F}}$, i.e., $-{\alpha }_1^F$ in Equations (19) and (20)) from tide gauge data depends on the stability of the RSLC linear constant ${\overline{R}}_c$, defined as $\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{\alpha }_1^F\right)$ in Equation (12). This study assumes that ${\overline{R}}_c$ remains stable within 0.01 mm/year since NOAA’s calculated RSLC trends are two decimals in millimeters/year. The LS rate (−${\alpha }_1^F$) can be assumed to be constant since this tide gauge is seated on Ordovician (?) Manhattan Formation bedrock [38] (pre-C). A linear RSLC function $\overline{R}$ of time $t$ is employed to find linear RSLC trend rate ${\overline{R}}_c$ [i.e., $\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{\alpha }_1^F\right)$ in Equation (16)]. Figure 5A shows how ${\overline{R}}_c$ varies with T under three conditions: (1) raw monthly mean relative sea-level data with sea-level rise acceleration since 1992, for T values ranging from 3.0 to 123.7 years, measured backward from the start year 2023; (2) monthly mean relative sea-level data without sea-level rise acceleration since 1992, for T values from 3.0 to 123.7 years, measured backward from 2023; and (3) monthly mean relative sea-level data without sea-level rise acceleration since 1992, for T values from 3.0 to 92.6 years, measured backward from 1992. The analysis reveals that (a) ${\overline{R}}_c$ stability improves as T increases; (b) the best estimate of a stable ${\overline{R}}_c$ is $2.99\pm 0.08$ mm/year for dataset (2) with T $\ge$ 122 years; and (c) removing the nonlinear trend (i.e., accelerated sea-level rise component) enhances the stability for data timescales shorter than about 72 years (short-term tide gauges), further supporting the existence of RSL acceleration since 1992 in Parris et al.’s framework. This implies that achieving ${\overline{R}}_c$ stability within 0.01 mm/year requires a tide gauge data period spanning at least 122 years (from 2023 back to 1902). Additionally, using tide gauge data periods shorter than 60 years may result in deviations in the RSLC linear trend, ranging from −1.43 mm/year for T = 9.4 years to approximately 28.64 mm/year for T = 3.1 years, compared to the long-term stability value of 2.99 mm/year. For tide gauge data spanning 46 and 100 years, deviations in the RSLC linear trend range from 2.74 mm/year to approximately 3.06 mm/year, with departures of −0.25 to 0.07 mm/year from the long-term stability of 2.99 mm/year (see Figure 5B). Among Chesapeake Bay tide gauges, only the Baltimore tide gauge has operated more than 122 years since 1902, while the other 14 tide gauges in the region range from 46 years (Wachapreague, VA, USA) to 100 years (Washington, DC, USA). This means the 14 short-term tide gauges cannot be directly employed to determine a constant LS rate $-\dot{\overline{F}}$ (i.e., ${-\alpha }_1^F$) in Equation (16) with precision better than 0.01 mm/year through simple linear or quadratic regression of RSLC over time. To overcome this limitation, we propose a new methodology to derive constant LS rates from the 14 short-term tide gauges by linking to the long-term Baltimore tide gauge. In this methodology, the Baltimore tide gauge serves as the Reference Tide Station in the Chesapeake Bay area for estimating the constant LS rate at the other 14 tide gauge locations. This is justified because it meets the ${\overline{R}}_c$ stability requirement of a 122-year data period and has a known LS rate of 1.86 mm/year [22] (see Figure 1).

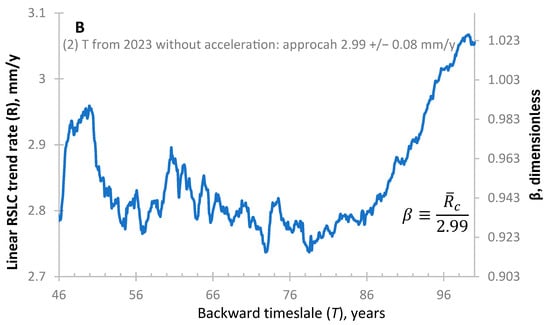
Figure 5. Variation in linear RSLR rate (R) with data timescale (T) at the New York tide gauge (NOAA ID: 8518750). (A) R changes with T from a start year (such as 2023) backward to an end year. The inset graph provides a zoomed-in illustration of T from 60 to 120 years. (B) Absolute error of R relative to a best R estimate of 2.99 mm/year with the end year of a T in A.

4.2. Equation for Estimating LS at a Short-Term Tide Gauge

Figure 6 shows that GSLC acceleration of 0.1016 mm/year² simulated from each tide gauge’s monthly mean sea-level time series can be reformed by removing climate-change-driven accelerated sea-level rise since 1992 [12] using the acceleration of 0.0991 mm/year² established in Figure 6. From the reformed sea-level data, linear RSLC trend equations can be written as Equation (21) for tide gauge Baltimore and (22) for any of the other 14 tide gauges with a data timescale T between 46 and 100 years in the study area according to Equation (19):

$${{\overline{R}}^{\prime }\left(t\right)}_{Bal}={{{\overline{R}}^{\prime }}_0}_{Bal}+{\beta }_{Bal}\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}\right)t$$

(21)

$${{\overline{R}}^{\prime }\left(t\right)}_{tg}={{{\overline{R}}^{\prime }}_0}_{tg}+{\beta }_{tg}\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{tg}\right)t$$

(22)

where $t$ is time in years; ${\beta }_{Bal}$ and ${\beta }_{tg}$ are constant to make the stable linear RSLC trend rates $\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}\right)={{\overline{R}}_c}_{Bal}$ and $\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{tg}\right)={{\overline{R}}_c}_{tg}$ vary to ${\beta }_{Bal}\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}\right)$ and ${\beta }_{tg}\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{tg}\right)$, respectively, due to a short data timescale T. Figure 5B shows the $\beta$ value of the tide gauge Battery varies from 0.916 to 1.025 for T between 46 and 100 years. ${{\overline{R}}^{\prime }\left(t\right)}_{tg}$ can be derived as a linear function of ${{\overline{R}}^{\prime }\left(t\right)}_{Bal}$ as Equation (23):

$${{\overline{R}}^{\prime }\left(t\right)}_{tg}={\displaystyle \frac{{\beta }_{tg}}{{\beta }_{Bal}}}{\displaystyle \frac{{\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{tg}}{{\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}}}{{\overline{R}}^{\prime }\left(t\right)}_{Bal} +{{\overline{R}}^{\prime }}_0$$

(23)

where ${\overline{R^{\prime }}}_0$ is a constant or an intercept. Equation (23) becomes Equation (24) if ${\beta }_{Bal}\approx {\beta }_{tg}$, which requires that variations in monthly mean sea levels are similar at all tide gauges in the Chesapeake Bay area.

$${{\overline{R}}^{\prime }\left(t\right)}_{tg}={k_{tg\sim Bal}{\overline{R}}^{\prime }\left(t\right)}_{Bal}+{{\overline{R}}^{\prime }}_0$$

(24)

where $k_{tg\sim Bal}=\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{tg}\right)/\left({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}\right)$. ${\beta }_{Bal}\approx {\beta }_{tg}$ may be supported by the similarity of monthly mean sea-level variations at the 15 tide gauges in the Chesapeake Bay area and the tide gauge Battery in New York shown in Figure 7. Supplementary Figure S1(A1–O1) shows similarity of 11-month moving average sea-level variations between tide gauge Baltimore and each of other 14 tide gauges and tide gauge Battery in New York in different time windows. Since we find ${\alpha }_1^h+ {\alpha }_1^{h^{\prime }}={\alpha }_1^{\eta }=1.26 \mathrm{m}\mathrm{m}/\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$ in the Chesapeake Bay region and the LS rate ${{\alpha }_1^F}_{Bal}$ at the Baltimore tide gauge location is 1.86 mm/year [22] (see Figure 1), then the LS rate ${{\alpha }_1^F}_{tg}$ at a short-term tide gauge can be solved by using Equation (24) if $k_{tg\sim Bal}$ is known:

$${{\alpha }_1^F}_{tg}=({\alpha }_1^h+{\alpha }_1^{h^{\prime }}-{{\alpha }_1^F}_{Bal}) k_{tg\sim Bal}-({\alpha }_1^h-{\alpha }_1^{h^{\prime }})=({\alpha }_1^{\eta }-{{\alpha }_1^F}_{Bal}) k_{tg\sim Bal}-{\alpha }_1^{\eta }$$

(25)

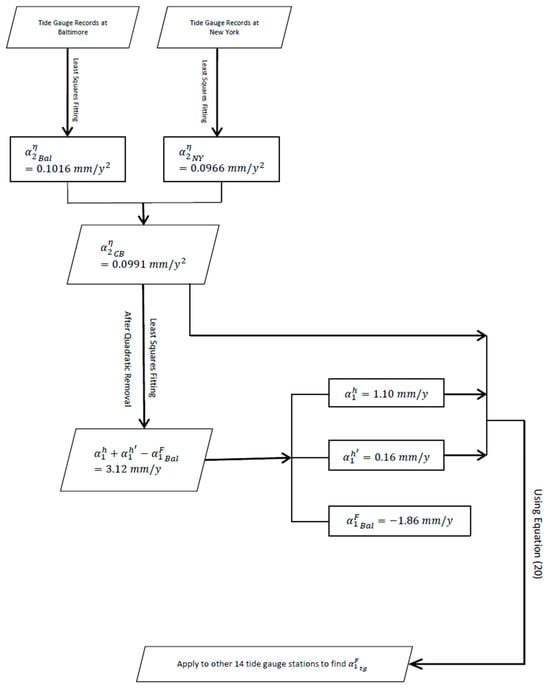
Figure 6. The flowchart illustrates the processes for determining LS rates ($-{{\alpha }_1^F}_{tg}$) at 14 short-term tide gauge sites in the Chesapeake Bay region.

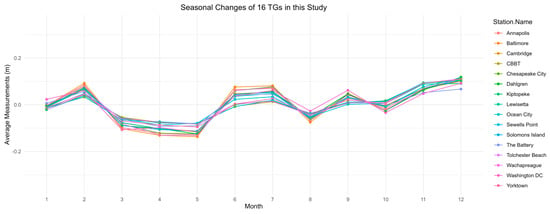
Figure 7. Seasonal changes in average water level measurements at the 16 tide gauge stations (15 in Chesapeake Bay and one at “The Battery” in New York), based on data released on the NOAA website. (Example for the tide gauge in Baltimore.)

Equation (25) shows the relationship of a long-term LS trend rate ($-{{\alpha }_1^F}_{tg}$) at each of the 14 short-term tide gauges with linear GMSLR rate ${\alpha }_1^h$, RSLR rate ${\alpha }_1^{h^{\prime }}$, and local LS rate $(-{{\alpha }_1^F}_{Bal})$ at the Baltimore tide gauge location through a linear regression coefficient $k_{tg\sim Bal}$ of RSLC between the short-term tide gauge and reference tide station Baltimore. In the Chesapeake Bay area, Equation (25) becomes

$${{\alpha }_1^F}_{tg}=(1.26-{{\alpha }_1^F}_{Bal}) k_{tg\sim Bal}+1.26$$

(26)

Supplementary Figure S1(A2–O2) shows $k_{tg\sim Bal}$ values for all the 14 short-term tide gauges with the R-squared values of 0.91 to 0.99 excluding Baltimore. LS rates (i.e., $-{{\alpha }_1^F}_{tg}$) at the 14 tide gauge locations can be found from the $k_{tg\sim Bal}$ values using Equation (26).

4.3. Evaluation of Uncertainty and LS Rate Range Under 95% Confidence Interval

4.3.1. Pearson Correlation Coefficient and Its Confidence Interval

In our methodology, linear correlations can be established as in Supplementary Figure S1(A2–O2) between each short-term tide gauge and reference tide station Baltimore, as well as between tide gauges Baltimore and New York, under short data timescale windows. To minimize the influence of high-frequency and seasonal variability, 11-month moving averages were applied to the relative sea level time series prior to calculating correlations. The original trends were preserved because the objective was to assess shared variability rather than to remove long-term signals. Time windows were defined based on overlapping observation periods between the Baltimore reference station and each short-term tide gauge to maximize data comparability. As the stations are located in the same estuarine system and subject to similar large-scale forcing, high correlation coefficients are expected and reflect regional coherence rather than purely site-specific dynamics. The Pearson correlation coefficient is the primary measure of the linear relationship, and its corresponding 95% confidence interval can be calculated by considering the sample size and the standard error of the Fisher-transformed correlation coefficient. The list of statistics is displayed in Table 1.

Table 1. The evaluation of uncertainty at each tide gauge station.

TG	Paring TG	C1	C2	D1	C3	C4	C5	C6	C7
Baltimore	New York	0.991	2.689	1420	0.027	2.637	2.741	0.990	0.992
Washington, D.C.	Baltimore	0.979	2.269	1063	0.031	2.209	2.329	0.976	0.981
	NY-Bal	0.984	2.393			2.333	2.453	0.981	0.985
Ocean City	Baltimore	0.954	1.877	321	0.056	1.766	1.987	0.943	0.963
	NY-Bal	0.973	2.145			2.035	2.255	0.967	0.978
Kiptopeke	Baltimore	0.979	2.266	831	0.035	2.198	2.335	0.976	0.981
	NY-Bal	0.973	2.141			2.073	2.210	0.969	0.977
Sewells Point	Baltimore	0.983	2.385	1106	0.030	2.326	2.444	0.981	0.985
	NY-Bal	0.985	2.452			2.393	2.511	0.984	0.987
Yorktown	Baltimore	0.981	2.329	807	0.035	2.210	2.398	0.978	0.984
	NY-Bal	0.972	2.132			2.063	2.201	0.968	0.976
Cambridge	Baltimore	0.990	2.628	684	0.038	2.553	2.703	0.988	0.991
	NY-Bal	0.978	2.255			2.180	2.330	0.978	0.981
Solomons Island	Baltimore	0.993	2.817	941	0.0330	2.753	2.881	0.992	0.994
	NY-Bal	0.979	2.262			2.198	2.326	0.976	0.981
Annapolis	Baltimore	0.994	2.904	1083	0.030	2.845	2.964	0.993	0.995
	NY-Bal	0.985	2.448			2.388	2.507	0.983	0.987
Lewisetta	Baltimore	0.969	2.076	581	0.042	1.994	2.157	0.964	0.974
	NY-Bal	0.968	2.054			1.973	2.136	0.962	0.973
Dahlgren	Baltimore	0.984	2.419	468	0.047	2.328	2.510	0.981	0.987
	NY-Bal	0.965	2.008			1.917	2.099	0.958	0.970
Tolchester Beach	Baltimore	0.992	2.779	325	0.056	2.670	2.888	0.990	0.994
	NY-Bal	0.920	1.586			1.477	1.695	0.901	0.935
Chesapeake City	Baltimore	0.996	3.072	323	0.056	2.962	3.181	0.995	0.997
	NY-Bal	0.980	2.293			2.183	2.402	0.975	0.984
Wachapreague	Baltimore	0.977	2.226	380	0.052	2.125	2.327	0.972	0.981
	NY-Bal	0.982	2.343			2.242	2.444	0.978	0.985
CBBT	Baltimore	0.971	2.112	548	0.043	2.028	2.196	0.966	0.976
	NY-Bal	0.963	2.034			1.950	2.118	0.960	0.972

Note: C1—Pearson correlation coefficient, for data series of $X_i$, and $Y_{i }(i=1, \dots , n)$, $\mathrm{C}1={\displaystyle \frac{1}{n-1}}{\sum }_{i=1}^n\left({\displaystyle \frac{X_i-\overline{X}}{\sigma X}}\right)\left({\displaystyle \frac{Y_i-\overline{Y}}{\sigma Y}}\right)$; C2—Fisher transformation coefficient, $\mathrm{C}2=0.5\ast \ln \left({\displaystyle \frac{1+\mathrm{C}1}{1-\mathrm{C}1}}\right)$; D1—sample size, for any tide gauge (TG), its comparison with the TG in Baltimore, and the comparison between TGs New York and Baltimore are the same D1 value; C3—Fisher transformed standard errors, $\mathrm{C}3= {\left(\sqrt{\mathrm{D}1-3}\right)}^{-1}$; C4—the lower limit of the 95% confidence interval of C2, $\mathrm{C}4=\mathrm{C}2-1.96\ast \mathrm{C}3$; C5—the upper limit of the 95% confidence interval of C2, $\mathrm{C}5=\mathrm{C}2+1.96\ast \mathrm{C}3$; C6—the lower limit of the 95% confidence interval of the inverse Fisher transformation coefficient, $\mathrm{C}6={\displaystyle \frac{e^{(2\ast \mathrm{C}4)}-1}{e^{(2\ast \mathrm{C}4)}+1}}$; C7—the upper limit of the 95% confidence interval of the inverse Fisher transformation coefficient, $\mathrm{C}7={\displaystyle \frac{e^{(2\ast C5)}-1}{e^{(2\ast C5)}+1}}.$ $\mathrm{C}1$ through $\mathrm{C}7$ are dimensionless.

Take the Annapolis tide gauge as an example. There are 1083 samples (see D1 values in column 5) on relative sea levels from the overlapping period between the Annapolis and Baltimore tide gauge stations. The statistical results suggest that there is 95% confidence that the Pearson correlation coefficient lies within the range of 0.993 to 0.995 (larger values in C6 and C7 columns at TG Annapolis). Similarly, there is 95% confidence that the Pearson correlation coefficient between the tide gauges of New York and Baltimore, within the same time window, lies within the range of 0.990 to 0.992 (C6 and C7 values at TG Baltimore).

4.3.2. Max and Min LS Rate Under the 95% Confidence Interval

Equation (25) or (26) suggest that the LS rate at any short-term tide gauge station can be calculated using the inferred $k_{NY\sim Bal}$ and $k_{tg\sim Bal}$ parameters, derived from the overlapping time window comparisons as described above. This approach allows the linear subsidence component to be inferred from stations with shorter records. Across the 15 stations, the inferred LS rates fall within the range of 1.86 to 2.88 mm/year, reflecting both shared regional forcing and local variability. Considering the upper and lower estimates under the 95% confidence interval, there are upper and lower ranges for the inferred $k_{NY\sim Bal}$ and $k_{tg\sim Bal}$ parameters. As a result, there exists a maximum and a minimum value for the LS rate ($-{{\alpha }_1^F}_{tg})$. The LS rate range at the 15 tide gauge stations under the 95% confidence interval is presented in Table 1 of Part 2.

5. Methods for Analyzing Components of LS

Categorization: We classify the LS ($-\overline{F})$ trend in Figure 4 into two major categories: bedrock-surface subsidence (BSS) from geological material bedrocks (pre-C) and the mantle below the bedrock surface in response to global glacial isostatic adjustment (GIA) processes (see details for BBS in Appendix B), and compaction subsidence (CS) of compressible sediments (C^OC, T^OC, and Q) between the sea floor and bedrock surface in response to local non-GIA processes [39] as shown in Table 2. Global GIA processes may include GIA itself, tectonics, earthquake, and volcano activities, etc. [40,41,42,43,44,45], while local non-GIA processes may include sediments’ creep, groundwater pumping from aquifers, weathering, land sliding, erosion, sedimentation, construction operation, biomass growth, among others, in human time. Sediments between the sea floor and bedrock surface in the Chesapeake Bay region include very thin (~50 m thick) Quaternary sediments (Q), Quaternary surficial aquifer (Q^W) (Figure 8), minor Tertiary aquifer-systems (T^OC), and major Cretaceous aquifer systems (C^OC) (Figure 8). The thickness of the sediments may be up to 2230 m (Figure 8). There may exist the following potential CS in the sediments in the Chesapeake Bay area: (1) primary consolidation subsidence (PCS) of the minor Tertiary aquifer systems (T^OC) and the major Cretaceous aquifer systems (C^OC) (Figure 8) due to groundwater pumping (see details for PCS in Appendix C); (2) the secondary consolidation subsidence (SCS) of normally consolidated Quaternary sediments (Q) and over-consolidated aquifer systems (T^OC and C^OC) resulted from natural overburden pressure [46,47] (see details for SCS in Appendix D); (3) construction-induced subsidence (CIS) attributable to the anthropogenic processes related to construction activities, such as tunnels and subways in the urbanization process [48,49] (see details for CIS in Appendix E); and (4) the negative subsidence (NS)—vertical expansion of surficial aquifers (Q^W) from its parent rock-like T^OC and C^OC sediments due to current weathering [50] or sedimentation and biomass growth of soils (Q) in wetland [51] (see details for NS in Appendix F).

Table 2. Geological type and symbol of tide gauges in the study area [modified from [47].

Geological Materials

Symbol of Station Type

Geological Time

Stress History

Consolidation Degree **

Type of VLM ($\Delta F)$ or LS ($-\Delta F)$

Period

Epoch

Start, MYBP

Experienced Effective Stress (${\mathsf{\sigma }}_{\mathrm{c}}^{\prime })$

Current Effective Stress (${\mathsf{\sigma }}_{\mathrm{o}}^{\prime })$

Sediments between see floor and bedrock surface

Surficial Aquifer ***

${\mathrm{Q}}^{\mathrm{W}}$

${\mathrm{Q}}_{\mathrm{h}}^{\mathrm{W}}$

Quaternary

Holocene

0.00117

Decreasing (losing)

${\mathsf{\sigma }}_{\mathrm{o}}^{\prime }<{\mathsf{\sigma }}_{\mathrm{c}}^{\prime }$

−1

Local non-GIA processes

NS $\le 0$ PCS $\approx$ 0

CS

${\mathrm{Q}}_{\mathrm{p}}^{\mathrm{W}}$

Pleistocene

2.58

$\mathrm{Q}$

${\mathrm{Q}}_{\mathrm{h}}$

Holocene

0.00117

Very low

${\mathsf{\sigma }}_{\mathrm{o}}^{\prime }\approx {\mathsf{\sigma }}_{\mathrm{c}}^{\prime }$

1

PCS $\approx$ 0 CIS $\ge$ 0

${\mathrm{Q}}_{\mathrm{p}}$

Pleistocene

2.58

Low

2

Aquifer Systems

TOC

Tertiary

Pliocene to Paleocene

66

High

${\mathsf{\sigma }}_{\mathrm{o}}^{\prime }<{\mathsf{\sigma }}_{\mathrm{c}}^{\prime }$

5

PCS $\ge 0$ $\mathrm{S}\mathrm{C}\mathrm{S}\approx 0$ *

COC

Cretaceous

145

Very high

Materials below bedrock surface

Bedrock

pre-C

Jurassic to Precambrian

4600

Highest

${\mathsf{\sigma }}_{\mathrm{o}}^{\prime }<{\mathsf{\sigma }}_{\mathrm{c}}^{\prime }$ ***

6

Global GIA processes

BSS

BSS

Mantle

n/a

n/a

n/a

n/a

Super high

n/a

?

* SCS from the T^OC and C^OC strata in the human observation period is assumed to be insignificant after a long-term accumulative creep such as Path C-D in Supplementary Figure S4 after an overburden removal event. ** The consolidation degree of geological strata is based on the strata’s stress history in column stress history; −1—Inverse consolidated for soil + saprolite + fractured rock due to weathering of Tertiary and Cretaceous strata during Quaternary (Q^w) (Figures S6 and S8); 1—Very unconsolidated for normal sediments during Holocene; 2—Unconsolidated for normal sediments during Pleistocene; 3—Semi-consolidated [52] for Tertiary strata (no distribution in this study area); 4—Highly semi-consolidated for Cretaceous strata (no distribution in this study area); 5—Over semi-consolidated for T^OC and C^OC; and 6—Consolidated (bedrock). Modified from [47]. *** [53] BSS—Bedrock-surface subsidence in response to global GIA (glacial isostatic adjustment) processes of Earth through mantle viscoelastic deformation (see Appendix B). CS—Compaction subsidence of compressible sediments in response to non-GIA processes, including PCS, SCS, CIS, NS, etc. PCS—Primary consolidation subsidence of compressible aquifer systems due to fluid withdrawal (see Appendix C). SCS—Secondary consolidation (creep) subsidence due to natural overburden pressure of the aquifer systems, which is taken to be zero in the C^OC and T^OC strata as Path C-D in Supplementary Figure S4 (see Appendix D). CIS—Construction-induced subsidence due to the complex construction process of big projects for a period; for instance, at subway constructions in Korea, the satellite monitored LS is presumably due to heterogeneous geologic stratigraphy with the spatially varying thickness of the compressible soil layers in the area of interest [48] (see Appendix E). At TG CBBT, we hypothesize that the vertical displacement observed may be correlated with changes in stress that were potentially influenced by nearby tunneling activities. NS—Negative subsidence (NS) due to bedrock-like weathering or sedimentation and soil biomass growth (see Appendix F).

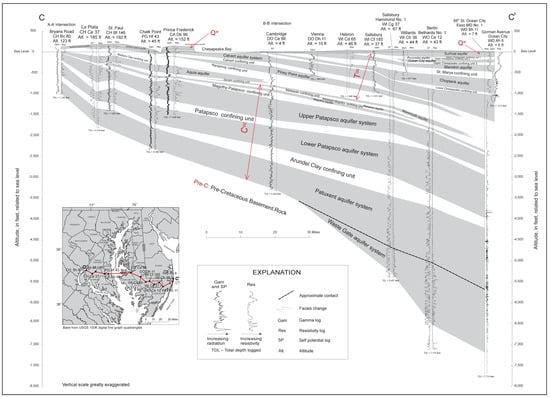
Figure 8. Typical cross-section of the Atlantic Coastal Plain aquifer system in the Chesapeake Bay region (modified from [53]). Surficial aquifer (Q^W) is weathered product of Tertiary aquifer system (see Supplementary Figure S8). Aquifer systems shaded in gray in the cross-section are in Cretaceous (C^OC) and Tertiary (T^OC) sediments.

LS estimating: Only LS of 1.86 mm/year at reference tide station Baltimore in Figure 1 is estimated from LS on the US east coast detected from InSAR image data by Ohenhen et al. (2023) [22]. LS ranges of 1.92 to 3.12 mm/year at the other 14 tide gauge locations are found by using Equation (19) from linear correlation coefficient $k_{tg\sim Bal}$ values in Supplementary Figure S1(B2–O2), which is shown in Part 2 in detail.

BBS contour mapping: LS = CS + BSS generally. LS = BSS if bedrock surface is equal to the sea floor, i.e., CS = 0 (see CS at location ① in Figure 4). Only tide gauge Washington, D.C. is seated on the pre-C bedrock surface without CS. CS is negligible at three tide gauge locations, Baltimore and Ocean City in Maryland, and Kiptopeke in Virginia, through analysis in Part 2 using comprehensive methods in Appendix B, Appendix C, Appendix D, Appendix E and Appendix F using groundwater level data in eight wells as shown in Supplementary Figure S2. LS values found by using methods in Section 3 and Section 4 can be determined to be their BBS values at the four tide gauge locations, respectively. The four BBS values allow us to map the first BSS contours in the range of 1.48 to 2.42 mm/year in the Chesapeake Bay region. Results are shown in Part 2 in detail.

CS estimating: CS in the range of 0 to 0.75 mm/year at the 15 tide gauge locations can be estimated from the determined LS above at each tide gauge location by removing BBS interpolated from the above BBS contours. Results are shown in Part 2 in detail.

CS type determination: Methods in Appendix C, Appendix D, Appendix E and Appendix F are employed to analyze PCS, SCS, CIS, and NS at each tide gauge location based on geological, geohydrological, and soil mechanical information. SCS in over-consolidated Tertiary and Cretaceous sediments (T^OC and C^OC in Figure 8 and Table 2) can be ignored since the sediment strata was uplifted during Quaternary. SCS of less than 0.01 mm/year in Quaternary sediments can be ignored as well since the Quaternary sediment thickness is thin (see Figure 8). PCS of up to 0.75 mm/year is present at nine tide gauge locations, including Cambridge, Solomons Island, Annapolis and Tolchester Beach in Maryland, and Sewells Point, Yorktown, Lewisetta, Dahlgren, and Wachapreague in Virginia. CIS of 0.52 mm/y during 1960–1990 is estimated at CBBT (Chesapeake Bay Bridge Tunnel) in Virginia. Results are shown in Part 2 in detail.

Figure 9 summarizes the above workflow for deciphering LS into BBS and CS and further dividing CS into PCS and CIS.

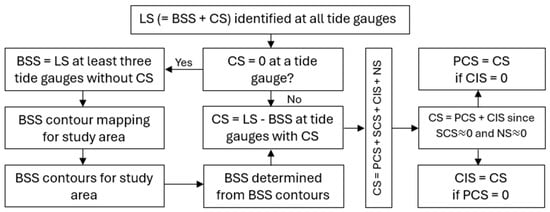
Figure 9. A flowchart for deciphering LS into BBS and CS and further dividing CS into PCS and CIS.

6. Projection Equation of RSLC in Terms of GMSLR, RSLR, and LS

Equation (20) can be built to project RSLC by 2100 for each of the 15 tide gauges in the Chesapeake Bay region with identified values for two GMSLR parameters ${\alpha }_1^h$ and ${\alpha }_2^{\eta }$, two RSLR parameters ${\alpha }_1^{h^{\prime }}$ and ${\alpha }_2^{h^{\prime }}$, LS $(-{\alpha }_1^F)$, and intercept ${\overline{R}}_0$ ($={\overline{h}}_0+{\overline{h^{\prime }}}_0-{\overline{F}}_0$). Contributions from GMSLR, RSLC, and LS can be computed over time. Projection results are shown in Part 2.

7. Conclusions

This study presents a novel, integrated methodology to decipher relative sea-level change (RSLC) in Chesapeake Bay by disentangling the contributions of global mean sea-level rise (GMSLR), regional sea-level rise (RSLR), and local land subsidence (LS). By combining long-term tide gauge records, satellite altimetry, and InSAR observations, we derive trend equations spanning from 1900 to 2100 and establish a robust framework to estimate both linear and nonlinear RSLC trends using trend equations and Maclaurin series expansions.

A key contribution of this work is the development of an innovative approach to estimate LS at short-term tide gauges by referencing long-term data from the Baltimore station, which meets the minimum 122-year threshold required for stable RSLC trend estimation. This technique enables more accurate LS assessments across Chesapeake Bay, even in locations lacking long-term data. Additionally, we classify LS into bedrock-surface subsidence (BSS) and compaction subsidence (CS), further subdividing CS into four types—primary consolidation, secondary consolidation, construction-induced, and negative subsidence—based on sediment types and geologic conditions. These classifications provide an important basis for identifying spatial heterogeneity in land motion and understanding underlying mechanisms.

The methodology proposed here not only advances sea-level trend analysis in sediment-rich and tectonically quiet estuarine environments like the Chesapeake Bay but also sets a foundation for applying similar techniques in other vulnerable coastal regions. By integrating geophysical, oceanographic, and geotechnical insights, this work enhances the precision of RSLC assessments, supporting long-term resilience planning, infrastructure design, and risk mitigation strategies in the face of accelerating sea-level rise.

In Part 2 of this two-part study, we will apply the methodology developed here to produce spatially distributed projections of RSLC, quantify uncertainties, and analyze site-specific risk across Chesapeake Bay. Together, both parts aim to provide a comprehensive framework for addressing the scientific and societal challenges posed by coastal sea-level changes.