Effects of Permeability and Pyrite Distribution Heterogeneity on Pyrite Oxidation in Flooded Lignite Mine Dumps
Abstract
1. Introduction
- How do different aspects of permeability and pyrite distribution heterogeneities (e.g., correlation lengths, variances) affect the spatial and temporal patterns of solute transport?
- What role does heterogeneity play in controlling oxygen consumption, acid generation, and sulfate mobilization?
- Under which conditions can simplified modeling approaches (e.g., homogeneous domains or equilibrium assumptions to reduce computational times) adequately represent the integrated geochemical response of heterogeneous mine dumps?
2. Materials and Methods
2.1. Reactive Transport Model Formulation and Implementation
2.2. Geostatistical Field Generation and Heterogeneity Implementation
2.3. Model Setup and Domain
2.4. Simulation Scenarios
3. Results
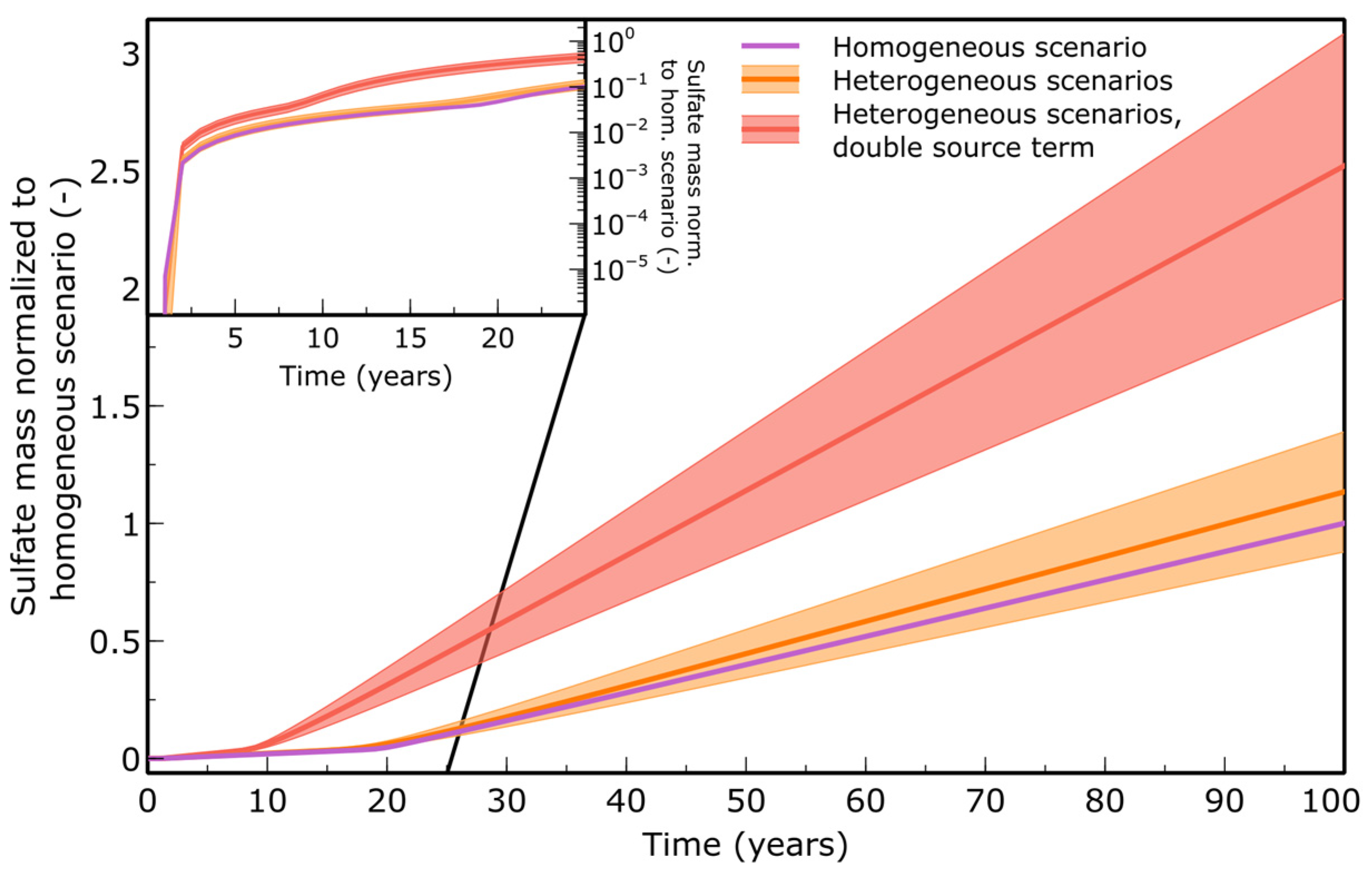
3.1. Solute Transport
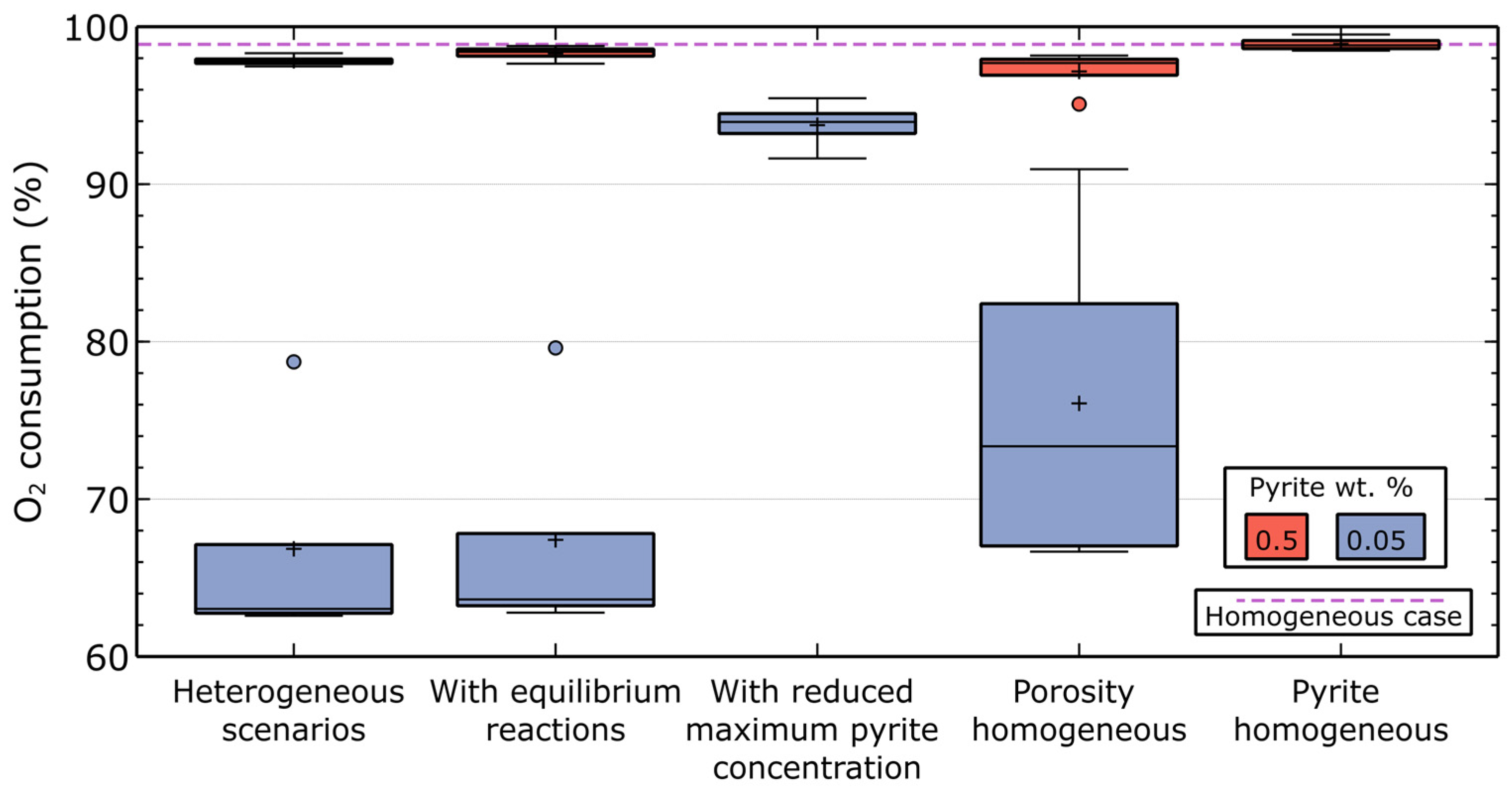
3.2. Oxygen Consumption
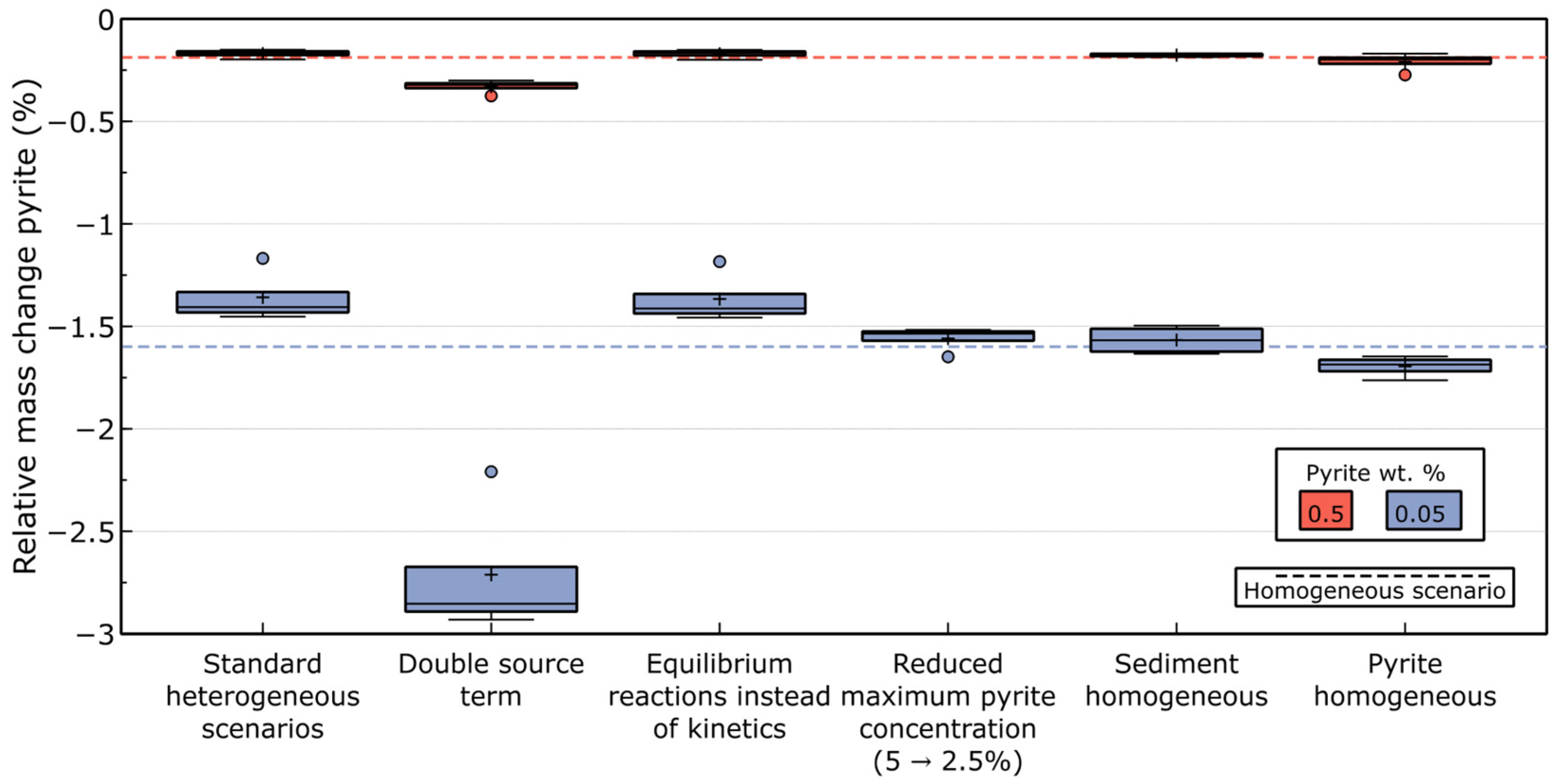
3.3. Mineral Balance
3.4. Ion Concentration and Speciation
4. Discussion
4.1. Heterogeneity Accelerates Solute Transport and Alters Reaction Fronts
4.2. Widespread Oxidation Is Promoted by Pyrite Concentrations
4.3. Equilibrium Assumptions Speed up Simulations but Distort Redox Speciation
4.4. Model Simplifications and Restrictions
4.5. Practical Implications for Mine Redevelopment and Management
- Sustained oxygen influx, e.g., by PHS operation will reactivate pyrite oxidation in internal mine dumps, especially in high-permeability zones. Monitoring should thus target flow paths, not just average pyrite content. Due to limited oxygen solubility and other oxygen-consuming processes, the extent of pyrite oxidation is low.
- Earlier contaminant breakthrough may occur in heterogeneous models than predicted by homogeneous ones.
- Low pyrite concentrations do not imply low environmental risk—dilute, widespread distributions may generate larger, longer-lasting plumes.
- Simplified geochemical models may suffice for estimating peak sulfate or pH, but lack simulating redox evolution and respective ion speciation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
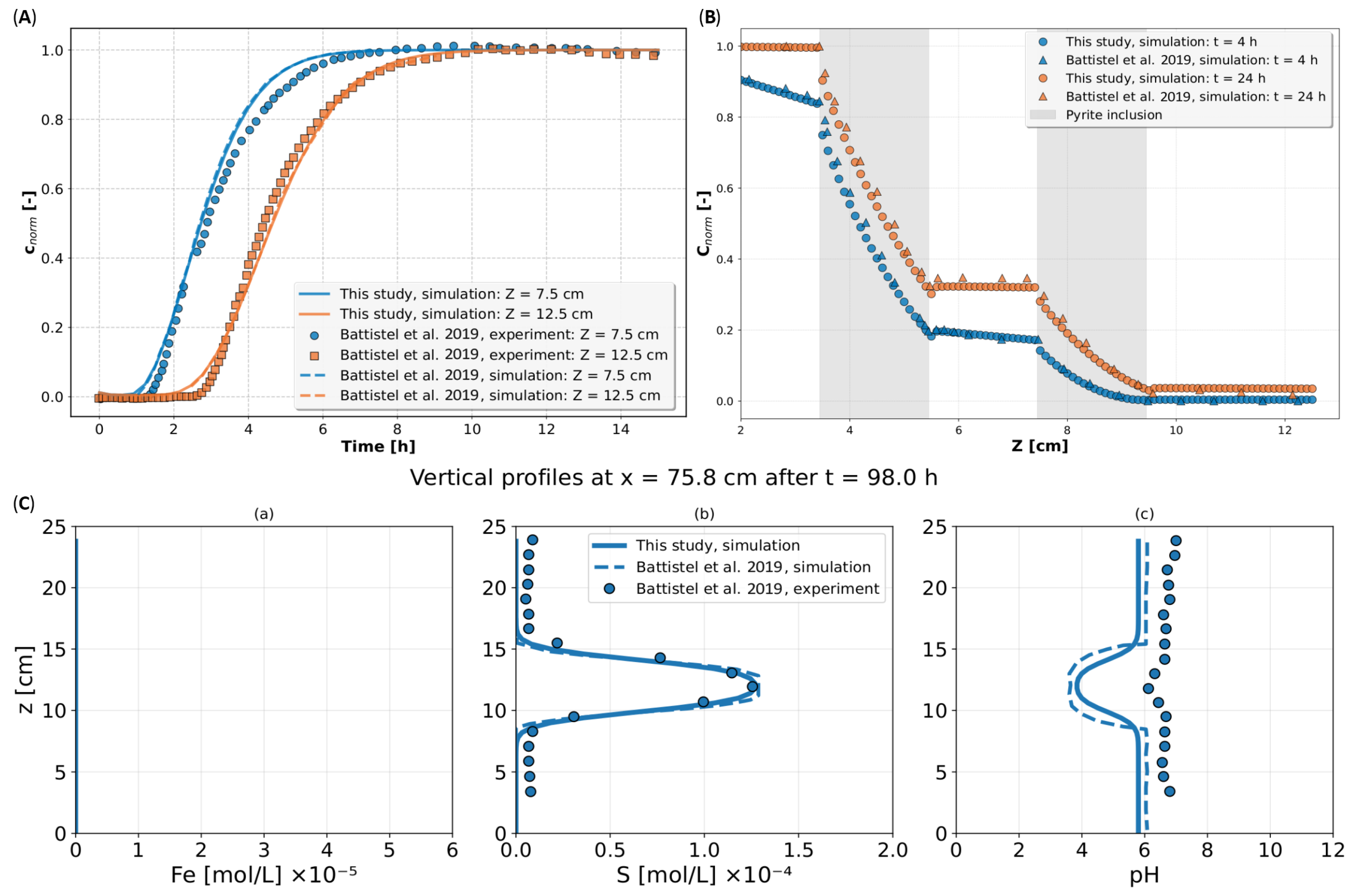
Appendix B
| ϕeff/K-Field | ϕeff/K-Field | Scenario Modification |
|---|---|---|
| Heterogeneous | Heterogeneous | 0.5 wt% initial pyrite concentration/0.05 wt% initial pyrite concentration |
| Heterogeneous | Heterogeneous | |
| Homogeneous | Homogeneous | |
| Homogeneous | Homogeneous | |
| Heterogeneous | Heterogeneous | Initial pyrite oxidation during equilibrium |
| No mineral–porosity feedback (Equations (8) and (9)) | ||
| No reaction kinetic (Equation (2)) | ||
| Reduced max. pyrite concentration per cell (2.5 wt%) | ||
| Double source term |
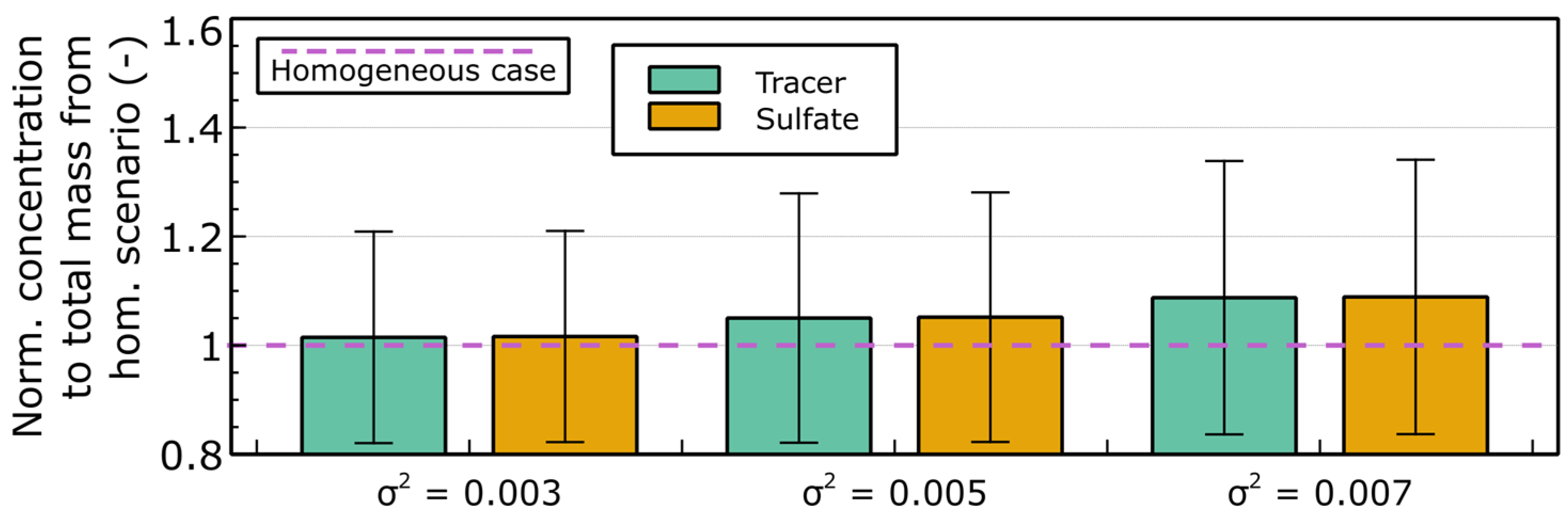
Appendix C
References
- Schultze, M.; Pokrandt, K.-H.; Hille, W. Pit Lakes of the Central German Lignite Mining District: Creation, Morphometry and Water Quality Aspects. Limnologica 2010, 40, 148–155. [Google Scholar] [CrossRef]
- Weber, A. Surrounded by Pit Lakes: New Landscapes After Lignite Mining in the Former German Democratic Republic. Mine Water Environ. 2020, 39, 658–665. [Google Scholar] [CrossRef]
- Korbmacher, J. Residual Lakes in the Rhineland Lignite Area. Min. Rep. 2016, 152, 233–244. [Google Scholar]
- Szczepiński, J. Hydrogeological Conditions of Lignite Basins in Poland and Its Influence on Reclamation Voids by Flooding. In An Interdisciplinary Response to Mine Water Challenges, Proceedings of the 12th Congress of International Mine Water Association, Xuzhou, China, 18–22 August 2014; China University of Mining and Technology Press: Xuzhou, China, 2014. [Google Scholar]
- Molenda, T.; Kidawa, J. Natural and Anthropogenic Conditions of the Chemical Composition of Pit Lake Waters (Based on Example Pit Lakes from Central Europe). Mine Water Environ. 2020, 39, 473–480. [Google Scholar] [CrossRef]
- Al Heib, M.; Varouchakis, E.A.; Galetakis, M.; Renaud, V.; Burda, J. A Framework for Assessing Hazards Related to Pit Lakes: Application on European Case Studies. Environ. Earth Sci. 2023, 82, 365. [Google Scholar] [CrossRef]
- McCullough, C.; Schultze, M.; Vandenberg, J. Realizing Beneficial End Uses from Abandoned Pit Lakes. Minerals 2020, 10, 133. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Roumpos, C.; Karlopoulos, E.; Koukouzas, N. Sustainable Rehabilitation of Surface Coal Mining Areas: The Case of Greek Lignite Mines. Energies 2020, 13, 3995. [Google Scholar] [CrossRef]
- Schmidt-Böcking, H.W.; Luther, G.; Düren, M.; Puchta, M.; Bender, T.; Garg, A.; Ernst, B.; Frobeen, H. Renewable Electric Energy Storage Systems by Storage Spheres on the Seabed of Deep Lakes or Oceans. Energies 2023, 17, 73. [Google Scholar] [CrossRef]
- Kempka, T.; Otto, C.; Chabab, E.; Ernst, P.; Schnepper, T. Best-Practice Guidelines on Hybrid Pumped Hydropower Storage of Excess Energy in Open-Pit Lignite Mines; Helmholtz Centre Potsdam—GFZ German Research Centre for Geosciences: Potsdam, Germany, 2024; p. 58. [Google Scholar] [CrossRef]
- Thema, J.; Thema, M. Pumpspeicherkraftwerke in Stillgelegten Tagebauen: Am Beispiel Hambach-Garzweiler-Inden; Wuppertal Papers; Wuppertal Institut für Klima, Umwelt, Energie: Wuppertal, Germany, 2019. [Google Scholar]
- Weber, T.; Stocks, R.; Blakers, A.; Nadolny, A.; Cheng, C. A Global Atlas of Pumped Hydro Systems That Repurpose Existing Mining Sites. Renew. Energy 2024, 224, 120113. [Google Scholar] [CrossRef]
- Quaranta, E.; Boes, R.M.; Hunt, J.D.; Szabò, S.; Tattini, J.; Pistocchi, A. Considerations on the Existing Capacity and Future Potential for Energy Storage in the European Union’s Hydropower Reservoirs and Pumped-Storage Hydropower. J. Energy Storage 2024, 104, 114431. [Google Scholar] [CrossRef]
- Schnepper, T.; Kühn, M.; Kempka, T. Reaction Path Modeling of Water Pollution Implications of Pumped Hydropower Storage in Closed Open-Pit Lignite Mines. Mine Water Environ. 2025, 44, 107–121. [Google Scholar] [CrossRef]
- Schnepper, T.; Kapusta, K.; Strugała-Wilczek, A.; Roumpos, C.; Louloudis, G.; Mertiri, E.; Pyrgaki, K.; Darmosz, J.; Orkisz, D.; Najgebauer, D.; et al. Potential Hydrochemical Impacts of Pumped Hydropower Storage Operation in Two European Coal Regions in Transition: The Szczerców-Bełchatów Mining Complex, Poland, and the Kardia Mine, Greece. Environ. Earth Sci. 2025, 84, 247. [Google Scholar] [CrossRef]
- Chandra, A.P.; Gerson, A.R. The Mechanisms of Pyrite Oxidation and Leaching: A Fundamental Perspective. Surf. Sci. Rep. 2010, 65, 293–315. [Google Scholar] [CrossRef]
- Evangelou, V.P.; Zhang, Y.L. A Review: Pyrite Oxidation Mechanisms and Acid Mine Drainage Prevention. Crit. Rev. Environ. Sci. Technol. 1995, 25, 141–199. [Google Scholar] [CrossRef]
- Fowler, T.A.; Holmes, P.R.; Crundwell, F.K. Mechanism of Pyrite Dissolution in the Presence of Thiobacillus ferrooxidans. Appl. Environ. Microbiol. 1999, 65, 2987–2993. [Google Scholar] [CrossRef]
- Blodau, C. A Review of Acidity Generation and Consumption in Acidic Coal Mine Lakes and Their Watersheds. Sci. Total Environ. 2006, 369, 307–332. [Google Scholar] [CrossRef]
- Geller, W.; Schultze, M.; Kleinmann, R.; Wolkersdorfer, C. Acidic Pit Lakes: The Legacy of Coal and Metal Surface Mines; Environmental Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-29383-2. [Google Scholar]
- Prein, A.; Mull, R. Oxygen as a Limiting Factor for Pyrite Weathering in the Overburden of Open Pit Lignite Areas. In Acidic Mining Lakes; Geller, W., Klapper, H., Salomons, W., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 237–250. ISBN 978-3-642-71956-1. [Google Scholar]
- van Berk, W.; Wisotzky, F. Sulfide Oxidation in Brown Coal Overburden and Chemical Modeling of Reactions in Aquifers Influenced by Sulfide Oxidation. Environ. Geol. 1995, 26, 192–196. [Google Scholar] [CrossRef]
- Wisotzky, F. Hydrogeochemische Reaktionen Im Sicker- Und Grundwasserbereich von Braunkohlentagebaukippen. Grundwasser 1996, 1, 129–136. [Google Scholar] [CrossRef]
- Castro, J.M.; Moore, J.N. Pit Lakes: Their Characteristics and the Potential for Their Remediation. Environ. Geol. 2000, 39, 1254–1260. [Google Scholar] [CrossRef]
- Lenk, S.; Wisotzky, F. Chemical Modelling of the Groundwater Composition in Aquifers Affected by Lignite Mine Dumps Discharge (Surface Mine Inden, Germany). Environ. Earth Sci. 2011, 62, 581–591. [Google Scholar] [CrossRef]
- Nixdorf, B.; Ramm, J.; van de Weyer, K. Übersicht Zur Ökologischen Situation Ausgewählter Tagebauseen Des Braunkohlebergbaus in Deutschland: UBA-FB 002383; Umweltbundesamt: Berlin, Germany, 2016. [Google Scholar]
- Hoth, N.; Feldmann, H.; Rinker, A.; Glombitza, F.; Häfner, F. Reductive Processes within Lignite Dumps—Chance of a Long-Term Natural Attenuation Process. Geoderma 2005, 129, 19–31. [Google Scholar] [CrossRef]
- Berkowitz, B.; Dror, I.; Hansen, S.K.; Scher, H. Measurements and Models of Reactive Transport in Geological Media. Rev. Geophys. 2016, 54, 930–986. [Google Scholar] [CrossRef]
- Muniruzzaman, M.; Pedretti, D. Mechanistic Models Supporting Uncertainty Quantification of Water Quality Predictions in Heterogeneous Mining Waste Rocks: A Review. Stoch. Environ. Res. Risk Assess. 2021, 35, 985–1001. [Google Scholar] [CrossRef]
- Battistel, M.; Muniruzzaman, M.; Onses, F.; Lee, J.; Rolle, M. Reactive Fronts in Chemically Heterogeneous Porous Media: Experimental and Modeling Investigation of Pyrite Oxidation. Appl. Geochem. 2019, 100, 77–89. [Google Scholar] [CrossRef]
- Raymond, K.E.; Seigneur, N.; Su, D.; Mayer, K.U. Investigating the Influence of Structure and Heterogeneity in Waste Rock Piles on Mass Loading Rates—A Reactive Transport Modeling Study. Front. Water 2021, 3, 618418. [Google Scholar] [CrossRef]
- Pedretti, D.; Mayer, K.U.; Beckie, R.D. Controls of Uncertainty in Acid Rock Drainage Predictions from Waste Rock Piles Examined through Monte-Carlo Multicomponent Reactive Transport. Stoch. Environ. Res. Risk Assess. 2020, 34, 219–233. [Google Scholar] [CrossRef]
- Buczko, U.; Gerke, H.H.; Hüttl, R.F. Spatial Distributions of Lignite Mine Spoil Properties for Simulating 2-D Variably Saturated Flow and Transport. Ecol. Eng. 2001, 17, 103–114. [Google Scholar] [CrossRef]
- Gerke, H.H.; Molson, J.W.; Frind, E.O. Modelling the Impact of Physical and Chemical Heterogeneity on Solute Leaching in Pyritic Overburden Mine Spoils. Ecol. Eng. 2001, 17, 91–101. [Google Scholar] [CrossRef]
- Gerke, H.H.; Molson, J.W.; Frind, E.O. Modelling the Effect of Chemical Heterogeneity on Acidification and Solute Leaching in Overburden Mine Spoils. J. Hydrol. 1998, 209, 166–185. [Google Scholar] [CrossRef]
- Gerke, H.H.; Badorreck, A.; Einecke, M. Single- and Dual-Porosity Modelling of Flow in Reclaimed Mine Soil Cores with Embedded Lignitic Fragments. J. Contam. Hydrol. 2009, 104, 90–106. [Google Scholar] [CrossRef]
- Ma, C.; Cai, Q.; Wang, H.; Shao, M.; Fan, J.; Shi, Z.; Wang, F. Modeling of Water Flow in Reclaimed Mine Spoil with Embedded Lignitic Fragments Using Hydrus-1D. Mine Water Environ. 2015, 34, 197–203. [Google Scholar] [CrossRef]
- Pujades, E.; Jurado, A.; Orban, P.; Ayora, C.; Poulain, A.; Goderniaux, P.; Brouyère, S.; Dassargues, A. Hydrochemical Changes Induced by Underground Pumped Storage Hydropower and Their Associated Impacts. J. Hydrol. 2018, 563, 927–941. [Google Scholar] [CrossRef]
- Pujades, E.; Orban, P.; Jurado, A.; Ayora, C.; Brouyère, S.; Dassargues, A. Water Chemical Evolution in Underground Pumped Storage Hydropower Plants and Induced Consequences. Energy Procedia 2017, 125, 504–510. [Google Scholar] [CrossRef]
- Strugała-Wilczek, A.; Basa, W.; Bzowski, Z.; Kempka, T.; Schnepper, T.; Pyrgaki, K.; Roumpos, C.; Louloudis, G.; Orkisz, D.; Najgebauer, D.; et al. Hydrogeochemical Effects of Pumped Hydropower Storage Operation in Open-Pit Lignite Mines in Greece and Poland. J. Clean. Prod. 2025, 501, 145286. [Google Scholar] [CrossRef]
- Kempka, T.; Steding, S.; Kühn, M. Verification of TRANSPORT Simulation Environment Coupling with PHREEQC for Reactive Transport Modelling. Adv. Geosci. 2022, 58, 19–29. [Google Scholar] [CrossRef]
- Kempka, T. Verification of a Python-Based TRANsport Simulation Environment for Density-Driven Fluid Flow and Coupled Transport of Heat and Chemical Species. Adv. Geosci. 2020, 54, 67–77. [Google Scholar] [CrossRef]
- Steding, S.; Kempka, T.; Zirkler, A.; Kühn, M. Spatial and Temporal Evolution of Leaching Zones within Potash Seams Reproduced by Reactive Transport Simulations. Water 2021, 13, 168. [Google Scholar] [CrossRef]
- Steding, S.; Kempka, T.; Kühn, M. How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams. Appl. Sci. 2021, 11, 9314. [Google Scholar] [CrossRef]
- Li, Z.; Spangenberg, E.; Schicks, J.M.; Kempka, T. Numerical Simulation of Coastal Sub-Permafrost Gas Hydrate Formation in the Mackenzie Delta, Canadian Arctic. Energies 2022, 15, 4986. [Google Scholar] [CrossRef]
- Li, Z.; Spangenberg, E.; Schicks, J.M.; Kempka, T. Numerical Simulation of Hydrate Formation in the LArge-Scale Reservoir Simulator (LARS). Energies 2022, 15, 1974. [Google Scholar] [CrossRef]
- Li, Z.; Chabab, E.; Spangenberg, E.; Schicks, J.M.; Kempka, T. Geologic Controls on the Genesis of the Arctic Permafrost and Sub-Permafrost Methane Hydrate-Bearing System in the Beaufort–Mackenzie Delta. Front. Earth Sci. 2023, 11, 1148765. [Google Scholar] [CrossRef]
- Kempka, T.; Kühn, M. Numerical Simulation of Spatial Temperature and Salinity Distribution in the Waiwera Geothermal Reservoir, New Zealand. Grund.-Z. Fachsekt. Hydrogeol. 2023, 28, 243–254. [Google Scholar] [CrossRef]
- Chabab, E.; Kühn, M.; Kempka, T. Upwelling Mechanisms of Deep Saline Waters via Quaternary Erosion Windows Considering Varying Hydrogeological Boundary Conditions. Adv. Geosci. 2022, 58, 47–54. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Techniques and methods; U.S. Geological Survey: Reston, VA, USA, 2013; p. 497.
- Müller, M.; Parkhurst, D.L.; Charlton, S.R. Programming PHREEQC Calculations with C++ and Python a Comparative Study. In Proceedings of the MODFLOW and More 2011: Integrated Hydrologic Modeling, Golden, CO, USA, 5–8 June 2011; Volume 1, pp. 632–636. [Google Scholar]
- Meyer, G.; Waschkies, C.; Hüttl, R.F. Investigations on Pyrite Oxidation in Mine Spoils of the Lusatian Lignite Mining District. Plant Soil 1999, 213, 137–147. [Google Scholar] [CrossRef]
- Wisotzky, F. Prevention of Acidic Groundwater in Lignite Overburden Dumps by the Addition of Alkaline Substances: Pilot-Scale Field Experiments. Mine Water Environ. 2001, 20, 122–128. [Google Scholar] [CrossRef]
- Bilek, F. Genetic Geochemical Model for Mining Affected Groundwaters of the Lusatian Post-Mining District. Appl. Geochem. 2012, 27, 1081–1088. [Google Scholar] [CrossRef]
- Williamson, M.A.; Rimstidt, J.D. The Kinetics and Electrochemical Rate-Determining Step of Aqueous Pyrite Oxidation. Geochim. Cosmochim. Acta 1994, 58, 5443–5454. [Google Scholar] [CrossRef]
- Fuchs, S.; Ziesche, M.; Nillert, P. Empirische Verfahren zur Ableitung verschiedener Porositätsarten aus Durchlässigkeitsbeiwert und Ungleichkörnigkeitszahl—Ein Überblick. Grundwasser 2017, 22, 83–101. [Google Scholar] [CrossRef]
- Pedretti, D.; Mayer, K.U.; Beckie, R.D. Stochastic Multicomponent Reactive Transport Analysis of Low Quality Drainage Release from Waste Rock Piles: Controls of the Spatial Distribution of Acid Generating and Neutralizing Minerals. J. Contam. Hydrol. 2017, 201, 30–38. [Google Scholar] [CrossRef]
- Müller, S.; Schüler, L.; Zech, A.; Heße, F. GSTools v1.3: A Toolbox for Geostatistical Modelling in Python. Geosci. Model Dev. 2022, 15, 3161–3182. [Google Scholar] [CrossRef]
- Kohfahl, C.; Pekdeger, A. Rising Groundwater Tables in Partly Oxidized Pyrite Bearing Dump-Sediments: Column Study and Modelling Approach. J. Hydrol. 2006, 331, 703–718. [Google Scholar] [CrossRef]
- Schöpke, R. Modeling Water Quality of AMD along the Flow Path. Adv. Environ. Eng. Res. 2023, 4, 23. [Google Scholar] [CrossRef]
- Graupner, B.J.; Koch, C.; Prommer, H.; Werner, F. Process Oriented Quantification of Mine Dump Pollutant Inventories on the Large Scale—The Case of the Lignite Mining District Lusatia, Germany. J. Geochem. Explor. 2012, 112, 161–173. [Google Scholar] [CrossRef]
- Rolland, W.; Wagner, H.; Chmielewski, R.; Grünewald, U. Evaluation of the Long Term Groundwater Pollution by the Open Cast Lignite Mine Jänschwalde (Germany). J. Geochem. Explor. 2001, 73, 97–111. [Google Scholar] [CrossRef]
- Nakaten, B. GEOMODELATOR—A Python Library to Generate Simple Structured 2d+ and 3d Cell-Based VTK Models/Files, Version 1.0; GFZ Data Services: Potsdam, Germany, 2024. [Google Scholar]
- Nakaten, B. GEOMODELATOR—A Python Library to Generate Simple Structured 2.5D and 3D Cell-Based VTK Models/Files with Layer, Fault and Seams as Corresponding Element/Zone Groups for Further Processing or Integrating into a Simulator Framework (TRANSPORTSE), Version 2.0; GFZ Data Services: Potsdam, Germany, 2025.
- Szczepinski, J.; Libicki, J. Modelling of the Bełchatów Open-Pit Impact on the Groundwater Environment. In Proceedings of the IMWA Proceedings 1999, Sevilla, Spain, 13–17 September 1999; pp. 69–77. [Google Scholar]
- Ustrnul, Z.; Marosz, M.; Biernacik, D.; Walus, K.; Chodubska, A.; Wasielewska, K.; Kusek, K. Climate of Poland 2022; Polish Climate Monitoring Bulletin; IMGW-PIB: Warszawa, Poland, 2023. [Google Scholar]
- Lahmira, B.; Lefebvre, R.; Aubertin, M.; Bussière, B. Effect of Heterogeneity and Anisotropy Related to the Construction Method on Transfer Processes in Waste Rock Piles. J. Contam. Hydrol. 2016, 184, 35–49. [Google Scholar] [CrossRef] [PubMed]
- Muniruzzaman, M.; Rolle, M. Multicomponent Ionic Transport Modeling in Physically and Electrostatically Heterogeneous Porous Media with PhreeqcRM Coupling for Geochemical Reactions. Water Resour. Res. 2019, 55, 11121–11143. [Google Scholar] [CrossRef]
- Muniruzzaman, M.; Rolle, M. Relevance of Charge Interactions for Contaminant Transport in Heterogeneous Formations: A Stochastic Analysis. Stoch. Environ. Res. Risk Assess. 2023, 37, 4399–4416. [Google Scholar] [CrossRef]
- Cogorno, J.; Stolze, L.; Muniruzzaman, M.; Rolle, M. Dimensionality Effects on Multicomponent Ionic Transport and Surface Complexation in Porous Media. Geochim. Cosmochim. Acta 2022, 318, 230–246. [Google Scholar] [CrossRef]
- Nordstrom, D.K.; Blowes, D.W.; Ptacek, C.J. Hydrogeochemistry and Microbiology of Mine Drainage: An Update. Appl. Geochem. 2015, 57, 3–16. [Google Scholar] [CrossRef]
- Wisotzky, F. Assessment of the Extent of Sulfate Reduction in Lignite Mining Dumps Using Thermodynamic Equilibrium Models. Water Air Soil Pollut. 1998, 108, 285–296. [Google Scholar] [CrossRef]
- Yu, B. Analysis of Flow in Fractal Porous Media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
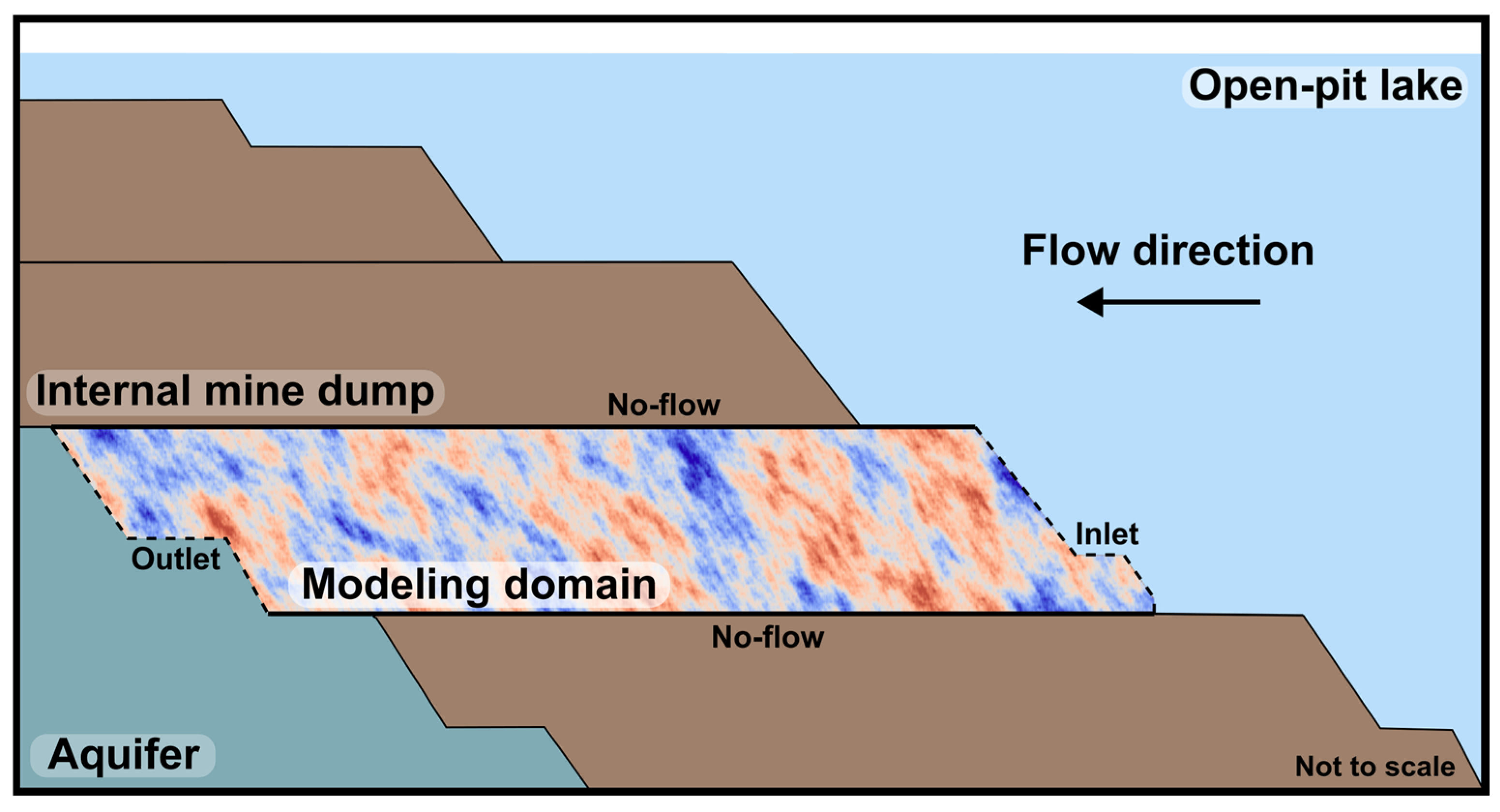
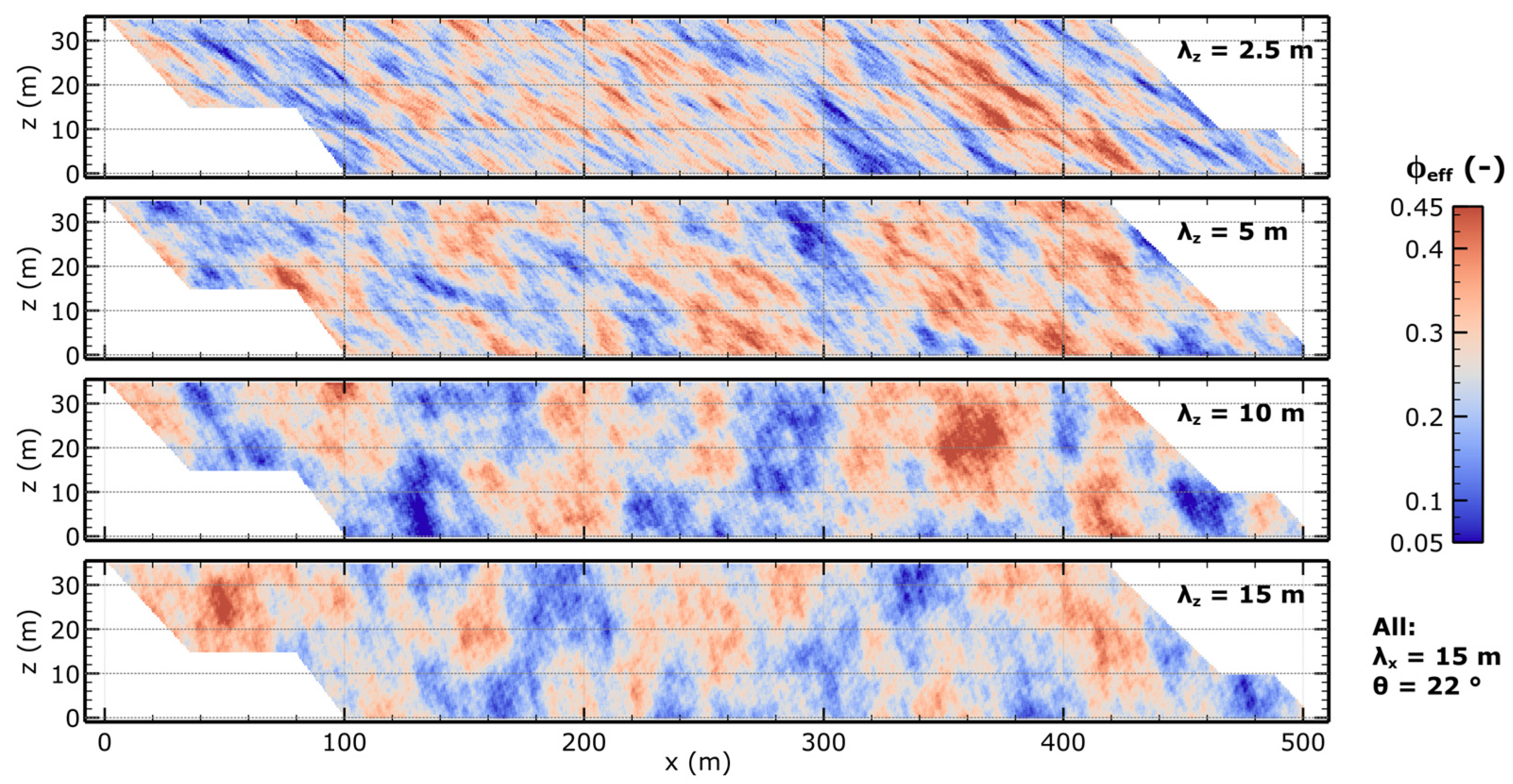
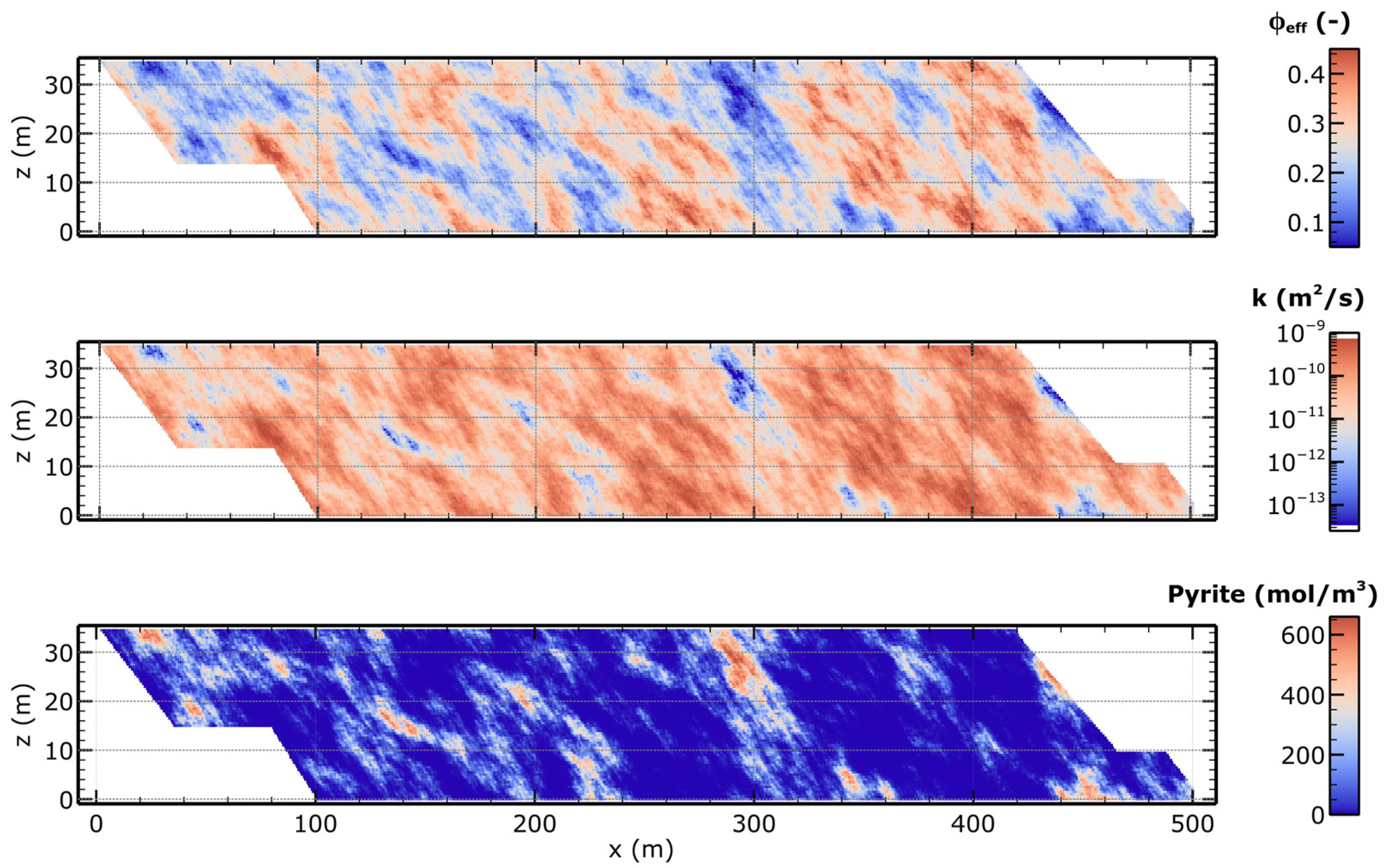
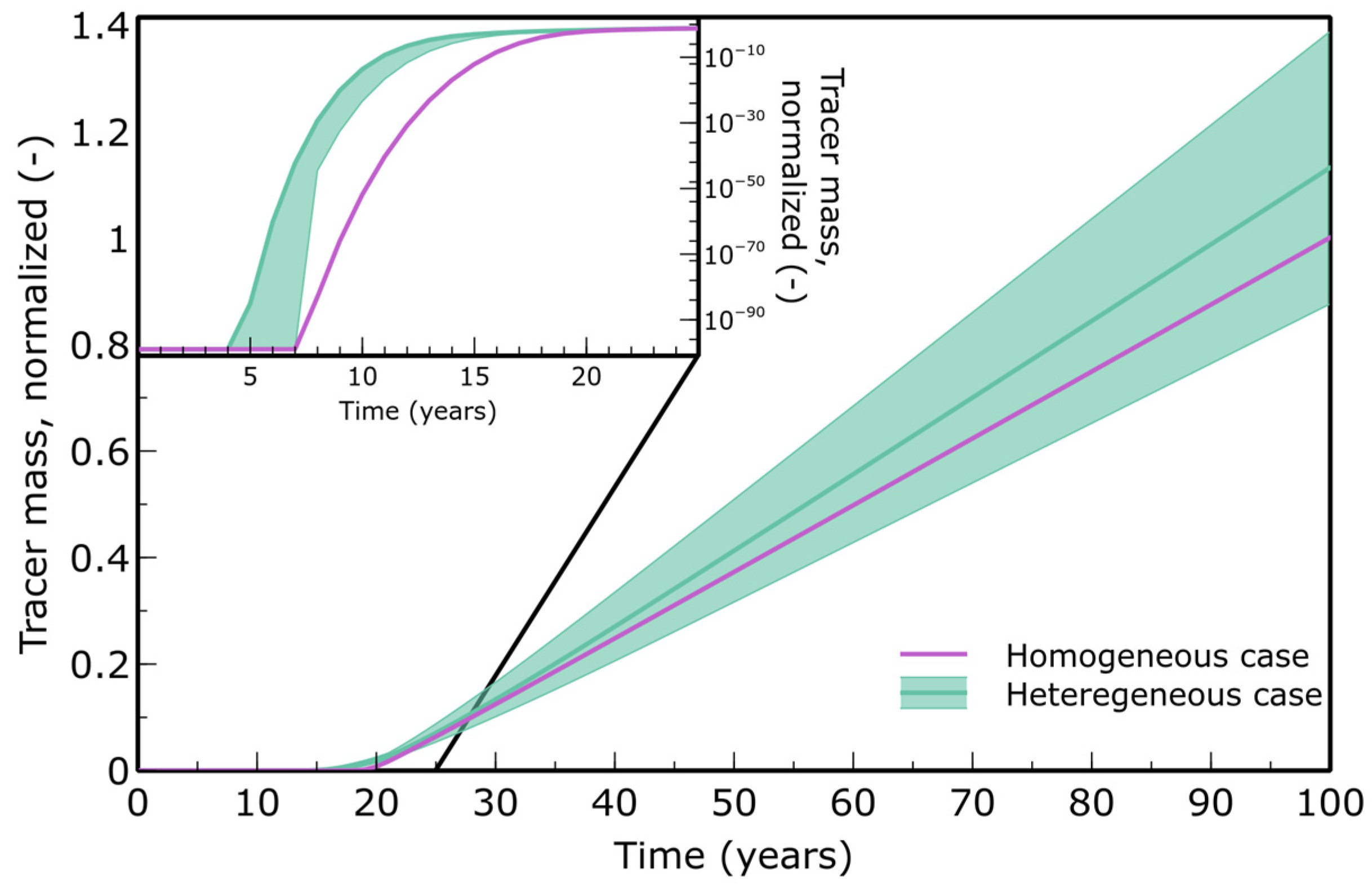
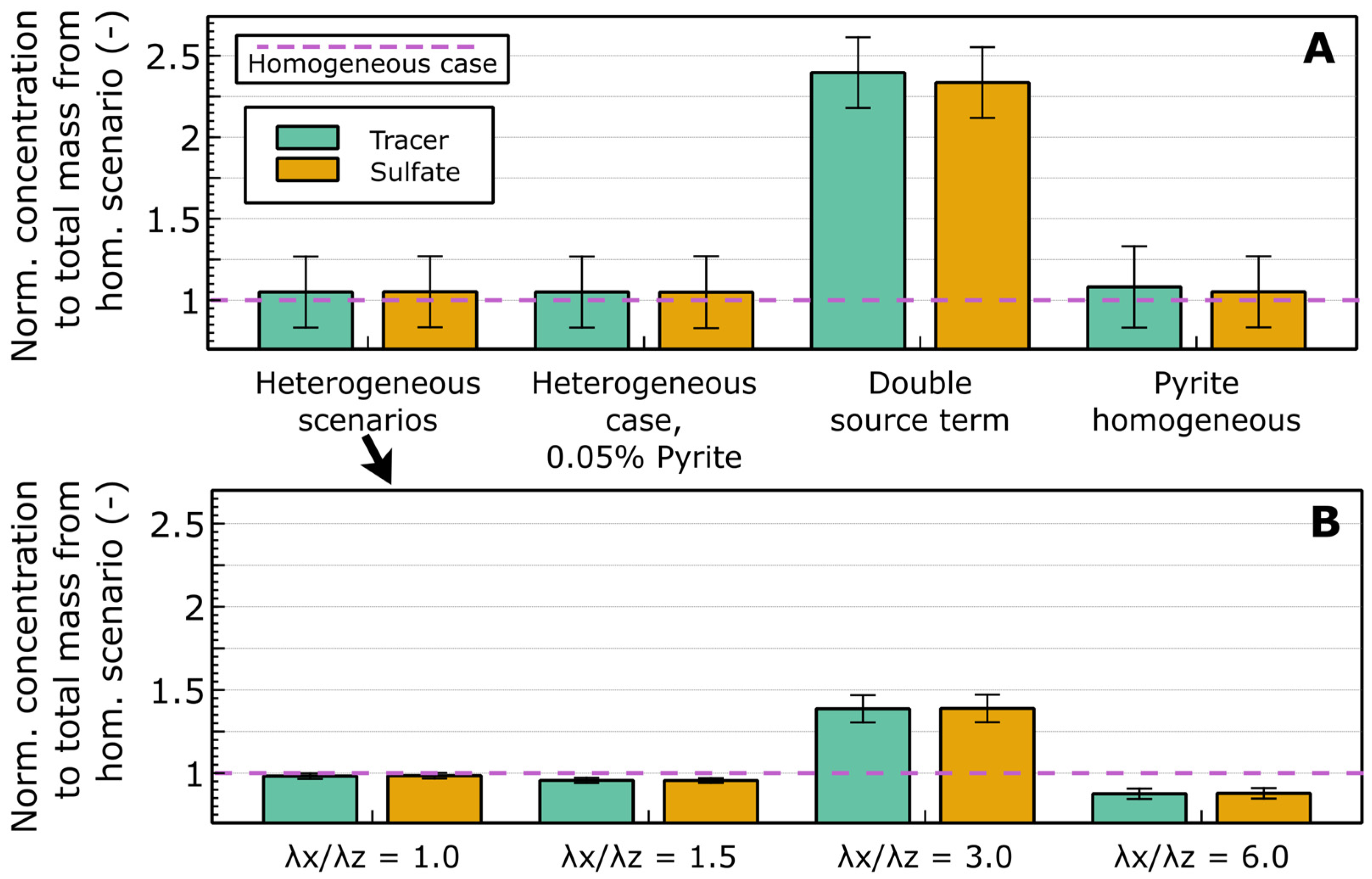
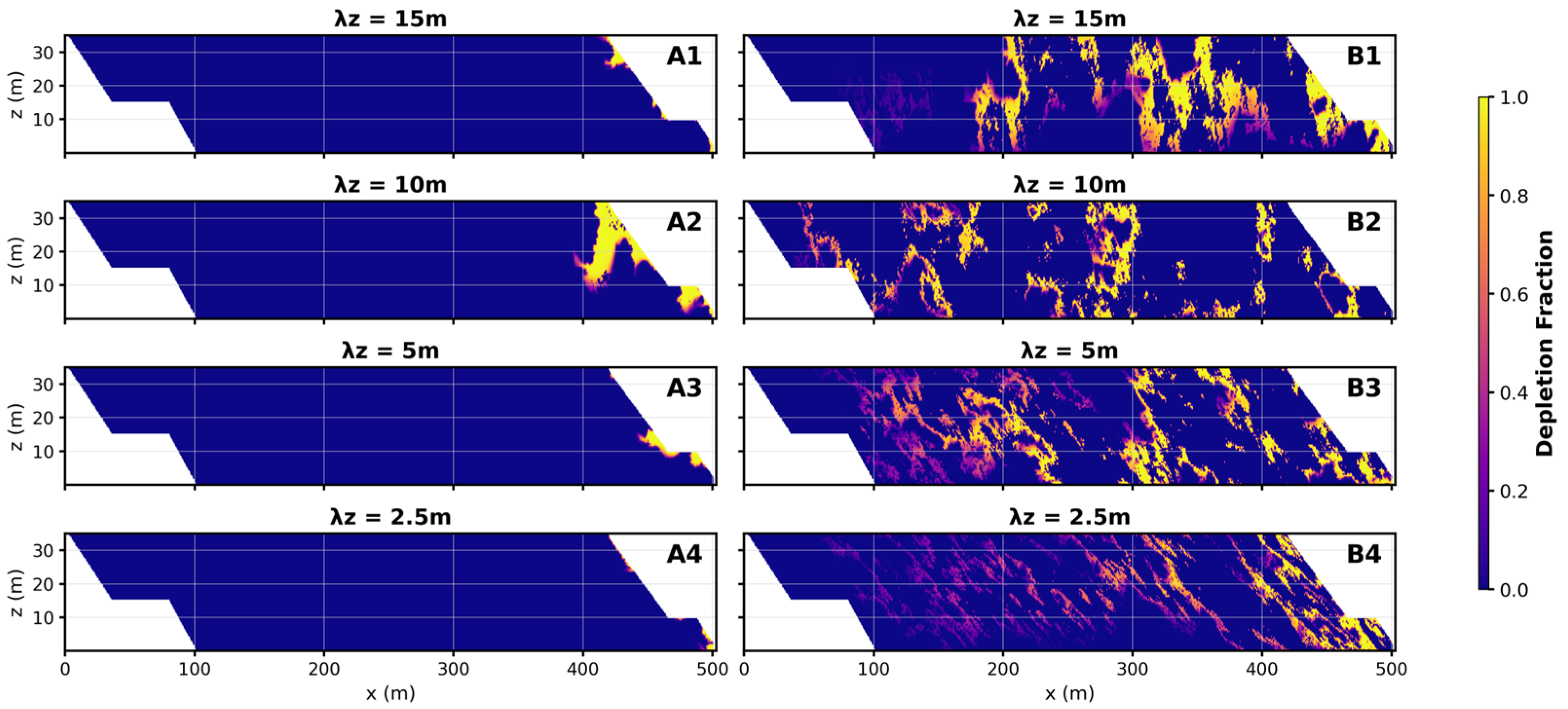

| Parameter | Value | Unit | Source |
|---|---|---|---|
| Domain length (x) | 503 | m | Internal project data |
| Domain length (z) | 35 | ||
| Grid cells (x × z × y) | 1006 × 70 × 1 | - | |
| Cell volume | 0.5 × 0.5 × 1 | m3 | |
| Diffusion coefficient | 2.0 × 10−9 | m2/s | [59] |
| Hydraulic gradient | 0.0036 | - | [65] |
| Average hydraulic conductivity | 1.5 | m/d | [65] |
| Bulk density | 1650 | kg/m3 | [62] |
| Temperature (constant) | 9.1 | °C | [66] |
| Simulation period | 100 | years | |
| Maximum allowed time step size | 2 | days |
| Solution | pH | pe | Ca2+ | Mg2+ | Na+ | K+ | HCO3− | Fe | Cl− | SO42− | O(0) | IBE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | mg/L | % | ||||||||||
| Groundwater | 7.38 | −1.70 | 67.90 | 8.30 | 15.07 | 1.09 | 231.74 | 0.00 | 16.04 | 40.18 | 0.00 | −3.38 |
| Post-mining lake | 7.99 | 14.07 | 101.07 | 8.93 | 13.32 | 1.11 | 99.98 | 0.00 | 14.12 | 210.50 | 11.34 | −0.26 |
| Parameter | Symbol | Value | Unit | Source |
|---|---|---|---|---|
| Correlation length x-direction | λx | 15 | m | Internal project data, derived from the cross-section |
| Correlation length z-direction | λz | 2.5, 5, 10, 15 | m | |
| Depositional angle | θ | 22 | ° | |
| Variance, effective porosity | σ2eff | 0.003, 0.005, 0.007 | - | - |
| Total initial pyrite concentration | 0.05, 0.5 | wt% | [19,22,61] | |
| Maximum pyrite concentration per cell | cmax | 2.5, 5 | wt% | [19] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnepper, T.; Kühn, M.; Kempka, T. Effects of Permeability and Pyrite Distribution Heterogeneity on Pyrite Oxidation in Flooded Lignite Mine Dumps. Water 2025, 17, 3157. https://doi.org/10.3390/w17213157
Schnepper T, Kühn M, Kempka T. Effects of Permeability and Pyrite Distribution Heterogeneity on Pyrite Oxidation in Flooded Lignite Mine Dumps. Water. 2025; 17(21):3157. https://doi.org/10.3390/w17213157
Chicago/Turabian StyleSchnepper, Tobias, Michael Kühn, and Thomas Kempka. 2025. "Effects of Permeability and Pyrite Distribution Heterogeneity on Pyrite Oxidation in Flooded Lignite Mine Dumps" Water 17, no. 21: 3157. https://doi.org/10.3390/w17213157
APA StyleSchnepper, T., Kühn, M., & Kempka, T. (2025). Effects of Permeability and Pyrite Distribution Heterogeneity on Pyrite Oxidation in Flooded Lignite Mine Dumps. Water, 17(21), 3157. https://doi.org/10.3390/w17213157






