Abstract
This study examined the diffusion of nutrients (NH4+, NO3−, and PO43−) in the pore water of intertidal sediments in Lake Komuke (located in the northeastern part of Hokkaido on the coast of Okhotsk Sea) across nine stations, at 0 cm to 40 cm depths, from 19 May to 23 August 2015. A comparison was made between the traditional version of Fick’s first law and a modified version to understand nutrient diffusion in the intertidal flat. The novelty of this study lies in establishing a flux correction factor as a function of the activity coefficient in intertidal sediments. The outcomes of the standard and modified versions of Fick’s law exhibited observable physical differences between stations for all nutrients. However, the statistical analysis demonstrated significant differences only for NO3− and PO43− at stations D, E, and F, suggesting that there is no statistically meaningful difference in NH4+ flux. A statistical comparison of 27 pairs of fluxes obtained by the classical and modified versions of Fick’s first law indicated that 88.9% of the differences were not statistically significant between the two methods, and 11.1% were statistically significant. This shows the consistency of the modified method, firstly in reproducing the classical version of Fick’s law, and secondly in improving upon it, in a porous medium. These findings indicate that the modified version of Fick’s first law is an accurate methodology for evaluating nutrient diffusion dynamics in intertidal environments, and is potentially applicable to coastal salt marshes, with practical implications for environmental management and conservation efforts.
1. Introduction
While coastal areas have recently garnered attention from researchers worldwide [,], the phenomenon of nutrient dynamics in coastal regions, especially in intertidal areas such as Lake Komuke’s intertidal zone, remains relatively underinvestigated []. An intertidal zone is a sandy area that is periodically submerged and exposed due to tidal fluctuations []. Sediments in tidal flat zones play two key roles in nutrient transformation: they act as both a source and a sink for dissolved nutrients, including NH4+, NO3−, and PO43− [,,]. Thus, nutrient exchange processes between the land, sea [], and atmosphere occur continuously in intertidal zones []. Understanding the processes of nutrient diffusion in the intertidal zone is essential for evaluating and predicting nutrient fluxes, and Fick’s first law of diffusion is the most empirical method that explains nutrient diffusion in porous media such as intertidal sediments [,].
In recent decades, intertidal areas have been extensively explored using various methods, including diffusion processes [,], numerical modeling [,,], and analytical solutions [,]. However, despite the existence of multiple approaches to evaluating nutrient flux in coastal zones, the role of the activity coefficient in optimizing this process remains poorly explored. Previous studies have not quantified the effect of the activity coefficient on the nutrient diffusion process in pore water of sediments using Fick’s first law. Instead, most studies assume ideal conditions and apply only concentration gradients and the effective diffusion coefficient without applying corrections that account for the nutrient activity coefficient, despite the variability in soil layers with increasing depth, which has a significant impact on the nutrient diffusion flux in intertidal sediments []. Furthermore, the complexity of the chemical reactions that take place in the redox reaction, along with the biogeochemical processes, ionic interactions, and microbiological activity in tidal flat sediments, has convoluted the traditional version of Fick’s law of diffusion [,,].
To fill the gap in our knowledge, this study aims to evaluate the impact of the activity coefficients of NH4+, NO3−, and PO43− in the pore water of Lake Komuke intertidal flat sediment by applying Fick’s first law of diffusion. The main objectives of this research are (i) to determine the activity coefficient of nutrients in intertidal sediment pore water using the Pitzer model; (ii) to estimate nutrient flux using the standard version of Fick’s law of diffusion; (iii) to estimate nutrient flux based on activity by using the calculated activity coefficient and establishing a modified version of Fick’s first law; (iv) to compare the fluxes of the classical and modified versions of Fick’s law to observe how the activity coefficient affects flux estimation; and (v) to conduct a statistical test to evaluate whether there are significant differences between the two methods. The major contributions of this study are its innovative approach, its field-based quantification of flux differences, and its theoretical formulation with statistical validation. Ultimately, these findings will help us better understand intertidal zones as natural habitats and enhance our insight into coastal ecosystems, biogeochemistry, and environmental management.
2. Materials and Methods
2.1. Study Area and Nutrient Sampling
Lake Komuke, located in northeastern Hokkaido, Japan, at coordinates of 44°14′58′′ N and 143°31′02′′ E, is connected to the Sea of Okhotsk by a human-made canal, resulting in a tidal flat formed due to tidal variations (Figure 1). This study highlights the intertidal zone as a crucial biological habitat for diverse organisms. With this in mind, nine stations were established in a cross-shore orientation, and the nutrient levels in pore water were assessed. It is important to note that this paper focuses on only three stations (D, E, and F) to make it more transparent and easier to understand. Pore water from tidal flats was collected at the nine locations between 19 May and 23 August 2015, utilizing syringes and buried tubes with inlets positioned at depths of 0 to 40 cm at and below the sediment surface. Following the suction and filtration of water samples through mixed cellulose ester filter paper with a pore size of 1 μm, the concentrations of nutrients, total dissolved nitrogen (TDN), and total dissolved phosphorus (TDP) were quantified using a continuous flow analyzer (QuAAtro, produced by SEAL/BLTEC, Osaka Japan). Furthermore, dissolved inorganic nitrogen (DIN: NO3− and NH4+) and dissolved inorganic phosphorus (DIP: PO43−) were measured from +0 cm to −40 cm throughout the specified period.
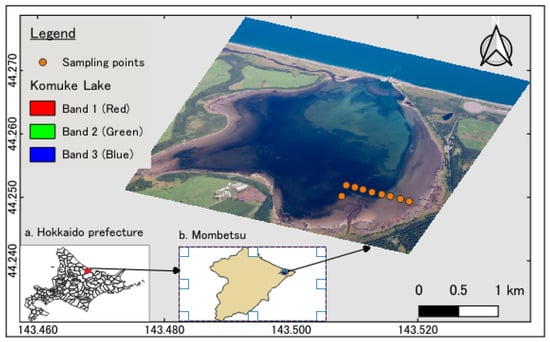
Figure 1.
Lake Komuke and the measurement points.
2.2. Modification of Fick’s First Law of Diffusion
The diffusion process in a porous medium is described by Fick’s first law of diffusion [] as follows:
where J is the flux (mol.m2.s−1); is the effective diffusion coefficient (m2/s); and is the concentration gradient (mol/L/m).
For this investigation, nutrient activity will be utilized rather than concentration, as the activity of a chemical species is equivalent to its real concentration.
Activity is defined by [] as
where is the activity of ion species (mol/L), is the activity coefficient (unitless), and C is the concentration (mol/L).
Since activity is the product of concentration and its activity coefficient, we examine to assess the influence of the activity coefficient on the diffusion process and establish the classical version of Fick’s law.
Then, we have
When considering the activity coefficient as a function of depth, we can assert that
Therefore, we rewrite the flux as follows:
Applying the fundamental principle of derivation, we obtain
The final expression of the modified version of Fick’s first law is as follows:
The specifics of deriving the flux correction factor and the conclusive formulation of the modified version of Fick’s first law are provided in the Appendix A.
2.3. Estimation of Activity Coefficient
The activity coefficients of the ions of interest were determined using the Pitzer model []. This model is based on the Debye–Hückel limiting law [] and is particularly useful in understanding the binary interaction between an anion and a cation, as well as the ternary interaction between two anions and one cation, or between two cations and one anion. In natural water, the activity coefficient is generally expressed as Equation (8).
Therefore, Equations (9)–(11) estimate the activity coefficients of , , and .
here represents the contribution of the Debye–Hückel limiting law. , and the coefficients , , and were determined from the values of , , and for the ions , , and in interstitial seawater of the tidal flat, while , , and were obtained for various ions from [,]. I is the ionic strength, and is the valence of the ion. B, , and C were obtained from the general formulas , , and and account for binary interactions. I is the ionic strength (molality), determined from the data on the salinity of the sediment’s pore water.
where S is the salinity level in pore water (ppt), and the coefficients originated from IUPAC’s Atomic Weights of the Elements 2013 [].
Thus, the activity coefficient as a function of depth, which has physicochemical properties that describe the non-ideal behavior of ion species, was fitted with a quartic polynomial. The quartic function was chosen after testing many functions, including exponential, logarithmic, logistic, sinusoidal, and piecewise functions, as well as polynomial orders two and three. Only the quartic function provided a perfect fit across all stations for the various ion species. Consequently, the quartic polynomial was chosen to fit our data because of its effectiveness in capturing the complex behavior of the depth-dependent activity coefficient. It is important to note that a quartic polynomial can have one to three turning points, where the function changes direction (up and down or down and up) depending on whether there is an increase or decrease in the ionic strength of the medium, which can indicate the behavior of the activity coefficient in sediment pore water.
2.4. Estimation of Effective Diffusion Coefficient, Porosity, and Tortuosity
The parameters used in this study were derived from our data collection and previously published peer-reviewed literature, accurately reflecting the characteristics of our study area. The effective diffusion coefficient is characterized by
where is the effective diffusion coefficient, is the diffusion in free water, is the water content (porosity) of the medium, m is an empirical factor (1–2 for sediment), and T is the tortuosity of the medium (how much the medium deviates from straight diffusion).
To more clearly visualize the contribution of this study, we present a comparative diagram between Fick’s first law and the modified version of Fick’s first law in Figure 2.
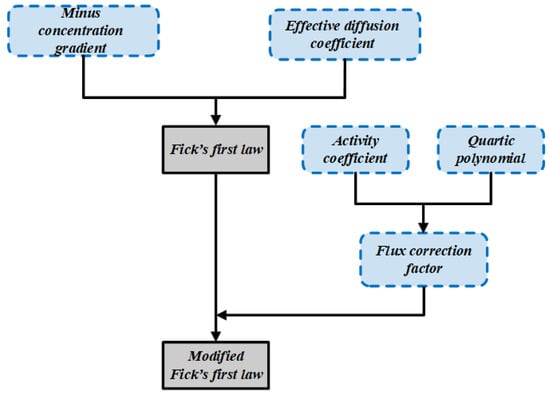
Figure 2.
Comparative diagram of Fick’s first law and the modified version of Fick’s first law.
2.5. Statistical Analysis
A paired-samples t-test was performed, as it is one of the most appropriate tests for comparative studies. In this study, we considered the population to be the estimated nutrient flux at the nine stations at five depth levels for NH4+, NO3−, and PO43−, and a sample was regarded as paired fluxes (nutrient fluxes determined by standard and modified versions of Fick’s first law). Each element population comprised 45 samples; therefore, the overall population was composed of 135 samples for the three ions. Using a specialized Python 3.12 script, we calculated the flux correction factor and flux of the various nutrients. The latter utilized the central method and forward–backward computation at the boundaries.
2.6. Data Analysis
R, OriginPro, Python, QGIS, and Excel were utilized to perform the data analysis. The activity coefficient, which possesses physicochemical properties, was used to fit the quartic polynomial function due to its non-ideal behavior. This enabled us to ascertain the various coefficients of the ions using our proposed method at the different stations. In addition, the dialog box in OriginPro provided an analysis of variance (ANOVA) table, as well as statistical parameters such as the standard error, sum of squared errors, p-value, and mean.
3. Results
This section discusses the outputs of the classical and modified versions of Fick’s first law of diffusion in a porous medium. A flux correction factor was introduced to evaluate the nutrient diffusion in the intertidal sediment’s pore water. We analyzed how the depth-dependent activity coefficient of nutrients affected the determination of diffusion flux by the classical version of Fick’s first law in the sediment’s pore water. Thus, the term “upward diffusion” will refer to negative flux, and the term “downward diffusion” will refer to positive flux throughout the Results and Discussion sections. Our results focused on three representative stations, but the measurements for all nine stations are available in the Supplementary Materials.
3.1. Flux Determination by Classical Version of Fick’s First Law of Nutrient Diffusion
The nutrient flux of NH4+, NO3−, and PO43− across stations D, E, and F at sediment depths of 0 m to 0.4 m, as determined by Fick’s first law of diffusion in a porous medium, is depicted in Figure 3. The flux results from the other stations are provided in the Supplementary Materials. The diffusion of nutrients across intertidal sediments was characterized by exclusive upward diffusion at the three stations. The maximum NH4+ flux, −223.664 μmol/m2/day, was recorded at St_F at the sediment surface (0 m) and exhibited a progressive decline with depth, reaching a minimum of −20.292 μmol/m2/day at a depth of 0.4 m (Figure 3).
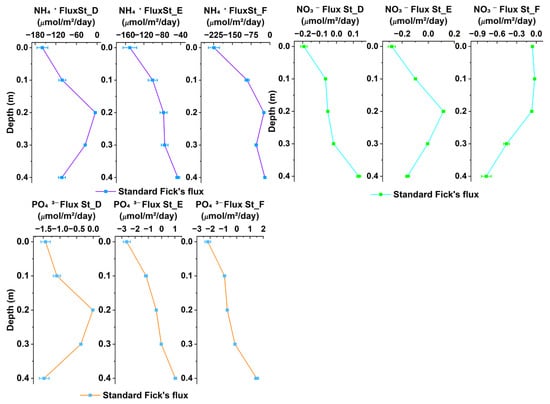
Figure 3.
Distribution of NH4+, NO3−, and PO43− classical flux across stations D, E, and F at intertidal flat sediment depths of 0 m to 0.4 m.
Nitrate diffusion peaked at St_F (0.4 m) with a flux of −0.765 μmol/m2/day, indicating significant upward diffusion flux (Figure 3). The minimum upward flux, −0.00519 μmol/m2/day, was recorded at St_E (0.3 m). In contrast, notable downward diffusion was observed at 0.2 m (St_E), corresponding to a value of 0.116 μmol/m2/day. The Supplementary Materials provide additional details about all of the nutrients for the other stations. PO43− flux was estimated in the same conditions as NH4+ and NO3−, further enriching our understanding of the nutrient diffusion process (Figure 3). The upward diffusion of PO43− was most prominent at three stations, with a peak of −2.628 μmol/m2/day at the sediment surface at St_E. Conversely, the lowest flux was recorded at St_D, with a value of −0.0124 μmol/m2/day at approximately a 0.2 m depth. Positive diffusion flux was observed at St_E and St_F at a maximum depth of 0.4 m, with flux values of 0.10321 μmol/m2/day and 1.493 μmol/m2/day, respectively.
3.2. Modified Version of Fick’s First Law and Its Flux Correction Factor
3.2.1. Flux Correction Factor
Figure 4 shows the results of fitting the activity coefficient using a quartic polynomial across stations D, E, and F for NH4+, NO3−, and PO43− at sediment depths of 0 m to 0.4 m. The fitted activity coefficients, a crucial component of our study, enabled us to calculate the flux correction factor for each ion. The activity coefficient profiles generally follow the same pattern with increasing depth, especially for NH4+ and NO3−, though their values differ. Figure 5 displays the flux correction factors at different depths. The flux correction factor peaked around 0.4 m (St_F) for NH4+, NO3−, and PO43−, with values of 1.048, 1.037, and 1.050, respectively. The lowest values were recorded at St_E (0.4 m) for NH4+, NO3−, and PO43−, with values of 0.937, 0.963, and 0.922, respectively. Details about the activity coefficient and correction factor are available in the Supplementary Materials.
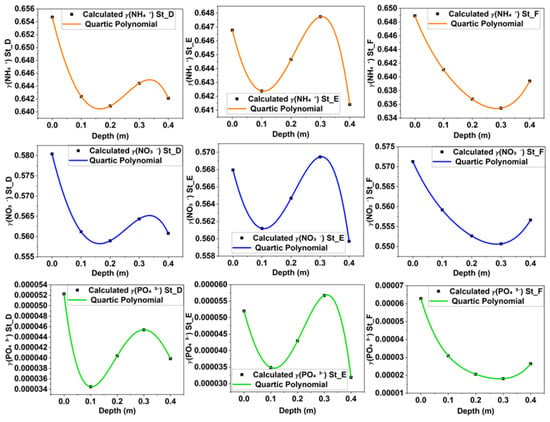
Figure 4.
Depth-dependent NH4+, NO3−, and PO43− activity coefficients fitted by a quartic polynomial function at stations D, E, and F.
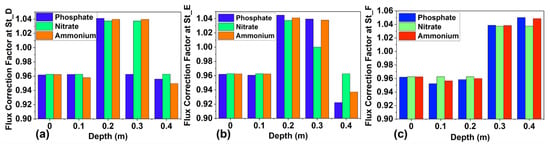
Figure 5.
(a) represent the flux correction factors for NH4+ at St_D, (b) represent the flux correction factor for NO3− at St_E, and (c) represent the flux correction factor for PO43− at St_F, ranging from 0 m to 0.4 m of depths.
3.2.2. Modified Version of Fick’s First Law of Nutrient Flux
The flux results from the modified version of Fick’s first law were compared to those of the standard version to evaluate their correlation and identify statistically significant differences due to variations in the activity coefficient. Figure 6 depicts the changes in NH4+ flux profiles from St_D to St_F across sediment depths (0 m to 0.4 m). The NH4+ fluxes obtained using the modified and standard versions of Fick’s law are expressed in μmol/m2/day to illustrate the effect of the correction factor. The diffusion of NH4+ occurred solely in the upward direction for both methods. High flux occurred at St_F (0 m), with values of −215.271 μmol/m2/day for the modified version of Fick’s law and −223.664 μmol/m2/day for the standard version. The statistical analysis revealed a p-value of 0.34, suggesting no statistically significant difference between the modified and classical versions of Fick’s first law at St_F. Figure 7 presents a comparison of the vertical profiles of NO3− diffusion flux (μmol/m2/day) obtained across five depth levels (0 m to 0.4 m) in intertidal sediments utilizing both methods. NO3− was observed globally to diffuse in upward and downward directions, with a predominance of negative diffusion across the three stations, as displayed in Figure 7. Our paired-samples t-test indicated a significant difference between the results obtained using the standard and modified versions of Fick’s law at St_E (p-value = 0.045). The vertical PO43− diffusion flux was estimated at St_D, St_E, and St_F, as presented in Figure 8. Upward diffusion was found at all stations, with a maximum flux of −2.628 μmol/m2/day obtained at St_E (0 m) using the standard version of Fick’s law, and of −2.528 μmol/m2/day using the modified version. The statistical comparison demonstrated moderate differences at St_D and St_F, with p-values of 0.047 for both.
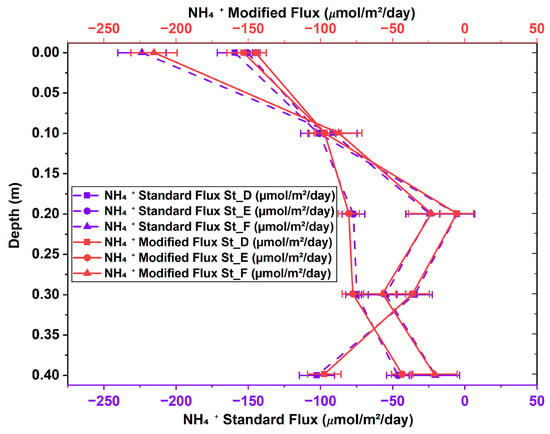
Figure 6.
NH4+ diffusion flux determined using modified and standard versions of Fick’s first law across stations D, E, and F at intertidal sediment depths of 0 to 0.4 m.
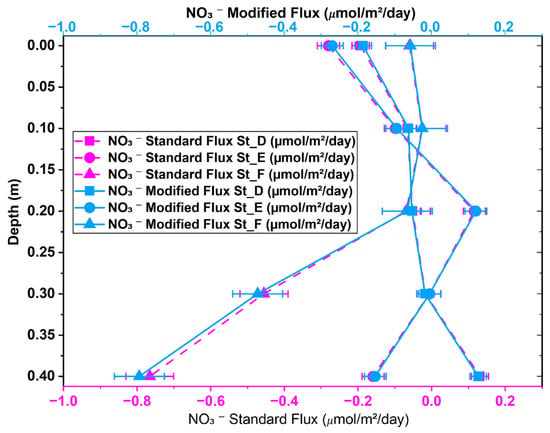
Figure 7.
NO3− diffusion flux obtained using modified and standard versions of Fick’s first law across stations D, E, and F at intertidal sediment depths of 0 to 0.4 m.
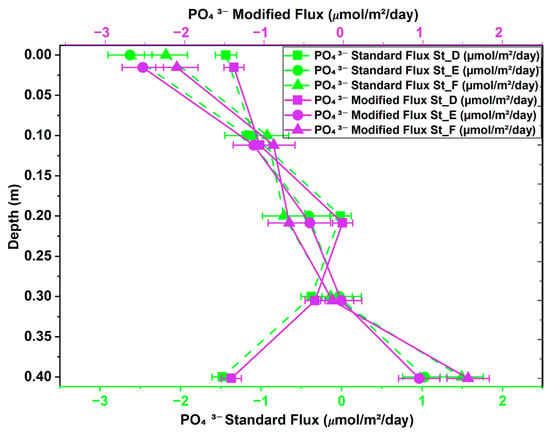
Figure 8.
PO43− diffusion flux obtained using modified and standard versions of Fick’s first law across stations D, E, and F at intertidal sediment depths of 0 to 0.4 m.
4. Discussion
This study analyzed Fick’s first law of nutrient diffusion flow in porous media, such as intertidal zones. It proposed a revised version of Fick’s first law of nutrient diffusion that accounts for the non-ideality of particles in sediment pores and incorporates a physicochemical parameter, namely the activity coefficient. A flux correction factor, derived from the activity coefficient, was implemented to amend Fick’s first law of diffusion. The original version of Fick’s law eventually failed to account for the significant physicochemical parameters that influence nutrient mobility in porous media.
4.1. Thermodynamic and Physicochemical Interpretation of the Activity Coefficient
The activity coefficient variations for NH4+, NO3−, and PO43− ions at stations D, E, and F exhibited polynomial-type profiles, as validated by statistical analyses. Figure 4 depicts the fitted activity coefficients of the three ions using a quartic polynomial function. The change in activity coefficient affected nutrient behavior across locations and depths due to changes in ionic strength. In fact, high ionic strength significantly influenced ionic interactions and pairing in a saline medium, causing nutrients in the mixture to behave non-ideally. Nutrient diffusion in pore water or sediment medium is reliant not solely on the concentration gradient, as posited by Fick’s law, but instead on the nutrients’ activity, which characterizes their effective behavior within a natural sedimentary environment. In a natural system, nutrients do not behave as they would in ideal conditions, such as in a dilute solution where all factors are controlled. Instead, non-ideal behavior dominates in ion species due to electrostatic interactions, ion pairing, and highly reactive reactions caused by changes in the activity coefficient driven by ionic strength. For example, in saline areas like intertidal flats and estuaries, the abundance of major ions like sodium (), chloride (), sulfate (), and potassium () can influence the behavior of minor ions, causing their activity coefficients to deviate from ideal values. Therefore, electrostatic shielding and ionic competitive binding can reduce their mobility in the medium, especially during significant fluctuations in salinity and ionic strength. Ignoring the activity coefficient when accurately estimating nutrient flux in high-salinity coastal environments can lead to over- or underestimation of nutrient flux. In this study, the NH4+ activity coefficient peaked at St_D (0 m), with a value of 0.655, suggesting that ionic strength was lower at other stations and depths (0.634 at St_F (0.3 m), for example). The activity coefficients at St_D, St_E, and St_F were slightly elevated compared to those reported in prior research []. This high activity coefficient could be attributable to variations in ionic strength within the pore water and to the low salinity at St_D. Indeed, past studies [,] have utilized ionic strengths in the order of 0.7 to 0.8 molality, while in our study, the ionic strength at St_D was 0.539 molality, which likely increased the activity coefficient. At St_I (cf Supplementary Materials), the lower activity coefficient of 0.624 around a depth of 0.3 m corresponded precisely with values reported in previous investigations [,], with an ionic strength of 0.86 molality. The fluctuations in the activity coefficient of NH4+ ions may be correlated with ionic interactions and pairing within the pore water of sediments, attributed to the influx of seawater from the Okhotsk Sea into the lake. The nitrate activity coefficient varied between 0.580 at St_D and 0.550 at St_F at depths of 0 m and 0.3 m, respectively. These values are perfectly situated between the values of 0.530 and 0.598 reported in [] and [], respectively. However, they are relatively lower than the values reported in [,]. These differences are due to the change in the ionic strength of pore water with depth and the physicochemical interactions of ions. Moreover, a significant increase in ionic strength induces a change in the activity coefficient []. The PO43− activity coefficient was fitted using a quartic polynomial function. The highest activity coefficient was observed at St_D (0.000104) near the surface (0 m), while the lowest was recorded at St_F (1.81 × 10−5) in the deeper sediment layer (0.3 m). Our results globally align with those documented by [,,] at stations D, E, and F at various depth levels. The elevated activity coefficient is attributed to the weak ionic strength (0.539 molality) resulting from the weak salinity (26.3 ppt) at this station. In contrast, the low activity coefficient is attributed to high ionic content (0.72 molality) resulting from the high salt concentration (35.1 ppt) at St_F. Thus, increased ionic strength can disrupt the electrostatic interactions between PO43− ions and sediment surfaces, leading to desorption and the release of PO43− into the water []. Consequently, the fluctuations in activity coefficients associated with the effects of ionic strength implicitly affected the concentration gradient of nutrients, thereby influencing nutrient flux across various locations and depths. According to [,], the adsorption capacity of chitosan and microalgae can decrease as the ionic strength increases.
4.2. Correction Factor and Flux Estimation Across Depths
Figure 5 presents a comparative bar chart illustrating the flux correction of NH4+, NO3−, and PO43− for enhanced visibility and comprehension of our findings. The figure shows variation in the correction factor of around one, typically indicating non-ideal nutrient flux behavior. Previous studies have also highlighted the inconsistency of Fick’s first law in capturing nutrient flux in pore water [,]. This study highlights the significance of correcting flux in environmental sediment studies, as such corrections have modestly improved standard flux-estimation methods in 11.1% of the cases. The extrema of the flux adjustment parameter for NH4+ were measured at St_F (0.4 m), with a numerical value of 1.048 (Figure 5a). This maximum flux correction ratio enhanced NH4+ diffusion at this specific location, indicating that the flux was underestimated by the standard Fickian diffusion model, as indicated by [,]. The peak of the NH4+ flux correction factor at St_F (0.4 m) indicates that the pore water at this station undergoes NH4+ remineralization due to an increase in ionic strength. Indeed, in the bottom sediments, NH4+ and ionic strength interact through adsorption and desorption, which influence nitrogen cycling and mobility []. Additionally, elevated ionic strengths can reduce adsorption and increase NH4+ levels in pore water. The minimum adjustment coefficient was recorded at St_E (0.4 m), with a numerical value of 0.937. The lower value of the flux correction factor of NH4+ limits its diffusion flux, leading to an overestimation of its diffusion flux at that point because the activity coefficient is ignored. Fick’s law, which overestimates NH4+ flux in interstitial water, was described in the Swan–Canning Estuary (Western Australia) by []. Nitrogen overestimation is driven by both aerobic and anaerobic conditions, particularly when redox reactions are present in the medium. In our study, the correction factor for NO3− varied across stations and depths, ranging from 1.0374 to 0.963 (Figure 5b). The most significant correction ratio is 1.0374 at St_F, indicating that NO3− flux is elevated at this specific station. However, the standard version of Fick’s law underestimated the NO3− diffusion flux, as indicated by the adjustment coefficient. The minimal NO3− flux adjustment parameter was recorded at St_D at 0 m and 0.4 m depths. The low flux correction factor (0.963) implies that flux is impeded at these stations, leading flux to be overrated under the classical version of Fick’s first law of diffusion. Consequently, we proposed a flux adjustment factor that modestly improved the estimation of the standard version of Fick’s law, particularly in intertidal zones where salinity is prevalent. From a global perspective, NO3− flux correction remained relatively consistent at about one, indicating that NO3− exhibits cautious behavior and has limited retention in the interstitial waters of intertidal flats. However, previous studies have identified situations where NO3− flux was either under- or overestimated, taking into account bioturbation conditions and whether the environments were anoxic and oxic [,]. The PO43− correction factor is shown alongside NO3− and NH4+ in Figure 5c, with a maximum of 1.050 observed at 0.4 m (St_F), and a minimum value of 0.922 recorded at St_E (0.4 m). The high PO43− correction ratio implies that the PO43− flux at St_F was underestimated due to the exclusion of the flux adjustment factor in the process. Indeed, underestimation of PO43− flux by Fick’s first law has been documented in previous studies, such as []. The elevated flux adjustment coefficient of PO43− at St_F (0.4 m) reflects a common occurrence in sedimentary environments experiencing iron reduction, which facilitates the release of PO43− ions into the pore water [,]. The fact that the lowest flux correction factor was obtained for these ions shows that the PO43− flux was overestimated at St_E because the flux calculation ignored the activity coefficient at about a 0.4 m depth. A study conducted on the Tancarville mudflat in Normandie (France) demonstrates that Fick’s law overlooks kinetic limitations and dynamic sediment reactivity, resulting in overestimation of instantaneous PO43− release during resuspension [].
This study demonstrated that the biogeochemical conditions of specific nutrients necessitate the incorporation of a flux correction parameter to prevent over- or underestimating the actual nutrient flux within the sediment matrix. Thus, past research has shown that depending on whether conditions are anoxic or oxic, the Fickian model may under- or overestimate nutrient flux [,,]. We found that our modified version of Fick’s first law, incorporating the activity coefficient, which was proposed to more accurately predict nutrient transport dynamics in sediments and their overlying water, will yield more precise chemical and physical diffusion flux values in dynamic environments, such as the intertidal zone of Lake Komuke’s coastal wetlands.
4.3. Statistically Significant Differences Between the Standard and Modified Flux
A statistical analysis demonstrated the significance of incorporating the nutrient activity coefficient into the diffusion flux process, highlighting the differences between the performance of the standard and modified versions of Fick’s first law of diffusion. A paired-samples t-test was conducted to compare the performance of the standard and modified versions in estimating the diffusion of NH4+, NO3−, and PO43−. The statistical comparison of the performance of the standard and modified versions of the Fickian model in determining the diffusion flux of NH4+ (Figure 6) revealed no significant differences, despite the observed physical variations. Consequently, the classical and modified versions of Fick’s first law across various stations were deemed statistically comparable after applying a flux correction ratio at a 95% confidence level. Stations D, E, and F demonstrated a p-value exceeding 0.05, as shown in Appendix B (Table A1). These statistically non-significant differences may be attributed to the small sample size of the stations and certain physical conditions, including bioturbation, tortuosity, microscale differences in porosity, and variations in organic matter content []. Our findings underscore that biogeochemical processes, ionic interactions, pairing, and redox reactions in the sediment’s pore water do not influence NH4+ diffusion. Therefore, Fick’s law does not require the NH4+ flux adjustment factor for slight variations in the activity coefficient. The paired-samples t-test for NO3− revealed a statistically significant difference at St_E (Appendix B, Table A2) and Figure 9b. This highlights the importance of an adjustment coefficient in addressing diffusion singularities, such as areas with significant ionic interactions and activity coefficient fluctuations resulting from enhanced ionic strength or other biogeochemical processes. Indeed, NO3− flux in pore water can be significantly influenced by ionic strength, which affects its mobility and interactions with the soil medium. Higher ionic strength can boost NO3− flux by reducing electrostatic interactions between NO3− and soil particles, whereas lower ionic strength can decrease flux due to stronger attraction and retention []. Our t-test for PO43− (Appendix B, Table A3) demonstrated statistically significant differences at two stations, St_D and St_F, with p-values of 0.0473 and 0.0468, respectively. A 95% confidence level was not achieved for most stations, indicating that the performance of the standard and modified versions of Fick’s law was comparable (Appendix B, Table A3). The effect of incorporating a flux correction factor to account for unusual nutrient behavior in Fick’s first law of diffusion is statistically significant, as illustrated in Figure 9c. This facilitated the identification of regions exhibiting significant activity coefficient fluctuations or chemical interactions resulting from heightened ionic strength or increased empirical porosity factors. The significant variation in physicochemical conditions, such as salinity or ionic strength, at St_D and St_F affects the flux calculated using the modified version of Fick’s law, either increasing or decreasing it. This fluctuation, which is only a part of the modified version of Fick’s law, created a gap between the flux values obtained using the standard and modified models, resulting in a notable difference in PO43− flux at St_D and St_F. Some of the direct effects of changes in salinity and ionic strength are fluctuations in the activity coefficient and increased ionic shielding within the sediment matrix, which decrease PO43− mobility and, consequently, its flux. This explains why in high-salinity areas, zones with high ionic strength, or locations with reduced iron, the nutrient flux differs significantly between the two methods, leading to statistically significant differences at St_D and St_F. Furthermore, in anoxic-sediment regions, iron ions predominate, and their abundance facilitates reactions with PO43− ions to form an insoluble mineral called vivianite []. However, under oxidized redox conditions, vivianite dissolves, releasing PO43− ions back into the pore water [,]. This reverse reaction in anoxic environments causes the PO43− flux calculated by the modified version of Fick’s law to fluctuate considerably. Therefore, the dominance of high salinity, high ionic strength, and anoxic conditions results in non-ideal PO43− behavior in the sediment, leading to unbalanced fluxes between the traditional and modified versions of Fick’s law, leading to statistically significant differences in PO43− ion flux at these locations. Our findings underscore the need to revise the classical version of Fick’s first law of diffusion in the case of sediment pore water, emphasizing the significant impact of ionic strength, biochemical conditions, sediment structure, and biogeochemical processes.
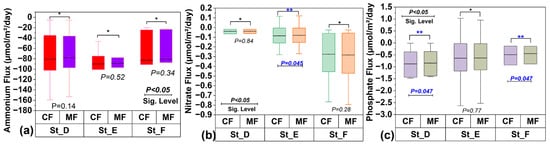
Figure 9.
(a) Pair comparison of classical and modified Fick’s first law flux for NH4+ at St_D, St_E, and St_F; (b) pair comparison of classical and modified Fick’s first law flux for NO3− at St_D, St_E, and St_F; and (c) and pair comparison of classical and modified Fick’s first law flux for PO43− at St_D, St_E, and St_F.
5. Conclusions
This study provides a physically and thermodynamically refined framework for estimating nutrient diffusion fluxes in sediment pore water, particularly in dynamic environments such as intertidal zones and brackish wetlands. By incorporating activity coefficients, the model reduces the risk of over- or underestimating nutrient fluxes in high-salinity and high-ionic-strength systems. The standard version and a modified version of Fick’s first law were employed to quantify and compare the diffusion fluxes of NH4+, NO3−, and PO43− in intertidal zones across nine stations, with a focus on stations D, E, and F, at five different depths. The revised version of Fick’s law was predicated on a novel parameter called the activity coefficient. The results of the comparison of the two methodologies exhibited certain physical discrepancies. A statistical test was performed to verify the observable physical differences, with three of the nine sites demonstrating a substantial disparity between the results obtained by the two approaches for NO3− and PO43− ions. St_E exhibited a meaningful difference in NO3− flux, with a p-value of 0.0454. Additionally, St_D and St_F showed a statistically significant difference in PO43− flux, with p-values of 0.0472 and 0.0468, respectively. The findings for NH4+ flux did not reveal any statistically meaningful variations across stations. This study emphasizes the need to use a correction factor associated with the activity coefficient to account for the atypical behavior of nutrients in sediment pore water, especially in regions where sediments have increased ionic strength, such as coastal salt marshes and semi-arid regions with saline pore water. This highlights the inadequacy of relying exclusively on Fick’s first law to estimate the nutrient flux of pore water in sediments, and underscores the necessity of introducing a correction ratio into Fick’s first law to enhance the accuracy of flux calculations. These improvements will improve the reliability of environmental monitoring data and numerical models, offering a more realistic basis for managing nutrient loading. Moreover, the findings of this study can be utilized to establish strategies for managing and protecting intertidal flat ecosystems, therefore helping to preserve the biodiversity and sustainability of these essential habitats.
Despite the rigorous methodology employed in this study, which yields significant results concerning the modified version of Fick’s first law, several limitations should be acknowledged for consideration in future research.
Firstly, although we adhered to a rigorous estimation procedure, the activity coefficient data were derived not from direct in situ measurements but from calculations based on ionic strength data. Future research should employ in situ-based activity coefficients to reduce uncertainties in the flux correction factor and flux estimation.
Secondly, this study focused solely on NH4+, NO3−, and PO43−, excluding other variables such as dissolved oxygen, dissolved organic carbon, trace metals, or silica, which could complicate and obscure the transport of nutrients due to complex chemical reactions and interactions, including redox reactions and kinetic reactions.
Thirdly, the diffusion process in sediment pore water often does not account for phenomena such as sorption, microbial activity, or precipitation and dissolution processes, which are prevalent in wetlands. The introduced flux correction factor fails to account for these phenomena. Thus, future research should focus on models that integrate reactive transport with diffusion flux to enhance the accuracy of nutrient predictions in pore water.
Additionally, the modification of Fick’s first law should be extended to Fick’s second law by including a flux adjustment parameter to examine the effect of temporal variation on nutrient mobility in the sediment matrix.
Finally, the depth profile resolution should be modified to accommodate minor fluctuations of one or two centimeters in the nutrient cycle, thereby enhancing the precision of the results. The same approach may also be applied to other unexplored geomorphological, hydrological, and biogeochemical zones to further clarify the applicability of the modified version of Fick’s law.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w17202958/s1, the supplementary figures are contained in this manuscript: Activity coefficient at station A, B, C, G, H, I (Figure S1), Flux correction factor at station A, B, C, G, H, I (Figure S2), Distribution of nutrient classical flux at station A, B, C, G, H, I (Figure S3), Diffusion flux obtained using modified and standard Fick’s first law across A, B, C, G, H, I at intertidal sediment depths of 0 to 0.4 m (Figure S4), Comparison of NH4+, NO3−, and PO43− flux values obtained using the classical and modified versions of Fick’s first law across stations A, B, C, G, H, I (Figure S5).
Author Contributions
M.S.A. and K.K.: conceptualization and methodology. M.S.A.: software, validation, formal analysis, and investigation. K.K.: resources. M.S.A.: data curation, writing—original draft preparation. M.S.A. and K.K.: writing—review and editing, and visualization. K.K.: supervision. M.S.A. and K.K.: funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The field observations used in this study were conducted with the support of the Grant-in-Aid for Scientific Research (C) from the Japan Society for the Promotion of Science (JSPS), Project No. 15K00514, entitled “Improvement of environmental dynamics analysis of river basin using specific substance information in cold region.” The first author, Abdoulkader Moussa Siddo, was financially supported by the JICA SDGs Global Leader Program during his doctoral studies at the Kitami Institute of Technology, Japan.
Data Availability Statement
The original contributions presented in this study are included in the article. For further inquiries, please contact the corresponding author.
Acknowledgments
Part of the dataset used in this study was obtained from field and laboratory work conducted in 2015 and 2016 by T. Takeuchi, a former student of Kitami Institute of Technology, to whom the authors express their sincere appreciation.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CF | Classical Fick |
| MF | Modified Fick |
| FCF | Flux Correction Factor |
| St | Station |
Appendix A. Introduction of Flux Correction Factor
To rectify the conventional Fickian flux model, Equation (6) is divided by its initial term on the right-hand side on both sides.
Let us call the left-side term A.
The primary aim of this study is to assess the influence of the activity coefficient on the diffusion process as a function of depth. Thus, we presume that the flux correction factor deviates from unity and exclusively focuses on the activity coefficient gradient when ascertaining the flux correction factor.
Consequently, Equation (A2) becomes
Therefore, we express the modified flux as the product of the effective diffusion coefficient, the activity coefficient, and the variable A as follows:
Finally, we define the flux correction factor as
The corrected flux is finally written as follows:
The function f must be defined. Subsequent fits revealed that it is an ideal polynomial function of degree 4.
where
- ▪
- , , , , and are the coefficients;
- ▪
- Z is the variable (accounting for depth in m);
- ▪
- 0, 1, 2, 3, and 4 are the degrees.
Following the calibration of the depth-dependent activity coefficient, distinct coefficients for various ions were established for each station.
Consequently, Equations (A3) and (A7) are incorporated into Equation (A5) to obtain the flux correction expression. And equation (A5) is introduced into Equation (A6) to get the final expression of the modified version of Fick’s first law (Equation A10).
Appendix B. Statistical Test Results

Table A1.
Statistical comparison of ammonium flux values obtained using classical and modified versions of Fick’s law.
Table A1.
Statistical comparison of ammonium flux values obtained using classical and modified versions of Fick’s law.
| Stations | Mean Flux Obtained Using Standard Method | Mean Flux Obtained Using Modified Method | Mean Difference in Flux | t-Value | Significance (p-Value < 0.05) |
|---|---|---|---|---|---|
| St_A | −3.63775 | −3.52471 | −0.11303 | −1.85913 | 0.13654 * |
| St_B | −6.25899 | −6.28696 | 0.02796 | 0.15384 | 0.88519 * |
| St_C | −6.96629 | −6.79534 | −0.17095 | −1.01444 | 0.36775 * |
| St_D | −3.36033 | −3.24471 | −0.11562 | −1.85787 | 0.13674 * |
| St_E | −3.74747 | −3.69467 | −0.05281 | −0.70432 | 0.52008 * |
| St_F | −3.45166 | −3.36634 | −0.08532 | −1.08316 | 0.33967 * |
| St_G | −3.96171 | −3.98111 | 0.01939 | 0.08736 | 0.93458 * |
| St_H | −4.10228 | −3.98201 | −0.12026 | −0.62248 | 0.56735 * |
| St_I | −3.15966 | −3.01441 | −0.14525 | −0.92015 | 0.40957 * |
Note: One asterisk (*) means there is no statistically significant difference between the values obtained by the standard and modified versions of Fick’s first law.

Table A2.
Statistical comparison of nitrate flux values obtained using classical and modified versions of Fick’s law.
Table A2.
Statistical comparison of nitrate flux values obtained using classical and modified versions of Fick’s law.
| Stations | Mean Flux Obtained Using Standard Method | Mean Flux Obtained Using Modified Method | Mean Difference in Flux | t-Value | Significance (p-Value < 0.05) |
|---|---|---|---|---|---|
| St_A | −0.0033 | −0.00319 | −1.10 × 10−4 | −2.12125 | 0.1012 * |
| St_B | −7.57 × 10−5 | 8.71 × 10−6 | −8.44 × 10−5 | −1.66061 | 0.17213 * |
| St_C | 9.91 × 10−5 | 9.34 × 10−6 | 8.97 × 10−5 | 1.18873 | 0.3003 * |
| St_D | −0.00163 | −0.00161 | −1.80 × 10−5 | −0.20977 | 0.8441 * |
| St_E | −0.00356 | −0.00336 | −2.03 × 10−4 | −2.87125 | 0.04541 ** |
| St_F | −0.01146 | −0.01179 | 3.32 × 10−4 | 1.25809 | 0.27679 * |
| St_G | −0.00965 | −0.00957 | −8.57 × 10−5 | −0.45648 | 0.67173 * |
| St_H | −0.00103 | −9.49 × 10−4 | −8.57 × 10−5 | −1.02396 | 0.36374 * |
| St_I | −0.00264 | −0.0026 | −3.90 × 10−5 | −0.14799 | 0.88951 * |
Note: Two asterisks (**) mean there is a statistically significant difference between the values obtained by the standard and modified versions of Fick’s first law. Note: One asterisk (*) means there is no statistically significant difference between the values obtained by the standard and modified versions of Fick’s first law.

Table A3.
Statistical comparison of phosphate flux values obtained using classical and modified versions of Fick’s law.
Table A3.
Statistical comparison of phosphate flux values obtained using classical and modified versions of Fick’s law.
| Stations | Mean Flux Obtained Using Standard Method | Mean Flux Obtained Using Modified Method | Mean Difference in Flux | t-value | Significance (p-value< 0.05) |
|---|---|---|---|---|---|
| St_A | −4.56 × 10−2 | −4.63 × 10−2 | 6.73 × 10−4 | 0.47037 | 0.66259 * |
| St_B | −4.71 × 10−2 | −4.67 × 10−2 | −4.08 × 10−4 | −0.32236 | 0.76332 * |
| St_C | −6.08 × 10−2 | −5.87 × 10−2 | −2.12 × 10−3 | −1.43809 | 0.22379 * |
| St_D | −3.66 × 10−2 | −3.52 × 10−2 | −1.46 × 10−3 | −2.83111 | 0.04729 ** |
| St_E | −2.67 × 10−2 | −2.63 × 10−2 | −3.88 × 10−4 | −0.30687 | 0.77425 * |
| St_F | −2.05 × 10−2 | −1.86 × 10−2 | −1.88 × 10−3 | −2.84086 | 0.04683 ** |
| St_G | −1.19 × 10−2 | −1.05 × 10−2 | −1.38 × 10−3 | −1.26816 | 0.27353 * |
| St_H | 4.18 × 10−5 | 3.85 × 10−5 | 3.29 × 10−6 | 0.55703 | 0.6072 * |
| St_I | 1.60 × 10−3 | 1.72 × 10−3 | −1.16 × 10−4 | −0.99619 | 0.37554 * |
Note: Two asterisks (**) mean there is a statistically significant difference between the values obtained by the standard and modified versions of Fick’s first law. Note: One asterisk (*) means there is no statistically significant difference between the values obtained by the standard and modified versions of Fick’s first law.
References
- Butt, A.; Iram, Z.; Saleem, J.; Jabeen, A. Importance of community involvement in coastal area management: A review of International and Pakistani scenario. Int. J. Biosci. (IJB) 2018, 12, 239–247. [Google Scholar] [CrossRef]
- Rizzo, A.; Anfuso, G. Coastal dynamic and evolution: Case studies from different sites around the world. Water 2020, 12, 2829. [Google Scholar] [CrossRef]
- Wilbur, L.; Louca, V.; Ibanez-Erquiaga, B.; Küpper, F.C. A case for trans-regional intertidal research in unstudied areas in the northeast and southeast Pacific: Filling the gaps. Coasts 2024, 4, 323–346. [Google Scholar] [CrossRef]
- Murray, N.; Phinn, S.; Fuller, R.; DeWitt, M.; Ferrari, R.; Johnston, R.; Clinton, N.; Lyons, M. High-resolution global maps of tidal flat ecosystems from 1984 to 2019. Sci. Data 2022, 9, 542. [Google Scholar] [CrossRef]
- Rios-Yunes, D.; Grandjean, T.; di Primio, A.; Tiano, J.; Bouma, T.J.; van Oevelen, D.; Soetaert, K. Sediment resuspension enhances nutrient exchange in intertidal mudflats. Front. Mar. Sci. 2023, 10, 1155386. [Google Scholar] [CrossRef]
- Sarkar, A.; Al-Said, T.; Naqvi, S.W.A.; Ahmed, A.; Fernandes, L.; Madhusoodhanan, R.; Thuslim, F.; Yamamoto, T.; Al-Yamani, F. A preliminary study on benthic nutrient exchange across sediment-water interfaces in a shallow marine protected area of the Northwestern Arabian Gulf. Mar. Environ. Res. 2024, 196, 106420. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, G.L.; Liu, S.M. Nutrient exchanges at the sediment-water interface and the responses to environmental changes in the Yellow Sea and East China Sea. Mar. Pollut. Bull. 2022, 176, 113420. [Google Scholar] [CrossRef]
- Liu, Y.; Jiao, J.J.; Liang, W.; Luo, X. Tidal pumping-induced nutrients dynamics and biogeochemical implications in an intertidal aquifer. J. Geophys. Res. Biogeosci. 2017, 122, 3322–3342. [Google Scholar] [CrossRef]
- Cooper, I.J.; Godbold, J.A.; Annett, A.L. Macrofaunal contributions to benthic nutrient fluxes revealed by radium disequilibrium. Limnol. Oceanogr. 2025, 70, 1345–1358. [Google Scholar] [CrossRef]
- Barrois, J.-M.; Mesnage, V.; Metzger, É.; Mouazé, D.; Denis, L.; Deloffre, J. Modeling of phosphate flux induced by flood resuspension on a macrotidal estuarine mudflat (Seine, France). Mar. Chem. 2024, 265, 104427. [Google Scholar] [CrossRef]
- Hong, Q.; Cheng, Y.; Qu, Y.; Wei, L.; Liu, Y.; Gao, J.; Cai, P.; Chen, T. Overlooked shelf sediment reductive sinks of dissolved rhenium and uranium in the modern ocean. Nat. Commun. 2024, 15, 3966. [Google Scholar] [CrossRef]
- Tamborski, J.J.; Eagle, M.; Kurylyk, B.L.; Kroeger, K.D.; Wang, Z.A.; Henderson, P.; Charette, M.A. Pore water exchange-driven inorganic carbon export from intertidal salt marshes. Limnol. Oceanogr. 2021, 66, 1774–1792. [Google Scholar] [CrossRef]
- Kwon, I.; Kim, T.; Park, S.Y.; Lee, C.; Lee, J.; Lee, J.; Kim, H.-G.; Kwon, B.-O.; Yoon, H.J.; Nam, J. National scale evaluation of nutrient purification capacity in marine sediments along the coast of South Korea: A mesocosm study based in situ assessment. Sci. Total Environ. 2025, 964, 178577. [Google Scholar] [CrossRef]
- Meyer, J.; Voynova, Y.G.; Van Dam, B.; Luitjens, L.; Daehne, D.; Thomas, H. Intertidal Regions Regulate Seasonal Coastal Carbonate System Dynamics in the East Frisian Wadden Sea. EGUsphere 2024, 2024, 1–40. [Google Scholar] [CrossRef]
- Fox, A.L.; Trefry, J.H. Nutrient fluxes from recent deposits of fine-grained, organic-rich sediments in a Florida estuary. Front. Mar. Sci. 2023, 10, 1305990. [Google Scholar] [CrossRef]
- Ospina-Álvarez, N.; Caetano, M.; Vale, C.; Santos-Echeandía, J.; Bernárdez, P.; Prego, R. Exchange of nutrients across the sediment–water interface in intertidal ria systems (SW Europe). J. Sea Res. 2014, 85, 349–358. [Google Scholar] [CrossRef]
- Yin, X.; Wang, W.; Zou, Y.; Song, Z.; Sardans, J.; Wiesmeier, M.; Guggenberger, G.; Li, Q.; Chen, J.; Peñuelas, J. Intertidal zonation of mangrove organic carbon fractions driven by vegetation biomass and soil nutrient levels. CATENA 2025, 250, 108722. [Google Scholar] [CrossRef]
- Rajyaguru, A.; Metzler, R.; Dror, I.; Grolimund, D.; Berkowitz, B. Diffusion in porous rock is anomalous. Environ. Sci. Technol. 2024, 58, 8946–8954. [Google Scholar] [CrossRef]
- Tartakovsky, D.M.; Dentz, M. Diffusion in porous media: Phenomena and mechanisms. Transp. Porous Media 2019, 130, 105–127. [Google Scholar] [CrossRef]
- Berkowitz, B.; Emmanuel, S.; Scher, H. Non-Fickian transport and multiple-rate mass transfer in porous media. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Fick, A.V. On liquid diffusion. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1855, 10, 30–39. [Google Scholar] [CrossRef]
- Lewis, G.N.; Randall, M. Thermodynamics and the Free Energy of Chemical Substances; McGraw-Hill: Columbus, OH, USA, 1923. [Google Scholar]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Debye, V.P. Zur theorie der electrolyte. Phyikalishce Zeitschrift. 1923, 185–206. [Google Scholar]
- Millero, F.J.; Pierrot, D. A chemical equilibrium model for natural waters. Aquat. Geochem. 1998, 4, 153–199. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Kim, J.J. Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef]
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, W.A.; De Bièvre, P.; Gröning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T. Atomic weights of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 265–291. [Google Scholar] [CrossRef]
- Millero, F. Use of models to determine ionic interactions in natural waters. Thalass. Jugosl. 1982, 18, 253–291. [Google Scholar]
- Pierrot, D.; Millero, F.J. The speciation of metals in natural waters. Aquat. Geochem. 2017, 23, 1–20. [Google Scholar] [CrossRef]
- Khoo, K.; Ramette, R.W.; Culberson, C.H.; Bates, R.G. Determination of hydrogen ion concentrations in seawater from 5 to 40. degree. C: Standard potentials at salinities from 20 to 45%. Anal. Chem. 1977, 49, 29–34. [Google Scholar] [CrossRef]
- Millero, F.J.; Schreiber, D.R. Use of the ion pairing model to estimate activity coefficients of the ionic components of natural waters. Am. J. Sci. 1982, 282, 1508–1540. [Google Scholar] [CrossRef]
- Harris, D.C. Quantitative Chemical Analysis; Macmillan: New York, NY, USA, 2010. [Google Scholar]
- Flower, H.; Rains, M.; Lewis, D.; Zhang, J.-Z.; Price, R. Saltwater intrusion as potential driver of phosphorus release from limestone bedrock in a coastal aquifer. Estuar. Coast. Shelf Sci. 2017, 184, 166–176. [Google Scholar] [CrossRef]
- Flores-Chaparro, C.E.; Rodriguez-Hernandez, M.C.; Chazaro-Ruiz, L.F.; Alfaro-De la Torre, M.C.; Huerta-Diaz, M.A.; Rangel-Mendez, J.R. Chitosan-macroalgae biocomposites as potential adsorbents of water-soluble hydrocarbons: Organic matter and ionic strength effects. J. Clean. Prod. 2018, 197, 633–642. [Google Scholar] [CrossRef]
- Ormeño-Martínez, M.; Guzmán, E.; Fernández-Peña, L.; Greaves, A.J.; Bureau, L.; Ortega, F.; Rubio, R.G.; Luengo, G.S. Roles of polymer concentration and ionic strength in the deposition of chitosan of fungal origin onto negatively charged surfaces. Biomimetics 2024, 9, 534. [Google Scholar] [CrossRef]
- Sheibley, R.W.; Paulson, A.J. Quantifying Benthic Nitrogen Fluxes in Puget Sound, Washington: A Review of Available Data; Scientific Investigations Report 2014-5033; U.S. Geological Survey: Reston, VA, USA, 2014.
- Tournassat, C.; Steefel, C.I.; Fox, P.M.; Tinnacher, R.M. Resolving experimental biases in the interpretation of diffusion experiments with a user-friendly numerical reactive transport approach. Sci. Rep. 2023, 13, 15029. [Google Scholar] [CrossRef]
- Du, C.; Pan, Y.a.; Tang, W.; Yue, Q.; Zhang, H. A Comparison Study of the Nutrient Fluxes in a Newly Impounded Riverine Lake (Longjing Lake): Model Calculation and Sediment Incubation. Water 2022, 14, 2015. [Google Scholar] [CrossRef]
- Lai, J.; Cheng, M.; Huang, R.; Yu, G.; Chong, Y.; Li, Y.; Zhong, Y. Mechanism of ammonium sharp increase during sediments odor control by calcium nitrate addition and an alternative control approach by subsurface injection. Environ. Res. 2020, 190, 109979. [Google Scholar] [CrossRef]
- Lavery, P.S.; Oldham, C.E.; Ghisalberti, M. The use of Fick’s First Law for predicting porewater nutrient fluxes under diffusive conditions. Hydrol. Process. 2001, 15, 2435–2451. [Google Scholar] [CrossRef]
- Moradi, N.; Klawonn, I.; Iversen, M.H.; Wenzhöfer, F.; Grossart, H.-P.; Ploug, H.; Fischer, G.; Khalili, A. A Novel Measurement-Based Model for Calculating Diffusive Fluxes Across Substrate-Water Interfaces of Marine Aggregates, Sediments and Biofilms. Front. Mar. Sci. 2021, 8, 689977. [Google Scholar] [CrossRef]
- Xia, L.; van Dael, T.; Bergen, B.; Smolders, E. Phosphorus immobilisation in sediment by using iron rich by-product as affected by water pH and sulphate concentrations. Sci. Total Environ. 2023, 864, 160820. [Google Scholar] [CrossRef] [PubMed]
- Slomp, C.P.; Mort, H.P.; Jilbert, T.; Reed, D.C.; Gustafsson, B.G.; Wolthers, M. Coupled dynamics of iron and phosphorus in sediments of an oligotrophic coastal basin and the impact of anaerobic oxidation of methane. PLoS ONE 2013, 8, e62386. [Google Scholar] [CrossRef]
- Lengier, M.; Szymczycha, B.; Brodecka-Goluch, A.; Kłostowska, Ż.; Kuliński, K. Benthic diffusive fluxes of organic and inorganic carbon, ammonium and phosphates from deep water sediments of the Baltic Sea. Oceanologia 2021, 63, 370–384. [Google Scholar] [CrossRef]
- Gibson, J.; Farnood, R. Some new ideas about porosity and diffusion in aquatic sediments. Next Res. 2025, 2, 100287. [Google Scholar] [CrossRef]
- Larson, J.H.; Bailey, S.W.; Maki, R.P.; Christensen, V.G.; Stelzer, E.A.; Smith, J.C.; LeDuc, J.F.; McWhorter, S. Possible influence of water level management on nutrient flux in nearshore sediments of Kabetogama Lake, Minnesota, USA. Ecosphere 2025, 16, e70176. [Google Scholar] [CrossRef]
- Cogorno, J.; Stolze, L.; Muniruzzaman, M.; Rolle, M. Dimensionality effects on multicomponent ionic transport and surface complexation in porous media. Geochim. Cosmochim. Acta 2022, 318, 230–246. [Google Scholar] [CrossRef]
- Münch, M.A.; van Kaam, R.; As, K.; Peiffer, S.; Ter Heerdt, G.; Slomp, C.P.; Behrends, T. Impact of iron addition on phosphorus dynamics in sediments of a shallow peat lake 10 years after treatment. Water Res. 2024, 248, 120844. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, L.; Rothe, M.; Braun, B.; Hupfer, M. Transformation of redox-sensitive to redox-stable iron-bound phosphorus in anoxic lake sediments under laboratory conditions. Water Res. 2021, 189, 116609. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).